Свойства и признаки параллелограмма

1.

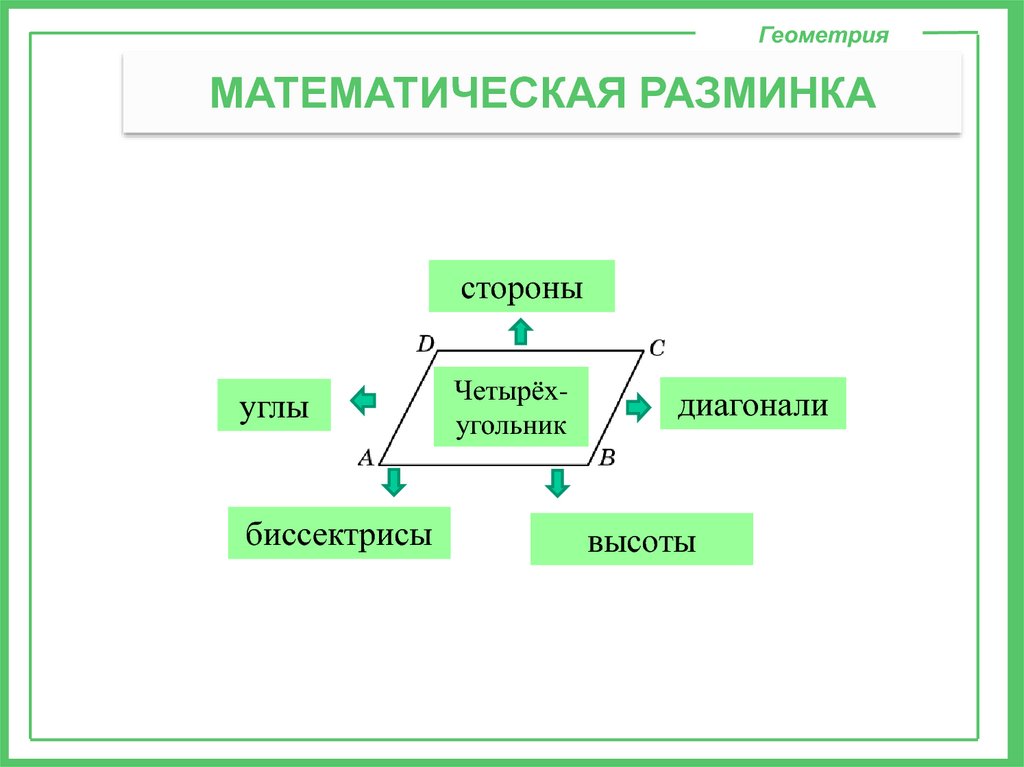
Геометрия
МАТЕМАТИЧЕСКАЯ РАЗМИНКА
стороны
углы
биссектрисы
Четырёхугольник
диагонали
высоты

2.

Геометрия
СВОЙСТВА ПАРАЛЛЕЛОГРАММА
1. Параллелограмм является выпуклым
четырёхугольником.
2. Противолежащие стороны
параллелограмма равны.
3. Противолежащие углы
параллелограмма равны.
4. Сумма углов параллелограмма равна
360º.

3.

Геометрия
СВОЙСТВА ПАРАЛЛЕЛОГРАММА
5. Сумма углов параллелограмма
прилегающих к любой стороне равна
180°.
6. Любая диагональ параллелограмма
делит его на два равных треугольника.
7. Диагонали параллелограмма
пересекаются и точкой пересечения
делят друг друга пополам.

4.

Геометрия
СВОЙСТВА ПАРАЛЛЕЛОГРАММА
8. Биссектрисы противоположных углов
параллелограмма всегда параллельны.
9. Биссектрисы соседних углов
параллелограмма всегда пересекаются
под прямым углом (90°).
10. Биссектриса параллелограмма
отсекает от него равнобедренный
треугольник.

5.

Геометрия
СВОЙСТВА ПАРАЛЛЕЛОГРАММА
11. Биссектрисы всех углов
параллелограмма при пересечении
образуют прямоугольник.
12. Высоты, опущенные из одной
вершины параллелограмма, образуют
угол, равный углу параллелограмма при
соседней вершине.

6.

Геометрия
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
1. Если в четырехугольнике
противоположные стороны попарно
равны, то этот четырехугольник —
параллелограмм.
2. Если в четырехугольнике
противоположные углы попарно
равны, то этот четырехугольник —
параллелограмм.

7.

Геометрия
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
3. Если в выпуклом четырехугольнике
сумма углов, прилежащих к каждой
из двух смежных сторон, равна 180⁰,
то этот четырехугольник —
параллелограмм.

8.

Геометрия
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
4. Если в четырехугольнике
диагонали, пересекаясь, точкой
пересечения делятся пополам, то
этот четырехугольник —
параллелограмм.
5. Если в четырехугольнике две
противоположные стороны равны и
параллельны, то этот
четырехугольник — параллелограмм.