Параллелограмм. Свойства и признаки параллелограмма

1. Параллелограмм. Свойства и признаки параллелограмма

Геометрия 8 класс
Параллелограмм. Свойства и
признаки параллелограмма

2. Задачи урока:

Повторить
Узнать
Научиться
• Определение и свойства
параллелограмма
• Понятие прямой и обратной
теоремы
• признаки параллелограмма
• применять признаки
параллелограмма при
решении задач

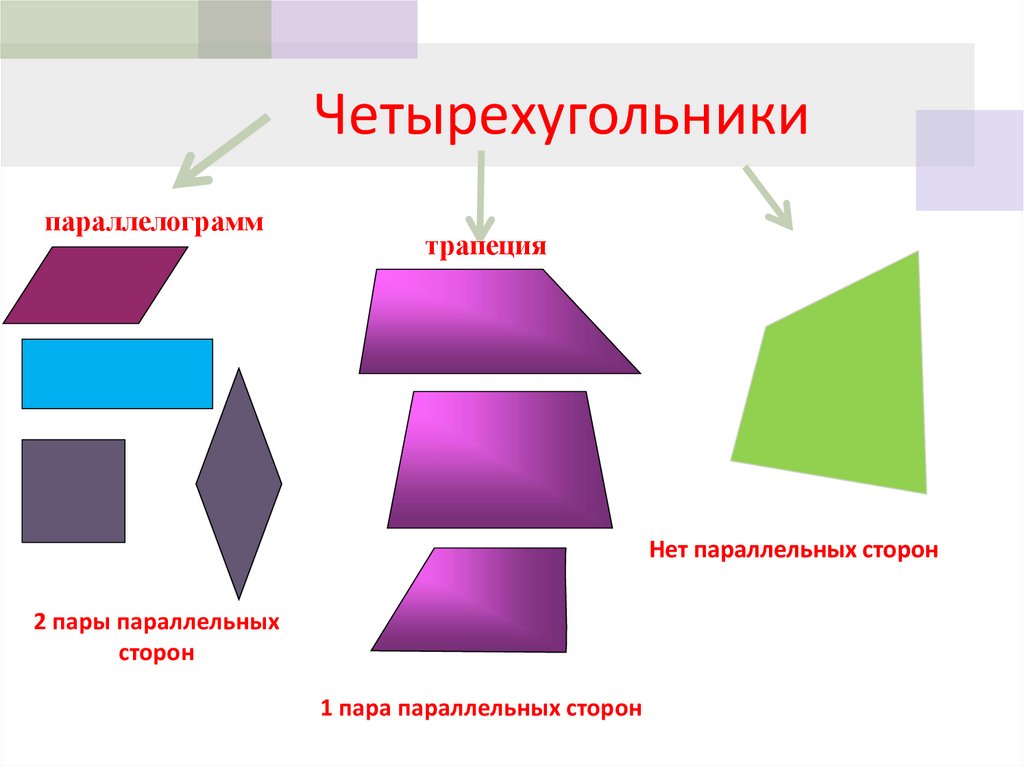
3. Четырехугольники

параллелограмм
трапеция
Нет параллельных сторон
2 пары параллельных
сторон
1 пара параллельных сторон

4.

Определение
Четырехугольник, у которого
противоположные стороны попарно
параллельны, называется параллелограммом
А
C
AB CD, AC BD
B
D

5.

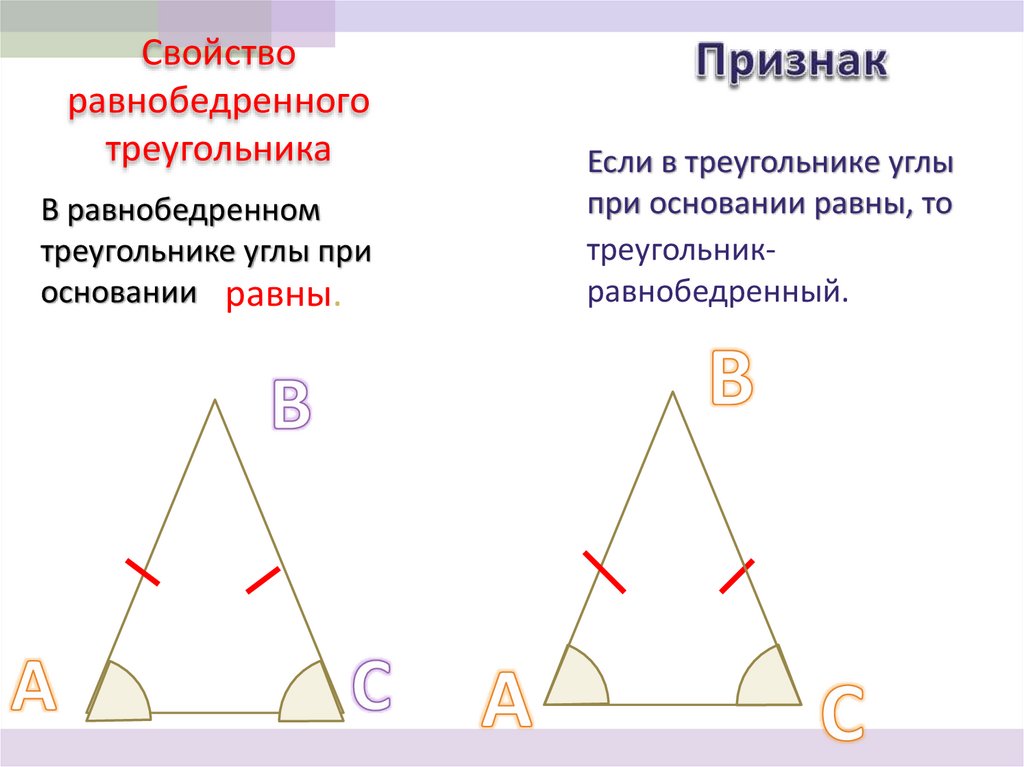
Определение

6. Свойство равнобедренного треугольника

В равнобедренном
треугольнике углы при
основании равны.
Если в треугольнике углы
при основании равны, то
треугольникравнобедренный.

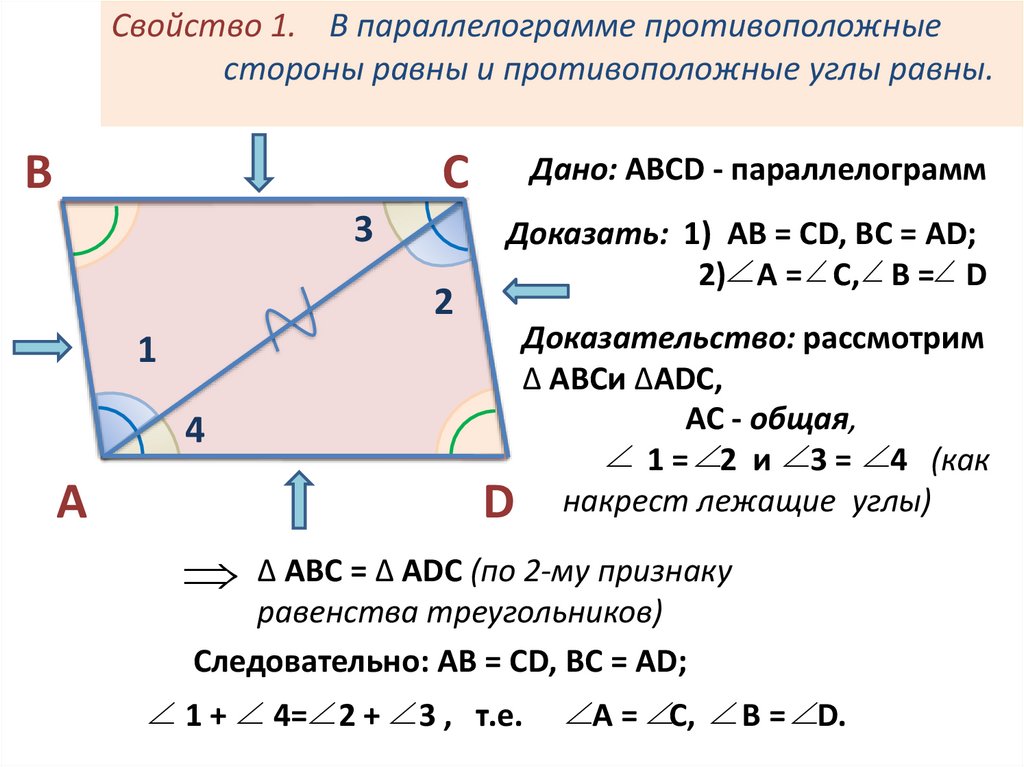
7. Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

В
С
3
2
1
4
А
Дано: ABCD - параллелограмм
Доказать: 1) АВ = СD, BC = AD;
2) A = C, B = D
Доказательство: рассмотрим
∆ ABCи ∆ADC,
AC - общая,
1 = 2 и 3 = 4 (как
D накрест лежащие углы)
∆ АВС = ∆ ADC (по 2-му признаку
равенства треугольников)
Следовательно: АВ = СD, BC = AD;
1 + 4= 2 + 3 , т.е.
A = C, B = D.

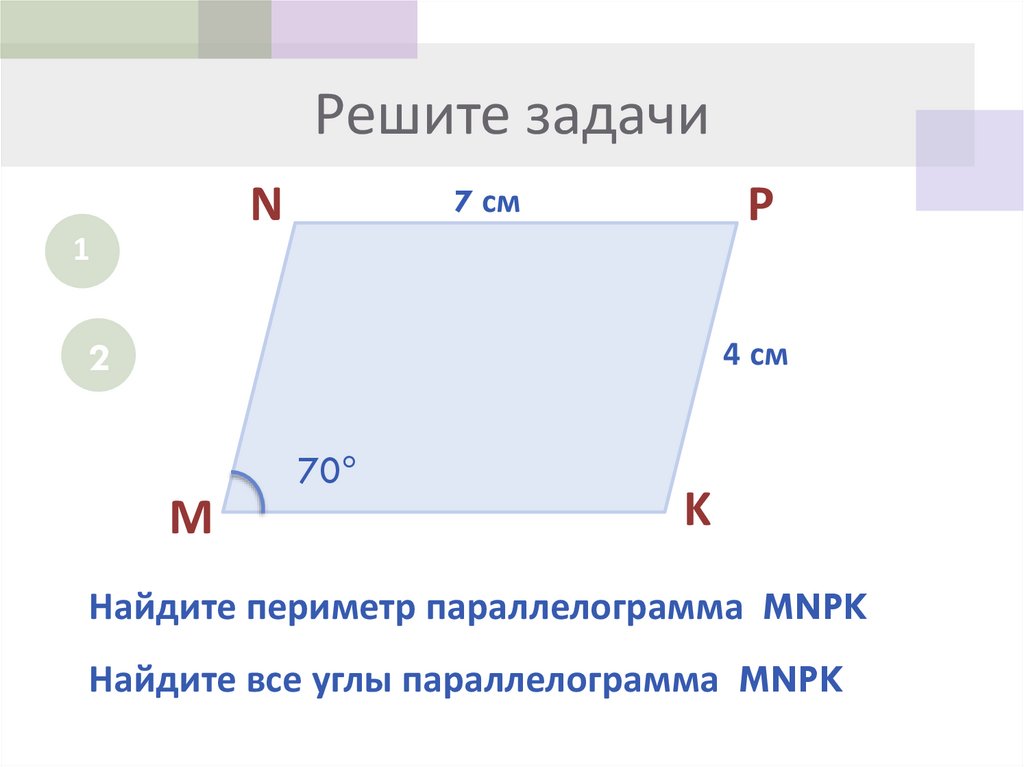
8. Решите задачи

N
P
7 см
1
2
4 см
70
M
K
Найдите периметр параллелограмма MNPK
Найдите все углы параллелограмма MNPK

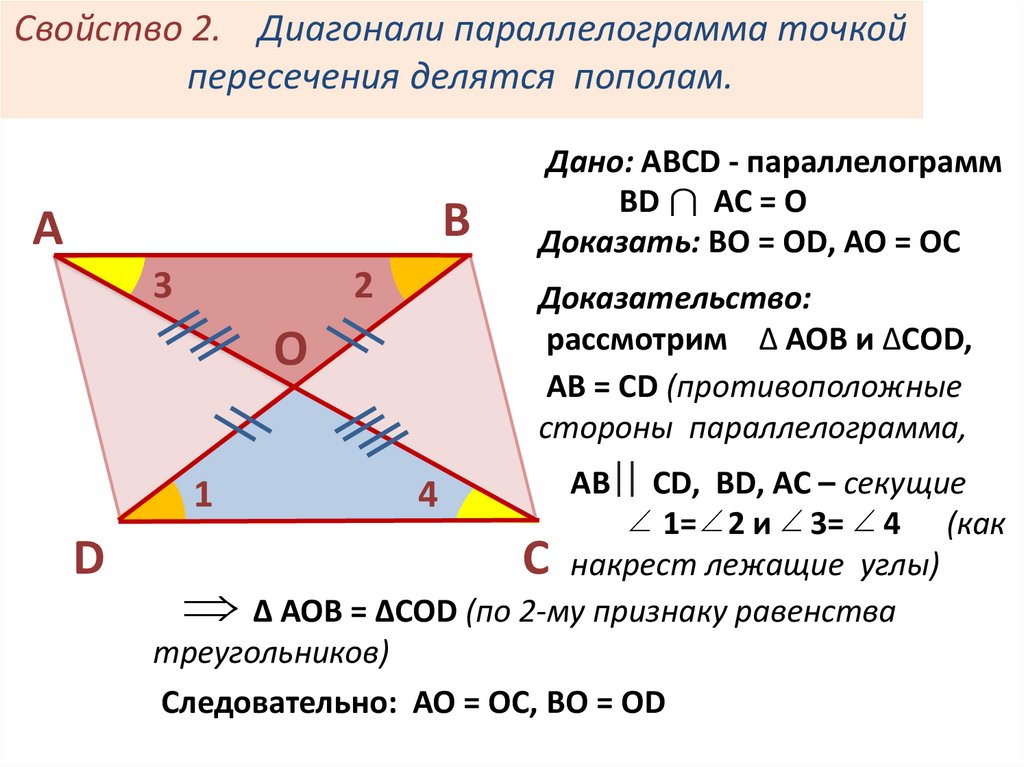
9. Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

В
А
3
2
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
АВ = СD (противоположные
стороны параллелограмма,
O
АВ СD, ВD, AC – секущие
1= 2 и 3= 4 (как
С накрест лежащие углы)
∆ АОВ = ∆СОD (по 2-му признаку равенства
треугольников)
Следовательно: АО = ОС, ВО = ОD
1
D
Дано: АВСD - параллелограмм
ВD AC = O
Доказать: ВО = ОD, АО = ОС
4

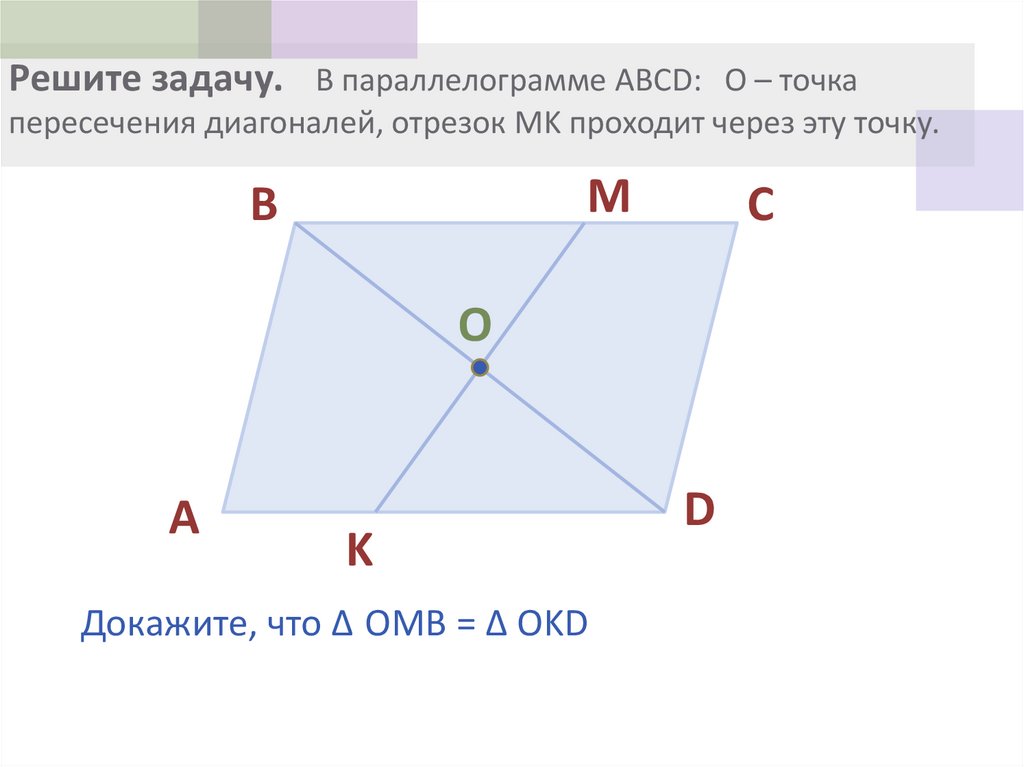
10. Решите задачу. В параллелограмме ABCD: О – точка пересечения диагоналей, отрезок MK проходит через эту точку.

M
B
C
1
O
2
A
K
Докажите, что ∆ OMB = ∆ OKD
D

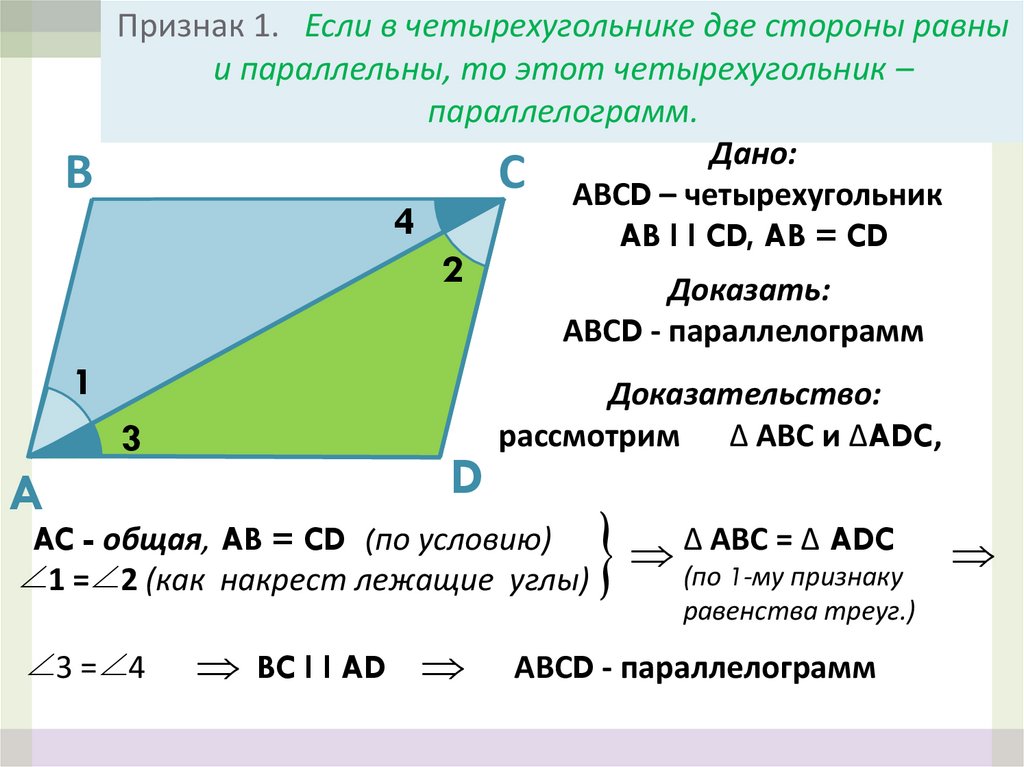
11. Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

В
Признак 1. Если в четырехугольнике две стороны равны
и параллельны, то этот четырехугольник –
параллелограмм.
Дано:
С АВСD – четырехугольник
4
AB l l CD, AB = CD
2
1
3
A
D
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
AC - общая, AB = CD (по условию)
1 = 2 (как накрест лежащие углы)
3 = 4
BC l l AD
= ∆ ADC
∆(поАВС
1-му признаку
равенства треуг.)
АВСD - параллелограмм

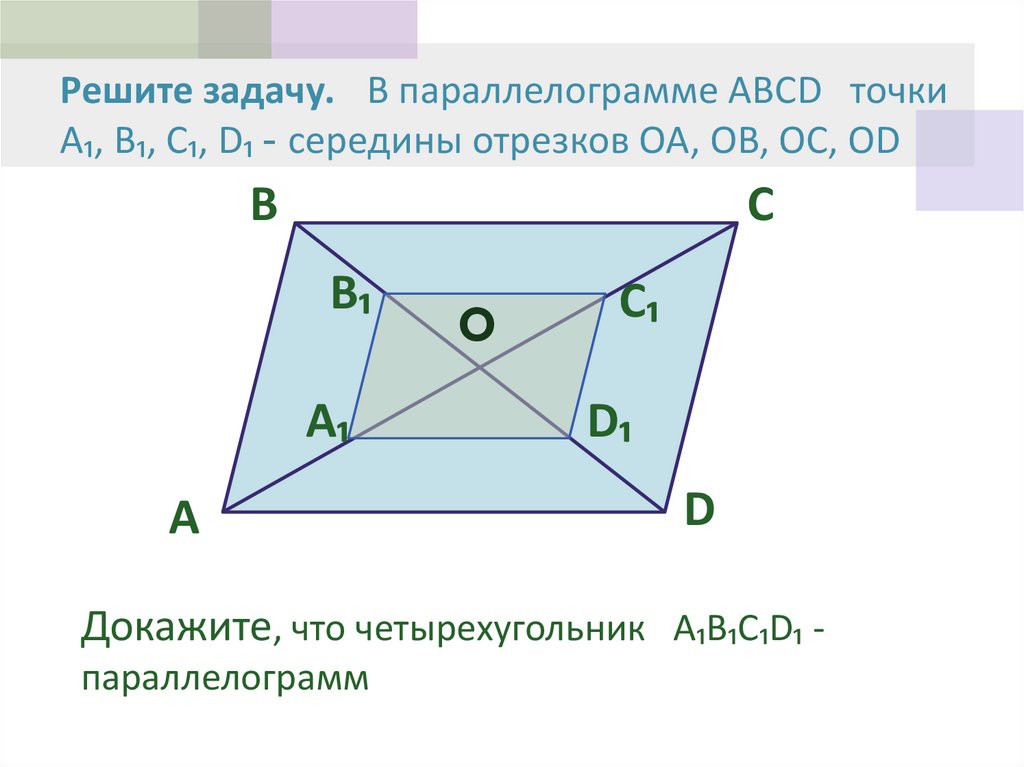
12. Решите задачу. В параллелограмме ABCD точки A₁, B₁, C₁, D₁ - середины отрезков OA, OB, OC, OD

B
C
B₁
A₁
A
O
C₁
D₁
D
Докажите, что четырехугольник A₁B₁C₁D₁ параллелограмм

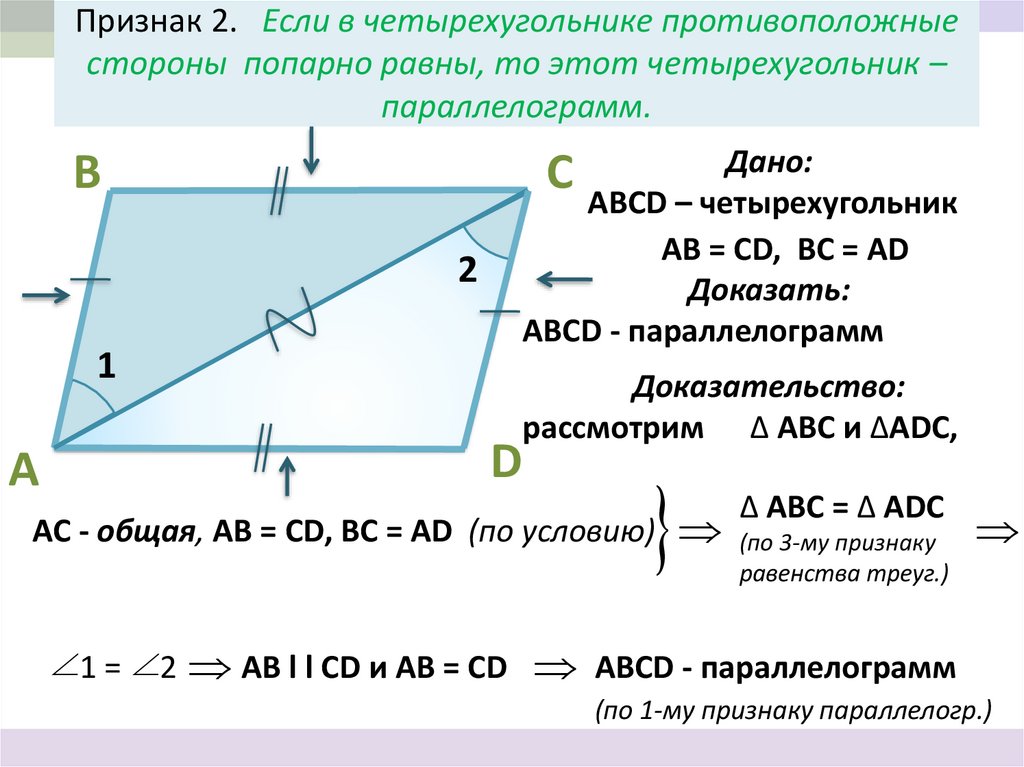
13. Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Дано:
С АВСD – четырехугольник
В
2
1
AB = CD, BC = AD
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
D
А
AC - общая, AB = CD, BC = AD (по условию)
1 = 2
∆ АВС = ∆ ADC
(по 3-му признаку
равенства треуг.)
AB l l CD и AB = CD АВСD - параллелограмм
(по 1-му признаку параллелогр.)

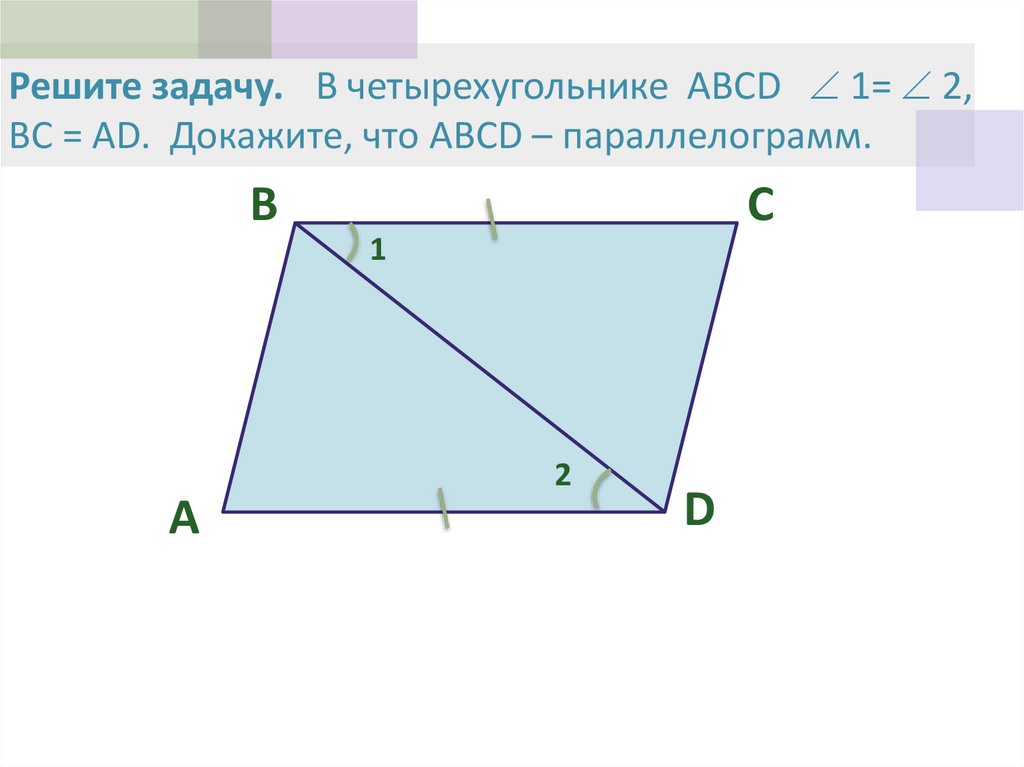
14. Решите задачу. В четырехугольнике ABCD  1=  2, ВС = АD. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ВС = АD. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

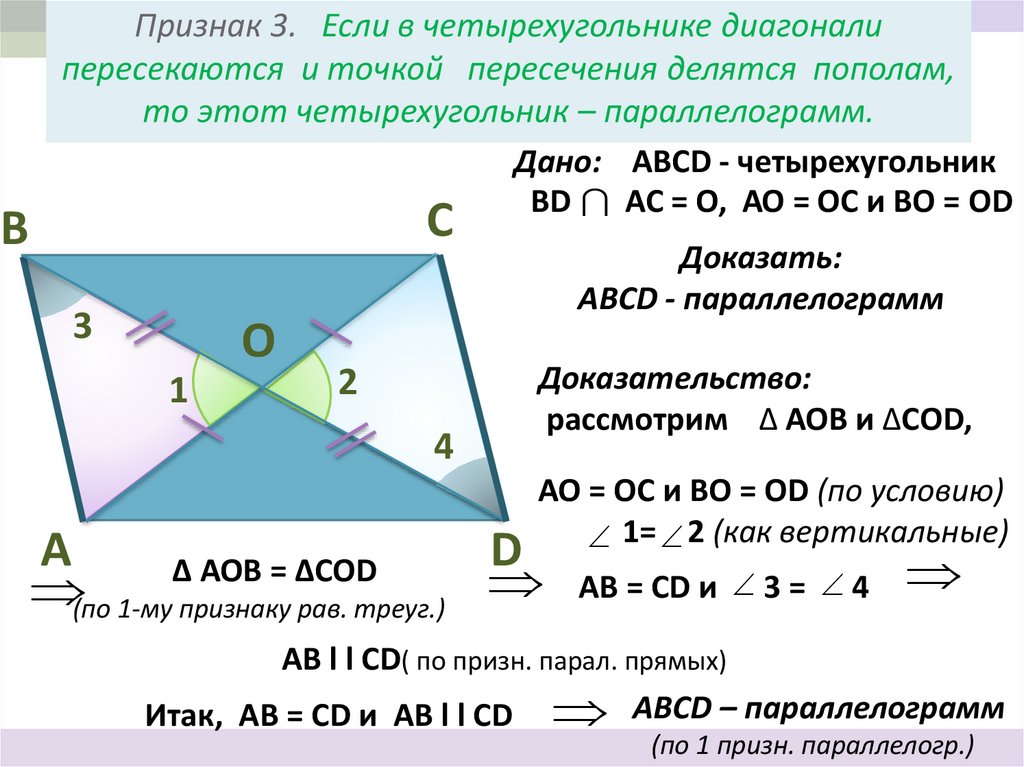
15. Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник –

В
Признак 3. Если в четырехугольнике диагонали
пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник – параллелограмм.
Дано: АВСD - четырехугольник
ВD AC = O, АО = ОС и ВО = ОD
С
3
O
1
Доказать:
ABCD - параллелограмм
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
2
4
А
D
АО = ОС и ВО = ОD (по условию)
1= 2 (как вертикальные)
(по 1-му признаку рав. треуг.)
∆ АОВ = ∆СОD
АВ = СD и 3 = 4
АВ l l СD( по призн. парал. прямых)
Итак, АВ = СD и АВ l l СD ABCD – параллелограмм
(по 1 призн. параллелогр.)

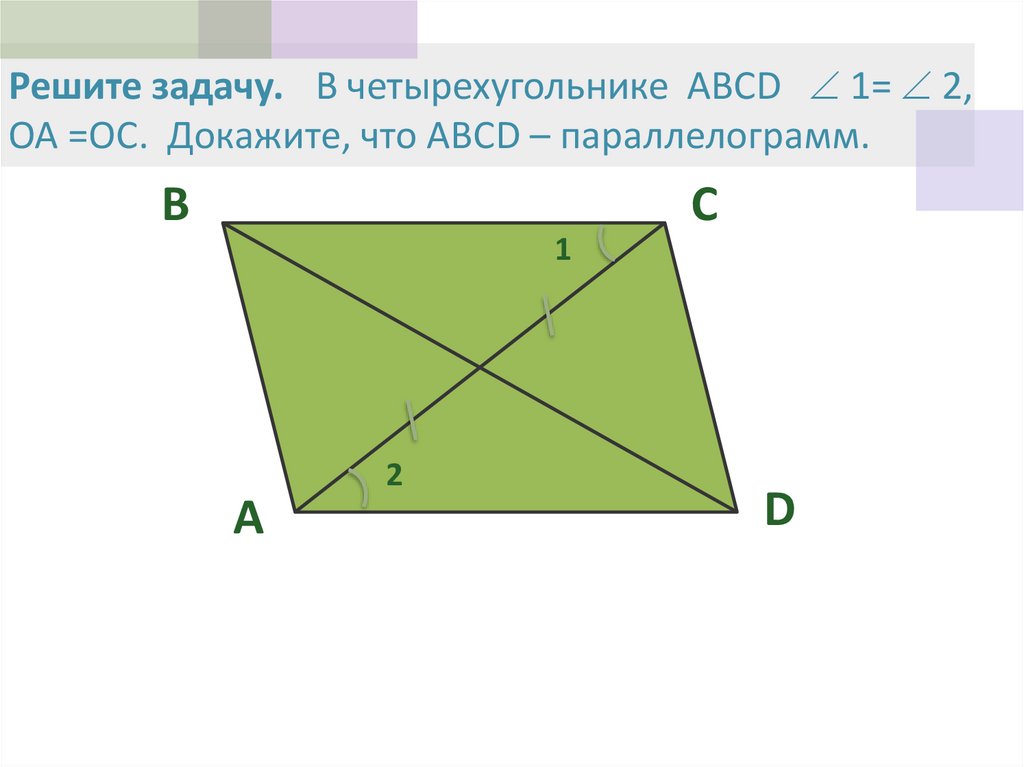
16. Решите задачу. В четырехугольнике ABCD  1=  2, ОА =ОС. Докажите, что ABCD – параллелограмм.

Решите задачу. В четырехугольнике ABCD 1= 2,
ОА =ОС. Докажите, что ABCD – параллелограмм.
B
C
1
2
A
D

17. Домашнее задание

Свойства, признаки выучить п. 42, 43
№ 372(б), № 376(в,г)