Колебания. Общие понятия

1.

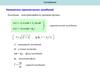
Колебания. Общие понятия.
Физические процессы, характеризующиеся определенной повторяемостью…
Период колебаний – время одного полного к – ия …
Т
Частота колебаний – ч. полных к- ий за 1 сек.
1
T
Циклическая ( круговая ) частота колебаний
2
sin( t )
Гармонические колебания…
Механические колебания ( свободные, вынужденные,
автоколебания, параметрические )...
Электрические колебания (свободные, вынужденные )…
cos( t )

2.

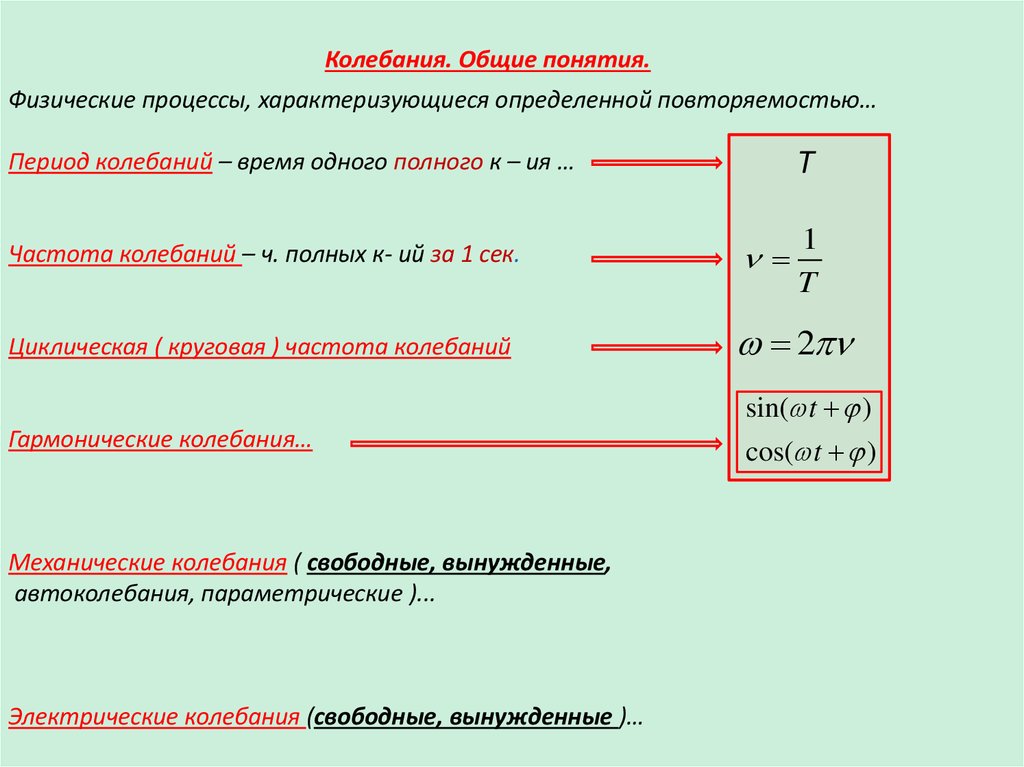
Свободные колебания в механической системе
1. Свободные колебания: колебания в системе, выведенной из положения
равновесия и предоставленной самой себе.
Необходимое условие существования свободных колебаний в
механической системе: наличие силы, направленной к положению
равновесия .
Упругая, квазиупругая сила…

3.

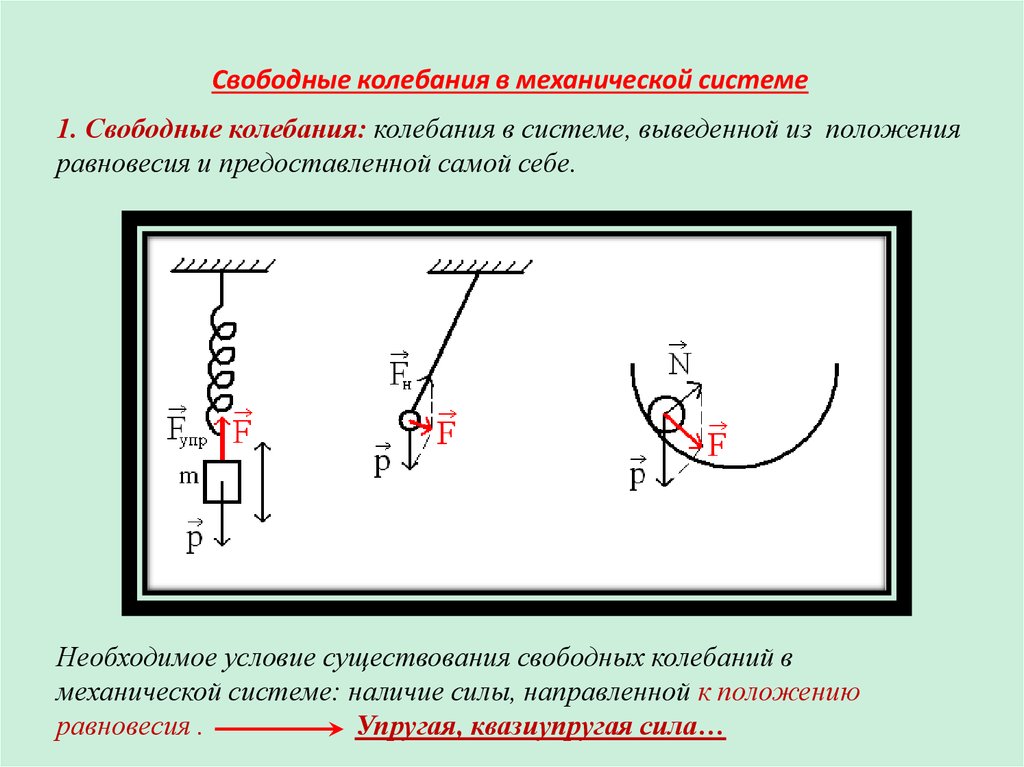
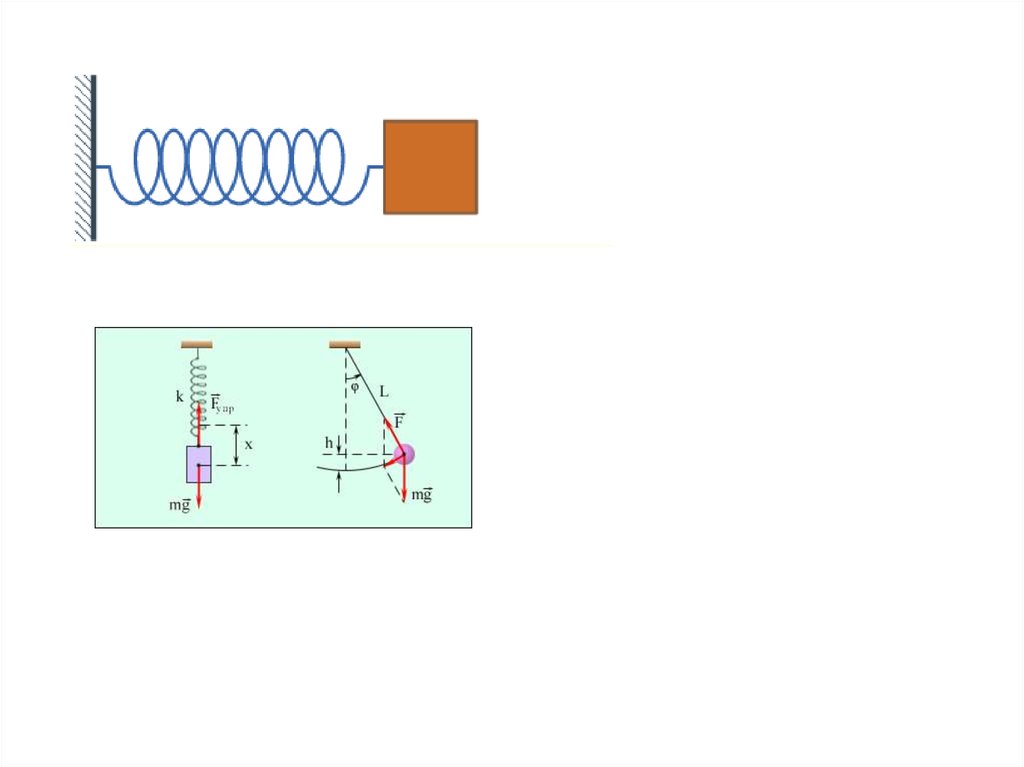
2. Модель свободных колебаний в механической системе.
На рис.:
деформация сжатия
r
N
m
x 0
Fynp
x
P
0
x 0

4.

r
dr
N
FTp
m
x 0
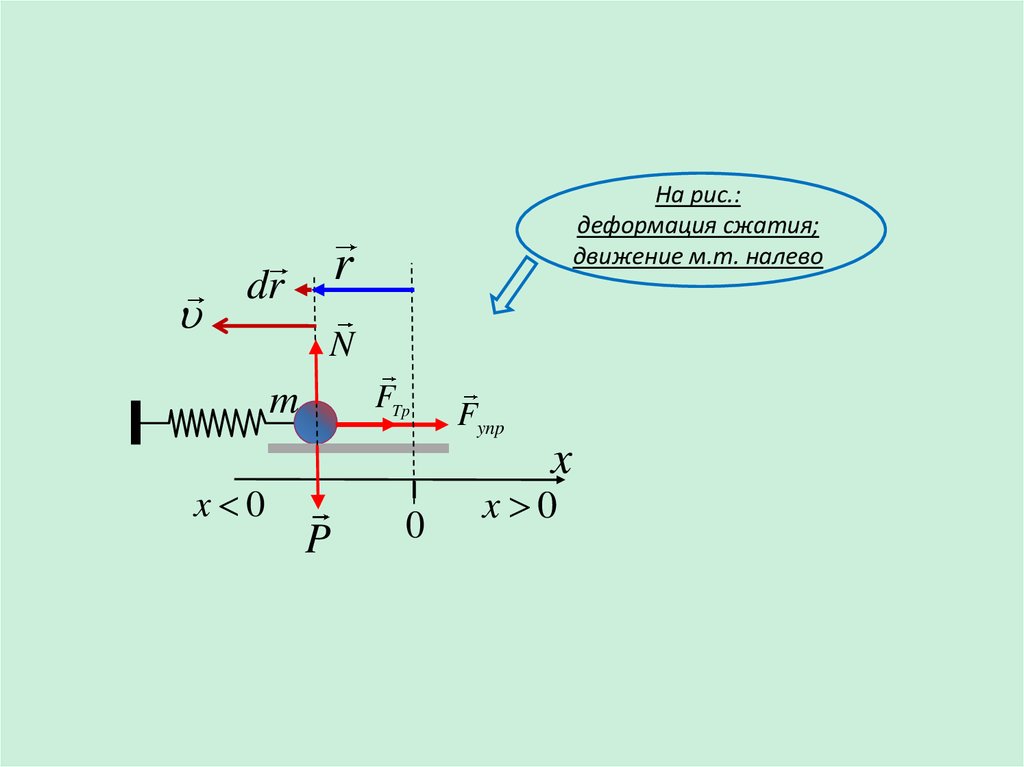
На рис.:
деформация сжатия;
движение м.т. налево
Fynp
x
P
0
x 0

5.

r
dr
N
FTp
m
x 0
Fynp
x
P
0
x 0
Fynp r
( Fynp ) x x
FTp
( FTp ) x dx
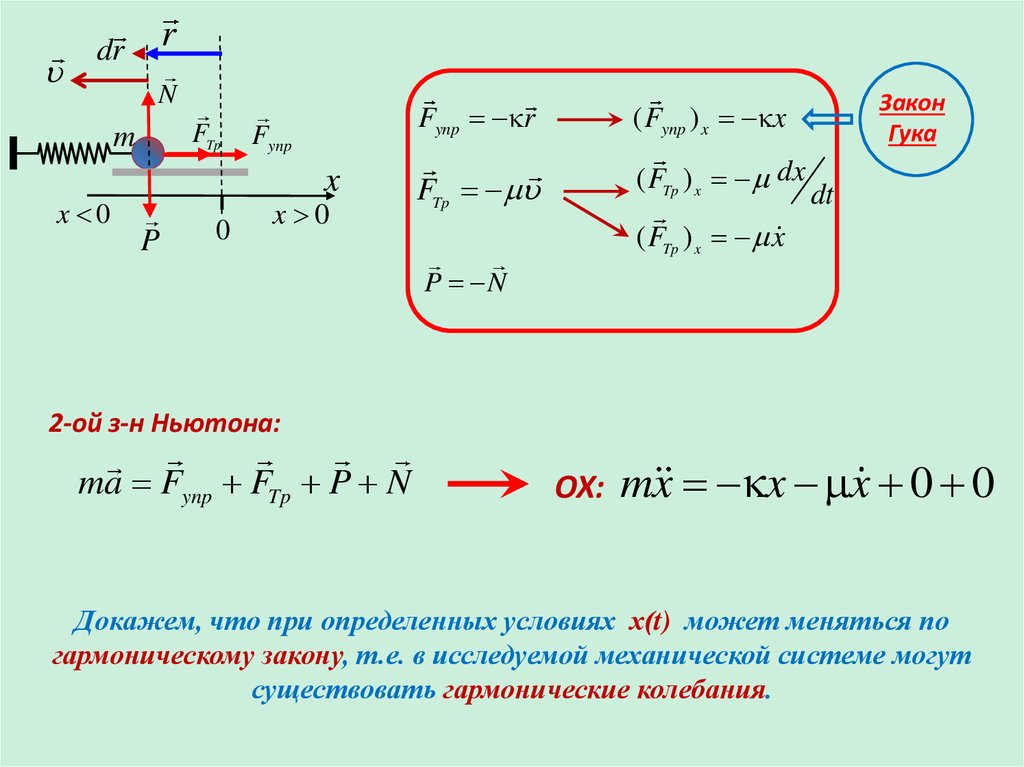
Закон
Гука
dt
( FTp ) x x
P N
2-ой з-н Ньютона:
ma Fynp FTp P N
ОХ:
mx x x 0 0
Докажем, что при определенных условиях х(t) может меняться по
гармоническому закону, т.е. в исследуемой механической системе могут
существовать гармонические колебания.

6.

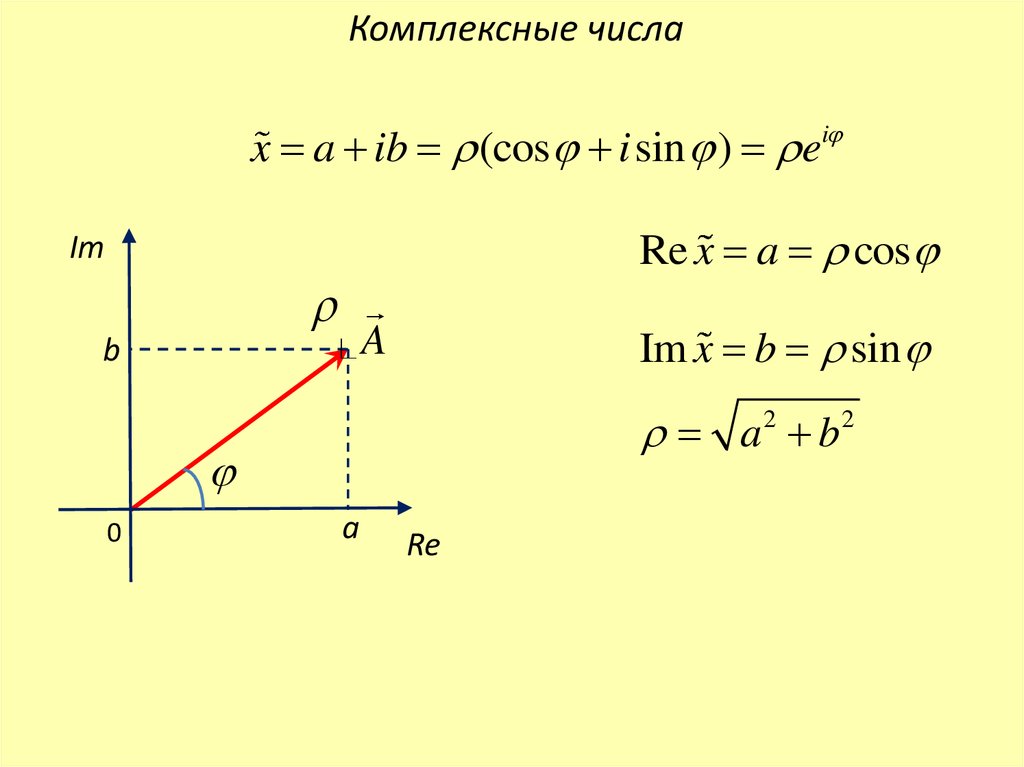
Комплексные числа
x a ib (cos i sin ) ei
Re x a cos
Im
Im x b sin
A
b
a 2 b2
0
a
Re

7.

3. Решение однородного дифференциального уравнения 2-го порядка
при помощи комплексных чисел
x
m
x
m
0 ,
x 0
m
02
m
2
Действительные числа,
характеризующие систему.
x x 2 x 0
2
0
x 02 x 2 x 0
x(t ) - Решение ур - ия
x(t ) - Решение ур - ия
x(t ) Re x(t )
Ищем решение в виде:
i ( t )
x a(t )e
a (t ) ? ? ?

8.

i ( t )
x a(t )e
i( t )
i( t )
x ae
ai e
i ( t )
i
(
t
)
x ae
ai e
i
(
t
)
2
i
(
t
)
ai e
a ( i ) e
x x 2 x 0
2
0
После подстановки и сокращения на
i( t )
e
:
a ai ai a 2 a 02 2 a 2 ai 0
Равенство нулю реальной и мнимой частей приводят к двум уравнениям:
1.
Re : a a( 02 2 ) 2 a 0
2.
Im : a a 0

9.

2.
da
da
a
dt
Im : a a 0
dt
a
da
a dt ln a t ln a0
a(t ) a0e
1.
t
, где
a0 - любое число
Re : a a( 02 2 ) 2 a 0
a a0e t ; a 2 a0e t ;
2 ( 02 2 ) 2 2 0
i( t )
t
x Re a0e
e
a0e t cos( t )
x a0e t cos( t ) , где a0 ,
- любые числа
02 2
0

10.

4. Свободные колебания без затуханий
З-н сохр.полн.мех.энергии:
0 0 0 ;a a0
x a0 cos( 0t )
a0
a0 cos
T0
x2
mx 2
const.
2
2
Амплитуда колебаний
a0 max x 0
Определяется…
Фаза колебаний
0
( 0t )
a0
x(t 0) a0 cos
Начальная фаза колебаний
Определяется моментом начала
отсчета времени.

11.

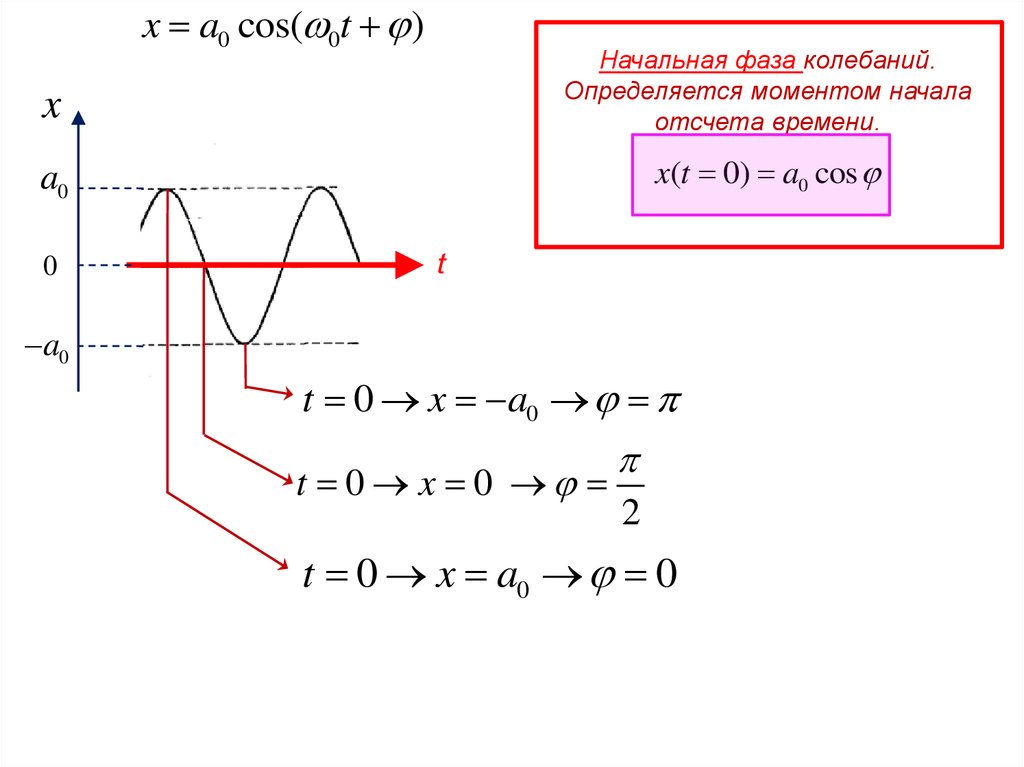
x a0 cos( 0t )
x
Начальная фаза колебаний.
Определяется моментом начала
отсчета времени.
a0
x(t 0) a0 cos
0
t
a0
t 0 x a0
t 0 x 0
2
t 0 x a0 0

12.

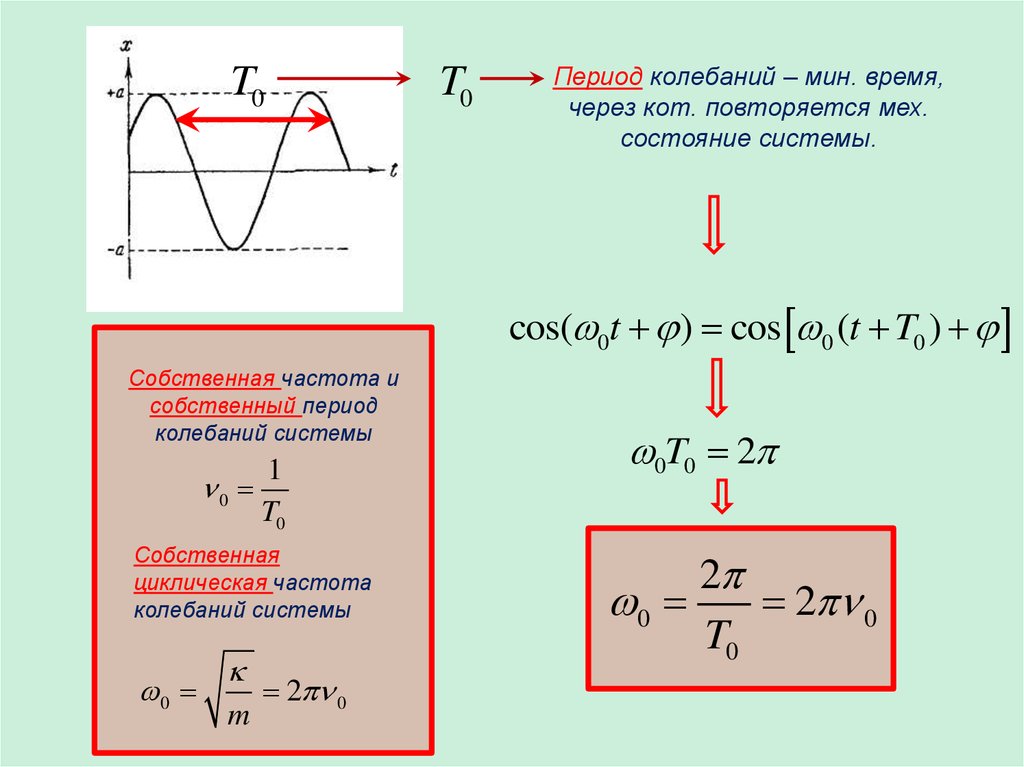
T0
T0
Период колебаний – мин. время,
через кот. повторяется мех.
состояние системы.
cos( 0t ) cos 0 (t T0 )
Собственная частота и
собственный период
колебаний системы
1
0
T0
Собственная
циклическая частота
колебаний системы
0
m
2 0
0T0 2
2
0
2 0
T0

13.

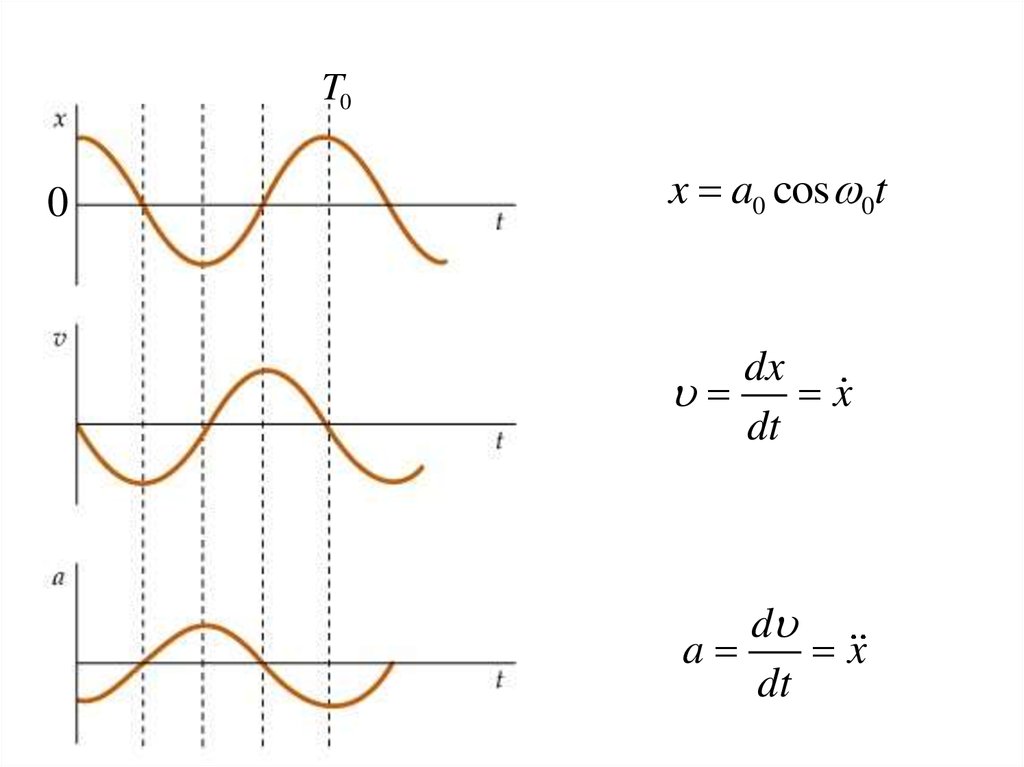
T0
0
x a0 cos 0t
dx
x
dt
d
a
x
dt

14.

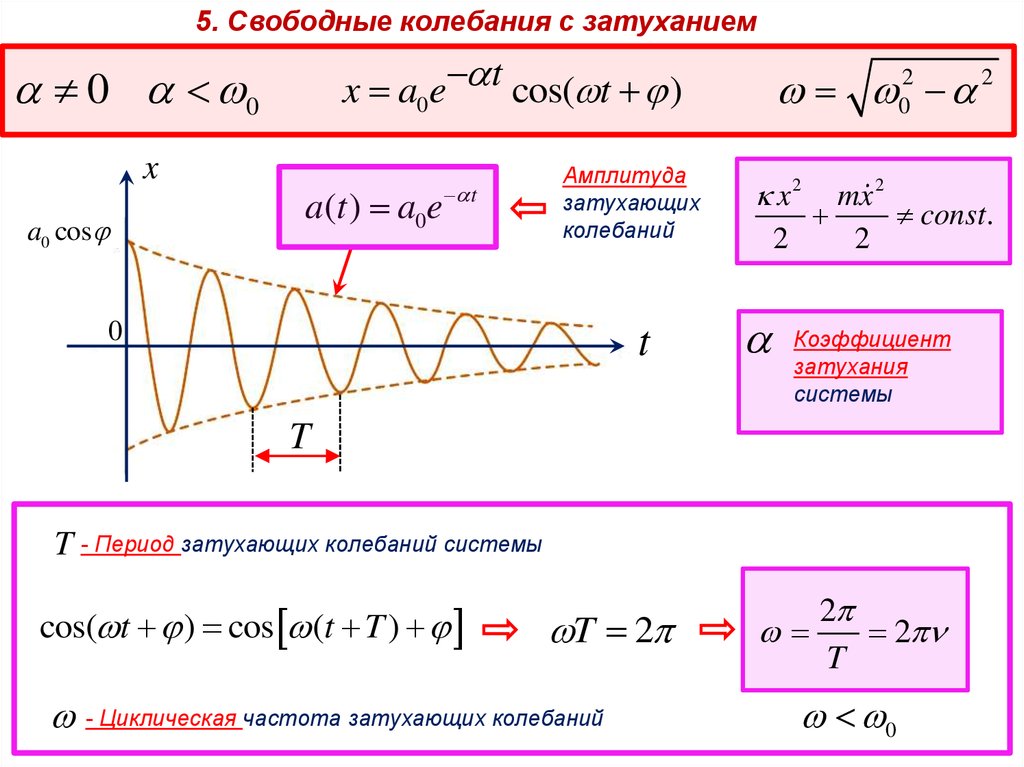
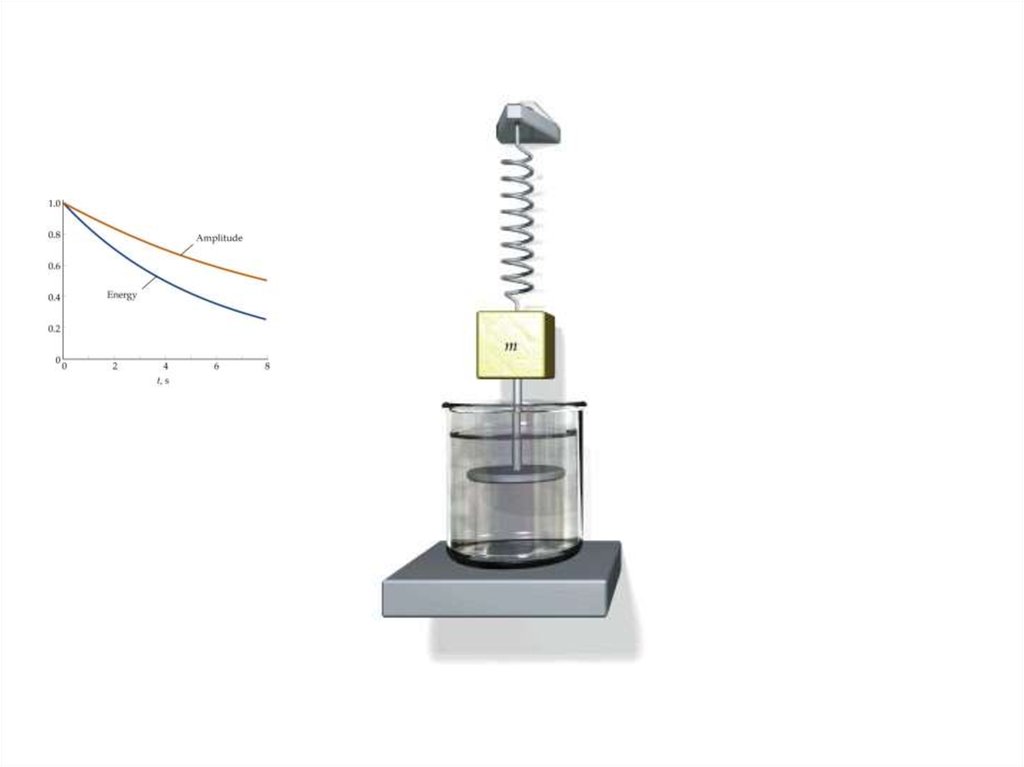
5. Свободные колебания с затуханием
x a0e t cos( t )
0 0
x
a0 cos
a(t ) a0e
t
Амплитуда
затухающих
колебаний
0
t
02 2
x2
mx 2
const.
2
2
Коэффициент
затухания
системы
T
T - Период затухающих колебаний системы
cos( t ) cos (t T )
T 2
- Циклическая частота затухающих колебаний
2
2
T
0

15.

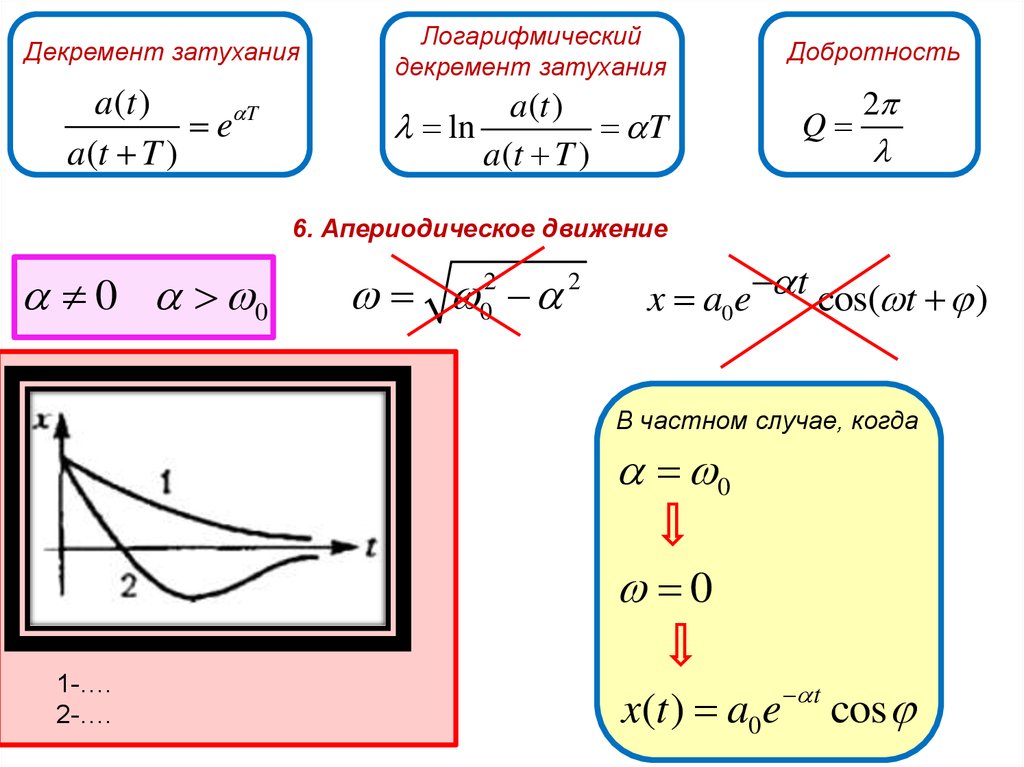
Декремент затухания
Логарифмический
декремент затухания
a (t )
e T
a (t T )
a (t )
ln
T
a (t T )
Добротность
Q
2
6. Апериодическое движение
0 0
2
0
2
x a0e t cos( t )
В частном случае, когда
0
0
1-….
2-….
x(t ) a0e t cos