Similar presentations:
Основные методы расчета линейных электрических цепей
1.
1Основные методы расчета (анализа) линейных
электрических цепей
Общая задача расчета – определение токов во всех участках цепи при
заданных параметрах элементов цепи и известной конфигурации.
Особенности разных методов рассмотрим на примере одной и той же
цепи.
2.
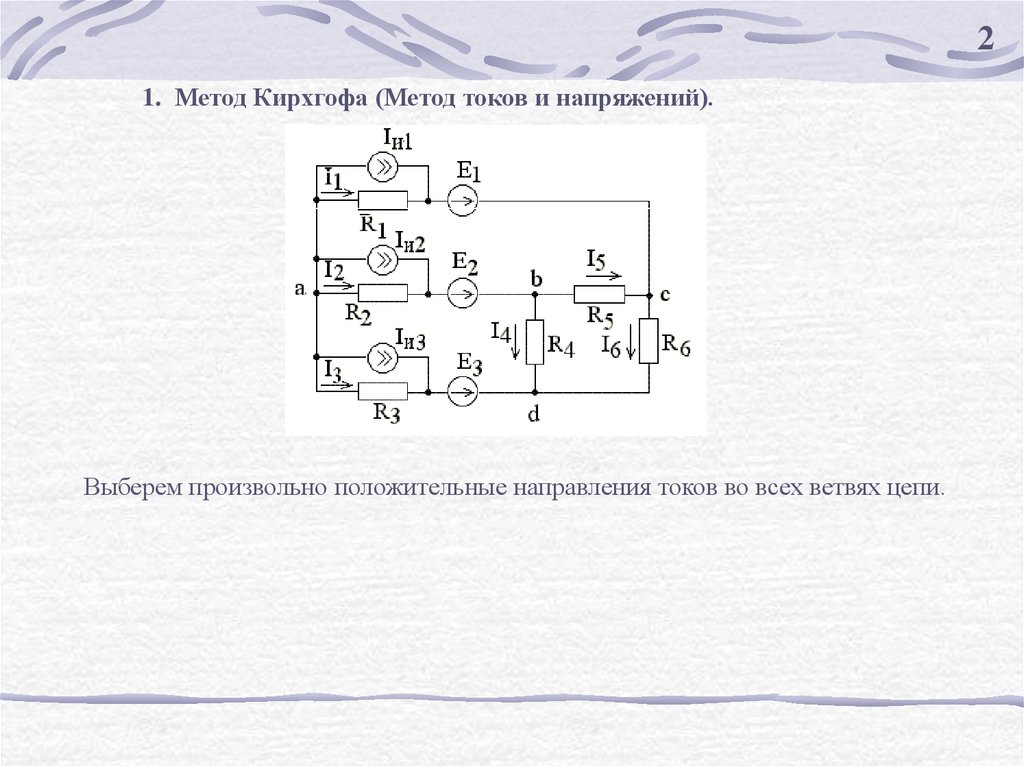
21. Метод Кирхгофа (Метод токов и напряжений).
Выберем произвольно положительные направления токов во всех ветвях цепи.
3.
3При записи уравнений для узлов по первому закону Кирхгофа – число
независимых уравнений на 1 меньше числа узлов n, т.е. нужно
составить n-1 уравнений.
При составлении уравнений по второму закону Кирхгофа для
получения независимой системы необходимо выбрать контуры так,
чтобы каждый следующий содержал хотя бы одну ветвь, не вошедшую
в контуры, для которых уже составлены уравнения.
Число токов равно числу ветвей m. Для их определения необходимо
составить m независимых уравнений. Т.к. по первому з-ну составляется
n-1 уравнений, то на основании второго з-на нужно составить m-(n-1)
уравнений.
4.
4Решая систему уравнений, найдем искомые токи, а, зная сопротивления ветвей,
можно найти напряжения между узлами.
5.
52. Метод контурных токов
При составлении уравнений используется только второй закон Кирхгофа.
E1 E2 ( R1 R5 R2 ) I11 R2 I 22 R5 I 33
E2 E3 R2 I11 ( R4 R2 R3 ) I 22 R4 I 33
0 R5 I11 R4 I 22 ( R6 R4 R5 ) I 33
для контура I;
для контура II;
для контура III.
Определив контурные токи из полученной системы уравнений, найдем токи в ветвях
I1 I11 ,
I 2 I 22 I11 ,
I 3 I 22 ,
I 5 I 33 I11 ,
I 6 I 33 .
I 4 I 22 I 33 ,
В общем случае для n контурной схемы получается n уравнений:
E11 R11I11 R12 I 22 ... R1n I nn ;
E R I R I ... R I ;
22
21 11
22 22
2 n nn
- - - - - - - - - - - - - - - - - - - - - Enn Rn1I11 Rn 2 I 22 ... Rnn I nn .
Согласно теореме Крамера, решение для любого
контурного тока может быть найдено как
1 n
I kk Eii ik
i 1
6.
63. Метод наложения
Ток в любой k ой ветви сложной электрической цепи можно найти, составив
уравнения по методу контурных токов, выбрав контуры так, чтобы k ая ветвь входила
только в один контур. Тогда ток в k ой ветви будет равен контурному току, определенному
выше:
1 n
I kk Eii ik E11 1k E22 2 k ... Enn nk
i 1
Таким образом, ток в k ой ветви, создаваемый несколькими источниками э. д. с.,
включенными в разных участках схемы, равен алгебраической сумме токов, вызываемых
каждой из э. д. с. в отдельности. Это и есть принцип суперпозиции или наложения.
Принцип суперпозиции справедлив только для линейных цепей и называется
принципом независимости действия, так как базируется на предположении, что каждое
слагаемое сложного воздействия на линейную цепь вызывает свой отклик независимо
от того, действуют ли в системе другие слагаемые.
7.
74. Метод узловых напряжений
При составлении уравнений используется только первый закон Кирхгофа
Для узлов a , b, с система уравнений, составленных
по первому закону Кирхгофа:
I 1 I 2 I 3 I1 I 2 I 3 0
I 2 I5 I 4 I 2 0
I 1 I1 I 5 I 6 0
Токи, протекающие через сопротивления
I1
Ua Uc
,
R1
I5
I2
U a Ub
,
R2
I3
Ub Uc
U
, I6 c .
R5
R6
Ua
,
R3
I4
Ub
,
R4
для узла а;
для узла b;
для узла c.
Подставив эти значения в последнюю
систему уравнений, получим:
( g1 g 2 g3 )U a g 2U b g1U c I 1 I 2 I 3 ;
g 2U a ( g 2 g 4 g5 )U b g5U c I 2 ;
g U g U ( g g g )U I .
1 a
5 b
1
5
6
c
1
где
gk 1/ Rk
Решив систему уравнений с помощью определителей, получим:
1 q 1
U k I ii ik
i 1
8.
85. Метод эквивалентного генератора
Метод эквивалентного источника напряжения. Этот метод основан на теореме
Тевенена, согласно которой ток в любой ветви линейной электрической цепи не
изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить
эквивалентным источником напряжения с э. д. с., равной напряжению холостого хода
на зажимах разомкнутой ветви, и внутренним сопротивлением, равным входному
сопротивлению пассивного двухполюсника со стороны разомкнутой ветви.
I I1 I 2
I1
=0
I2 I
EЭ 2
U
XX
Ri R Ri R
При переходе от эквивалентного
генератора напряжения к
эквивалентному источнику тока
IЭ
I
EЭ
I КЗ GU
i XX
Ri
RRi 1
Ri
U
I КЗ
I КЗ
R
R Ri R
R Ri
9.
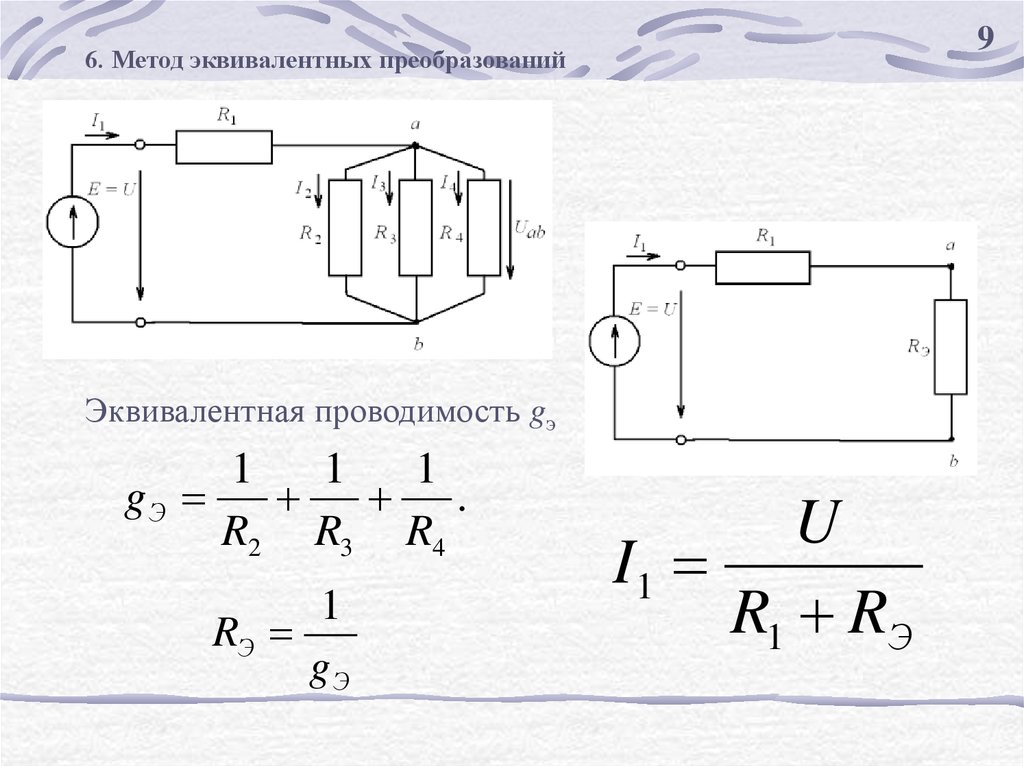
96. Метод эквивалентных преобразований
Эквивалентная проводимость gэ
1
1
1
gЭ
.
R2 R3 R4
1
RЭ
gЭ
U
I1
R1 RЭ
10.
1011. Решение задач
11Решение задач
12.
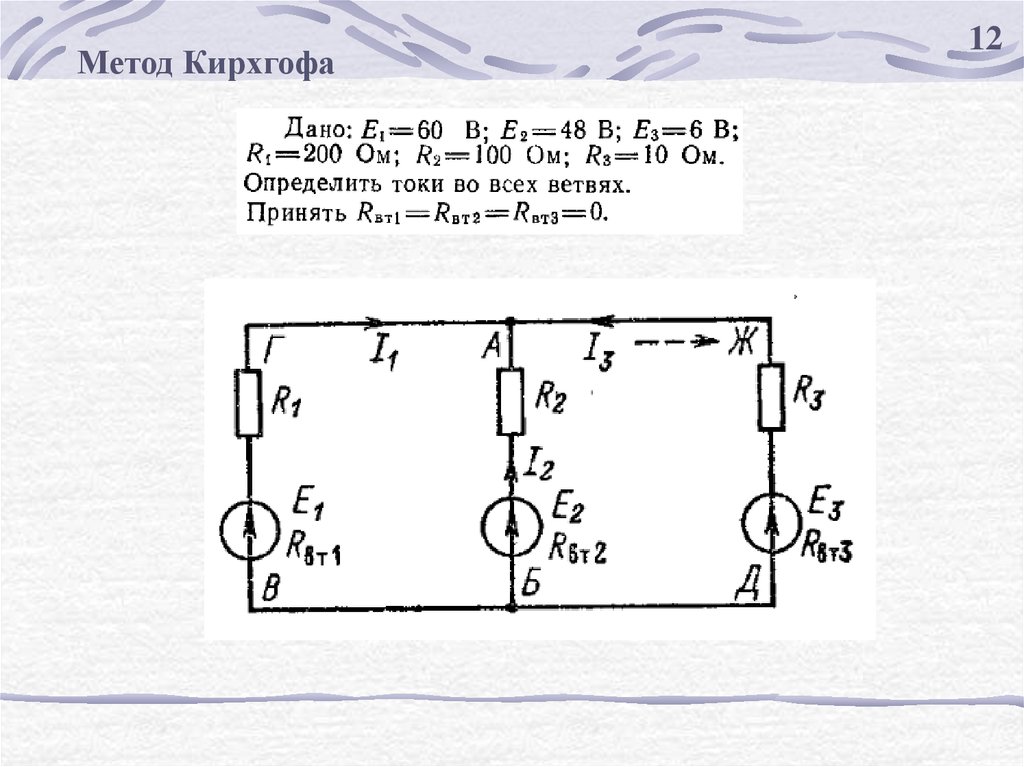
Метод Кирхгофа12
13.
1314.
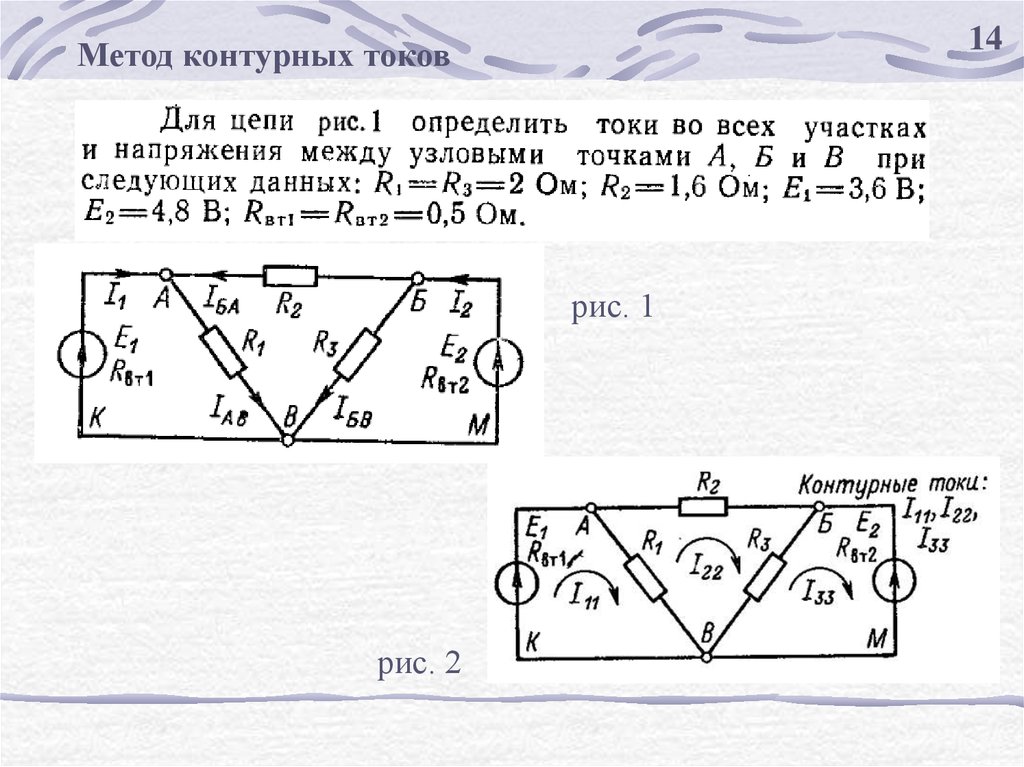
14Метод контурных токов
рис. 1
рис. 2
15.
1516.
1617.
1718.
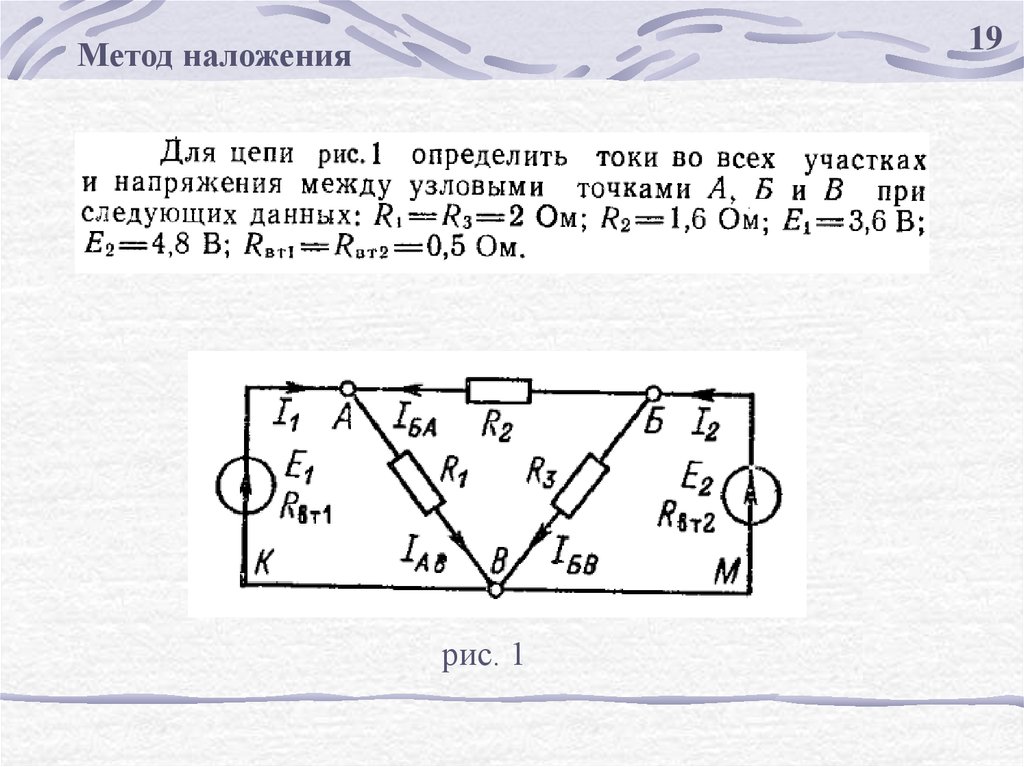
1819.
19Метод наложения
рис. 1
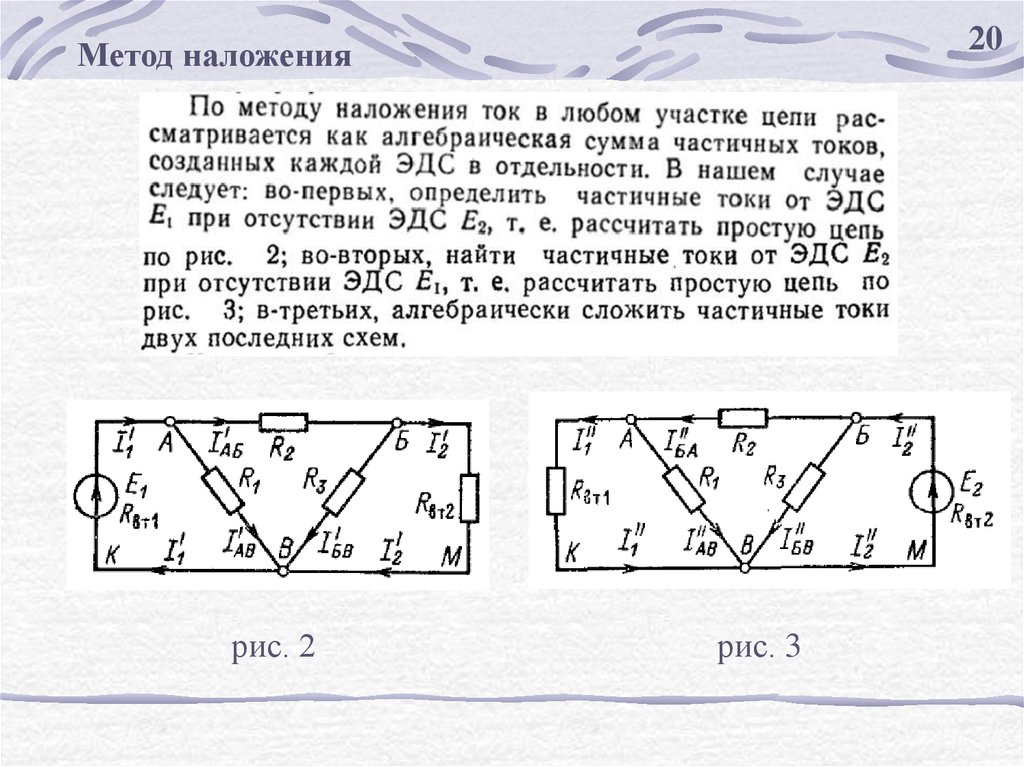
20.
20Метод наложения
рис. 2
рис. 3
21.
Метод наложения21
22.
Метод наложения22
23.
Метод наложения23
24.
Метод наложения24



















 physics
physics








