Similar presentations:
Показательная и логарифмическая функции
1.
Показательная илогарифмическая функции
2.
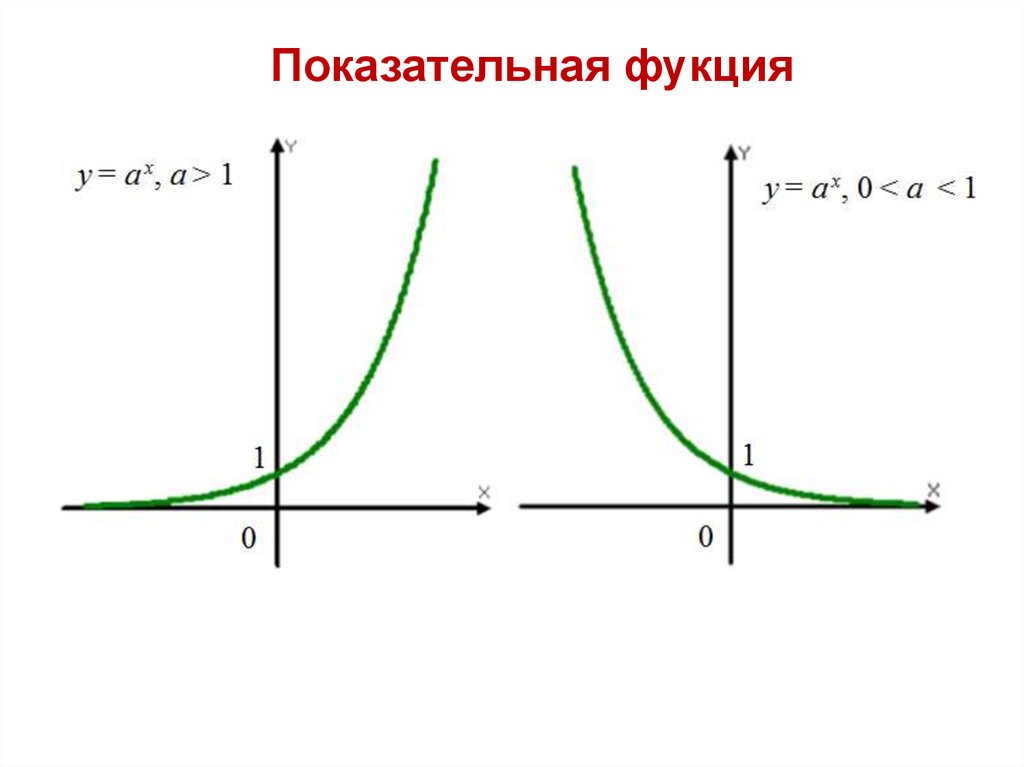
Показательная фукция3.
Показательные уравнения.
1) a
f ( x)
2
2)
a
x 1
1 a
1, 2
f ( x)
2
x 1
a
2
f ( x)
x 1
g ( x)
x 2 2
a f ( x) 0
0
2 , x 1 0......
0
f ( x) g ( x)
, x 1 x 2......
2
4.
Показательные уравнения.
3)
2
4)
Вынесение за скобки общего
множителя
x 2
2 12,
x
2 (2 1) 12.....
x
2
Приведение к квадратному
уравнению
4 3 2 4 0,
x
x
2 3 2 4 0,
2x
Пусть 2 t , тогда....
x
x
5.
Показательные уравнения.
5)
Однородные уравнения
5 4 3 6 9 0,
х
x
x
,
Делим обе части на 4 или на 9
x
x
Плучаем уравнение квадратное
6.
Показательные уравнения.
6) 2
x 2
2
2 x
15
2
2
2 2 x 15 0
2
4
x
4 2 x 15 0
2
x
Пусть 2 t , тогда
2
x
4
4 t 15 0 | t
t
2
4t 15t 4 0......
7.
Показательные неравенства1)
a
f ( x)
a
g ( x)
,
если 0 a 1, то f ( x) g ( x)
0,2
x 1
0,2
x2 2
Так как 0,2 1, то
x 1 x 2......
2
8.
Показательные неравенства1)
a
f ( x)
a
g ( x)
,
если a 1, то f ( x) g ( x)
2
x 1
2
x2 2
Так как 2 1, то
x 1 x 2......
2
9.
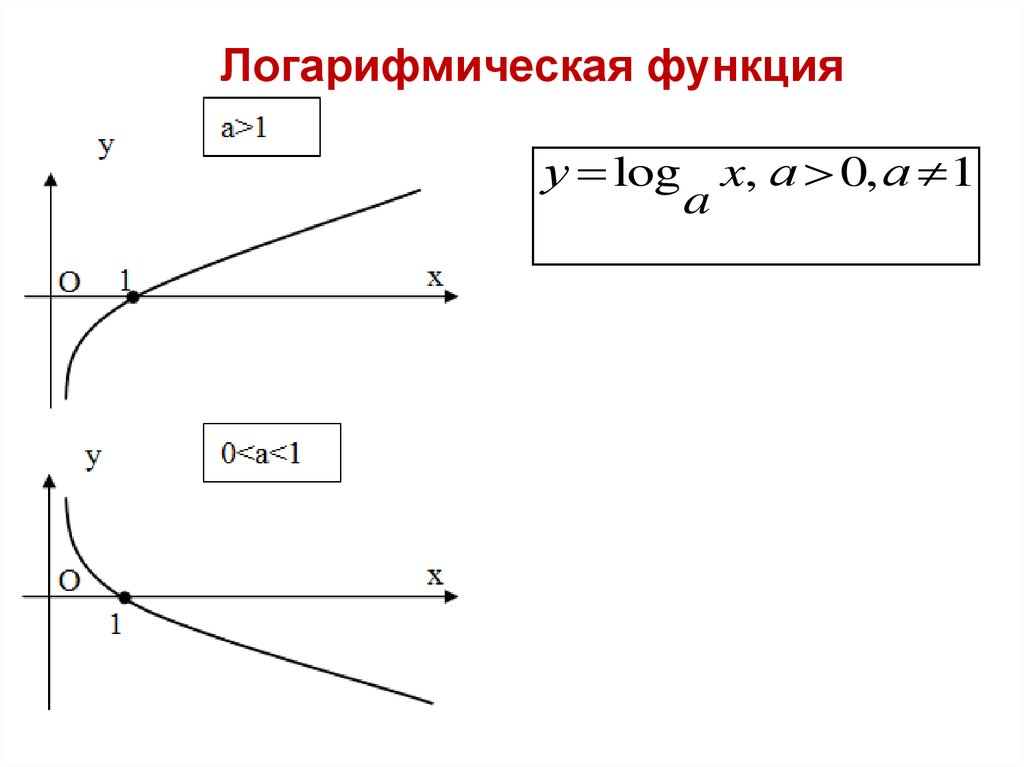
Логарифмическая функцияу log x, а 0, а 1
a
10.
Основные свойства логарифмов1. log a 1 0
2. log a a 1
3. log a ( xy) log a x log a y
x
4. log a log a x log a y
y
5. log a x p p log a x
log b x
6. log a x
log b a
7.log a g x 1 log a x
g
1
8.log a b
log b a
11.
Логарифмические уравнения1)
log a f ( x) b f ( x) a
b
log 2 ( x 4) 5 x 4 2 ......
5
f ( x) g ( x)
2) log a f ( x) log a g ( x)
f ( x) 0 или g ( x) 0
2
x 4 x 1
2
log 2 ( x 4) log 2 ( x 1)
x 4 0.....
12.
3)Приведение к квадратному
уравнению
log 22 x 5 log 2 x 4 0
Пусть log 2 x t......
4)
Применение свойств
логарифмов
log a f ( x) log a g ( x) log a h( x),
log a ( f ( x) g ( x)) log a h( x),
f ( x ) g ( x ) h( x )
f ( x) 0
g ( x) 0
h( x) 0......
13.
Логарифмические уравнения5)
log g ( x )
f ( x) g ( x) a
f ( x) a g ( x) 0
g ( x) 1
x 4 x2
log x ( x 4) 2 x 0
x 1
14.
Логарифмические неравенстваlog a f ( x) log a g ( x)
Если a 1, то f ( x) g ( x)
x 4 x 1
log 2 ( x 4) log 2 ( x 1) 2
x 1 0....
2
2
(обязательно проверяем меньшее в системе…)
15.
Логарифмические неравенстваlog a f ( x) log a g ( x)
Если 0 a 1, то f ( x) g ( x)
x 4 x 1
log 2 ( x 4) log 2 ( x 1)
3
3
x 4 0....
2
2
(обязательно проверяем меньшее в системе…)
16.
Логарифмические неравенстваlog g ( x ) f ( x) log g ( x ) h( x)
g ( x) 1
0 g ( x) 1,
f ( x ) h( x ) f ( x ) h( x )
или
f ( x) 0
f ( x) 0
h( x) 0
h( x) 0














 mathematics
mathematics








