Ковариация и собственный вектор

1. Тема 2. Ковариация и собственный вектор

1
1

2.

Временной ряд рассматривается либо как некоторая
выборка из генеральной совокупности либо как
описание некоторой детерминированной функции.
Все значения каждого признака в различные моменты
времени образуют временной ряд, который обозначается
вектором
0
xi {x1i ,
2
0
x2i , ,
0 T
xmi }
2

3.

Среднеарифметические значения временных
рядов:
1 m 0
xi =
∑ xk i
m
k
Мода — это наиболее часто наблюдаемая
величина изучаемого временного ряда
Медиана — это значение наблюдения, которое
находится в середине ранжированного ряда
данных, т.е. наблюдение, занимающее
срединное положение
3
3

4.

Дисперсия – отклонение наблюдаемого значения
(для каждого наблюдения) от среднего
арифметического (несмещенная оценка) :
m
x1
∑ ( xk01 x1 )( xk01 x1 )
k 1
m
Если размер выборки относительно ограничен,
то для более точного расчета применяется
формула смещенной (исправленной)
дисперсии:
m
4
x1
∑ ( xk01 x1 )( xk01 x1 )
k 1
m 1
4

5.

Среднеквадратическое (стандартное)
отклонение показывает абсолютное отклонение
измеренных значений от среднего
арифметического и определяется по формуле :
m
x
1
5
∑ ( xk01 x1 )( xk01 x1 )
k 1
m
x1
5

6.

Ковариация двух случайных величин
определяется следующим образом (несмещенная
оценка)
m
cov(x10 x20 ) x1 x2
∑ ( xk01 x1 )( xk02 x 2 )
k 1
m
Если размер выборки относительно ограничен,
то для более точного расчета применяется
формула смещенной (исправленной)
m
ковариации:
0
0
∑ ( xk1 x1 )( xk 2 x 2 )
cov(x10 x20 ) x1 x 2 k 1
6
m 1
6

7.

Коэффициент корреляции
rx x
1 2
x1x2
x0 x0
1
2
Коэффициент корреляции– это безразмерная величина,
которая может принимать значения из отрезка :
1– имеет место абсолютная положительная
корреляция между рассматриваемыми величинами
-1– имеет место абсолютная отрицательная
корреляция между рассматриваемыми величинами
0 – линейная корреляционная связь отсутствует.
7
7

8.

Пространство признаков описывается
матрицей
0
0
0
0
или
x11
0
x21
0
X 0
xi1
0
xm1
x12
x1i
0
x22
x20i
xi02
xii0
0
xm0 2 xmi
X 0 [ x10
8
x20
x1n
x20n
0
xin
0
xmn
xn0 ]
8

9.

При вычислении ковариационной и
корреляционной матриц используются операции
вычитания средних (центрирование) и деления
на стандарты (нормирование).
Операция нормирования в пространстве
соответствует изменению масштабов по всем
осям координат так, чтобы величина рассеяния,
характеризуемая величиной дисперсии, стала
равной единице.
9
9

10.

При вычислении ковариационной
матрицы используется операция
«центрирование».
1 T
A X X
m
X
[ x1
x ji
10
x2
0
x ji
xn ]
xi
10

11.

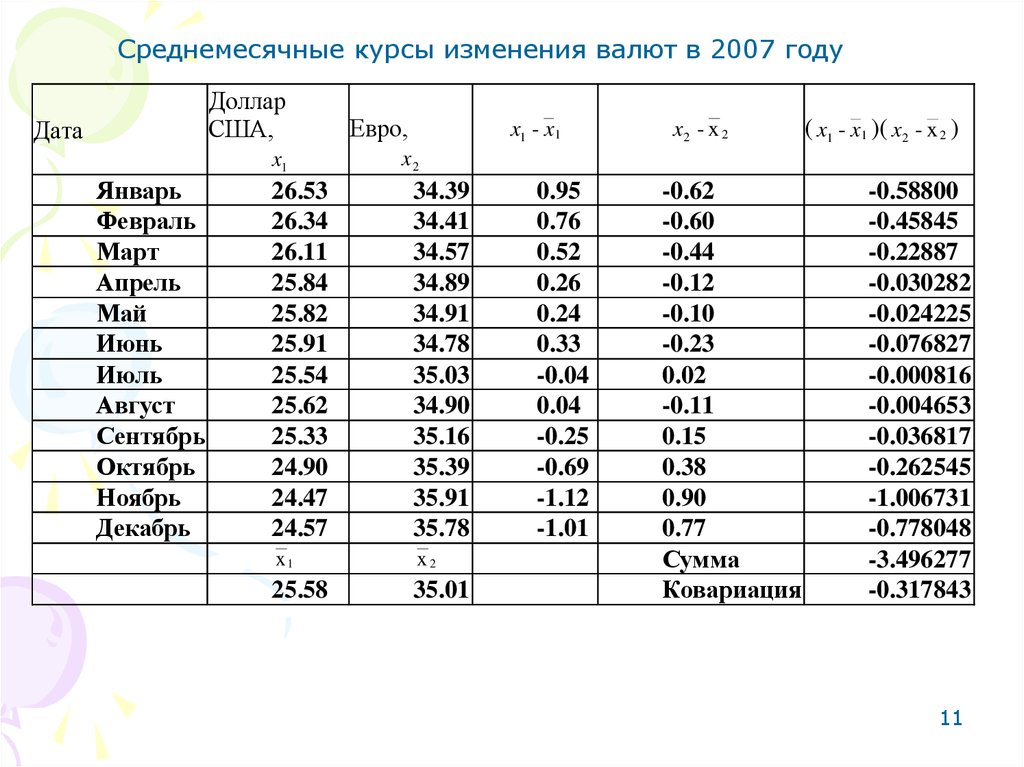
Среднемесячные курсы изменения валют в 2007 году
Доллар
США,
Дата
x1
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
11
Евро,
x1 - x1
x2 - x 2
( x1 - x1 )( x2 - x 2 )
x2
26.53
26.34
26.11
25.84
25.82
25.91
25.54
25.62
25.33
24.90
24.47
24.57
34.39
34.41
34.57
34.89
34.91
34.78
35.03
34.90
35.16
35.39
35.91
35.78
x1
x2
25.58
35.01
0.95
0.76
0.52
0.26
0.24
0.33
-0.04
0.04
-0.25
-0.69
-1.12
-1.01
-0.62
-0.60
-0.44
-0.12
-0.10
-0.23
0.02
-0.11
0.15
0.38
0.90
0.77
Сумма
Ковариация
-0.58800
-0.45845
-0.22887
-0.030282
-0.024225
-0.076827
-0.000816
-0.004653
-0.036817
-0.262545
-1.006731
-0.778048
-3.496277
-0.317843
11

12.

Ковариационная матрица
Доллар США
Доллар США
Евро
12
0.4345
-0.318
Евро
-0.318
0.2372
12

13.

При вычисление корреляционной матрицы
используются операции центрирование и
нормирование
r
x10 x20
x1x2
x0 x0
1
E
13
2
A k EAE
- диагональная матрица (нормирование)
Доллар США
Евро
Доллар
США
1,0
-0,989
Евро
-0,989
1,0
13

14.

m
Вычисление вторых моментов
x
1 x2
0 0
x
∑ k 1 xk 2
k 1
m 1
1
A
(X0 ) T X0
m 1
0
Доллар США
14
Евро
Доллар
США
714,35
976,72
Евро
976,72
1337,4
14

15.

При вычислении матрицы нормированных
начальных вторых моментов используется
операция нормирование
x10 x 20
Доллар США
Евро
15
x10 x 20
0
x1
0
Ak
x 20
PA P
0
Доллар США
Евро
1,0
0,999
0,999
1,0
15

16.

Матрица
x
11
x 21
X
x
i1
x
m1
x12
x1i
x 22
x 2i
xi 2
xii
x m 2 x mi
x1n
x2n
xin
x mn
Транспонированная матрица
X
16
0T
x
11
x12
x
1i
x
1n
xi1 x m1
x 22 xi 2 x m 2
x 2i xii x mi
x 2n xin x mn
x 21
16

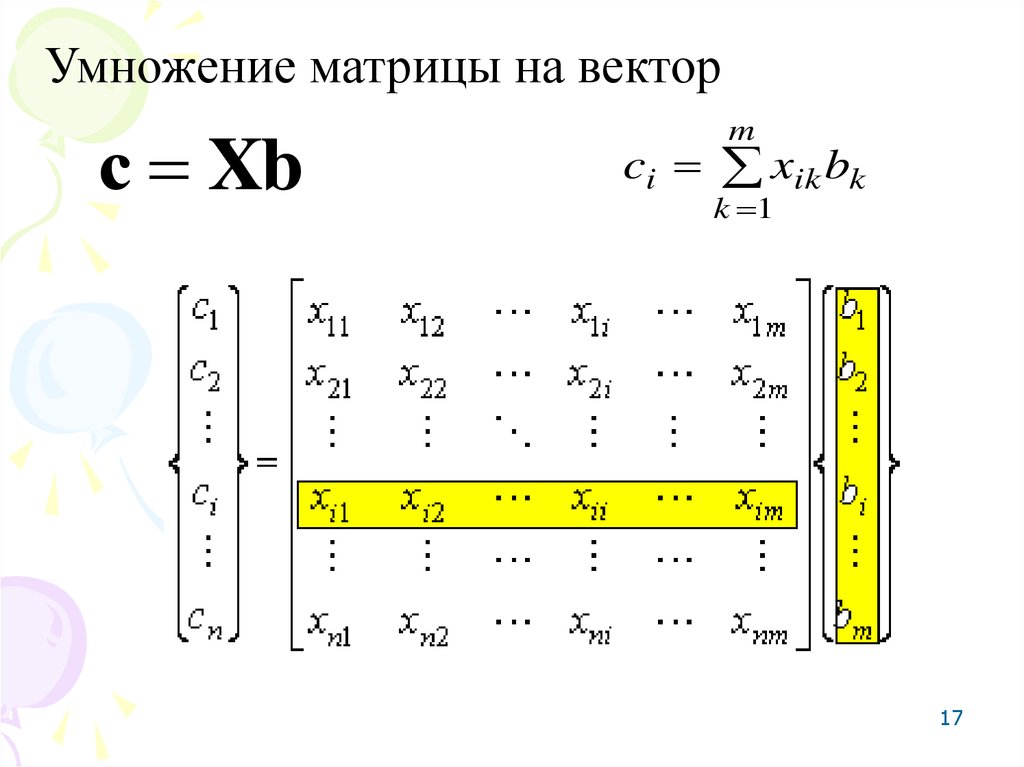
17.

Умножение матрицы на вектор
с Xb
17
m
ci xik bk
k 1
17

18.

Пример вектора и собственного вектора
2 3 1 2 1 3 3 11
2 1 3 2 1 1 3 5
4 3 3 4 3 3 2 18
3
3 1,5 2 3 3 1,5 2 12 6 2
4 3 2 4 2 3 3 1
2
3 1,5 3 3 2 1,5 3 1 0,5 3
18
18

19.

Уравнение собственных векторов
Xb b 0
4 3 3
3 18
3
3 1,5 2 6 2 12 6 2 0
19
19

20.

1. Выбрать произвольное начальное (нулевое)
приближение собственного вектора b
0
Положить k=0
2. Найти
.
b1* Аb 0
(1) max( b1* )
Вычислить первое приближение собственного вектора
b1(i ) b1*(i ) / 1
20
.

21.

,
3. Найти
b*k 1 Аb k ( k 1) max( b* )
k 1
.
Вычисляем k+1 приближение собственного вектора
*
bk 1(i ) bk 1(i )
.
k 1
/
Вычисляется норма ошибки b k 1 b k
Полагаем k=k+1.
4. Шаг 3 повторяется пока
lim
21

22.

Свойства собственных векторов.
1. Матрица n x n имеет n собственных
векторов.
2. Если собственный вектор умножить на
ненулевой коэффициент, то
результирующий вектор также является
собственным вектором.
22
22

23.

3. Ортогональность собственных векторов
ai i j
T
b j Abi
0 i j
ai i j
T
b j bi
0 i j
23
23

24.

3. Ортогональность собственных векторов
24
24

25.

Упражнение. Для следующей квадратной
матрицы определить какие векторы
являются собственными
3 0 1
4 1 2
6 0 2
Векторы
2
2
1
25
1
0
2
1
1
3
0
1
0
3
2
1
25