Similar presentations:
Метод главных компонент
1. Тема 3. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
11
2.
Предположим, что x – это вектор p случайныхили детерминированных величин.
Дисперсия этих величин и структуры
ковариации или корреляции между
переменными представляют для нас интерес.
Если p мало или структура слишком проста, то
зачастую бесполезно оценивать p дисперсий и
все ½ p(p-1) корреляций и ковариаций.
2
2
3.
Альтернативным вариантом является поисктаких комбинаций факторов, которые
сохраняют большую часть информации/
T'x
z
— линейной
1
1
Поиск нового фактора
комбинации элементов , имеющей максимальную
дисперсию
p
z1 1T x 11x1 12 ... 1 p x p 1 j x j
j 1
Далее, ищется x линейная комбинация
T
2
исходных факторов, которая не коррелированна с
3
z31 и имеет максимальную дисперсию, и так далее
4.
Далее, ищется x — линейная комбинацияT
2
исходных факторов, которая не коррелированна с
1T x и имеет максимальную дисперсию, и т.д.
Главный смысл выделения главных компонент
заключается в том чтобы достаточно хорошо
описать изменчивость x с помощью m главных
компонент, где m<<p.
4
4
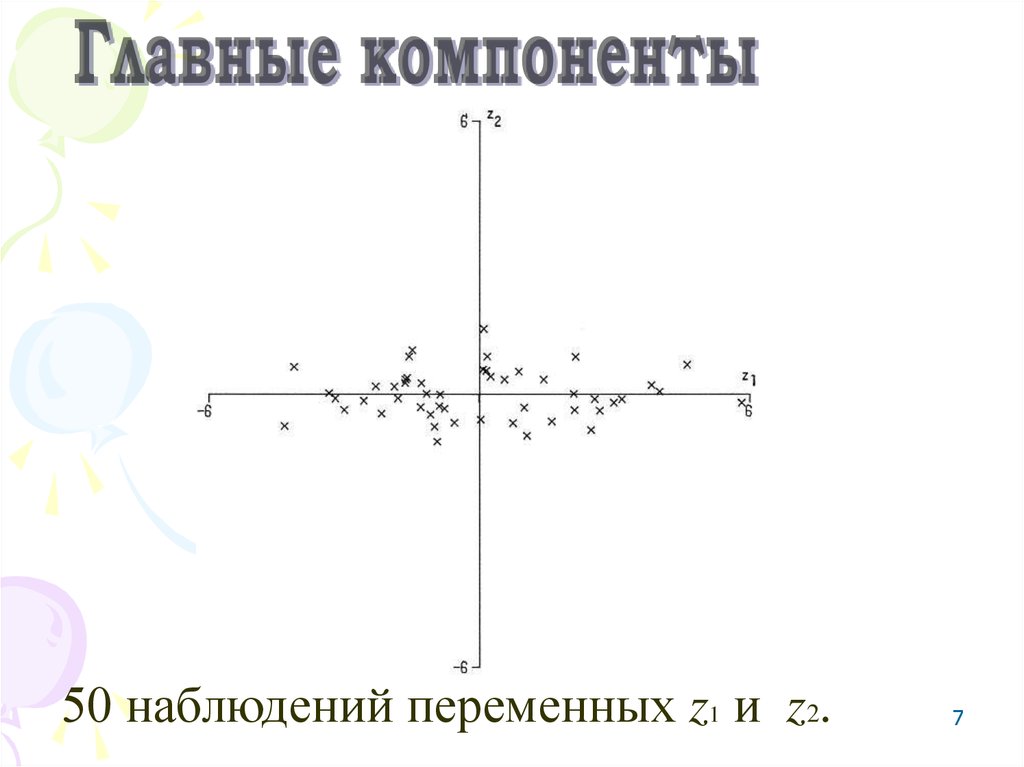
5.
50наблюдений
переменных
x
1 и x2.
5
5
6.
Комбинируя переменные, мы можемнайти две комбинации имеющих разные
дисперсии
z1 11 ( x1 x1 ) 12 ( x2 x2 )
z 2 21 ( x1 x1 ) 22 ( x2 x2 )
6
6
7.
50наблюдений
переменных
z
1 и z2.
7
7
8.
Переменные x можно достаточно хорошоописать с помощью первой главной компоненты.
x1 x1 11z1
x2 x2 12 z1
(1)
Если мы знаем значение переменной x1
то используя первое уравнение системы (1)
получим
z1 ( x1 x1 ) / 11
8
8
9.
Прогнозирование по главным компонентам9
9
10.
Рассмотрим задачу поиска такой линейнойкомбинации 1T x , которая максимизирует.
дисперсию равной
1T A 1
Чтобы максимизировать
1T A 1
с учетом
1T 1 1
необходимо использовать метод множителей
Лагранжа. Функция Лагранжа имеет вид
T
T
L( 1, ) 1 A 1 ( 1 1 1)
10
10
11.
Необходимым условием экстремума функцииЛагранжа является равенство нулю градиента
L 1 Дифференцируем по 1
A 1 1 0
Величина, которая максимизируется, равна
T
1 A 1
11
T
1 1
T
1 1
11
12.
Вторая комбинацияT
2 A 2
x
максимизирует
T
2
с сохранением некоррелированности с
x , т.е.
T
1
cov[ 1T x, 2T x] 0
,
При этом
T
T
T
T
T
T
T
T
cov[ 1 x, 2 x] 1 A 2 2 A, 1 2 1 2 1 1 1 2
В связи с этим, любое из уравнений
0 1 0 2 0
может быть использовано для определения
нулевой корреляции между 1 и 2 главными
12
12
компонентами
1T A 2
0
T2 A 1
T
2
T
1
13.
Опять используем множители Лагранжа. Приэтом функция Лагранжа равна
T
T
T
2 A 2 ( 2 2 1) 2 1
Дифференцирование по 2 дает
A 2 2 1 0
а умножение уравнения на
T
1 A 2
13
T
1 2
T
1
приводит к
T
1 1
0
13
14.
Таким образомA 2 2 0
приводят к тому, что и 2 вновь становятся
собственным значением и собственным
вектором матрицы A
Наши доказательства приведены для k=2, для
k > 2 доказательство более сложное, но в
целом выполняется по аналогичной схеме.
14
14
15.
Ковариационная матрица определяетсяпо формуле
1 T
A
m
X X
Собственные векторы ковариационной
матрицы определяются из уравнения
A λI v
15
0
=0
15
16.
Формируется матрица собственныхвекторов, которым соответствуют
наибольшие собственные значения
[
V0 = v 01 , v 02 ,..., v 0 p
16
]
16
17.
На основе собственных вектороввычисляются главные компоненты
zi
17
T
v 0i
n
xi v 0ij x j
j 1
17
18.
Пусть рынок акций описывается наборомпризнаков
1. Курс доллара (USD)
2. Курс евро (EURO)
3. Индекс РТС (RTC)
4. Цена на нефть Юралс (OIL)
5. Доходность ГКО-ОФЗ, % (GKO)
6. Межбанковская ставка, % (MB)
18
18
19.
Ковариационная матрицаUSD
USD
RTC
OIL
GKO
MB
12,090
-1592,4
-53,381
6,030
4,852
EURO 12,090 16,571
RTC -1592,4 -1483,1
-1483,1
31919
-29,258
6,839
8883,7 -1020,14
4,409
-1074,5
OIL
11,635
EURO
-53,381 -29,258 8883,74
526,48
-23,89
-27,46
GKO
6,030
6,839
-1020,1
-23,897
4,377
3,826
MB
4,852
4,409
-1074,5
-27,468
3,826
8,64
19
19
20.
Корреляционная матрицаUSD
EURO
RTC
OIL
GKO
MB
USD
1,00
0,87
-0,83
-0,68
0,84
0,48
EURO
0,87
1,00
-0,64
-0,31
0,80
0,37
RTC
-0,83
-0,64
1,00
0,69
-0,86
-0,65
OIL
-0,68
-0,31
0,69
1,00
-0,50
-0,41
GKO
0,84
0,80
-0,86
-0,50
1,00
0,62
MB
0,48
0,37
-0,65
-0,41
0,62
1,00
20
20
21.
Z1 (t ) 0,00498 (USD(t ) USD) 0,00464 ( EUR(t ) EUR) 0,9995 ( PTC (t ) PTC )0,0278 (OIL (t ) OIL ) 0,00319 (GKO(t ) GKO) 0,00336 ( MB (t ) MB )
Z 2 (t ) 0,0318 (USD(t ) USD) 0,0440 ( EUR(t ) EUR) 0,0276 ( PTC (t ) PTC )
21
21
0997 (OIL (t ) OIL ) 0,0164 (GKO(t ) GKO) 0,0089 ( MB (t ) MB
)
22.
Первая главная компонента22
22
23.
USD(t ) USD 0,00498 Z1 0,0318 Z 223
Реконструкция курса доллара США по двум ГК
23
24.
Пусть состояние динамической системы описывается набором показателей0
xki
Модель динамической системы формируется
из p ( p<< n) главных компонент.
et
xki
24
p
xi vhi zkh
h 1
24
25.
Таким образом, n показателейдинамической системы зависят от p
главных компонент.
Сценарное прогнозирование
заключается в задание сценария в виде
изменения p показателей динамической
системы и вычисление по этим
сценарным показателям значений
главных компонент
25
25
26.
1. Жесткий алгоритм. В жесткомалгоритме прогнозирование ведется
по сценарию, который содержит
число показателей равное числу
главных компонент модели.
p
sc
xk1 x1 v hi zkh
h 1
p
sc
xk 2 x2 v hi zkh
h 1
p
sc
xkp x p h 1 v hi zkh
26
26
27.
Однако полученные главныекомпоненты не являются
ортогональными ортогональности, т.е.
ковариационная матрица главных
компонент не является диагональной.
Поэтому используется процедура
ортогонализации.
27
27
28.
Мягкий алгоритм.При использовании мягкого алгоритма
число показателей в сценарии
прогнозирования может быть не равно
числу главных компонент модели.
28
28
29.
Шаг 1. Формируется учебная выборка,которая используется для вычисления
матрицы весовых коэффициентов
главных компонент и матрицы главных
компонент .
Шаг 2. Главные компоненты тестовой
выборки вычисляются по сценарным
значениям показателей
r
29
z ik v ij ( xkjsc x jsc )
j 1
29
30.
Шаг 3. Показатели динамическойсистемы вычисляются по формуле
p
xi = ∑ v 0 ki z k
k
Шаг 4. Главные компоненты уточняются
по формуле
n
z ik v ij ( xkj x j )
j 1
30
30
31.
Оценка ошибок прогнозаОшибки прогноза
ei yi yˆi
Среднее абсолютное отклонение (Mean
Absolute Derivation, MAD)
e MAD
31
1 m
y i yˆ i
m i 1
31
32.
Оценка ошибок прогнозаСреднеквадратическая ошибка (Mean Squared
Error, MSE)
e MSE
1 m
2
( y i yˆ i )
m i 1
Средняя абсолютная ошибка в процентах
(Mean Absolute Percentage Error, МАРЕ)
32
1 n yi yˆ i
MAPE
n i 1 yi
32
33.
Оценка ошибок прогнозаСтандартная ошибка оценки
m
( yi yˆ i ) 2
eSSE
i 1
m n 1
Относительная среднеквадратическая ошибка
m
2
(
y
y
)
i ˆi
eMSEN
i 1
m
2
y
i
33
i 1
33
34.
Рассматривается задача прогнозирование курсоввалют. В качестве независимых переменных
используются курс китайского юаня, курс доллара
США, курс Евро, цена на нефть.
Китайский Курс
Курс
Цена на
юань
доллара
евро
нефть
CNY
USD
EURO OIL
CNY
1,00
0,97
0,92
-0,55
USD
0,97
1,00
0,87
-0,70
EURO
0,92
0,87
1,00
-0,33
OIL
-0,55
-0,70
-0,33
1,00
34
34
35.
Для построения модели используем обучающую выборку,которая включает первые 700 наблюдений.
Весовые коэффициенты главных компонент
Дисперсия
Доля %
Кумулятив. доля %
Китайский юань
Курс доллара
Курс евро
Цена на нефть
35
617
93,0
93,0
-0,15
-0,10
-0,06
0,98
44,7
6,74
99,8
0,74
0,35
0,55
0,18
1,09
0,165
99,96
-0,58
-0,03
0,81
-0,04
0,23
0,036
100
-0,32
0,93
-0,18
0,04
35
36.
Модель на основе первых двух главных компонент.Полученная модель является двух факторной, в связи
с этим в качестве сценария будем использовать
значения двух показателей цена на нефть и курс
доллара
Ошибки прогноза (жесткий алгоритм)
CNY USD EURO OIL
MPE, %
0,04 0,02
0,3
0
MAPE, % 2,34 0,33 2,43 0,01
MSEN, % 2,93 0,51 3,19 0,01
36
36
37.
37Прогноз курса юаня (жесткий алгоритм)
37
38.
38Прогноз курса евро(жесткий алгоритм)
38
39.
Ошибки прогноза (мягкий алгоритм)CNY USD EURO OIL
MPE, %
-0,16 -0,07
0,2
0
MAPE, %
3,48
1,6
3,04
0,03
MSEN, %
3,81
1,92
3,81
0,03
39
39
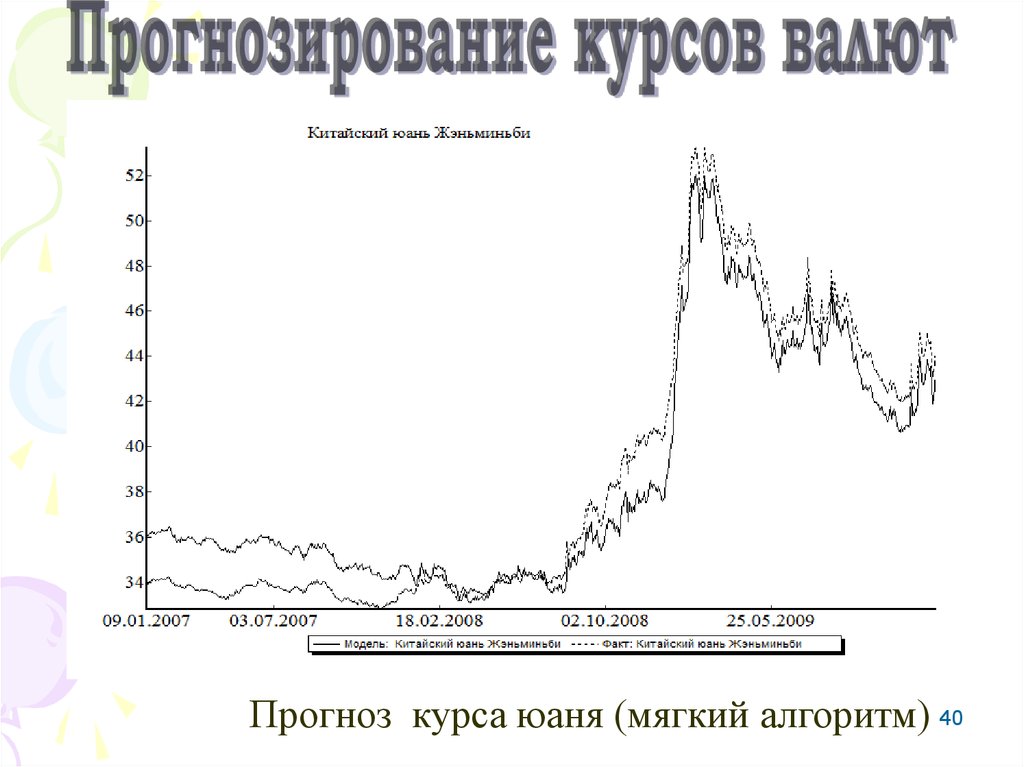
40.
40Прогноз курса юаня (мягкий алгоритм) 40
41.
41Прогноз курса евро(мягкий алгоритм)
41







































 mathematics
mathematics








