Ранг матрицы. Собственные числа и собственные векторы

1. Линейная алгебра

Лекция 4
Ранг матрицы.
Собственные числа и собственные
векторы

2. План лекции

Определение и свойства ранга
Методы вычисления ранга
–
Метод элементарных преобразований
–
Метод окаймляющих миноров
Теорема Кронекера-Капелли
Определение и примеры собственных чисел и столбцов
матрицы.
Характеристический многочлен матрицы и его свойства.
Общий план решения задачи о собственных
числах и собственных столбцах матрицы.
2

3. Минор k-го порядка

Определение.
Пусть А - прямоугольная матрица размеров mxn, k - любое целое
число,
1 k min m, n .
Выберем в матрице произвольные k строк и k столбцов. Элементы,
стоящие на пересечении этих строк и столбцов образуют
квадратную матрицу порядка k. Определитель полученной матрицы
называется минором k-го порядка матрицы А.
3

4. Ранг матрицы. Определение

Рангом rgA матрицы А = {aij} называется целое число r ,
такое, что среди миноров r–го порядка матрицы А имеется хотя
бы один, отличный от нуля,
а все миноры (r+1)-го порядка равны нулю или миноров порядка
(r+1) вообще нет.
Примеры:
1 0
; rgA 2 ;
1 A
0 1
Замечание: очевидно, что
1
0
2 A
0
0
2 3
4 5
; rgA 3.
0 6
0 0
1 rgA min m, n .
4

5. Инвариантность ранга

Введём обозначение A ~ B для матриц, полученных друг из
друга элементарными преобразованиями.
Теорема (об инвариантности ранга матрицы относительно
элементарных преобразований):
если A ~ B , то
rgA = rgB
5

6. Базисный минор

Минор r-го порядка называется базисным, если он отличен от
нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще
не существует.
Таким образом, определение ранга матрицы можно
сформулировать так:
рангом матрицы называется порядок ее базисного минора.
Замечание. В нулевой матрице базисного минора нет. Поэтому
ранг нулевой матрицы по определению полагают равным
нулю.
6

7. Свойства ранга

T
rgA
rgA
1.
2. rg A B m i n rgA, rgB
3.
rg A B rgA rgB
4. Если A - невырожденная квадратная матрица, то
rg A B rgB
и
rg C A rgC
,
т.е. ранг матрицы не изменяется при умножении ее слева или
справа на невырожденную квадратную матрицу.
7

8. Методы вычисления ранга матрицы. Метод элементарных преобразований

Метод элементарных преобразований основан на том, что
элементарные преобразования матрицы не меняют ее ранга.
Используя эти преобразования, матрицу можно привести к
трапециевидному виду, т.е. такому виду, когда все элементы a '
при i r , j i
нулевыми.
a11
a21
...
ar1
...
...
am1
a12
a22
...
ar 2
...
...
am 2
ij
равны нулю и все строки с номерами i > r являются
a13 ... ... ... a1n 1 a12' a13'
a23 ... ... ... a2 n 0 1 a23'
... ... ... ... ... ... ... ...
ar 3 ... ... ... arn 0 0 0
... ... ... ... ... 0 0 0
... ... ... ... ... ... ... ...
am3 ... ... ... amn 0 0 0
Тогда
...
...
...
...
...
...
1 ar ,'r 1
0
0
...
...
0
0
... a1n'
'
... a2 n
... ...
... ar ,'n
0 0
... ...
0 0
rgA = r
8

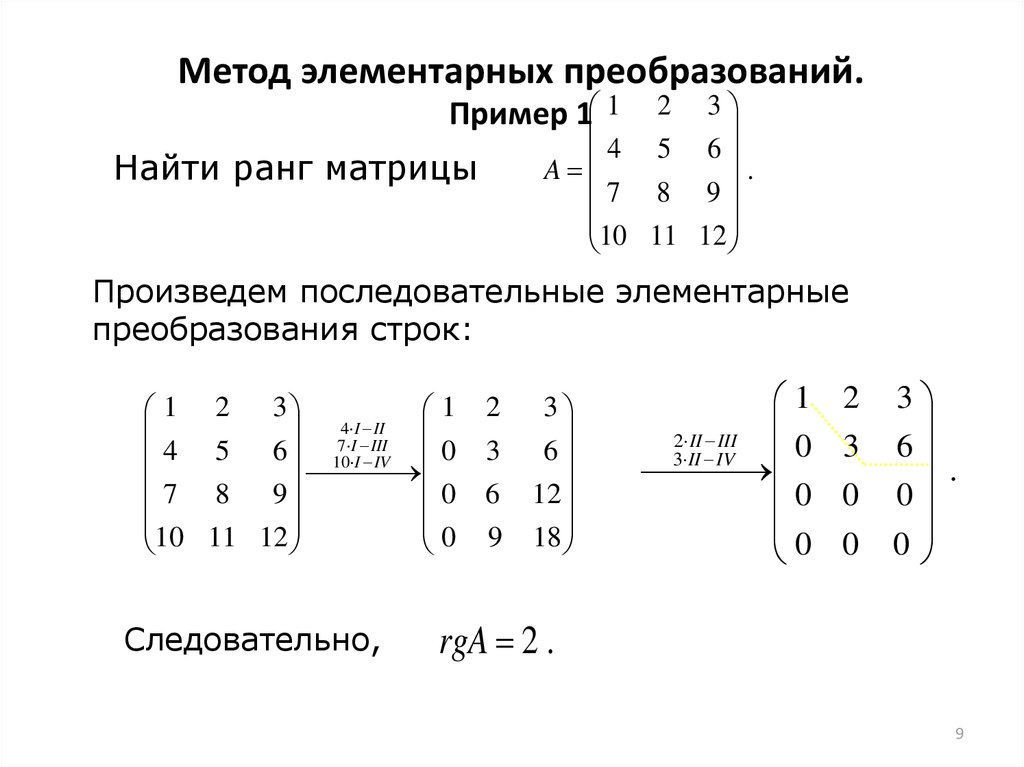
9. Метод элементарных преобразований. Пример 1

1
3
4
5
6
A
.
7 8 9
10 11 12
Найти ранг матрицы
2
Произведем последовательные элементарные
преобразования строк:
1 2 3
1
74 II IIIII
4 5 6 10 I IV 0
7 8 9 0
10 11 12
0
Следовательно,
2
3
6
9
3
6
12
18
1
2 II III
0
3 II IV
0
0
2
3
0
0
3
6
.
0
0
rgA 2 .
9

10. Методы вычисления ранга матрицы. Метод окаймляющих миноров

Пусть в матрице найден минор M k-го порядка, отличный
от нуля. Рассматривают те миноры (k+1)-го порядка,
которые содержат в себе (окаймляют) минор M. Если все
они равны нулю, то
rgA = k.
В противном случае среди окаймляющих миноров найдется
ненулевой минор (k+1)-го порядка, и вся процедура
повторяется.
10

11. Метод окаймляющих миноров. Пример 2

2 4 3 1
1 2 1 4
A
0
1 1 3
4 7 4 4
Найти ранг матрицы
2 4
Минор
M
3
3
0
2
.
1
5
1 2
0
1 1 - отличен от нуля.
1 1
Оба минора 4-го порядка, окаймляющие M3 , равны нулю:
M
41
2 4
3
1 2
1 4
0
1 1
4 7
4
Следовательно,
1
3
0;
4
M
42
2 4
3
0
1 2
1
2
1 1
1
0
4 7
4
0.
5
rgA 3 .
11

12. Теорема Кронекера-Капелли

СЛУ совместна (т.е. имеет хотя бы одно решение)
тогда и только тогда, когда ранг матрицы
коэффициентов равен рангу расширенной
матрицы системы:
x10
0
x2
X 0 R n : A X 0 B rg ( A) rg ( A1 )
...
x0
n
12

13. Пример

Исследовать совместность СЛУ
x1 x2 x3 2
2 x1 x2 x3 5
x 7x 7x
2
3
1
1
1
1
2
1
1 1 2
1
1
1
2
IIIII 2I I
III 2 II
5 0 3 2 1 0 3 2 1
2 1
0
0
1
6 6 2
0
2
2
7
7
1
1 1 2
3 1 , rg ( A) 2, rg ( A1 ), 3
При 1 A1 0 3
0
СЛУ несовместна
0
0
1
При
1 rg ( A) rg ( A1 ) 3 , СЛУ совместна
13

14. Теорема о числе решений СЛУ

Пусть дана совместная СЛУ от n неизвестных с матрицей
коэффициентов ранга r .
Тогда:
1. если r = n , то система имеет единственное решение;
2. если r < n , то система имеет бесконечно много решений,
причем (n – r) неизвестным можно присвоить произвольные
значения, а остальные r неизвестных выражаются через них
единственным образом.
14

15. Собственные числа и собственные столбцы матрицы. Определение

Собственным числом (значением) квадратной
матрицы
R
А порядка n
называется такое число
, для которого выполняется следующее
условие:
X R : X 0 R ,
n
n
X R
A X X
n
При этом столбец
называется собственным
вектором (столбцом) матрицы А, соответствующим
собственному числу
.
R
15

16. Пример

Проверить, что 5 – собственное число,
1
X 1 –
1
отвечающий ему собственный вектор матрицы
1 2 2
A 2 1 2 .
2 2 1
Вычислим AX и 5X :
1 2 2 1 5
AX 2 1 2 1 5 ;
2 2 1 1 5
1 5
5 X 5 1 5 .
1 5
16

17. Характеристический многочлен матрицы. Определение

Характеристическим многочленом квадратной
матрицы
А порядка n называется следующий
многочлен:
a11 t
A (t ) det( A t E )
a21
a12
...
a1n
a22 t ...
a2 n
...
...
...
...
a n1
an 2
... ann t
17

18. Теорема

Пусть φА(t) – характеристический многочлен
матрицы A . Тогда:
*
*
A t 0 ;
1. t R - собственное число A
n
2. X R - собственный вектор A, соответствующий t*, X – решение однородной СЛУ
(A t * E)X 0 .
Следствие.
У матрицы размера nxn не может быть более n
различных собственных чисел.
18

19. Общий план решения задачи о собственных числах и собственных столбцах матрицы

1. Составить характеристический многочлен
A (t ) det( A tE ) .
2. Найти собственные числа как корни
характеристического уравнения
t1 , t 2 , ... , t k
A (t ) .0
3. Для каждого собственного числа ti определить
собственный вектор Xi, решив однородную СЛУ
( A t E) X 0.
i
i
19

20. Пример 1

Найти собственные числа и
собственные столбцы матрицы
0 1
.
A
1 0
Составим характеристический многочлен
t A tE
Многочлен
φ(t)
t
1
1 t
t 2 1
не имеет действительных корней.
Матрица A не имеет собственных чисел и собственных
столбцов.
20

21. Пример 2

1 2 2
A 2 1 2 .
2 2 1
Найти собственные числа и
собственные столбцы матрицы
1. Составим характеристический многочлен
1 t
A (t ) 2
2
2
1 t
2
2
5 t 5 t 5 t
2 2
1 t
2
1 t
2
1
1
2 5 t 0 1 t
1 t
0
0
1
0
1 t
5 t 1 t t 1 5 t
2
2
2. Найдем корни характеристического уравнения
t 1 t 5 0 :
2
t1 1, t2 5
21

22. Пример (продолжение)

3.
Пример (продолжение)
Найдем собственные столбцы
а) для
t1 1
X 1 R 3 : ( A t1 E ) X 1 0 R 3
2 x1 2 x2 2 x3 0
2 x1 2 x2 2 x3 0
2 x 2 x 2 x 0
2
3
1
x3 ,
2 2 2 0
2 2 2 0 ~ 1 1 1 | 0 x2 ,
2 2 2 0
x1
X
1
α β
1
1
β α 0 β 1 R3, α, β R
α
1
0
22

23. Пример (продолжение)

Найдем собственные столбцы
б) для
t2 5
X 2 R 3 : ( A t2 E ) X 2 0 R 3
4 x1 2 x2 2 x3 0
2 x1 4 x2 2 x3 0
2x 2x 4x 0
1
2
3
2
2 0
x3 ,
4
2
1 1 0
x2 ,
2 0 ~
2 4
1
2
1
0
2
2 4 0
x1 ,
X
2
1
1 R 3 , R
1
23