Определенный интеграл. Его основные свойства. Методы вычислений

1. Тема: Определенный интеграл. Его основные свойства. Методы вычислений.

2.

Опр: Если при любом разбиении отрезка
[a, b] на части и при любом выборе
точек ci на каждой части
интегральная сумма стремится к
одному и тому же пределу, то его
называют определенным интегралом
и обозначают:
b
a
f ( x) dx lim
xi 0
f (c ) x
i 1
i
i
(2)

3.

Теорема: Если функция f (x) непрерывна на
отрезке [a, b], а функция F (x )
f
(x
)
является первообразной для
на этом отрезке, то справедлива
b
формула:
f ( x)dx F ( x)
b
a
F (b) F (a ) (3)
a
формула Ньютона-Лейбница

4.

b
a
b
f ( x) dx lim
xi 0
f ( x)dx F ( x)
a
b
a
f (c ) x
i 1
i
F (b) F (a )
i

5.

Свойства определенного интеграла:
b
1)
c
a
2)
3)
b
f ( x ) dx c f ( x ) dx.
a
b
b
b
a
a
a
b
c
b
a
a
c
( f ( x) ( x))dx f ( x)dx ( x)dx.
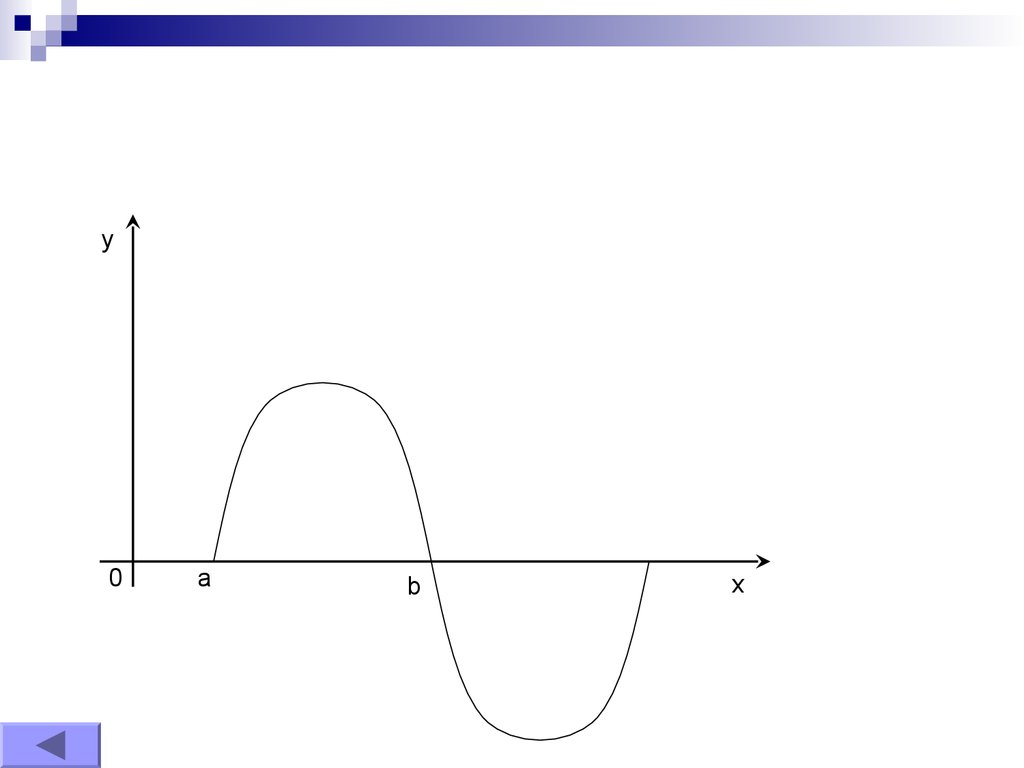
Если a c b, то
f ( x)dx f ( x)dx f ( x)dx.
b
4)
Если f ( x) 0, x [ a, b], то
f ( x)dx 0.
a
5)
Если f ( x) ( x) для всех x [a, b], то
b
b
a
a
f ( x)dx ( x)dx.

6.

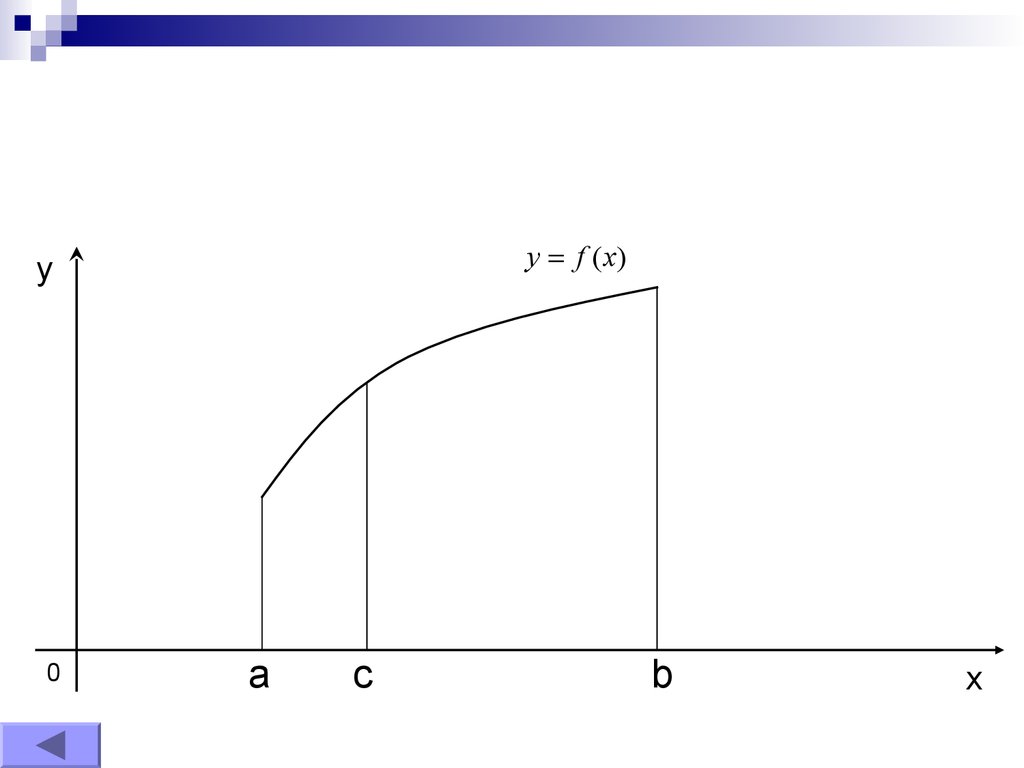
y f (x)
y
0
a
с
b
x

7.

y
0
a
b
x

8.

b
f ( x)dx F ( x)
b
a
F (b) F (a)
a
Пример:
4
4
4
4 4
x
x
dx
2xdx
1
1 ( x 2 x)dx 1
4
3
3
1
2 4
x
2
2
1
4 4
x
4
1
x
2 4
1
256 1
255
4 4 14
2
2
) (16 1)
15 78,75
( ) (4 1 ) (
4
4
4
4 4