Similar presentations:
Определённый интеграл
1. Определённый интеграл
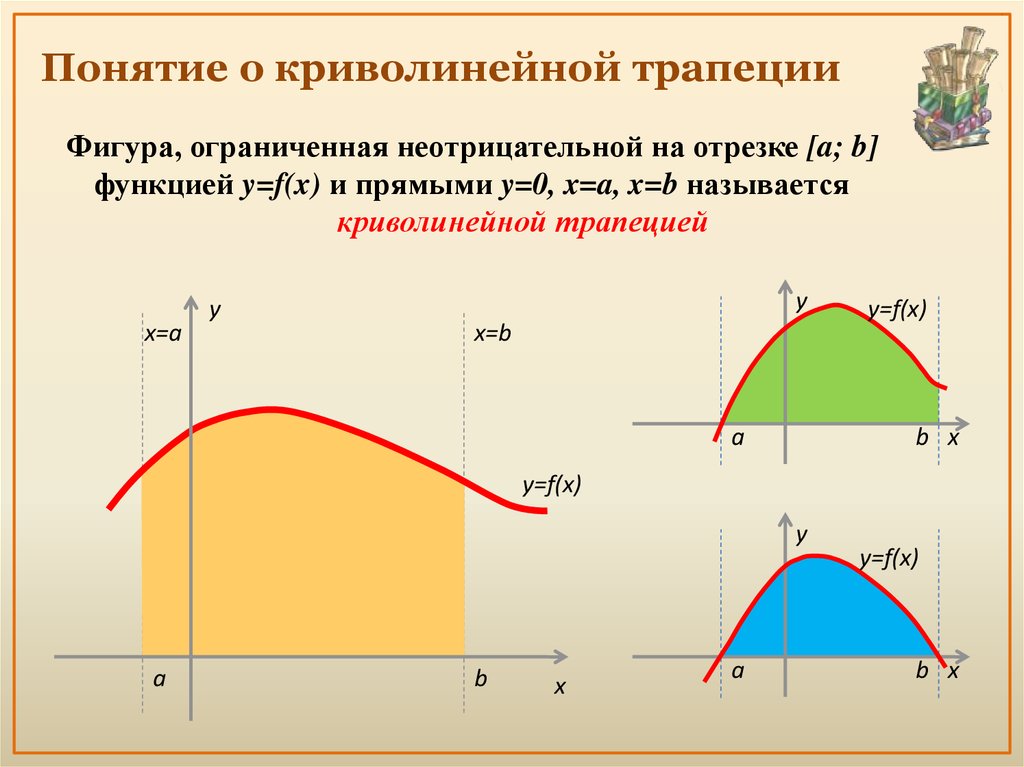
Алгебра2. Понятие о криволинейной трапеции
Фигура, ограниченная неотрицательной на отрезке [a; b]функцией y=f(x) и прямыми y=0, x=a, x=b называется
криволинейной трапецией
x=a
y
y
x=b
a
y=f(x)
b x
y=f(x)
y
a
b
x
a
y=f(x)
b x
3. Задачи, приводящие к понятию определённого интеграла
Решение различных задач привелок одной и той же математической модели:
Для функции y=f(x) на отрезке [a;b]:
1.Разбить отрезок [a;b] на n равных частей
2.Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xn
3.Вычислить предел этой суммы при n→∞
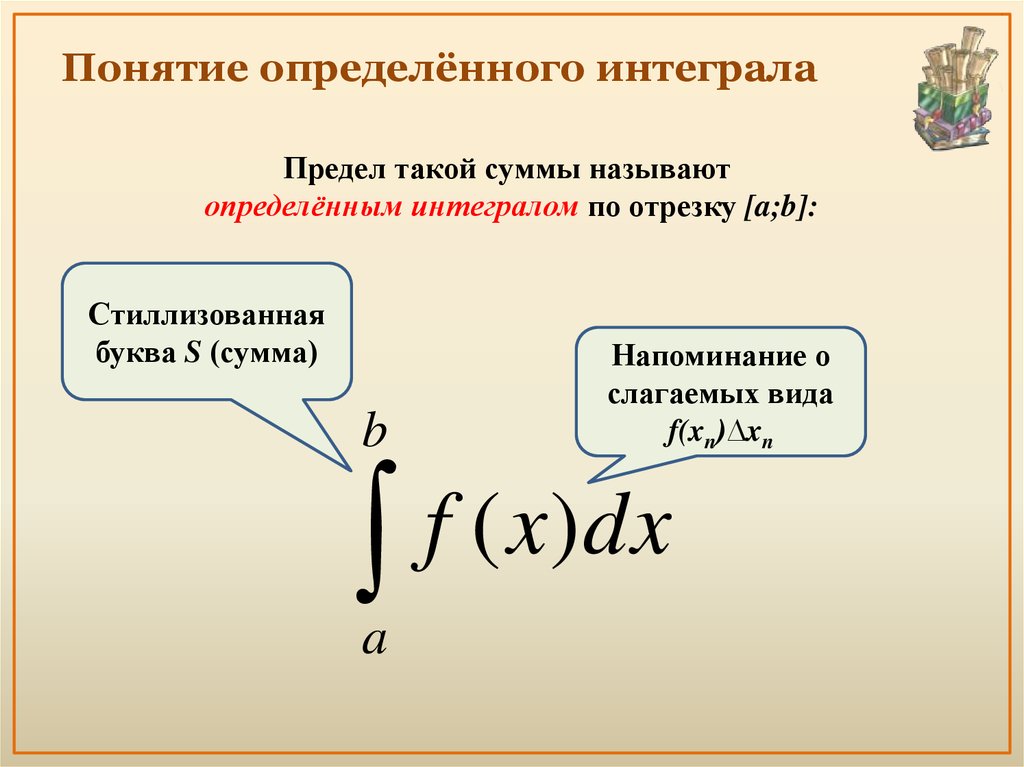
4. Понятие определённого интеграла
Предел такой суммы называютопределённым интегралом по отрезку [a;b]:
Стиллизованная
буква S (сумма)
b
a
Напоминание о
слагаемых вида
f(xn)∆xn
f ( x)dx
5. Геометрический и физический смысл определённого интеграла
Вернёмся к трём рассмотренным задачам:Геометрический смысл интеграла: S a f ( x)dx
b
Физический смысл интеграла:
s v(t )dt
b
a
m p ( x)dx
b
a
6. Формула Ньютона-Лейбница
bf ( x)dx F (b) F (a ),
a
где F(x) – первообразная
для функции f(x)
Исаак Ньютон
1642-1727
b
b
Или
a
f ( x)dx F ( x)
a
Готфрид Лейбниц
1646-1716
7. Вычисление определённого интеграла
Вычислить интеграл:2
2
2
2
2 Формула
Постоянный
множитель
Ньютона-Лейбница:
dx можно
от
суммы
функций
равен
3 вынести
( 2 Интеграл
3x3 1за
)dx
2
3
x
dx
dx
2
знак
интеграла
сумме интегралов
x
x
1
1
2
1
4 2
1
4
2
1
x
2 3x
2
b 2( ) 3
x b1 ( b x)
xf ( x1 b)dx4 1F ( x) b Fx (b)4 F (a )1
( f ( x) gkf( x( x)))dx k f (fx()xdx
)dx g ( x)dx
a
3 a aa
1 a
a
a
( 1 12 2) (2 1) 11
4
4
1
Ответ : 11
4
b
b
8. Примеры вычисления определённых интегралов
13
21.4б
2dx
10 3 x
2
21.8в
x
2
sin
3 dx
2
4
21.16а
0 , 5 х 1
е
dx
0
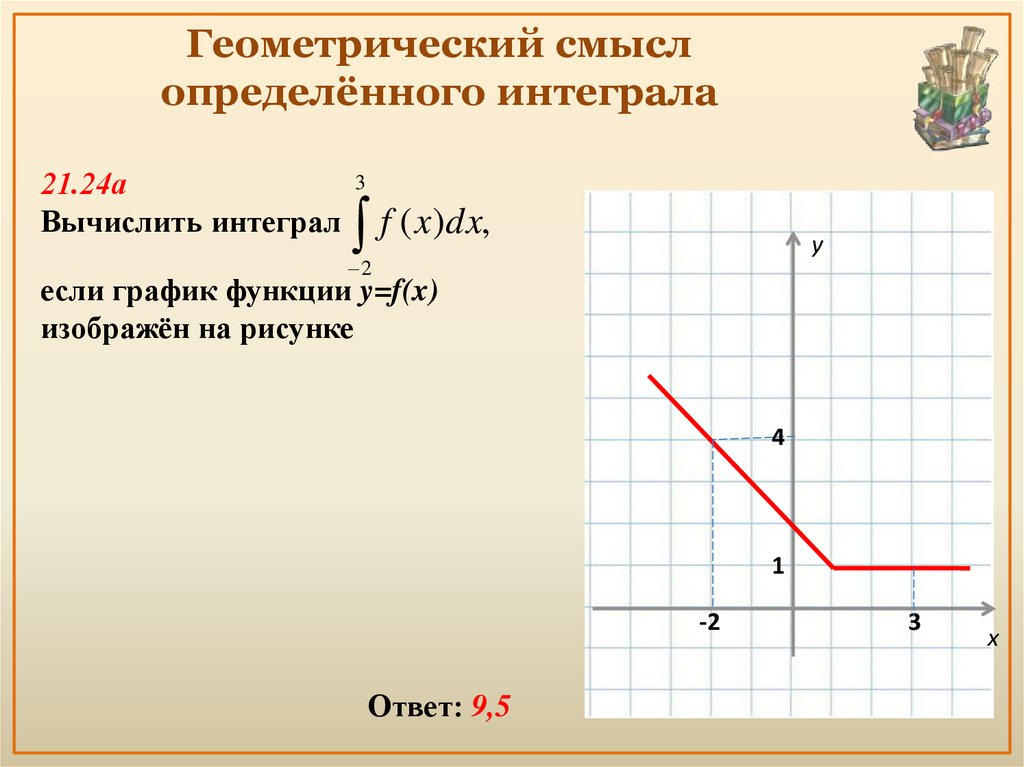
9. Геометрический смысл определённого интеграла
21.24аВычислить интеграл
3
f ( x)dx,
y
2
если график функции y=f(x)
изображён на рисунке
4
1
-2
Ответ: 9,5
3
x
10. Физический смысл определённого интеграла
21.40а Материальная точка движется по прямой со скоростью,определяемой формулой v = 3t2-4t+1, (время измеряется в
секундах, скорость – в cантиметрах в секунду).
Какой путь пройдёт точка за 3 секунды,
считая от начала движения (t=0)?
Ответ: 12см
11. Физический смысл определённого интеграл
21.42а Дан прямолинейный неоднородный стержень [0;6], егоплотность в точке х определяется по формуле р(х) = х2+х+1.
Найдите массу стержня.
Ответ: 96
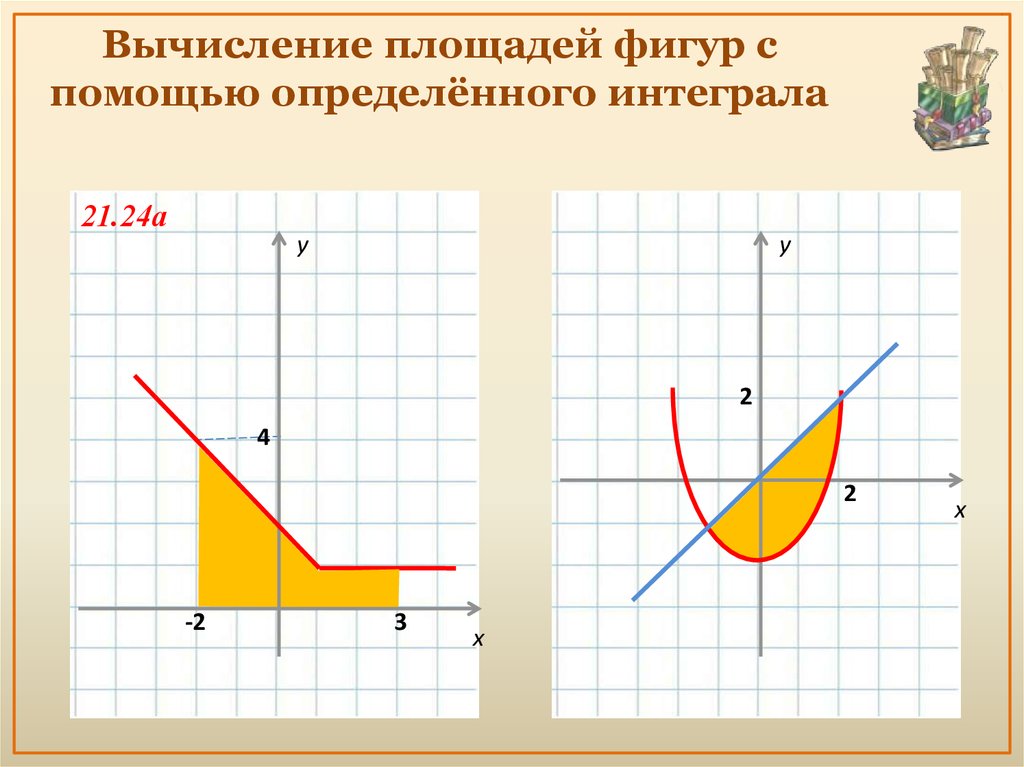
12. Вычисление площадей фигур с помощью определённого интеграла
21.24аy
y
2
4
2
-2
3
x
x
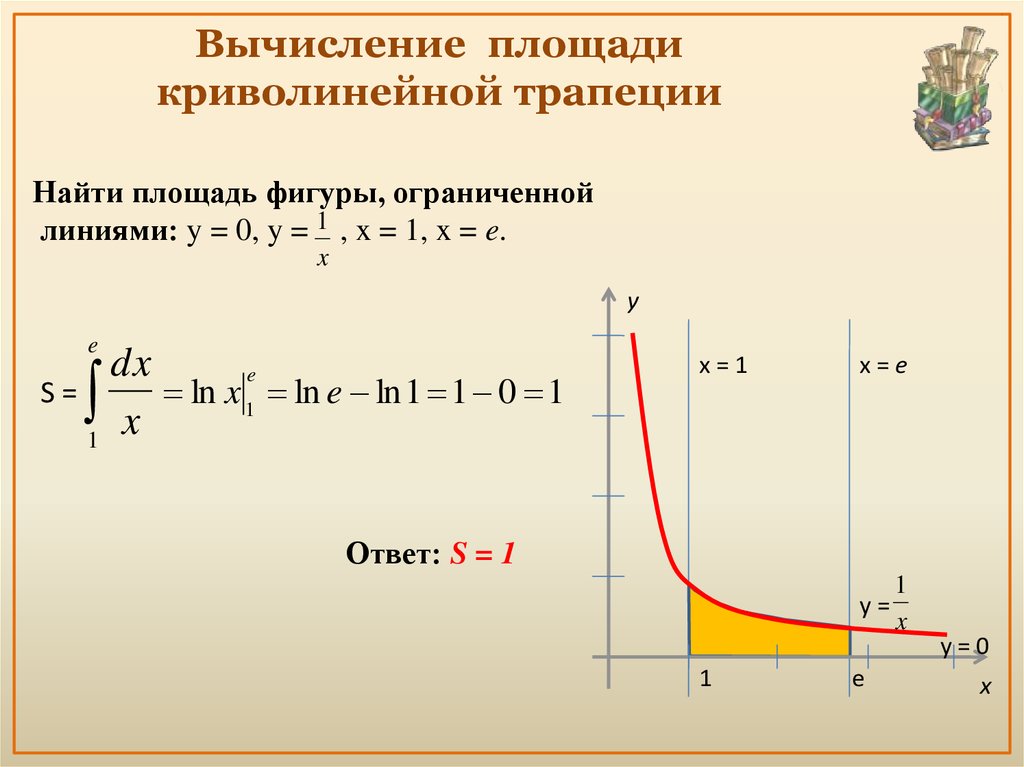
13. Вычисление площади криволинейной трапеции
Найти площадь фигуры, ограниченнойлиниями: y = 0, y = 1 , x = 1, x = e.
x
y
e
dx
e
S=
ln x 1 ln e ln 1 1 0 1
x
1
x=1
x=e
Ответ: S = 1
y=
1
e
1
x
y=0
x
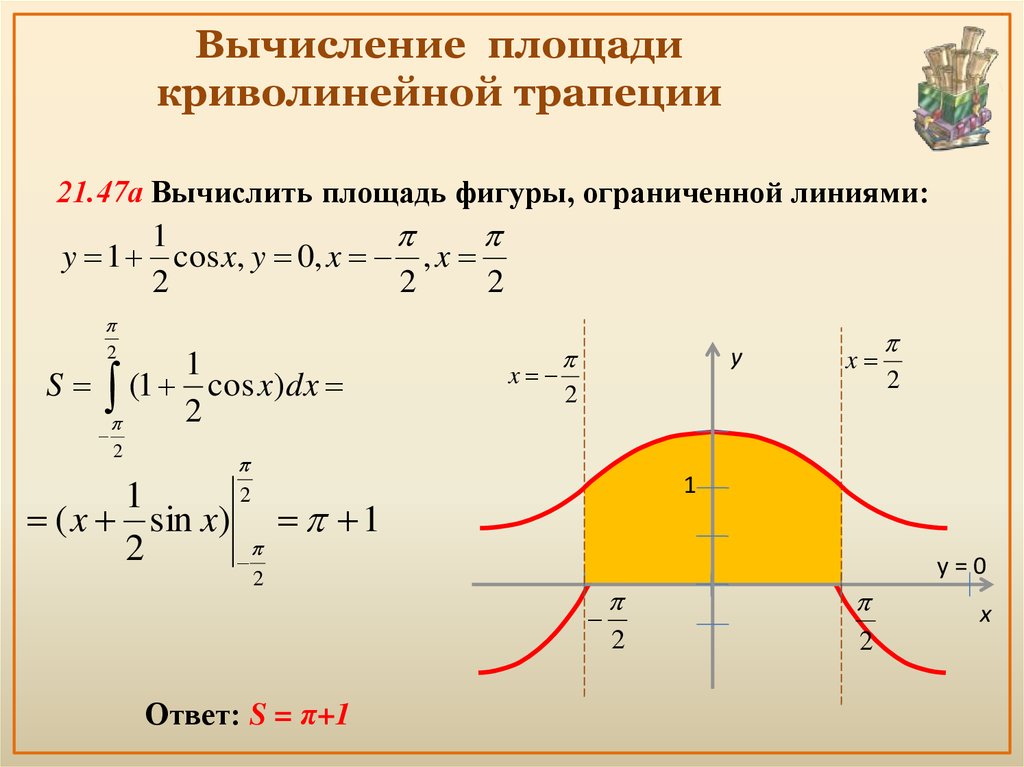
14. Вычисление площади криволинейной трапеции
21.47а Вычислить площадь фигуры, ограниченной линиями:1
y 1 cos x, y 0, x , x
2
2
2
2
1
S (1 cos x)dx
2
2
x
y
2
2
1
2
1
( x sin x) 1
2
y=0
2
Ответ: S = π+1
x
2
2
x
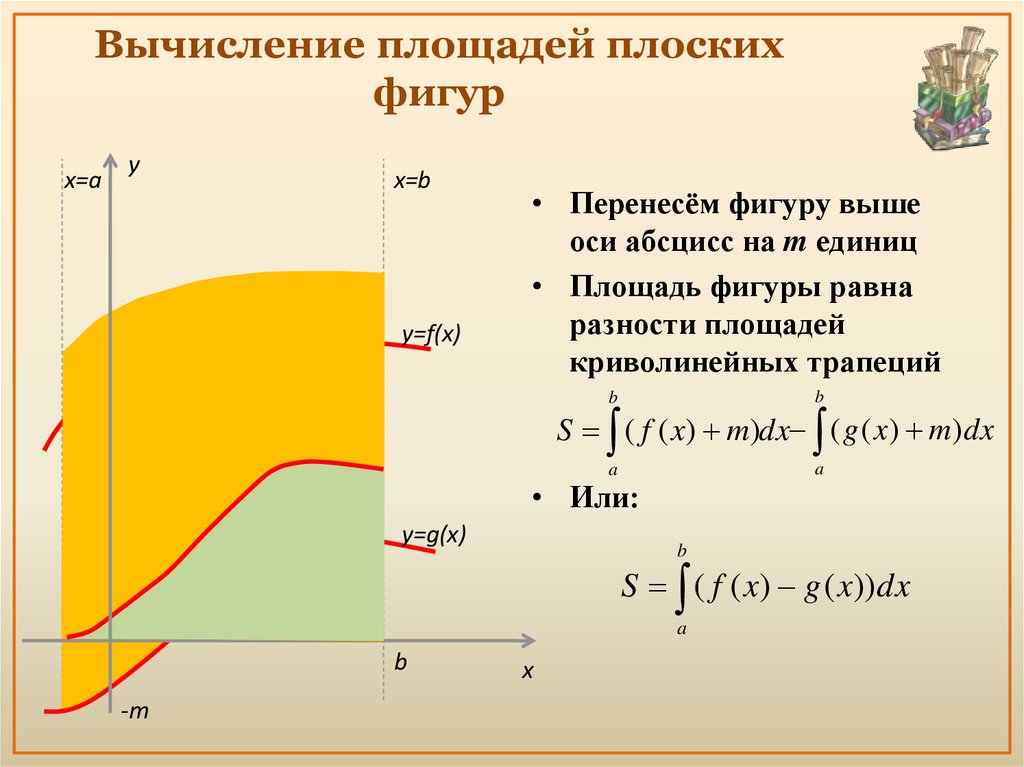
15. Вычисление площадей плоских фигур
x=ay
x=b
y=f(x)
• Перенесём фигуру выше
оси абсцисс на m единиц
• Площадь фигуры равна
разности площадей
криволинейных трапеций
b
b
a
a
S ( f ( x) m)dx ( g ( x) m)dx
• Или:
y=g(x)
b
S ( f ( x) g ( x)) dx
a
a
b
-m
x
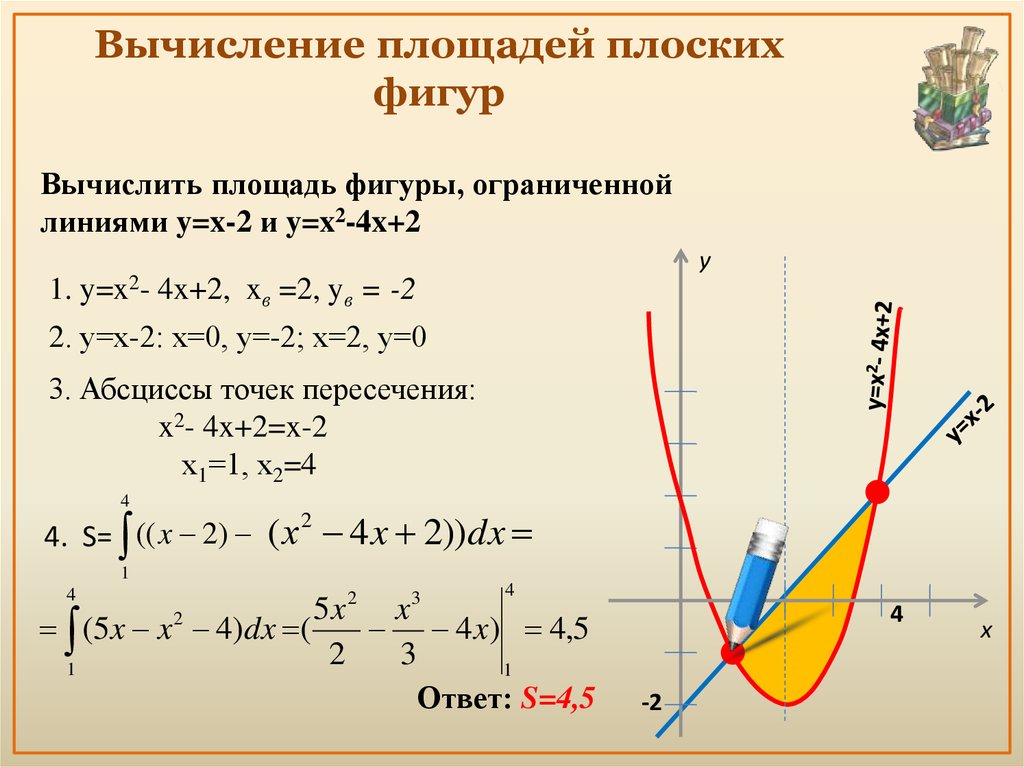
16. Вычисление площадей плоских фигур
Вычислить площадь фигуры, ограниченнойлиниями y=x-2 и y=x2-4x+2
y
1.
y=x2-
4x+2, xв =2, yв = -2
2. у=х-2: х=0, у=-2; х=2, у=0
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4
4. S= ((x 2) ( х 4 x 2))dx
2
1
4
2
3
4
5x
x
(5 x x 4)dx (
4 x) 4,5
2
3
1
1
Ответ: S=4,5
1
2
-2
4
x
17. Рефлексия
• Криволинейная трапеция• Формула Ньютона-Лейбница
• Геометрический и физический смысл определённого
интеграла
• Формула для вычисления площади фигуры, ограниченной
графиками y = f(x) и y = g(x)
18.
Формула Ньютона-Лейбница19.
Формула Ньютона-ЛейбницаНьютон открыл новый метод раньше, но
опубликовал его позже Лейбница, написав ему:
«Надеюсь, что я при этом не написал ничего,
что было бы тебе неприятно, если же это
случилось, то прошу сообщить, потому что
друзья мне дороже математических открытий»
Лейбниц ответил в резкой форме. Распря двух
гениев дорого обошлась науке: английская
математическая школа увяла на целый век,
а европейская проигнорировала многие
выдающиеся идеи Ньютона.
Спор тянулся почти 40 лет, пока аббат Конти не
сообщил Ньютону: «Лейбниц умер – диспут окончен»
20. Структура презентации
Титульный слайдСведе
ния об
авторе
Источ
ники
Струк
тура
презен
тации
Задачи, приводящие к понятию определённого
интеграла
Понятие определённого
интеграла
Смысл определённого
интеграла
Задача
1
Задача
2
Формула Ньютона –
- Лейбница
Вычис
ления
интегр
.ала
Приме
ры
Допол
нитель
ная
инфор
мация
Вычисление
площадей
фигур
S
трапец
ии
S
фигур
ы
Приме
р
Приме
р
Рефле
ксия
Задача
3
Использованная литература
21. Использованные ресурсы
• А.Г. Мордкович, П.В. Семёнов. Алгебра и начала анализа.Учебник (профильный уровень)
• А.Г. Мордкович, Л.О. Денищева и др. Алгебра и начала анализа.
Задачник (профильный уровень)
• Картинка "книги“
• Материал Википедии Лейбниц Ньютон
• Рисунок карандаш
• Значок Информация
• Видео Величайший из учёных – Исаак Ньютон












 mathematics
mathematics








