Геометрический смысл определённого интеграла

1.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
a
∫f(x)dx
y
b
a
0
b
x

2.

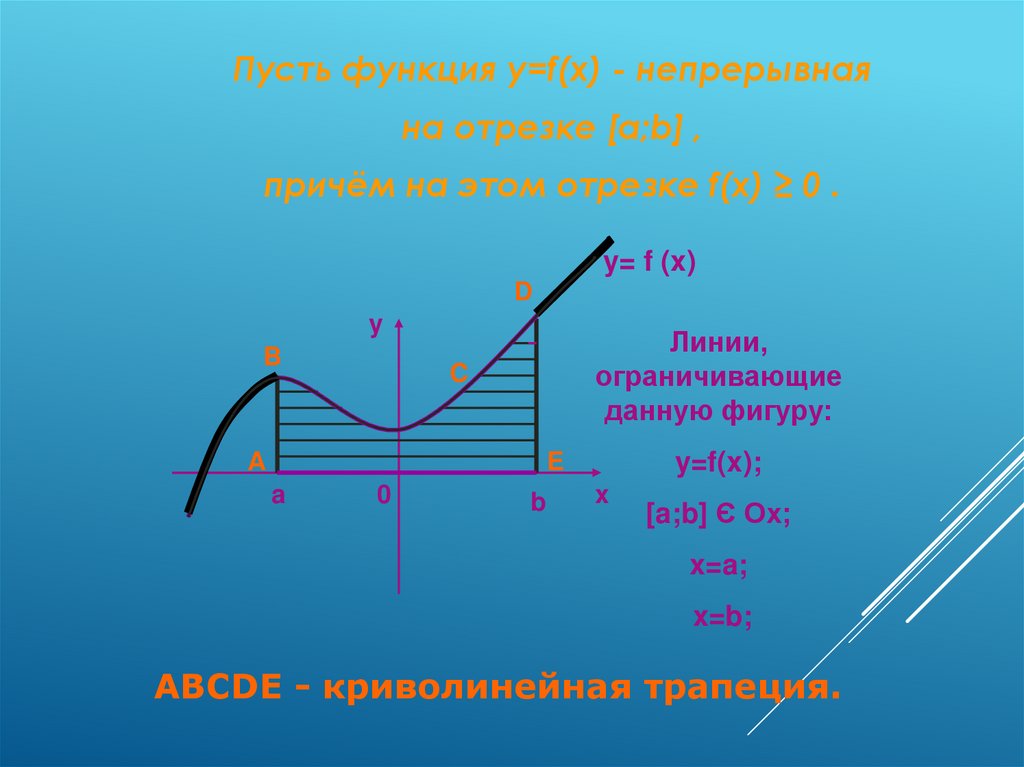
Пусть функция y=f(x) - непрерывная
на отрезке [a;b] ,
причём на этом отрезке f(x) ≥ 0 .
y= f (x)
D
y
B
Линии,
ограничивающие
данную фигуру:
C
A
y=f(x);
E
a
0
b
x
[a;b] Є Ох;
x=a;
x=b;
ABCDE - криволинейная трапеция.

3.

2.Площадь криволинейной трапеции.
SABCDE =?
y
SABCDE ≈ S1 S2
D
+
B
C
Sn
S2
A S1
y=f(x)
a
Если
SABCDE
E
0
b
n
+…+
Sn
∞, тогда
Σ
Sn.
x
ΣSn - интегральные суммы.
b
limΣSn =∫f(x)dx
n
∞
a
b
∫f(x)dx = SABCDE
a

4.

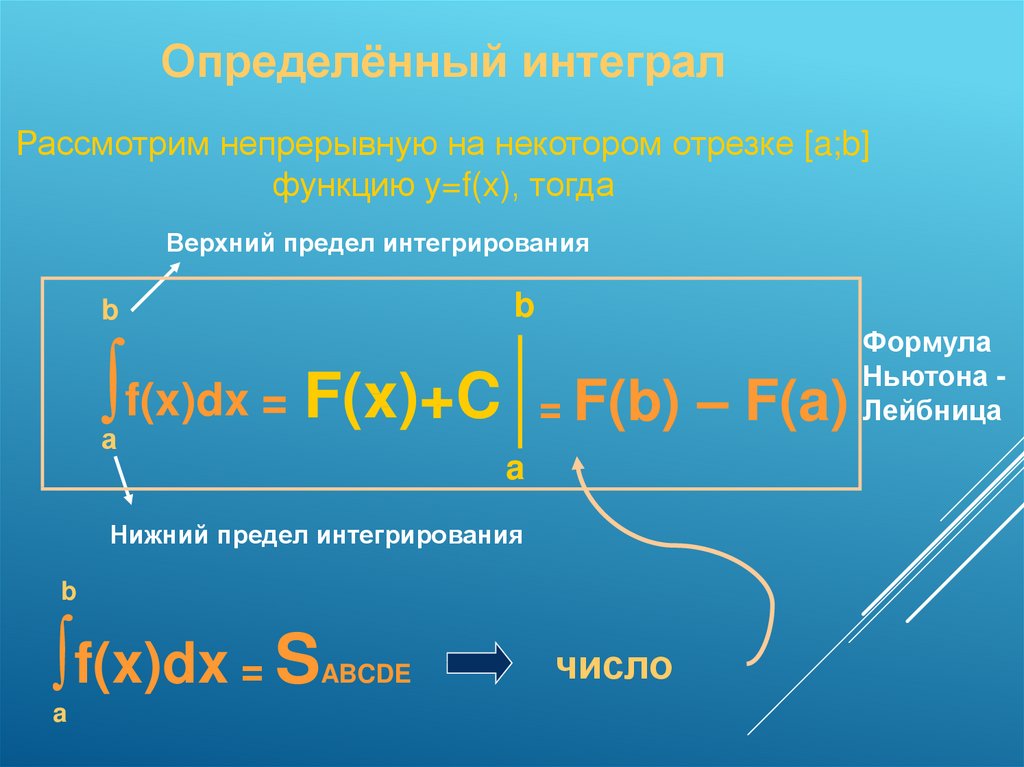
Определённый интеграл
Рассмотрим непрерывную на некотором отрезке [a;b]
функцию y=f(x), тогда
Верхний предел интегрирования
b
b
∫f(x)dx = F(x)+C
а
= F(b)
a
Нижний предел интегрирования
b
∫f(x)dx = S
a
ABCDE
число
– F(a)
Формула
Ньютона Лейбница

5.

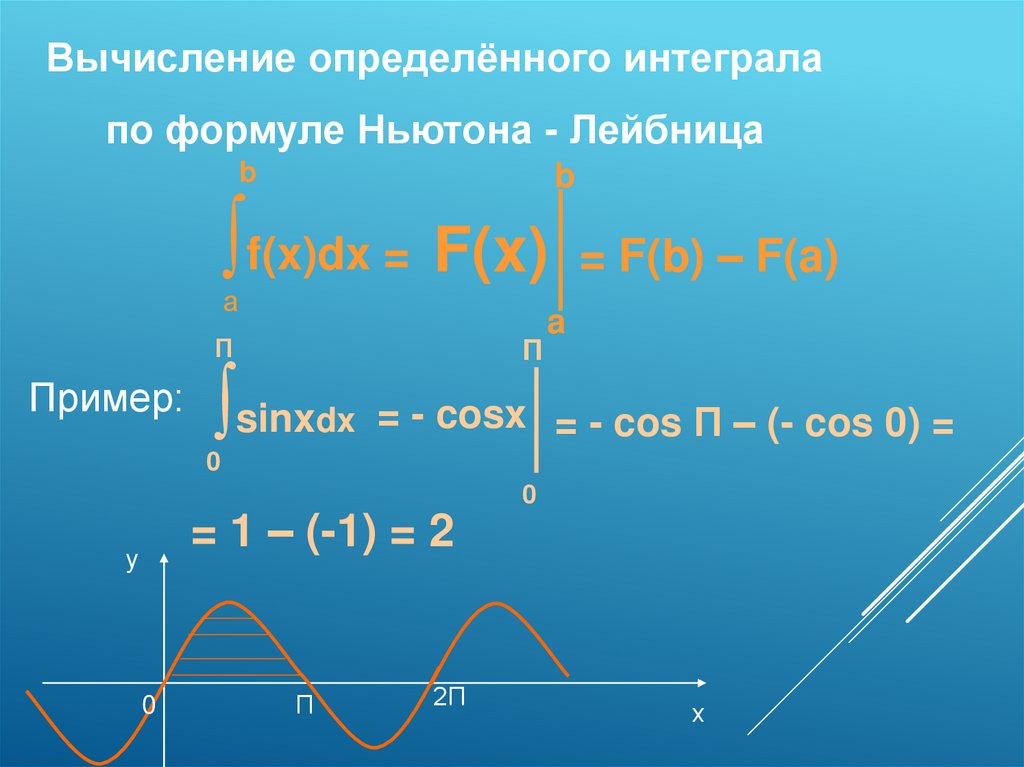
Вычисление определённого интеграла
по формуле Ньютона - Лейбница
b
∫f(x)dx = F(x)
а
П
Пример:
П
∫sinxdx = - cosx
b
= F(b) – F(a)
a
= - cos П – (- cos 0) =
0
= 1 – (-1) = 2
у
0
П
2П
0
х

6.

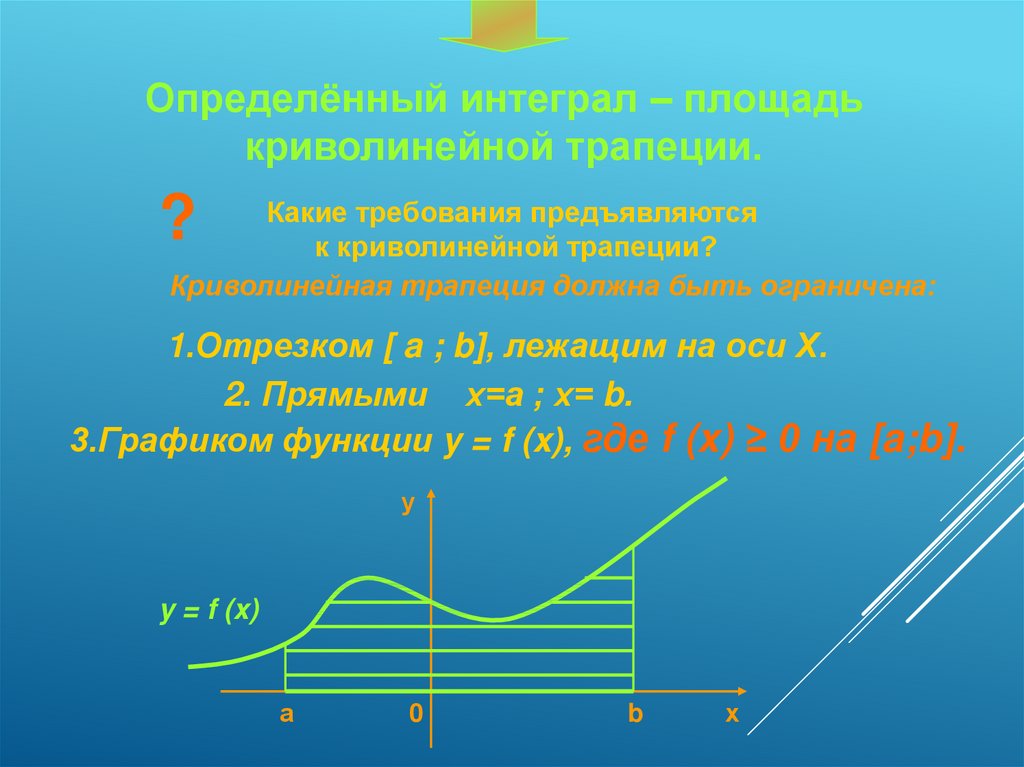
Определённый интеграл – площадь
криволинейной трапеции.
?
Какие требования предъявляются
к криволинейной трапеции?
Криволинейная трапеция должна быть ограничена:
1.Отрезком [ a ; b], лежащим на оси Х.
2. Прямыми х=а ; х= b.
3.Графиком функции y = f (x), где f (x) ≥ 0 на [a;b].
у
y = f (x)
а
0
b
х

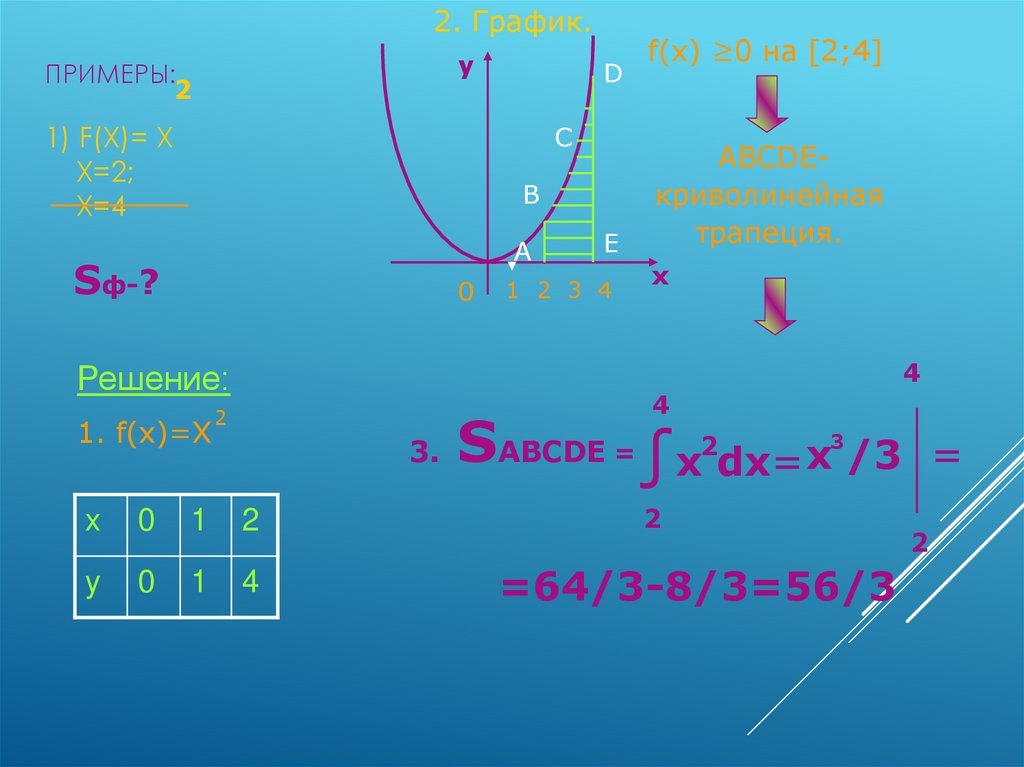
7. Примеры: 1) f(x)= x x=2; x=4

2. График.
y
ПРИМЕРЫ:
2
1) F(X)= X
X=2;
X=4
D
C
B
A
Sф-?
0
1 2 3 4
ABCDEкриволинейная
трапеция.
x
4
Решение:
1. f(x)=X
E
f(x) ≥0 на [2;4]
4
2
3.
x
0
1
2
y
0
1
4
SABCDE =∫x2dx= x /3
=
3
2
=64/3-8/3=56/3
2

8.

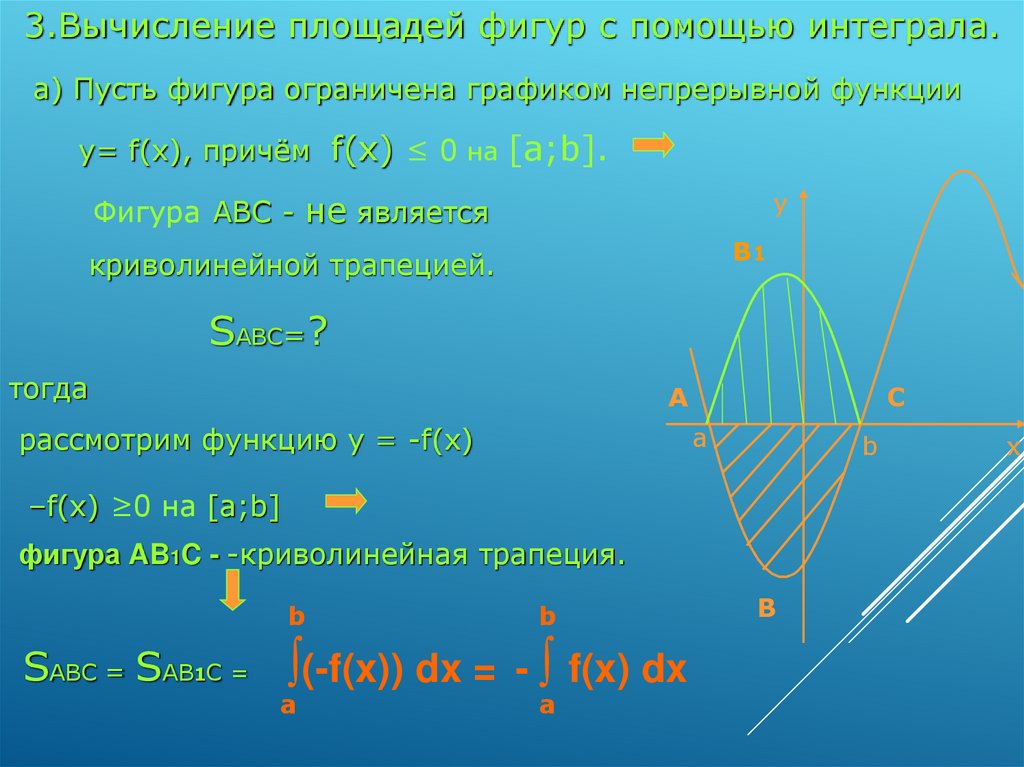
3.Вычисление площадей фигур с помощью интеграла.
а) Пусть фигура ограничена графиком непрерывной функции
y= f(x), причём f(x) ≤ 0 на [a;b].
y
Фигура ABC - не является
B1
криволинейной трапецией.
SABC=?
тогда
A
C
a
рассмотрим функцию y = -f(x)
b
–f(x) ≥0 на [a;b]
фигура AB1C - -криволинейная трапеция.
b
SABC = SAB1C =
b
∫(-f(x)) dx = - ∫ f(x) dx
a
a
B
x

9.

Задачи по готовым чертежам:
2. График.
Дано:
f(x)=-√x
x=0
x=4
Sф-?
f(x) ≤ 0 на [0;4]
0
1
4
y
0
-1 -2
0
x
B
4
S OABC= - ∫(-√x)dx =
4
x
1 2 3 4
A
Решение:
1. f (x)=-√x
y
=
∫√x dx
0
4
= 3x √x /2 =
0
=3* 4√4/2 – 0 = 12
0

10.

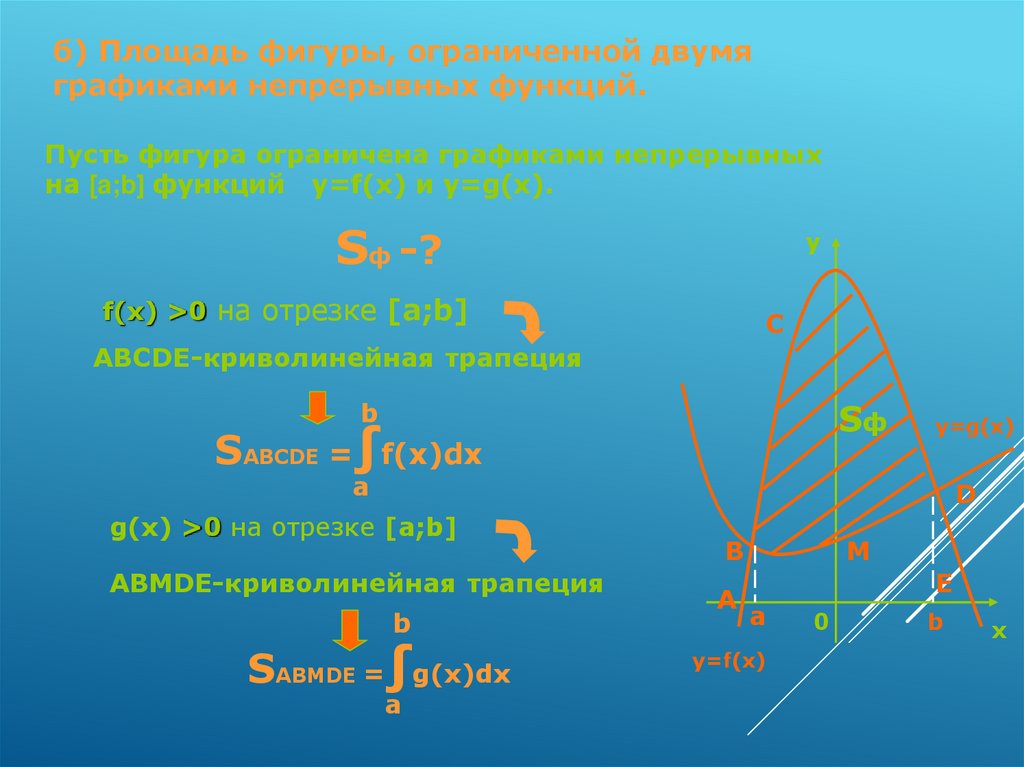
б) Площадь фигуры, ограниченной двумя
графиками непрерывных функций.
Пусть фигура ограничена графиками непрерывных
на [a;b] функций y=f(x) и y=g(x).
Sф -?
y
f(x) >0 на отрезке [a;b]
C
ABCDE-криволинейная трапеция
Sф
b
SABCDE =∫f(x)dx
y=g(x)
a
D
g(x) >0 на отрезке [a;b]
ABМDE-криволинейная трапеция
b
SABMDE =∫g(x)dx
a
B
A
М
E
a
y=f(x)
0
b
x

11.

b
b
SABMDE =∫g(x)dx
SABCDE =∫f(x)dx
Sф -?
a
Sф= SABCDE
-
a
SABMDE
y
b
b
Sф =∫f (x)dx -∫g (x)dx=
a
C
y=g(x)
Sф
a
b
=
∫(f (x)- g (x))dx,
a
где f(x) ≥ g(x) на отрезке [a;b]
D
B
A
М
a
y=f(x)
E
0
b
x

12.

Разбор решения задачи по алгоритму.
Дано:
y
y=f(x)
f(x) = (x – 2)²;
g(x)= - (х-2)² + 2 ;
S
S ф -?
Решение:
0
1
1. Фигура ограничена графиками
двух непрерывных функций.
3
x
y=g(x)
2. Найдём пределы интегрирования:
- (x – 2)² + 2 = (х-2)² ;
Х1 = 1;
Х2 = 3.
3. Найдём площадь полученной фигуры S: 3
Т.к. на [1;3]
3
g(x) ≥ f(x), то
Sф = ∫ (g(x) - f(x)) dx=
1
3
=∫(- (х-2)²+2-(x – 2)²)dx= ∫(-2x²+8x-6) dx=
1
1
(-
2X³
3 + 4x² - 6x
)=
1
2
2
3

13.

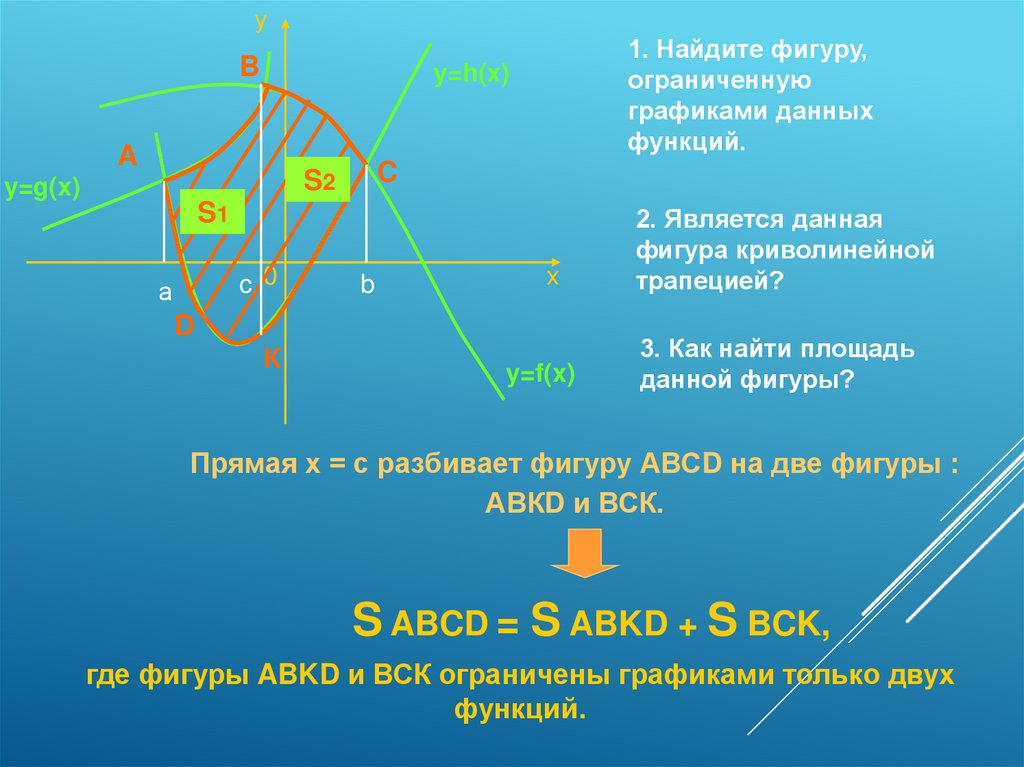
у
B
1. Найдите фигуру,
ограниченную
графиками данных
функций.
y=h(x)
A
C
S2
y=g(x)
S1
c 0
а
b
х
D
К
y=f(x)
2. Является данная
фигура криволинейной
трапецией?
3. Как найти площадь
данной фигуры?
Прямая х = с разбивает фигуру АВСD на две фигуры :
АВКD и ВСК.
S ABCD = S ABKD + S BCK,
где фигуры ABKD и ВСК ограничены графиками только двух
функций.

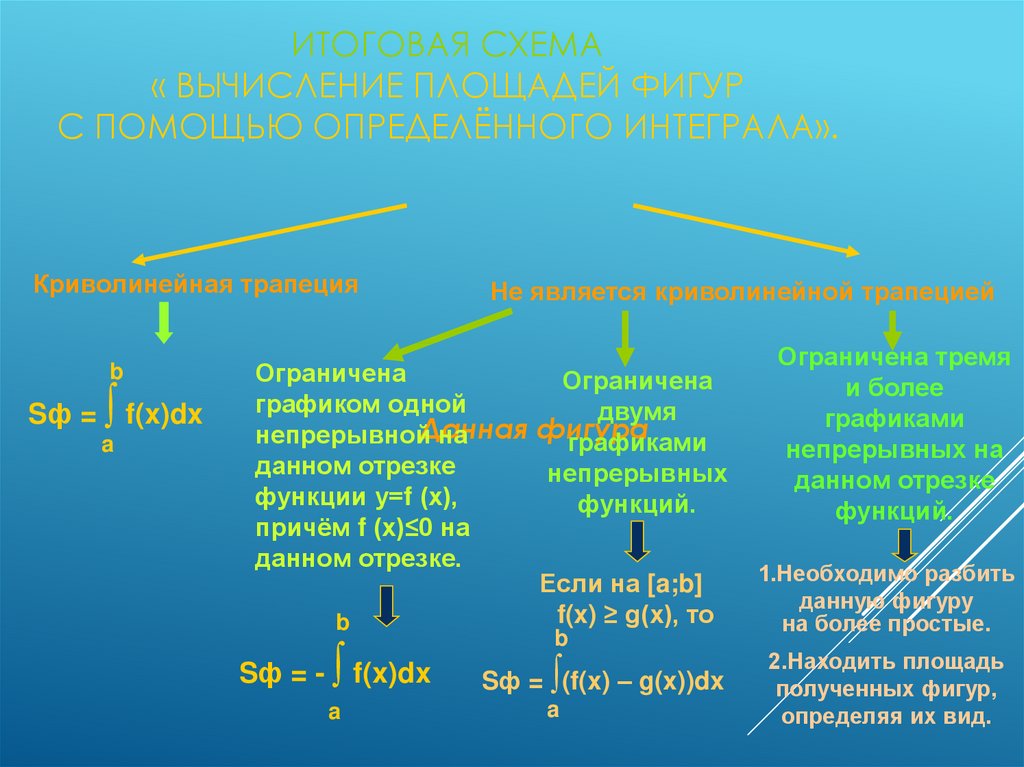
14. Итоговая схема « Вычисление площадей фигур с помощью определённого интеграла».

ИТОГОВАЯ СХЕМА
« ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР
С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА».
Криволинейная трапеция
b
Sф = ∫ f(x)dx
a
Не является криволинейной трапецией
Ограничена
Ограничена
графиком одной
двумя
фигура
непрерывнойДанная
на
графиками
данном отрезке
непрерывных
функции у=f (х),
функций.
причём f (х)≤0 на
данном отрезке.
Если на [a;b]
f(x) ≥ g(x), то
b
Sф = - ∫ f(x)dx
a
b
Sф = ∫(f(x) – g(x))dx
a
Ограничена тремя
и более
графиками
непрерывных на
данном отрезке
функций.
1.Необходимо разбить
данную фигуру
на более простые.
2.Находить площадь
полученных фигур,
определяя их вид.

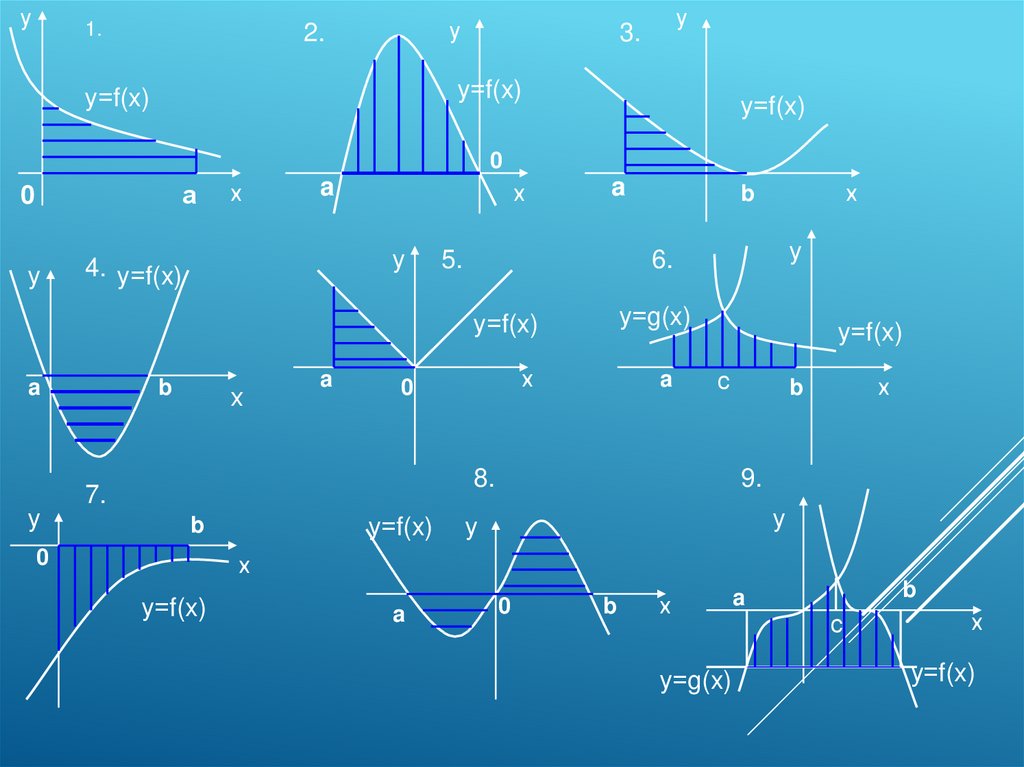
15.

Самостоятельная работа
На предложенных далее рисунках изображены
различные фигуры.
1. Выберете из них те, на которых изображены
криволинейные трапеции (запишите их номера)
2. Запишите формулы для вычисления площадей этих
криволинейных трапеций.
3. Определите способы вычисления площадей всех
оставшихся фигур.

16.

у
1.
у
2.
у
3.
у=f(x)
у=f(x)
у=f(x)
0
а
0
у
х
a
х
у
4. у=f(x)
a
5.
у
b
х
a
у
6.
у=g(x)
у=f(x)
a
х
0
a
у=f(x)
с
8.
7.
у=f(x)
b
0
х
b
х
b
9.
у
у
х
у=f(x)
a
0
b
х
у=g(x)
a
b
с
х
у=f(x)

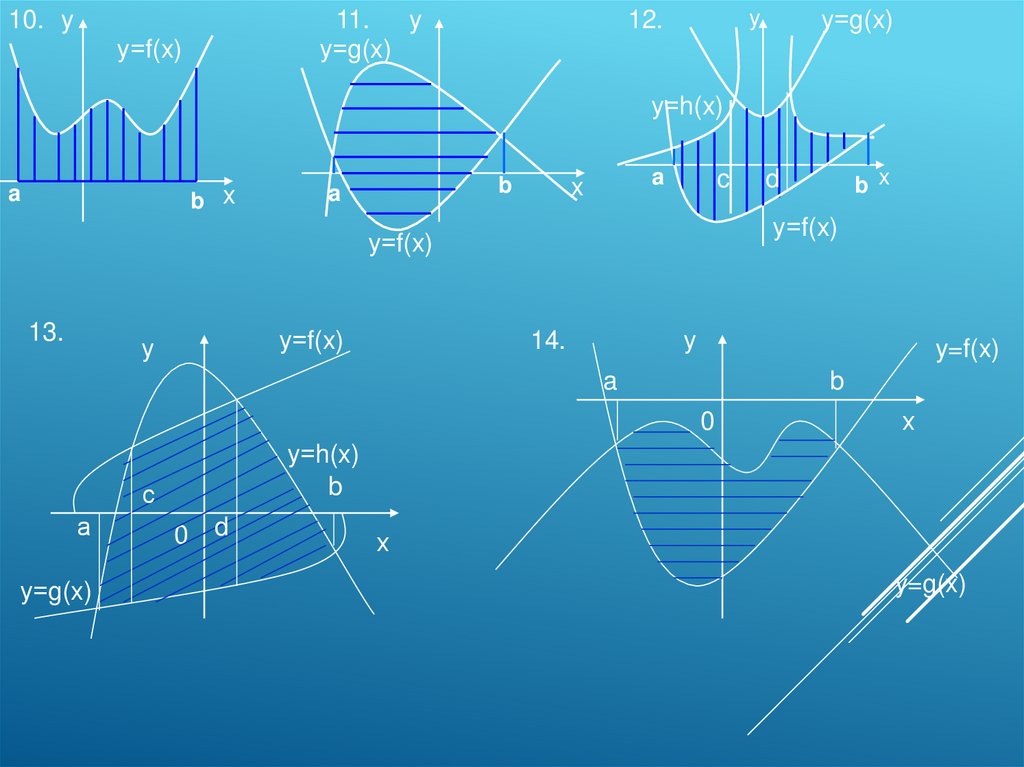
17.

10. y
11.
y
у=g(x)
у=f(x)
у=g(x)
y
12.
у=h(x)
a
b x
b
a
a
x
c
у=f(x)
у=f(x)
13.
у=f(x)
у
у
14.
y=f(x)
a
b
0
у=g(x)
х
у=h(x)
b
с
а
b x
d
0
d
х
y=g(x)