Similar presentations:
Приложение определённого интеграла. Тема 18
1.
2.
Тема 18.Приложение
определенного
инетграла.
3.
Основными геометрическимиприложениями определенного
интеграла являются:
вычисление площади плоской
фигуры, вычисление объемов
тел вращения вокруг осей
координат и вычисление
длины дуги плоской кривой.
4.
Площадь всякой фигуры впрямоугольной системе
координат может быть
составлена из площадей
криволинейных трапеций,
прилегающих к оси Ох
или к оси Оу.
5.
При вычислении площадейплоских фигур с помощью
определённого интеграла мы
ограничимся рассмотрением
только тех фигур, которые
часто встречаются на
практике.
6.
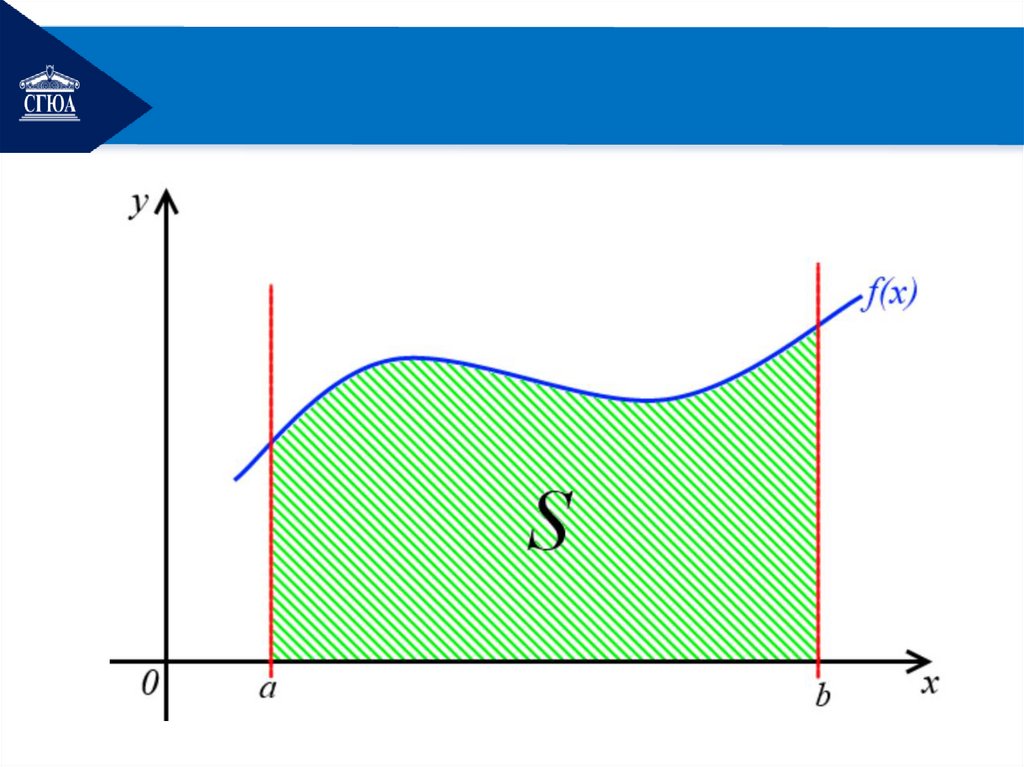
Случай 1. Пустькриволинейная трапеция
ограничена графиком
функции y = f(x) сверху,
осью Ox снизу и двумя
прямыми
x = a и x = b.
7.
8.
Тогда площадь такой фигурывычисляется по формуле
b
S f ( x)dx
a
9.
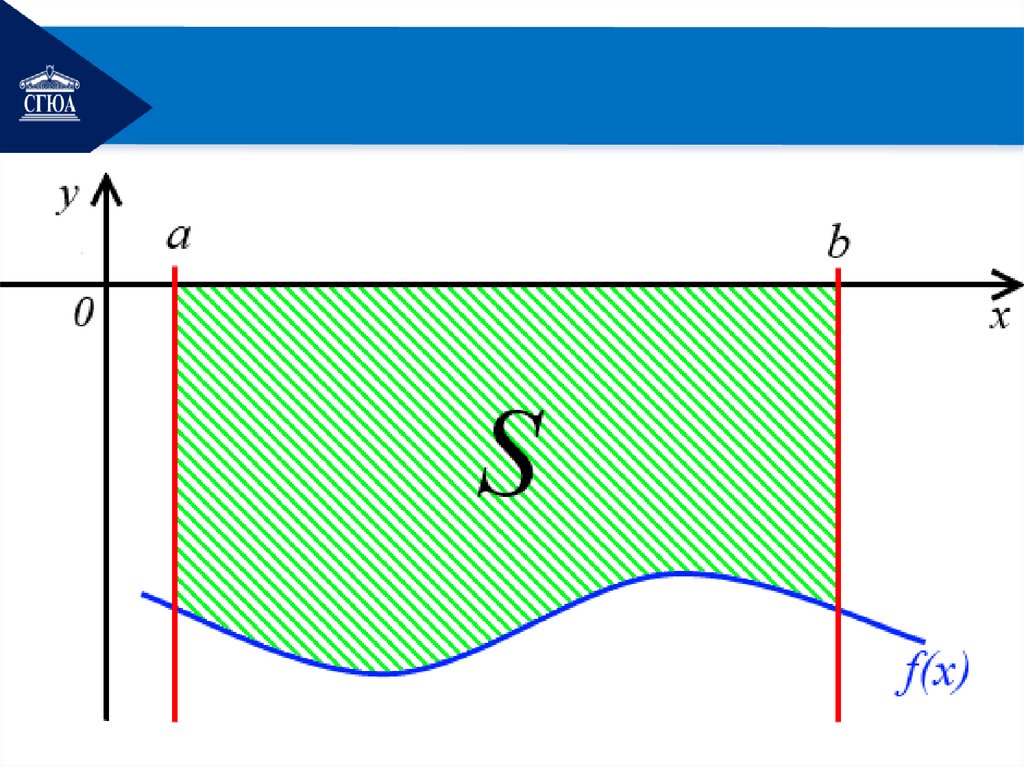
Случай 2. Пустькриволинейная трапеция
ограничена графиком
функции y = f(x) снизу, осью
Ox сверху и двумя прямыми
x = a и x = b.
10.
11.
Тогда площадь такой фигурывычисляется по формуле
b
S f ( x) dx
a
12.
Также можно использоватьформулу
b
S f ( x)dx
a
13.
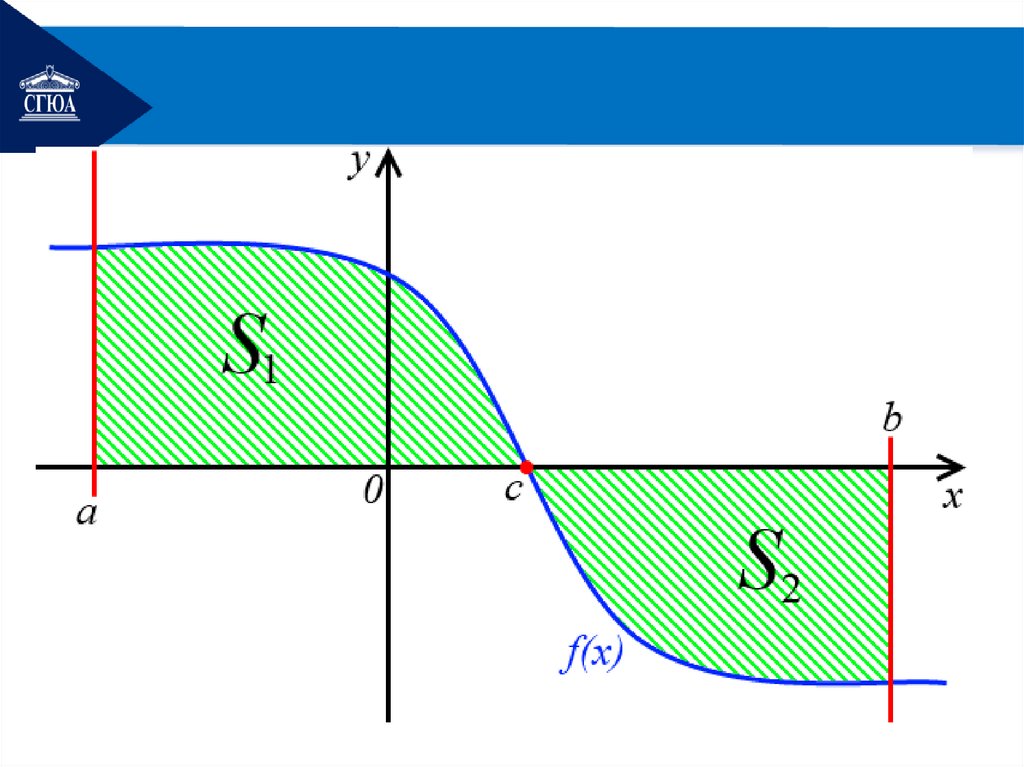
Случай 3. Пустькриволинейная трапеция
ограничена осью Ox,
графиком функции y = f(x),
прямыми x = a и x = b,
расположена по обе стороны
оси Ox.
14.
15.
Тогда площадь такой фигурывычисляется по формуле
с
b
a
c
S f ( x)dx f ( x) dx
16.
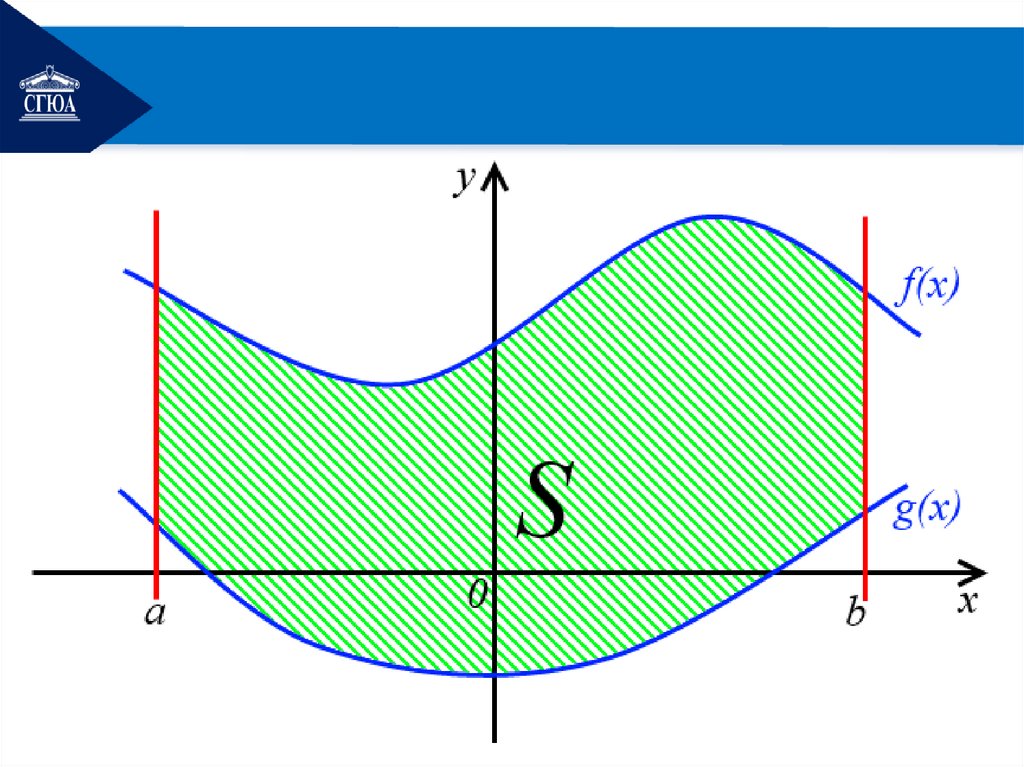
Случай 4. Пустькриволинейная фигура
ограничена двумя
пересекающимися кривыми
y = f(x), y = g(x),
прямыми x = a и x = b,
где
f(x) ≥ g(x).
17.
18.
Тогда площадь такой фигурывычисляется по формуле
b
S f ( x) g ( x) dx
a
19.
Так же используют формулуb
S yв ун dx
верхняя
кривая,
в
нижняя
кривая.
где y
yн
a
20.
График функций строитсяпоточечно, но для параболы
можно составить алгоритм,
который значительно
упростит задачу построения
графика, а затем и
вычисления площади.
21.
Алгоритм построения ивычисления площади искомой
фигуры.
1. Вычислим вершину
параболы O(x; y). Сначала
найдём абсциссу вершины из
условия x= b/2a,
22.
затем находим ординату y,для этого подставляем
найденное x в исходное
уравнение параболы.
2. Построим параболу по
точкам относительно оси
симметрии, то есть
относительно абсциссы
вершины.
23.
Если кроме параболы заданапрямая
y=kx+b,
то её нужно построить по двум
точкам. Если кроме параболы
задана ещё одна парабола, то
её строят аналогично по
алгоритму.
24.
3. Найдём абсциссы точекпересечения параболы и
прямой(параболы и
параболы), для этого решим
уравнение
y = y.
25.
4. Смотрим к какому случаюотносится искомая фигура.
Применяем данную формулу и
вычисляем интеграл.
26.
Примеры.1. Вычислить площадь
фигуры, ограниченной
линиями
y x 2; y 0;
x 2; x 1.
2
27.
2. Вычислить площадьфигуры, ограниченной
линиями
y x 1; y 0;
x 1; x 1.
2
28.
3. Вычислить площадьфигуры, ограниченной
линиями
y x ; y 0;
x 1; x 2.
3
29.
4. Вычислить площадьфигуры, ограниченной
линиями
y x 1;
y 2 x 2;
2






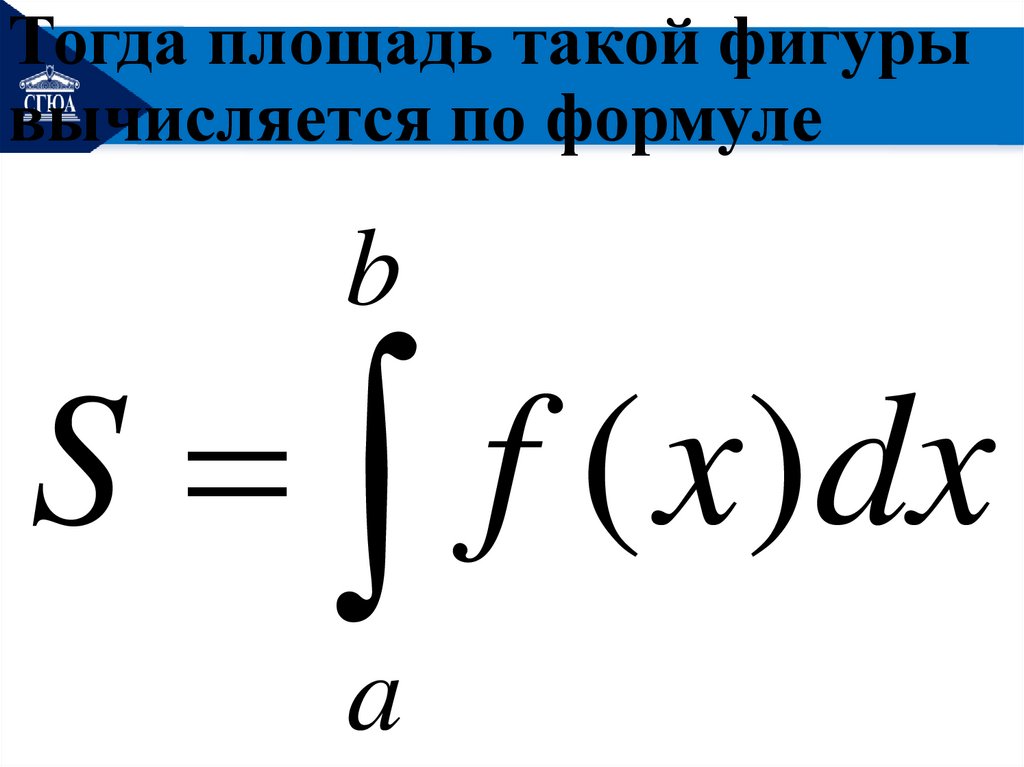

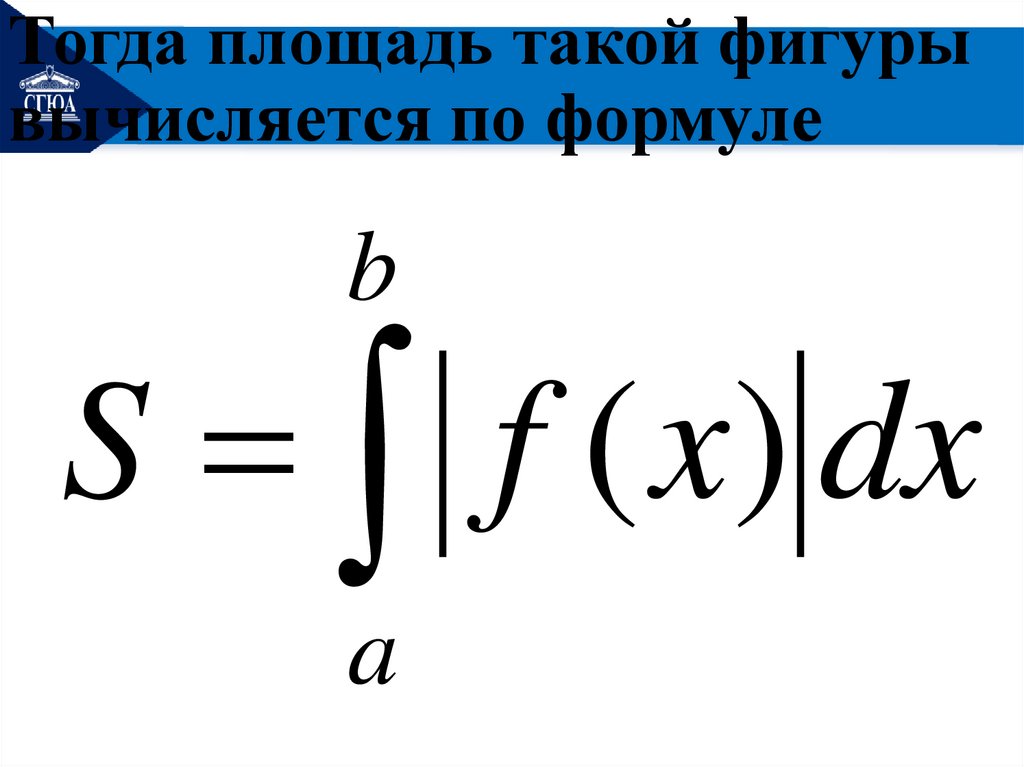
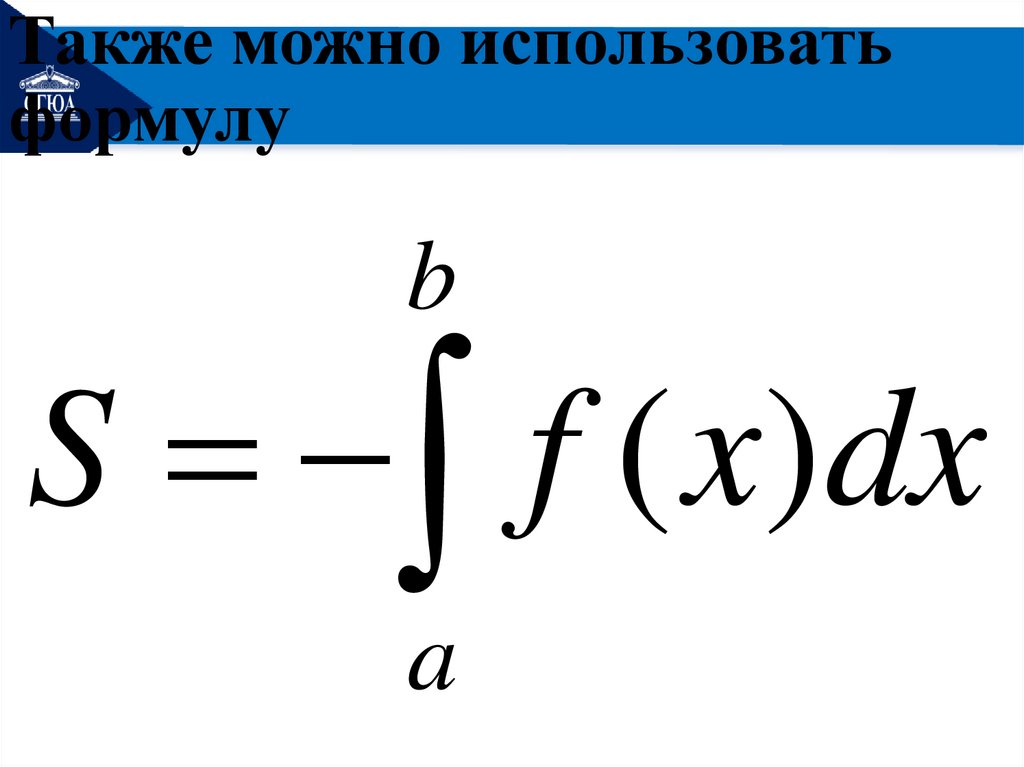
















 mathematics
mathematics








