Similar presentations:
Эконометрика-II. Оценивание SVAR в EViews 6
1. Эконометрика-II
Лекция 62. Оценивание SVAR в EViews 6
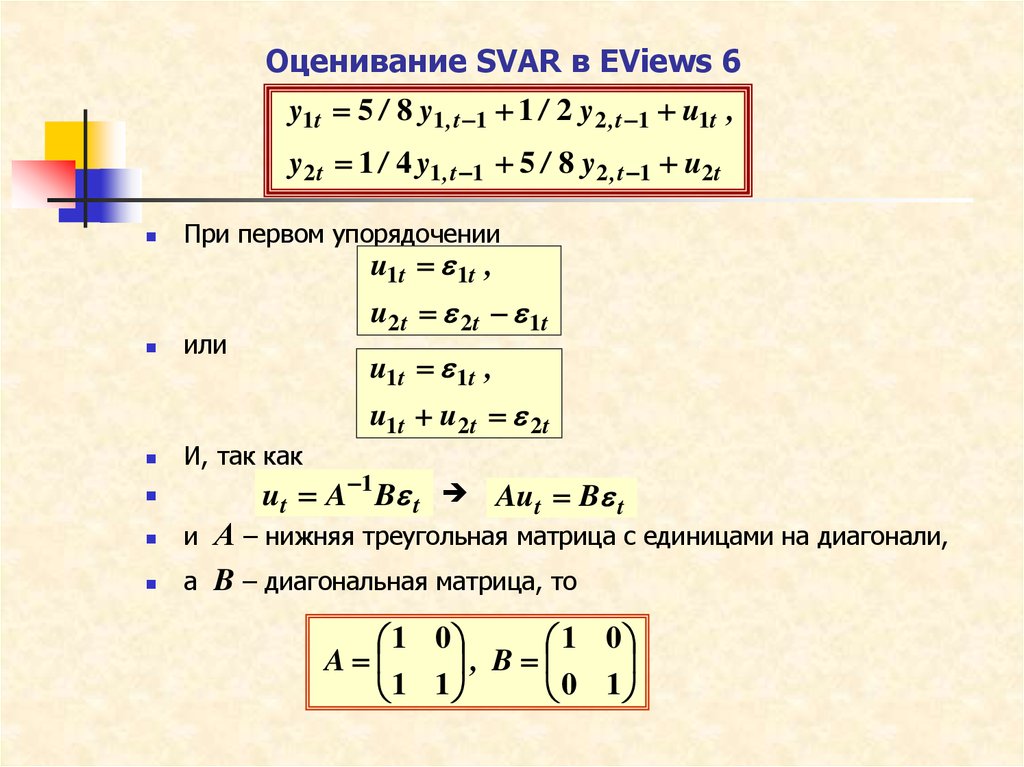
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 u1t ,y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 u2 t
При первом упорядочении
u1t 1t ,
u2 t 2 t 1t
или
u1t 1t ,
u1t u2 t 2 t
И, так как
ut A 1 B t Aut B t
А – нижняя треугольная матрица с единицами на диагонали,
а B – диагональная матрица, то
и
1 0
1 0
A
, B
1 1
0 1
3.
1 01 0
A
, B
1 1
0 1
Таким образом, при первом упорядочении SVAR (структурная
VAR) принимает вид:
1 0 y1t 1 0 5 8 1 2 y1 ,t 1 1t
1 1 y2 t 1 1 1 4 5 8 y2 ,t 1 2 t
5 8 1 2 y1 ,t 1 1t
7 8 9 8 y2 ,t 1 2 t
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,
y1t y 2 t 7 / 8 y1 , t 1 9 / 8 y 2 , t 1 2 t
4.
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,y1t y 2 t 7 / 8 y1 , t 1 9 / 8 y 2 , t 1 2 t
В рекурсивной структуре, полученной с использованием
изложенного метода, случайные ошибки в разных уравнениях
являются взаимно некоррелированными случайными
величинами. Это означает, что соответствующую систему
одновременных уравнений можно оценивать, используя обычный
метод наименьших квадратов (OLS).
Статистическая модель:
y1t c11 y1 , t 1 c12 y 2 , t 1 1t
y 2 t a 21 y1t c 21 y1 , t 1 c 22 y 2 , t 1 2 t
5. y1=c(1)*y1(-1)+c(2)*y2(-1) y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1)
C(1)C(2)
C(3)
C(4)
C(5)
Результаты оценивания:
Coefficient
Std. Error
t-Statistic
--------------------------------------------------------0.610340
0.041871
14.57663
0.497220
0.047645
10.43600
-0.988495
0.122953
-8.039596
0.810082
0.090567
8.944557
1.156414
0.084061
13.75689
y1t 5 / 8 y1 , t 1 1 / 2 y2 , t 1 1t ,
y1t y2 t 7 / 8 y1 , t 1 9 / 8 y2 , t 1 2 t
Prob.
0.0000
0.0000
0.0000
0.0000
0.0000
6. EViews 6: Оценивание матриц A и B структурной формы
Создав объект VAR и оценив коэффициенты приведенной VAR,можно получить в рамках этого объекта и оценки указанных
матриц.
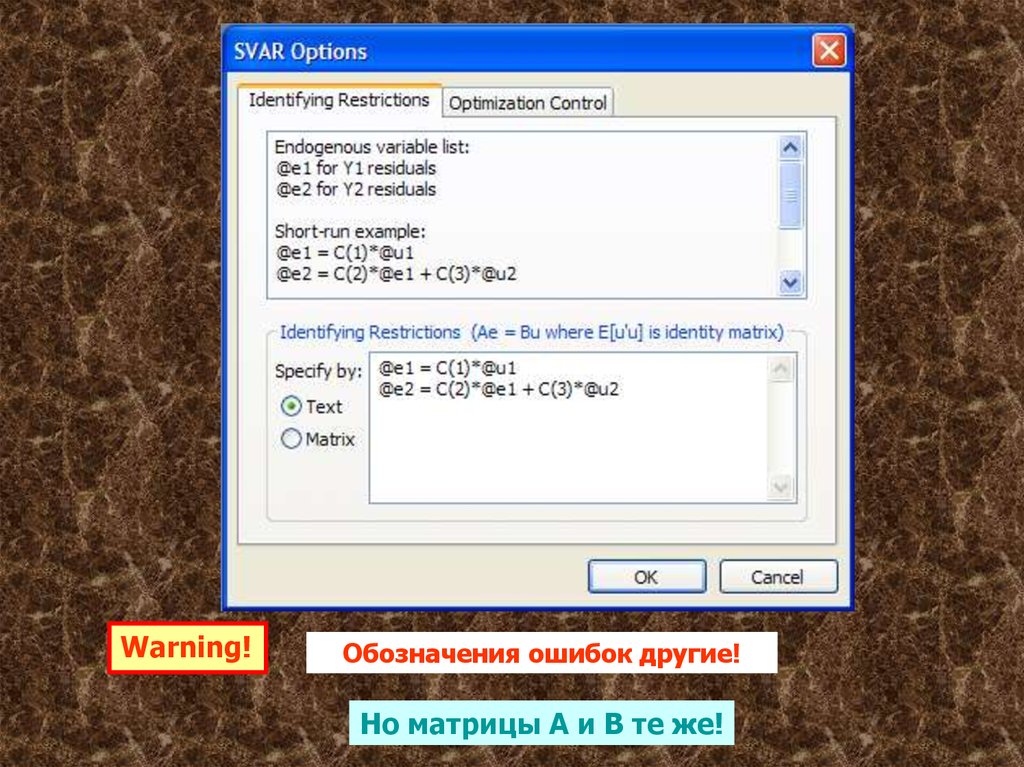
Для этого заказываем: Proc Estimate Structural Factorization
В открывшемся окне указываем форму связи между ошибками в
приведенной VAR и фундаментальными инновациями,
соответствующую выбранному упорядочению в схеме Холецкого.
7.
Warning!Обозначения ошибок другие!
Но матрицы A и B те же!
8.
Результаты оценивания матриц A и BModel: Ae = Bu where E[uu']=I
Restriction Type: short-run text
form
@e1 = C(1)*@u1
@e2 = C(2)*@e1 + C(3)*@u2
where
@e1 represents Y1 residual
@e2 represents Y2 residuals
Coefficient
C(2)
C(1)
C(3)
Estimated B matrix:
0.962944
0.000000
0.000000
1.143882
-0.997582
0.962944
1.143882
Estimated A matrix:
1.000000
0.000000
0.997582
1.000000
9. Замечания
Принимая различные порядки последовательноговхождения переменных, мы получаем и различное
поведение импульсных функций отклика, что дает
возможность сравнивать альтернативные теории.
В рекурсивной структуре, полученной с использованием
изложенного метода, случайные ошибки в разных уравнениях
являются взаимно некоррелированными случайными
величинами. Это означает, что соответствующую систему
одновременных уравнений можно оценивать, используя обычный
метод наименьших квадратов (OLS).
10. Пример. В модели двумерной VAR переменная y1t может представлять объем производства (output), а переменная y2t – “деньги”
(money).Упорядочение
1t
2t
y1t
y2t
соответствует схеме
u1t
u2t
В этой схеме шоки в объеме производства оказывают немедленное
воздействие и на объем производства и на деньги, тогда как
шоки в деньгах оказывают немедленное воздействие только на
деньги.
Такое упорядочение соответствует представлению, согласно
которому денежная политика имеет только запаздывающее
влияние на объем производства.
11. Пример (продолжение)
Упорядочение2t
y2t
y1t
1t
соответствует схеме
u2t
u1t
В этой схеме шоки в объеме производства оказывают немедленное
воздействие только на объем производства, тогда как шоки в
деньгах оказывают немедленное воздействие и на деньги и на
объем производства.
Это соответствует представлению о том, что деньги поставляются
центральным банком, а объем производства становится известным
центральному банку лишь с опозданием. Поэтому деньги не
могут немедленно реагировать на шоки в объеме
производства.
12. Методология VAR: Эмпирические исследования
13. Sims (1980): сравнение динамики экономики США в период между двумя мировыми войнами (IW) и в период после Второй Мировой войны
(AW)VAR с 3 переменными (месячные данные)
M1 – денежный агрегат M1 (сезонно скорректированная);
IP – индекс промышленного производства (сезонно
скорректированная);
P – индекс оптовых цен (сезонно скорректированная).
Все переменные брались в логарифмах, в правые части уравнений
включались константы и по 12 лагов каждой переменной.
Упорядочение:
Денежная масса Объем производства Цены
Соответственно,
y2t y3t , где
y1t = M1 , y2t = IP , y3t = P .
y1t
14.
Денежная масса Объем производства ЦеныСхема влияния фундаментальных инноваций
Упорядочение
y1t
y2t y3t
соответствует схеме:
1t
u1t
2t
u2t
3t
u3t
M1 – “ наименее эндогенная” переменная, P – “ наиболее
эндогенная“ переменная)
15. Декомпозиции дисперсий ошибок прогнозов трех переменных на 48 месяцев вперед
Денежная масса Объем производства ЦеныДекомпозиции дисперсий ошибок прогнозов трех
переменных на 48 месяцев вперед
Объясняемы
е
переменные
Объясняются шоками в переменных
M1
IP
P
IW
AW
IW
AW
IW
AW
M1
92
97
4
2
4
1
IP
66
37
28
44
6
18
P
38
14
19
7
43
80
Для обоих периодов дисперсия M1 почти полностью
объясняется инновациями M1.
Инновации M1 объясняют значительную часть дисперсии
IP и существенную часть дисперсии P.
Все это вполне в духе монетаризма, если понимать монетаризм как
точку зрения, согласно которой денежная политика играет
центральную роль в цикле деловой активности, а динамика
денежной массы является хорошим показателем денежной
политики.
16. Влияние процентной ставки
VAR с 4 переменными –добавляется Rt – процентная ставка по 4-6 месячным
первоклассным коммерческим бумагам (prime commercial papers).
Упорядочение: R M1 P IP
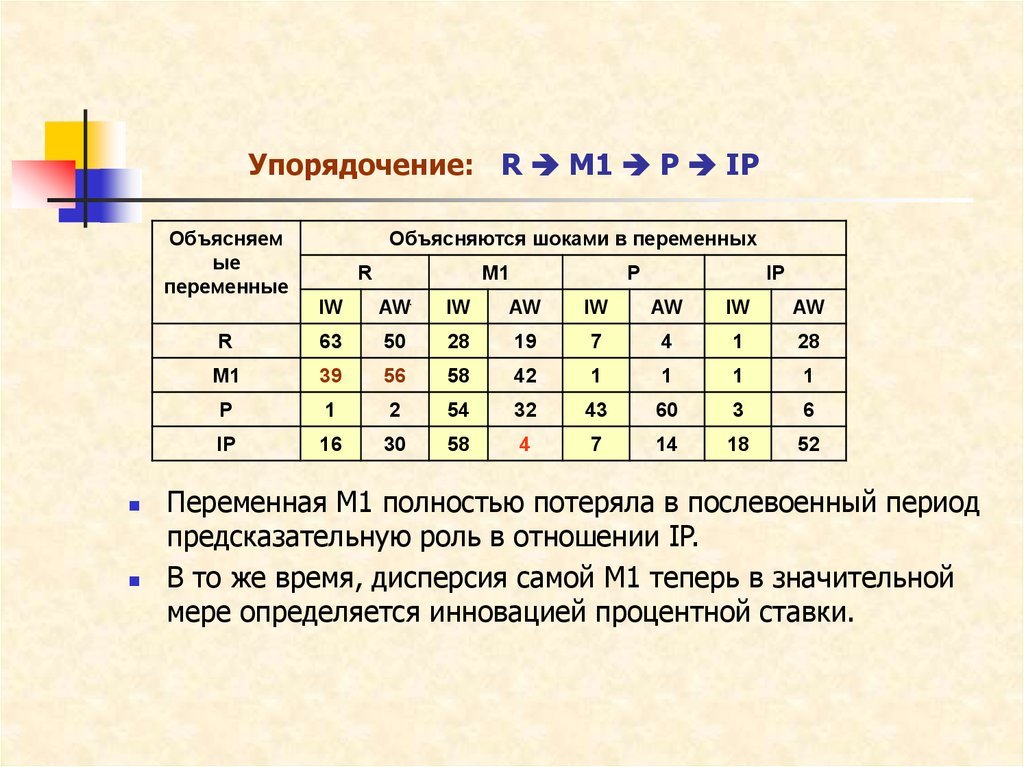
17. Упорядочение: R M1 P IP
Упорядочение: R M1 P IPОбъясняем
ые
переменные
Объясняются шоками в переменных
R
M1
P
IP
IW
AW
IW
AW
IW
AW
IW
AW
R
63
50
28
19
7
4
1
28
M1
39
56
58
42
1
1
1
1
P
1
2
54
32
43
60
3
6
IP
16
30
58
4
7
14
18
52
Переменная M1 полностью потеряла в послевоенный период
предсказательную роль в отношении IP.
В то же время, дисперсия самой M1 теперь в значительной
мере определяется инновацией процентной ставки.
18. Leeper, Sims, Zha (1996): модели VAR с 3, 4 и 5 переменными
VAR с 3 переменнымиПеременные:
LP 100 ln CPI _ SA ,
LY 100 ln RGDP _ MON
LM 2 100 ln M 2 _ SA
Оценивание на периоде 1960:01 – 1996:03 ( T=435)
В уравнения включались константы и по 6 лагов каждой
переменной.
Упорядочение: P Y M2
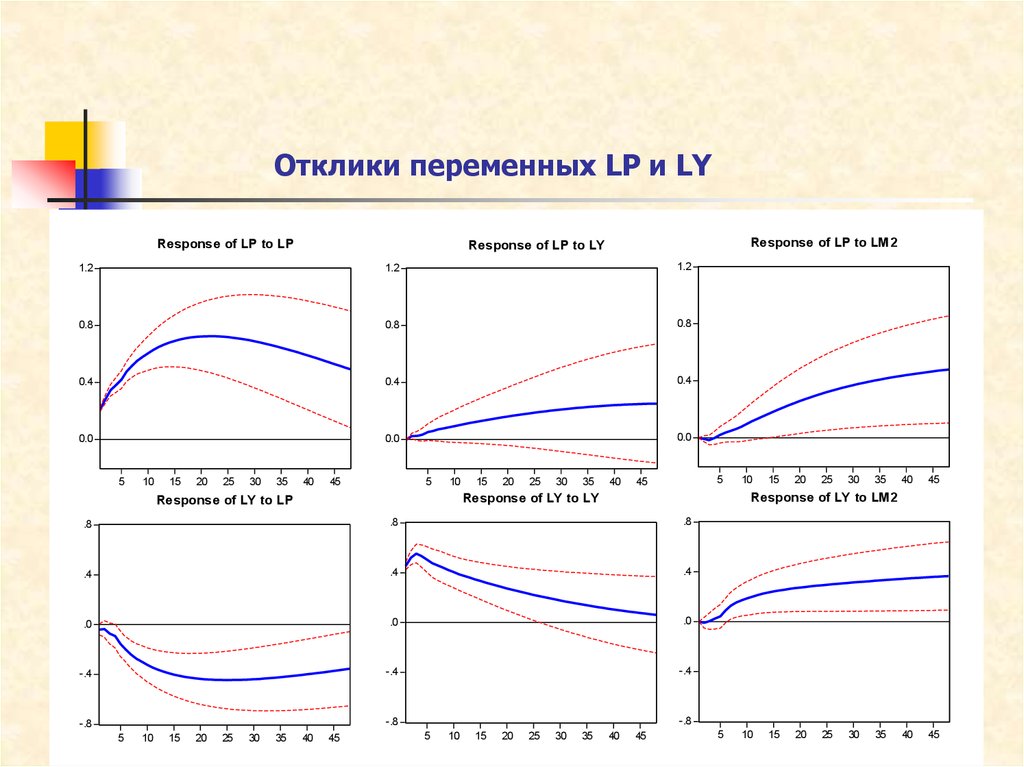
19. Отклики переменных LP и LY
Response of LP to LPResponse of LP to LM2
Response of LP to LY
1.2
1.2
1.2
0.8
0.8
0.8
0.4
0.4
0.4
0.0
0.0
0.0
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
40
5
45
.8
.8
.8
.4
.4
.4
.0
.0
.0
-.4
-.4
-.4
5
10
15
20
25
30
35
40
45
20
25
30
35
40
45
40
45
-.8
-.8
-.8
15
Response of LY to LM2
Response of LY to LY
Response of LY to LP
10
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
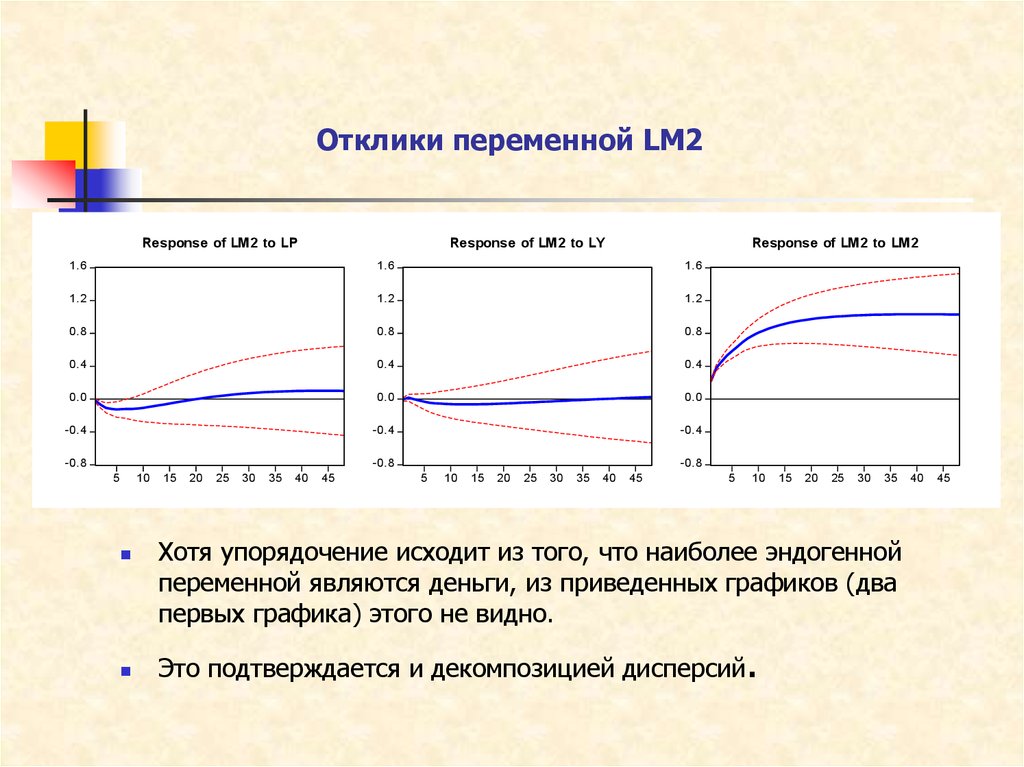
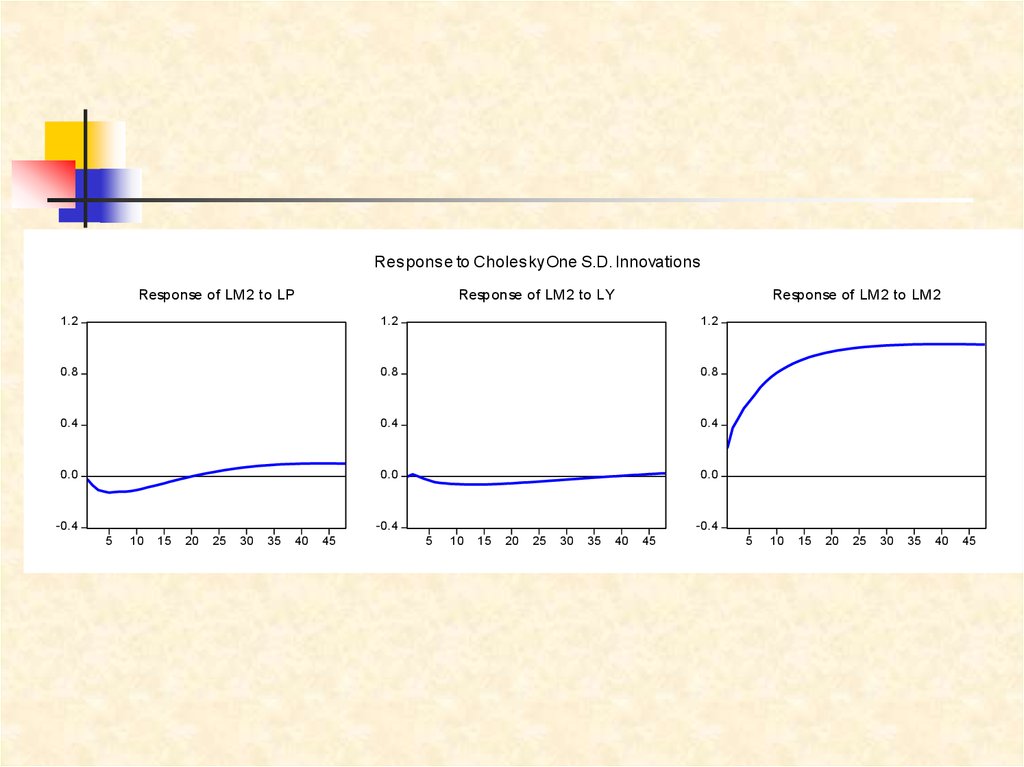
20. Отклики переменной LM2
Response of LM2 to LPResponse of LM2 to LY
Response of LM2 to LM2
1.6
1.6
1.6
1.2
1.2
1.2
0.8
0.8
0.8
0.4
0.4
0.4
0.0
0.0
0.0
-0.4
-0.4
-0.4
-0.8
-0.8
5
10
15
20
25
30
35
40
45
-0.8
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
Xотя упорядочение исходит из того, что наиболее эндогенной
переменной являются деньги, из приведенных графиков (два
первых графика) этого не видно.
Это подтверждается и декомпозицией дисперсий.
40
45
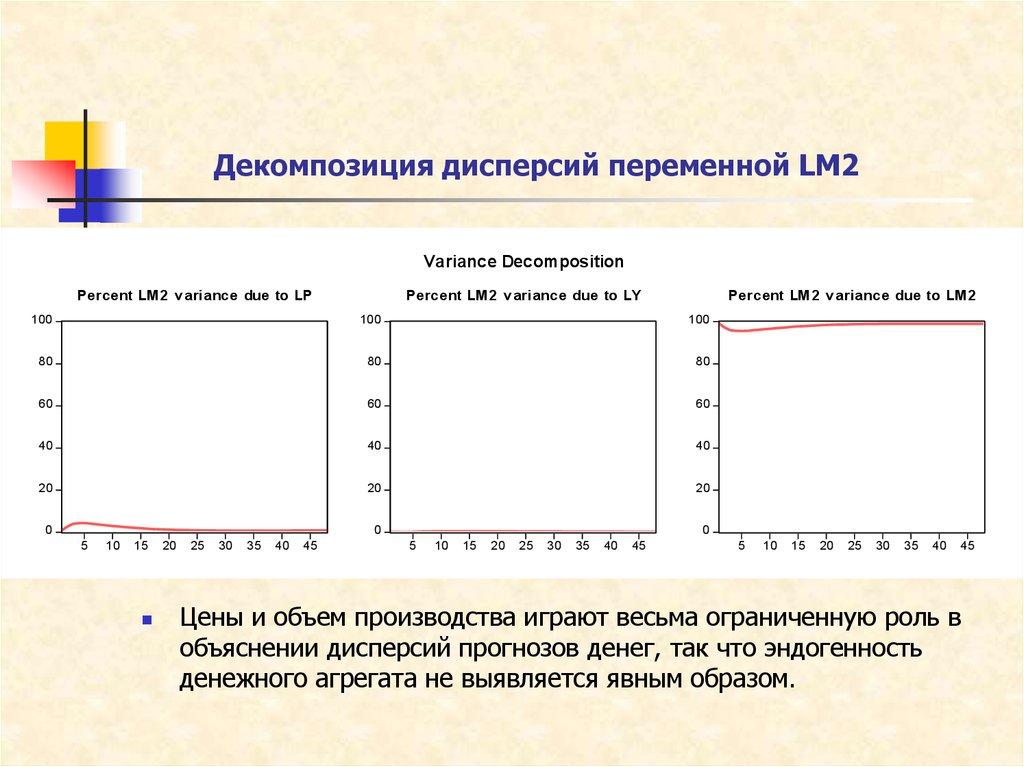
21. Декомпозиция дисперсий переменной LM2
Variance DecompositionPercent LM2 v ariance due to LP
Percent LM2 v ariance due to LY
Percent LM2 v ariance due to LM2
100
100
100
80
80
80
60
60
60
40
40
40
20
20
20
0
0
5
10
15
20
25
30
35
40
45
0
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
40
45
Цены и объем производства играют весьма ограниченную роль в
объяснении дисперсий прогнозов денег, так что эндогенность
денежного агрегата не выявляется явным образом.
22.
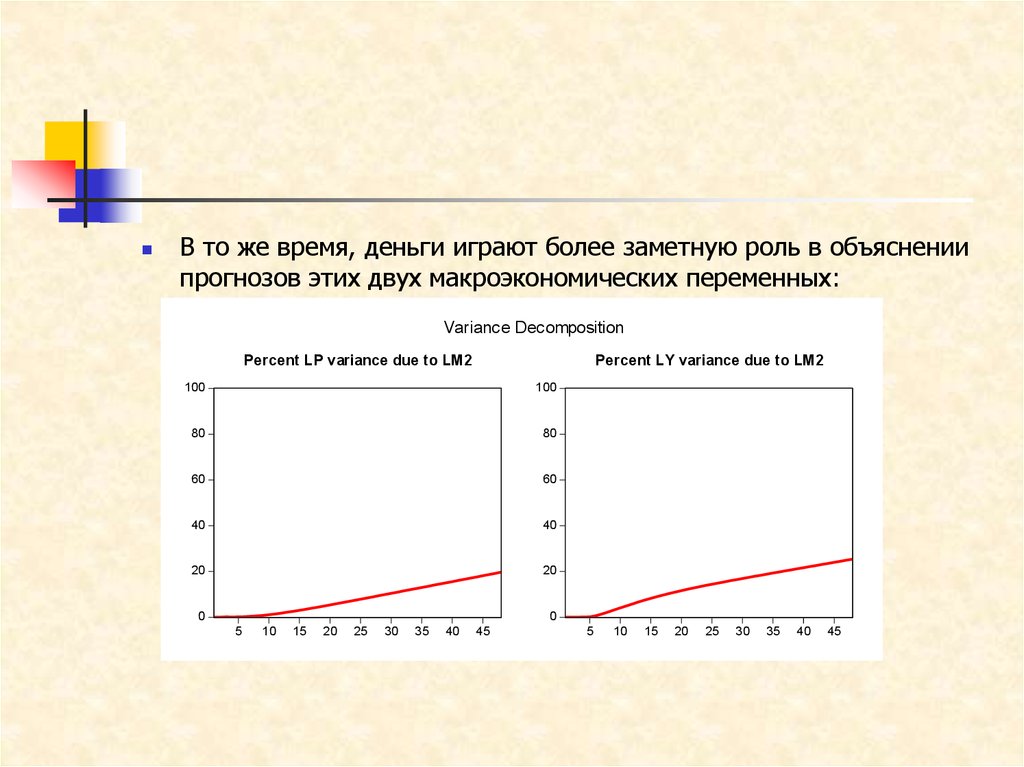
В то же время, деньги играют более заметную роль в объяснениипрогнозов этих двух макроэкономических переменных:
Variance Decomposition
Percent LP variance due to LM2
Percent LY variance due to LM2
100
100
80
80
60
60
40
40
20
20
0
0
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
40
45
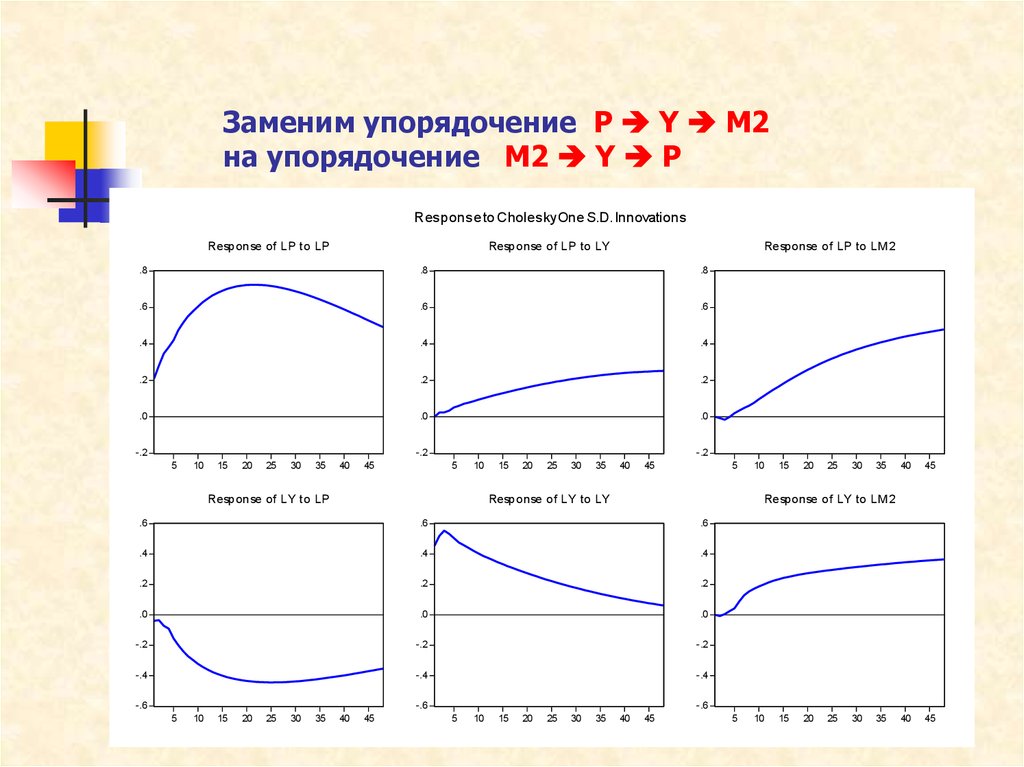
23. Заменим упорядочение P Y M2 на упорядочение M2 Y P
Заменим упорядочение P Y M2на упорядочение M2 Y P
Response to Cholesky One S.D. Innovations
Response of LP to LP
Response of LP to LY
Response of LP to LM2
.8
.8
.8
.6
.6
.6
.4
.4
.4
.2
.2
.2
.0
.0
.0
-.2
-.2
5
10
15
20
25
30
35
40
45
-.2
5
10
Response of LY to LP
15
20
25
30
35
40
45
5
Response of LY to LY
.6
.6
.4
.4
.4
.2
.2
.2
.0
.0
.0
-.2
-.2
-.2
-.4
-.4
-.4
-.6
5
10
15
20
25
30
35
40
45
15
20
25
30
35
40
45
40
45
Response of LY to LM2
.6
-.6
10
-.6
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
24.
Response to Cholesky One S.D. InnovationsResponse of LM2 to LP
Response of LM2 to LY
Response of LM2 to LM2
1.2
1.2
1.2
0.8
0.8
0.8
0.4
0.4
0.4
0.0
0.0
0.0
-0.4
-0.4
5
10
15
20
25
30
35
40
45
-0.4
5
10
15
20
25
30
35
40
45
5
10
15
20
25
30
35
40
45
25. Графики очень похожи!
Почему все так похоже?Получается, что порядок вхождения переменных для этих
данных не имеет значения.
Но это возможно только если инновации в приведенной VAR
не коррелированы между собой.
Корреляции между остатками на сей раз имеют вид:
LP
LY
LM2
1.000000
-0.086962
-0.094147
-0.086962
1.000000
-0.002022
-0.094147
-0.002022
1.000000
Во всяком случае, в обоих вариантах:
эндогенность M2 незаметна ;
M2 играет более заметную роль в объяснении дисперсий
прогнозов реального GDP.
26. Причинность по Грейнджеру, функции импульсного отклика и декомпозиция дисперсий.
Тесты на наличие причинности по Грейнджеру/блочнуюэкзогенность фактически только выявляют наличие Gпричинности в рамках имеющейся выборки, но не указывают
на динамику усиления/ослабления влияния одних переменных на
другие с течением времени.
В то же время, функции импульсного отклика и
декомпозиции дисперсий позволяют проследить динамику
влияния шоковых воздействий на будущие значения
переменных.
Свойство отсутствия G-причинности между переменными двух
групп является исключительным свойством двух
подмножеств переменных данного процесса. В то же время,
декомпозиция дисперсий ошибок прогнозов не
единственна: она зависит от матрицы, приводящей к
фундаментальным инновациям.
27.
Если набор переменных в составеy t 1
y t 2
yt
yt
разбивается на две части:
и переменные второй группы не являются Грейнджерпричиной для переменных первой группы, то это
вовсе не означает, что доли дисперсий ошибок прогнозов
переменных группы 1, соответствующие инновациям в уравнениях
для переменных второй группы, равны нулю.
Последнее может иметь место только если отсутствует
перекрестная коррелированность инноваций в уравнениях
для переменных группы 1 с инновациями в уравнениях для
переменных группы 2.
Если же это условие нарушено, то доли дисперсий ошибок
прогнозов переменных группы 1, соответствующие инновациям в
уравнениях для переменных группы 2 отличны от нуля.
28. Leeper, Sims, Zha (1996): модель VAR с 3 переменными
Переменные: LP 100 ln CPI _ SA ,LY 100 ln RGDP _ MON
LM 2 100 ln M 2 _ SA
Упорядочение: P Y M2
При оценивании на периоде 1974:01 – 1980:03 ( T=75
наблюдений) ранее было выявлено наличие G-причинной
связи в направлении от LY к LM2.
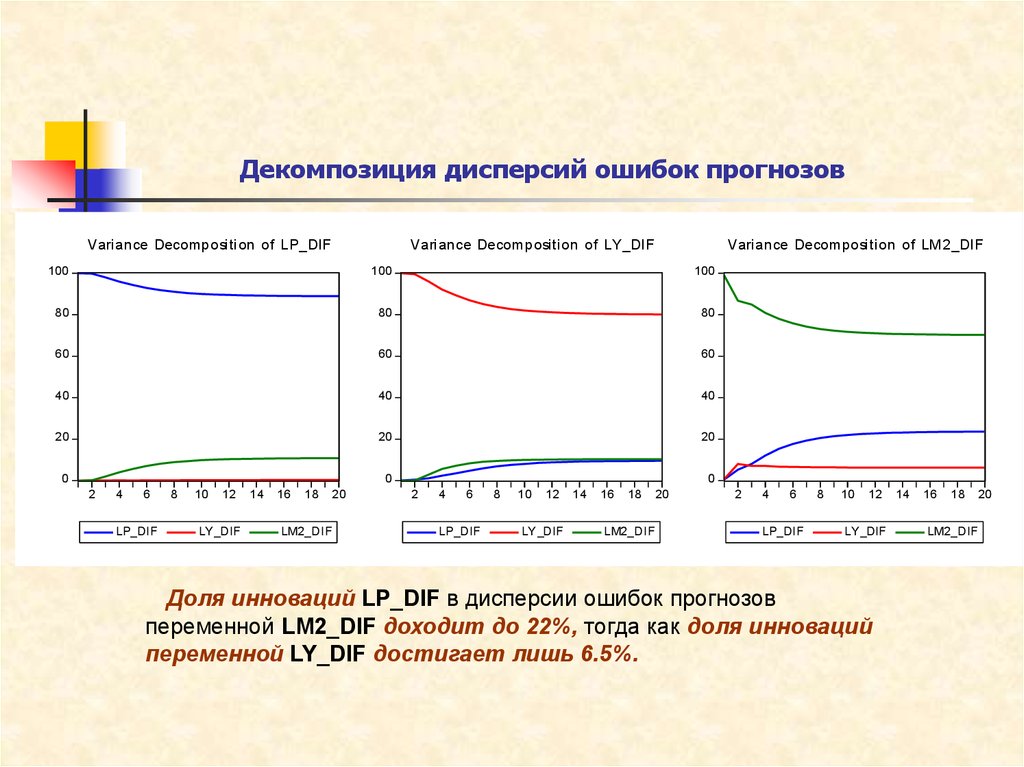
29. Декомпозиция дисперсий ошибок прогнозов
Variance Decomposition of LP_DIFVariance Decomposition of LY_DIF
Variance Decomposition of LM2_DIF
100
100
100
80
80
80
60
60
60
40
40
40
20
20
20
0
0
2
4
6
LP_DIF
8
10
12
LY_DIF
14
16
18
20
LM2_DIF
0
2
4
6
LP_DIF
8
10
12
LY_DIF
14
16
18
LM2_DIF
20
2
4
6
LP_DIF
8
10
12
LY_DIF
Доля инноваций LP_DIF в дисперсии ошибок прогнозов
переменной LM2_DIF доходит до 22%, тогда как доля инноваций
переменной LY_DIF достигает лишь 6.5%.
14
16
18
20
LM2_DIF
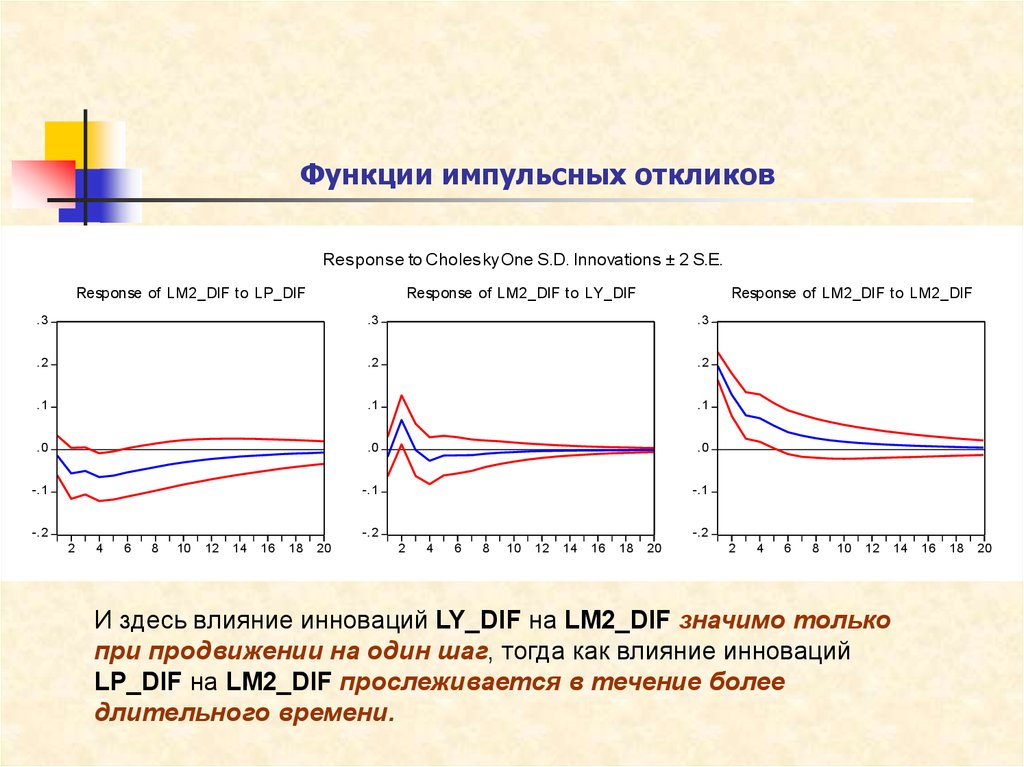
30. Функции импульсных откликов
Response to Cholesky One S.D. Innovations ± 2 S.E.Response of LM2_DIF to LP_DIF
Response of LM2_DIF to LY_DIF
Response of LM2_DIF to LM2_DIF
.3
.3
.3
.2
.2
.2
.1
.1
.1
.0
.0
.0
-.1
-.1
-.1
-.2
-.2
2
4
6
8
10
12
14
16
18
20
-.2
2
4
6
8
10
12
14
16
18
20
2
4
6
8
10
12
И здесь влияние инноваций LY_DIF на LM2_DIF значимо только
при продвижении на один шаг, тогда как влияние инноваций
LP_DIF на LM2_DIF прослеживается в течение более
длительного времени.
14
16
18
20
31. Нестабильные VAR
Законно ли использование инструментария,предназначенного для анализа стабильных моделей
VAR, в случаях, когда условие стабильности не
выполнено?
32. Филлипс [Phillips (1995)]
При наличии единичных корней или корней, близких кединице:
Импульсные отклики, полученные на основании оцененной
приведенной VAR без ограничений, в долговременном плане
сходятся в пределе не к истинным откликам, а к
некоторым случайным величинам.
Предельное распределение не является нормальным и
несимметрично.
Предсказания на основании нестационарной VAR без ограничений
не сходятся к оптимальным прогнозам (по крайней мере, на
больших горизонтах прогнозов), а дисперсия оптимального
прогноза, как правило занижается.
33. Филлипс [Phillips (1995)]
Если имеет место коинтегрированность рядов, образующихVAR, и оценивается модель VAR, учитывающая
ограничения, накладываемые коинтеграцией, то тогда:
Построенные по оцененной модели импульсные отклики и
декомпозиции дисперсий прогнозов состоятельны, а прогнозы
асимптотически оптимальны.
Правда, для этого надо или
правильно специфицировать ранг коинтеграции или
получить для него состоятельную оценку.
34.
Смоделирована VAR(1):y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 u1t ,
y 2 t 1 / 4 y1 , t 1 2 / 3 y 2 , t 1 u2 t
В этой модели один из корней характеристического уравнения
равен 1, так что VAR нестабильна.
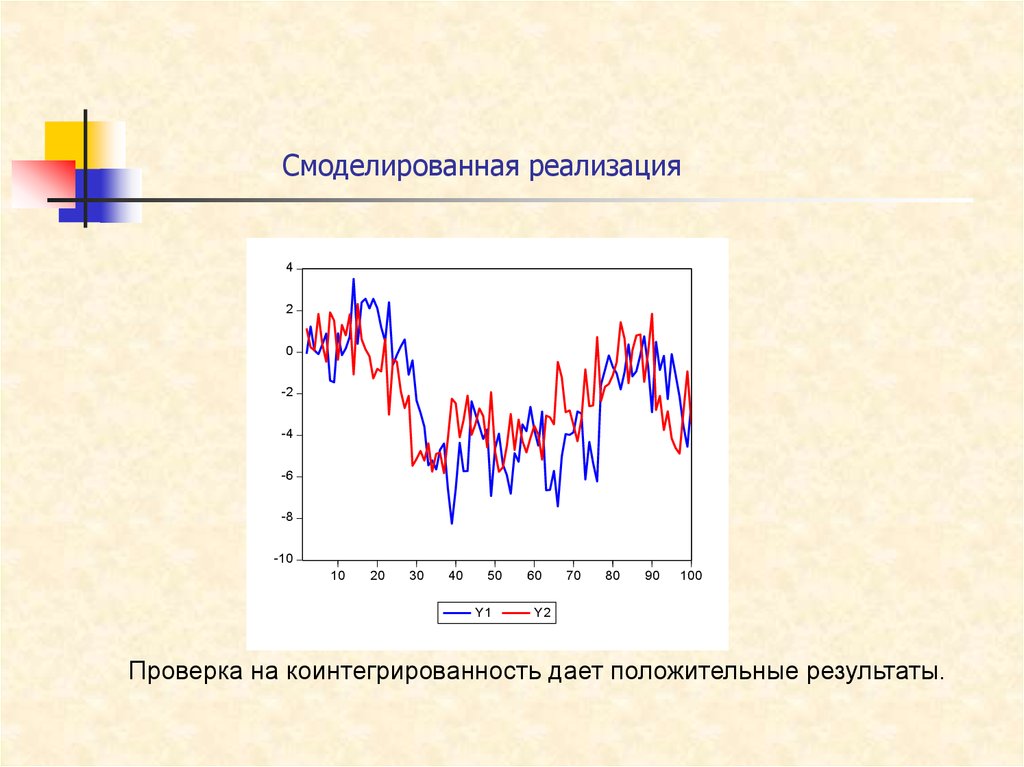
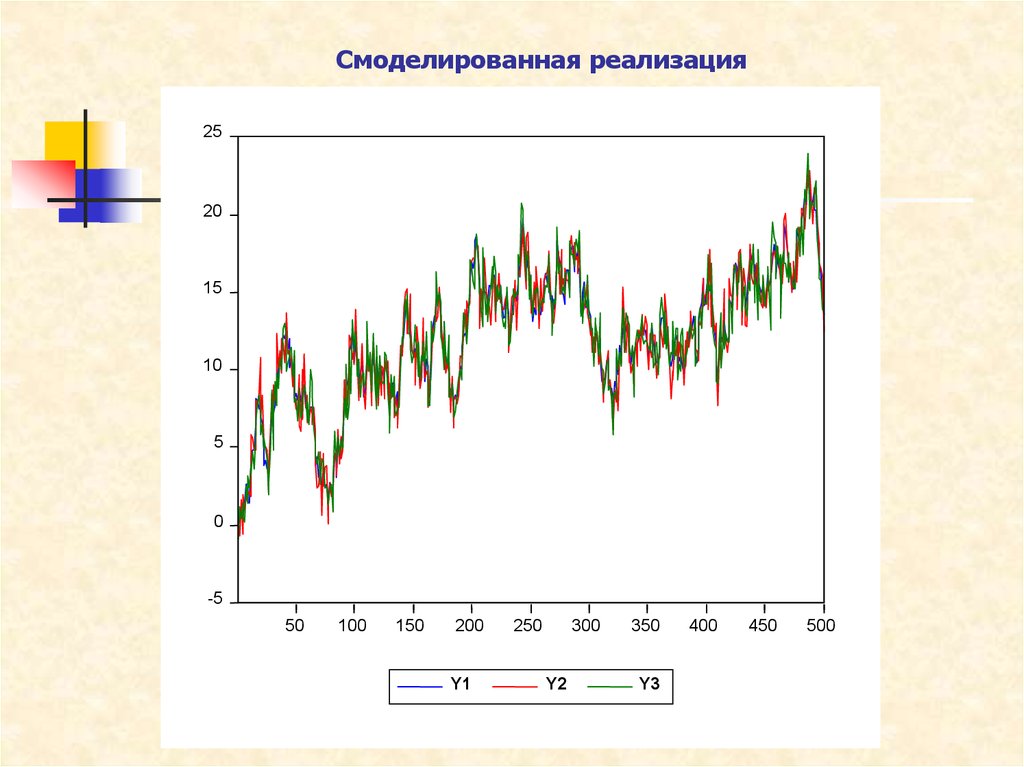
35. Смоделированная реализация
42
0
-2
-4
-6
-8
-10
10
20
30
40
50
Y1
60
70
80
90
100
Y2
Проверка на коинтегрированность дает положительные результаты.
36.
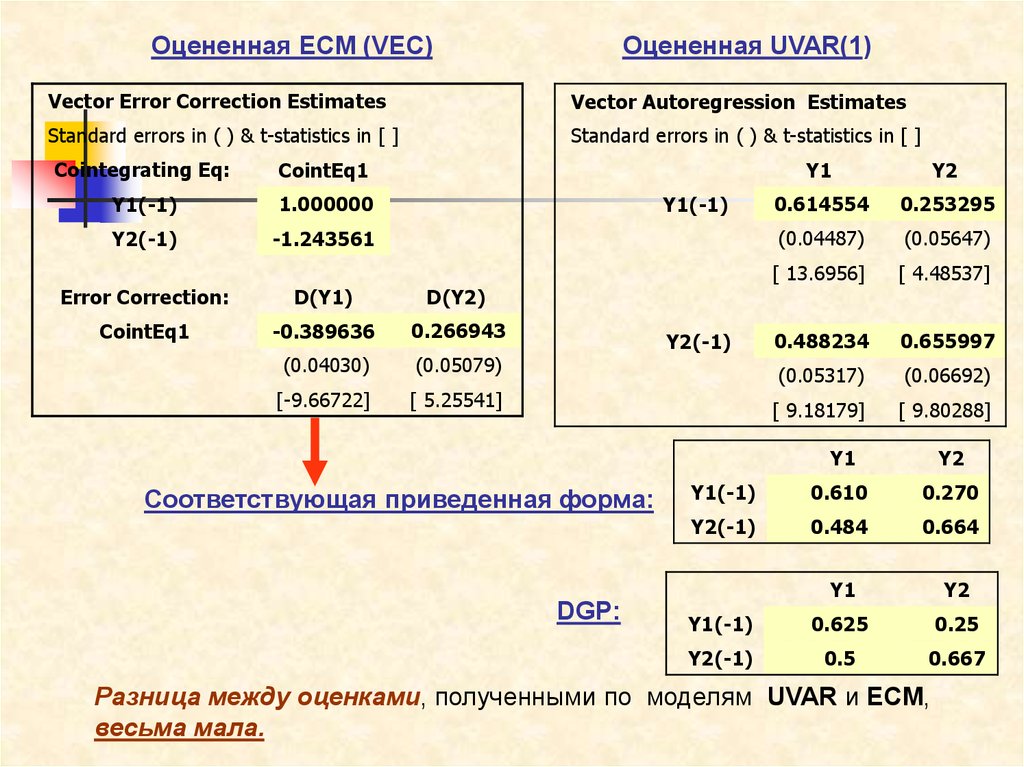
Оцененная ECM (VEC)Оцененная UVAR(1)
Vector Error Correction Estimates
Vector Autoregression Estimates
Standard errors in ( ) & t-statistics in [ ]
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:
CointEq1
Y1(-1)
1.000000
Y2(-1)
-1.243561
Y1(-1)
Error Correction:
D(Y1)
D(Y2)
CointEq1
-0.389636
0.266943
(0.04030)
(0.05079)
[-9.66722]
[ 5.25541]
Y2(-1)
Соответствующая приведенная форма:
DGP:
Y1
Y2
0.614554
0.253295
(0.04487)
(0.05647)
[ 13.6956]
[ 4.48537]
0.488234
0.655997
(0.05317)
(0.06692)
[ 9.18179]
[ 9.80288]
Y1
Y2
Y1(-1)
0.610
0.270
Y2(-1)
0.484
0.664
Y1
Y2
Y1(-1)
0.625
0.25
Y2(-1)
0.5
0.667
Разница между оценками, полученными по моделям UVAR и ECM,
весьма мала.
37.
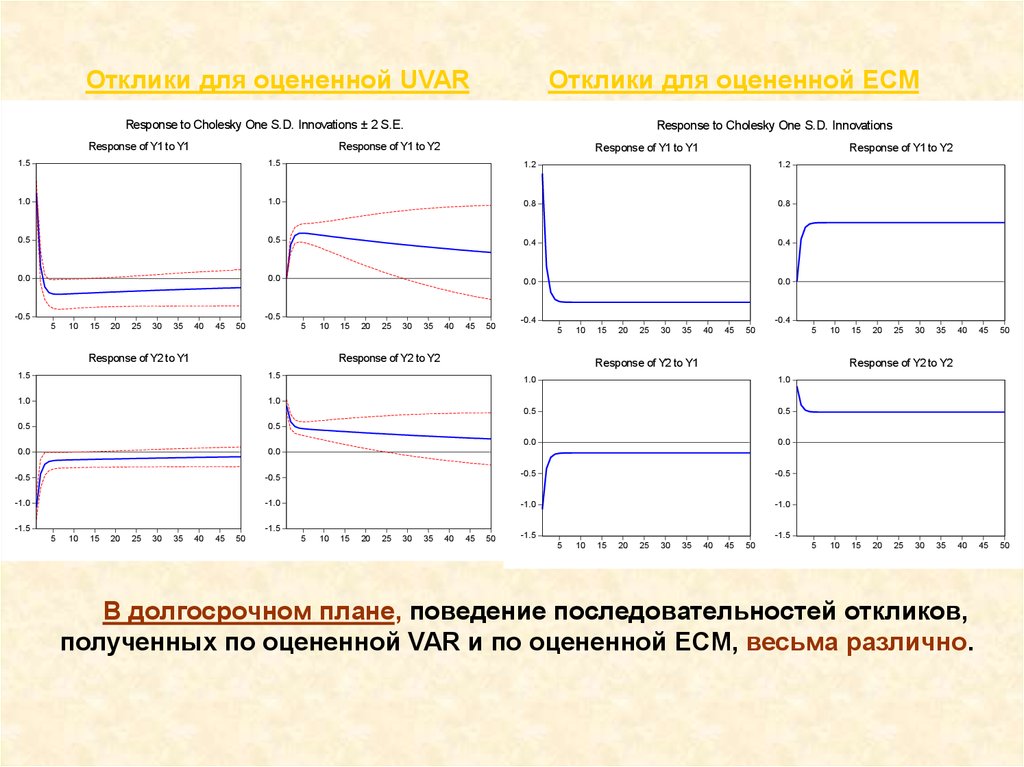
Отклики для оцененной UVARОтклики для оцененной ECM
Response to Cholesky One S.D. Innovations ± 2 S.E.
Response of Y1 to Y1
Response to Cholesky One S.D. Innovations
Response of Y1 to Y2
Response of Y1 to Y1
Response of Y1 to Y2
1.5
1.5
1.2
1.2
1.0
1.0
0.8
0.8
0.5
0.5
0.4
0.4
0.0
0.0
0.0
0.0
-0.5
-0.5
5
10
15
20
25
30
35
40
45
50
5
10
Response of Y2 to Y1
15
20
25
30
35
40
45
50
1.5
1.0
1.0
0.5
0.5
0.0
0.0
-0.5
-1.0
-1.5
15
20
25
30
35
10
40
45
50
15
20
25
30
35
40
45
50
5
0.5
0.5
0.0
0.0
-0.5
-0.5
-0.5
-1.0
-1.0
-1.0
10
15
20
25
30
35
40
45
50
15
20
25
30
35
40
45
50
40
45
50
Response of Y2 to Y2
1.0
5
10
Response of Y2 to Y1
1.0
-1.5
10
-0.4
5
Response of Y2 to Y2
1.5
5
-0.4
-1.5
-1.5
5
10
15
20
25
30
35
40
45
50
5
10
15
20
25
30
35
В долгосрочном плане, поведение последовательностей откликов,
полученных по оцененной VAR и по оцененной ECM, весьма различно.
38. Поведение последовательностей откликов в модели, использованной в DGP
IMP_Y1_TO_Y1_DGP1.2
0.8
0.4
0.0
-0.4
5
10
15
20
25
30
35
40
45
50
40
45
50
IMP_Y2_TO_Y1_DGP
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2
5
10
15
20
25
30
35
Из графиков видно, что, в долговременном
плане,
поведение функций отклика
при использовании UVAR не соответствует
поведению функций отклика в DGP,
тогда как поведение функций отклика
при использовании ECM соответствует
поведению функций отклика в DGP.
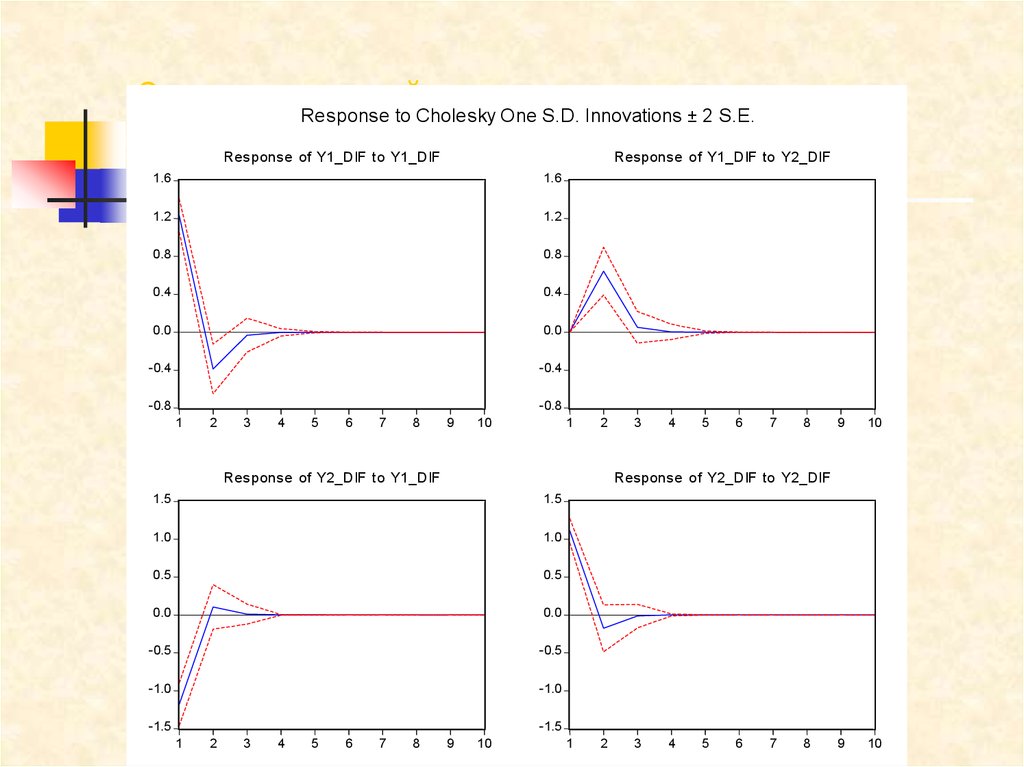
39. Отклики приращений
Response to Cholesky One S.D. Innovations ± 2 S.E.Response of Y1_DIF to Y1_DIF
Response of Y1_DIF to Y2_DIF
1.6
1.6
1.2
1.2
0.8
0.8
0.4
0.4
0.0
0.0
-0.4
-0.4
-0.8
-0.8
1
2
3
4
5
6
7
8
9
10
1
2
Response of Y2_DIF to Y1_DIF
3
4
5
6
7
8
9
10
9
10
Response of Y2_DIF to Y2_DIF
1.5
1.5
1.0
1.0
0.5
0.5
0.0
0.0
-0.5
-0.5
-1.0
-1.0
-1.5
-1.5
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
40. Пример с тремя рядами
DGP:где
y1t 1t
y2 t y1t 2 t
y3 t y1t 3 t
1t , 2 t , 3 t
– не коррелированные между собой
гауссовские инновации с нулевыми средними и единичными
дисперсиями, y10=0.
Получаемые I(1) ряды коинтегрированы, ранг коинтеграции
равен 2.
41. Смоделированная реализация
2520
15
10
5
0
-5
50
100
150
200
Y1
250
300
Y2
350
Y3
400
450
500
42.
Импульсные отклики: упорядочение Y1 Y2 Y3UVAR
Response of Y3 to Y1
Response of Y3 to Y2
Response of Y3 to Y3
1.2
1.2
1.2
1.0
1.0
1.0
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
0.0
0.0
0.0
-0.2
-0.2
-0.2
-0.4
-0.4
5
10
15
20
25
30
35
40
45
50
-0.4
5
10
15
20
25
30
35
40
45
50
5
10
15
20
25
30
35
40
45
50
40
45
50
40
45
50
ECM rank 1
Response of Y3 to Y1
Response of Y3 to Y2
Response of Y3 to Y3
1.2
1.2
1.2
1.0
1.0
1.0
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
0.0
0.0
0.0
-0.2
-0.2
5
10
15
20
25
30
35
40
45
50
-0.2
5
10
15
20
25
30
35
40
45
50
5
10
15
20
25
30
35
ECM rank 2
Response of Y3 to Y1
Response of Y3 to Y2
Response of Y3 to Y3
1.2
1.2
1.2
1.0
1.0
1.0
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
0.0
0.0
0.0
-0.2
-0.2
5
10
15
20
25
30
35
40
45
50
-0.2
5
10
15
20
25
30
35
40
45
50
5
10
15
20
25
30
35
43. Выводы
Использование при оценивании ECM различныхпредположений о ранге коинтеграции приводит к
различным результатам в отношении функций
импульсного отклика.
Это весьма затрудняет интерпретацию результатов VAR
анализа при обращении к данным экономической
статистики.




















![Филлипс [Phillips (1995)] Филлипс [Phillips (1995)]](https://cf.ppt-online.org/files1/slide/d/dRTLCPDmcOfzBxJqyhFSoHp26WV3Z19kKts4I8AYg/slide-31.jpg)
![Филлипс [Phillips (1995)] Филлипс [Phillips (1995)]](https://cf.ppt-online.org/files1/slide/d/dRTLCPDmcOfzBxJqyhFSoHp26WV3Z19kKts4I8AYg/slide-32.jpg)





 economics
economics








