Similar presentations:
Эконометрика. Методология VAR
1. Эконометрика
Лекция 42.
Методология VAR3.
1932 г. – учреждение Комиссии Коулса(The Cowles Commission for Research in Economics)
1932 г. – решение об издании журнала “Econometrica”
1933 г. (январь) – выход первого номера журнала
Два принципа журнала:
(1) экономика – это наука,
(2) в этой науке очень важен количественный аспект.
4. Комиссия Коулса: Период с 1943 г. – Джейкоб Маршак (Jacob Marschak)
Комиссия Коулса:Период с 1943 г.
–
Джейкоб Маршак (Jacob Marschak)
Методы исследования должны быть обусловлены
следующими характеристиками экономических данных и
экономической теории:
Теория есть система одновременных уравнений, а не
отдельное уравнение;
некоторые из этих уравнений включают "случайные"
составляющие, отражающие многочисленные
неустойчивые причины, в дополнение к нескольким
"систематическим.
Многие данные выражены в виде временных рядов,
причем последующие события зависят от предыдущих.
Многие опубликованные данные относятся скорее к
агрегатам, а не к отдельным субъектам.
5.
Комиссия КоулсаРазвитие соответствующих математических и
статистических методов не менее важно, чем получение
немедленных результатов.
Применение математических результатов в практических
исследованиях сопровождается также и обратным
движением : возникновение новых ситуаций в процессе
практической работы ставит и новые задачи перед
математиками.
6. Комиссия Коулса
Значительное место в исследованиях под эгидой Комиссии заняларазработка моделей и методов анализа моделей систем
одновременных уравнений.
Цель –количественный анализ влияния изменений в переменных,
контролируемых неким монетарным "полисмейкером“, на
макроэкономические переменные, представляющие конечные цели
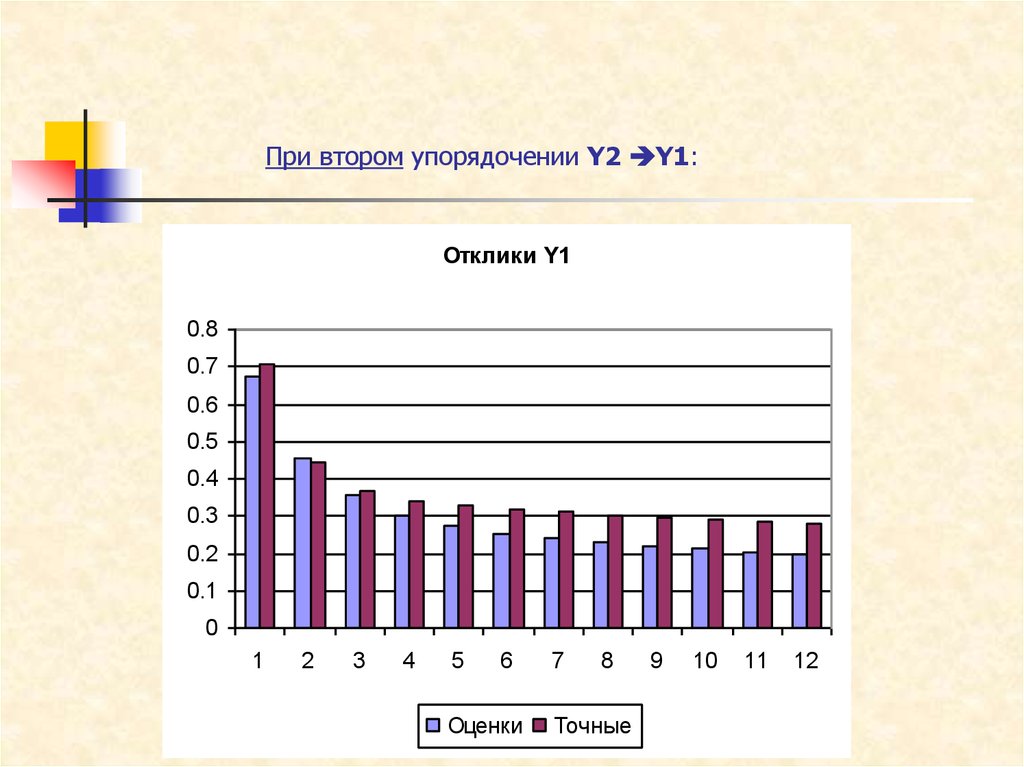
этого полисмейкера.
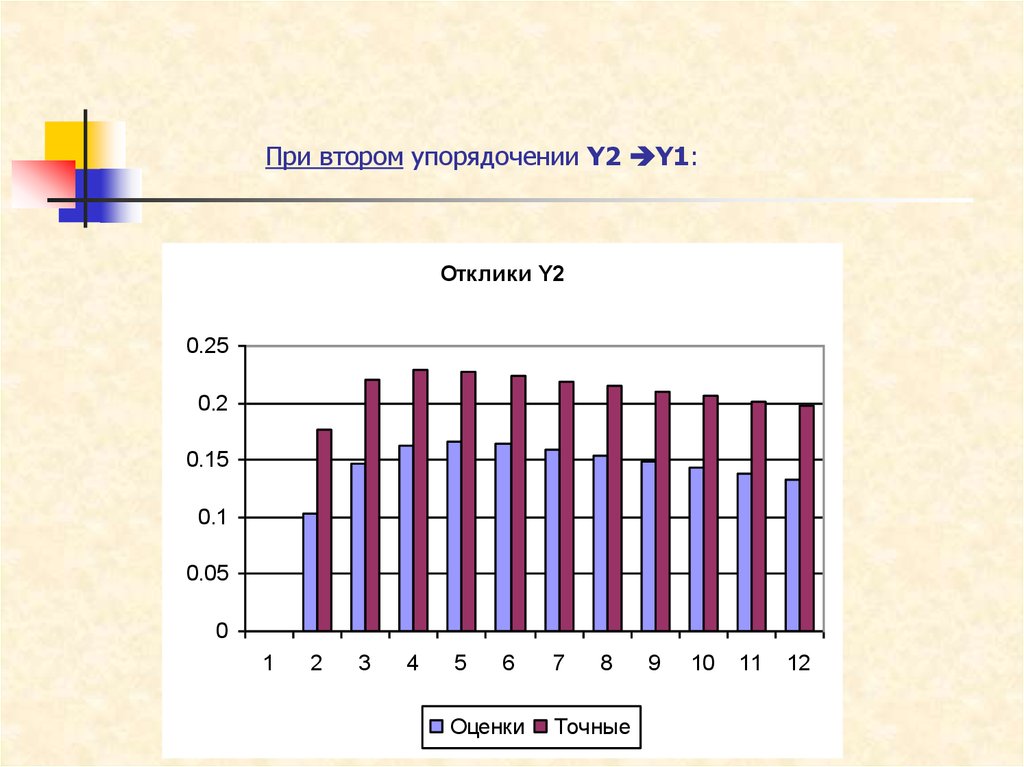
Такой анализ предусматривает:
спецификацию и идентификацию теоретической модели,
оценивание параметров,
расчет динамических свойств модели с особым акцентом на
долговременные свойства,
симуляцию динамической модели,
анализ последствий различных политик.
7.
Комиссия Коулса: системы одновременных уравнений(simultaneous equations model – SEM)
Cпецификация модели производится с априорным разделением
переменных на экзогенные и эндогенные.
Идентификация достигается как результат накладывания
большого количества ограничений.
При выявлении тех или иных отклонений от стандартных
предположений метода наименьших квадратов модифицируется
не модель, а метод оценивания.
Базовая симуляция обычно производится на основе имеющейся
выборки; результаты базовой симуляции сравниваются с
результатами, полученными в альтернативной симуляции,
основанной на модификации соответствующих экзогенных
переменных.
Анализ альтернативных политик базируется на динамических
мультипликаторах.
8.
Методология Комиссии КоулсаСобственно эконометристы остаются отделенными от
выбора модели, который является прерогативой экономистов,
формулирующих теоретическую модель.
9. Методология Комиссии Коулса: критика Лукаса и Симса (Lucas (1978), Sims (1980)
Лукас:Традиционные структурные макромодели бесполезны для целей
симуляции политики, поскольку такие модели не принимают в
расчет в явной форме ожидания экономических агентов.
Симс:
В моделях Комиссии идентификация достигается за счет произвольного
объявления некоторых переменных экзогенными. Однако в мире
агентов, поведение которых зависит от решения некоторых впередсмотрящих межвременных оптимизационных моделей, никакая из
переменных не может считаться экзогенной.
Кроме того, в теоретическую априорную модель может быть включено
недостаточное количество переменных (и тогда возникает эффект
пропущенных переменных) и недостаточное количество
запаздываний.
10.
Для преодоления указанных недостатков методологииКомиссии были предложены:
методология Лондонской Школы экономики (LSE),
методология VAR (векторных авторегрессий).
11. Методология LSE (Sargan, Hendry)
Акценты смещаются с методов оценивания (априорно заданноймодели) на получение адекватной данным спецификации и
на идентифицируемость модели.
Строится достаточно широкая базовая модель в виде
векторной ADL в приведенной форме с достаточно большим
количеством переменных и достаточно большим количеством
запаздываний (если, конечно, это позволяют данные).
Эта модель редуцируется путем упрощения динамики
(отбрасывания незначимых лагов) и уменьшения размерности
(отбрасывания уравнений для тех переменных, для которых не
отвергается гипотеза экзогенности).
Накладываются ограничения на матрицу, определяющую
долговременное равновесие, и производится идентификация
коинтегрирующих векторов.
12. Методология LSE
Это приводит к статистической модели для данных с возможнымразделением краткосрочной динамики и долговременного
равновесия; эта модель идентифицируется и оценивается.
Если система идентифицируема точно, то на этом все
заканчивается.
Если система сверхидентифицирована, то проверяется
выполнение "лишних" ограничений.
13. Методология VAR (Sims)
Разделение изменений в монетарной политике на два типа:изменения, которые агенты экономики предвидят правильно;
изменения, которые являются неожиданными для агентов
экономики.
Изменения первого типа должны производить нейтральные
эффекты: пропорциональные изменения цен и других
номинальных переменных и отсутствие влияния на реальные
переменные.
Неожиданные изменения второго типа, напротив, могут
отражаться и на реальных переменных.
В методологии Симса делается акцент на исследование
откликов системы экономических показателей на
неожиданные (шоковые) воздействия, которым подвергаются
отдельные переменные.
14.
В основе методологии VAR (как и в основе методологии LSE)лежит общая структура вида:
A yt C L yt 1 t C1 yt 1 C p yt p t
y t y1 , , yk T
ζ t – инновационная последовательность
i.i.d. случайных (k х 1)- векторов с нулевым
математическим ожиданием.
В приведенной форме:
yt 1 yt 1 p yt p ut
j A 1C j , ut A 1 t
ut
– инновационная последовательность
i.i.d. случайных (k х 1)- векторов с нулевым
математическим ожиданием и ковариационной
матрицей Σ .
15. Простая VAR(1) для двух рядов (k = 2, p = 1)
yt yt 1 uty1t 11 y1 , t 1 12 y 2 , t 1 u1t ,
y 2 t 21 y1 , t 1 22 y 2 , t 1 u2 t
На сколько изменяются значения
y1 , t s , y2 , t s при изменении инновации
u1t или u2 t на одно стандартное отклонение?
Вычисляя эти изменения последовательно для значений s = 0, 1, … ,
получаем функции откликов на шоки инноваций.
16. Пример
11 5 / 8 , 12 1 / 2 , 21 1 / 4 , 22 5 / 8y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 u1t ,
y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 u2 t
Эту VAR можно записать в виде:
(1 0.625 L) y1t
или
( 0.5 L) y 2 t u1t ,
( 0.25 L) y1t (1 0.625 L) y 2 t u2 t
0.5 L y1t u1t
(1 0.625 L)
(1 0.625 L) y2t u2t
0.25 L
17.
При этом,0.5 z
(1 0.625z )
det
(1 0.625z )
0.25 z
(1 0.625z ) 2 0.125z 2 (1 0.978z )(1 0.271z )
Корни уравнения
0 .5 z
(1 0.625 z )
det
0
(1 0.625 z )
0.25 z
лежат за пределами единичного круга, так что
рассматриваемая VAR стационарна (стабильна).
18.
Поэтому можно записать:0.5 L
y1t (1 0.625 L)
(1 0.625 L)
y2t 0.25 L
1
u1t
u2t
0.25 L u1t
(1 0.625 L)
1
(1 0.978 L)(1 0.271L)
0.5 L
(1 0.625 L) u2t
1 0.978L 0.9782 L2 1 0.271L 0.1272 L2
0.25 L u1t
(1 0.625 L)
0.5 L
(1 0.625 L) u2t
Тем самым, мы имеем возможность построения функций откликов
обеих переменных на шоки инноваций.
19. Однако:
Из-за того, что общем случаеCov u1 t , u2 t 0 , возникают
затруднения с интерпретацией этих функций.
Из-за перекрестной коррелированности инноваций в приведенной
форме, невозможно полностью изолировать шок для u1t
от шока для u2t , т.е.,
Нельзя произвольно изменять значение u1t , сохраняя при
этом значения u2t , u2 , t 1 , , u2 , t s , неизменными.
20. “Фундаментальные” инновации
Для преодоления указанного затруднения предполагают, чтосистема изменяется благодаря воздействию
некоррелированных между собой “фундаментальных”
инноваций 1t , , kt .
Обычно предполагается, что все они имеют единичные
дисперсии, так что , , T– i.i.d. с нулевым
t
1t
kt
математическим ожиданием и единичной ковариационной
матрицей
Ik .
При этом предполагается, что инновации u1t , , ukt
являются линейными комбинациями фундаментальных
инноваций, так что
ut D t
21. В примере с двумерной VAR(1):
ut D tПоскольку
yt yt 1 D t
, то
,
y2 t 21 y1 , t 1 22 y2 , t 1 d 21 1t d 22 2 t
y1t 11 y1 , t 1 12 y2 , t 1 d11 1t d12 2 t ,
Изменение
u1t
изменений
на одно стандартное отклонение складывается из
1t и 2t , которые, в свою очередь,
вызывают одновременное изменение
u2t .
22. Импульсные функции отклика (impulse response function – IRF )
С экономической точки зрения, первоочередной интереспредставляют реакции значений y1 , t s , y2 , t s на
единичные импульсные изменения отдельных
фундаментальных инноваций 1t , , kt при
фиксированных значениях всех остальных
фундаментальных инноваций во все моменты времени.
Именно на построение таких импульсных функций отклика
нацелены алгоритмы, реализуемые в пакетах статистических
программ.
23. Проблема отыскания матрицы D
ut D tЕсли матрица
11 12
Cov ut
21 22
известна, то как найти матрицу
D?
24.
y2 t 21 y1 , t 1 22 y2 , t 1 d 21 1t d 22 2 ty1t 11 y1 , t 1 12 y2 , t 1 d11 1t d12 2 t ,
u1t d11 1t d12 2t , u2t d 21 1t d 22 2t
Отсюда:
2
2
11 D u1t d11
d12
,
2
2
22 D u2 t d 21
d 22
,
12 Cov u1t , u2 t d11d 21 d12d 22
Для нахождения четырех неизвестных
имеется всего три уравнения.
d1 , d2 , d3 , d4
идентифицировать невозможно,
если не накладывать априорных ограничений на ее структуру.
Следовательно, матрицу
D
25. упорядочивание инноваций в системе.
Предложение Симса:упорядочивание инноваций в системе.
Пример двумерной VAR(1)
Пусть фундаментальная инновация
2t
воздействует только
y2t , а фундаментальная инновация 1t воздействует и на
y1t и на y2t .
на
2t воздействует только на
u2t , а фундаментальная инновация 1t воздействует и на u1t
Тогда фундаментальная инновация
и на
u2t .
1t
2t
u1t
u2t
26. Пример двумерной VAR(1)
u1t d11 1t d12 2t , u2t d 21 1t d 22 2t1t
u1t
u2t
2t
2
11 D u1t d11
,
2
2
22 D u2 t d 21
d 22
,
12 Cov u1t , u2 t d11d 21
d12 0
11
D 12
11
2
12
22
11
0
27.
D P BПредставим:
0
1
P
d 21 d11 1
Тогда
Обозначим
yt yt 1 P B t
A P
d11 0
B
0 d 22
1
1
0
d 21 d11 1
Умножим обе части VAR(1) на матрицу A :
Ay t A yt 1 AP B t Cyt 1
Получаем структурную модель
Ayt C L yt 1 t
в которой
t B t
B t
28.
Пусть в приведенной VAR(1) ковариационная матрица ошибок имеетвид
1 1
Cov ut
1 2
так что
11
D 12
11
1 0 1 0 1 0
2
12
22
1 1 1 1 0 1
11
0
Тогда структурная VAR имеет вид :
1 0 y1t 1 0 11 12 y1 , t 1 1t
1 1 y2 t 1 1 21 22 y2 , t 1 2 t
12 y1 , t 1 1t
1 0 y1t 11
1 1 y2t 11 21 12 22 y2 , t 1 2t
y1t 11 y1 , t 1 12 y2 , t 1 1t ,
y1t y2t 11 21 y1 , t 1 12 22 y2 , t 1 2t
29. Изменим теперь упорядочение инноваций
,,
.
Пусть
Тогда:
1t
2t
u1t
u2t
u1t d11 1t d12 2t ,
u2t d 22 2t
11 d112 d122 , 22 d 222 , 12 d12d 22
2
11 12
D
22
0
12 2 2 2 2
22
2
0
22
30.
Представляем:2 2 2 2 1 1 2 2 2
D
1 0
2 0
0
0
2
Структурная VAR имеет вид:
1 1 / 2 y1t 1 1 / 2 11 12 y1 ,t 1 2 2 1t
1 y 2 t 0
1 21 22 y2 ,t 1
2 2t
0
1 1 / 2 y2 t 11 1 2 21 12 1 2 22 y1 ,t 1 2 2 1t
21
22
1 y1t
2 2t
0
y2 ,t 1
y1t 1 / 2 y2 t 11 1 / 2 21 y1 ,t 1 12 1 / 2 22 y2 ,t 1 2 2 1t
y2 t 21 y1 ,t 1 22 y2 ,t 1 2 2 t
31. Резюме:
При первом упорядочении инноваций:y1t 11 y1 , t 1 12 y2 , t 1 1t ,
y1t y2t 11 21 y1 , t 1 12 22 y2 , t 1 2t
При втором упорядочении инноваций:
y1t 1 / 2 y2 t 11 1 / 2 21 y1 ,t 1 12 1 / 2 22 y2 ,t 1 2 2 1t
y2 t 21 y1 ,t 1 22 y2 ,t 1 2 2 t
В обоих случаях выбранная форма матрицы A приводит к
рекурсивной системе .
32. Рекурсивная система (первое упорядочение: Y1 Y2 )
Рекурсивная система(первое упорядочение: Y1 Y2 )
В первое уравнение с текущим значением входит только одна
переменная y1t , т.е.,
y1t
объясняется только запаздывающими значениями
переменных
y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят обе
переменные y1t и y2t , т.е. ,
y2t
объясняется с помощью
y1t
и
yt – 1 , yt – 2 , . . .
,
Такой порядок вхождения переменных интерпретируется как
последовательное включение переменных в порядке
возрастания их эндогенности, так что последней в систему
включается наиболее эндогенная переменная.
33.
Вернемся к двумерной VAR(1)y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 u1t ,
y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 u2 t
Сравним функции отклика переменных y1t и
шок фундаментальной инновации 1t .
y2t
на импульсный
При первом упорядочении:
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,
y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 2 t 1t
Пусть в момент
t = 1 имеет место шок фундаментальной
инновации для переменной
рекурсивной системы), так что
а
2t
y1t
(в первом уравнении
1t 1 для t 1,
~
1t
1t для t 1,
не изменяется ни при каком t
34.
При этом мы получаем измененную реализацию~
y1t
~
yt ~
y2t
~
y1 ,0 y1 ,0 , ~
y2 ,0 y2 ,0 и
для которой
~
y1t 5 / 8 ~
y1 , t 1 1 / 2 ~
y 2 , t 1 ~1t ,
~
y 1 / 4~
y
5/ 8~
y
~
2t
1 , t 1
2 , t 1
2t
1t
Для простоты, пусть
y1 ,0 y 2 ,0 0 . Тогда при t =1
y11 11 ,
~
y11 11 1 y11 1 ,
~
y 21 21 11 1 y 21 1
y 21 21 11
а при t =2
~
y12 5 / 8 ~
y1 ,1 1 / 2 ~
y 2 ,1 ~12 y12 1 / 8 ,
~
y 22 1 / 4 ~
y1 ,1 5 / 8 ~
y 2 ,1 22 ~12 y 22 3 / 8
35.
~y11 11 1 y11 1 ,
~
y 21 21 11 1 y 21 1
~
y12 5 / 8 ~
y1 ,1 1 / 2 ~
y 2 ,1 ~12 y12 1 / 8 ,
~
y 22 1 / 4 ~
y1 ,1 5 / 8 ~
y 2 ,1 22 ~12 y 22 3 / 8
Таким образом, мы получили следующие значения функций
импульсного отклика на единичный шок инновации
t
Imp y1t 1t
Imp y2t 1t
1
2
1
0.125
–1
– 0.375
1t :
36.
При втором упорядоченииy1t 5 / 8 y1 , t 1 1 / 2 y2 , t 1 2 2 1t 2 2 2 t ,
y2 t 1 / 4 y1 , t 1 5 / 8 y2 , t 1 2 2 t
Получаются следующие значения функций импульсного отклика
на единичный шок инновации 1t :
t
Imp y1t 1t
Imp y2t 1t
1
2
0.707
0.441875
0
0.17675
Принимая различный порядок последовательного вхождения
переменных, мы получили и различное поведение функций
импульсного отклика.
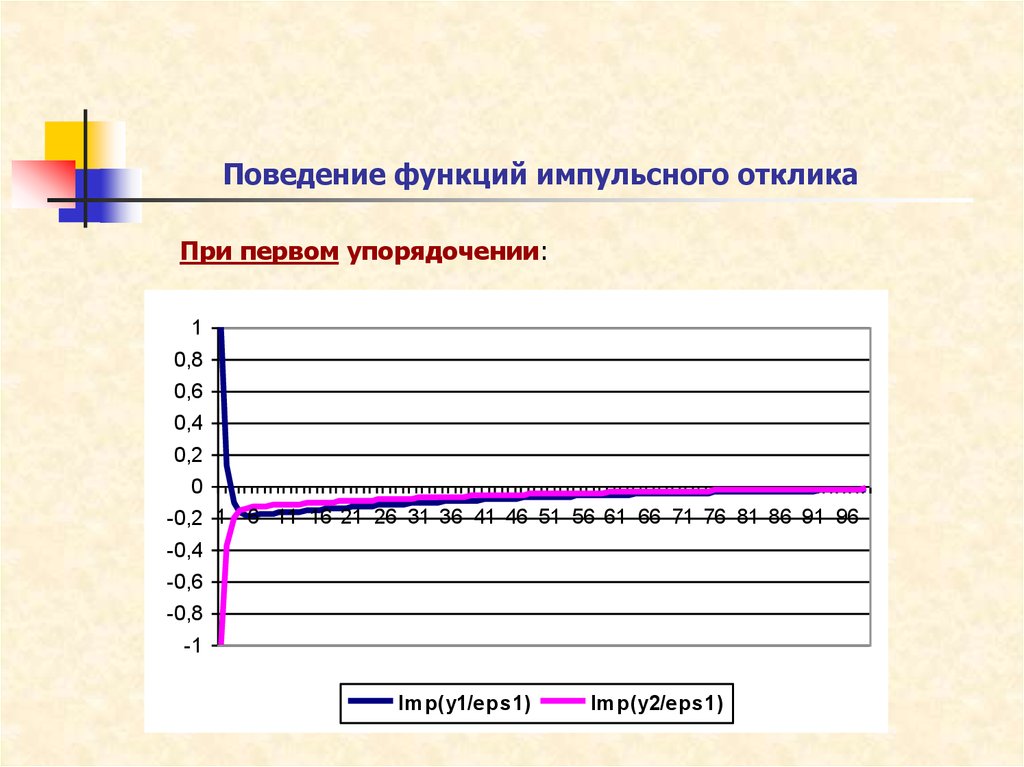
37. Поведение функций импульсного отклика
При первом упорядочении:1
0,8
0,6
0,4
0,2
0
-0,2 1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96
-0,4
-0,6
-0,8
-1
Im p(y1/eps1)
Im p(y2/eps1)
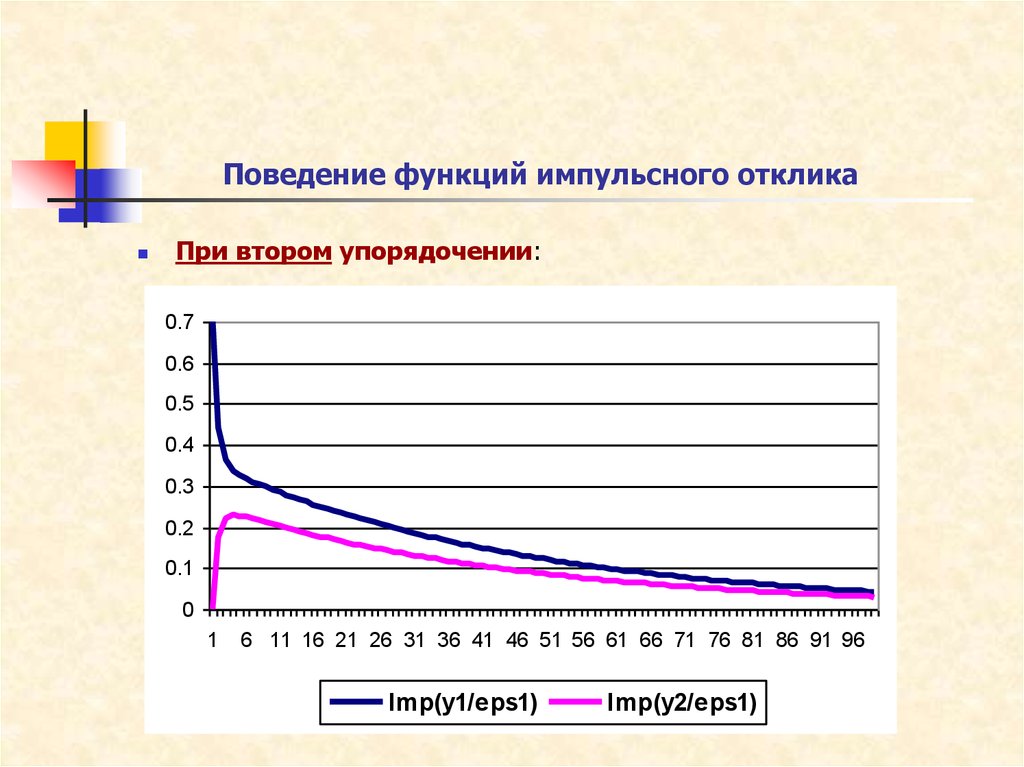
38. Поведение функций импульсного отклика
При втором упорядочении:0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96
Imp(y1/eps1)
Imp(y2/eps1)
39. Проблема: В примере функции импульсного отклика были построены, опираясь на известные коэффициенты приведенной формы и на
известную ковариационную матрицу вектора инноваций вприведенной форме.
Будем считать теперь эти параметры неизвестными и
использовать для построения функций отклика их оценки,
построенные по смоделированным реализациям длины 100.
40. В нашем примере:
11 22 5 / 8 0.62512 1 / 2 0.5
21 1 / 4 0.25
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,
y1t 5 / 8 y1 , t 1 1 / 2 y2 , t 1 2 2 1t 2 2 2 t ,
y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 2 t 1t
y2 t 1 / 4 y1 , t 1 5 / 8 y2 , t 1 2 2 t
Vector Autoregression Estimates
Vector Autoregression Estimates
Первый вариант упорядочения Y1
Y2
Второй вариант упорядочения Y2 Y1
Y1(-1)
Y2(-1)
Y1
Y2
0.677859
0.154110
Y1
Y2
0.610340
0.206764
(0.03880)
(0.06036)
(0.04187)
(0.06525)
[ 17.4726]
[ 2.55303]
[ 14.5766]
[ 3.16883]
0.418677
0.734929
0.497220
0.664915
(0.04350)
(0.06769)
(0.04764)
(0.07425)
[ 9.62382]
[ 10.8573]
[ 10.4360]
[ 8.95554]
(impulse_new.wf1)
Y1(-1)
Y2(-1)
(impulse_new_reord.wf1)
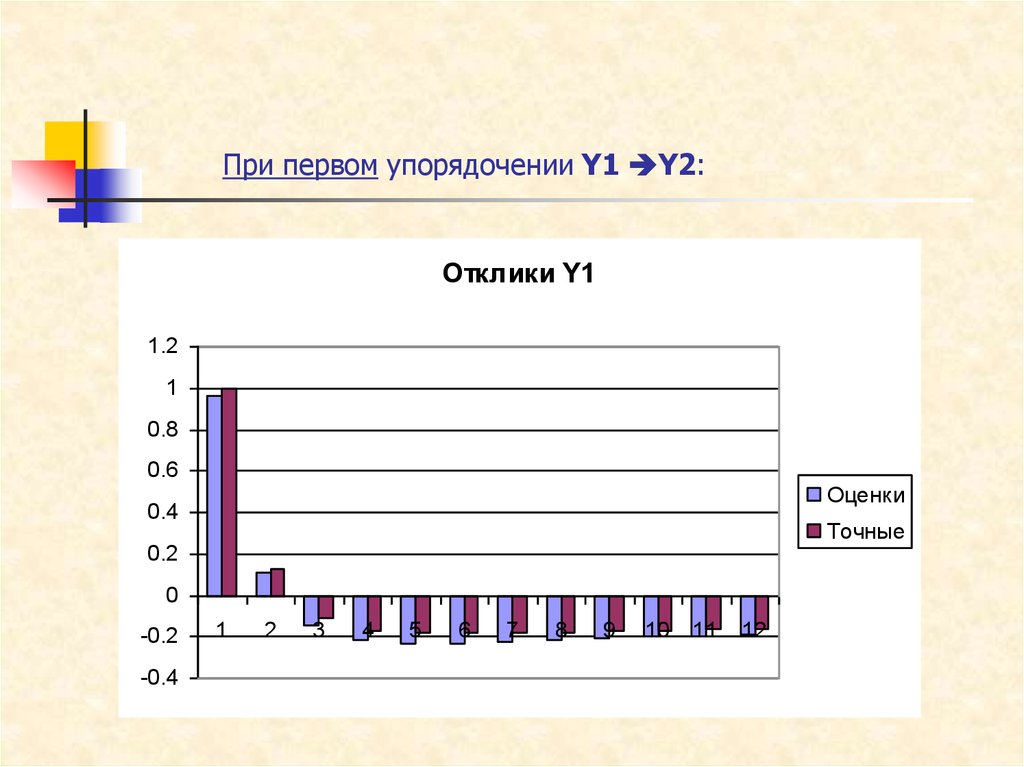
41. При первом упорядочении Y1 Y2:
При первом упорядочении Y1 Y2:Отклики Y1
1.2
1
0.8
0.6
Оценки
0.4
Точные
0.2
0
-0.2
-0.4
1
2
3
4
5
6
7
8
9
10
11
12
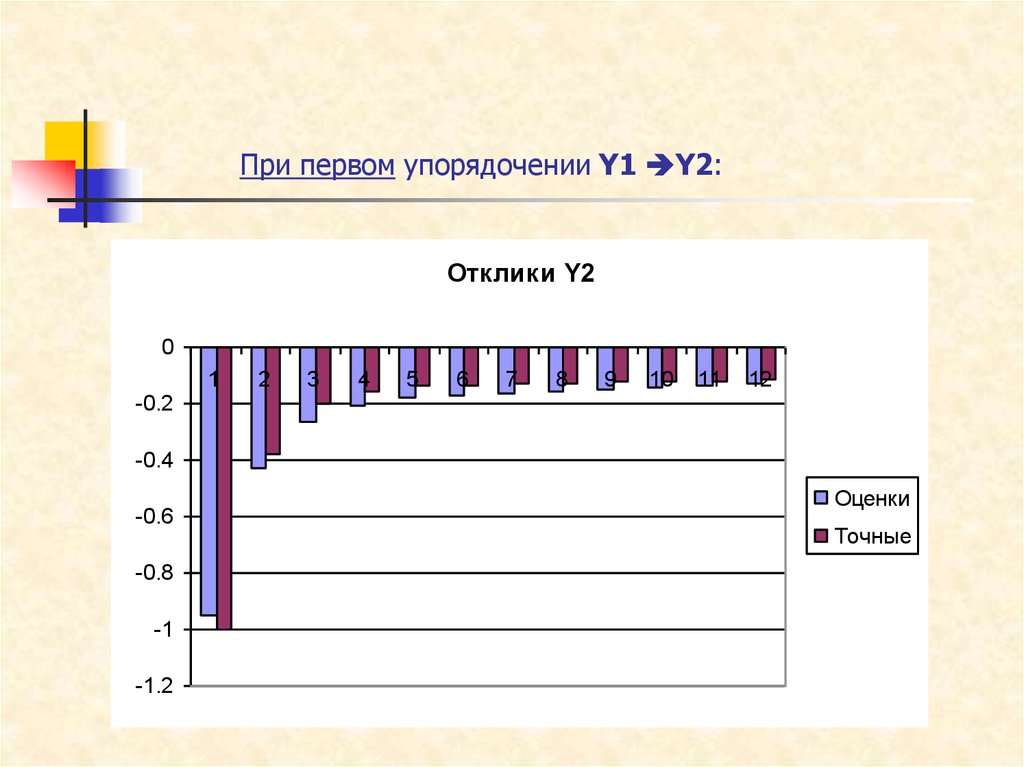
42. При первом упорядочении Y1 Y2:
При первом упорядочении Y1 Y2:Отклики Y2
0
-0.2
1
2
3
4
5
6
7
8
9
10
11
12
-0.4
-0.6
-0.8
-1
-1.2
Оценки
Точные
43.
При втором упорядочении Y2 Y1:Отклики Y1
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
2
3
4
5
6
Оценки
7
8
Точные
9
10
11
12
44.
При втором упорядочении Y2 Y1:Отклики Y2
0.25
0.2
0.15
0.1
0.05
0
1
2
3
4
5
6
Оценки
7
8
Точные
9
10
11
12
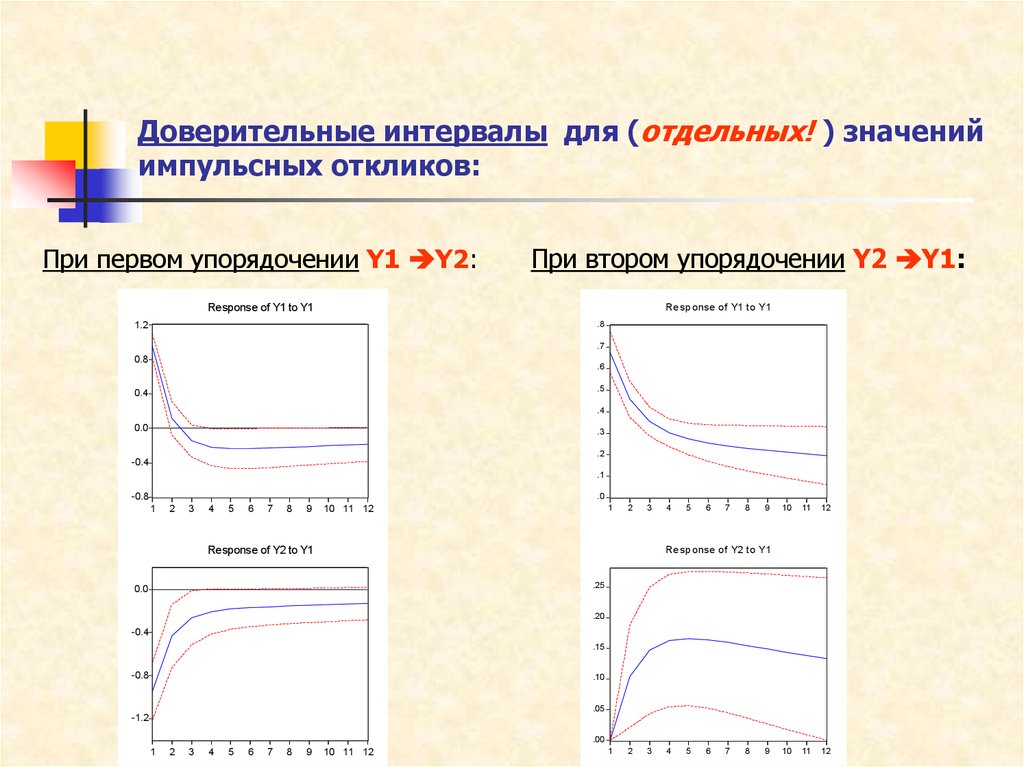
45. Доверительные интервалы для (отдельных! ) значений импульсных откликов:
При первом упорядочении Y1 Y2:При втором упорядочении Y2 Y1:
Response of Y1 to Y1
Re sp onse of Y1 to Y1
1.2
.8
.7
0.8
.6
.5
0.4
.4
0.0
.3
.2
-0.4
.1
-0.8
.0
1
2
3
4
5
6
7
8
9
10 11 12
1
2
3
Response of Y2 to Y1
4
5
6
7
8
9
10
11
12
10
11
12
Re sp onse of Y2 to Y1
.25
0.0
.20
-0.4
.15
-0.8
.10
.05
-1.2
.00
1
2
3
4
5
6
7
8
9
10 11 12
1
2
3
4
5
6
7
8
9
46. Замечание
Столь существенное различие в поведении функцийимпульсного отклика при альтернативных упорядочениях
связано с существенной перекрестной
коррелированностью инноваций в приведенной
форме VAR.
В сгенерированных данных эта корреляция равна
-0.628, а для остатков от оцененной VAR она равна
-0.634.
47. k -мерная VAR(p)
В общем случае предполагают, что структурная модель VAR имеетвид
Ayt C L yt 1 B t
т.е.
t B t
где
t 1t , , kt T
– i.i.d. с нулевым
математическим ожиданием и единичной ковариационной
матрицей
Ik , так что инновации 1t , , k , t
в структуре
являются линейными комбинациями "ортогонализованных"
(“фундаментальных”) инноваций 1t , , kt .
Соответственно, в приведенной форме
ut A 1 t A 1 B t D t
48.
Ayt C L yt 1 B tПриведенная форма:
yt A 1C L yt 1 A 1 B t L yt 1 ut
Структурная форма:
Здесь
Приведенную форму оцениваем OLS, получаем оценки матриц
Ayt A L yt 1 B t
L 1 p L p 1 .
1 , , p . Но по этим оценкам не всегда удается
восстановить структурную форму, т.к. не известны матрицы A
и
B.
49. Проблема идентификации структурных уравнений по приведенной форме
В рассматриваемой ситуацииCov ut Cov A B t A B Cov t A B
1
1
A BB
A
1
Замена
на
ˆ
T
1 T
Оценив приведенную VAR, мы можем получить и оценку
ковариационной матрицы
T
1
ˆ
.
приводит к оценочному уравнению для
ˆ 1 Bˆ Bˆ T A
ˆ 1
ˆ A
T
A и B:
50.
ˆ 1 Bˆ Bˆ 1
ˆT A
ˆ A
Матрица
ˆ
симметрична, и поэтому достаточно оценить
ее элементов.
T
k
k2 k
k
2
2
Общее количество неизвестных элементов в матрицах
равно 2k 2 .
ˆ и Bˆ
A
Поэтому идентификация возможна лишь при наложении на
ˆ и Bˆ достаточного количества ограничений.
матрицы A
51. Разложение Холецкого (Cholesky factorization)
Методология Симса, которую мы применили выше, фактическиоснована на следующем результате (разложение Холецкого).
Всякую положительно полуопределенную матрицу
можно представить в виде произведения QT Q , где Q –
верхняя треугольная матрица с положительными
диагональными элементами, причем такая матрица Q
единственна.
Обозначая
D QT , запишем указанное представление в виде:
DDT
Здесь
D – нижняя треугольная матрица с положительными
диагональными элементами.
52. Факторизация матрицы D
d11d 21
D
d k1
0
d 22
dk2
0
0
d kk
1
d 21
d 31
d
k1
d11
0
D* 0
0
0 d11
0 0
0 0
1 0
0
0
1
0
d 32
1
d k 2
d k 3
0
0
d 22
0
0
d 33
0
0
0
0
0
d kk
0
0
d 22
0
0
d 33
0
0
0
0
0
d kk
53.
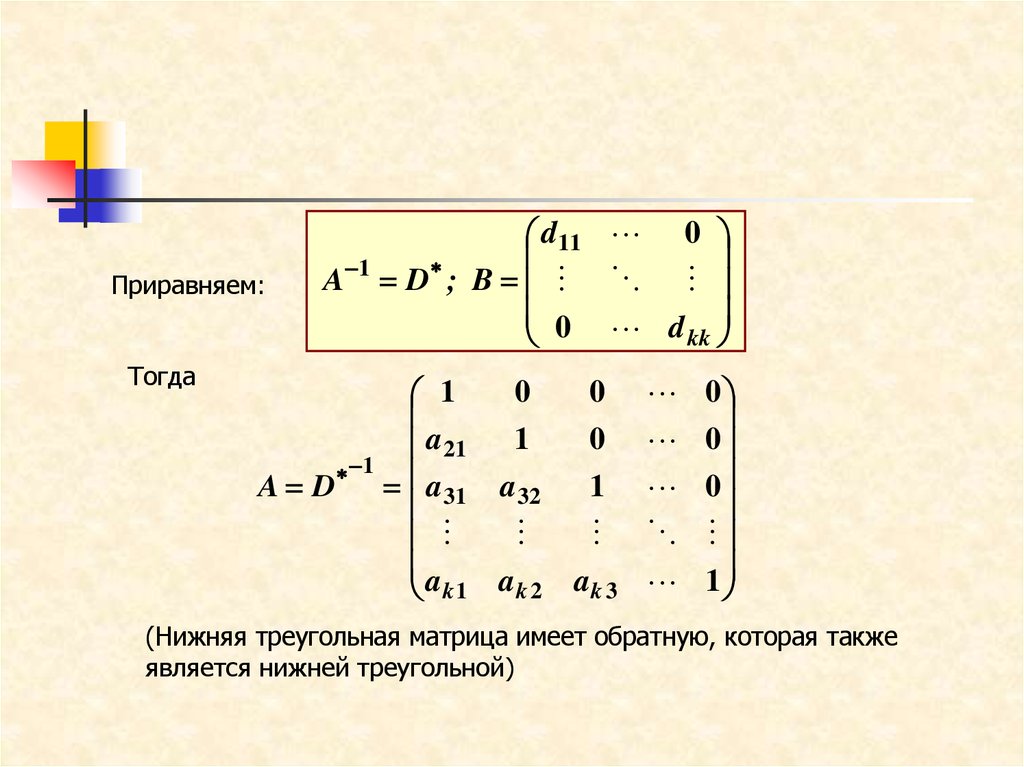
Приравняем:Тогда
d11 0
1
A D ; B
0 d
kk
1
a 21
1
A D
a 31
a
k1
0
0
1
0
a 32
1
ak 2
ak 3
0
0
0
1
(Нижняя треугольная матрица имеет обратную, которая также
является нижней треугольной)
54. Резюме
Если наложить на матрицыA
B
AиB
ограничения:
– нижняя треугольная матрица с единицами на
диагонали;
– диагональная матрица с положительными
диагональными элементами,
то уравнение
1
1
A B A B
T
имеет единственное решение, т.е. имеет место точная
идентифицируемость матриц A и B .
Диагональные элементы bjj матрицы B можно рассматривать как
с.к.о. инновации в i-м уравнении структуры, а форма матрицы A
соответствует рекурсивной системе .
55. Рекурсивная система
В первое уравнение с текущим значением входит только
одна переменная y1t , т.е.,
y1t
объясняется только запаздывающими значениями
переменных y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят только
переменные y1t и y2t , т.е. ,
y2t
объясняется с помощью
y1t
и
yt – 1 , yt – 2 , . . . ,
...
В последнее, k-е уравнение с текущими значениями входят
все переменные y1t , y2t , . . . , ykt , т.е.,
• ykt
объясняется с помощью y2t
, . . . , yk-1,t
и
yt – 1 , yt – 2 , . . .
Такой порядок вхождения переменных интерпретируется как
последовательное включение переменных в порядке
возрастания их эндогенности, так что последней в систему
включается наиболее эндогенная переменная.
При выбранной нормализации (единицы на диагонали матрицы ),
y1t
ykt
– “наименее эндогенная” переменная,
– “наиболее эндогенная” переменная
56. Вернемся к k -мерной VAR(p)
Приведенная форма:yt 1 yt 1 p yt p ut
1 Lyt p Lp yt ut L Lyt ut
Запишем ее в виде:
I L L yt ut
Если все корни уравнения
det I L L 0
лежат за пределами единичного круга, то VAR стабильна, и можно
записать:
yt I L L 1 ut
57. k -мерная VAR(p)
I L L yt utyt I L L
1
ut I 1 L p L
p 1
ut
ut 1ut 1 2 ut 2 3 ut 3 L ut
Это есть векторное MA-представление
k -мерного ряда y1t ,
основанное на инновационной последовательности ut .
Если для некоторого k-мерного случайного вектора
выполнено соотношение
то
ut D t
Cov ut Cov D t D Cov t DT
t
58.
и еслиCov t I k , то
D Cov t DT DDT
так что матрица
D является корнем из матрицы и имеет
левую нижне-треугольную форму:
d11
d 21
D d 31
d
k1
0
0
d 22
0
d 32
dk2
d 33
dk3
0
0
0
d kk
Ее элементы легко вычисляются рекуррентным образом
по элементам ковариационной матрицы .
59.
МатрицуD можно представить в виде
d11
d 21
D d 31
d
k1
1
d 21
d 31
d
k1
0
0
d 22
0
d 32
dk 2
d 33
dk 3
0
0
1
0
d 32
1
d k 2
d k 3
При этом, представление
0
0
0 P B
d kk
0
0
0
1
d11 0
0 d 22
0
0
0
0
DD P B P B
T
разложением Холецкого матрицы
.
0
0
d 33
T
0
0
0
0
d kk
называют
60. Разложение Холецкого (Cholesky factorization)
DD P B P BT
T
P* – левая нижне-треугольная матрица с единицами на
диагонали,
B – диагональная матрица.
Мы уже фактически использовали такую факторизацию ранее для
матрицы
1 1
Cov ut
1 2
где
1 0 1 0 1 0
D
1 1 1 1 0 1
61. Функция импульсных откликов
Теперь мы можем возвратиться к векторному MA-представлениюряда yt , основанному на инновационной последовательности ut :
yt ut 1ut 1 2 ut 2 3 ut 3 L ut
и произвести подстановку
ut D t
.
В результате получаем разложение
yt D t 1 D t 1 2 D t 2 3 D t 3
основанное на инновационной последовательности
Элемент матрицы
h D
с индексом
переменной в момент времени
ij
t+h
t
равен изменению
i-ой
в ответ на единичное
изменение шока j-ой переменной в момент времени t
при сохранении неизменными всех остальных шоков во
все моменты времени.
62. Декомпозиция (разложение) дисперсии ошибок прогнозов (variance decomposition)
yt ut 1ut 1 2 ut 2 3 ut 3yt 1 ut 1 1ut 2 ut 1 3 ut 2
Прогноз по VAR на один шаг вперед:
ˆyt 1 t E yt 1 ut , ut 1 , 1ut 2 ut 1 3 ut 2
Ошибка прогноза по VAR на один шаг вперед:
et 1 t yt 1 ˆyt 1 t ut 1
63.
Ошибка прогноза по VAR на один шаг вперед:yt 1 ˆy t 1 t ut 1 D t 1
Рассмотрим матрицу
e t 1
t et 1 t T
u 1 , t 1
u2 , t 1
2
u
1 ,t 1
u1 , t 1 , u2 , t 1
u
1 , t 1 u2 , t 1
u 1 , t 1 u2 , t 1
u22,t 1
Ee математическое ожидание есть матрица
E yt 1 ˆyt 1
T
ˆ
y
y
t 1
t
t 1 t
на диагонали которой находятся значения дисперсий ошибок
прогнозов на один шаг вперед рядов y1 и y2 .
64.
НоT
ˆ
y
y
t 1
t
t 1 t
E u12,t 1
E u 1 , t 1 u2 , t 1
Cov u
E y t 1 ˆy t 1
E u
1 , t 1 u2 , t 1
u22,t 1
t
Cov D t DCov t D T DD T
DDT d1d1T d 2d 2T
dj
– j-й столбец матрицы
D
d11 T
, d1 d11 d 21 ,
d1
d 21
d 12 T
, d 2 d 1T d 12
d2
d 22
d 22
65.
DDT d1d1T d 2d 2Td11 T
, d1 d11 d 21 ,
d1
d 21
d12 T
, d 2 d12
d2
d 22
d 22
Дисперсия ошибки прогноза на один шаг вперед ряда y1
D e1 , t 1
t d112 d122
Дисперсия ошибки прогноза на один шаг вперед ряда y2
2
2
D e2 , t 1 t d 21
d 22
66.
Дисперсия ошибки прогноза на один шаг вперед ряда y1D e1 , t 1
t d112 d122
Дисперсия ошибки прогноза на один шаг вперед ряда y2
2
2
D e2 , t 1 t d 21
d 22
Получили декомпозиции дисперсий ошибок прогноза
– разложение каждой из них на две компоненты.
Что представляют собой эти компоненты?
67.
u 1 , t 1u2 , t 1
d11 1 , t 1
1 , t 1
D
2 , t 1
d 11
d 21
d 12 1 , t 1
d 22 2 , t 1
d11 1 , t 1 d12 2 , t 1
d 21 1 , t 1 d 22 2 , t 1
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией 1 , t 1
d12 2 , t 1
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией 2 , t 1
2
2
D d11 1 , t 1 d12 2 , t 1 d11
d12
– дисперсия ошибки прогноза на один шаг вперед ряда y1
68.
d11 1 , t 1– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией 1 , t 1
d12 2 , t 1
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией 2 , t 1
2
2
D d11 1 , t 1 d12 2 , t 1 d11
d12
– дисперсия ошибки прогноза на один шаг вперед ряда y1
2
D d11 1 , t 1 d11
– составляющая дисперсии ошибки прогноза на один шаг вперед
D
ряда y1, обусловленная фундаментальной инновацией
2
d12 2 , t 1 d12
1 , t 1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
2 , t 1
69.
22
D d11 1 , t 1 d12 2 , t 1 d11
d12
– дисперсия ошибки прогноза на один шаг вперед ряда y1
2
D d11 1 , t 1 d11
– составляющая дисперсии ошибки прогноза на один шаг вперед
D
ряда y1, обусловленная фундаментальной инновацией
2
d12 2 , t 1 d12
1 , t 1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией 2 , t 1
2
d 11
– доля дисперсии ошибки прогноза на один шаг вперед
2
2 ряда y , обусловленная фундаментальной инновацией
d 11
d 12
1 , t 1
1
2
d12
2
2
d11
d12
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией 2 , t 1
70.
22
D d 21 1 , t 1 d 22 2 , t 1 d 21
d 22
D
– дисперсия ошибки прогноза на один шаг вперед ряда y2
2
d 21 1 , t 1 d 21
– составляющая дисперсии ошибки прогноза на один шаг вперед
D
ряда y2, обусловленная фундаментальной инновацией
2
d 22 2 , t 1 d 22
1 , t 1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией 2 , t 1
2
d 21
– доля дисперсии ошибки прогноза на один шаг вперед
2
2
ряда y2, обусловленная фундаментальной инновацией 1 , t 1
d 21
d 22
2
d 22
2
2
d 21
d 22
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией 2 , t 1
71.
Вернемся к двумерной VAR(1)y1t 5 / 8 y1 , t 1 1 / 2 y2 , t 1 u1t ,
y2 t 1 / 4 y1 , t 1 5 / 8 y2 , t 1 u2 t
При упорядочении Y1 Y2
1 0
D
1 1
72.
1 0D
1 1
1
1 – доля дисперсии ошибки прогноза на один шаг вперед
1 0
ряда y1, обусловленная фундаментальной инновацией 1 , t 1
– доля дисперсии ошибки прогноза на один шаг вперед
0
0
ряда y1, обусловленная фундаментальной инновацией 2 , t 1
1 0
1
1 – доля дисперсии ошибки прогноза на один шаг вперед
1 1 2 ряда y2, обусловленная фундаментальной инновацией 1 , t 1
1
1 – доля дисперсии ошибки прогноза на один шаг вперед
1 1 2 ряда y2, обусловленная фундаментальной инновацией 2 , t 1
73.
Декомпозиция дисперсии ошибок прогнозовОшибка прогноза по VAR на h шагов вперед вычисляется по
формуле:
yt h ˆyt h t ut h 1ut h 1 2ut h 2 h 1ut 1
E ( yt h ˆyt h t )( yt h ˆyt h t )T
1 1T h 1 hT 1
DDT 1 DDT 1T h 1 DDT hT 1
d j d Tj 1d j d Tj 1T h 1d j d Tj hT 1
k
j 1
где
dj – j-й столбец матрицы D.
74.
Декомпозиция дисперсии ошибок прогнозовОшибка прогноза по VAR на h шагов вперед вычисляется по
формуле:
yt h ˆyt h t ut h 1ut h 1 2ut h 2 h 1ut 1
E ( yt h ˆyt h t )( yt h ˆyt h t )T
1 1T h 1 hT 1
DDT 1 DDT 1T h 1 DDT hT 1
d j d Tj 1d j d Tj 1T h 1d j d Tj hT 1
k
j 1
Вкдад j-й ф.и. в дисперсию прогноза ряда ym равен m-у
диагональному элементу матрицы, заключенной в скобки под
знаком суммы.
75. Декомпозиция дисперсии ошибок прогнозов
Обычно результат такой декомпозиции представляется какперечень долей каждого из слагаемых в общей сумме.
В пакетах программ статистического анализа предлагаются
также графики, показывающие динамику изменений
каждой такой доли с изменением h, h =1, 2, . . .
76.
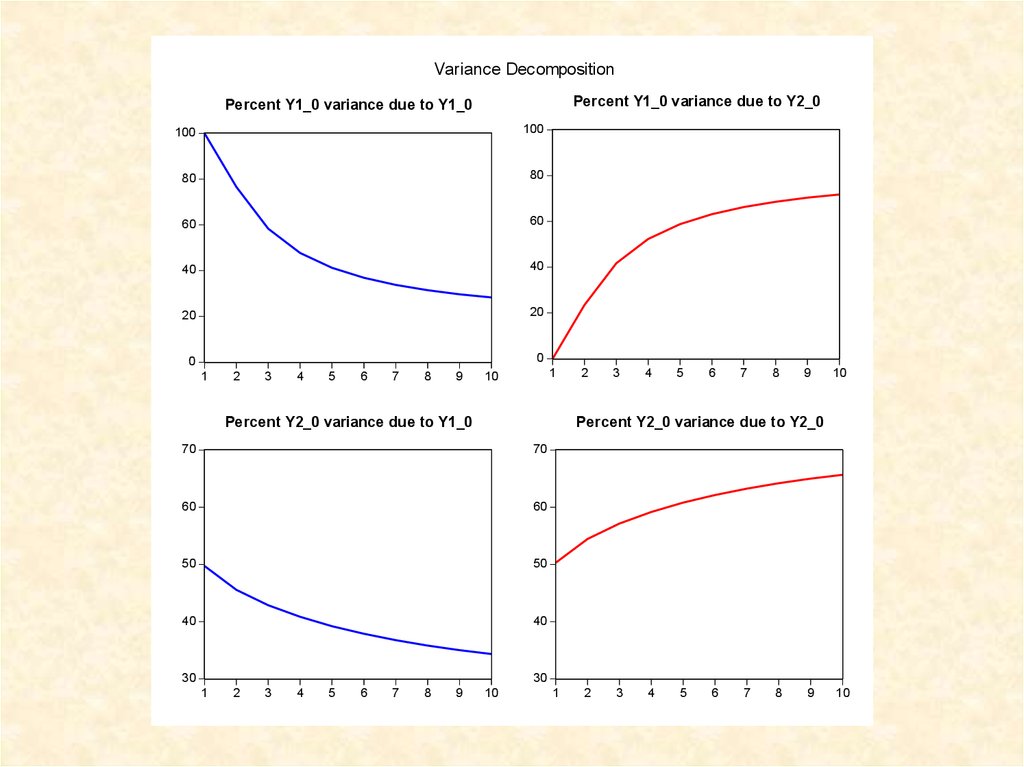
CholeskyOrdering: Y1 Y2
Variance Decomposition
Percent Y1_0 variance due to Y2_0
Percent Y1_0 variance due to Y1_0
100
100
80
80
60
60
40
40
20
20
0
0
1
2
3
4
5
6
7
8
9
1
10
Percent Y2_0 variance due to Y1_0
2
3
4
5
6
7
8
9
10
Percent Y2_0 variance due to Y2_0
70
70
60
60
50
50
40
40
30
30
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
77.
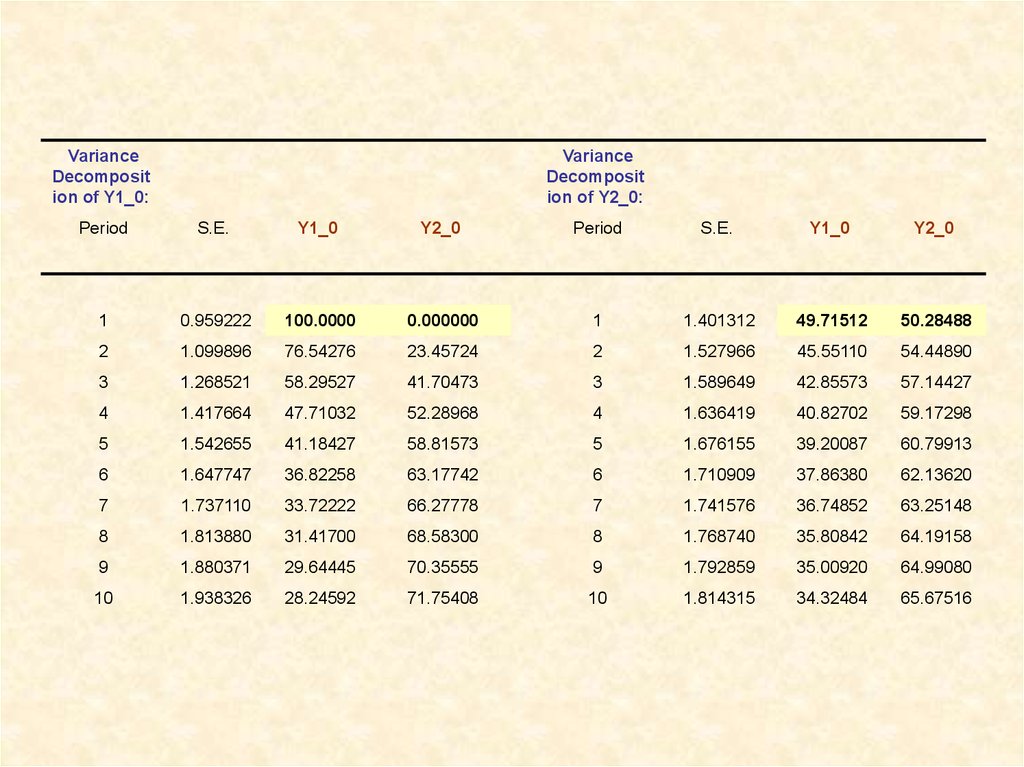
VarianceDecomposit
ion of Y1_0:
Variance
Decomposit
ion of Y2_0:
Period
S.E.
Y1_0
Y2_0
Period
S.E.
Y1_0
Y2_0
1
0.959222
100.0000
0.000000
1
1.401312
49.71512
50.28488
2
1.099896
76.54276
23.45724
2
1.527966
45.55110
54.44890
3
1.268521
58.29527
41.70473
3
1.589649
42.85573
57.14427
4
1.417664
47.71032
52.28968
4
1.636419
40.82702
59.17298
5
1.542655
41.18427
58.81573
5
1.676155
39.20087
60.79913
6
1.647747
36.82258
63.17742
6
1.710909
37.86380
62.13620
7
1.737110
33.72222
66.27778
7
1.741576
36.74852
63.25148
8
1.813880
31.41700
68.58300
8
1.768740
35.80842
64.19158
9
1.880371
29.64445
70.35555
9
1.792859
35.00920
64.99080
10
1.938326
28.24592
71.75408
10
1.814315
34.32484
65.67516
78.
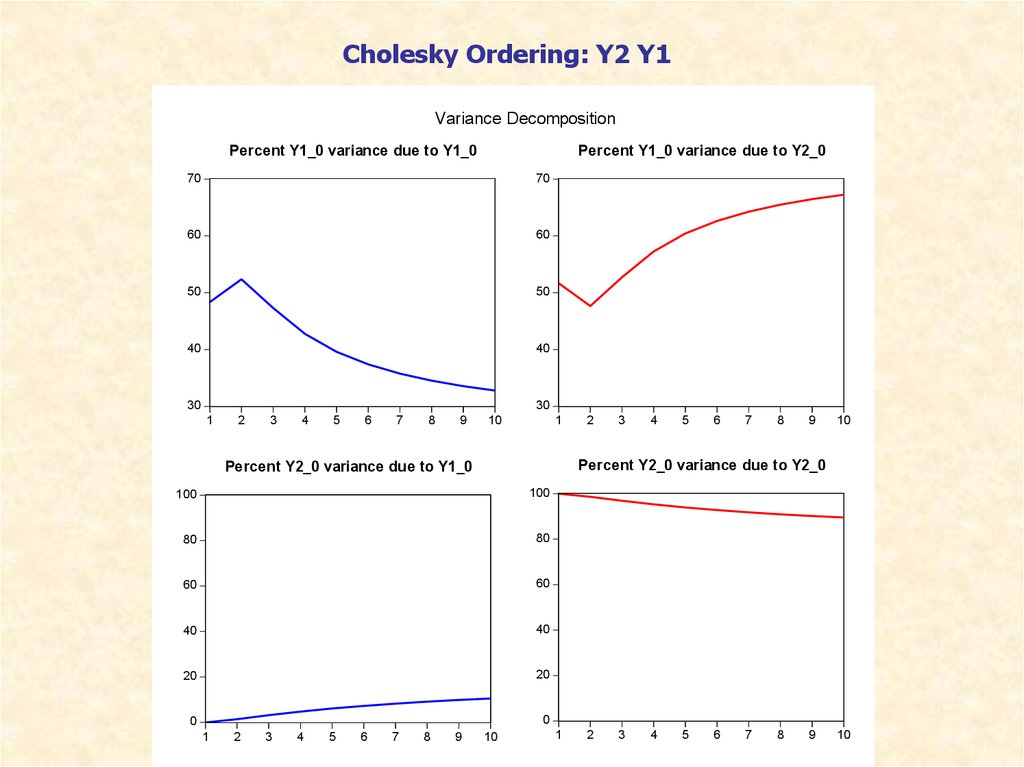
Cholesky Ordering: Y2 Y1Variance Decomposition
Percent Y1_0 variance due to Y1_0
Percent Y1_0 variance due to Y2_0
70
70
60
60
50
50
40
40
30
30
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
Percent Y2_0 variance due to Y2_0
Percent Y2_0 variance due to Y1_0
100
100
80
80
60
60
40
40
20
20
0
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
79.
VarianceDecompos
ition of
Y1_0:
Period
Variance
Decomposi
tion of
Y2_0:
S.E.
Y1_0
Y2_0
1
0.959222
50.28488
49.71512
2
1.099896
53.52920
3
1.268521
4
Period
S.E.
Y1_0
Y2_0
1
1.401312
0.000000
100.0000
46.47080
2
1.527966
1.182727
98.81727
48.33907
51.66093
3
1.589649
2.584105
97.41590
1.417664
44.19547
55.80453
4
1.636419
3.818615
96.18138
5
1.542655
41.44300
58.55700
5
1.676155
4.847692
95.15231
6
1.647747
39.56726
60.43274
6
1.710909
5.701919
94.29808
7
1.737110
38.22719
61.77281
7
1.741576
6.416083
93.58392
8
1.813880
37.22952
62.77048
8
1.768740
7.018400
92.98160
9
1.880371
36.46213
63.53787
9
1.792859
7.530525
92.46947
10
1.938326
35.85661
64.14339
10
1.814315
7.969058
92.03094
80. Оценивание SVAR в EViews
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 u1t ,y 2 t 1 / 4 y1 , t 1 5 / 8 y 2 , t 1 u2 t
При первом упорядочении
u1t 1t ,
u2 t 2 t 1t
или
u1t 1t ,
u1t u2 t 2 t
И, так как
ut A 1 B t Aut B t
А – нижняя треугольная матрица с единицами на диагонали,
а B – диагональная матрица, то
и
1 0
1 0
A
, B
1 1
0 1
81.
1 01 0
A
, B
1 1
0 1
Таким образом, при первом упорядочении SVAR (структурная VAR)
принимает вид:
1 0 y1t 1 0 5 8 1 2 y1 ,t 1 1t
1 1 y2 t 1 1 1 4 5 8 y2 ,t 1 2 t
5 8 1 2 y1 ,t 1 1t
7 8 9 8 y2 ,t 1 2 t
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,
y1t y 2 t 7 / 8 y1 , t 1 9 / 8 y 2 , t 1 2 t
82.
y1t 5 / 8 y1 , t 1 1 / 2 y 2 , t 1 1t ,y1t y 2 t 7 / 8 y1 , t 1 9 / 8 y 2 , t 1 2 t
В рекурсивной структуре, полученной с использованием
изложенного метода, случайные ошибки в разных уравнениях
являются взаимно некоррелированными случайными
величинами. Это означает, что соответствующую систему
одновременных уравнений можно оценивать, используя обычный
метод наименьших квадратов (OLS).
Статистическая модель:
y1t c11 y1 , t 1 c12 y 2 , t 1 1t
y 2 t a 21 y1t c 21 y1 , t 1 c 22 y 2 , t 1 2 t
83. y1=c(1)*y1(-1)+c(2)*y2(-1) y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1)
C(1)C(2)
C(3)
C(4)
C(5)
Результаты оценивания:
Coefficient
Std. Error
t-Statistic
--------------------------------------------------------0.610340
0.041871
14.57663
0.497220
0.047645
10.43600
-0.988495
0.122953
-8.039596
0.810082
0.090567
8.944557
1.156414
0.084061
13.75689
y1t 5 / 8 y1 , t 1 1 / 2 y2 , t 1 1t ,
y1t y2 t 7 / 8 y1 , t 1 9 / 8 y2 , t 1 2 t
Prob.
0.0000
0.0000
0.0000
0.0000
0.0000
84. EViews: Оценивание матриц A и B структурной формы
Создав объект VAR и оценив коэффициенты приведенной VAR,можно получить в рамках этого объекта и оценки указанных
матриц.
Для этого заказываем: Proc Estimate Structural Factorization
В открывшемся окне указываем форму связи между ошибками в
приведенной VAR и фундаментальными инновациями,
соответствующую выбранному упорядочению в схеме Холецкого.
85.
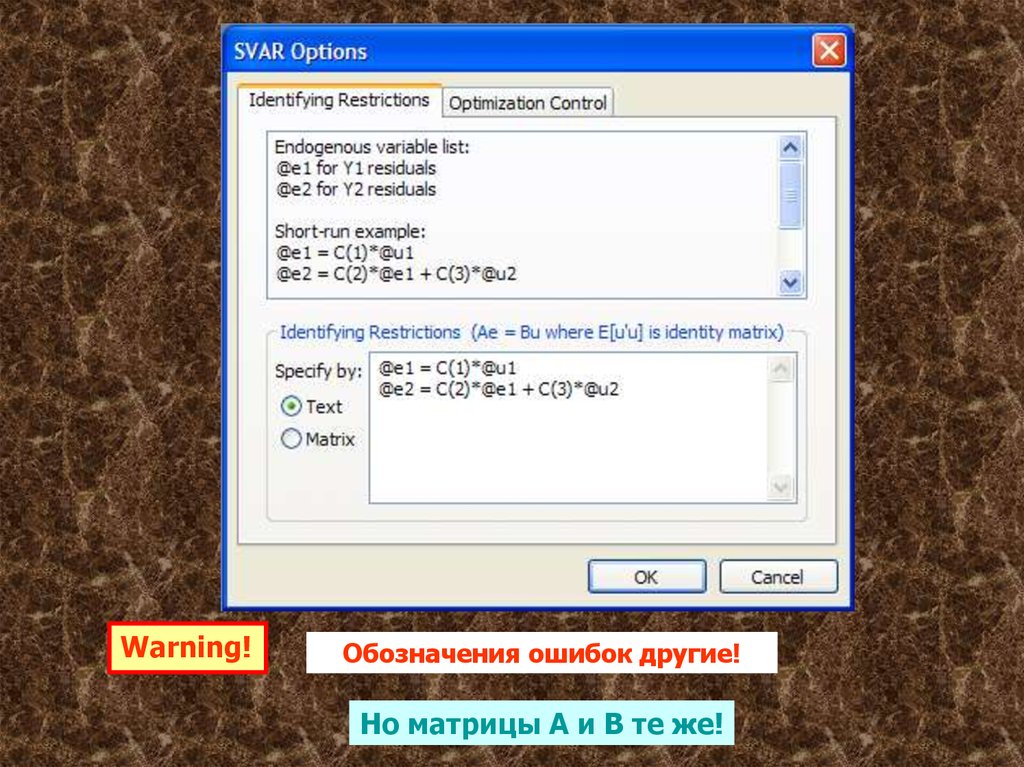
Warning!Обозначения ошибок другие!
Но матрицы A и B те же!
86.
Результаты оценивания матриц A и BModel: Ae = Bu where E[uu']=I
Restriction Type: short-run text
form
@e1 = C(1)*@u1
@e2 = C(2)*@e1 + C(3)*@u2
where
@e1 represents Y1 residual
@e2 represents Y2 residuals
Coefficient
C(2)
C(1)
C(3)
Estimated B matrix:
0.962944
0.000000
0.000000
1.143882
-0.997582
0.962944
1.143882
Estimated A matrix:
1.000000
0.000000
0.997582
1.000000
87. Замечания
Принимая различные порядки последовательноговхождения переменных, мы получаем и различное
поведение импульсных функций отклика, что дает
возможность сравнивать альтернативные теории.
В рекурсивной структуре, полученной с использованием
изложенного метода, случайные ошибки в разных уравнениях
являются взаимно некоррелированными случайными
величинами. Это означает, что соответствующую систему
одновременных уравнений можно оценивать, используя обычный
метод наименьших квадратов (OLS).
88. Пример. В модели двумерной VAR переменная y1t может представлять объем производства (output), а переменная y2t – “деньги”
(money).Упорядочение
1t
2t
y1t
y2t
соответствует схеме
u1t
u2t
В этой схеме шоки в объеме производства оказывают немедленное
воздействие и на объем производства и на деньги, тогда как
шоки в деньгах оказывают немедленное воздействие только на
деньги.
Такое упорядочение соответствует представлению, согласно
которому денежная политика имеет только запаздывающее
влияние на объем производства.
89. Пример (продолжение)
Упорядочение2t
y2t
y1t
1t
соответствует схеме
u2t
u1t
В этой схеме шоки в объеме производства оказывают немедленное
воздействие только на объем производства, тогда как шоки в
деньгах оказывают немедленное воздействие и на деньги и на
объем производства.
Это соответствует представлению о том, что деньги поставляются
центральным банком, а объем производства становится известным
центральному банку лишь с опозданием. Поэтому деньги не
могут немедленно реагировать на шоки в объеме
производства.























































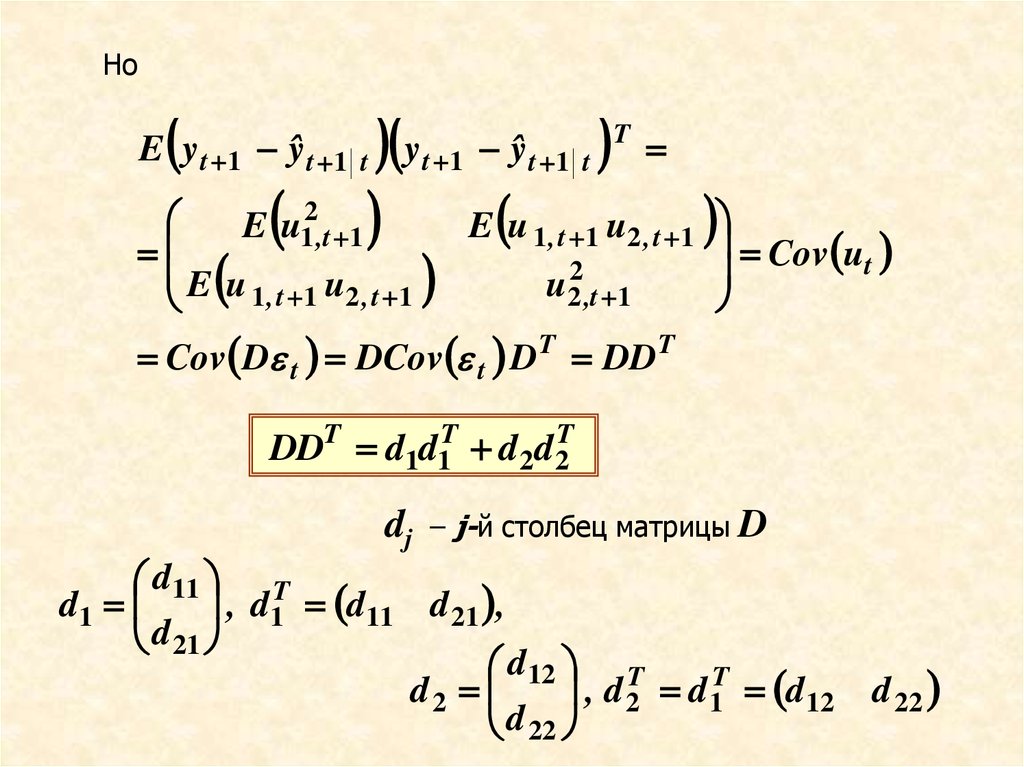





















 economics
economics








