Similar presentations:
Выбор и поведение потребителя
1. Микроэкономика уровень II (упрощенный)
Практика (4 часа)Преподаватель:
к.э.н., доцент Павлова
Елена Евгеньевна
2. Выбор и поведение потребителя
Задача №1Функция полезности индивида имеет вид U(X, Y) = X Y.
а) Какое количество товаров X и Y будет приобретать индивид, если
его доход равен 100 ден. ед., цены товаров X и Y соответственно
равны PX = 5 ден. ед., PY = 5 ден. ед.?
б) Найдите количество товаров X и Y при приобретении которых,
максимизируется полезность индивида, если цена товара X
возрастет до 20 ден. ед.
в)* Определите величину эффекта замены и эффекта дохода по Хиксу
и по Слуцкому, общего эффекта изменения цены.
г)* Определить компенсирующее и эквивалентное изменение
дохода.
д) Вывести функцию спроса на благо Х.
г) Определить коэффициенты прямой эластичности спроса по цене.
Все этапы решения представить графически.
к.э.н., доцент Павлова Е.Е.
2
3. а) Дано: U(X, Y) = X Y, I=100, PX = 5, PY = 5 Найти: Х1, Y1
Решение:Оптимум потребителя:
Бюджетное ограничение:
MRS XY
Y Y TU MU X PX
X X TU MU Y
PY
I PX X Py Y
Оптимальную комбинацию благ (точка Е1) ищем, решая систему
уравнений:
100 5 X 5Y
Y 5
X 1 10; Y1 10
X 5
к.э.н., доцент Павлова Е.Е.
3
4. Для упрощения расчетов
• Для функции Кобба-Дугласа вида:U X Y
MU X Y
MU Y X
к.э.н., доцент Павлова Е.Е.
4
5. б) Дано: U(X, Y) = X Y, I=100, PX = 20, PY = 5 Найти: Х1, Y1
Оптимальную комбинацию благ при росте цены товара Х (точка Е2)ищем, решая систему уравнений:
100 20 X 5Y
Y 20
X 2 2,5; Y2 10
X
5
к.э.н., доцент Павлова Е.Е.
5
6. Изменение оптимума потребителя при росте цены товара Х
YU1
tg = PX/PY
1
PX повысилась до PX1
2
tg = PX1/PY
U2
Y2 = Y1=10
E2
E1
X2 =2,5
X1=10
к.э.н., доцент Павлова Е.Е.
X
6
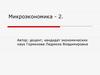
7. Общий эффект изменения цены. Эффект замены и эффект дохода по Хиксу
Общий эффект изменения цены по Хиксу составит:X = X2 – X1 = 2,5 – 10= –7,5;
Y = Y2 – Y1 = 10 – 10 = 0
При разложении общего эффекта сохраняется первоначальный
уровень полезности: U1=XY = 10 10=100.
Т.е. Эффект замены (E1 E3 ):
U 1 const
PX
PX 1
PY
PY
Эффект дохода (E3 E2 ):
U1 U 2
PX 1
const
PY
к.э.н., доцент Павлова Е.Е.
7
8. Общий эффект изменения цены. Эффект замены и эффект дохода по Хиксу
Точка Е3:XY 100
U 1 XY 100 const
MU X
PX Y 20 X 3 5; Y3 20
MRS XY
X
5
MU Y
PY
Следовательно, эффект замены:
X = X3 – X1 = 5 – 10= –5;
Y = Y3 – Y1 = 20 – 10 = 10,
эффект дохода:
X =X2 – X3 =2,5 – 5 = –2,5;
Y = Y2 – Y3 = 10 – 20 = –10.
к.э.н., доцент Павлова Е.Е.
8
9. Общий эффект изменения цены. Эффект замены и эффект дохода по Хиксу
Y3
U1
tg = PX/PY
1
PX повысилась до PX1
Y3
tg = PX1/PY
U2
ЭД
Y2 Y1
E3
2
E2
ЭЗ
E1
ЭЗ
ЭД
X2
X3
X1
к.э.н., доцент Павлова Е.Е.
X
9
10. Общий эффект изменения цены. Эффект замены и эффект дохода по Слуцкому
• Общий эффект по Слуцкому тот же самый• После изменения цены товара уровень удовлетворения
потребителя останется прежним, если он будет иметь
возможность купить первоначальный товарный набор.
Для этого ему потребуется:
I = PхX + PуY= 20 10+5 10 = 250 ден.ед.
к.э.н., доцент Павлова Е.Е.
10
11. Общий эффект изменения цены. Эффект замены и эффект дохода по Слуцкому
Точка Е3:250 20 X 5Y
MU X PX
Y 20
X 3 6,25; Y3 25
MU Y
PY
X
5
Следовательно, эффект замены:
X = X3 – X1 = 6,25 – 10= –3,75;
Y = Y3 – Y1 = 25 – 10 = 15,
эффект дохода:
X =X2 – X3 =2,5 – 6,25 = –3,75;
Y = Y2 – Y3 = 10 – 25 = –15.
к.э.н., доцент Павлова Е.Е.
11
12. Общий эффект изменения цены. Эффект замены и эффект дохода по Слуцкому
Y3
1
U1
tg = PX/PY
PX повысилась до PX1
Y3=25
E3
2
ЭД
Y2=Y1=10
U3
U2
E2
ЭЗ
tg = PX1/PY
E1
ЭЗ
X2=2,5
ЭД
X3=6,25 X1=10
к.э.н., доцент Павлова Е.Е.
X
12
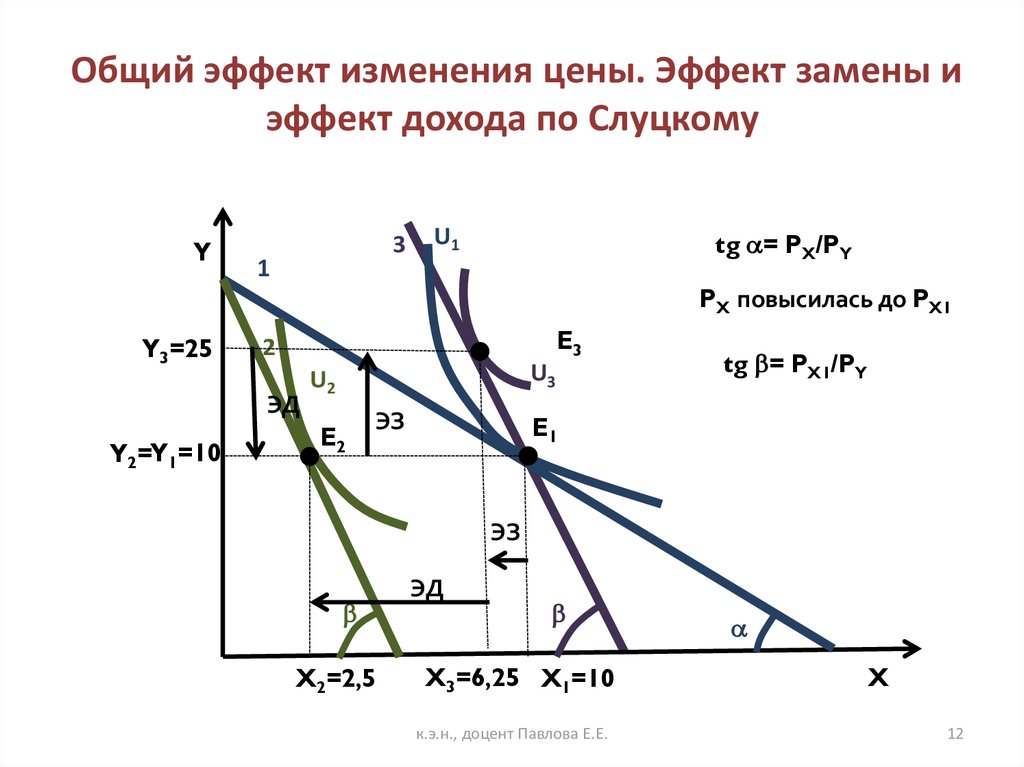
13. Компенсирующее изменение дохода
• Для нахождения на первоначальной кривойбезразличия при новой цене блага X индивиду
нужно иметь бюджет:
I = (20·5 + 5·20) = 200 ден. ед.
Компенсирующее изменение дохода по Хиксу
составит: 200 – 100 = 100
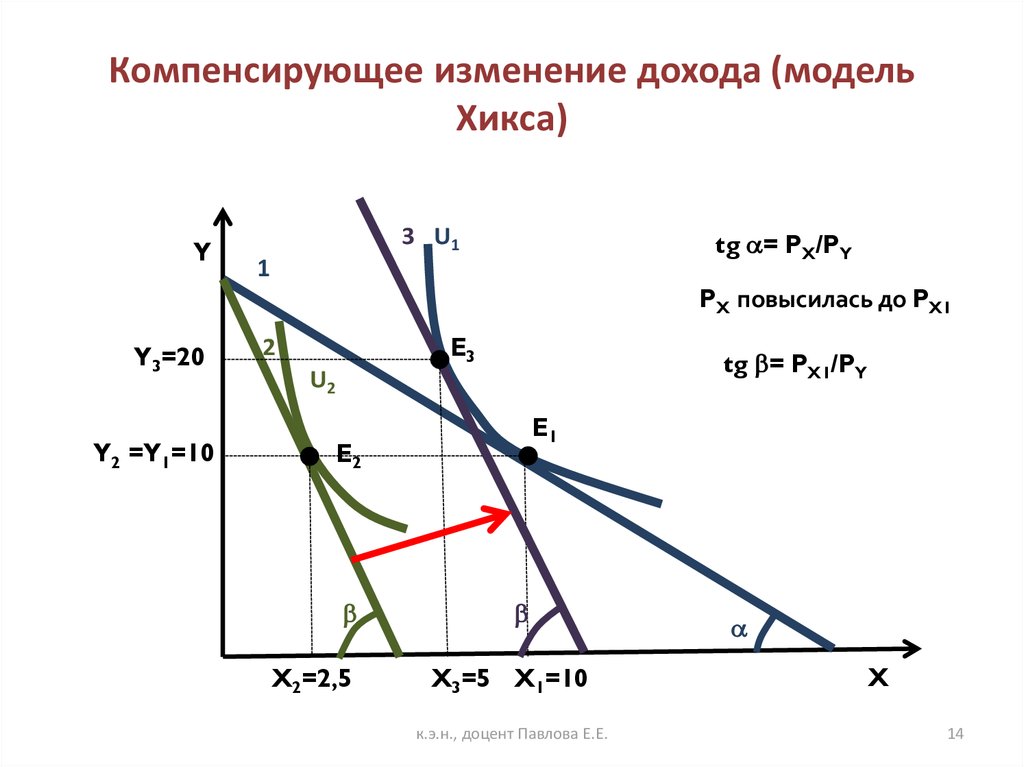
• Для покупки исходной потребительской корзины
при новой цене блага X индивиду нужно иметь
бюджет:
I = (20·6,25 + 5·25) = 250 ден. ед.
Компенсирующее изменение дохода по Слуцкому
составит: 250 – 100 = 150
к.э.н., доцент Павлова Е.Е.
13
14. Компенсирующее изменение дохода (модель Хикса)
Y3 U1
tg = PX/PY
1
PX повысилась до PX1
Y3=20
Y2 =Y1=10
E3
2
tg = PX1/PY
U2
E1
E2
X2=2,5
X3=5 X1=10
к.э.н., доцент Павлова Е.Е.
X
14
15. Компенсирующее изменение дохода (модель Слуцкого)
YY3=25
Y2 =Y1=10
3
1
tg = PX/PY
U3
U1
PX повысилась до PX1
E3
2
E2
X2=2,5
tg = PX1/PY
E1
X3=6,25 X1=10
к.э.н., доцент Павлова Е.Е.
X
15
16. Эквивалентное изменение дохода
Точка Е3:U 2 XY 2,5 10 25
MU X
PX
Y
5
X 3 5; Y3 5
MU Y
PY
X
5
При исходных ценах такой набор благ можно купить при бюджете:
I = 5·5 + 5·5 = 50 ден. ед.
Эквивалентное изменение дохода равно: 100 – 50 = 50.
к.э.н., доцент Павлова Е.Е.
16
17. Эквивалентное изменение дохода
YU1
tg = PX/PY
1
PX повысилась до PX1
2
tg = PX1/PY
U2
Y2 =Y1=10
E1
E2
3
E3
Y3=5
X2=2,5
X3=5
X1=10
к.э.н., доцент Павлова Е.Е.
X
17
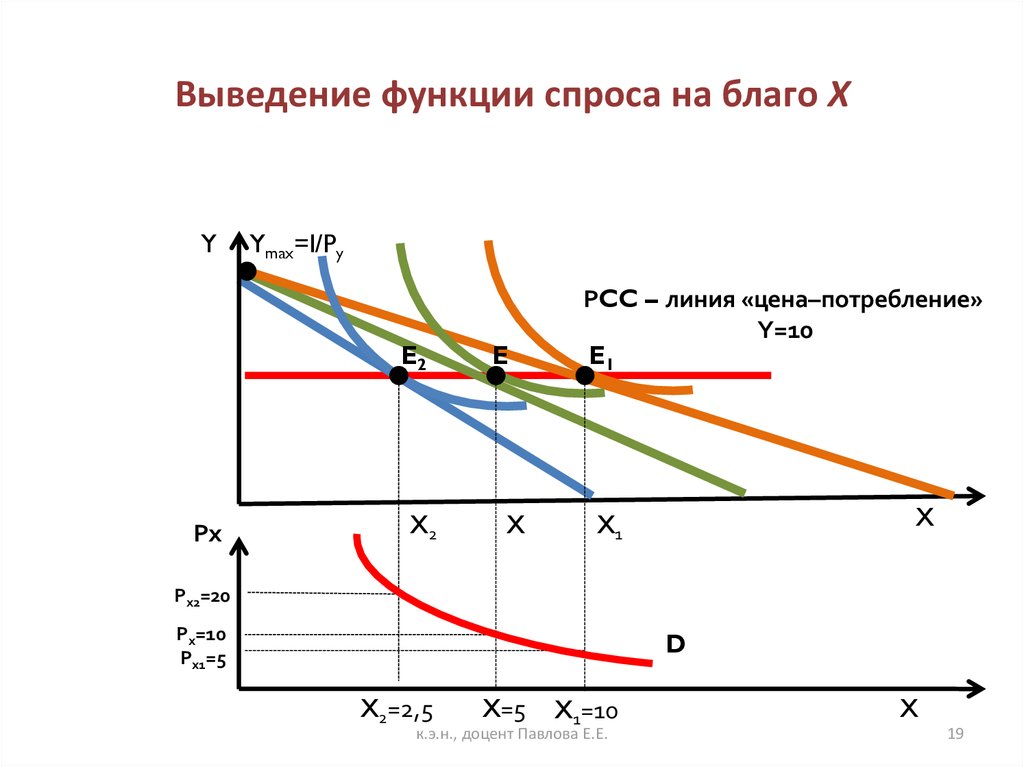
18. Выведение функции спроса на благо Х
В функции спроса объединены только оптимальные объемы благапри соответствующем уровне цены:
I PX X PY Y
MU X
PX
MU Y
PY
100 PX X PY Y
50
PX
Y
100
2
P
X
X
X
PX X PY Y
PX
X
PY
к.э.н., доцент Павлова Е.Е.
18
19. Выведение функции спроса на благо Х
YYmax=I/Py
E2
Рх
X2
E
X
РCC – линия «цена–потребление»
Y=10
E1
X
X1
Рх2=20
Рх=10
Рх1=5
D
X2=2,5
X=5
X1=10
к.э.н., доцент Павлова Е.Е.
X
19
20. Коэффициенты прямой эластичности спроса по цене
• Дуговая эластичность:ei
2,5 10 20 5
7,5 25
1
20 5 2,5 10
15 12,5
• Точечная эластичность:
50 Pi
50 Pi
50
ei 2
1
Pi Qi
50 Pi
Pi Qi
к.э.н., доцент Павлова Е.Е.
20
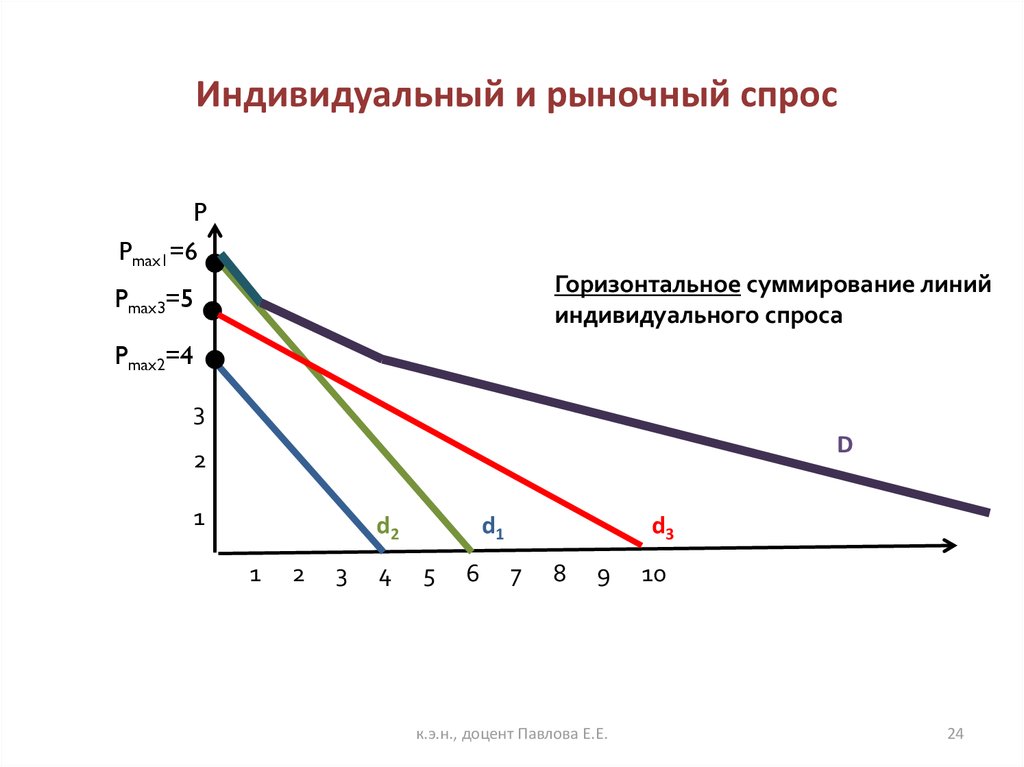
21. Индивидуальный и рыночный спрос
Задача №2На рынке имеются три покупателя со следующими
функциями спроса: qD1=6-Р; qD2 =4-Р; qD3=10-2Р.
Определить:
1. Сколько единиц товара будет продано на рынке при
Р = 3?
2. При какой цене можно будет продать 12 единиц
товара?
3. Какова эластичность спроса по цене при Р = 4?
4. Какова эластичность спроса по цене при Q = 1?
к.э.н., доцент Павлова Е.Е.
21
22. Индивидуальный и рыночный спрос
Функции спроса трех потребителей линейны:qD1=6-Р
qD2 =4-Р
qD3=10-2Р
Для каждого потребителя существует своя область
допустимых значений цены:
Pmax1=6,
Pmax2=4,
Pmax3=5,
когда 0 ≤ Р 4, на рынке присутствуют все три
покупателя, в интервале 4 ≤Р 5 — первый и третий, а
в интервале 5 ≤Р 6 — только один первый
покупатель.
к.э.н., доцент Павлова Е.Е.
22
23. Индивидуальный и рыночный спрос
Следовательно: Функция рыночного спросаQD= qD1 + qD2+ qD3= 20 - 4Р, при 0 ≤ Р 4
QD= qD1 + qD3=16 - 3Р,
при 4 ≤ Р 5
QD= qD1=6-Р,
при 5 ≤ Р 6
примет вид:
и 4 Q ≤ 20
и 1 Q≤4
и 0 Q≤1
1. Р = 3 QD= 20 - 4Р = 20-12=8
2. Q = 12 QD= 20 - 4Р 12= 20-4P P = 2
3. Р = 4 QD= 16 – 3P Q= 4
4. Q = 1
QD= 6-P
ei 3
1= 6 - P P = 5
к.э.н., доцент Павлова Е.Е.
4
3
4
5
e i 1 5
1
23
24. Индивидуальный и рыночный спрос
PPmax1=6
Горизонтальное суммирование линий
индивидуального спроса
Pmax3=5
Pmax2=4
3
D
2
1
d2
1
2
3
4
d3
d1
5
6
7
8
9
к.э.н., доцент Павлова Е.Е.
10
24
25. Индивидуальное предложение труда
Задача № 4Предпочтения индивида относительно денег и
свободного времени отображается функцией
полезности U = (I + 27)0,5F0,25, где I = wL –
заработная плата, F – свободное время,
равное разности между календарным
временем (Т) и рабочим временем: F = Т – L.
Сколько часов индивид будет работать в
течение календарного времени Т = 33 при
цене труда w = 3 и какова эластичность
предложения труда по цене?
к.э.н., доцент Павлова Е.Е.
25
26. Дано: U = (I + 27)0,5F0,25, Т = 33, w = 3
Решение:0,5
Цель индивида − максимизировать функцию U I 27 F 0,25
при F = 33 – L и I = wL.
MU F w
MRS
FI
Оптимум индивида достигается при:
MU I
1
wL 27 w
wL 27 66w 2wL
2(33 L) 1
9
w
Следовательно, при w = 3 индивид будет работать 19 часов.
Определим коэффициент эластичности предложения труда по его
L w
цене:
e
3wL 66w 27 L 22
S
w
L
к.э.н., доцент Павлова Е.Е.
26
27. Дано: U = (I + 27)0,5F0,25, Т = 33, w = 3
eS9 w 9 1
0,16
2
L 3 19
w
I
Максимальный доход за 33 часа работы:
Imax = 33 3 =99(точка В),
tg = w
Imax=99 В
Е
IЕ==57
U1
F Е= 14 рабочее
А
33
F (часов в сутки)
время – L=19
к.э.н., доц. Павлова Е.Е.
27
28. Индивидуальная функция предложения капитала
Задача № 5Предпочтения индивида относительно
нынешнего (С0) и будущего (С1) потребления
благ отображаются двухпериодной функцией
полезности U C00,6C10,4 . Его доход в текущем
периоде I0 = 250, в будущем I1 = 120.
Определите объемы его сбережений в
текущем периоде и объемы потребления в
обоих периодах при ставке процента i = 20%.
к.э.н., доцент Павлова Е.Е.
28
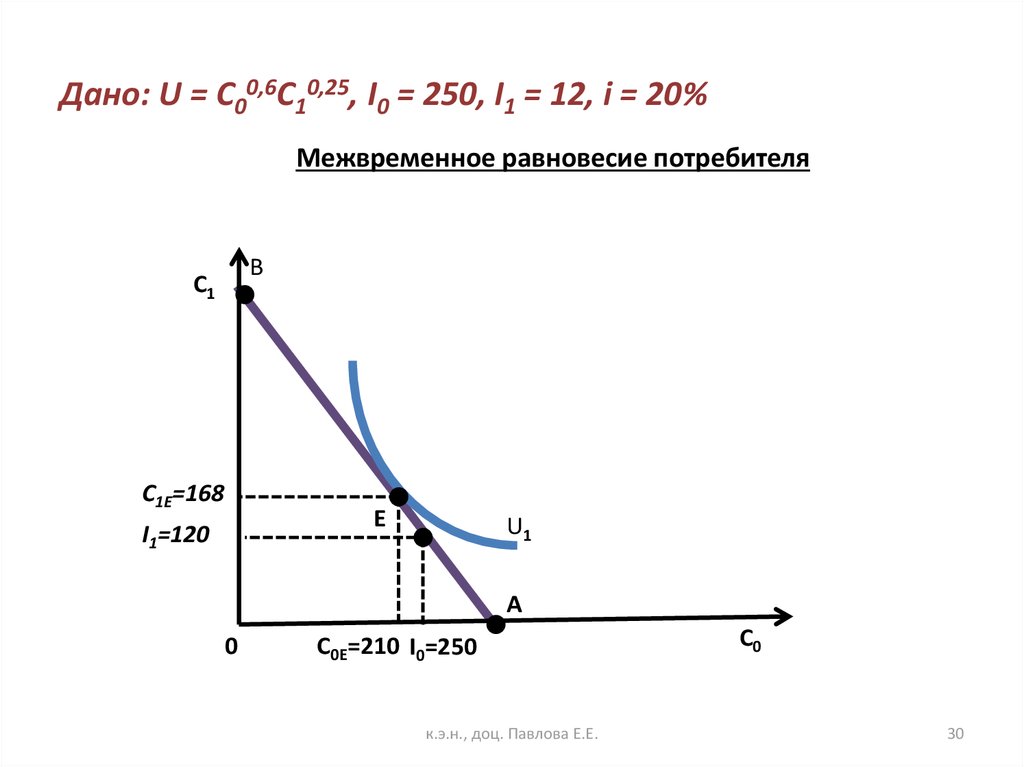
29. Дано: U = C00,6C10,4, I0 = 250, I1 = 120, i = 20%
Решение:Индивид максимизирует функцию
когда
U C00,6C10,4
при ограничении С1 = I1 + (I0 – С0)(1+i)
С1 120 (1 0,2)( 250 С 0 )
0,6С1
1 0,2
0,4С 0
С1 0,8С0
С0 210, С1 168, S 0 40
0,8С0 120 300 1,2С0
т. е. индивид дает взаймы.
к.э.н., доцент Павлова Е.Е.
29
30. Дано: U = C00,6C10,25, I0 = 250, I1 = 12, i = 20%
Межвременное равновесие потребителяB
С1
С1Е=168
Е
I1=120
U1
А
0
С0Е=210 I0=250
к.э.н., доц. Павлова Е.Е.
С0
30
31. Теория фирмы
.Задача № 6
• Зависимость выпуска продукции от количества
используемого труда отображается функцией:
Q 50L 5L2 0,5L3
1. При каком количестве используемого труда
достигается максимум: а) общего выпуска; б)
предельной производительности (предельного
продукта) труда; в) средней производительности
(среднего продукта) труда.
2. Определите эластичность выпуска по труду при
использовании 5 ед. труда.
к.э.н., доцент Павлова Е.Е.
31
32. Дано: Q=50L+5L2-0,5L3
а) Функция от одной переменной достигает максимума,когда ее производная равна нулю.
dQ dL 50 10L 1,5L 0 L 10
2
б) Предельная производительность труда: MPL Q' L 50 10L 1,5L2
достигает максимума при
MP' 10 3L 0 L 3,3
L
АPL
Q
50 5 L 0,5L2
L
в) Средняя производительность труда:
достигает максимума при
AP' L 5 L 0 L 5
к.э.н., доцент Павлова Е.Е.
32
33. Дано: Q=50L+5L2-0,5L3
TPC
B
A
0
MPL
APL
L
1
A1
2
3
4
B1
При L = 5 средняя и
предельная
производительности равны
следовательно еQL=1.
C1
0
LA=3,3 LB=5
LC=10
L
34. Теория фирмы
Задача № 7Фирма, максимизирующая прибыль, работает по
технологии Q = L0,25K0,25. Факторы
производства она покупает по неизменным
ценам: w = 2; r = 8 и продает свою продукцию
по цене Р = 320. Определите: а) выпуск фирмы;
б) общие затраты на выпуск; в) средние
затраты; г) предельные затраты; д) объем
спроса фирмы на труд; е) объем спроса фирмы
на капитал; ж) прибыль фирмы; з) излишки
продавца.
к.э.н., доцент Павлова Е.Е.
34
35. Дано: Q = L0,25K0,25, w = 2, r = 8, Р = 320
Решение:Если в условии производственная функция, то:
TC(K,L) TC(Q) MC(Q) MC=P QS(P)
ТС=Kr+Lw=8K+2L
В оптимуме: MRTSLK = МРL / МРK = w/r
MPL 0,25K 2
L 4K
MPK 0,25L 8
TC=8K+8K=16K
Из производственной функции:
Q=(4K)0,25K0,25=(2K)0,5 K=0,5Q2
TC=8Q2
к.э.н., доцент Павлова Е.Е.
35
36. Дано: Q = L0,25K0,25, w = 2, r = 8, Р = 320
TC=8Q2MC=TC’(Q)=16Q
MC=P 16Q=P QS = P/16
a) QS = P/16 = 320/16=20
б) LTC = 8·202 = 3200
в) LAC = 3200/20 = 160
г) LMC = 16·20 = 320
д) L = 4·200 = 800
е) K = 0,5·400 = 200
ж) = TR-TC = 20·320 – 3200 = 3200
з) RS = 0,5 (P-Pmin)Q=0,5·20·320 = 3200
к.э.н., доцент Павлова Е.Е.
36
37. Теория затрат, теория предложения
Задача № 8Фирма с функцией общих затрат TC 8 8Q 2Q2 может
продать любое количество своей продукции по
цене Р = 20.
1. Определите выпуск фирмы: а) минимизирующий
средние затраты; б) максимизирующий прибыль.
2. Рассчитайте максимальную величину: а) прибыли;
б) излишка производителя.
3. Определите эластичность предложения фирмы по
цене, когда она получает максимум прибыли.
к.э.н., доцент Павлова Е.Е.
37
38. Дано: Q=8+8Q+2Q2,Р = 20. Найти: а) Q, ATC min б) Q, П max
Дано: Q=8+8Q+2Q2,Р = 20.Найти: а) Q, ATC min
б) Q, П max
Решение:
АТС
ТС 8
8 2Q
Q Q
АТС ' (Q)
8
2 0 Q 2
Q2
Условие максимизации прибыли:
Р=МС
MC TC ' (Q) 8 4Q
8 4Q 20 Q 3
к.э.н., доцент Павлова Е.Е.
38
39. Дано: Q=8+8Q+2Q2,Р = 20. Найти: а) Пmax б) RS
Решение:П TR TC
= 20 3 – 8 – 8 3 – 2 9 = 10
RS TR VC
RS = 20 3 – 8 3 – 2 9 = 18
Выводим функцию предложения:
QS P MC
8 4Q P QS 0,25Q 2
еS
Q P
20 5
0,25
P Q
3 3
к.э.н., доцент Павлова Е.Е.
39
40. Оптимум по Парето в обмене
Задача № 11Первый индивид произвел 200 ед. блага А, а второй – 240 ед.
блага В. Предпочтения индивидов относительно данных
благ отображаются функциями полезности: U1 QA0,51 QB0,25
,
1
0,75
. Индивиды договорились о
U 2 QA0,25
Q
2
B2
распределении блага А: QA1 = 120; QА2 = 80.
а) Сколько блага В должен получить 1-й индивид для
достижения оптимального по Парето распределения благ?
б) При какой цене блага А рынок обеспечивает оптимальное
по Парето распределение, если РВ = 1?
в) Рассчитать величину бюджета первого и второго
индивидов.
к.э.н., доцент Павлова Е.Е.
40
41. Дано: , , QA = 200, QВ = 240, QA1 = 120; QА2 = 80
0,25 0,75Дано: U1 QA0,51 QB0,25
, QA = 200, QВ = 240, QA1 =
1 , U 2 QA 2 QB 2
120; QА2 = 80
Решение:
а) Условие оптимального по Парето распределения благ:
MRS AI , B MRS AII, B
MRS 1AB
MU A
0,5QB1
Q
B1
MU B 0,25Q A1
60
2
MRS AB
MU A 0,25QB 2 QB 2
MU B 0,75Q A2 240
QB1 QB 2
QB 2 4QB1
60 240
QB QB1 QB 2 5QB1 QB1 48, QB 2 192
к.э.н., доцент Павлова Е.Е.
41
42. Дано: , , QA = 200, QВ = 240, QA1 = 120; QА2 = 80
0,25 0,75Дано: U1 QA0,51 QB0,25
, QA = 200, QВ = 240, QA1 =
1 , U 2 QA 2 QB 2
120; QА2 = 80
Решение:
б) Условие оптимума отдельного потребителя:
MRS 1AB
MRS
в)
1
AB
MU A PA
MU B PB
0,5QB1
PA
0,5 48
PA 0,8
0,25Q A1 0,25 120 1
I PAQA PB QB
бюджет 1-го индивида 0,8 120 + 48 = 144
бюджет 2-го 0,8 80 + 192 = 256
к.э.н., доцент Павлова Е.Е.
42
43. Оптимум по Парето в производстве
Задача № 12Для производства двух благ А и В имеется 240 ед. труда и
160 ед. капитала. Технологии производства представлены
0,25 0,5
0,5 0,25
Q
L
Q
L
K
,
функциями
B
B KB .
A
A
A
При производстве блага А используется 16 ед. капитала, а
при производстве блага В – 144 ед. Сколько ед. труда
должно быть в отрасли А, чтобы обеспечить
эффективность по Парето в производстве?
к.э.н., доцент Павлова Е.Е.
43
44. Дано: , L=240, K=160 KA = 16, KВ = 144
0,5 0,250,25 0,5
Q
L
K
,
Дано: A
Q
L
A
A
B
B K B , L=240, K=160 KA = 16, KВ
= 144
Решение:
а) Условие оптимального по Парето распределения ресурсов:
A
B
MRTS LK
MRTS LK
A
MRTS LK
MPL
0,5K A
32
MPK 0,25L A L A
B
MRTS LK
MPL 0,25K B 72
MPK
0,5LB
LB
32 72
LB 2,25L A
L A LB
L LA LB 3,25LA LA 80, LB 180
к.э.н., доцент Павлова Е.Е.
44
45. Парето-оптимальность в производстве и обмене
Задача № 13*Кривая производственных возможностей
описывается уравнением:
2
QA 800 QB ,
а функция общественной полезности:
U QA0,25QB0,5 .
Определите оптимальные объемы
производства каждого блага.
к.э.н., доцент Павлова Е.Е.
45
46. Парето-оптимальность в производстве и обмене
Решение:Рассмотрим два способа решения
Первый способ:
MRSBA = MRPTBA
MU B
2Q A
MRS BA
MU A
QB
QА
MRPTBA =
= ( QA 800 QB2)′= |–2 QB| = 2QB
QВ
Решая систему:
2QA
Q 2QB ;
B
Q 800 Q 2 .
B
A
получаем: QA= 400;QB = 20.
к.э.н., доцент Павлова Е.Е.
46
47. Парето-оптимальность в производстве и обмене
Объем производства QAR
400
U3общ
20
Объем производства QB
В точке R наклон границы производственных
возможностей (MRPTBA) и кривой безразличия общества
(MRSBAобщ) равны
к.э.н., доцент Павлова Е.Е.
48. Парето-оптимальность в производстве и обмене
Второй способ:Производственные возможности выступают в роли
бюджетного ограничения при максимизации функции
полезности:
QA0,25QB0,5 QA 800 QB2 max .
QA 400; QB 20.
2 QB 0
0, 25QB0,5
0
0,75
QA
QA
0,5QA0,75
QB
QB0,5
к.э.н., доцент Павлова Е.Е.
48
49. Монополия
Задача №16Отраслевой спрос QD = 180 – 2P удовлетворяет единственная
фирма с функцией общих затрат: TC = 120 + 12Q + 0,5Q2.
1. Определите цену и объем продаж, если фирма максимизирует:
а) прибыль; б) выручку; в) объем продаж.
2. Определите параметры работы фирмы, если бы она могла
осуществлять ценовую дискриминацию первой степени.
3. Определите величину дотации за каждую проданную единицу
товара, при которой фирма, стремясь максимизировать
прибыль, будет продавать 45 ед.
4. Определите цену и объем продаж, если фирма максимизирует
прибыль при наличии 20%-го налога на выручку.
к.э.н., доцент Павлова Е.Е.
49
50. Дано: TC = 120 + 12Q + 0,5Q2 QD = 180 – 2P P=90-0,5Q
Дано: TC = 120 + 12Q + 0,5Q2QD = 180 – 2P P=90-0,5Q
Решение:
а) Условие максимизации прибыли: MR=MC
MR TR' ( PQ)' (90Q 0,5Q 2 )' 90 Q
MC TC ' 12 Q
12 Q 90 Q
Q 39, P 90 0,5 39 70,5
TR TC 39 70,5 120 12 39 0,5 392 1401
б) Условие максимизации выручки: MR=0
MR TR' 90 Q 0
Q 90, P 90 0,5 90 45
2
TR TC 90 к.э.н.,
45
120
12
90
0
,
5
90
1200
доцент Павлова Е.Е.
50
51. Дано: TC = 120 + 12Q + 0,5Q2 QD = 180 – 2P P=90-0,5Q
Дано: TC = 120 + 12Q + 0,5Q2QD = 180 – 2P P=90-0,5Q
Решение:
в) Условие максимизации выпуска: P=MC
MC TC ' 12 Q
12 Q 90 0,5Q
Q 52, P 90 0,5 52 64
TR TC 52 64 120 12 52 0,5 522 1232
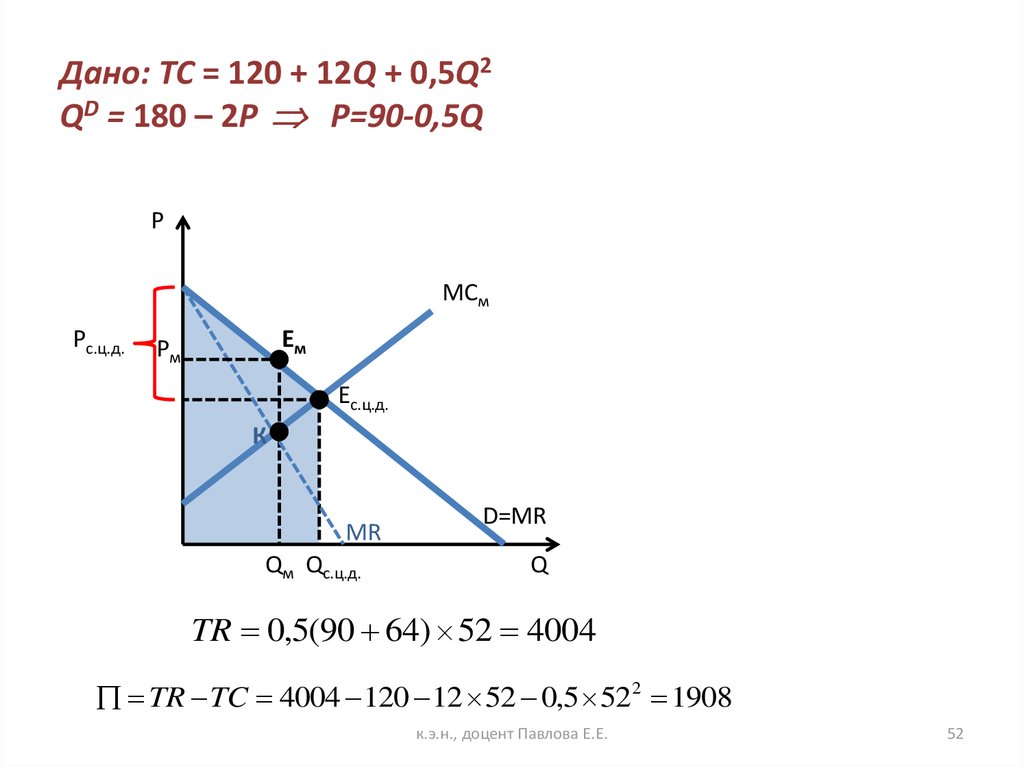
2. Условие для осуществления ценовой дискриминации первой
степени: Р=МС, Р const
Q 52, P [ Рпосл. , Рmax ) P [64;90)
к.э.н., доцент Павлова Е.Е.
51
52. Дано: TC = 120 + 12Q + 0,5Q2 QD = 180 – 2P P=90-0,5Q
Дано: TC = 120 + 12Q + 0,5Q2QD = 180 – 2P P=90-0,5Q
P
МСм
Pс.ц.д.
Ем
Pм
Eс.ц.д.
К
MR
Qм Qс.ц.д.
D=MR
Q
TR 0,5(90 64) 52 4004
TR TC 4004 120 12 52 0,5 522 1908
к.э.н., доцент Павлова Е.Е.
52
53. Дано: TC = 120 + 12Q + 0,5Q2 QD = 180 – 2P P=90-0,5Q, QД=45
Дано: TC = 120 + 12Q + 0,5Q2QD = 180 – 2P P=90-0,5Q, QД=45
3. Условие максимизации прибыли с учетом дотации: MR=MCД
TС Д ТС Д 120 12Q 0,5Q2 dQ
MC Д TС ' Д 12 Q d
MR TR' ( PQ)' (90Q 0,5Q 2 )' 90 Q
12 Q d 90 Q
d 90 12 2Q 12
Д 45 12 540
Q 45, P 90 0,5 45 67,5
TR TC 45 67,5 120 12 45 0,5 452 540 1972,5
к.э.н., доцент Павлова Е.Е.
53
54. Дано: TC = 120 + 12Q + 0,5Q2 QD = 180 – 2P P=90-0,5Q, T=0,2TR
Дано: TC = 120 + 12Q + 0,5Q2QD = 180 – 2P P=90-0,5Q, T=0,2TR
4. Условие максимизации прибыли с учетом налога: MR=MCТ
TСТ ТС Т 120 12Q 0,5Q 2 0,2PQ
MCТ TС'Т 12 Q 0,2Р
MR TR' ( PQ)' (90Q 0,5Q 2 )' 90 Q
12 Q 0,2(90 0,5Q) 90 Q
Q 31,6; P 90 0,5 31,6 74,2
Т 0,2(74,2 31,6) 469
TR TC 74,2 31,6 120 12 31,6 0,5 31,6 2 469 877,24
к.э.н., доцент Павлова Е.Е.
54
55. Ценовая дискриминация 3 степени
Задача №17Монополия может продавать продукцию на
двух сегментах рынка с различной
эластичностью спроса: Q1 = 200 – 4P1; Q2 = 160
– 2P2. Ее функция общих затрат TC = 10 + 12Q +
0,5Q2. Определить:
а) При каких ценах на каждом из сегментов
рынка монополия получит максимум
прибыли?
б) Какую цену установит монополия в случае
запрета ценовой дискриминации?
к.э.н., доцент Павлова Е.Е.
55
56. Дано: TC = 10 + 12Q + 0,5Q2, Q1 = 200 – 4P1 P1=50-0,25Q1 Q2 = 160 – 2P2 P2=80-0,5Q2
Дано: TC = 10 + 12Q + 0,5Q2,Q1 = 200 – 4P1 P1=50-0,25Q1
Q2 = 160 – 2P2 P2=80-0,5Q2
Решение:
1. Условие максимизации прибыли при осуществлении ценовой
дискриминации третьей степени следующее:
MR1 MC
MR2 MC
MR1 TR1 ' ( P1Q1 )' (50Q1 0,25Q1 )' 50 0,5Q1
2
MR2 TR2 ' ( Р2Q2 )' (80Q2 0,5Q2 )' 80 Q2
2
MC TC' 12 Q 12 Q1 Q2
50 0,5Q1 12 Q1 Q2
80 Q2 12 Q1 Q2
76 2
Q
Q
1 3 3 2
80 Q 12 76 2 Q Q
2
2
2
3 3
к.э.н., доцент Павлова Е.Е.
Q1 4
Q2 32
P1 49
P2 64
56
57. Дано: TC = 10 + 12Q + 0,5Q2, Q1 = 200 – 4P1 P1=50-0,25Q1 Pmax=50 Q2 = 160 – 2P2 P2=80-0,5Q2 Pmax=80
Дано: TC = 10 + 12Q + 0,5Q2,Q1 = 200 – 4P1 P1=50-0,25Q1 Pmax=50
Q2 = 160 – 2P2 P2=80-0,5Q2 Pmax=80
Определим прибыль монополии
TR1 TR2 TC 32 64 4 49 10 12(32 4) 0,5(32 4) 2 1154
2. Для определения условий достижения максимума прибыли
при запрете ценовой дискриминации выведем
функцию суммарного спроса:
160 2 P, P 50,80
QD
360 6 P, P 0,50
80 Q, Q 0,60
MR
60 1 Q, Q 60,360
3
80 0,5Q, Q 0,60
PD
60 1 Q, Q 60,360
6
80 Q 12 Q Q 34, Q 0,60 P 63
MR MC
60 1 Q 12 Q Q 36, Q 60,360
3
На втором рынке продукция продаваться не будет
TR TC 34 63 10 12 34 0,5 342 1146
к.э.н., доцент Павлова Е.Е.
57
58. Ценовой лидер
Задача №21В отрасли функционируют 80 мелких фирм с
одинаковыми функциями затрат TCаут = 2 +
8q2аут и еще одна крупная фирма,
выступающая в роли лидера, с функцией
затрат TCл = 20 + 0,275Qл2 . Отраслевой спрос
представлен функцией QD = 256 – 3P. Какая
цена сложится на рынке и как он будет
поделен между лидером и аутсайдерами?
Определите прибыль лидера и каждого из
аутсайдеров.
к.э.н., доцент Павлова Е.Е.
58
59. Дано: TCа= 2 + 8q2а , n=80, TCл = 20 + 0,275Qл2, QD = 256 – 3P
Решение:а) Условие максимизации прибыли лидера: MRЛ =MCЛ
QDЛ QD QSа
QSа PЛ MCа
MCа ТС 'а 16qа
QSа 80 qа 80
Р 16qа qа
Р
16
Р
5P
16
QDЛ QD QSа 256 3Р 5Р 256 8Р
РЛ 32 1 Q МRЛ 32 0,25Q
8
МС Л ТС ' Л 0,55QЛ
к.э.н., доцент Павлова Е.Е.
59
60. Дано: TCа = 2 + 8qа2, n=80, TCл = 20 + 0,275Qл2, QD = 256 – 3P
MRЛ =MCЛ0,55Q 32 0,25Q
QЛ 40, PЛ 32 1 40 27
8
Л TR TC 27 40 20 0,275 40 2 440
б) Аутсайдеры
qа
Р
1,6875
16
а TR TC 27 1,6875 2 8 1,68752 20,78
в) Рынок в целом
QD 256 3Р 256 3 27 175
QS QЛ QSа 40 80 1,6875 175
к.э.н., доцент Павлова Е.Е.
60





















































 economics
economics