Подобие. Признаки подобия треугольников

1. Подобие. Признаки подобия треугольников.

1.
I в.
Какие фигуры являются подобными?
1
2
1
3
5
Ответ: 1 и 4; 2 и 3
4
6
II в.
2
3
4
5
6
Ответ: 1 и 5; 2 и 3; 4 и 6
Подобные фигуры - фигуры, одинаковые по форме, но
разные по размерам.

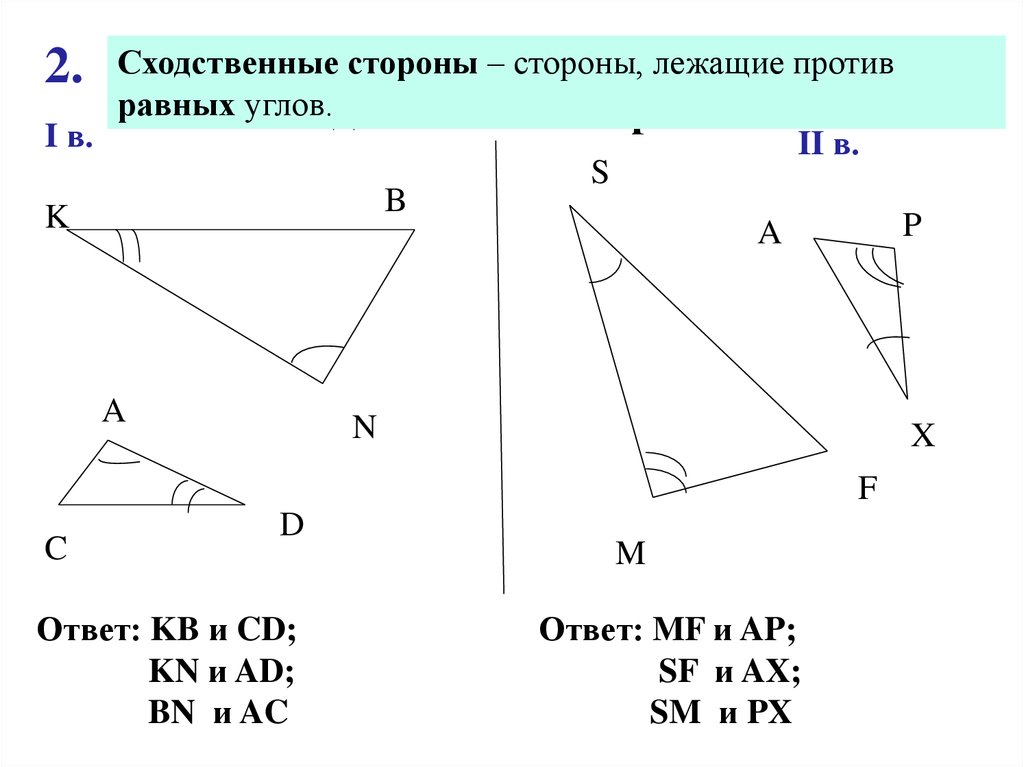
2. Треугольники подобны, найдите сходственные стороны

Треугольники
найдите
Сходственные
стороныподобны,
– стороны, лежащие
против
равных углов.
сходственные
стороны
I в.
II в.
S
B
K
P
A
2.
A
N
X
F
C
D
Ответ: KB и CD;
KN и AD;
BN и AC
M
Ответ: MF и AP;
SF и AX;
SM и PX

3.

3.
I в.
а). 5
Найти коэффициент подобия,
если сходственные стороны
треугольников равны:
и 25
в). 10 и 2
с). 20 и 21
Ответ:
5 1
k
25 5
10
k
5
2
20
k
21
а). 3 и 6
в). 30 и 10
с). 5 и
7
II в.
Ответ:
3 1
k
6 2
30 3
k
10 1
5
k
7
Коэффициент подобия – равен отношению сходственных
сторон подобных треугольников.

4.

4.
Периметры
подобных
треугольников
относятся
Найти
коэффициент
подобия,
как коэффициент подобия k.
P1
если периметры подобных
k
треугольников равны:
P2
I в.
а). 20 и 40
в). 9 и 10
5.
20 1
40 2
9
k
10
k
II в.
2 1
4 2
19
k
1,9
10
k
а). 2 и 4
в). 19 и 10
Найти
коэффициент
подобия,
Площади
подобных
треугольников
относятся как
еслиподобия
площади
подобных
2
коэффициент
в квадрате
k2. S
k
треугольников равны:S
2
1
а). 1 и 4
в). 8 и 2
1 1
k
4 2
8
k
4 2
2
а). 32 и 2
k
32
16 4
2
k
18
6
3
в). 18 и 3

5.

6.
Подобные треугольники – это треугольники, у которых
ли быть
1). углы Могут
соответственно
равныподобны
2). сходственные
стороныупропорциональны
треугольники,
которых углы
равны:
I I в.
I в.
ΔA B C ~ Δ D E F
ΔA B C ~ Δ D E F
<А = 30 ° <F = 110 °
<А = 10 ° <F = 50 °
<B = 40 ° <D = 30 °
<B = 20 ° <D = 100 °
и
и
почему?
Ответ: Да, так как
<A = <D = 30º
<C = 180º - 30º - 40º = 110º = <F
<E = 180º - 110º - 30º = 40º = <B
почему?
Ответ: Нет, так как
<C = 180º - 20º - 10º = 150º
<E = 180º - 50º - 100º = 30º

6.

Подобные треугольники
– это треугольники,
Могут ли быть
подобны у которых
1). углы соответственно равны
треугольники,
у которых
7. 2). сходственные
стороны пропорциональны
стороны равны:
I в.
II в.
ΔA B C ~ Δ D E F
ΔA B C ~ Δ D E F
АB = 12
DF = 7
АB = 8
DF = 7
АС = 21
FE = 10
АС = 14
FE = 10
ВС = 30
ED = 4
ВС = 20
и
почему?
Ответ: Да, так как
AB AC BC
3
k
ED DF FE
1
и
ED = 4
почему?
Ответ: Да, так как
AB AC BC
2
k
ED DF FE
1

7.

Площадиплощади
подобных треугольников
как
Заданы
подобных относятся
треугольников
8. коэффициент
2.
подобия
в
квадрате
k
2
S1
и одна сторон второго треугольника.
k
S2 ей.
Найти сторону, сходственную
II в.
I в.
S 1 = 270
S 1 = 144
S 2 = 30
S 2 = 36
Сторона 2 Δ = 4 см
Сторона 2 Δ = 10
Найти сходственную
сторону 1 Δ -?
Ответ: 12см 2 S1 270
k
S2
k 9 3
30
Найти сходственную
сторону 1 Δ -?
9
Ответ: 20
2
k
S1 144
4
S2
36
k 4 2
Сход. сторона 1Δ: 4 ∙ k = 4∙3 = 12 Сход. сторона 1Δ: 10∙k = 10 ∙2=20

8. Теория

I признак подобия Δ:
III признак подобия Δ:
(по
(по пропорциональности трех
9.равенству двух углов) Теория
Если два угла одного
сторон )
I в.
II в.
треугольника
соответственно
Если три стороны одного
равны двум углам другого
треугольника пропорциональны
1.
Первый то
признак
треугольника,
такие
трем сторонам другого
1. Третий признак
подобия
подобияподобны.
треугольников треугольника,
треугольники
то такие
треугольников
треугольники
подобны.
II признак подобия Δ:
(по пропорциональности двух
сторон и равенству угла между
2.
Второй признак
ними)
треугольников
Еслиподобия
двe стороны
одного
треугольника пропорциональны
двум сторонам другого
треугольника и углы между
ними равны, то такие
треугольники подобны.
Коэффициент подобия – это
2. Коэффициент подобия –
число, показывающее во сколько
это…
раз один
треугольник больше (или
меньше) другого, подобного ему.
Равен отношению сходственных
сторон подобных Δ.