Similar presentations:
Решение систем уравнений
1.
19.02Классная работа
Тема. Решение систем уравнений
2
ax bx c 0
2
D b 4ac
b D
x1
2a
b D
x2
2a
D 0 x1, x2
D 0 x
D 0 Нет
действительных
корней
2.
Приведенное квадратное уравнение2
x px q 0
à 1
Теорема Виета
x1 x2 p
x1 x2 q
Разложение на множители квадратного уравнения
2
ax bx c a( x x1 )( x x2 )
3.
Биквадратное уравнение4
2
ax bx c 0
2
x t
t 0
2
at bt c 0
I II ( I II ) ( I II )
2
2
2
I 2 I II II
2
2
( I II )
( I II )
2
I 2 I II II
2
2
4.
Решить уравнение:2
1)
x 5
2
x 0
5 0
Ответ: Нет действительных корней
2)
2
x 3
x1, 2
Ответ:
x1
3
3,
x2 3
5.
2ax 0
x 0
2
2
ax bx 0
x ( ax b) 0
x 0 ax b 0
ax ñ 0
2
ax ñ
ñ
2
ñ
x1, 2
x
a
a
6.
Системы уравненийI Способ подстановки. Универсальный.
3x y 5 (1)
2 x y 10 (2)
1.
(1)
3x y 5
Ответ: (- 5; 20)
y 5 3x
y 5 3 ( 5)
y 5 15
y 5 15 20
2 x y 10
2 x (5 3x ) 10
(2)
2 x 5 3x 10
5 x 10
x 10 5
x 5
x 5
7.
II Способ сложения3x y 5
-
2 x y 10
(1)
(2)
(1) - (2):
3x y 2 x y 5 10
x 5
Тогда подставим х в любое из уравнений системы
(2) 2 x y 10
y 20
2 ( 5) y 10
Ответ: (- 5; 20)
10 y 10
y 10 10
8.
III Способ «теорема Виета»2.
x y 3
x y 10
x 5; y 2
и
Ответ: (5; - 2), (- 2; 5)
x 2; y 5
9.
IY Способ «разность квадратов»3.
2
2
I II ( I II ) ( I II )
x y 9
x y 1
2
(1)
2
2
x y 9
+
x y 1
(1)
(2)
2
x y 9
( x y) ( x y) 9
1 ( x y) 9
(1)
(2)
(1) + (2):
x y x y 9 1
2 x 10
x 5
Тогда подставим х в (2):
5 y 1
Ответ: (5; 4)
y 4
10.
Y Способ «Сложение до полного квадрата»2
2
2
2
2
2
( I II ) I 2 I II II
( I II ) I 2 I II II
4.
x y 13
2
2
x y 6 / 2
2
2
x y 13
+
2 x y 12
2
2
x 2 xy y 1
2
( x y) 1
( x y ) 1
Сначала рассмотрим
x y 1
x y 6
11.
Сначала рассмотримx y 1
x y 6
x 3; y 2
и
x 2; y 3
Теперь рассмотрим
x y 1
x y 6
и
x 2; y 3
Ответ: (3; -2), (-2;3)
или (-3;2), (2;-3)
x 3; y 2
12.
Учебникстр. 203 №496, 497 (все 1),
498, 504
508, 510 (все 1),
520, 522
13.
Домашнее задание:§32, 34, № 537, 539,
542
В пятницу 26.02 Контрольная работа.
Хороших выходных!




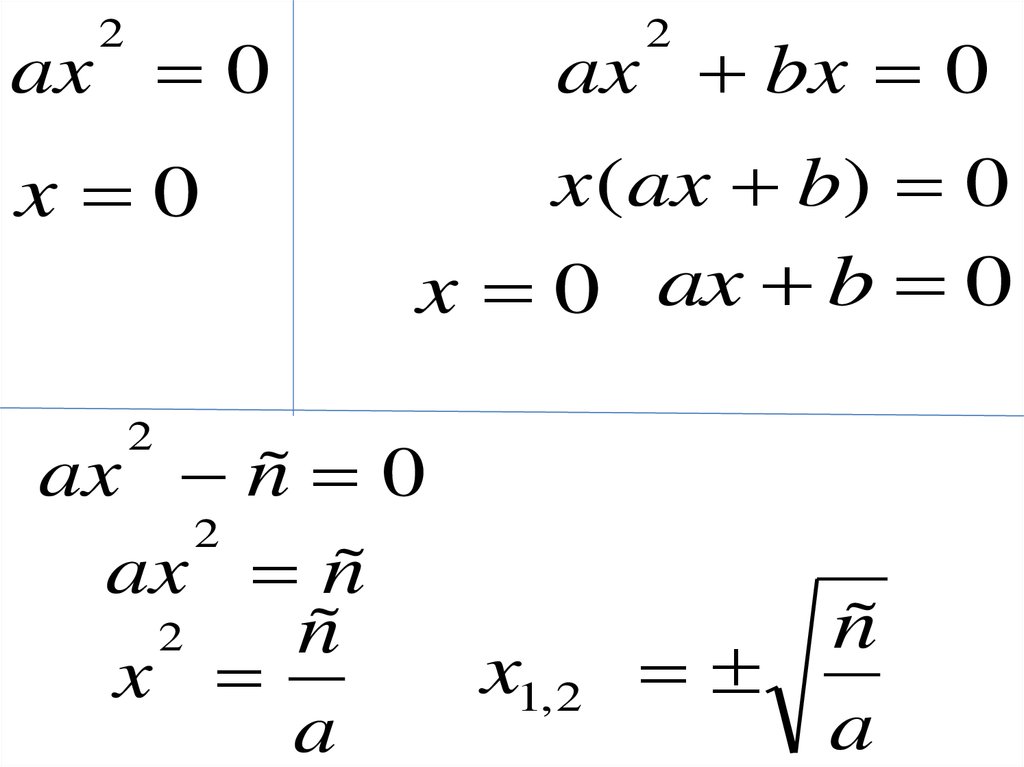








 mathematics
mathematics