Сапалық белгілердің арасындағы байланысты орнату

1.

БИОСТАТИСТИКА
№23 Дәріс
Тақырыбы:
САПАЛЫҚ БЕЛГІЛЕРДІҢ
АРАСЫНДАҒЫ БАЙЛАНЫСТЫ
ОРНАТУ

2.

Дәріс жоспары
1. Юлдың ұқсастық коэффициенті.
2. Пирсонның түйіндес коэффициенті.
3. Пирсон және Чупровтың өзара
коэффициенттері. φ2 көрсеткіш.
түйіндес

3. Корреляциялық тәуелділікті бағалау әдістері

Корреляцилық талдау – бұл екі немесе одан көп кездейсоқ
шамалардың арасындағы байланыстың тығыздығын (күшін)
және бағытын анықтайтын сандық әдіс.
Сандық белгілердің корреляциялық тәуелділігін бағалау үшін:
- Пирсонның жұптасқан сызықты корреляция коэффициенті;
- Спирменнің шендік корреляция коэффициенті қолданады.
Сапалық белгілердің корреляциялық тәуелділігін бағалау
үшін:
- Юлдың ұқсастық коэффициенті;
- Пирсонның түйіндес коэффициенті;
- Пирсон және Чупровтың өзара түйіндес коэффициенттері
және т.б. қолданады.

4.

Юлдың ұқсастық коэффициенті
Егер «иә - жоқ», «тірі - өлі», «ауырып қалды –
ауырған жоқ» және т.б. түрлерінің екі балама
нәтижесі ұсынылған белгілер қарастырылса, онда
байланыс тығыздығының көрсеткіштері
2x2
өлшемді түйіндес кестелерімен есептеледі.

5.

Юлдың ұқсастық коэффициенті
2-ші белгі
1-ші белгі
Иә
Жоқ
Барлығы
Иә
а- жағдайдың
кездесу жиілігі
b -жағдайдың
кездесу жиілігі
a+b
Жоқ
с -жағдайдың
кездесу жиілігі
d -жағдайдың
кездесу жиілігі
c+d
Барлығы
n1=a+c
n2=b+d
Юлдың ұқсастық коэффициенті (Кұ)
ad bc
Kў
ad bc
формула бойынша есептеледі.
n=a+b+c+d

6.

Юлдың ұқсастық коэффициентін
түсіндіру
Ұқсастық коэффициенті (Кұ) [-1, 1] аралығындағы мәндерді
қабылдайды
Егер a, b, c, d төрт санның біреу нөл, немесе a=d=0 немесе
с=b=0 болса, Кұ=±1
Егер Кұ=±1 болса, онда белгілер арасындағы байланыстың
тығыздығы ең күшті болып саналады.
Егер Кұ=0 болса, онда белгілер арасында байланыс жоқ.
Корреляция коэффициенті сияқты, Кұ-ның оң немесе теріс
белгісі, белгілердің мәндері арасында тура немесе кері
байланыс бар екенін білдіреді.

7.

Дәріс жоспары
1. Юлдың ұқсастық коэффициенті.
2. Пирсонның түйіндес коэффициенті.
3. Пирсон және Чупровтың өзара
коэффициенттері. φ2 көрсеткіш.
түйіндес

8. Пирсонның түйіндес коэффициенті.

Сапалық
белгілердің
арасындағы
байланыс
тығыздығының
басқа
сипаттамасы
Пирсоның
түйіндес коэффициенті Кт болып табылады:
ad bc
KТ
(a d )(c b)( a c)(b d )
Түйіндес коэффициентінің мәндері (Кт) әрқашан
ұқсастық коэффициентінің (Кұ) мәндерінен аз болады.
Пирсоның түйіндес коэффициенті Кт мағынасы
Юлдың ұқсастық коэффициенті Кұ мағынасымен
бірдей, бірақ байланыстың тығыздығы туралы нақты
баға бере алмайды.

9.

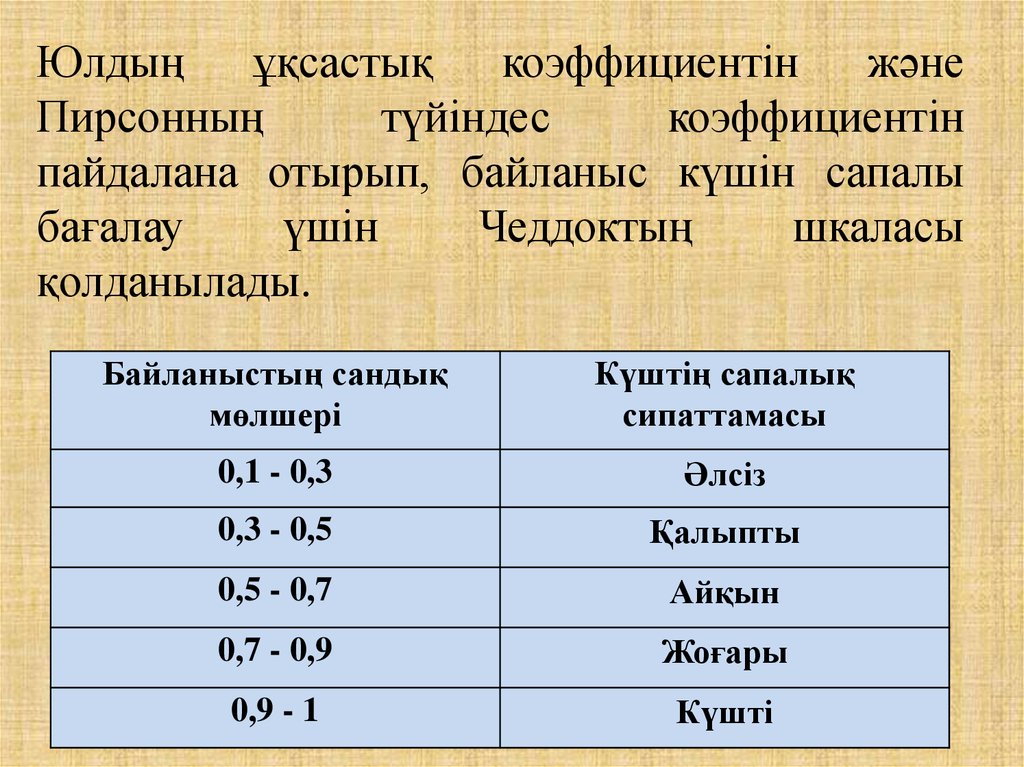
Юлдың
ұқсастық
коэффициентін
және
Пирсонның
түйіндес
коэффициентін
пайдалана отырып, байланыс күшін сапалы
бағалау
үшін
Чеддоктың
шкаласы
қолданылады.
Байланыстың сандық
мөлшері
Күштің сапалық
сипаттамасы
0,1 - 0,3
Әлсіз
0,3 - 0,5
Қалыпты
0,5 - 0,7
Айқын
0,7 - 0,9
Жоғары
0,9 - 1
Күшті

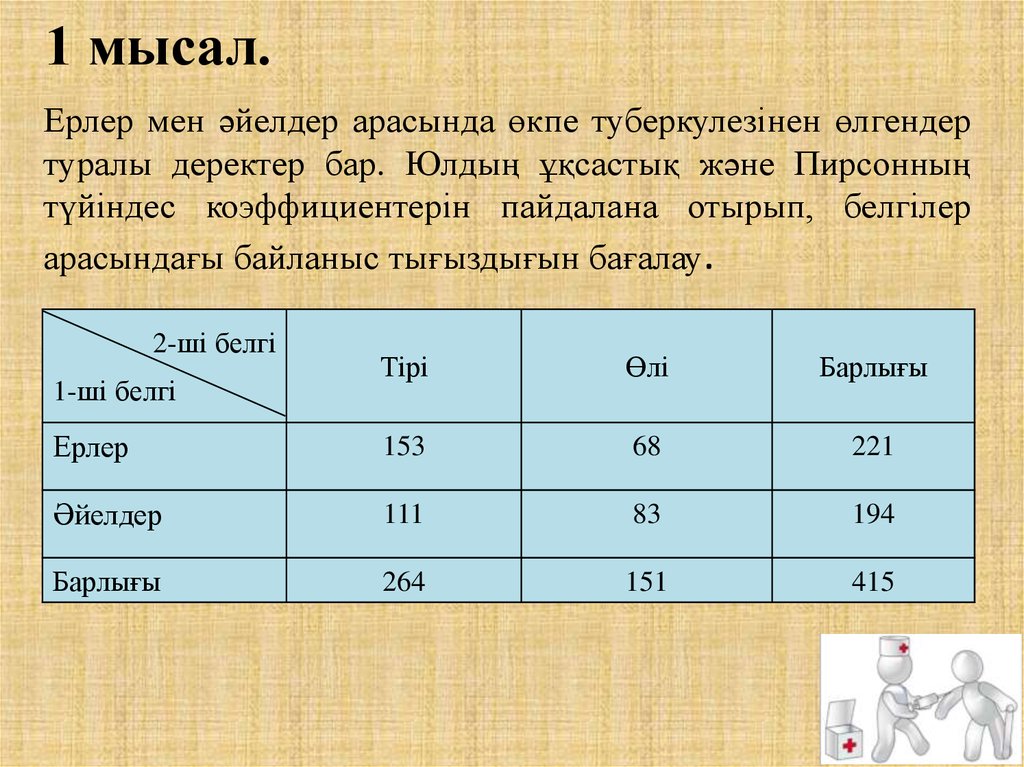
10. 1 мысал.

Ерлер мен әйелдер арасында өкпе туберкулезінен өлгендер
туралы деректер бар. Юлдың ұқсастық және Пирсонның
түйіндес коэффициентерін пайдалана отырып, белгілер
арасындағы байланыс тығыздығын бағалау.
2-ші белгі
Тірі
Өлі
Барлығы
Ерлер
153
68
221
Әйелдер
111
83
194
Барлығы
264
151
415
1-ші белгі

11. 1 мысал.

Шешуі.
ad bc 153 83 68 111
Kў
0,254
ad bc 153 83 68 111
ad bc
153 83 68 111
KТ
0,125
(a d )(c b)( a c)(b d )
221 194 264 151
Кұ және КТ мәндері әр түрлі болса да, бірақ екі жағдайда да
байланыс тікелей әлсіз болып табылады.
Демек, «жынысы» белгісі және «өкпе туберкулезінен өлім»
белгісі бір-біріне әлсіз тәуелді.

12.

Дәріс жоспары
1. Юлдың ұқсастық коэффициенті.
2. Пирсонның түйіндес коэффициенті.
3. Пирсон және Чупровтың өзара
коэффициенттері. φ2 көрсеткіш.
түйіндес

13. Өзара түйіндес коэффициент

Егер екі сапалық белгілердің әрқайсысының сатылары
екіден асатын болса, онда осы қасиеттердің
тығыздығы өзара түйіндес коэффициентпен
өлшенеді.
Айырмашылық:
- Пирсон өзара түйіндес коэффициент (ТП);
- Чупров өзара түйіндес коэффициент (ТЧ).

14.

Пирсонның өзара түйіндес коэффициенті:
ТП
2
1
2
Чупровтың өзара түйіндес коэффициенті:
ТЧ
2
(r 1)( s 1)
,
мұндағы r х s – тиісті түйіндес белглер кестесінің
өлшемі, φ2 – өзара түйіндес көрсеткіш.

15.

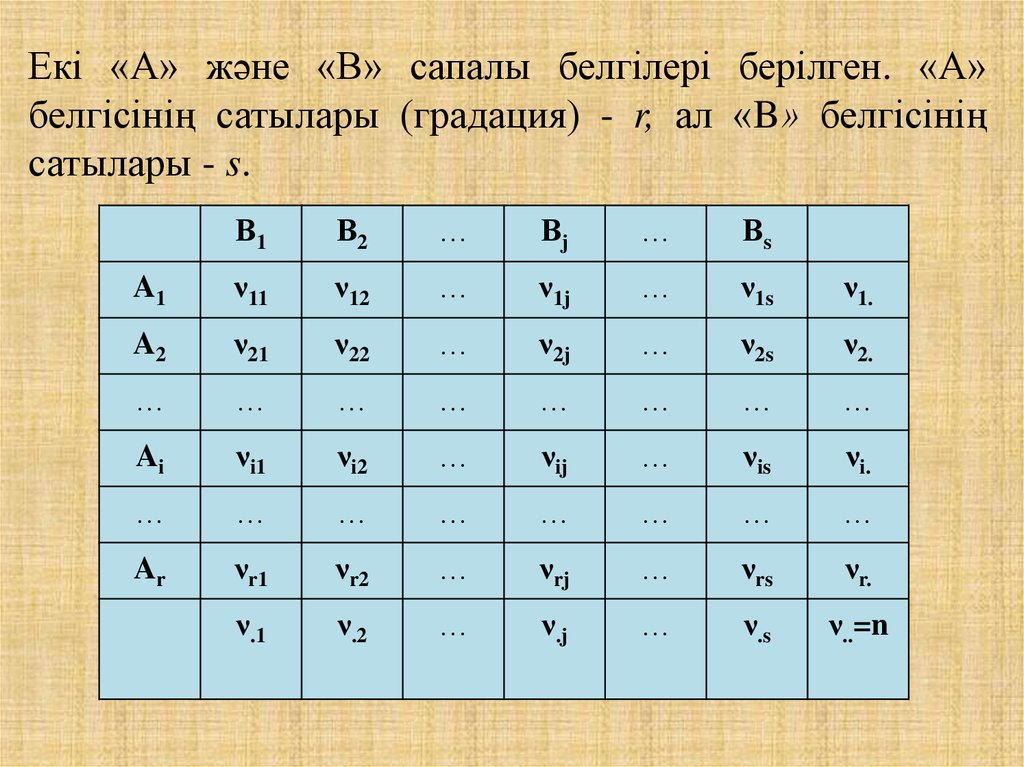
Екі «А» және «В» сапалы белгілері берілген. «А»
белгісінің сатылары (градация) - r, ал «B» белгісінің
сатылары - s.
В1
В2
…
Вj
…
Вs
A1
ν11
ν12
…
ν1j
…
ν1s
ν1.
A2
ν21
ν22
…
ν2j
…
ν2s
ν2.
…
…
…
…
…
…
…
…
Ai
νi1
νi2
…
νij
…
νis
νi.
…
…
…
…
…
…
…
…
Ar
νr1
νr2
…
νrj
…
νrs
νr.
ν.1
ν.2
…
ν.j
…
ν.s
ν..=n

16. φ2 түйіндес көрсеткіш

φ2 –көрсеткішін есептеудің сызбасы:
112 122
12s
1 сызық
z1
... : 1.
.s
.1 .2
2
2
21
22s
22
: 2.
z2
...
.s
.1 .2
2 сызық
…………………………..
соңғы сызық
r21 r22
Содан кейін
rs2
zr
... : r .
.s
.1 .2
z1 z2 ... zr 1
2

17.

Чупровтың коэффициенті (ТЧ) әрқашан
Пирсон коэффициентіне (ТП) қарағанда аз
болады.
Өзара түйіндес коэффициентінің белгісі
байланыс
қатынастардың
бағытын
көрсетпейді.

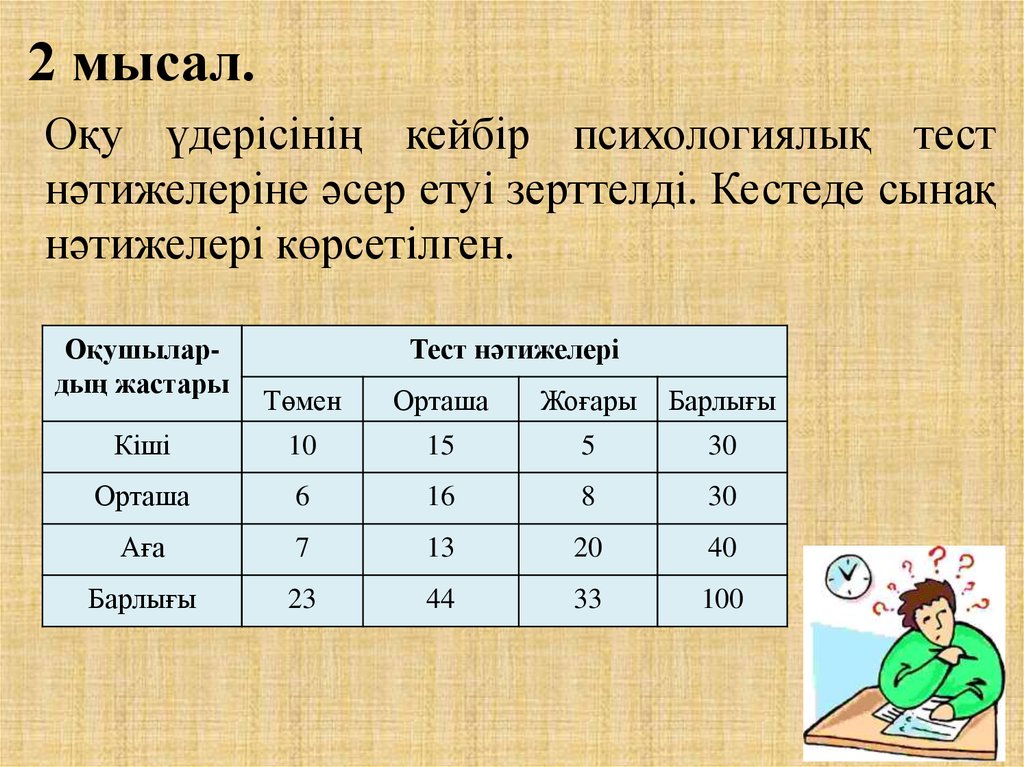
18. 2 мысал.

Оқу үдерісінің кейбір психологиялық тест
нәтижелеріне әсер етуі зерттелді. Кестеде сынақ
нәтижелері көрсетілген.
Оқушылардың жастары
Тест нәтижелері
Төмен
Орташа
Жоғары
Барлығы
Кіші
10
15
5
30
Орташа
6
16
8
30
Аға
7
13
20
40
Барлығы
23
44
33
100

19. 2 мысал.

Шешуі.
Өзара түйіндес белгісінің φ2 көрсеткішінің мәнін есептеу:
112 122 132
102 152 52
: 1.
z1
: 30 0,34
23 44 33
.1 .2 .3
2
2
2
21
62 162 82
23
22
: 2.
z2
: 30 0,31
23 44 33
.1 .2 .3
2
31
7 2 132 202
322 332
: 3.
: 40 0,45
z3
23 44 33
.1 .2 .3
2 z1 z2 z3 1 0,34 0,31 0,45 1 0,1

20. 2 мысал.

Шешуі (жалғасы).
Өзара түйіндес коэффициенттерді есептеу:
0,1
ТП
0,3
2
1
1 0,1
2
ТЧ
2
(r 1)( s 1)
0,1
0,22
(3 1)(3 1)
Бұл сынақтың нәтижесі оқу уақытына
байланысты, бірақ белгілер арасындағы
байланыс әлсіз.

21.

Бақылау сұрақтары:
1.
2.
3.
4.
Корреляциялық
талдау
не
үшін
қолданылады?
Сапалық
белгілердің
корреляциялық
тәуелділігін
бағалау
үшін
қандай
сипаттамалар қолданылады?
Қандай жағдайларда Юлдың ұқсастық және
Пирсонның түйіндес
коэффициенттері
қолданылады?
Қандай
жағдайларда
Пирсон
және
Чупровтың өзара түйіндес коэффициенттері
қолданылады?