Similar presentations:
Геометрия. Төртбұрыштар. Көпбұрыштар. Параллелограмм. Трапеция. Фалес теоремасы
1. Геометрия.
Райымбекова А.АНИШ ФМН Астана
2. Мазмұны
ТөртбұрыштарКөпбұрыштар
Параллелограмм
Трапеция
Фалес теоремасы
Тіктөртбұрыш
Ромб
Остік және централік симметрия
Аудан
Ауданның қасиеттері
Тіктөртбұрыштың ауданы
Параллелограмның ауданы
Үшбұрыштың ауданы
Трапецияның ауданы
Пифагор теоремасы
Ұқсас үшбұрыштар
Ұқсас үшбұрыштар анықтамасы
Үшбұрыштардың ұқсастық белгілері
Үшбұрыштың орта сызығы
Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасында ғы қатынас
3.
4.
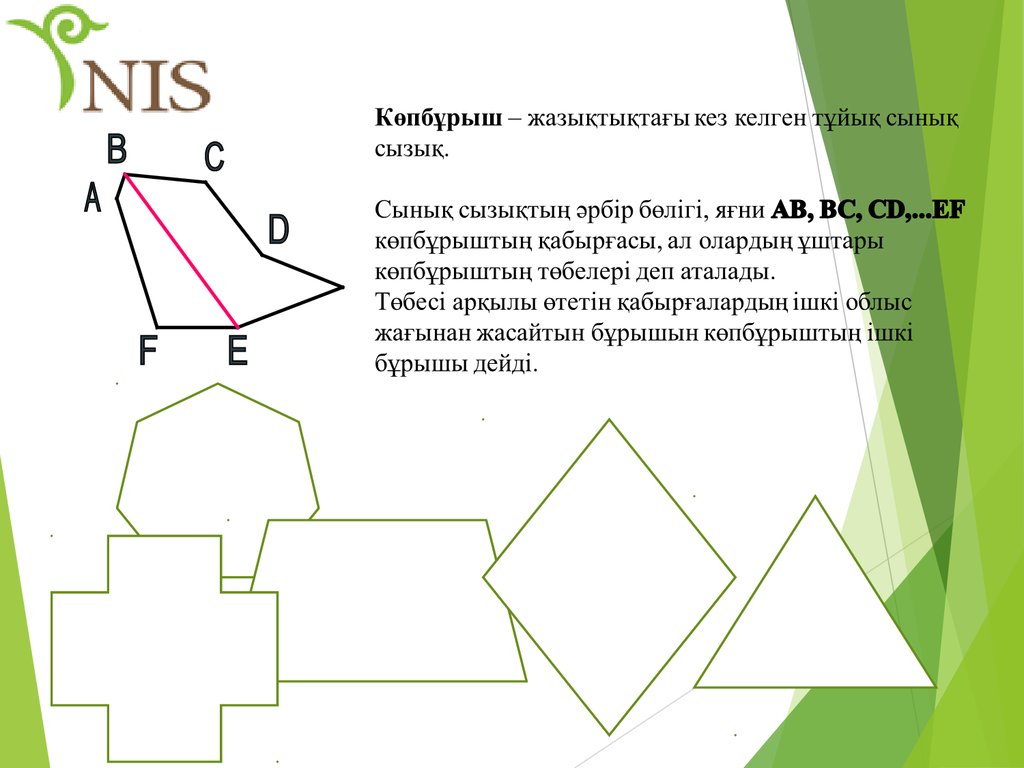
(көпбұрыш жазықтығынан тыс жазықтық бөлігі)(көпбұрыш жазықтығы)
5.
6. Төртбұрыш
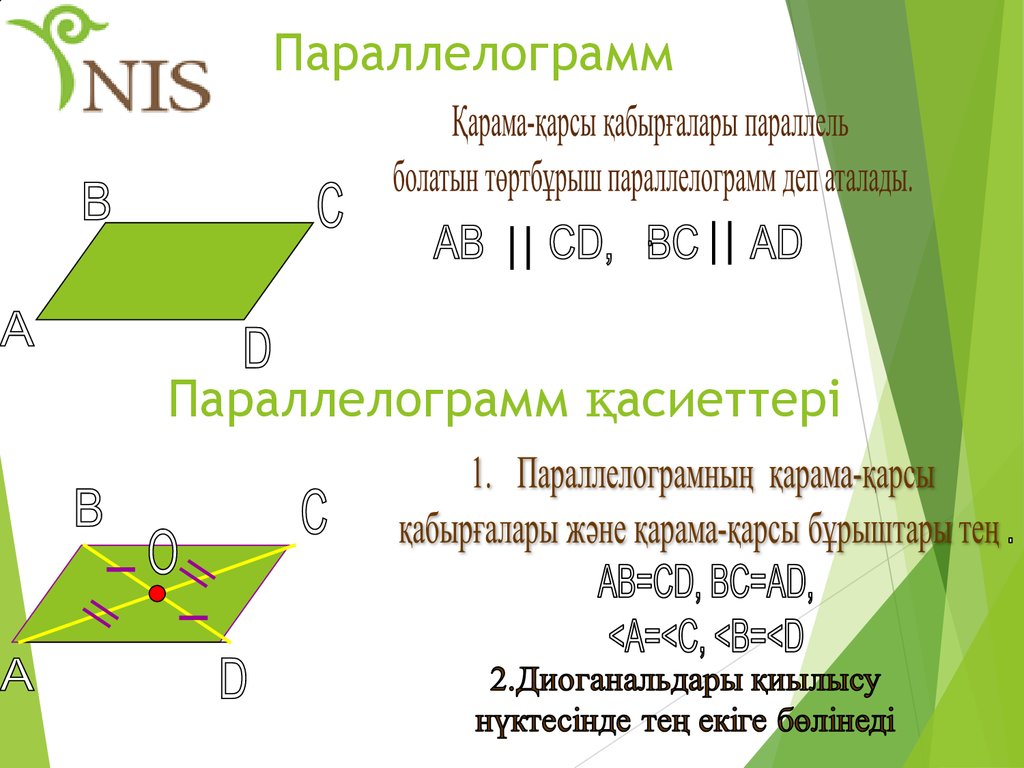
7. Параллелограмм
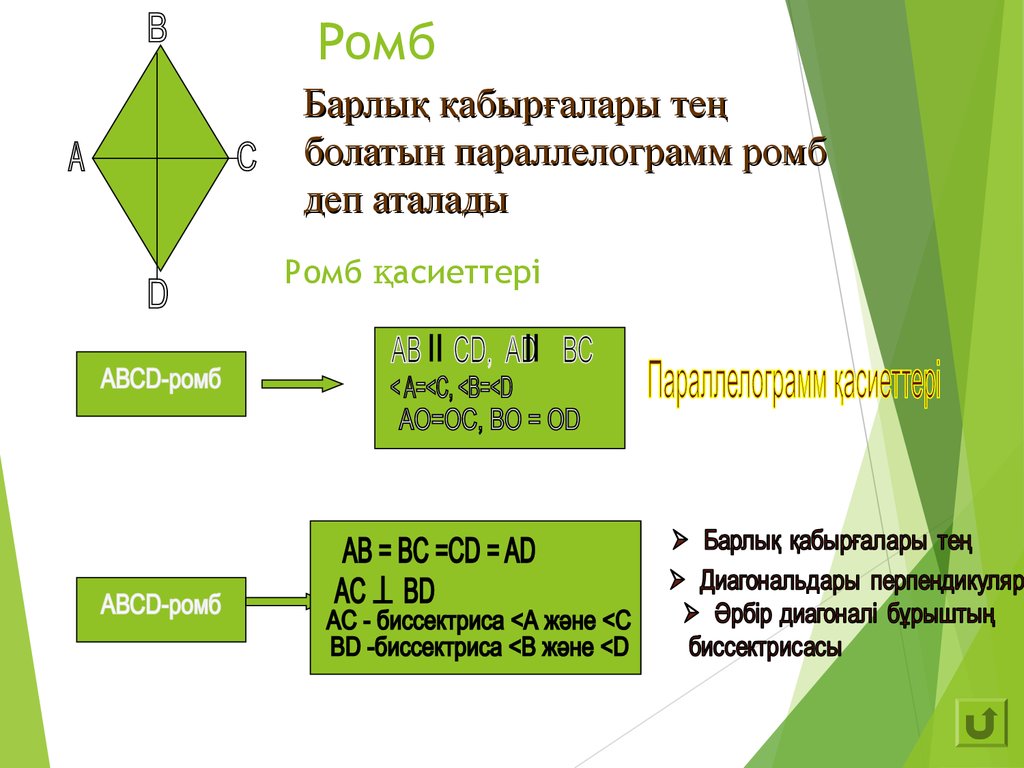
Параллелограмм қасиеттері8.
Егер төртбұрыштың екіқабырғасы тең және параллель
болса, онда ол-параллелограмм
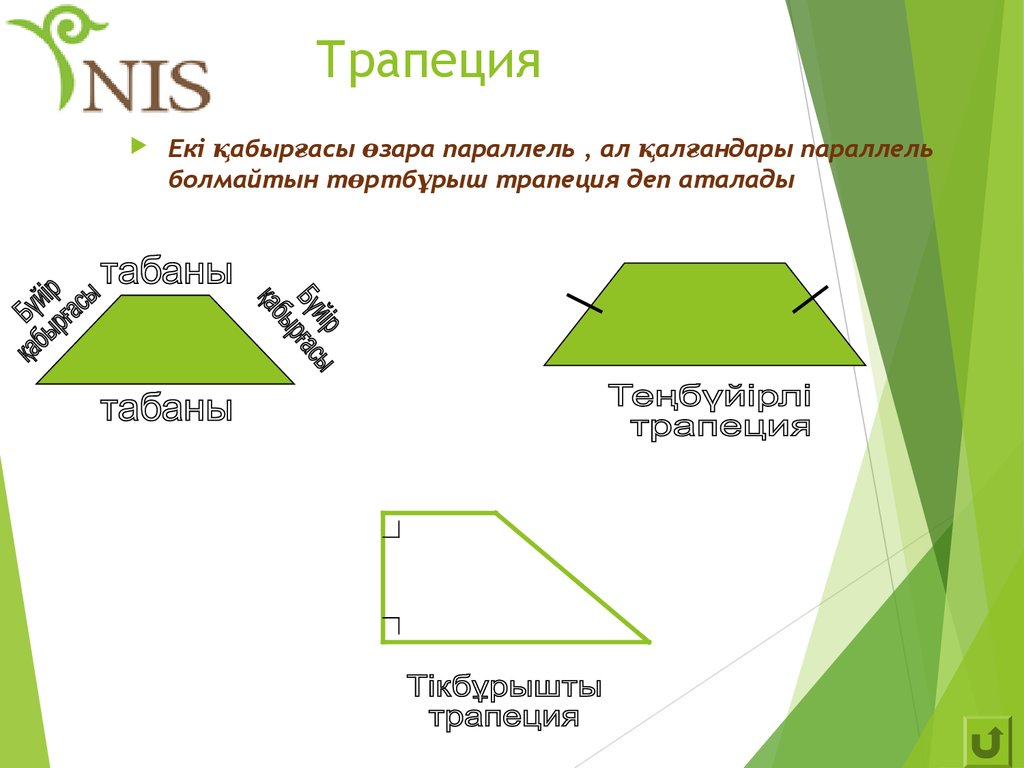
9. Трапеция
Екі қабырғасы өзара параллель , ал қалғандары параллельболмайтын төртбұрыш трапеция деп аталады
10.
Фалес теоремасыЕгер бұрыштың қабырғаларын қиып өтетін
параллель түзілер оның бір қабырғасынан тең
кесінділер қиып түсетін болса, онда ол
түзулер бұрыштың екінші қабырғасынан да тең
кесінді қиып түседі.
А1
А1
В1
В1
А2
1
А2
3
В2
В2
А3
А3
4
D
В3
А4
В4
С
А4
2
В3
В4
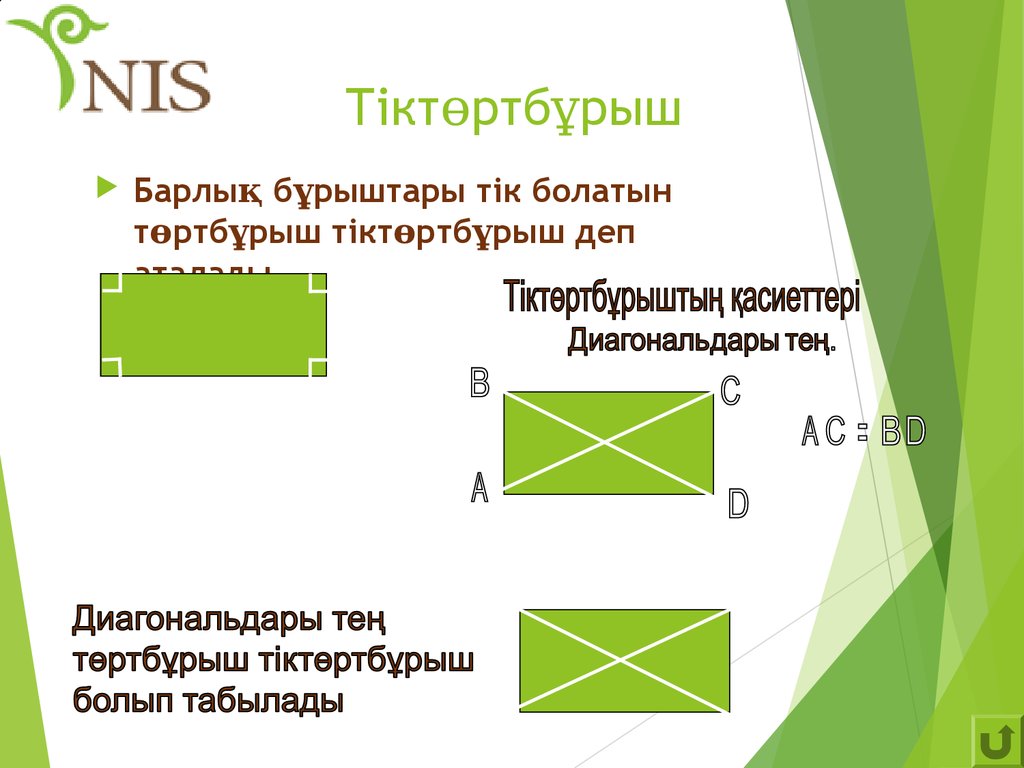
11. Тіктөртбұрыш
Барлық бұрыштары тік болатынтөртбұрыш тіктөртбұрыш деп
аталады.
12. Ромб
Барлық қабырғалары теңболатын параллелограмм ромб
деп аталады
Ромб қасиеттері
13.
Аа
А1
Екі А және А1нүктелері а түзуіне қарағанда
симметриялы деп аталады, егер а түзуі
АА1 кесіндісінің ортасынан өтіп оған
перпендикуляр болса
а симметрия осі деп аталады.
14.
Фигураа
түзуіне
қарағанда
симметриялы деп аталады, егер
фигураның
а
түзуіне
қарағанда
симметриялы әрбір нүктесі осы
фигураға тиісті болса
а
түзуі фигураның симетрия осі деп
аталады
а
15.
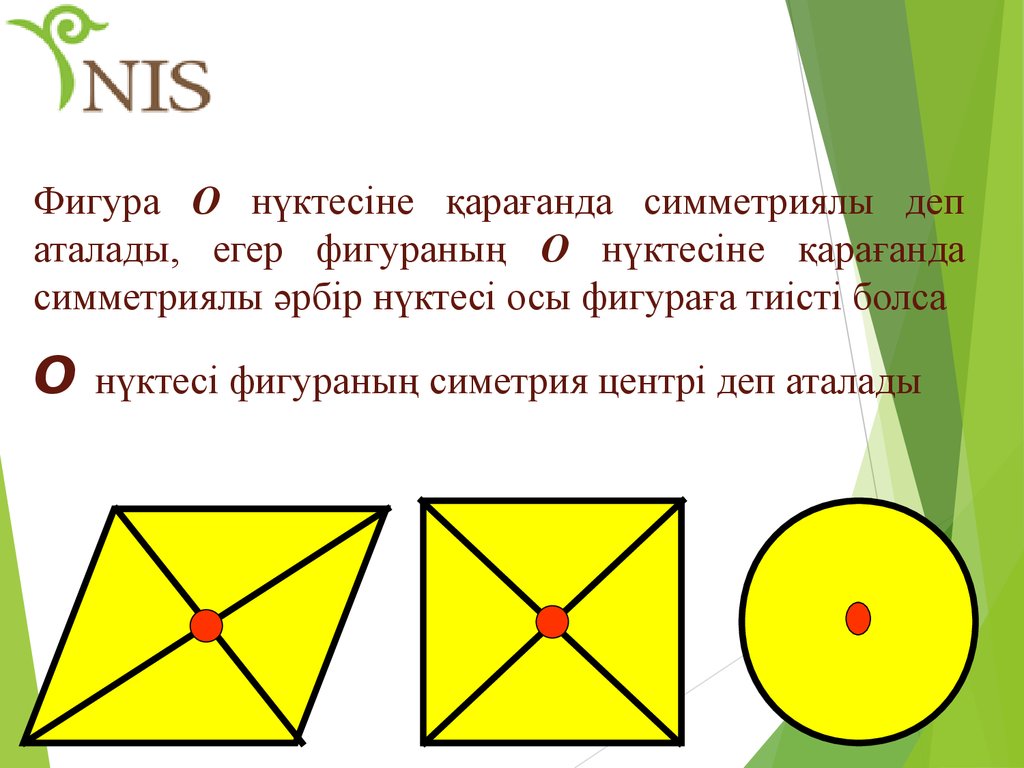
Фигура О нүктесіне қарағанда симметриялы депаталады, егер фигураның О нүктесіне қарағанда
симметриялы әрбір нүктесі осы фигураға тиісті болса
О
нүктесі фигураның симетрия центрі деп аталады
16. Аудан ұғымы. Ауданның қасиеттері.
Жазық пішіндерді қамтитын бірлік квадраттардың(қабырғалары ұзындықтың бірлігіне тең) санымен
анықталады
17.
Аудан ұғымы.Ауданның қасиеттері.
1. Тең фигуралар аудандары тең болады.
F1 F 2 S F 1 S F 2
F1
F2
2. Егер фигура бөліктерге бөлінсе , оның ауданы осы
бөліктердің аудандарының қосындысынан тұрады.
S1
S2
S3
S S1 S 2 S3
18.
Теорема.Тіктөртбұрыштың ауданы оның іргелес
қабырғаларының көбейтіндісіне тең
В
b
А
a
С
S =ab
S ab
D
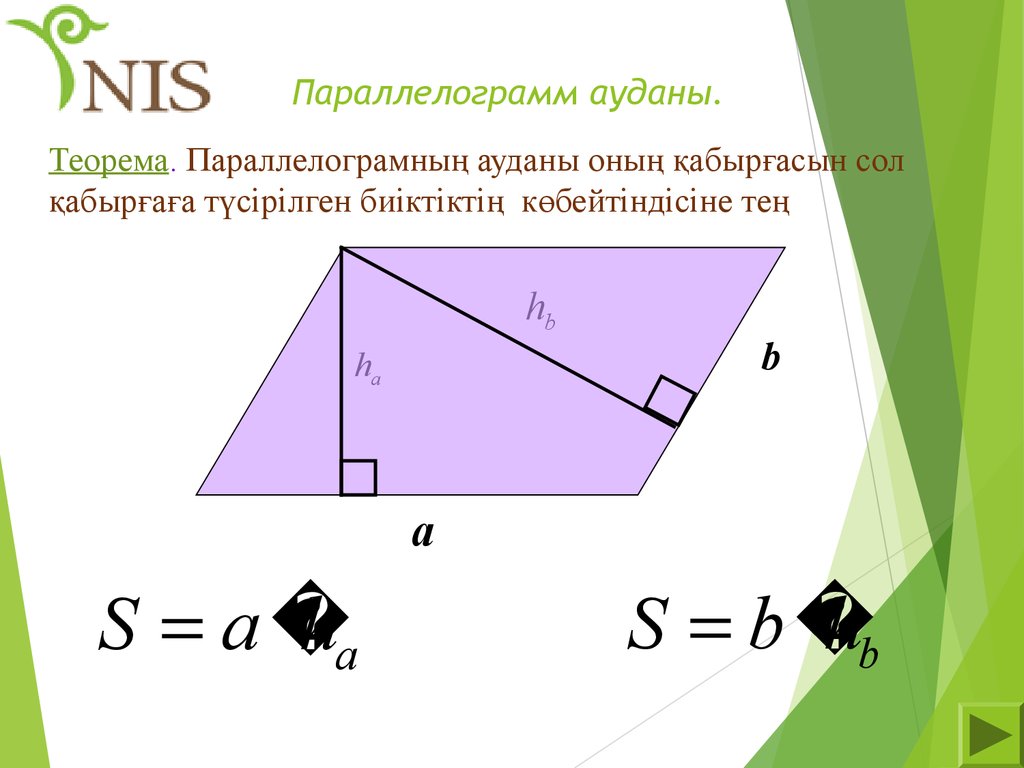
19. Параллелограмм ауданы.
Теорема. Параллелограмның ауданы оның қабырғасын солқабырғаға түсірілген биіктіктің көбейтіндісіне тең
hb
ha
b
a
S a
ha
S b
hb
20.
Үшбұрыштың ауданы.Теорема. Үшбұрыштың ауданы оның кез келген қабырғасы мен осы
қабырғаға түсірілген биіктіктің жарым көбейтіндісіне тең.
1
S b
hb
2
b
c
hb
hc
1
S a
ha
2
1
S c
hc
2
ha
1
S ab
2
a
b
a
21.
Трапеция ауданы.Теорема. Трапецияның ауданы оның биіктігін табандарының
жарым қосындысына көбейткенге тең.
b
h
а
1
S ( a b)
h
2
22.
Пифагор теоремасыТікбұрышты үшбұрыштың гипотенузасының квадраты оның
катеттерінің квадраттарының қосындысына тең
c²=a²+b²
с – гипотенуза
a,b – катеттер.
23. Үшбұрыштар ұқсастығы
Екі үшбұрыш ұқсас болып табылады, егер олардыңсәйкес бұрыштары тең және қабырғалары
пропорционал болса.
В
B1
А
A1
C1
AB и A1B1, BC и B1C1, AC и A1C1
– сходственные стороны
С
24.
Теорема!I ұқсастық белгісі
Егер бір
үшбұрыштың екі
бұрышы екінші
үшбұрыштың екі
бұрышына тең
болса, онда бұл
үшбұрыштар ұқсас
II ұқсастық белгісі
Егер бір үшбұрыштың
екі қабырғасы екінші
үшбұрыштың екі
қабырғасына
пропорционал және
олардың арасындағы
бұрыштар тең болса,
онда бұл үшбұрыштар
ұқсас.
25.
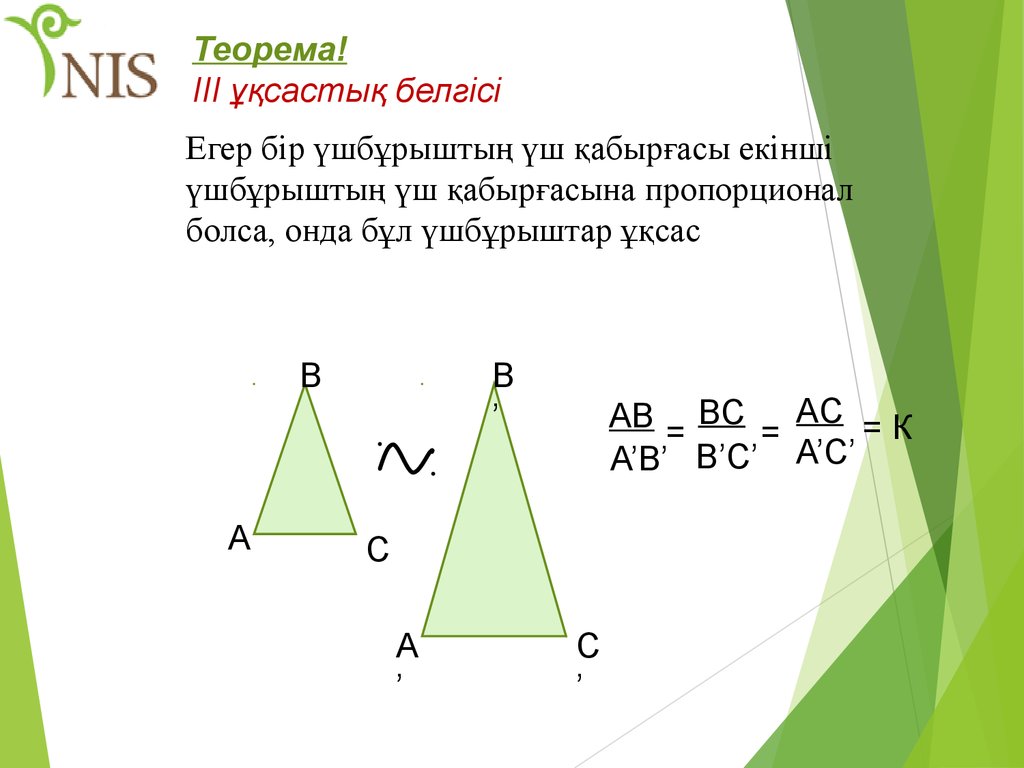
Теорема!III ұқсастық белгісі
Егер бір үшбұрыштың үш қабырғасы екінші
үшбұрыштың үш қабырғасына пропорционал
болса, онда бұл үшбұрыштар ұқсас
В
А
B
’
АВ = BС = AC = К
A’B’ B’C’ A’C’
С
A
’
C
’
26.
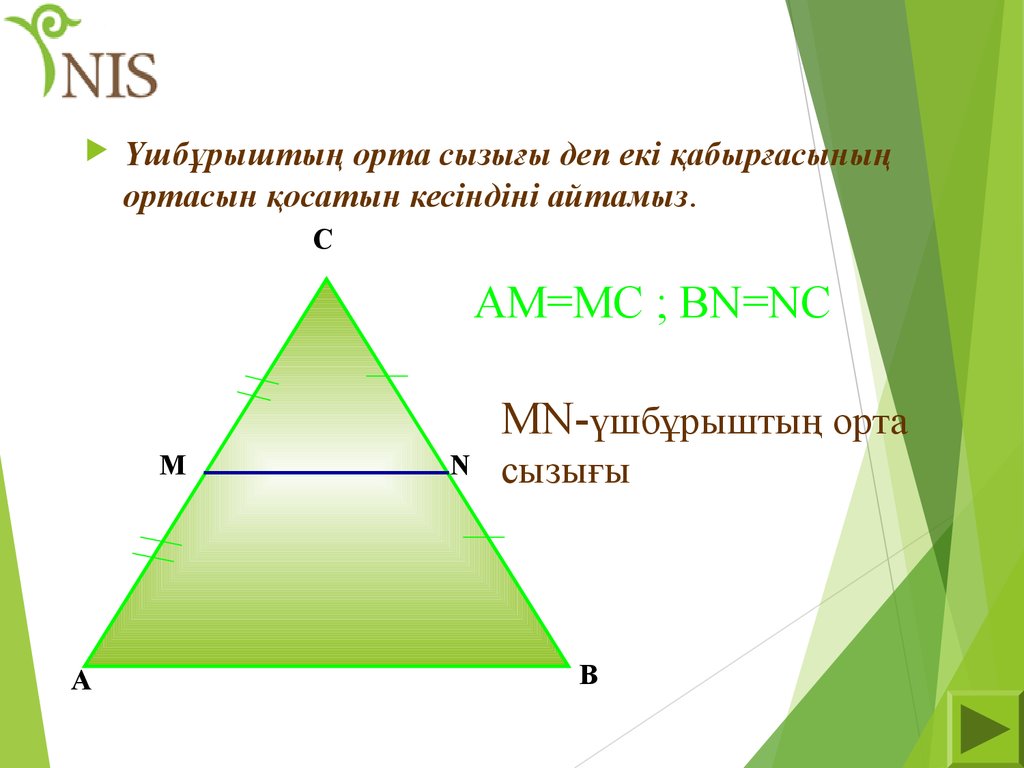
Үшбұрыштың орта сызығы деп екі қабырғасыныңортасын қосатын кесіндіні айтамыз.
С
AM=MC ; BN=NC
MN-үшбұрыштың орта
М
А
N
сызығы
В
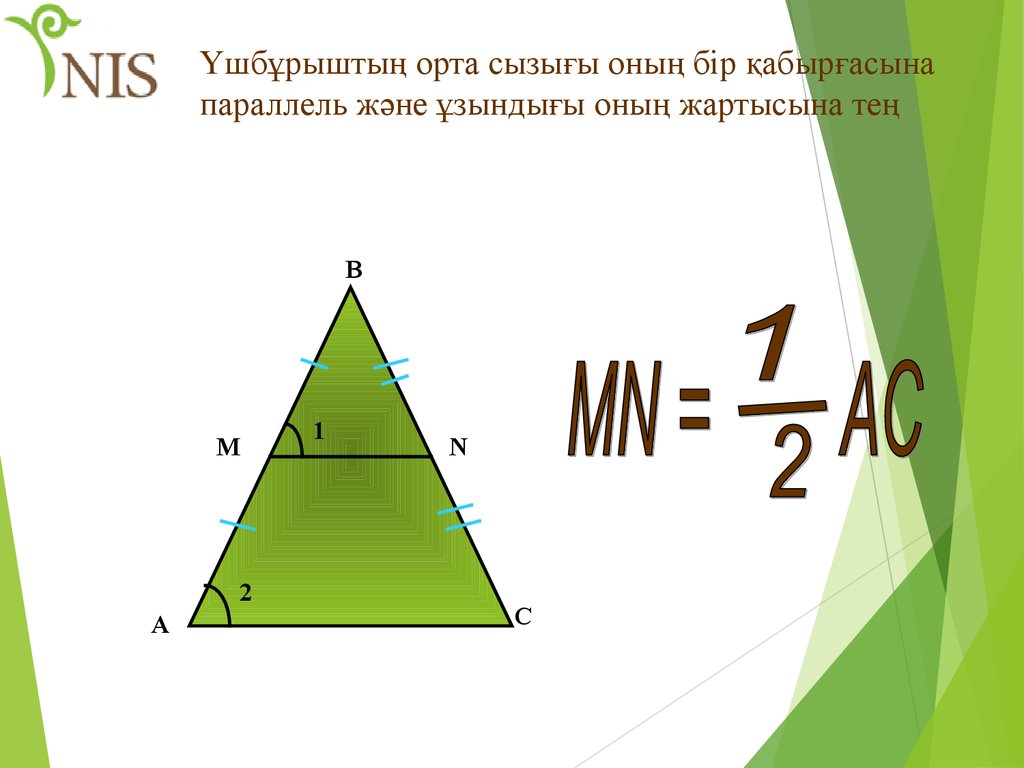
27. Үшбұрыштың орта сызығы оның бір қабырғасына параллель және ұзындығы оның жартысына тең
ВM
2
А
1
N
С
28.
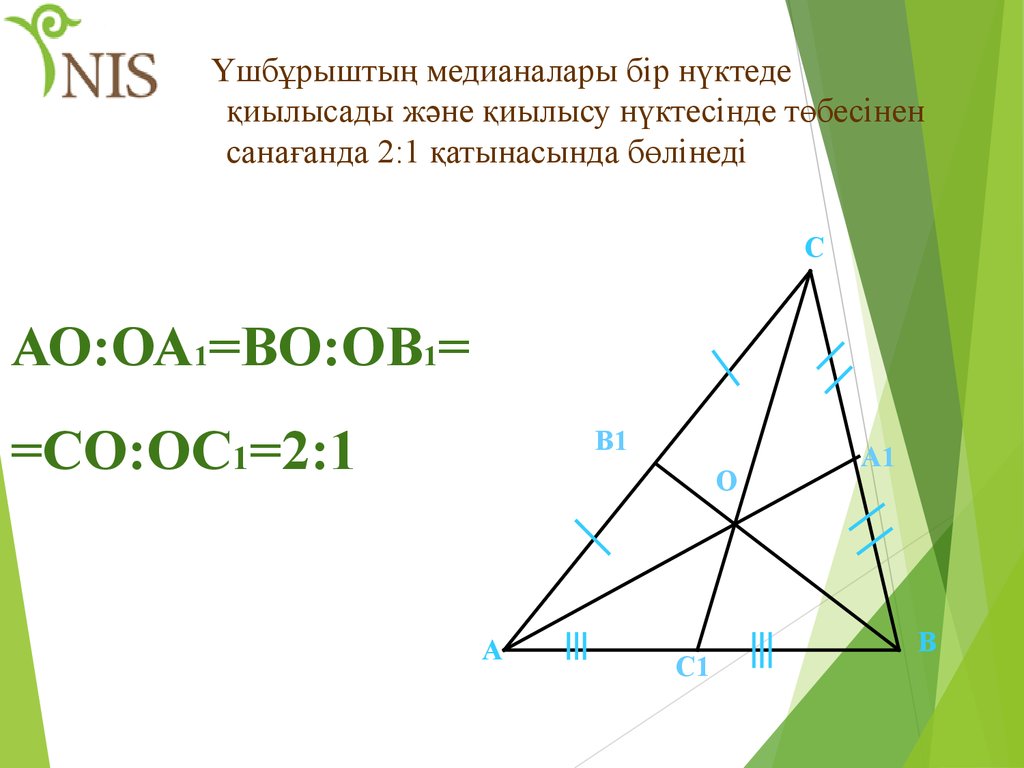
Үшбұрыштың медианалары бір нүктедеқиылысады және қиылысу нүктесінде төбесінен
санағанда 2:1 қатынасында бөлінеді
С
АО:ОА1=ВО:ОВ1=
=СО:ОС1=2:1
В1
О
А
С1
А1
В
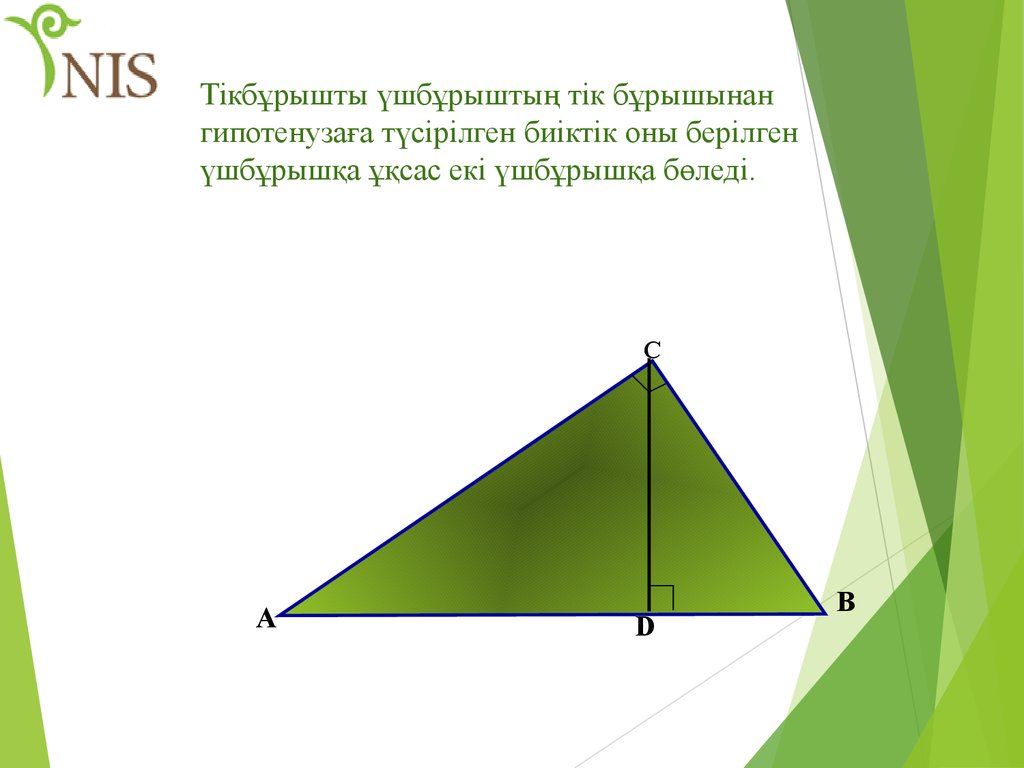
29. Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға түсірілген биіктік оны берілген үшбұрышқа ұқсас екі үшбұрышқа бөледі.
СА
D
В
30.
Тік бұрышты үшбұрыштың тік бұрышынантүсірілген биіктік, гипотенузаның бойынан
бөлінетін
кесінділер
үшін
орташа
пропорционал болып табылады
В
А
D
BD
AD DC
С
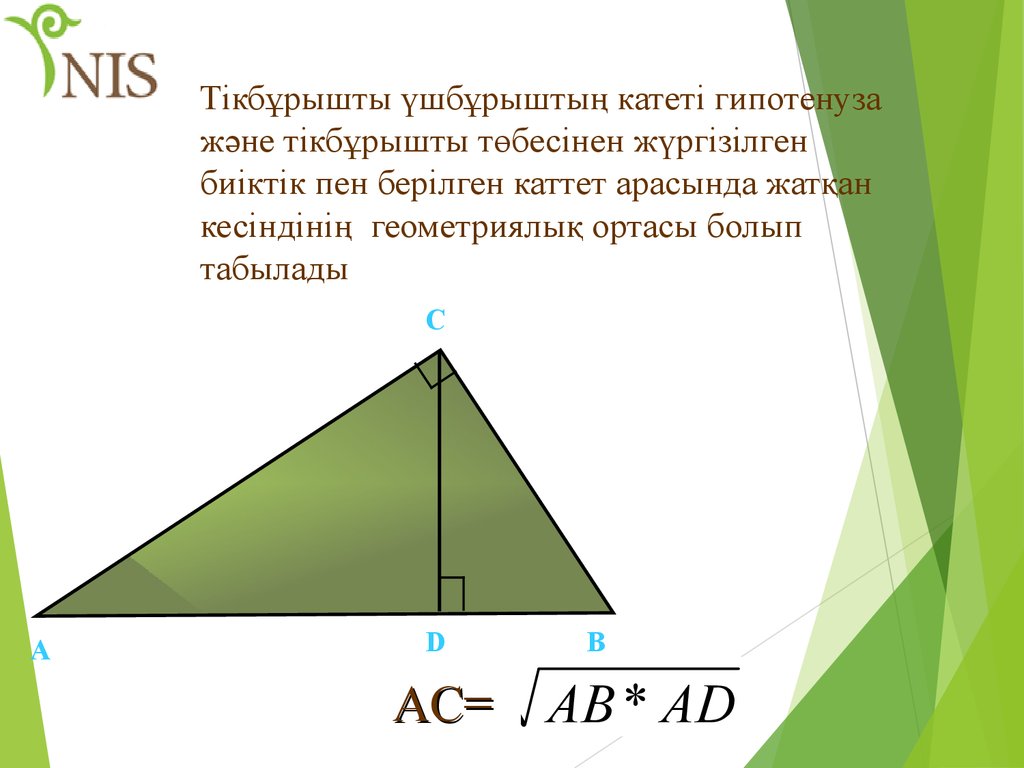
31. Тікбұрышты үшбұрыштың катеті гипотенуза және тікбұрышты төбесінен жүргізілген биіктік пен берілген каттет арасында жатқан
кесіндінің геометриялық ортасы болыптабылады
С
А
D
AC=
В
AB * AD
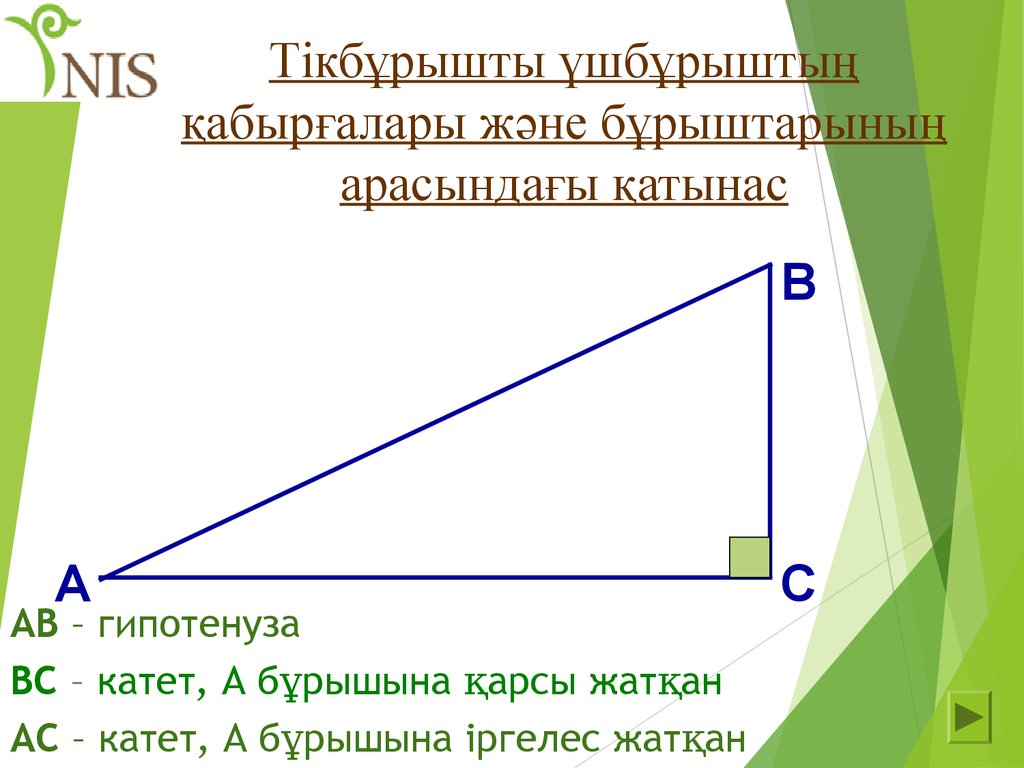
32. Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасындағы қатынас
ВА
АВ – гипотенуза
ВС – катет, А бұрышына қарсы жатқан
АС – катет, А бұрышына іргелес жатқан
С
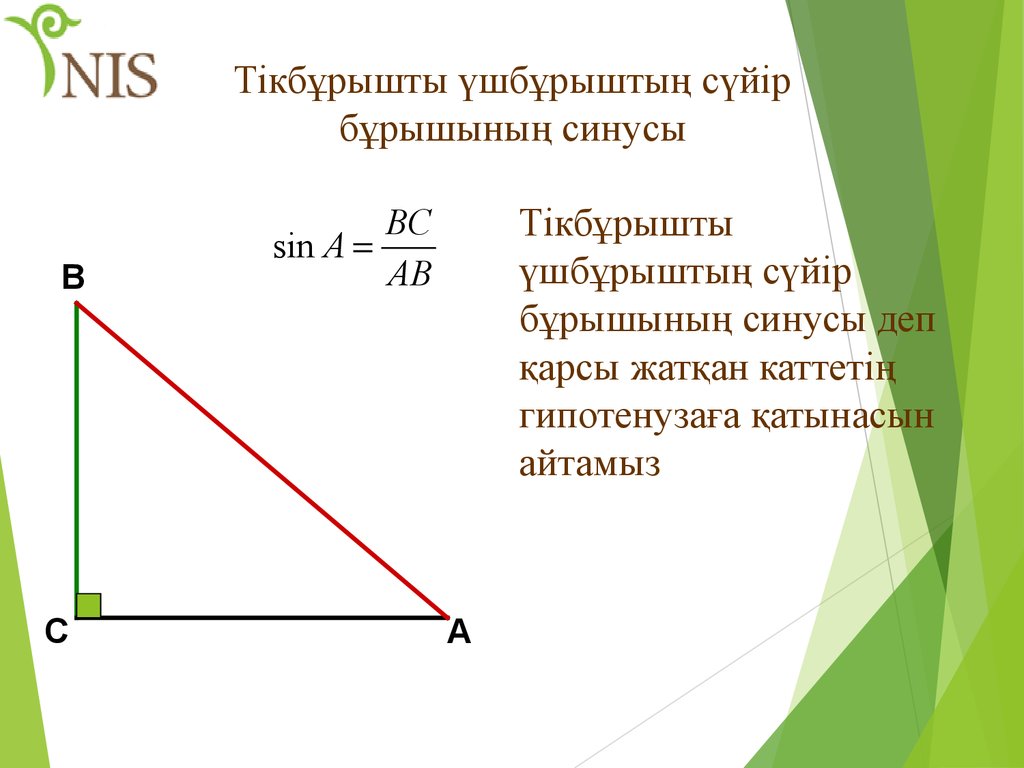
33. Тікбұрышты үшбұрыштың сүйір бұрышының синусы
ВС
Тікбұрышты
үшбұрыштың сүйір
бұрышының синусы деп
қарсы жатқан каттетің
гипотенузаға қатынасын
айтамыз
BC
sin A
AB
А
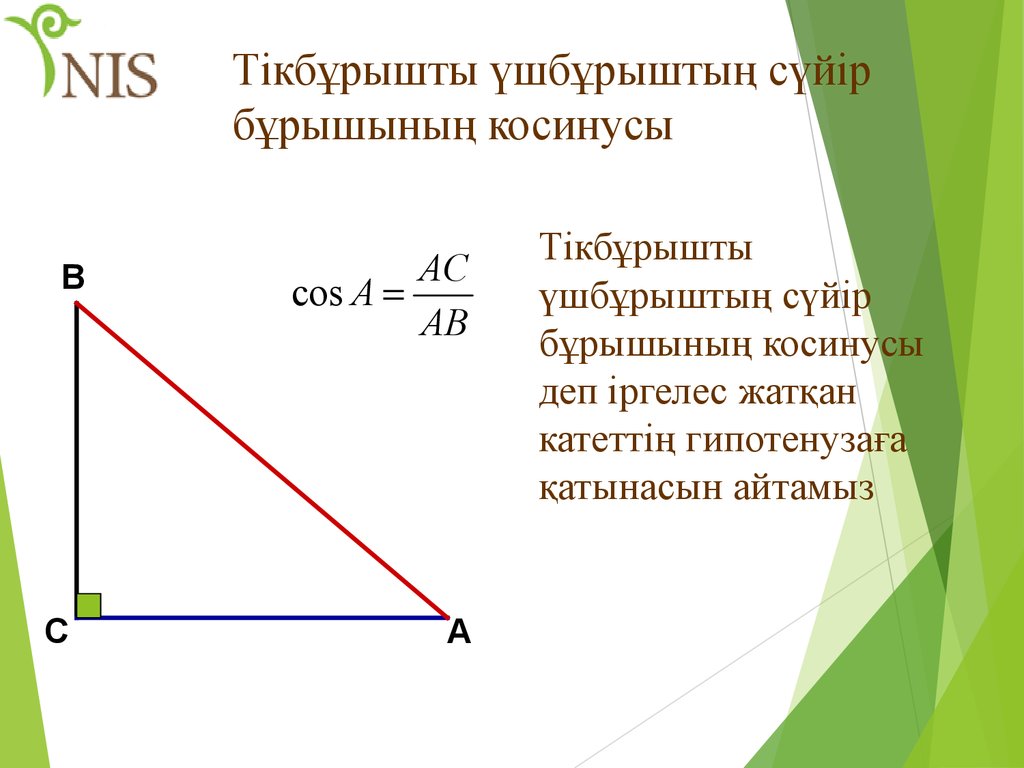
34. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы
ВС
AC
cos A
AB
А
Тікбұрышты
үшбұрыштың сүйір
бұрышының косинусы
деп іргелес жатқан
катеттің гипотенузаға
қатынасын айтамыз
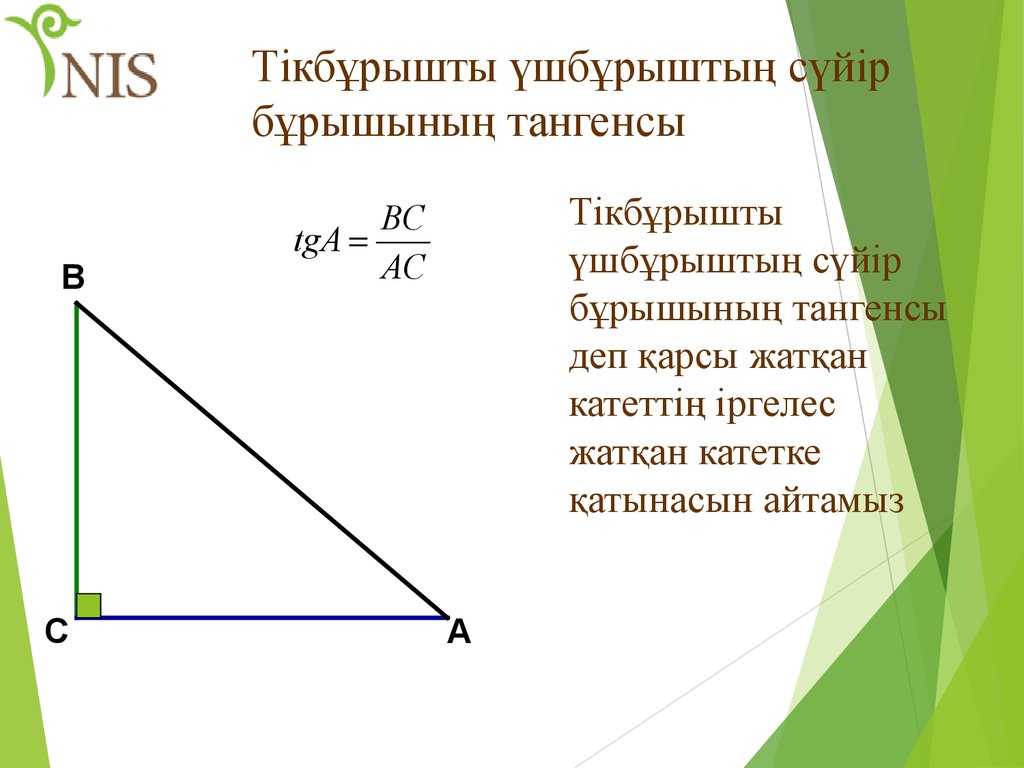
35. Тікбұрышты үшбұрыштың сүйір бұрышының тангенсы
ВС
Тікбұрышты
үшбұрыштың сүйір
бұрышының тангенсы
деп қарсы жатқан
катеттің іргелес
жатқан катетке
қатынасын айтамыз
BC
tgA
AC
А
36. Тригонометриялық теңбе-теңдіктер
1)Негізгі тригонометриялық теңбң-теңдік
sin A cos A 1
2
2
2) Бұрыштың тангенсы осы бұрыштың синусының косинусына
қатынасына тең.
sin A
tgA
cos A



















 mathematics
mathematics








