Геометрия курсында ұқсастық және гомотетия қасиеттерін зерттеу

1.

Геометрия курсында ұқсастық және
гомотетия қасиеттерін зерттеу
Орындаған: Мажитов Дастан.
Сапаов Саржан.
Қабылдаған: Мұратбекова М.

2.

МАЗМҰНЫ

3.

IІ Мектепте гомотетия тақырыбын
оқытудың теориялық негізі

4.

Гомотетияның анықтамасы және нүктені
гомотетиялы көшіру.
1-анықтама. S нүкте және k ≠ 0 саны берілген болсын, S тен басқа
кез келген М нүктеге төмендегі шарттарды қанағаттандыратын М
нүктеге сәйкес келтіретін көшіру гомотетиялы көшіру немесе
гомотетия деп аталады.
2-анықтама. F фигураны құраушы барлық нүктелерді берілген S
центр және берілген k ≠ 0 коэффицентпен гомотетиялы көшірудан
құралған нүктелер жиыны F фигураға гомотетиялы (перспектив
ұқсау) фигура деп аталып, ол F пен белгіленеді.

5.

Гомотетияның қасиеттері.

6.

Гомотетиялық түзулер.
Теорема. Түзудің нүктелерін гомотетиялық орын ауыстырғанда олар тағы
түзудің нүктелеріне көшеді, яғни кез келген түзуге гомотетиялы фигура тағы
түзу сызық болады.
Дәлелдеу. Гомотетия центрі ,гомотетия коэффиценті болсын.
Бір неше жағдайларын тексеріп көрейік.
1) Ауыстырылып жатқан түзу гомотетия центріден өтеді.Гомотетияның
сипаттамасына көре түзуінде жатушы кез келген М нүктеге гомотетиялы М'
нүкте сол түзуде жатады.Екіншіден, түзуінде жатушы кез келген М' нүкте үшін
түзуінде жатушы сондай М нүкте табу мүмкін, Г М болады.Демек,бұл жағдай
үшін теорема дұрыс болды. түзуге гомотетиялы фигура сол түзудің өзінен
құралады.
Г
2) Берілген түзу гомотетия центрінен өтпейді және
а) Біріншіден болған жағдайды қарастырайық.
Берілген түзудің кез келген А және В нүктелерін алып,оларға гомотетиялы
сәйкес нүктелерді А' және В' мен белгілейік.

7.

8.

Гомотетиялық көпбұрыштар.
Теорема. Кез келген көпбұрышқа гомотетиялық фигура берілген
көпбұрышқа ұқсас көпбұрыш.

9.

1- мысал.Қандайда бір үшбұрыш алып берілген гомотетия центріне байланысты
оған k 1 гомотетиялы үшбұрыш салыңдар [2].
2
1
Талдау: k
болғандықтан салынатын үшбұрыш берілген үшбұрыштан екі
есе кіші болуы2керек.Берілген үшбұрыштың ұштарынан гомотетия центріне
дейінгі қашықтық салынған үшбұрыштың ұштарынан S ке дейінгі
қашықтықтың жартысына тең болуы керек.
Салу: 1) SА, SВ, SС біріктіреміз;
2) SВ -ны тең екіге бөлеміз;
3) SА- ны тең екіге бөлеміз;
4) SС- ны тең екіге бөлеміз;
5) B' A' C' біріктіреміз.

10.

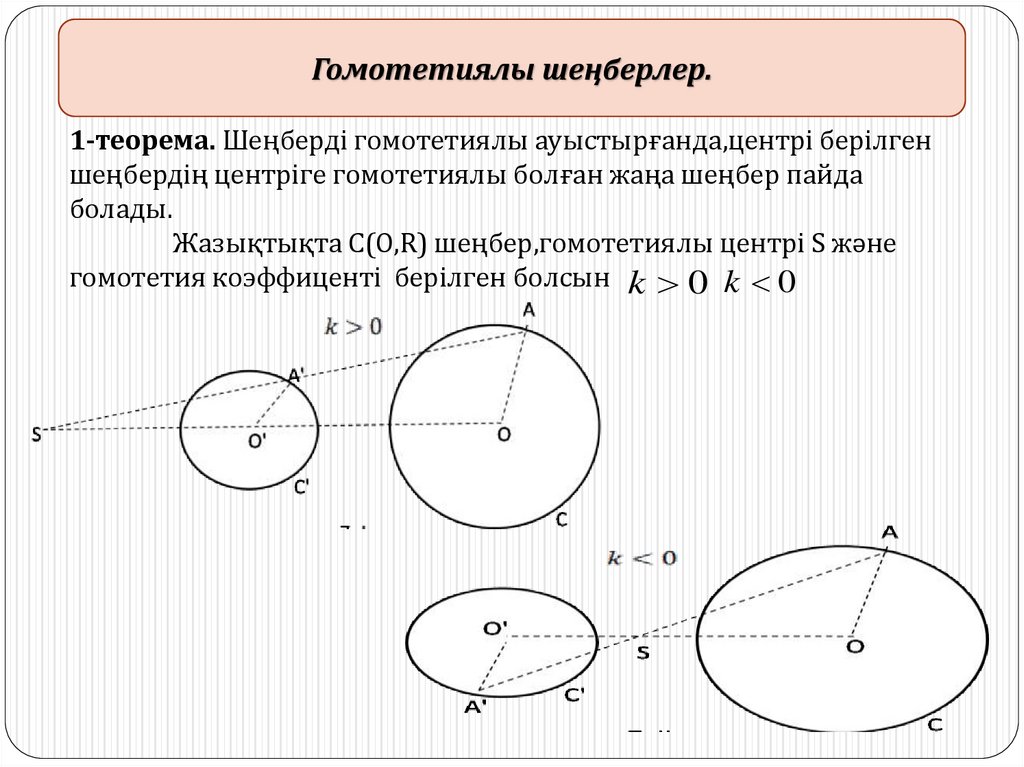
Гомотетиялы шеңберлер.
1-теорема. Шеңберді гомотетиялы ауыстырғанда,центрі берілген
шеңбердің центріге гомотетиялы болған жаңа шеңбер пайда
болады.
Жазықтықта С(О,R) шеңбер,гомотетиялы центрі S және
гомотетия коэффиценті берілген болсын k 0 k 0

11.

Трансверсаль және Менелай теоремасы.
Трансверсаль сөзі - көлденең өтуші немесе көлденең жатушы
мағынадағы латынның transversus сөзінен алынған, үшбұрыштың
қабырғаларын қиып өтетін түзуді білдіреді.Жалпы түзулер
системасында қиюшы түзу-трансверсаль деп аталады. Төмендегі
теоремалар трансверсал жайындағы тура және кері теоремалар
болып,олар көп теоремаларды дәлелдеуде (мысалы, Монж, Паскаль
және Чева теоремаларын дәлелдеуде) және салу есептерінде
қолданылады.
1.Менелай теоремасы. Егер үшбұрыштың АВ,ВС,АС
қабырғаларын немесе олардың жалғасын қандайда түзу
сәйкесінше А'В'С' нүктелерде кессе, АС ВА СВ
теңдігі шығады.
С В
А С
В А
1

12.

Әр екеуі гомотетиялы болған үш
фигура туралы теорема
Теорема. Егер екі фигураның әр бірі үшінші бір фигураға
гомотетиялы болса, ол екі фигурада өзара гомотетиялы болып,бұл
үш фигурадан әр қайсысы екеуінің ұқсастық центрлері бір түзуде
жатады.Бұл теореманы үшбұрыштарға дәлелдейік.

13.

Ұқсас түрлендіруді мектепте оқыту

14.

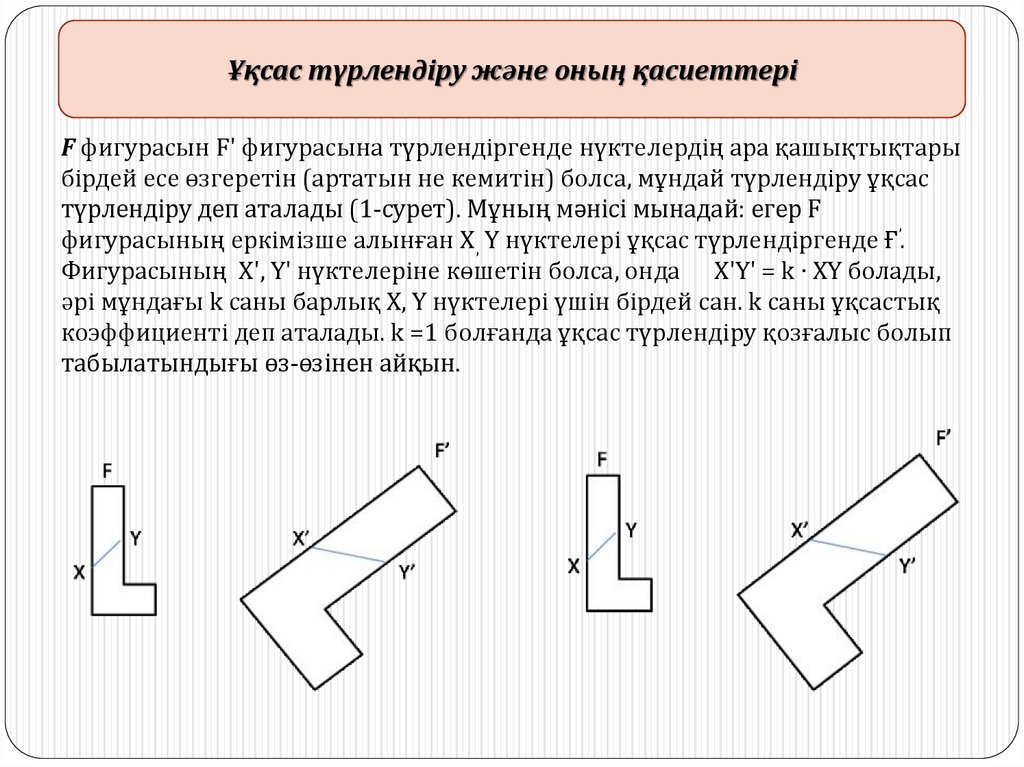
Ұқсас түрлендіру және оның қасиеттері
F фигурасын F' фигурасына түрлендіргенде нүктелердің ара қашықтықтары
бірдей есе өзгеретін (артатын не кемитін) болса, мұндай түрлендіру ұқсас
түрлендіру деп аталады (1-сурет). Мұның мәнісі мынадай: егер F
фигурасының еркімізше алынған Х , Y нүктелері ұқсас түрлендіргенде Ғ’.
Фигурасының X', Y' нүктелеріне көшетін болса, онда X'Y' = k ∙ XY болады,
әpi мұндағы k саны барлық X, Y нүктелері үшін бірдей сан. k саны ұқсастық
коэффициенті деп аталады. k =1 болғанда ұқсас түрлендіру қозғалыс болып
табылатындығы өз-өзінен айқын.

15.

Үшбұрыштардың екі бұрышы бойынша ұқсастық белгісі.

16.

Үшбұрыштардың екі қабырғасы және олардың
арасындағы бұрышы бойынша ұқсастық белгісі.
Теорема3. Егер бір үшбұрыштың eкi қабырғасы екінші үшбұрыштың
қабырғасына пропорционал болып және осы қабырғалар жасайтын
бұрыштар тең болса, ондай үшбұрыштар ұқсас болады.

17.

Үшбұрыштың ұқсастығын іс жүзінде қолданылуы.
Салу есептерінде
Үшбұрыштарды салуға берілген көптеген есептерді шешу
кезінде ұқсастық әдісі қолданылады. Ол алдымен кейбір берілген
деректер негізінде іздеп отырылған үшбұрышқа ұқсас
үшбұрышты, содан кейін қалған деректерді пайдалана отырып
ізделген үшбұрышты салудан тұрады.
Мысал келтірейік.
1-есеп. Екі бұрышы мен үшінші бұрышының
биссектрисасы бойынша үшбұрыш салу керек.
Шешуі. 15, а-суретте берілген екі бұрыш пен берілген
кесінді кескінделген. Екі бұрышы сәйкес берілген екі бұрышқа тең,
ал үшінші бұрышының биссектрисасы берілген кесіндіге тең
болатын үшбұрышты салу керек.
Алдымен іздеген үшбұрышқа ұқсас кез келген үшбұрышты
саламыз. Ол үшін қалауымызша алынған А1 В1 кесіндісін сызып, А1
мен В1 бұрыштары сәйкес берілген бұрыштарға тең болатындай,
А1 В1 С үшбұрышын тұрғызамыз (1, б- сурет).

18.

19.

Ұқсас үшбұрыштар тақырыбын оқыту.
Геометрияны оқытуда есептерді шеше білу дағдысын
қалыптастыру және оны жалпы түрде дамыту аса маңызды
мәселелердің бірі болып табылады. Геометриялық есептерді шешу
туралы жалпы білік - дағдылар әдетте көптеген есептерді шешу
арқылы қалыптасады. Олай болса, мұғалім мен оқушының жүйелі
түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім,
әр түрлі теориялық фактілерді байланыстыруды қажет ететін,
оқушылар шығара алмайтын жаңа есептер де жиі кездеседі.
Сондықтан оқушыларды кез келген геометриялық есепті шешудің
жалпы тәсілдерімен қаруландыру керек. Бұл талап математикалық
есептерді шешу бағдарламасында да айтылған. Бағдарлама белгілі
бір есептердің түрлерін және оларды шешудің тәсілдерін
таныстыруға бағытталып қана қоймай, қайта дәлелдеудің
барынша жалпы әдістерін ойлауды меңгерту болып табылады.

20.

21.

Пайдаланылған әдебиеттер.
1. Рахымбек Д., Мадияров Н.К. Геометриялық салу есептері. Оқу
құралы / Д. Рахымбек, Н.К. Мадияров. – Алматы: Эверо, 2015. – 287 б.
2. Отажонов .Р.К. Геометрик ясаш методлари - Тошкент:
Укитувчи,1965. - 205 бет
3. Шыныбеков Ә.Н. Геометрия: Жалпы білім беретін мектептің 9сыныбына арналған оқулық. – Алматы:Атамұра,2013. – 224 бет.
4. Погорелов А.В. «Геометрия» Жалпы білім беретін мектептің 7-11
сыныптарына арналған оқулық. Алматы. Просвещение-Қазақстан.
2003
5. Рахымбек Д., Кенеш Ә.С. Мектеп геометрия (планиметрия) курсын
оқыту әдістемесі: Оқу құралы. / Д. Рахымбек, Ә.С.Кенеш –Алматы:
Эверо,2015. – 320 б.
6. Атанасян Л. С., Бутузов В. Ф., Геометрия: Жалпы білім беретін
мектептің 7-9 сыныбына арналған оқулық. – Алматы:Мектеп,2002. –
132 бет.
7. Атанасян Л. С., В. Ф. Бутузов В. Ф., Глазков Ю.А., Некрасов В. Б.,
Юдина И. И., Изучение геометрии в 7-9 классах. Москва 2010.- 113ст.

22.

8. Жүнісов Т. Планиметриялық салу есептерін шығару әдістері. Алматы,
1998.
9. Жазықтықтағы геометриялық салу теориясы мен практикасы.
Методикалық талдау. – Алматы: Республикалық оқу-методика
кабинеті, 1976. – 101 бет
10. Бекбоев И.Б. және т.б. Геометрия: Жалпы білім беретін мектептің 9сыныбына арналған оқулық. – Алматы:Мектеп, 2008.
11. Әбдімәжитов К., Қаңдыбаев Қ. Геометрия есептерін шешудің кейбір
методтары. – Алматы:Абай атындағы ҚазПИ, 1978. – 72 бет.
12. Cенников Г.П. VI-VIII кластарда салу есептерін шешу: Оқытушылар
үшін. – А., 1959. -165б.
13. Методика и технология обучения математике. Курс лекций:пособие
для вузов / под научн. ред. Н.Л. Стефановой, Н.С. Подходовой. =
М.:Дрофа, 2005. – 414 с.
14. Методика преподавания математики в средней школе. Частная
методика. Учебное пособие. Огоносьян В.Г., Колягин Ю.М., Луканин Г.Л.,
Санинский В.Я. -М: Просвещение.1980, - 368 с.
15. Гусев А.А., Кожухов И.В., Прокофьев А.А. Геометрия. Полный
справочник. – М.: Махон, 2006. 320 с.

23.

Назарларыңызға рахмет !