Сызықтық геометрия курсы. Геометриялық объектілер

1.

Сызықтық геометрия курсы геометриялық объектілер,
олардың ара-қатынасы және олардың жазықтықтағы кесіні
жайлы ақпаратты сипаттаудың теориялық негіздірін құрайды.
Объект(зат) элементтерінің өзара байланысын анықтайтын
кескінді объектінің толық кескіні деп атайды.
Объектінің(заттың)
өлшемдері
анықталатын
метрикалық анықталған кескін деп атайды
Кескінді салу ережелері проекциялық әдіске негізделген
кескінін

2.

Сызықтық геометрия курсында қарастырылатын
тақырыптар:
Кеңістік объектілерін жазықтықта кескіндеу ;
Түрлі геометриялық тапсырмаларды
сараптамалық шешімін табу жолдары;
Кескінделген объектінің геометриялық
түрлендіру және зерттеу әдістері;
графиктік
және
сипаттамаларын
Геометриялық объектілерді модельдеу негіздері;
Графиктік редактор(программалар)
кескінін тұрғызу.
көмегімен
объектінің

3.

Кеңістікте кез-келген
S нүктесі
проекциялау центрі
ретінде таңдап
алынады және осы нүкте арқылы
өтпейтін кез-келген
Пi
жазықтығы
проекцяилау
жазықтығы
таңдап
алынады
А нүктесін Пi жазықтығына проекциялау
үшін, S проекциялау центрі арқылы SА
сәулесін Пi жазықтығымен Аi нүктесінде
қиылысқанша жүргізеді. Аi нүктесі А
нүктесінің центрлік проекциясы, ал SА –
проекциялаушы сәуле деп аталады.
Центрлік проекциялау

4.

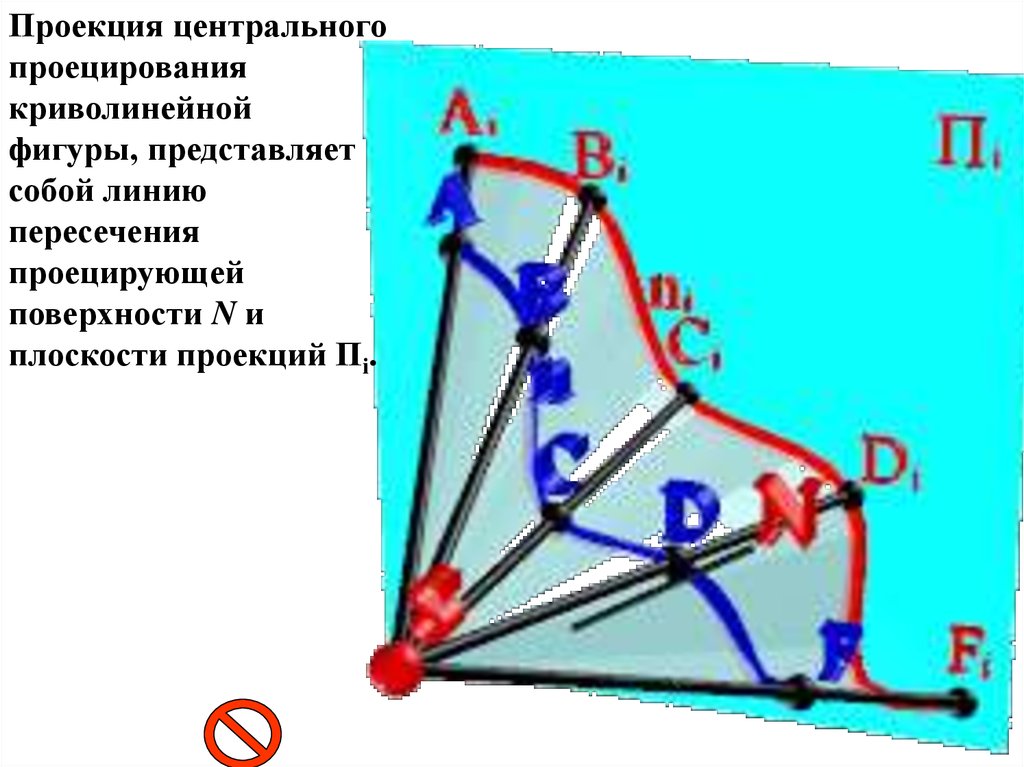
Проекция центрального
проецирования
криволинейной
фигуры, представляет
собой линию
пересечения
проецирующей
поверхности N и
плоскости проекций Пi.

5.

Конустық беттің проекциясы Ki сызығын береді, бұл сызықты
фигура очеркі деп атайды.

6.

Центрлік проекциялаудың дербес бір түрі – параллель проекциялау, яғни
проекциялау центрлін шексіз алыс қашықтыққа ұзартсақ, проекциялау
сәулелерін өзара параллель деп айтуға болады. Параллель проекциялар
тікбұрышты және көлбеубұрышты болады.

7.

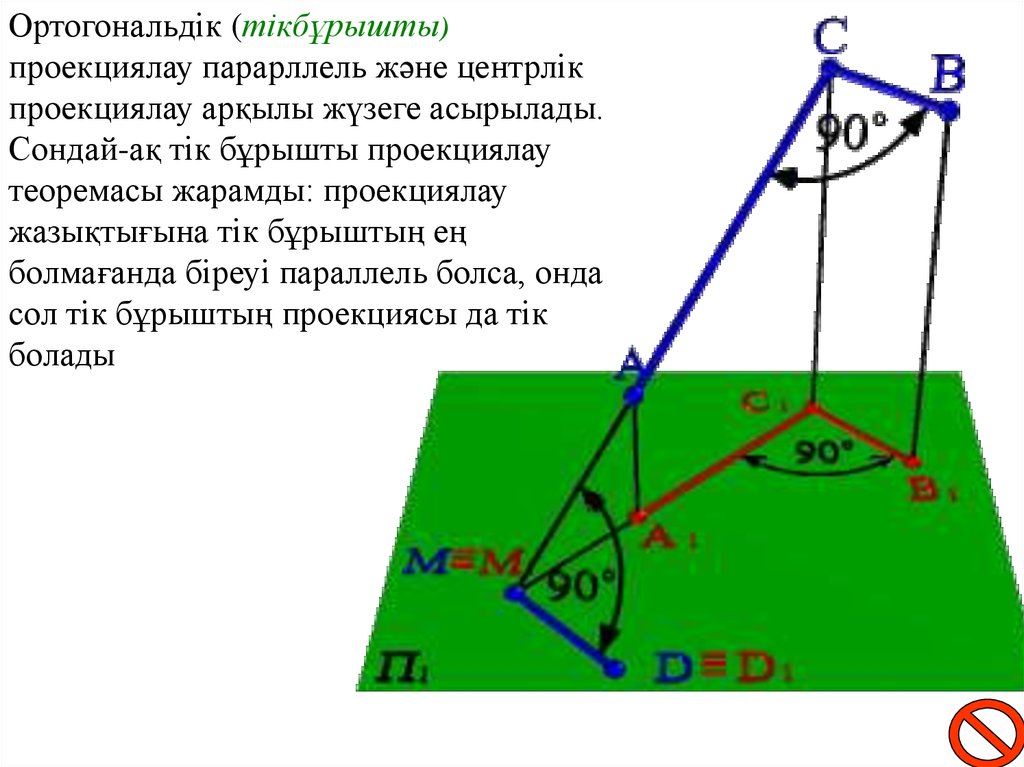
Ортогональдік (тікбұрышты)
проекциялау парарллель және центрлік
проекциялау арқылы жүзеге асырылады.
Сондай-ақ тік бұрышты проекциялау
теоремасы жарамды: проекциялау
жазықтығына тік бұрыштың ең
болмағанда біреуі параллель болса, онда
сол тік бұрыштың проекциясы да тік
болады

8.

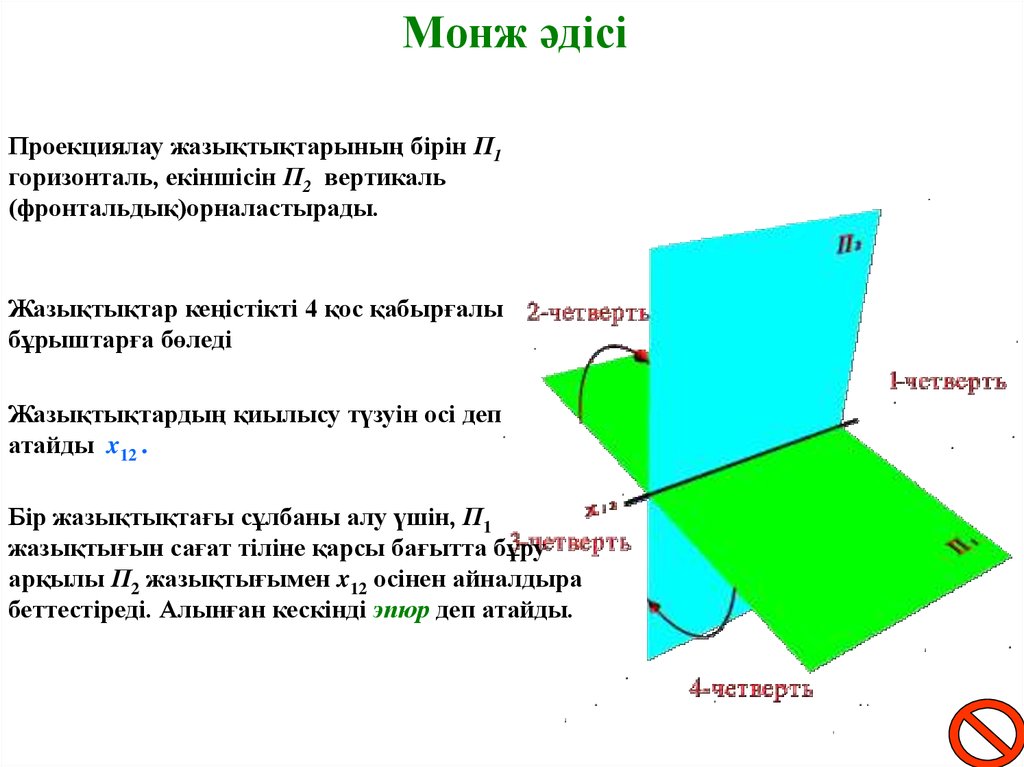
Монж әдісі
Проекциялау жазықтықтарының бірін П1
горизонталь, екіншісін П2 вертикаль
(фронтальдық)орналастырады.
Жазықтықтар кеңістікті 4 қос қабырғалы
бұрыштарға бөледі
Жазықтықтардың қиылысу түзуін осі деп
атайды x12 .
Бір жазықтықтағы сұлбаны алу үшін, П1
жазықтығын сағат тіліне қарсы бағытта бұру
арқылы П2 жазықтығымен x12 осінен айналдыра
беттестіреді. Алынған кескінді эпюр деп атайды.

9.

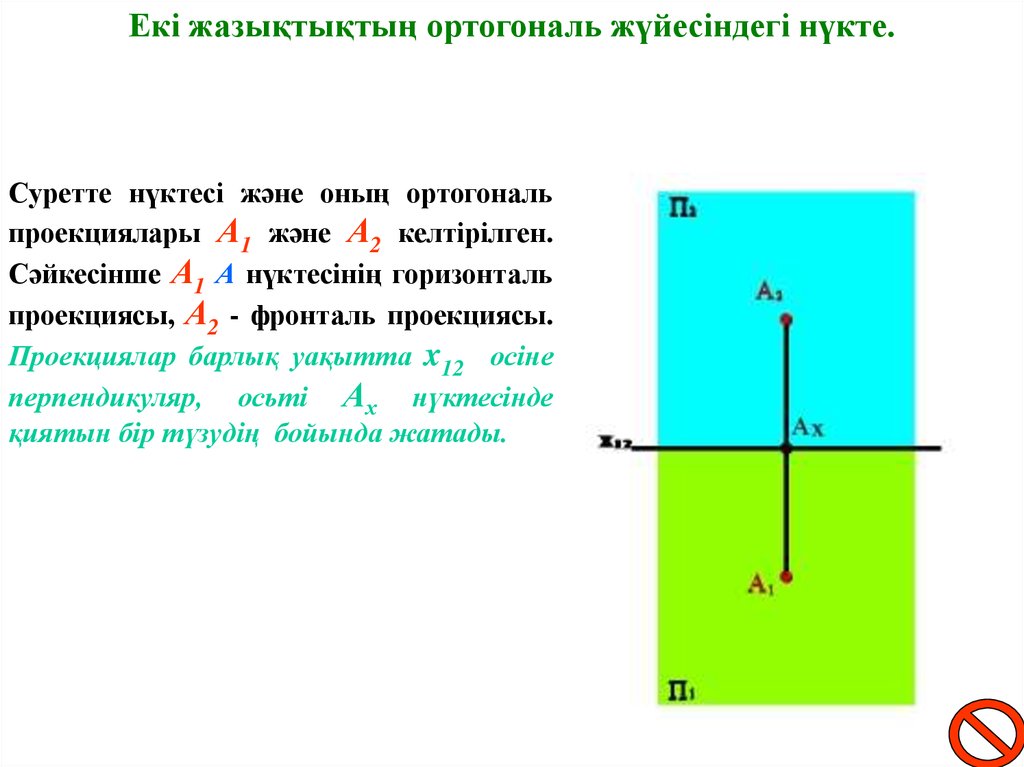
Екі жазықтықтың ортогональ жүйесіндегі нүкте.
Суретте нүктесі және оның ортогональ
проекциялары А1 және А2 келтірілген.
Сәйкесінше А1 А нүктесінің горизонталь
проекциясы, А2 - фронталь проекциясы.
Проекциялар барлық уақытта x12 осіне
перпендикуляр, осьті Ах нүктесінде
қиятын бір түзудің бойында жатады.

10.

Кеңістіктің
түрлі
ширектерінде
жататын
нүктелер

11.

Үш жазықтықтың ортогональ жүйесінде орналасқан нүкте
Шынайы өмірде П1 , П2 ден басқа қосымша П3 профильдік жазықтықты
қолдану қаже.

12.

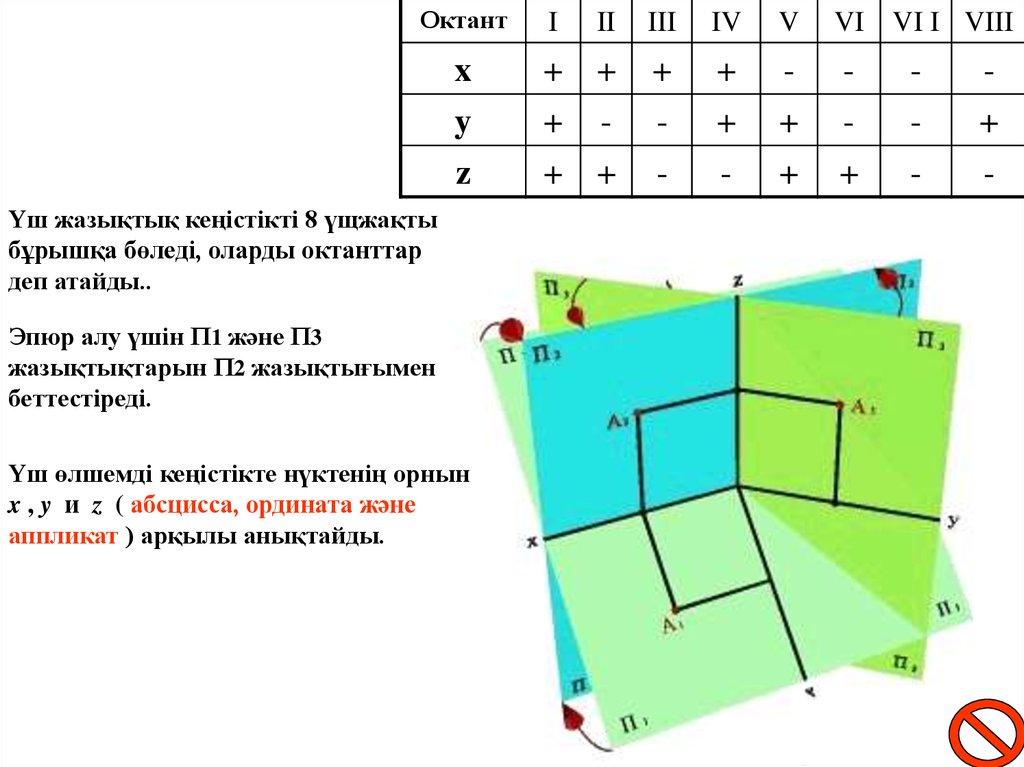
Октант
II
III
IV
V
x
+ +
+
+
-
-
-
-
y
+
-
-
+
+
-
-
+
z
+ +
-
-
+
+
-
-
Үш жазықтық кеңістікті 8 үщжақты
бұрышқа бөледі, оларды октанттар
деп атайды..
Эпюр алу үшін П1 және П3
жазықтықтарын П2 жазықтығымен
беттестіреді.
Үш өлшемді кеңістікте нүктенің орнын
x , y и z ( абсцисса, ордината және
аппликат ) арқылы анықтайды.
I
VI VI I VIII

13.

Нүктелердің өзара орналасуы

14.

Егер нүктенің сәйкес координаттары мәні тең болса,
ондай координаттар бәсекелес деп аталады. Бәсекелес
нүктелер бір проекцияланушы түзу бойында жатады.
Суретте осындай 3 жұп нүутелер көрсетілген, мұндағы:
•XА=XD;YА=YD;ZА < ZD;
• XA=XC;ZA=ZC;YA < YC;
• YA=YB;ZA=ZB;XA < XB;
Айырмашылықтары: горизонталь бәсекелес А және
D нүктелері горизонталь проекцияланушы АD
түзуінің бойында жатыр; фронталь бәсекелес А
және С нүктелері фронталь проекцияланушы АС
түзуінің бойында жатыр; профиль бәсекелес А және
В нүктелері профиль проекцияланушы АВ түзуінің
бойында жатыр; .

15.

16.

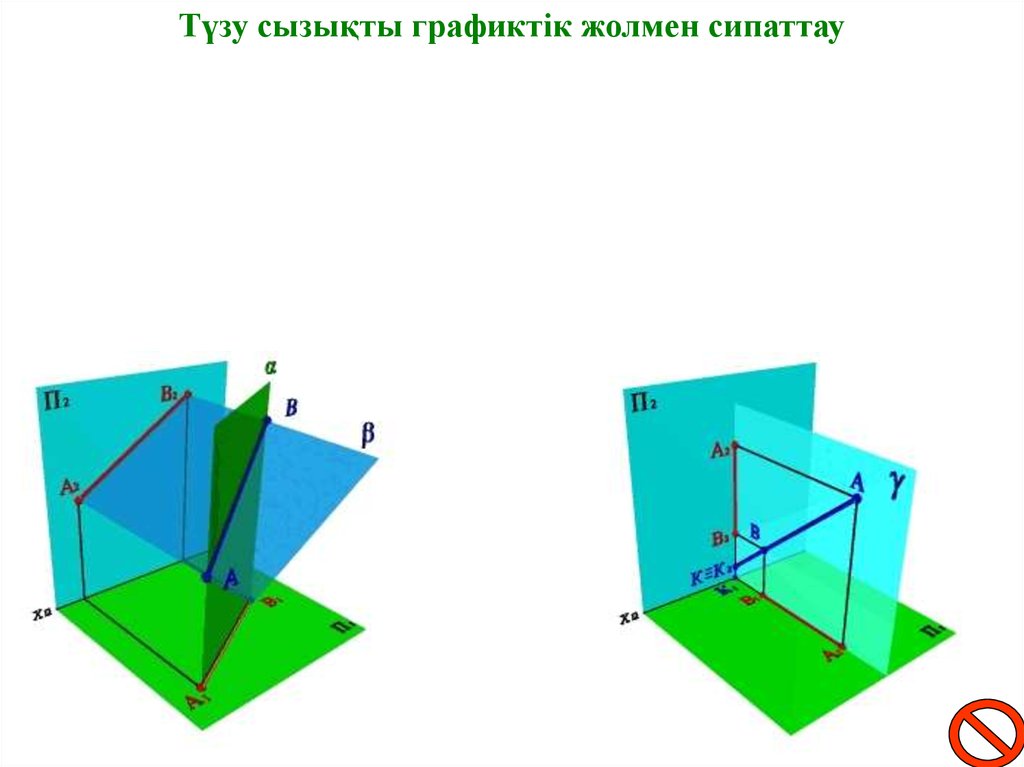
Түзу сызықты графиктік жолмен сипаттау

17.

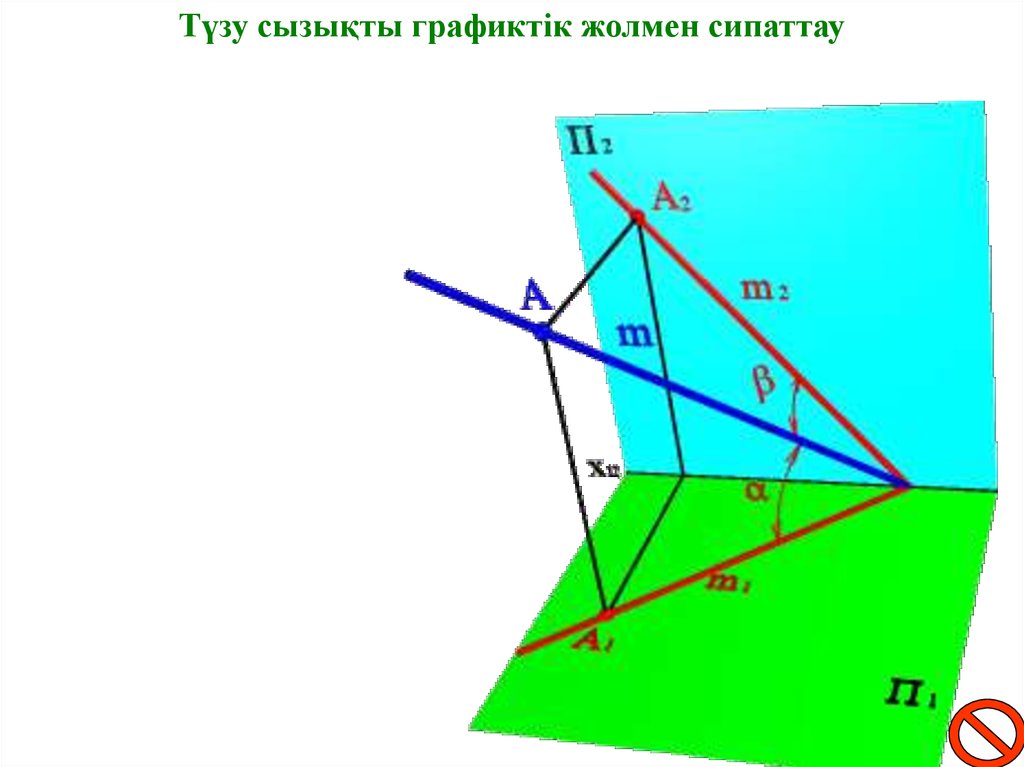
Түзу сызықты графиктік жолмен сипаттау

18.

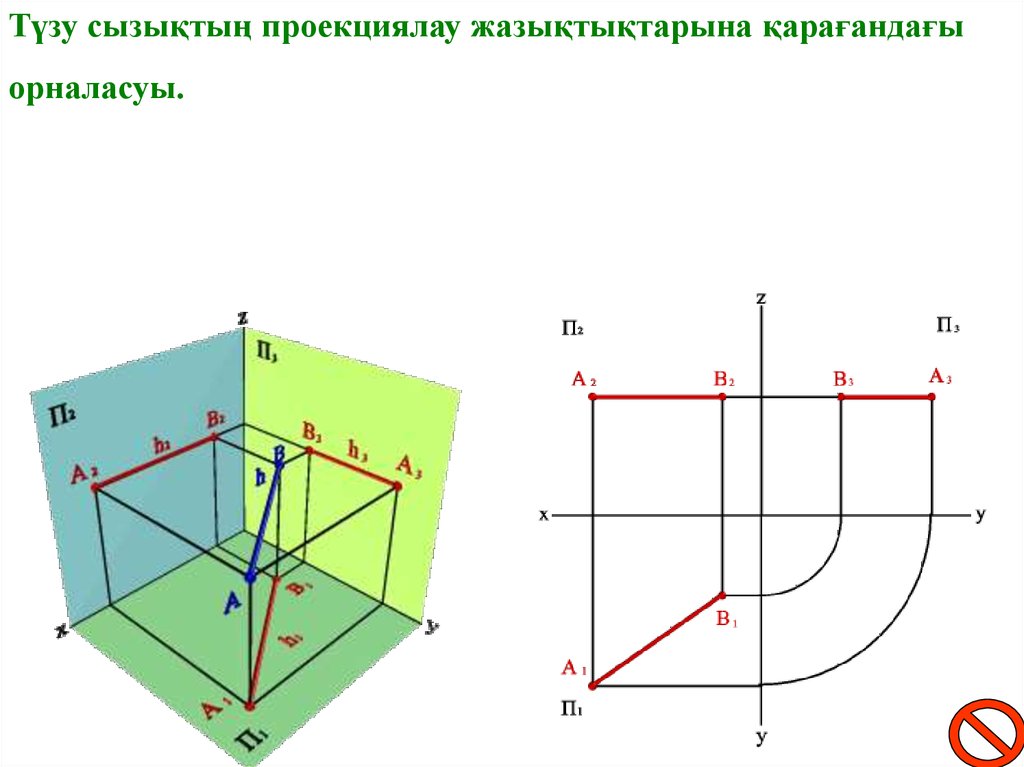
Түзу сызықтың проекциялау жазықтықтарына қарағандағы
орналасуы.

19.

Түзу сызықтың проекциялау жазықтықтарына қарағандағы
орналасуы.

20.

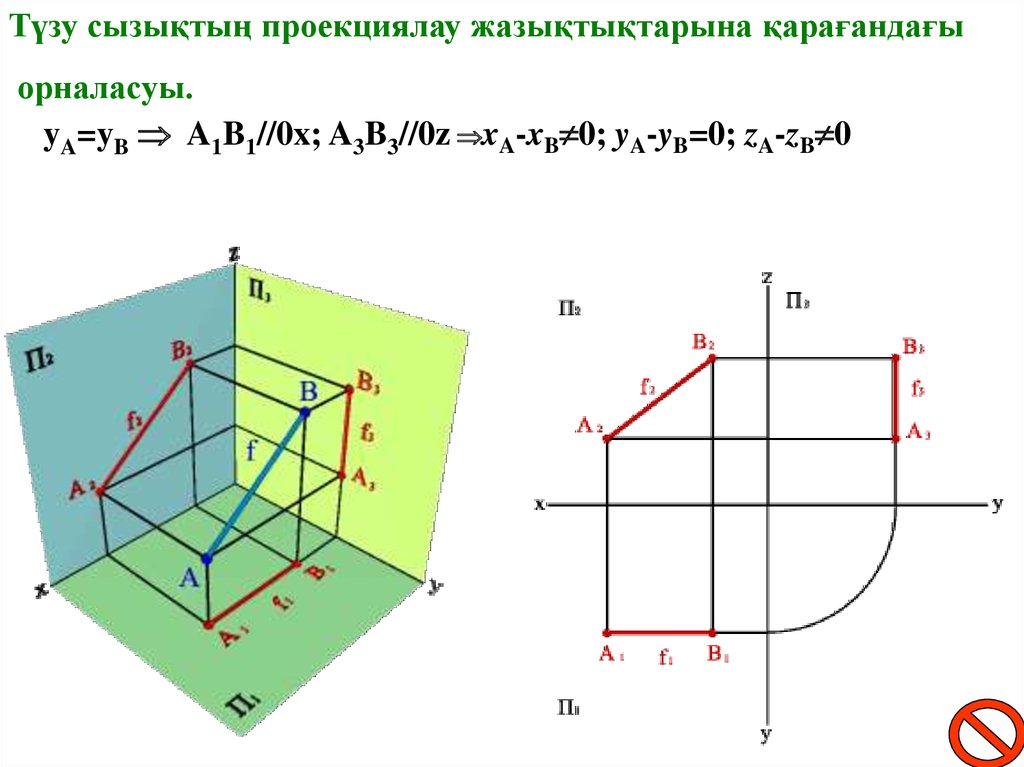
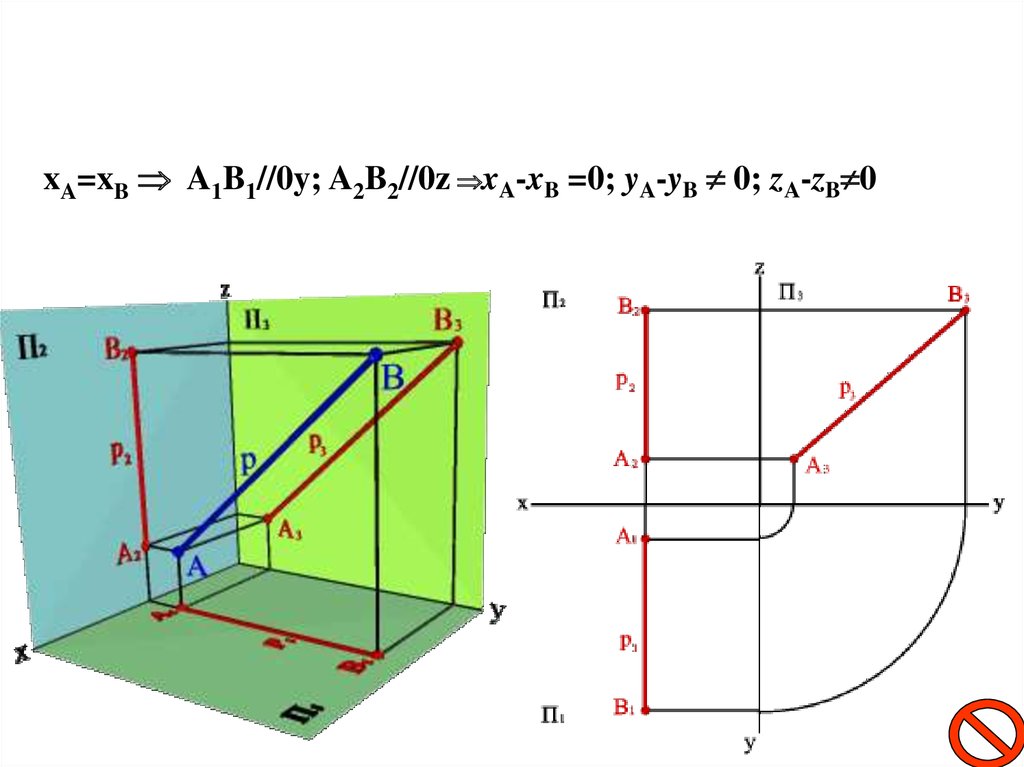
Түзу сызықтың проекциялау жазықтықтарына қарағандағы
орналасуы.
yA=yB A1B1//0x; A3B3//0z xA-xB 0; yA-yB=0; zA-zB 0

21.

xA=xB A1B1//0y; A2B2//0z xA-xB =0; yA-yB 0; zA-zB 0