Similar presentations:
Квадрат суммы и квадрат разности для матриц размером 2х2
1.
Исследовательская работа на тему „Квадратсуммы и квадрат разности для матриц
размером 2х2 “
МАОУ КУГ №1 – Универс
Профильнгая лаборотория математики
г.Красноярск
Выполнила :Исаенко Ю.А.
2.
Цель и задачи:Цель: изученить некоторые свойства квадратных матриц размерности
2х2 .
Задачи:
1.Исследовать некоторые свойства матриц
2.Исследовать справедливость некоторых формул сокращенного
умножения для квадратных матриц размерности 2х2
3.Исследовать справедливость свойства возведение в степень
произведения квадратных матриц размерности 2х2 .
3.
Обьект исследования - матрицыМатрица-это прямоугольная таблица специального вида, состоящая
из n строк и m столбцов, заполненная числами.
Например:
Матрица А называется
матрицей размера mхn,
числа aij называются ее
элементми ,где i показывает
номер строки , j - номер столбца
Единиичная маитрица — квадратная матрица, элементы главной
диагонали которой равны единице, а остальные равны нулю.
Обозначается такая матрица Е.
Е=
Например:
4.
Виды матриц.Если в матрице число
строк равно числу
столбцов, то матрица
называется квадратной.
Матрица, в которой число
строк не равно числу
столбцов, называется
прямоугольной.
a 11 a 12 a 13
1 1 2 0
п р и м е р
3 9 8
a 21 a 22 a 23
a 11 a 12 a 13
a 21 a 22 a 23 п р и м е р
a a a
31 32 33
4 12 4
1 3 8
- 5 9 10
5.
1.Умножение матрицы начисло
Для того чтобы умножить матрицу размерностью (m x n) надо каждый
элемент матрицы умножить на число.
Например:
а
а
А 11 12
а
а
21 22
а к
А к 1 1
а к
21
к
12
а к
22
а
Справедливо переместительное свойство
Ak=kA
6.
2.Сумма (разность) матрицСкладываются соответствующие элементы матриц. Количество суммируемых
матриц может быть произвольным. Для сложения матриц матрицы должны быть
одной размерности m x n.
a 11 a 12 a 13 b11 b12 b13 a 11 b11 a 12 b12 a 13 b13
a 21 a 22 a 23 b 21 b 22 b 23 a 21 b 21 a 22 b 22 a 23 b 23
прим ер :
1 5 2 5 2 1 1 5 5 2 2 ( 1 ) 6 7 1
1 7 1 2 4 1 1 2 7 ( 4 ) 1 1 3 3 0
7.
Умножение матриц.Чтобы одну матрицу можно было умножить на другую матрицу
нужно, чтобы число столбцов первой матрицы равнялось числу строк
второй матрицы.
Умножение выполняется по следующему алгоритму:
a 11 a 12
a 21 a 22
прим ер
1
0
2
1
b11
b 21
3
2
b12
b 22
a 11 b11 a 12 b 21
a 21 b11 a 22 b 21
4 1 3 2 ( 2 )
1 0 3 ( 1) ( 2 )
a 11 b12 a 12 b 22
a 21 b12 a 22 b 22
1 4 2 1 1
0 4 ( 1 ) 1 3
6
1
Произведение двух матриц в общем случае зависит от порядка
сомножителей, то есть оно не коммутативно:
AB≠BA
8.
Исследование некоторых свойств матрицВыведем формулу для возведения матрицы X в n-ую
степень.
X
X
X
2
3
4
1
X X
1
X
X
2
3
1
1
1
1
1
1
2
X
2
2
2
4
X
4
4 1
4 1
1
1
1
1
2
2
2
2
4
4
4
4
1 8
1 8
X
8
8
X
X
1
1
2
1
1
1
1
2
2
3
4
2
1
1
1
1
2 1
3
3 1
1
1
1
1
1
1
1
1
4
1
2
1
4 1
1
1
Исходя из вышеописанных примеров, предполагаем, что
общей формулой будет
X = 2 X
n
n -1
(1)
1
1
9.
Докажем истинность формул с помощью метода
математической индукции
(1)
1)Пусть
1 1
1 1
1 *
1 1
1 1
-верно
1 1
1 1
1 1
1 1 2)В предположении ,что (1) верна для n=N
докажем ,что формула(1) верна для n=N+1
Итак ,
.Значит, формула(1) верна для всех значений x€ N
10.
Формула для возведения матрицы Y в n-ую степень.Выведем формулу для возведения матрицы Y в n-ую
степень.
Y
Y
Y
2
3
4
1 1
1 1
1
Y Y
1
2
2
Y Y
2
4
3
Y Y
4
2
2
1
1
4 1
4 1
1 2
1 2
2
2
1 4
1 4
1 8
1 8
Y
n
4
4
8
8
= 2
Y
2
Y
Y
n -1
4
3
2
1
1
1
2
1
1
1
1
2
1
1
1
2 1
3
3 1
4
1
2
1
4 1
Y
И с т и н н о с т ь ф о р м у л ы (2 ) д о к а з ы в а е т с я а н а л о г и ч н о ф о р м у л е (1 ) .
1
1
1
1
1
1
1
1
1
1
1
1
11.
Выведем формулу для возведения суммы матриц X иY в n-ую степень.
1
1
Y
1
1
1
X
1
1
1
1 2
1 0
1
( X Y )
1
1 1
1 1
2
( X Y )
0
0
2
2
0
0
2
4
0
0
4
2 1
2
0
0
1
2 2 E
4
( X Y )
0
0
4
2
0
0
2
8
0
0
8
3 1
2
0
0
1
2 3 E
2
3
0
2
1
2
0
0
1
2 E
За м е ча е м за ко н о м е р н о сть , ко то р а я в ы р а ж е н а ф о р м ул о й
(X + Y ) = 2 E
n
n
(3 )
12.
Докажем истинность формулы (3) с помощью метода
математической индукции
(X + Y ) n = 2 n E
( X Y )1 2 1 * E 2 E
n 1;
1)
2)П уст ь
(3 )
(3)
верно
для
n k,
докаж ем,
чт о
(3)
верна
для
n k 1
k
k 1
1
0
2
0
2
0
2
0
2
0
k 1
k
k
k
( X Y ) ( X Y ) ( X Y ) 2 E ( X Y ) 2
k
k 1
0 1 0 2 0 2 0 2 0 2
1 0
k 1
k 1
2
И т ак
0
1
2
E
( X Y ) k 1 2 k 1 E ;
З н а ч и т ф о р м у л а (3 ) в е р н а д л я в с е х x € N
13.
22
.И с с л е д у е м и с т и н н о с т ь ф о р м у л ы (X Y ) X 2 X Y Y
( X Y )
b
а
X
с
d
a m
c g
b k
d z
Y
m
g
2
k
z
2
а
X Y
с
b
d
m
g
2 a m
( X Y )
c g
k
z
b k a m
d z c g
b k (a m )2 (b k )(c g )
d z ( c g ) ( a m ) ( d z ) ( c q )
(a m )(b k ) (b k )(d z )
2
(c q )(b k ) (d z )
14.
во втор ом сл уч ае, сл о ж и м к вад рат м атри ц ы X с удвоен н ы м п р ои зведен и ем м атри ц X Y и п ри бави мквадрат м атриц ы Y
X
2
2 X Y Y
2 а
X
с
2
b a 2 b c
d c a d c
b а
d с
а
2 * X * Y X Y 2
с
b m
d g
2
2
2 a bc
X 2 X Y Y
ca d c
k
ab bd
2
cb d
a k b z
k m
z g
2 a m 2 bg
2
ck d z
2cm 2d g
m 2 kg
2
a
m
2
b
g
2
a
k
2
b
z
ab bd
2 2 c m 2 d g 2 c k 2 d z
cb d
gm zg
2
a bc 2 a m 2 bg m 2 kg
ca d c 2cm 2d g gm zg
a m bg
2
z
cm d g
2 m
Y
g
ab bd 2ak 2bz m k kz
2
2
cb d 2ck 2d z gk z
k m 2 k g
z
gm zg
2 a k 2 b z
2 c k 2 d z
m k kz
2
gk z
m k kz
2
gk z
15.
ср а вн и м п о л у ч и в ш и е ся м атр и ц ы п о эл ем е н тн о ,то есть к аж д ы й эл ем ен т о д н о й м ат р и ц ыс со о тветств ую щ и м эл ем ен то м д р уго й м атр и ц ы
( X Y )
2
2
( a m ) ( b k )( c g ) ( a m )( b k ) ( b k )( d z )
2
( c g )( a m ) ( d z )( c q ) ( c q )( b k ) ( d z )
2
X 2 X Y Y
2
О б о з н а ч и м p .q п о з и ц и ю э л е м е н т а м а т р и ц ы .П о л у ч а е м
1 .1
kc gb
1 .2
m b kd ak bz
(2 )
2 .1
cm dg ga zc
(3)
2 .2
gb ck
(1 )
(4 )
з а м е т и м , ч т о у с л о в и е (1 ) ( 4 ) с о в п а д а ю т
и з (1 ) сл е д у е т
k
b
g
c
С р а в н и м (2 ) и (3 ) :
2
2
a b c 2 a m 2 b g m k g a b b d 2 a k 2 b z m k k z 1 .2 b ( m - z ) k ( a - d )
2
2
c a d c 2 c m 2 d g g m z g c b d 2 c k 2 d z g k z 2 .1 c ( m - z ) g ( a - d )
c
g
a d
m z
16.
В итоге получаем условие, при котором выполняетсяравенство (X+Y)2=X2+2XY+Y2
Это будет пропорция:
( k,g, m-z≠0)
17.
Проверим истинность формулы для особогослучая, когда (k,g,m-n=0)
0
m
Тогда матрица Y имеет вид Y
а
X
с
(X Y )
b
d
X
X
X
X
2
m
0
0
m
2
0
m
0
m
b
a m
d m
c
а
X Y
с
(X Y )
Y
0
2
b
d
2 X Y Y
a m
c
a m
c
b
d m
b
(a m )2 bc
d m ( a m ) c ( d m ) c
2
b a 2 bc ab bd
а
m
2
Y
2
с
d
c
a
d
c
c
b
d
0
b m
0
bm
2bm
а
am
2am
2
2
Y 2
с
d
0
m
c
m
d
m
2
c
m
2
d
m
2
2
2bm m
a bc ab bd 2am
0
2
2 X Y Y 2
2 d m 0
c b d 2 2 c m
m 2
ca dc
a 2 bc 2am m 2
ab bd 2bm
2
2
c
a
d
c
2
c
m
c
b
d
2
d
m
m
2
а
с
b
d
(a m )b b (d m )
2
cb (d m )
0
m
m
0
0
m
m 2
0
0
m 2
m
18.
C равниваемкаж ды й
э лем ен т о д н о й м а т р и ц ы с элем ен т о м д р уго й м а т р и ц ы .
(X Y )2
(a m )2 bc
(a m )b b (d m )
2
( a m ) c ( d m ) c
cb (d m )
X 2 2XY Y 2
a 2 bc 2am m 2
ab bd 2bm
2
2
cb d 2dm m
ca dc 2cm
1 .1 ( a m ) 2 b c a 2 b c 2 a m m 2
1 .2 ( a m ) b b ( d m ) a b b d 2 b m
2 .1
(a m )c (d m )c c a d c 2 c m
2 .2
cb (d m )2 cb d 2 2dm m
В частном случае когда
одна из матриц имеет вид
m
Y
0
,то формула
2
2
2
(X Y ) X 2 X Y Y
(1 )
(2 )
является истинной
(3)
2
0
m
(4 )
19.
Исследование показали что все выводы сделанные дляквадрата суммы двух матриц 2х2 ,справедливы и для
квадрата разности таких матриц
20.
Результат:1.В общем случае для квадратных матриц порядка
2х2 формулы квадрата суммы ,квадрата разности,
разности квадратов не являются истинными ,но
при этом формулы истинны если выполняются
пропорция.












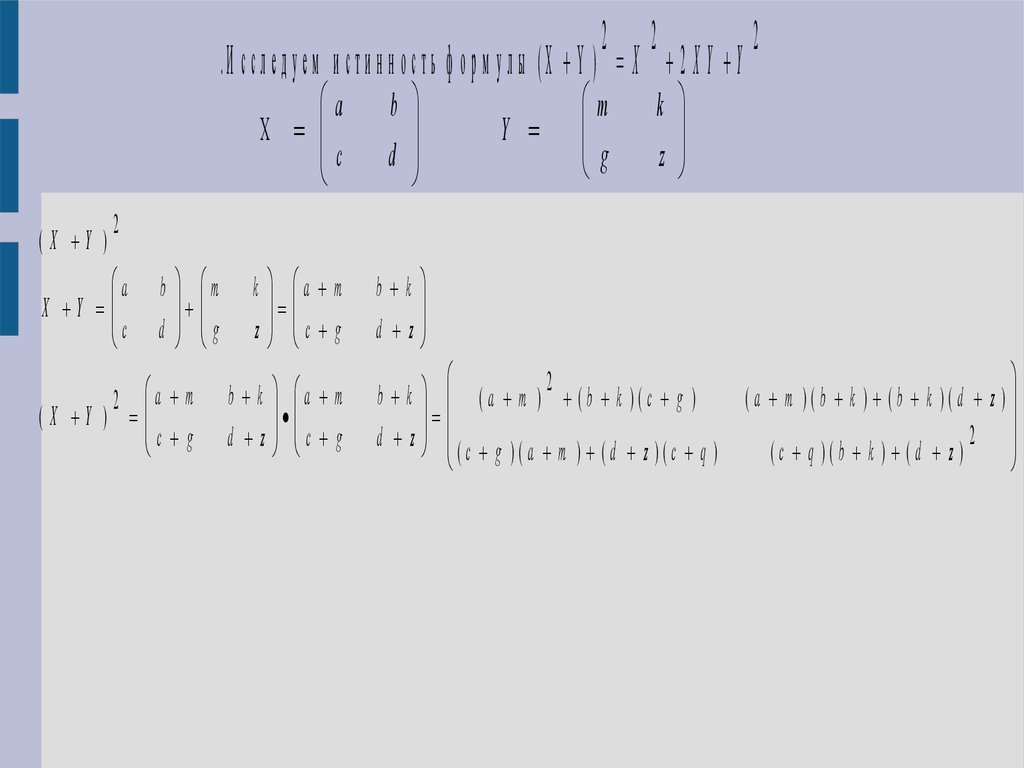







 mathematics
mathematics








