Similar presentations:
Квадрат суммы. Квадрат разности
1. Квадрат суммы. Квадрат разности.
2. 1.Прочитайте выражения:
• а2; аb; 2ху; a + b;(а +b)2; (а –b)2.
х – у; а2 – b2;
• 2.Найдите удвоенное произведение чисел:
х и у;
1 и с; 3 и m; 2р и 5к.
• 3. Упрости: а + а; ху + ху; -аb – ab.
• 4. Найдите квадрат числа: 22; 42 ; 502; (3х)2;
(сх)2; (ур3)2.
• 5. Представь в виде квадрата: 25; 81с2; 4х2;
49у2; 0,01а2; с2у2.
3. Верные и неверные утверждения.
1. (a + b )2 = ( a + b )( a + b )
2. ( a – b )2 = ( a – b )( a – b)
3. 492 = 2401
4. 522 = 2704
5. Некоторые правила сокращенного
умножения были сформулированы
около 4 тыс. лет тому назад в
буквенном виде.
4. Найти более простой способ возведения в квадрат суммы и разности двух чисел.
• Упрости, проанализируй результат.• 1. ( а + b )2
• 2. ( х + у )2
• 3. ( m + 1)2
• 4. ( c - d )2
• 5. ( m – 2 )2
5.
• ( a + b = + 2ab +2
2
2
• ( a - b ) = a – 2ab + b
2
)
2
a
2
b
Формулы
сокращенного
умножения
6.
ab
2
a
ab
a
ab
2
b
b
7. Возвести в квадрат, используя формулы сокращенного умножения:
• 1. (p + k• 2. ( x + 1 )2
• 3. ( a + 2)2
2
)
• 4. (p – k
• 5. ( x – 1 )2
• 6. ( a – 2 )2
2
)
8. Решить задания из учебника:
• № 370(1,3)• № 371(1,3)
• № 372(1)
• № 373(3)
9. Вычислите, используя формулы сокращенного умножения:
2• 49
=
2
• 52 =
10.
• 492 = (50 -1)2 =2
2
= 50 - 2· 50 ·1 + 1 =
= 2500 – 100 + 1 = 2401
• 532 = ( 50 + 3 )2=
= 502 +2 · 50 ·3 + 32 =
= 2500 + 300 + 9= 2809
11. Самостоятельная работа.
• 1 вариант2 вариант
• Упрости, применяя формулы сокращенного
умножения:
• 1. ( n + m )2
• 2. (3x – 2y)2
• 3. ( 0,3x2 + 4ab)2
1. ( k + p )2
2. ( 2a – 3b )2
3. (0,1xy + 3a2 )2
• Вычисли, используя формулы сокращенного
умножения:
• 4. 992
• 5. 812
4. 912
5. 892
12. Решение:
1.(n+m)2=n2+2nm+m2
1.(k+p)2=k2+2kp+p2
2.(3x-2y)2=9x2-12xy+4y2 2.(2a-3b)2=4a2-12ab+9b2
3.(0,3x2+4ab)2=
3.(0,1xy+3a2)2=
= 0,09x4+2,4x2ab+16a2b2 = 0,01x2y2+0,6a2xy+9a4
• 4. 992=(100-1)2=
• = 1002-2 · 100 · 1+ 12=
• =9801
• 5. 812=(80+1)2 =
=802+ 2 ·80 ·1 +12 =
=6400+160+1=6561
4. 912=(90+1)2=
= 902 + 2 · 99 ·12=
=8281
5. 892=(90-1)2=
=902 - 2 ·90 · 1 + 12=
=8100-180+1=7921
13. Оценка:
• «3»• №1
«4»
№1, №2.
«5»
№1, №2, №3.
Дополнительно «5»
№4, №5.
14.
Спасибо за урок!15.
)·( + )2
2
= + + +
2
2
= + 2 +
2
( + ) =( +














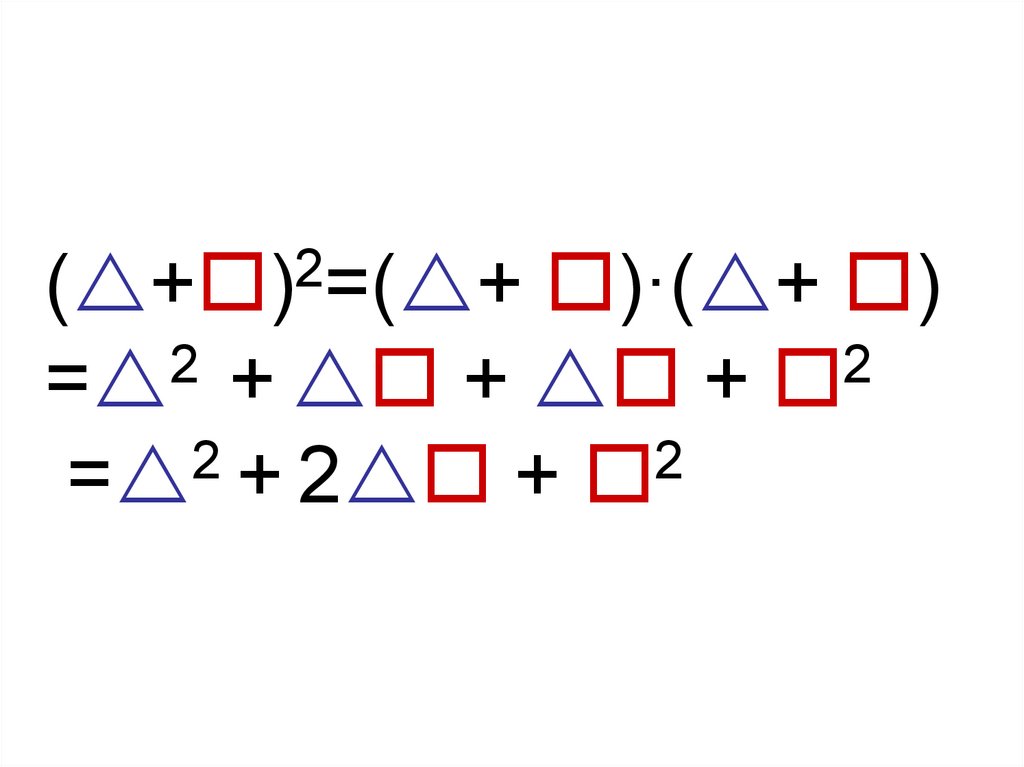
 mathematics
mathematics








