Similar presentations:
Магнитостатическое поле в вакууме. Часть 3
1. Магнитостатическое поле в вакууме. Часть 3.
2.
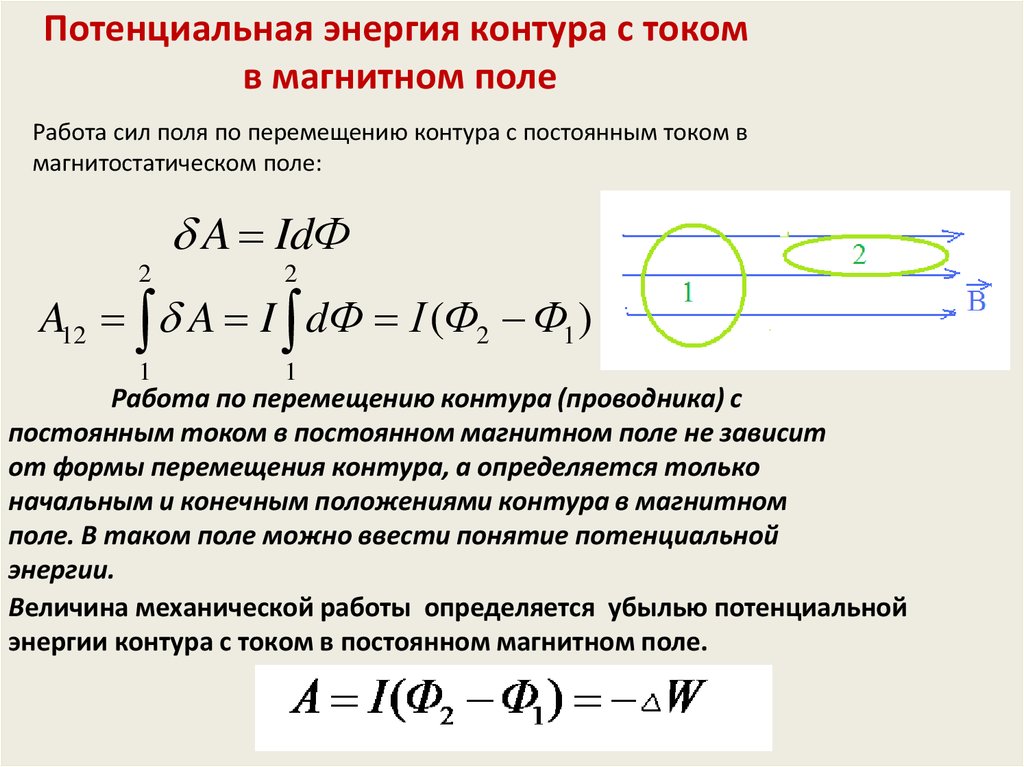
Потенциальная энергия контура с токомв магнитном поле
Работа сил поля по перемещению контура с постоянным током в
магнитостатическом поле:
A IdФ
2
2
1
1
A12 A I dФ I (Ф2 Ф1 )
Работа по перемещению контура (проводника) с
постоянным током в постоянном магнитном поле не зависит
от формы перемещения контура, а определяется только
начальным и конечным положениями контура в магнитном
поле. В таком поле можно ввести понятие потенциальной
энергии.
Величина механической работы определяется убылью потенциальной
энергии контура с током в постоянном магнитном поле.
3.
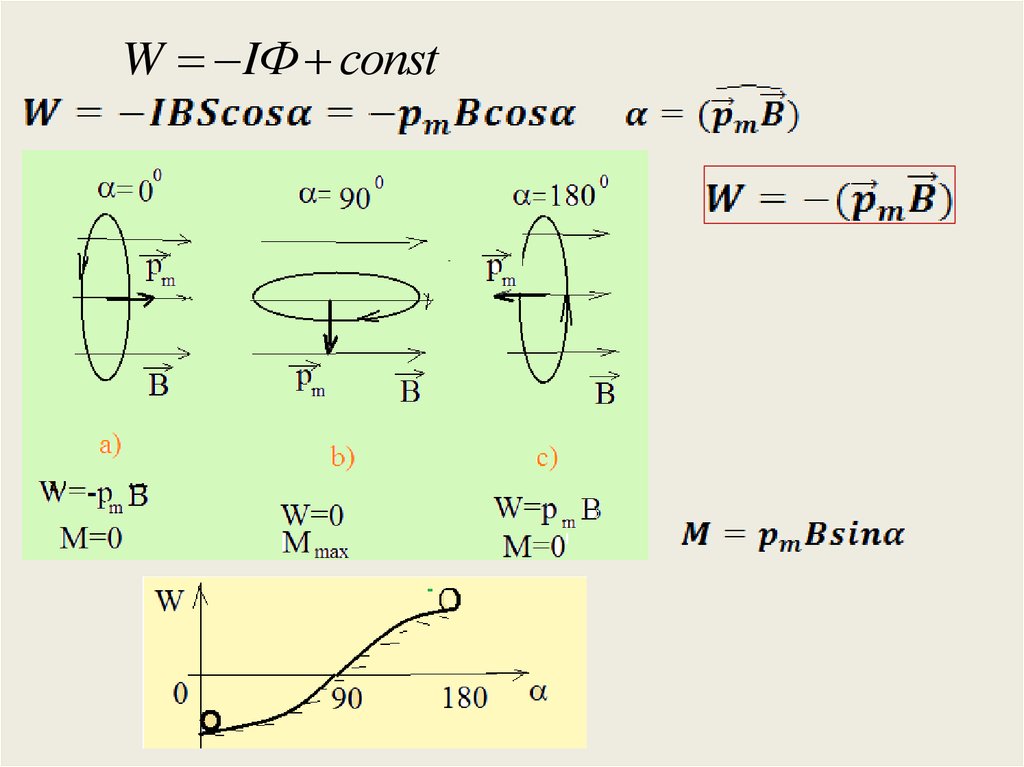
W IФ const4.
W pm B cos( pm B)
Положение контура
0 pm B
соответствует минимуму его потенциальной энергии,
т.е. состоянию устойчивого равновесия.
5.
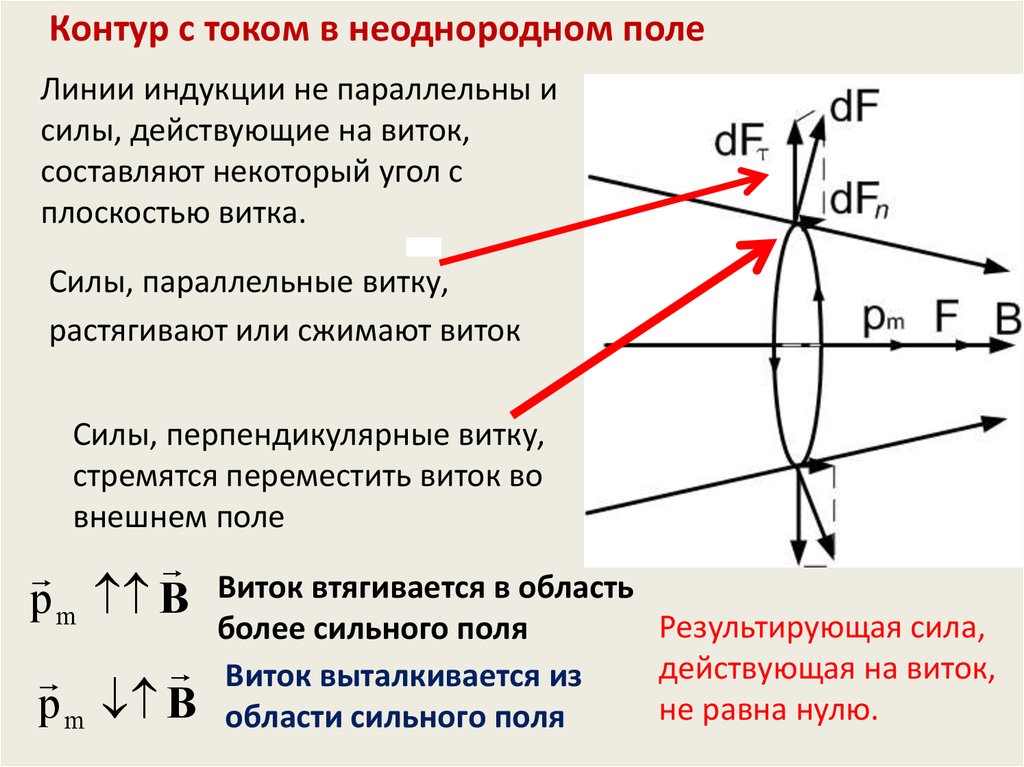
Контур с током в неоднородном полеЛинии индукции не параллельны и
силы, действующие на виток,
составляют некоторый угол с
плоскостью витка.
Силы, параллельные витку,
растягивают или сжимают виток
Силы, перпендикулярные витку,
стремятся переместить виток во
внешнем поле
p m B
p m B
Виток втягивается в область
Результирующая сила,
более сильного поля
действующая на виток,
Виток выталкивается из
не равна нулю.
области сильного поля
6.
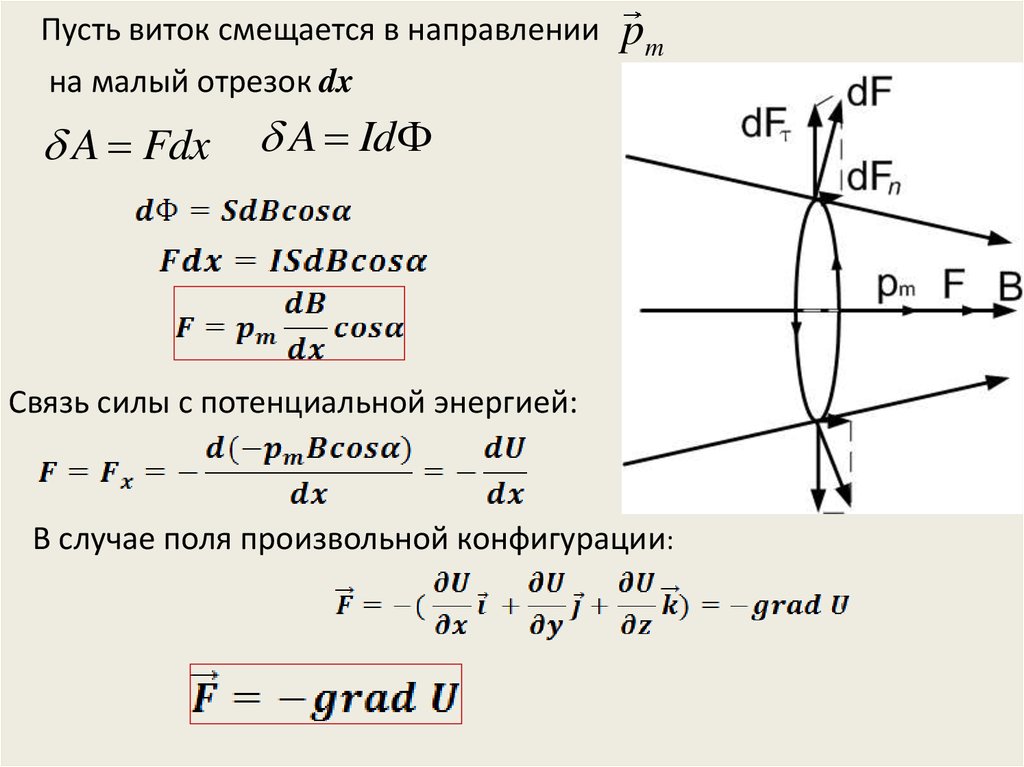
Пусть виток смещается в направленииpm
на малый отрезок dx
A Fdx
A Id
Связь силы с потенциальной энергией:
В случае поля произвольной конфигурации:
7.
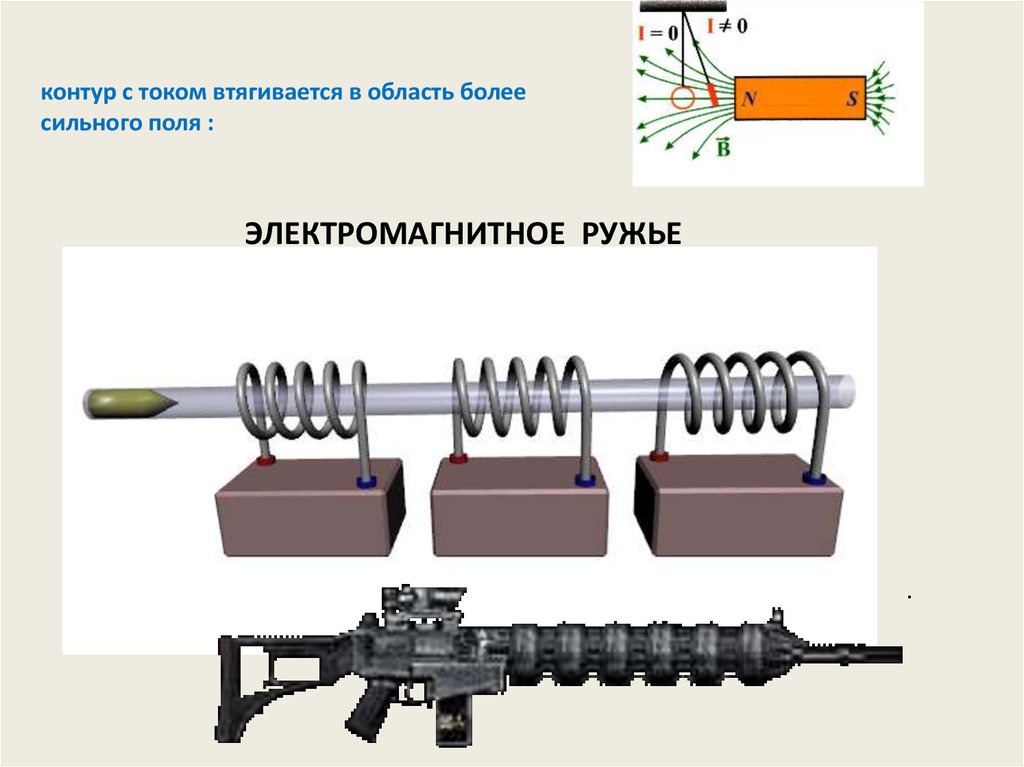
контур с током втягивается в область болеесильного поля :
ЭЛЕКТРОМАГНИТНОЕ РУЖЬЕ
8.
Основные уравнения магнитостатическогополя в вакууме
1. Теорема Гаусса для магнитного поля в вакууме
Линии магнитной индукции всегда замкнуты, т.е. не имеют ни
начала, ни конца.
Отсутствие в природе магнитных зарядов приводит к
тому, что для произвольной замкнутой поверхности,
расположенной в магнитном поле, поток вектора B сквозь нее
всегда равен нулю.
ФВ ( BdS ) 0 -интегральная
S
форма записи
теоремы
Гаусса.
9.
2. Теорема о циркуляции вектора индукциимагнитного поля.
Эксперимент:
(Bd
L
N
) 0 I k
k 1
Циркуляция вектора индукции магнитного поля в вакууме по
произвольному замкнутому контуру равна алгебраической сумме
токов, охватываемых данным контуром, умноженной на
магнитную постоянную .
10.
IВ
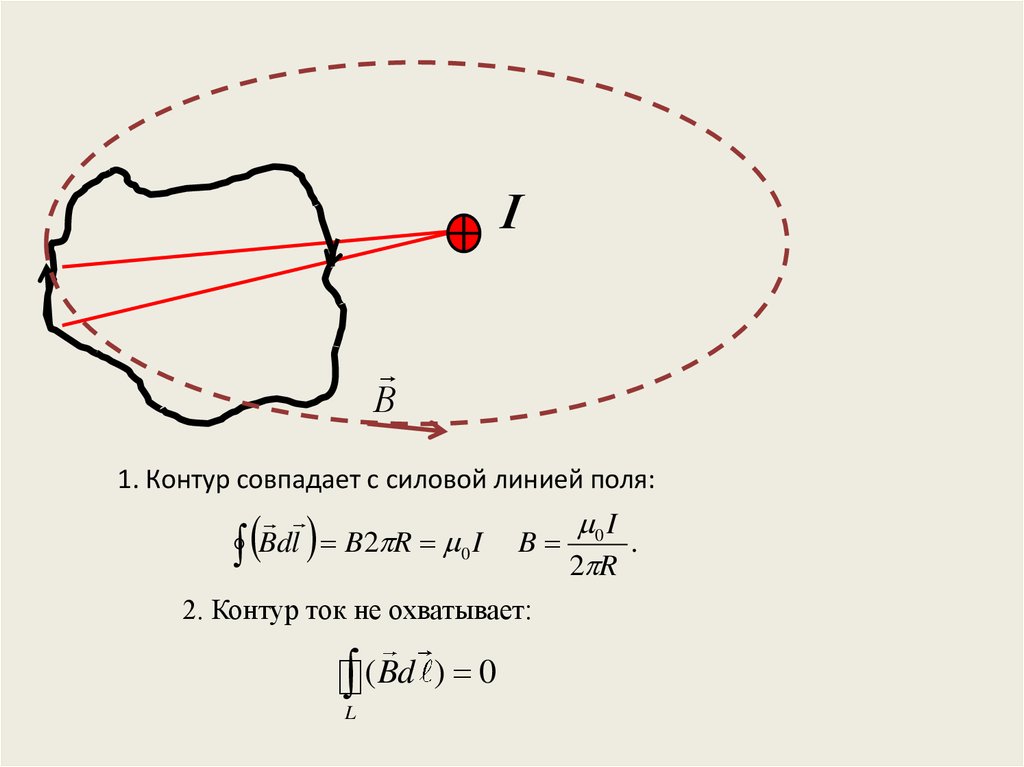
1. Контур совпадает с силовой линией поля:
0 I
B
d
l
B
2
R
I
B
.
0
2 R
2. Контур ток не охватывает:
( Bd
L
) 0
11.
3. Контур охватывает несколько токов:(Bd
N
) 0 I k
L
Каждый ток
учитывается столько
раз, сколько раз он
охватывается
контуром.
Знак тока
определяется
правилом правого
винта.
k 1
(
Bd
)
?
L
12.
N(Bd ) 0 I k
L
k 1
-интегральная форма записи теоремы о
циркуляции вектора B .
Циркуляция вектора индукции магнитного поля в вакууме по
произвольному замкнутому контуру равна алгебраической сумме токов,
охватываемых данным контуром, умноженной на магнитную
постоянную .
Отсюда следует, что источниками стационарного магнитного поля являются
постоянные токи проводимости.
13.
(BdL
N
) 0 I k
k 1
Справка из векторной алгебры: векторное поле, в котором
циркуляция вектора по замкнутому контуру не равна нулю, является
вихревым.
Стационарное магнитное поле является вихревым.
14.
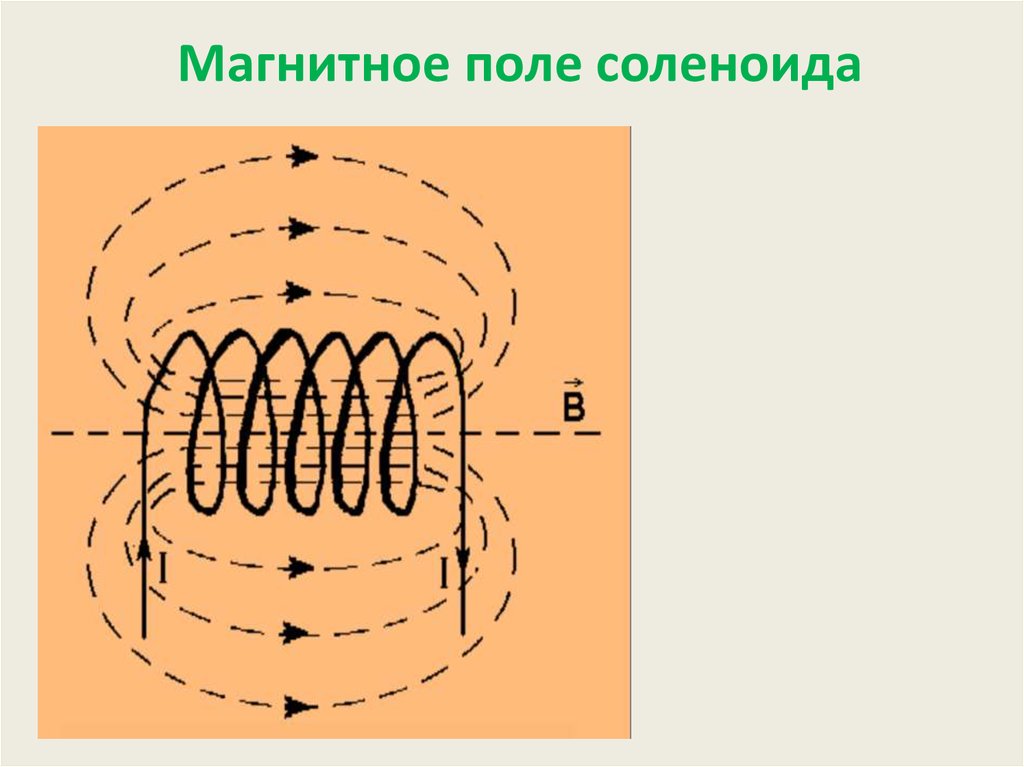
Магнитное поле соленоида15.
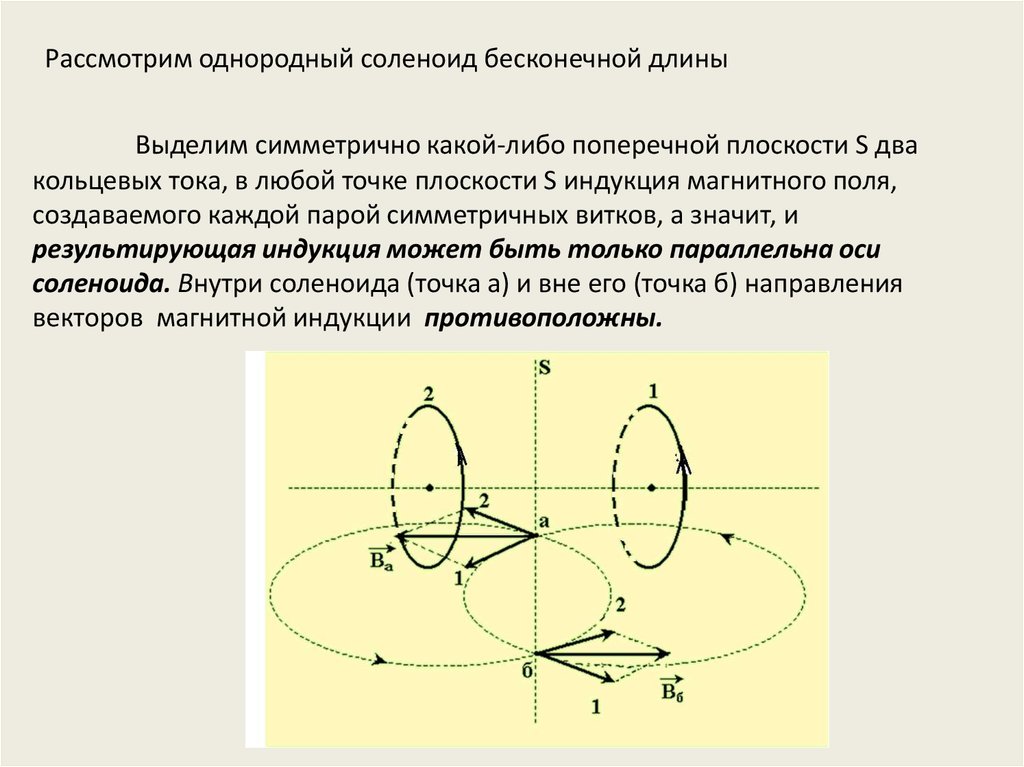
Рассмотрим однородный соленоид бесконечной длиныВыделим симметрично какой-либо поперечной плоскости S два
кольцевых тока, в любой точке плоскости S индукция магнитного поля,
создаваемого каждой парой симметричных витков, а значит, и
результирующая индукция может быть только параллельна оси
соленоида. Внутри соленоида (точка а) и вне его (точка б) направления
векторов магнитной индукции противоположны.
16.
Магнитное поле бесконечного соленоида однороднои полностью сосредоточено в объеме соленоида.
Величина индукции магнитного поля внутри
бесконечно длинного соленоида:
B 0 nI 0
N
I
17.
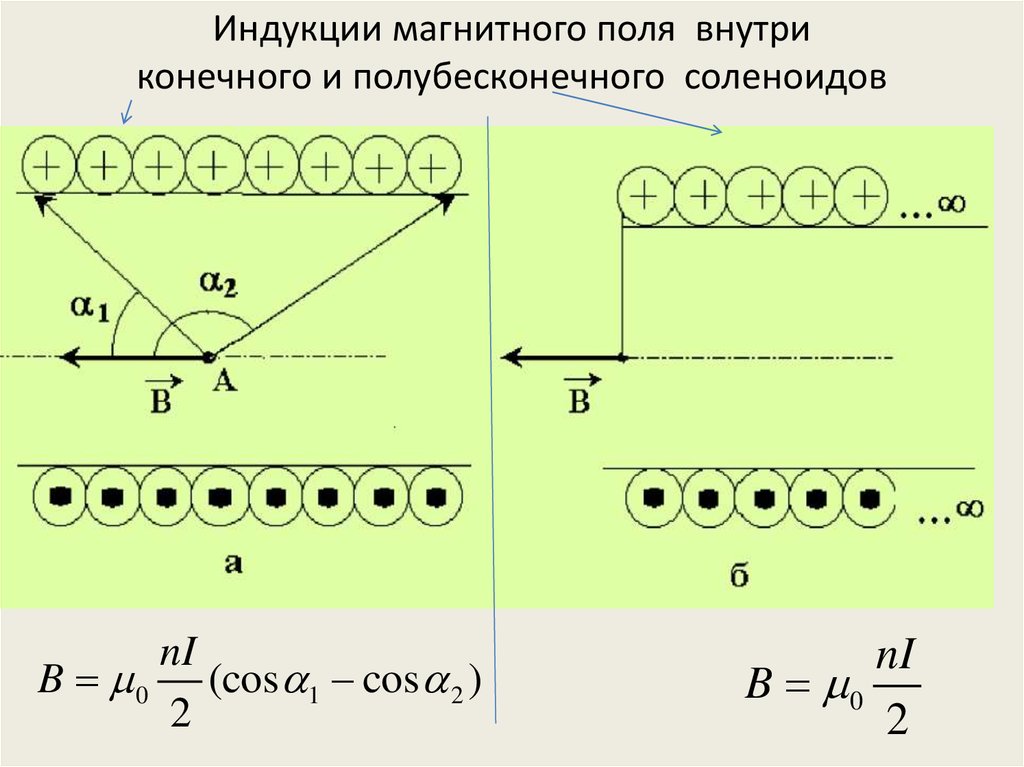
Индукции магнитного поля внутриконечного и полубесконечного соленоидов
nI
B 0 (cos 1 cos 2 )
2
nI
B 0
2
18.
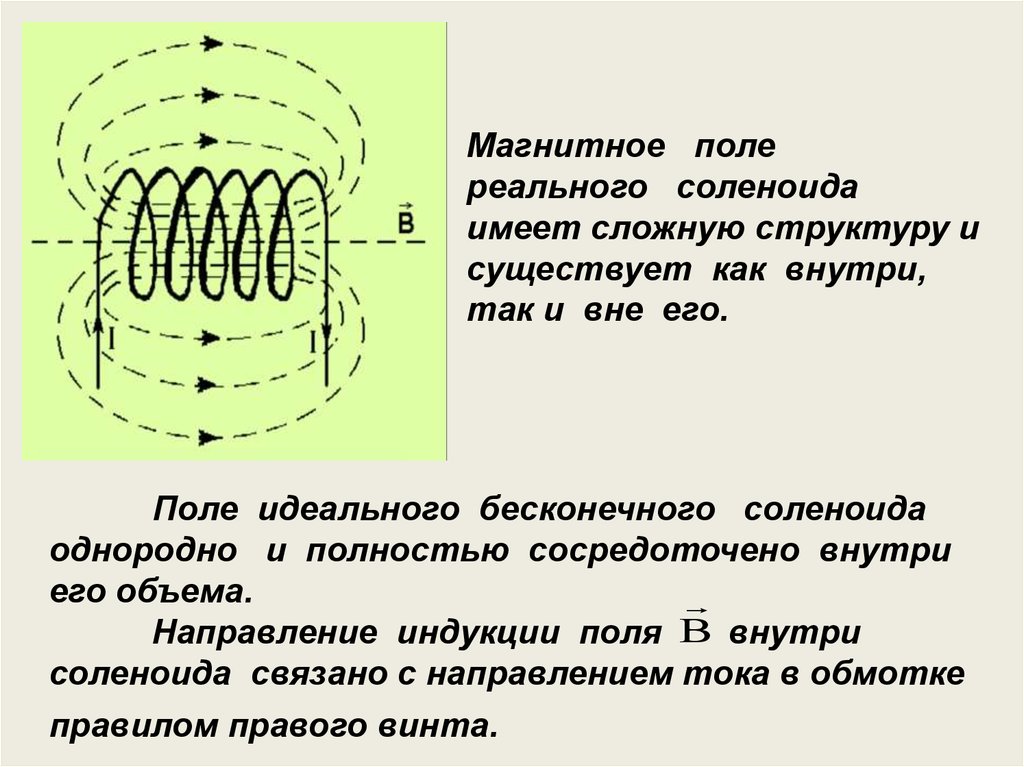
Магнитное полереального соленоида
имеет сложную структуру и
существует как внутри,
так и вне его.
Поле идеального бесконечного соленоида
однородно и полностью сосредоточено внутри
его объема.
Направление индукции поля B внутри
соленоида связано с направлением тока в обмотке
правилом правого винта.
19.
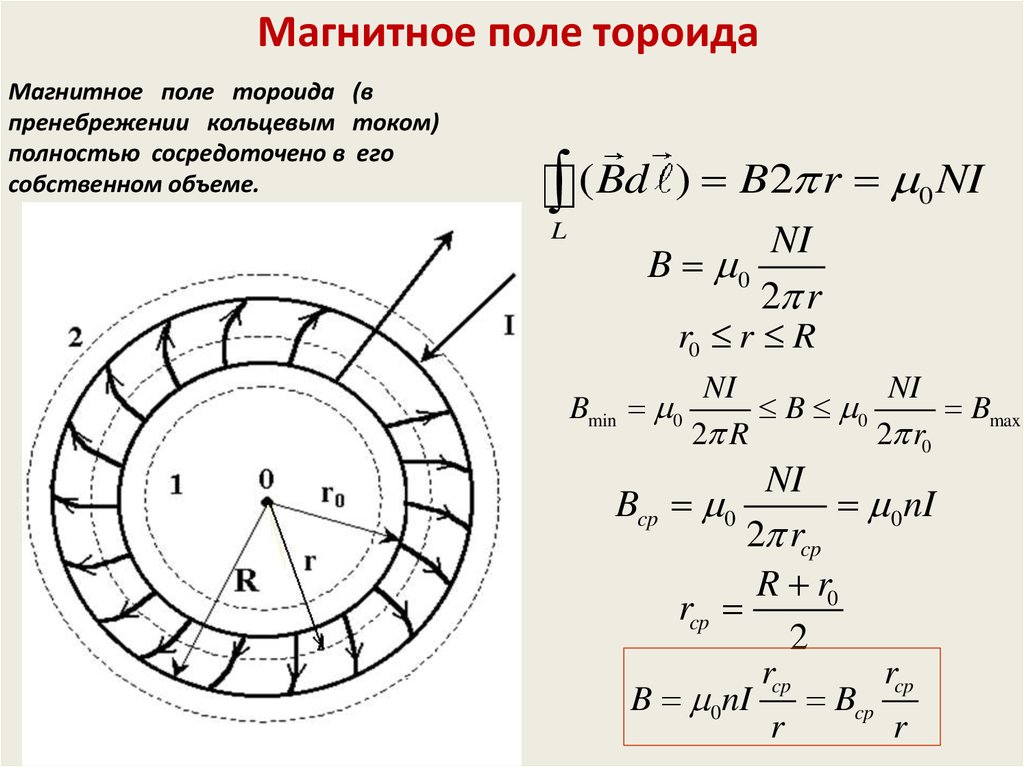
Магнитное поле тороидаМагнитное поле тороида (в
пренебрежении кольцевым током)
полностью сосредоточено в его
собственном объеме.
( Bd
L
) B2 r 0 NI
NI
B 0
2 r
r0 r R
Bmin
NI
NI
0
B 0
Bmax
2 R
2 r0
NI
Bcp 0
0 nI
2 rcp
R r0
rcp
2
B 0 nI
rcp
r
Bcp
rcp
r
20.
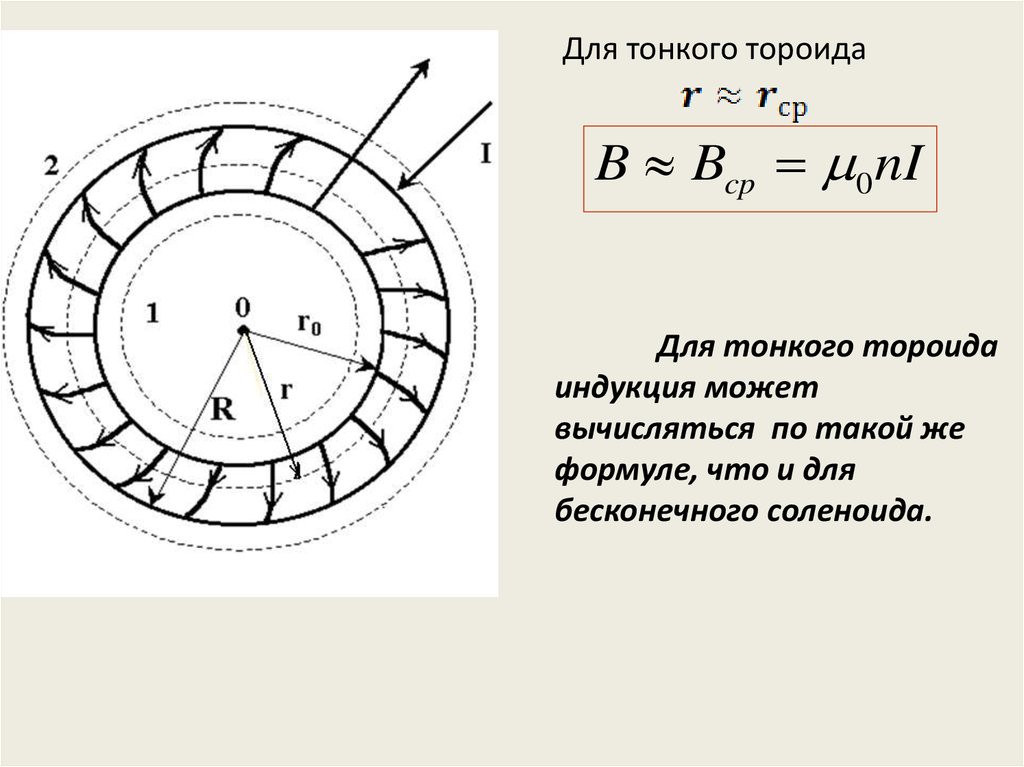
Для тонкого тороидаB Bcp 0 nI
Для тонкого тороида
индукция может
вычисляться по такой же
формуле, что и для
бесконечного соленоида.
21.
Резюме по теме «Магнитостатическое поле в вакууме».Любое магнитостатическое поле в вакууме можно описать
двумя уравнениями.
1. Теорема Гаусса для вектора B :
Из нее следует, что линии магнитной индукции всегда замкнуты или
уходят на бесконечность, т.е. в природе отсутствуют магнитные
заряды, на которых обрывались бы эти линии .
2. Теорема о циркуляции вектора B , которая является
обобщением закона Био-Савара_Лапласа:
Из нее следует, что источниками стационарного магнитного поля
являются постоянные токи проводимости.









 physics
physics








