Окружность и эллипс

1.

Окружность и эллипс относятся к кривым
второго порядка, которые описываются
уравнениями второй степени с двумя
переменными.
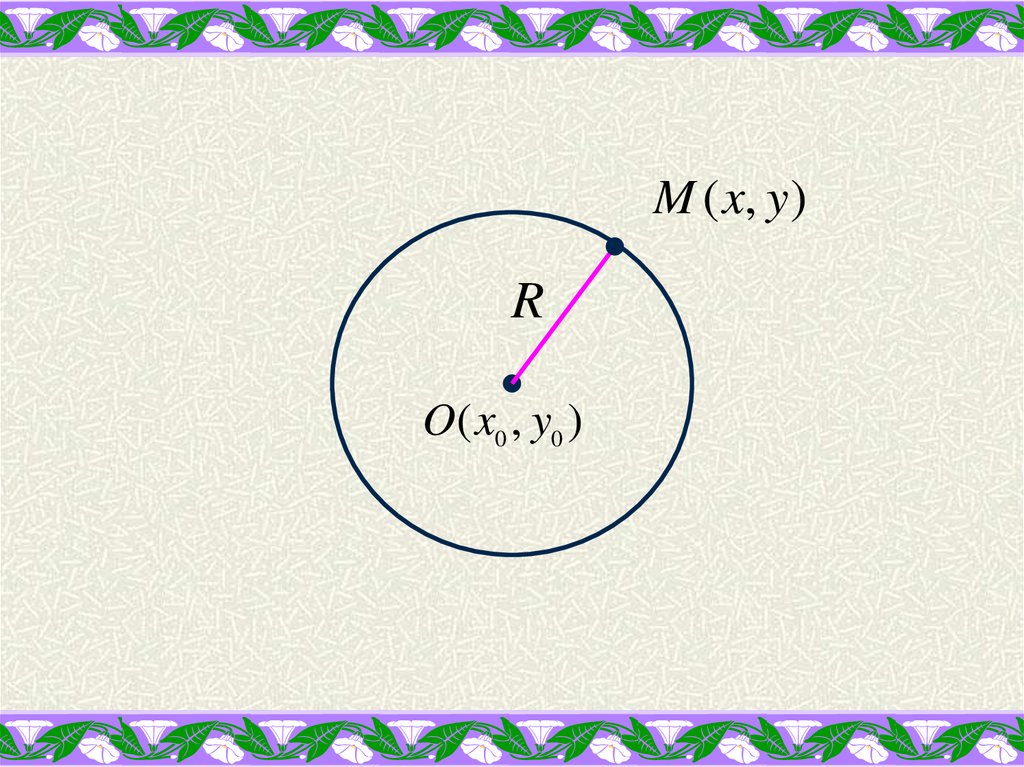
Пусть дана окружность радиуса R с центром в
точке О(х0,у0). Найдем ее уравнение.
Выберем на окружности произвольную точку
М(х,у).

2.

M ( x, y)
R
O( x0 , y0 )

3.

Для точки М выполняется равенство:
OM R
Используем формулу расстояния между двумя
точками:
( x x0 ) ( y y0 ) R
2
2
Возводим обе части выражения в квадрат:
( x x0 ) ( y y0 ) R
2
2
2

4.

Если центр окружности
координат (0,0):
лежит
x y R
2
2
2
в
начале

5.

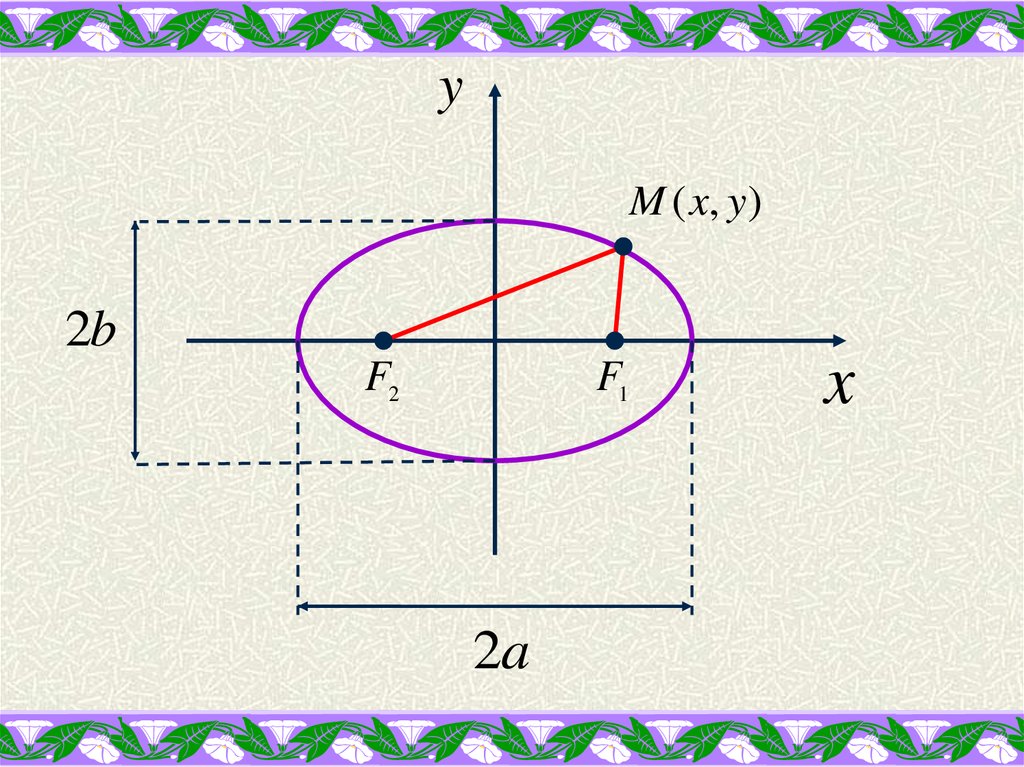
ЭЛЛИПСОМ называется множество
точек плоскости, сумма расстояний от
каждой до двух данных точек,
называемых фокусами, есть величина
постоянная.

6.

y
M ( x, y)
2b
F2
F1
2a
x

7.

Введем обозначения:
F1 (c;0)
F2 ( c;0)
F1F2 2c
a – большая полуось эллипса
b – малая полуось эллипса
Для любой точки М(х,у), принадлежащей
эллипсу,
по
определению
выполняется
равенство:
F1M MF2 2a

8.

Для того, чтобы точка М(х,у)
принадлежала эллипсу, необходимо и
достаточно, чтобы ее координаты
удовлетворяли уравнению
2
2
x
y
2 1
2
a
b
где
b a c
2
2
2
1

9.

2
2
x
y
1
2
2
a
b

10.

Отношение фокусного расстояния к
длине большой оси эллипса называется
ЭКСЦЕНТРИСИТЕТОМ
2c c
2a a