Кривые второго порядка. Лекция 7

1.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Кривые второго порядка.

2.

КРИВЫЕ ВТОРОГО ПОРЯДКА.
Ax2+Bxy+Cy2+Dx+Ey+Q=0

3.

ОКРУЖНОСТЬ
x2+y2=R2
центр (0; 0) и радиус R
y
(x-x0)2+(y-y0)2=R2
x2+y2-2x
центр (x0; y0) и радиус R
M0
2
2 2
0x-2y0y+x0 +y0 -R =0
A=1, B=0, C=1, D=-2x0, E=-2y0, Q=
эксцентриситет ε=0
R
M
D2 E 2
Q
4
4
x02+y02-R2,
R
A=C 0
0
D2 E 2
Q 0 -действительная окружность
4
4
D2 E 2
Q 0
4
4
D2 E 2
Q 0
4
4
-точка
-мнимая окружность
x

4.

ЭЛЛИПС
F1F2=2c
F1(-c; 0) и F2(c; 0) - фокусы
F1M+MF2=2a (2a>2c)
a2-c2=b2
B2
y
M (x; y)
А1 F1 ( c;0) 0 F2 (c;0)
А2 x
B1
.
x 2 y 2 центр
2 1
2
a
b
(0; 0)
с эксцентриситет (0<ɛ<1)
a
(x x 0 ) 2
a
2
(y y0 ) 2
b
2
1
центр (x0; y0)

5.

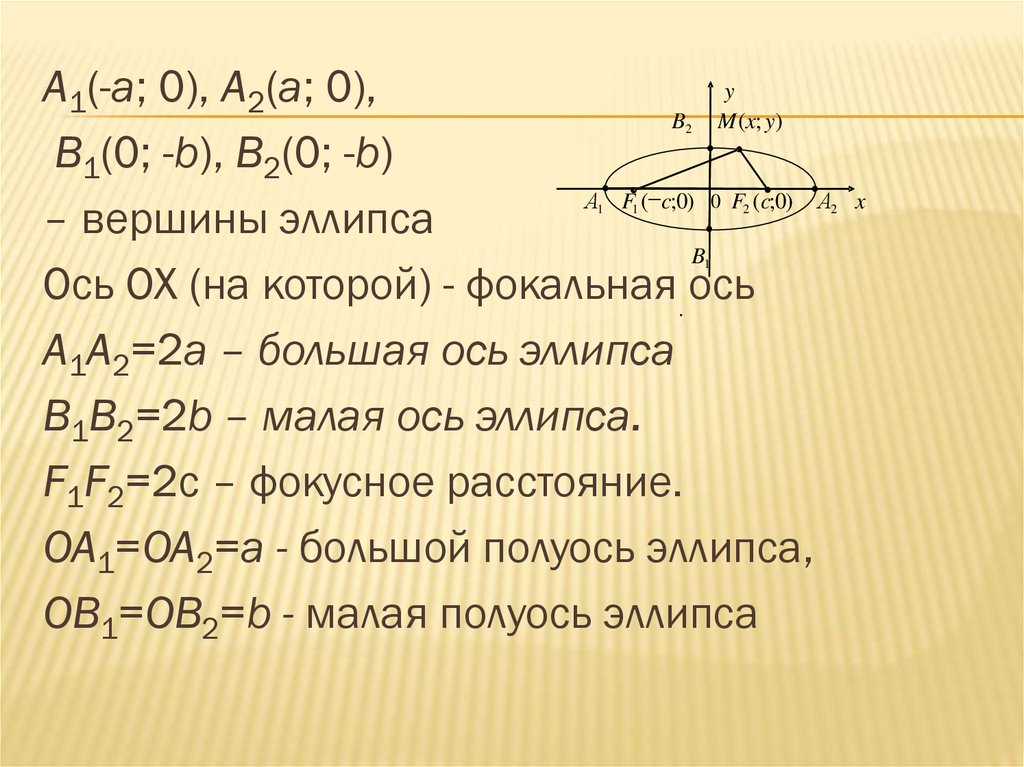
y
A1(-a; 0), A2(a; 0),
B M (x; y)
B1(0; -b), B2(0; -b)
А F ( c;0) 0 F (c;0) А
– вершины эллипса
B
Ось OX (на которой) - фокальная . ось
A1A2=2a – большая ось эллипса
B1B2=2b – малая ось эллипса.
F1F2=2c – фокусное расстояние.
OA1=OA2=a - большой полуось эллипса,
OB1=OB2=b - малая полуось эллипса
2
1
1
2
1
2
x

6.

ГИПЕРБОЛА
F1F2=2c – фокусное расстояние
F1(-c; 0) и F2(c; 0) - фокусы
|F1M - MF2|=2a (2a<2c)
a2-c2=b2
c2-a2=b2
каноническое уравнение гиперболы
x2 y2
2 1
2
a
b
центр
B2
A1
асимптоты
эксцентриситет (ɛ>1)
(x x 0 ) 2
a2
(y y0 ) 2
b2
1
A2
F1
(0; 0)
b
y x
a
c
a
y
центр (x0; y0)
F2
B1
x

7.

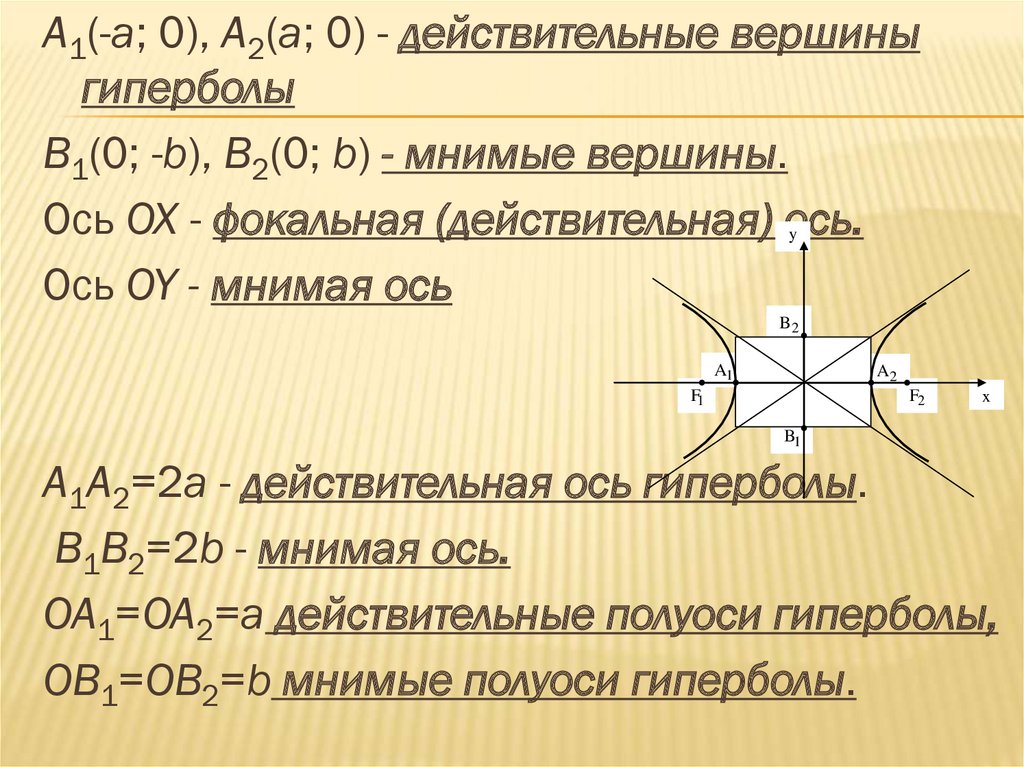
A1(-a; 0), A2(a; 0) - действительные вершины
гиперболы
B1(0; -b), B2(0; b) - мнимые вершины.
Ось OX - фокальная (действительная) ось.
Ось OY - мнимая ось
y
B2
A1
A2
F1
F2
x
B1
A1A2=2a - действительная ось гиперболы.
B1B2=2b - мнимая ось.
OA1=OA2=a действительные полуоси гиперболы,
OB1=OB2=b мнимые полуоси гиперболы.

8.

ПАРАБОЛА
p
F ;0
2
y
фокус
( )
p
директрисой
x
2
FP=p>0 – параметр параболы
y2=2px
O(0; 0) вершина параболы
Ось OX - фокальная ось
(y-y0)2=2p(x-x0) - (x0; y0) вершина параболы
M x, y
N
p
P ; 0 ÷
2
0
p
F ; 0 ÷
2
x

9.

ИССЛЕДОВАНИЕ ОБЩЕГО УРАВНЕНИЯ КРИВОЙ
ВТОРОГО ПОРЯДКА, НЕ СОДЕРЖАЩЕГО ЧЛЕНА
С ПРОИЗВЕДЕНИЕМ ТЕКУЩИХ КООРДИНАТ
Ax2+Bxy+Cy2+Dx+Ey+Q=0
B =0=>Ax2+Cy2+Dx+Ey+Q=0=>окружность, эллипс, гипербола, парабола,
пара прямых, точка или мнимая кривая
1) A>0, C>0=>либо эллипс, либо окружность, либо точка, либо мнимый
эллипс.
2) A>0, C<0 => либо гипербола, либо пара пересекающихся прямых.
3) A>0, C=0=>либо парабола с осью симметрии параллельной оси OY, либо
пара параллельных прямых, либо мнимое место точек
4) A=0, C>0 => либо парабола с осью симметрии, параллельной оси OX,
либо пара параллельных прямых, либо мнимое место точек.
Алгебраическое уравнение Ax2+Bxy+Cy2+Dx+Ey+Q=0 при любых старших
коэффициентах A, B и C всегда определяет либо окружность, либо эллипс,
гиперболу, параболу, либо вырожденную кривую (точку, прямые, мнимые
кривые).