Similar presentations:
Кривые второго порядка
1. Кривые второго порядка
2.
Кривые второго порядкаОбщее уравнение кривой второго порядка:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
Ax2 + 2Bxy + Cy2 - главная часть уравнения (кв.ф.)
2Dx + 2Ey + F - линейная часть уравнения
3. Эллипс
Декартово уравнение: x2/a2 + y2/b2 = 1Параметрическое уравнение:
x = a cos(t), y = b sin(t)
4. Окружность
Декартово уравнение: x2 + y2 = a2Параметрическое уравнение:
x = a cos(t), y = a sin(t)
5. Парабола
Декартово уравнение:y = ax2 + bx + c
6.
7. Гипербола
• Декартово уравнение:x2/a2 - y2/b2 = 1
• Параметрическое уравнение:
x = a sec(t) = a/cos(t), y = b
tan(t)
8.
9.
Общее уравнение кривой второго порядка:Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
10.
Параллельный перенос системы координатПусть на плоскости заданы две декартовы прямоугольные
системы координат: ("старая") и ("новая"), причем как оси
абсцисс, так и оси ординат обеих систем параллельны и
одинаково направлены. В этом случае говорят, что одна
система координат получается из другой "параллельным
переносом".
x x a
y y b
x x a
y y b
11. Преобразование уравнения кривой при параллельном переносе
x x aAx2 + 2Bxy + Cy2 + 2Dx +2 Ey + F = 0
y y b
Подставляем
A( x a) 2 2B( x a)( y b) C ( y b) 2 2D( x a) 2E ( y b) F
A( x ) 2 2Bx y C ( y ) 2
2( Aa Bb D) x 2( Ba Cb E ) y ( Aa 2 2Bab Cb2 2Da 2Eb F ) 0
Главная часть не меняется, можно упростить только
линейную часть
12. Преобразование уравнения кривой при параллельном переносе
x x ay y b
так, чтобы коэффициенты при переменных в линейной части
Подберем a и b в
стали равными 0:
Aa Bb D 0
Ba Cb E 0
Для нахождения a и b получили систему уравнений,
которая имеет единственное решение при условии
A B
B C
0 AC B 2 0.
13. 1 случай. Преобразование уравнения кривой при параллельном переносе при .
1 случай. Преобразование уравнения кривой приA B
параллельном переносе при B C 0 .
Преобразованное уравнение:
A( x ) 2 2Bx y C ( y ) 2 ( Aa 2 2Bab Cb2 2Da 2Eb F )
A( x ) 2 2Bx y C ( y ) 2 а( Aa Bb D) b( Ba Cb E ) Da Eb F
A( x ) 2 2Bx y C ( y ) 2 Da Eb F 0
Таким образом, в новой системе координат уравнение
принимает вид
Ax2 + 2Bxy + Cy2 + F= 0
Для дальнейшего упрощения повернем систему
координат.
14. По часовой стрелке
15. Против часовой стрелки
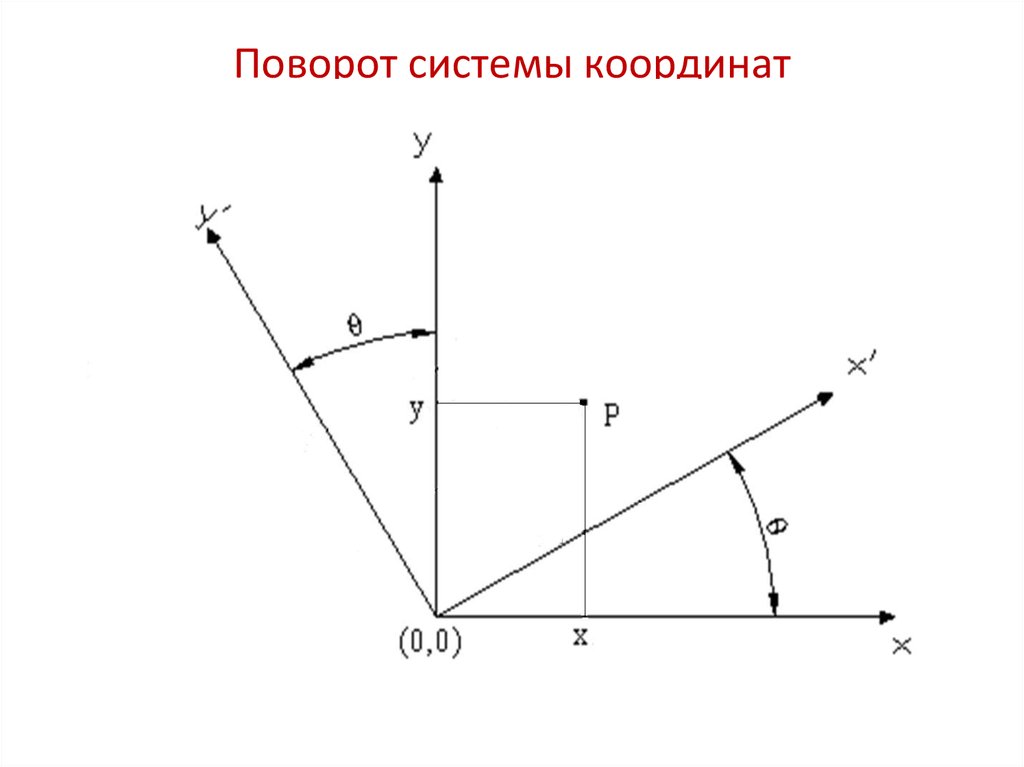
16. Поворот системы координат
17. Поворот системы координат
18.
Поворот системы координатx x cos y sin
y x sin y cos
x cos
y sin
где
sin x
cos y
cos
R
sin
x x cos y sin
y x sin y cos
x cos
y sin
sin
cos
есть матрица поворота
(ортогональная матрица)
sin x
cos y
19. 1 случай. Преобразование уравнения кривой при повороте при .
1 случай. Преобразование уравнения кривой приповороте при A B 0 .
B C
Преобразованное уравнение:
Ax2 + 2Bxy + Cy2 + F= 0
x cos
y sin
sin x
cos y
Главная часть уравнения – квадратичная форма,
а преобразование – ортогональное – приведение к главным осям.
Тогда после подстановки в уравнение получаем
A ( x ) 2 C ( y ) 2 F 0
20. Как найти θ
A Cctg 2
2B
A C 2 900 450
Пример.
4 x 2 2 xy 3 y 2 5 x 3 y 2 0
4 3 1
ctg 2
2
2
21. Классификация центральных кривых ( ).
Классификация центральных кривых(
A B
B C
0
).
Преобразованное уравнение:
1 x 2 2 y 2 F 0
Уравнения для нахождения коэффициентов при квадратах:
A
B
B
C
1
0
0
2
2
2
( A )(C ) B 2 ( A C ) ( AC B )
( 1 )( 2 )
2 ( 1 2 ) 1 2 0
λ1 λ2 A C
λ1 λ2 δ
22. Классификация центральных кривых ( ).
1 x 2 2 y 2 F 0A
Классификация центральных кривых ( B
B
C
0
).
Вырожденные центральные кривые
1. 1 2 0, F 0 1 x 2 2 y 2 0 точка
2
2
x
y
0
2. 1 2 0, F 0
1
2
y
1
x пара
2
пересекающихся прямых
Невырожденные центральные кривые
5. 1 2 0, F 0
2
2
x2
y2
x
y
1
1 действительный
2
2
F
F
a
b
1
2
или мнимый эллипс
2
2
x
y
6. 1 2 0, F 0
1
F
F
1
2
x2 y 2
2 2 1 гипербола
a
b
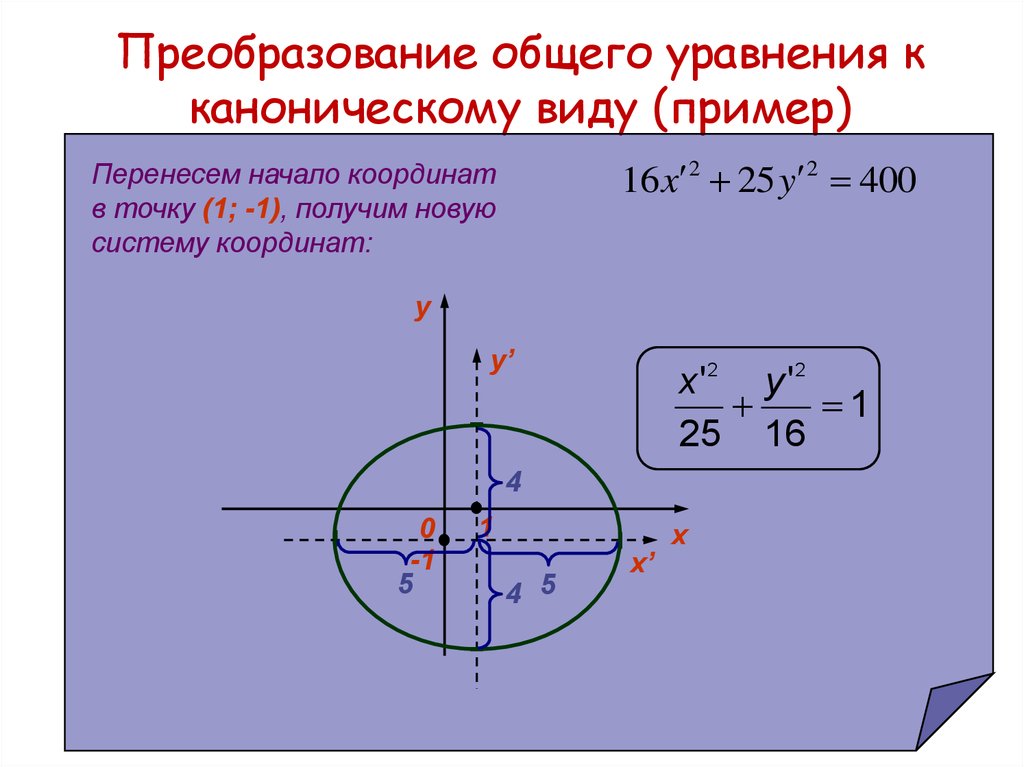
23. Преобразование общего уравнения к каноническому виду (пример)
16 x 2 25 y 2 32 x 50 y 359 016
0
0
25
0 (центр.кривая )
16a 16 0
a 1, b 1(коорд. нового центра)
25b 25 0
x' x 1;
y ' y 1 x x' 1;
y y ' 1
2
2
16 x 1 25 y 1 32 x 1 50 y 1 359 0
16 x 2 25 y 2 400
24. Преобразование общего уравнения к каноническому виду (пример)
16 x 2 25 y 2 400Перенесем начало координат
в точку (1; -1), получим новую
систему координат:
y
y’
x'2 y '2
1
25 16
4
0
-1
5
1
4 5
x’
х
25. 2 случай. Преобразование уравнения кривой Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 в случае .
2 случай. Преобразование уравнения кривойAx2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 в случае
A B
B C
x cos
y sin
Сразу производим поворот
0
.
sin x
cos y
1 ( x ) 2 2 ( y ) 2 2D1 x 2E1 у F 0
Так как λ1λ 2 δ λ1λ 2 0
квадрат, например, для y:
, остается только один
y 2 2 Dx 2 Eу F 0
Для дальнейшего упрощения (предполагаем D,F ненулевые)
( x 2 Ey
2
E
E2
) 2 Dx F
E2
E2
0
( y ) 2 Dx F
0
2
x x
y y
E
26. Классификация нецентральных кривых ( ).
Классификация нецентральных кривых (A B
B C
0 ).
Преобразованное уравнение:
y 2 2Dx F 0
Вырожденные нецентральные кривые
1. 1 2 0, D 0, F 0
2. 1 2 0, D 0, F 0
x 2 0 пара совпадающих прямых
x 2 a 2 прямые
действительные или мнимые
Невырожденные нецентральные кривые
F
x
x
F
2
y
2 D( x
) 0
2D
3. D 0
2D
y y
y 2 2 px парабола
y 2 2 Dx 0























 mathematics
mathematics








