Similar presentations:
Кривые второго порядка
1. Кривые второго порядка
Общее уравнение кривой второго порядка
Окружность
Эллипс
Гипербола
Парабола
2. Общее уравнение кривой второго порядка
К кривым второго порядка относятся: эллипс, частным случаемкоторого является окружность, гипербола и парабола.
Они задаются уравнением второй степени относительно x и y:
Ax 2 2Bxy Cy 2 2Dx 2Ey F 0
Общее уравнение кривой
второго порядка
В некоторых частных случаях это уравнение может определять
также две прямые, точку или мнимое геометрическое место.
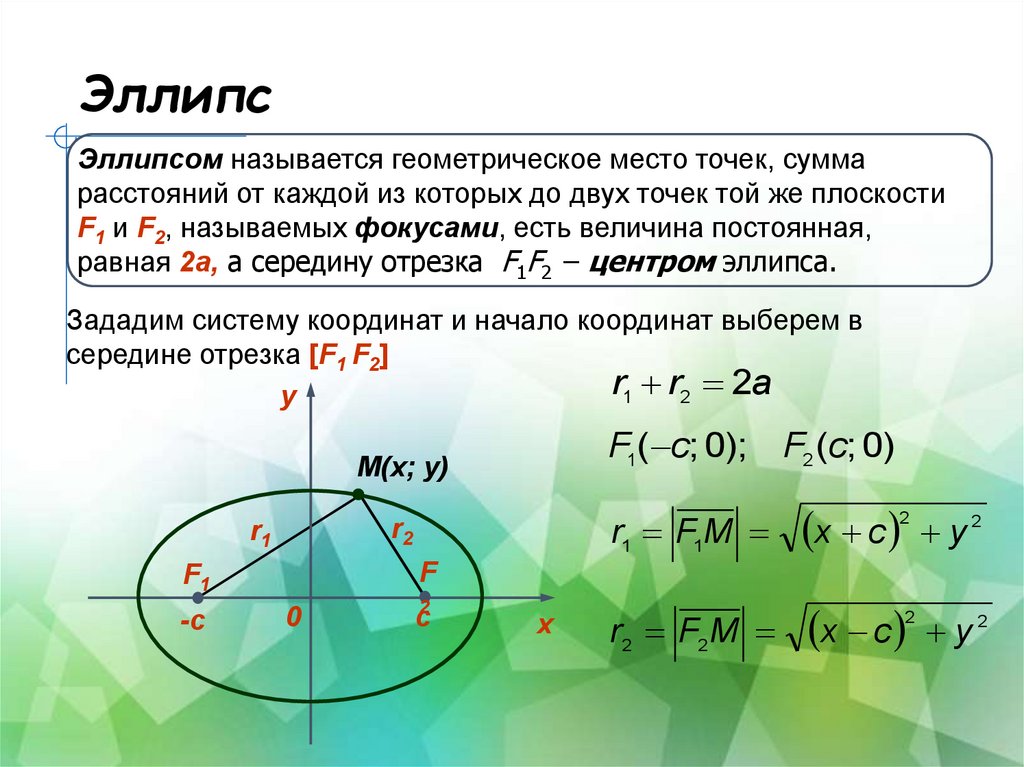
3. Эллипс
Эллипсом называется геометрическое место точек, суммарасстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а, а середину отрезка F1F2 – центром эллипса.
Зададим систему координат и начало координат выберем в
середине отрезка [F1 F2]
r1 r2 2a
y
F1( c; 0);
M(x; y)
r2
r1
r1 F1M
x c
r2 F2M
x c
2
y2
F
F1
-c
F2 (c; 0)
0
c2
х
2
y2
4. Эллипс
x c2
x c
y2
2
y 2 2a
x c y 2a 2 a x xc c y y
2
2
x c
2
4a
y 4a 4a
2
x c
2
2
2
2
2
22
x c
2
y
2
x c
2
22
2
a cb x a y a (ba : (ca22)b2 )
22
2
2
2
x2 y 2
2 1
2
a
b
2
22
a 2 x 2 2a 2 xc a 2c 2 a 2 y 2 a 4 2a 2 xc x 2c 2
2
y2
y 2 4a 2 x 2 2 xc c 2 x 2 2 xc c 2
22
2
4a
a xx
cc
yy 4a
4
xc
a xc : 4
22
2
2
b2
Каноническое уравнение
эллипса
5. Гипербола
Гиперболой называется геометрическое место точек, разностьрасстояний от каждой из которых до двух точек той же плоскости
F1 и F2, называемых фокусами, есть величина постоянная,
равная 2а, а середину отрезка F1F2 – центром гиперболы.
y
r1 r2 2a
M(x; y)
F1( c; 0);
r1
F
F1
-c
0
2
c
r2
х
F2 (c; 0)
r1 F1M
x c
r2 F2M
x c
2
2
y2
y2
6. Гипербола
x c2
y2
x c
2
y 2 2a
x c
2
y2
x c
2
y 2 2a
После тождественных преобразований уравнение примет вид:
c ab2 2 x 2 a2 y 2 a2 (bc22 : (a22b) 2 )
2
x2 y 2
2 1
2
a
b
b2
Каноническое уравнение
гиперболы
7. Пример
Составить уравнение гиперболы, проходящей через точкуА(6; -4), если ее асимптоты заданы уравнениями:
6
y
x
3
b
6
a
3
3b 6a
x2 y 2
62 ( 4)2
2 1 2
1
Точка А лежит на гиперболе
2
2
a
b
a
b
36b 2 16a 2 a 2b 2
2
3b 6a
b2 a2
Решим систему:
3
2
2
2 2
2
2
2 2
36b 16a a b
36
b
16
a
a
b
2 2
2
2
b a
a 2 3
a
12
3
2
2
b 8
b 2 2
24a 2 16a 2 a 4
3
8. Парабола
Параболой называется геометрическое место точек наплоскости, для каждой из которых расстояние до некоторой
фиксированной точки той же плоскости
p
p , называемой фокусом, равно расстоянию до прямой:
x
F ( ;0)
2
2
Фиксированную прямую называют директриссой параболы.
y
d
r d
M(x; y)
r
p
2
0
p
2
p 0
2
p
r FM x y 2
2
F
p
F ( ; 0)
2
х
d x
p
2
9. Преобразование общего уравнения к каноническому виду
Общее уравнение кривой называется пяти-членным, если 2Bxy=0:Ax 2 Cy 2 2Dx 2Ey F 0
Приведение пяти-членного уравнения к каноническому виду
рассмотрим на примере:
16 x 2 25y 2 32x 50y 359 0
16x 2 32x 25y 2 50y 359 0
16 x 2 2x 25 y 2 2y 359
16 x 2 2x 1 25 y 2 2y 1 359 16 25
16 x 1 25 y 1 400
2
2
x 1
2
25
y 1
2
16
1








 mathematics
mathematics








