Similar presentations:
Кривые второго порядка
1. Кривые второго порядка
1. Окружность2. Эллипс
3. Гипербола
4. Парабола
2. Общее уравнение кривых второго порядка
Ax 2Bxy Cy 2Dx 2Ey F 02
2
А, В, С не равны нулю одновременно
3. 1. Окружность
( x x0 ) ( y y0 ) r2
2
2
У
М(х;у)
r
у0
A( x0 ; y0 ) – центр окружности;
r – радиус окружности.
О
А(х0;у0)
х0
Х
4. Каноническое уравнение окружности
x y r2
2
2
У
r
О (0;0) – центр окружности;
r
r
О
r – радиус окружности.
(0;0)
r
Х
5. 2.Эллипс
( x x0 ) ( y y0 )1
2
2
a
b
2
2
У
В
r1
b
A( x0 ; y0 )
– центр эллипса;
В,С,Д,Е – вершины эллипса.
Е
r2
А (х0;у0)
F1
а
F1, F2 – фокусы эллипса;
r1 , r2– фокальные радиусы.
а – большая полуось эллипса;
b – меньшая полуось эллипса.
M(x;y)
F2
С
Х
Д
6.
F1F2 =2сL1
L2
У
с – половина расстояния
между фокусами.
c a b
2
2
2
- эксцентриситет эллипса,
c
; 0 <1
.
a
F1
А (х0;у0)
F2
c
О
Х
a/
7. Каноническое уравнение эллипса
22
x
y
1
2
2
a
b
О (0;0) – центр эллипса;
F1 (-c;0), F2 (c;0) –
фокусы эллипса;
c a b
2
L1:
x
2
2
a
x
; L2:
У
L2
М(х;у)
b
r2
r1
F1
F2
О (0;0)
c
a
Х
a/
.
a
– директрисы эллипса.
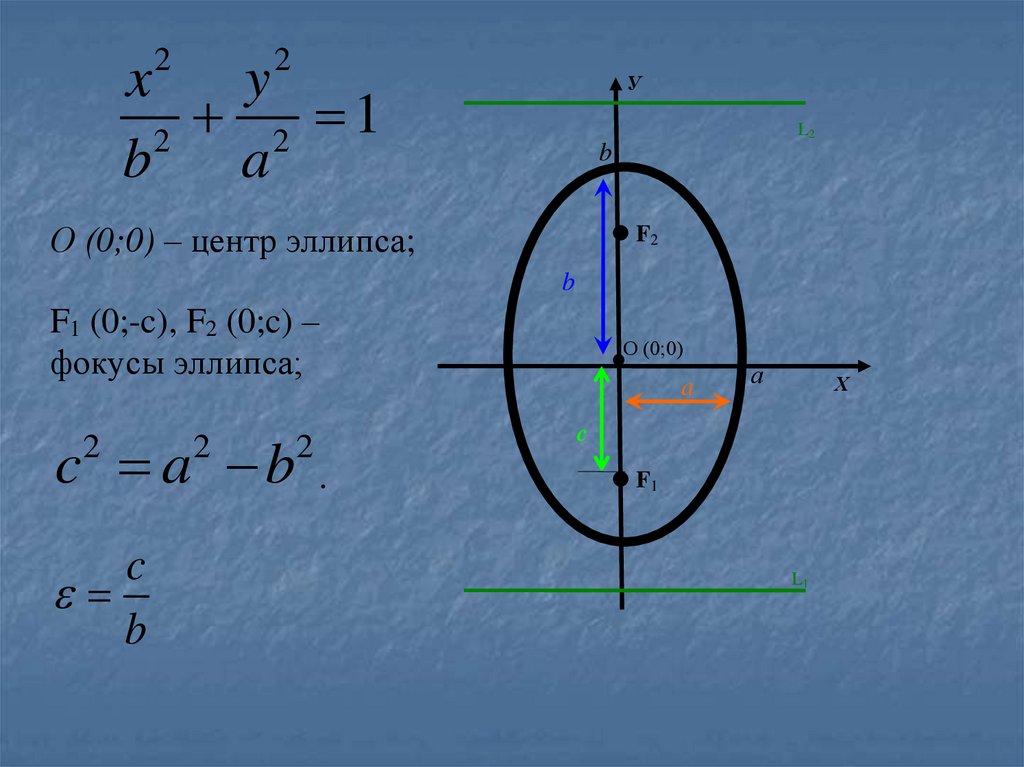
8.
22
x
y
2 1
2
b
a
У
L2
b
О (0;0) – центр эллипса;
F2
b
F1 (0;-c), F2 (0;c) –
фокусы эллипса;
c a b
2
c
b
2
2
О (0;0)
a
а
Х
c
.
F1
L1
9. 3. Гипербола
2У
2
x
y
1
2
2
a
b
О (0;0)– центр гиперболы;
А,В – вершины гиперболы.
F1, F2 – фокусы гиперболы;
r1 , r2– фокальные радиусы.
|r1 - r2|=2a
r1
М (х;у)
r2
F1
F2
А
О
В
Х
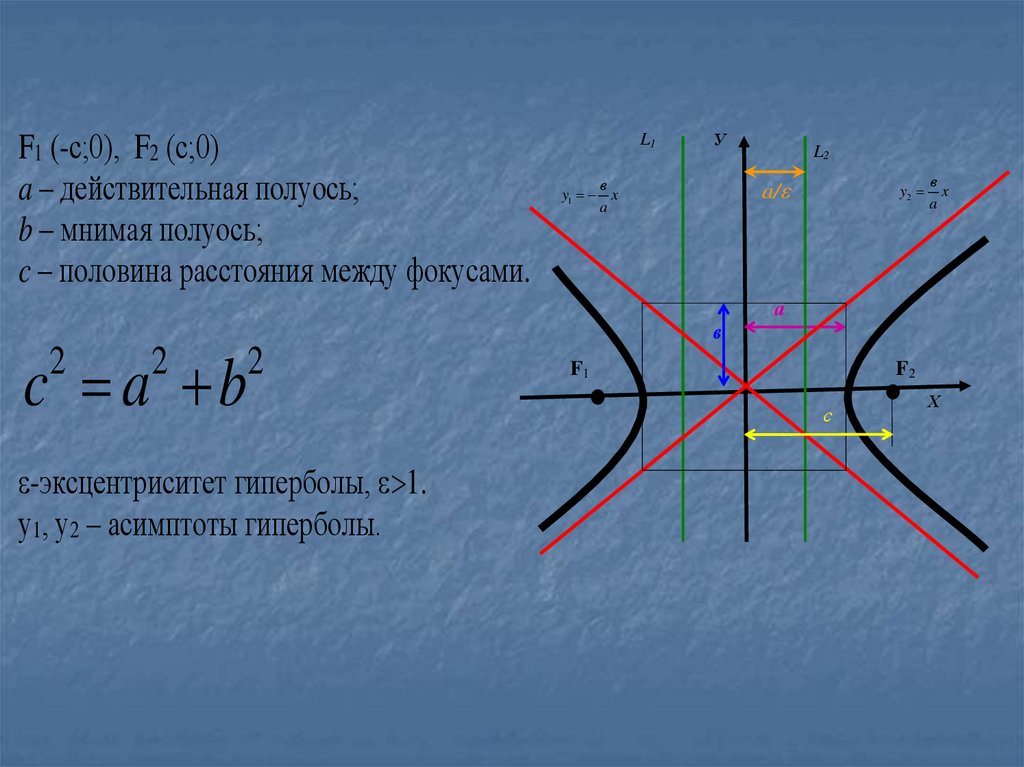
10.
F1 (-с;0), F2 (с;0)a – действительная полуось;
b – мнимая полуось;
c – половина расстояния между фокусами.
L1
У
L2
a/
в
y1 x
a
y2
в
x
a
а
c a b
2
2
в
2
-эксцентриситет гиперболы, 1.
у1, у2 – асимптоты гиперболы.
F1
F2
с
Х
11.
22
y
x
1
2
2
a
b
y2
в
x
a
У
F2
L2
в
F1 (0;-с), F2 (0;с)
а
a – действительная полуось;
b – мнимая полуось;
c – половина расстояния между
в
фокусами.
y x
1
c
a
в/
a
Х
с
L1
F1
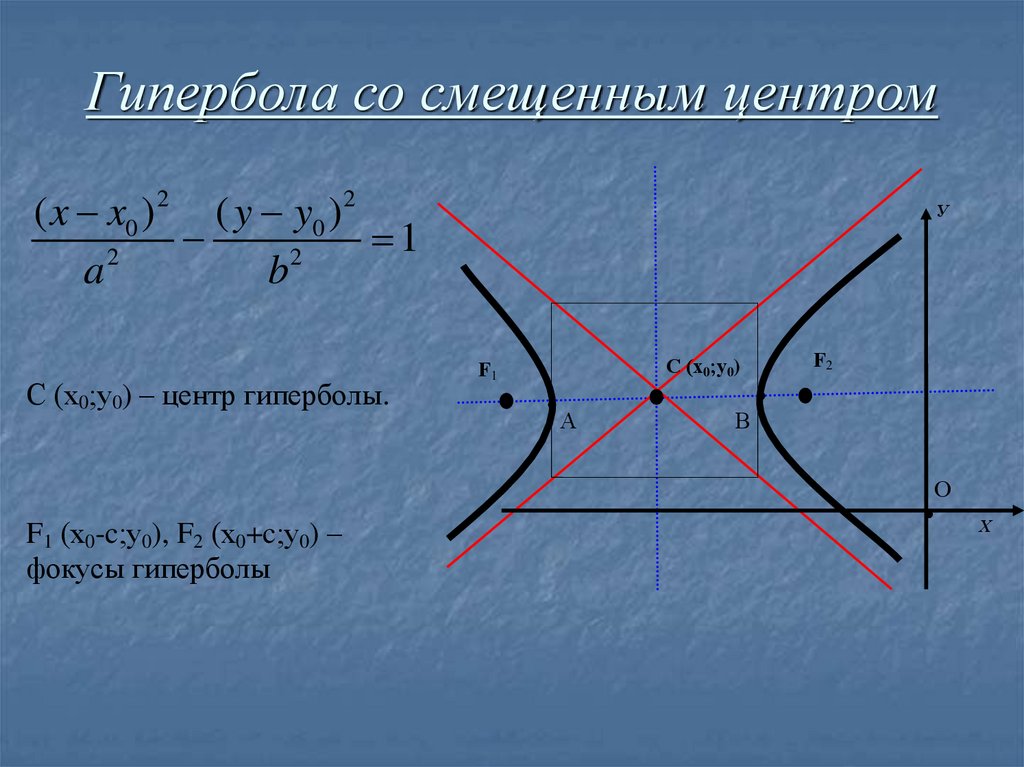
12. Гипербола со смещенным центром
( x x0 )2 ( y y0 ) 21
2
2
b
a
С (х0;у0) – центр гиперболы.
У
С (х0;у0)
F1
А
F2
В
О
F1 (х0-c;у0), F2 (х0+c;у0) –
фокусы гиперболы
Х
13. 4. Парабола
y 2 px2
У
L
р 0
р – расстояние от фокуса до
директрисы.
r1; r2 - фокальные радиусы.
r1
М
r2
r1 r2
О(0;0) – вершина параболы.
p
F ( ;0) - фокус параболы.
2
p/2 О
p/2
F
Х
14.
x 2 pyУ
2
О(0;0) – вершина параболы.
p
F (0; ) - фокус параболы
2
F
р\2
О
р\2
Х
L
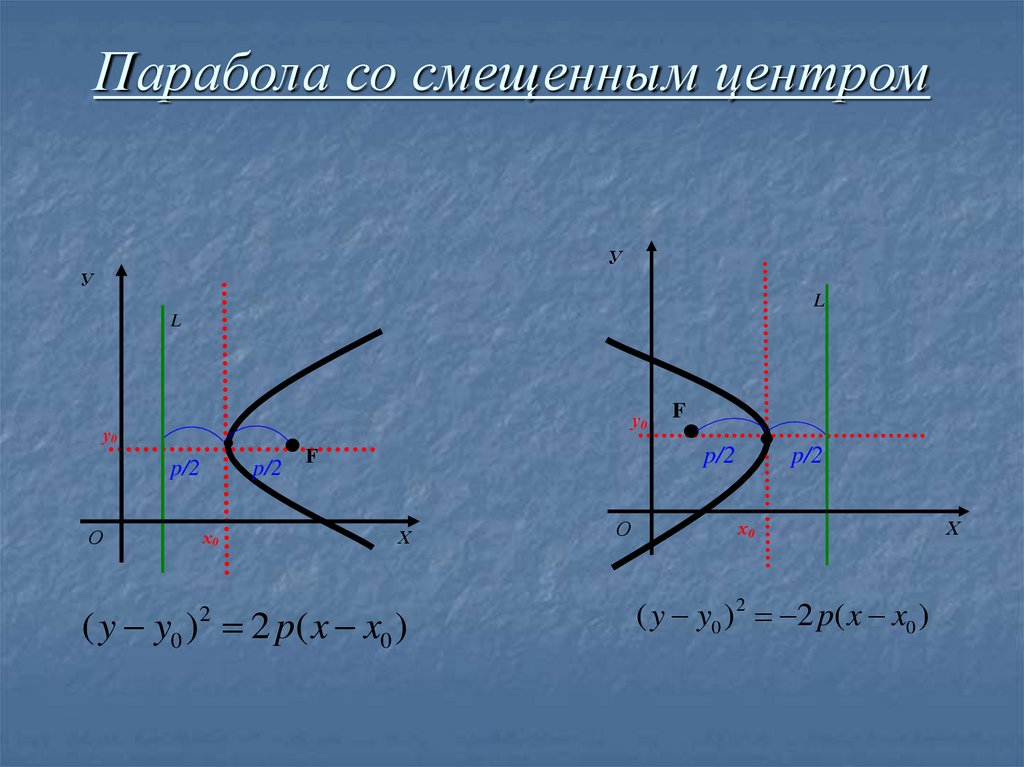
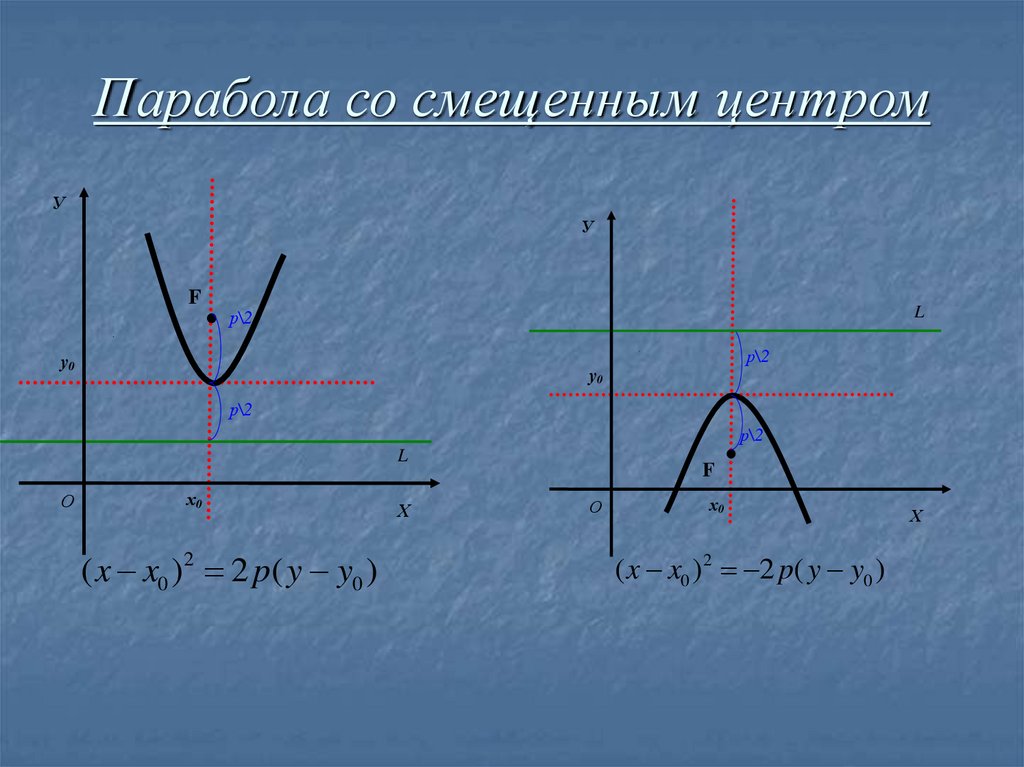
15. Парабола со смещенным центром
УУ
L
L
у0
у0
p/2
О
p/2
х0
p/2
F
Х
( y y0 ) 2 p( x x0 )
2
F
О
p/2
х0
( y y0 )2 2 p( x x0 )
Х
16. Парабола со смещенным центром
УУ
F
L
р\2
у0
р\2
у0
р\2
р\2
L
О
х0
( x x0 )2 2 p( y y0 )
Х
F
О
х0
( x x0 )2 2 p( y y0 )
Х
17. Вырожденные кривые второго порядка
Пара прямыхa x b y e c x d y m 0
Совпадающие прямые
a x b y
2
0
Точка (вырожденный
эллипс)
2
a x b y
c x d y 0
Пустое множество
a x b y
2
2
c x d y 1
2
18. Задачи-1
Определить тип следующих кривых, найти их полуоси,фокусные расстояния, координаты центра, координаты
фокусов. Для гипербол записать уравнения асимптот.
Построить графики кривых.
1)
2)
3)
4)
5)
4 x 9 y 24 x 36 y 36 0
2
2
36 x y 72 x 6 y 11 0
2
2
36 x 144 y 108x 192 y 1 0
2
2
4 x 8 y 4 x 16 y 23 0
2
4 y x 16 y 19 0
2
2
19. Задачи-2
6)7)
8)
9)
10)
11)
12)
4 x 24 x 2 y 37 0
2
2
3x 4 y 18x 16 y 43 0
2
2
27 x 36 y 18x 24 y 101 0
2
x 3x 2 0
2
2
2 x 2 y 3xy 7 x y 3 0
2
2
9x 9 y x 8 y 1 0
2
2
4 x 4 y 16 x 24 y 43 0
2
20. Задачи-3
13) При каком радиусе окружность с центром в точкеQ(1, 2) будет касаться прямой, проходящей через точки
A(-3, -2) и B(1, 5) ?
14) Найти точки пересечения эллипса с фокусами
F1(1, 2), F2(5,2) и большой полуосью 2.5 с прямой,
проходящей через точки A(1, -1) и B(4, 8).
















 mathematics
mathematics








