Интеграл с переменным верхним пределом

1.

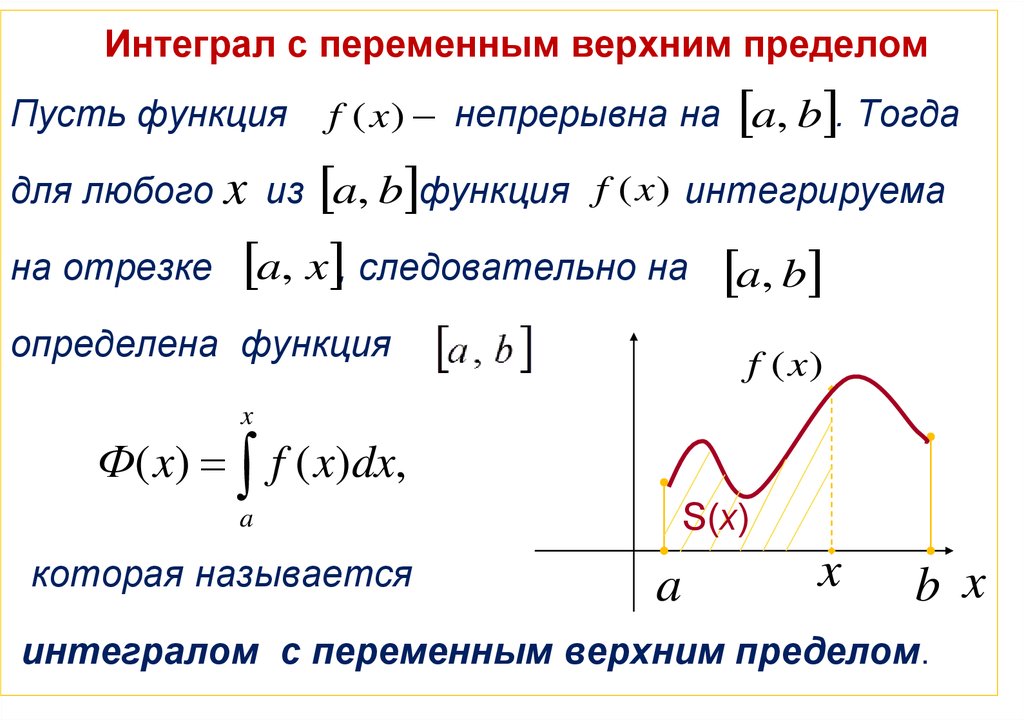
Интеграл с переменным верхним пределом
Пусть функция
f (x ) непрерывна на a, b . Тогда
для любого x из a, b функция f (x ) интегрируема
на отрезке
a, x , следовательно на a, b
определена функция
f (x )
x
Ф( x) f ( x)dx,
S(x)
a
которая называется
a
x
b x
интегралом с переменным верхним пределом.

2.

Значение функции Ф(x) в точке x из a, b равно
площади S (x ) под кривой y f (x) на отрезке a, x .
Т Е О Р Е М А 1.
Пусть функция f (x ) непрерывна на a, b . Тогда
x
функция Ф(x) заданная формулой Ф( x)
обладает следующими свойствами:
• непрерывна на отрезке
;
• имеет производную для всех
x
удовлетворяющую равенству
из
f ( x)dx,
a
,
Ф ( x) f ( x).

3.

Формула Ньютона – Лейбница.
Пусть функция
f (x ) непрерывна на a, b ,
функция Ф (x ) любая ее первообразная на
. Тогда определенный интеграл от функции
f (x ) по отрезку
a, b равен
b
f ( x)dx Ф(b) Ф(а)
( ),
a
где Ф (b) u Ф ( а )
значения функции в точках а и b соответственно.
Ф( x) ba Ф(b) Ф( a )

4.

Формула
b
f ( x)dx Ф(b) Ф(а)
a
называется формулой Ньютона –
Лейбница.
Исаак Ньютон (1643-1727) – английский физик, математик и
астроном. Один из создателей классической физики. Автор
фундаментального труда «Математические начала натуральной
философии» , в котором он изложил Закон всемирного
тяготения и три закона механики. Разработал
дифференциальное и интегральное исчисление.
Лейбниц Готфрид Вильгельм (1646-1716)
математик, физик и изобретатель,
юрист, историк, языковед. Основные математические
сочинения:
"Об истинном отношении круга к квадрату" (1682),
"Новый метод максимумов и минимумов" (1684),
"О скрытой геометрии и анализе неделимых..." (1686).

5. Вычисление определенных интегралов

Вычисление
определенных
интегралов
с
использованием
формулы Ньютона-Лейбница осуществляется в два шага.
• На
первом
шаге,
неопределенного
первообразную Ф(x)
используя
интеграла,
технику
нахождения
получают
некоторую
для подынтегральной функции f (x ) .
на втором этапе применяется собственно формула Ньютона-
Лейбница.

6.

Примеры.
1
2
x
dx.
Пример 1. Вычислить
0
Решение. Произвольная первообразная для функции
f ( x) x 2
x3
F ( x)
C.
3
имеет вид
Применяя формулу Ньютона – Лейбница, получим
3 2
2
x
1 x dx 3
2
Ответ:
7
.
3
1
8 1 7
.
3 3 3

7.

• Пример 2. Вычислить
2
2
1
3 x 4
2
dx.
1
Решение.
2
2
3 x 4
1
1
7
.
4
3 ln 2
2 6 ln 2
Ответ:
1
1
3 x 4
dx
2
23 x 4
3 ln 2
1 3 ln 2
7
.
6 ln 2
2
1

8.

Замена переменной в определенном интеграле
Теорема. Пусть функция (t ) имеет непрерывную
производную на , , a ; b и функция
f (x ) непрерывна в каждой токе x t ,где
t , . Тогда справедливо следующее равенство
b
f ( x)dx f (t ) (t )dt.
a
Эту формулу называют формулой
замены переменной в определенном интеграле.

9.

Примеры
x 2 x dx.
1
Пример 3. Вычислить
2 5
0
Решение. Пусть
2
2
2
t 2 x , dt d 2 x 2 x dx 2 xdx,
1
2
xdx dt. При x 0, то t 2 0 ; при x 1,
2
то t 2 12 1.
Следовательно,
x 2 x
1
0
2 5
1
1 5
1 t
1
dx t dt t dt
22
2 6 2
2
2
1
1
5
1 61
1
21
6
t 1 2 .
2
12
12
4
6

10.

Интегрирование по частям
в определенном интеграле
Теорема. Пусть функция u u (x) и v v (x ) имеют
непрерывные производные на
a, b,
тогда справедливо следующее равенство
b
udv u v
a
где
b
b
a
vdu,
( )
a
u v a u (b)v(b) u (a)v(a ).
b
Эту формулу называют формулой интегрирования
по частям для определенного интеграла.

11.

Примеры.
1
Пример 4. Вычислить
ln( x 1)dx.
0
Решение. u ln( x 1), du d (ln( x 1)
dx
(ln( x 1)) dx
; vdv dx, v dx x.
x 1
1
1
dx
1
0 ln( x 1)dx ( x ln( x 1)) 0 0 x x 1 ;
1
1
dx
0 x x 1 0
1
1
x 1 1 dx
x 1
1
1
1
0 dx 0 x 1 dx x ln( x 1) 0 1 ln 2.
0
0

12.

1
1
dx
0 ln( x 1)dx ( x ln( x 1)) 0 0 x x 1
1
ln 2 0 1 ln 2 2 ln 2 1 ln 4 1;
Ответ:
ln 4 1.
Пример 5. Найти площадь фигуры, ограниченной линиями
x y , x 0, y 4.
Решение. Из рисунка следует, что площадь искомой фигуры
равна: SOABC SOBC , каждая их
которых находится по
Y
y 4
B
y x
A
геометрическому смыслу
определенного интеграла.
0
C
2
x

13.

Решая систему y 4,
x
2
получим координаты точки В(2;4).
y,
2
SOABC 4dx 4 x 8; SOBC
0
0
8 16
S 8 (ед.2 ).
3 3
16
2
(
ед
.
).
ОТВЕТ:
3
3 2
2
x
x dx
3
0
2
0
8
;
3

14.

Несобственный интеграл
Определение:
интервале
Пусть
(a ; ) .
функция
f(x)
Если существует lim
непрерывна
на
f ( x)dx,
то
t
t
a
этот предел называется несобственным интегралом и
обозначается
t
f ( x)dx lim f x dx.
t
a
Если
предел,
существует
стоящий
и
конечен,
в
то
правой
части
несобственный
равенства,
интеграл
называется сходящимся, в противном случае - расходящимся.