Определенный интеграл как функция верхнего предела

1.

Пусть функция y=f(x) интегрируема на [a,b].
Тогда она будет интегрируема и на
произвольном отрезке [a,х], где a<x<b.
Пусть
x
x
a
a
f ( x)dx f (t )dt Ф( x)
Функция Ф(x) называется интегралом
с переменным верхним пределом.

2.

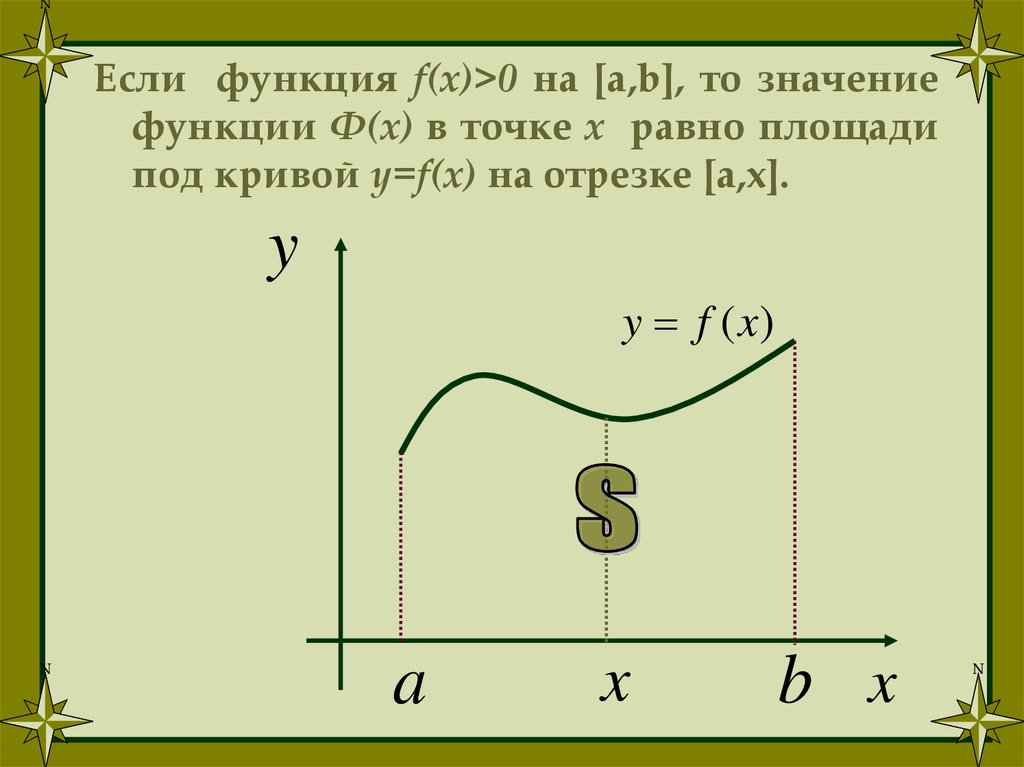
Если функция f(x)>0 на [a,b], то значение
функции Ф(x) в точке x равно площади
под кривой y=f(x) на отрезке [a,х].
y
y f (x)
a
x
b x

3.

Если функция f(x) непрерывна на
отрезке [a,b], то функция Ф(x)
также непрерывна на [a,b].

4.

Пусть приращение Δх таково, что x x a, b
По свойству определенного интеграла
x x
x
x x
a
a
x
f (t )dt f (t )dt f (t )dt
Ф( x x)
x x
Ф( x)
f (t )dt
x
По теореме о среднем найдется
что
x x
x, x x
f (t )dt f ( ) x
x

5.

Ф( x x) Ф( x) f ( ) x
Так как
a, b то m f ( ) M
где m и M - наименьшее и наибольшее
значения функции на [a,b].
Переходим в последнем равенстве к
пределу при x 0
lim Ф( x x) Ф( x) lim f ( ) x Ф( x)
x 0
x 0
0
Это и будет означать, что функция Ф(х)
непрерывна на [a,b].

6.

Пусть функция f(x) непрерывна на
отрезке [a,b]. Тогда в каждой точке
x a, b
производная
функции
Ф(x)
по
переменному
верхнему
пределу
равна подынтегральной функции:
Ф ( x)
a
x
f ( x)dx f ( x)

7.

Из теоремы 1 следует, что
Ф( x x) Ф( x) f ( ) x
Ф( x x) Ф( x)
f ( )
x
где
x, x x
Переходим к пределу при x 0

8.

Ф( x x) Ф( x)
lim f ( ) lim
x 0
x 0
x
Ф (x)
В силу непрерывности функции f(x)
lim f ( ) f ( x)
x 0
Ф ( x) f ( x)

9.

Если функция y=f(x) непрерывна
на отрезке [a,b], то на этом отрезке
существует первообразная этой
функции.

10.

Одной
из
функция
первообразных
является
x
f (t )dt Ф( x)
a
Поскольку любая другая первообразная
отличается от Ф(х) на постоянную
величину,
то
связь
между
неопределенным
и
определенным
интегралом имеет вид:
x
f ( x)dx f (t )dt C
a