Функциональная схема скоростной САР

1.

Министерство образования и науки Российской Федерации
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ВОЕНМЕХ» им. Д.Ф. УСТИНОВА
Кафедра Н1
Мехатроника и робототехника
К.т.н., доцент Савельев Б.Н.
Иллюстративный материал
к конспекту лекций
Часть вторая
Санкт – Петербург
2015 г.

2.

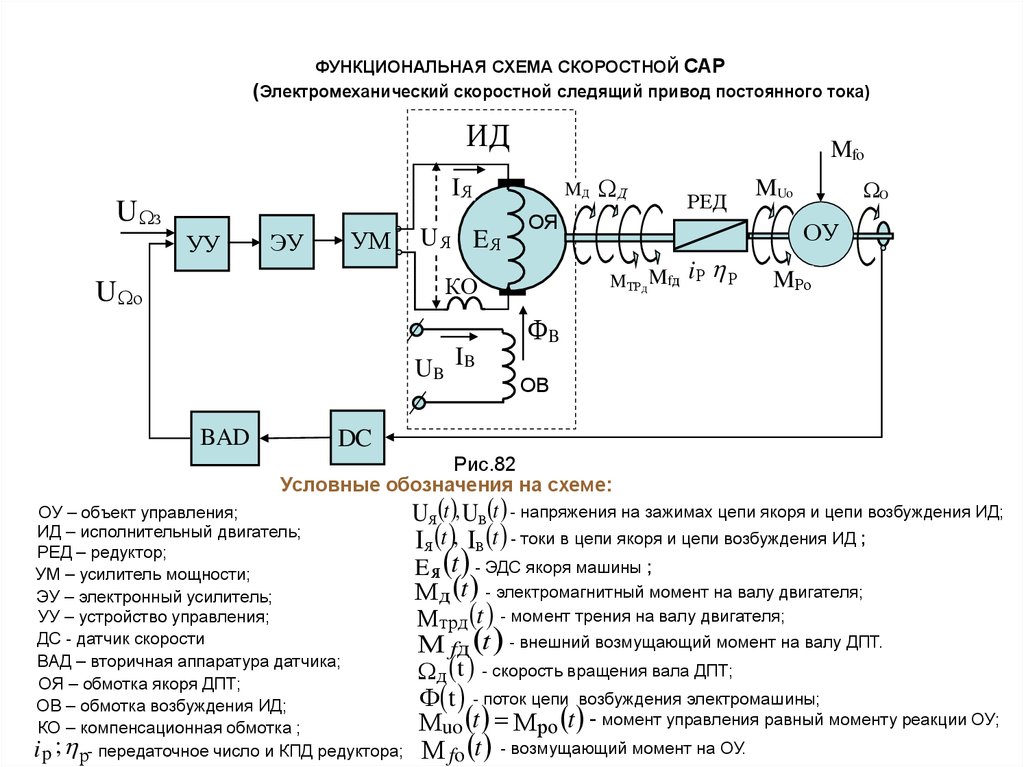
ФУНКЦИОНАЛЬНАЯ СХЕМА СКОРОСТНОЙ САР
(Электромеханический скоростной следящий привод постоянного тока)
ИД
Mfo
IЯ
U з
УУ
ЭУ
УM
U Я EЯ
MД
ОЯ
РЕД
O
MUo
ОУ
MТР Д Mfд i Р
КО
U о
Д
Р
MРo
ФB
U B IB
BAD
ОВ
DC
Рис.82
Условные обозначения на схеме:
ОУ – объект управления;
ИД – исполнительный двигатель;
РЕД – редуктор;
УМ – усилитель мощности;
ЭУ – электронный усилитель;
УУ – устройство управления;
ДС - датчик скорости
ВАД – вторичная аппаратура датчика;
ОЯ – обмотка якоря ДПТ;
ОВ – обмотка возбуждения ИД;
КО – компенсационная обмотка ;
i p ; р- передаточное число и КПД редуктора;
Uя t , Uв t - напряжения на зажимах цепи якоря и цепи возбуждения ИД;
Iя t , Iв t - токи в цепи якоря и цепи возбуждения ИД ;
E я t - ЭДС якоря машины ;
М д t - электромагнитный момент на валу двигателя;
Мтрд t - момент трения на валу двигателя;
М fд t - внешний возмущающий момент на валу ДПТ.
д t - скорость вращения вала ДПТ;
Ф t - поток цепи возбуждения электромашины;
Мuo t Мро t - момент управления равный моменту реакции ОУ;
М fo t - возмущающий момент на ОУ.

3.

Математическая модель скоростной САР
Математическая модель исполнительного двигателя
Принимаемые допущения:
- параметры ИД на рассматриваемом интервале времени не изменяются;
- реакция якоря полностью скомпенсирована компенсационной обмоткой ДПТ;
- гистерезисом магнитной цепи машины пренебрегаем;
- кривая намагничивания аппроксимирована кусочно-линейной характеристикой “насыщение”;
- трения на валу машины хорошо описываются характеристикой «сухое трение».
Уравнения равновесия ЭДС в цепях исполнительного электродвигателя
В цепи якоря:
d I я t
t
t
t
t
t
E я t
Uя
U Rя
U Lя
Eя
R я Iя
Lя
В цепи возбуждения:
dt
d Iв t
, где
Uв t U Rв t U Lв t R в Iв t Lв
dt
(136)
(137)
Uя t , Uв t - напряжения на зажимах цепи якоря и цепи возбуждения машины ;
URя t , ULя t - падение напряжения на активном и реактивном сопротивлении якоря;
URв t ; ULв t - падение напряжения на активном и реактивном сопротивлении ОВ;
Iя t , Iв t - токи в цепи якоря и цепи возбуждения машины ;
E я t
R я,Rв
L я , Lв
- ЭДС якоря машины ;
- активные сопротивления цепи якоря и цепи возбуждения машины ;
- индуктивности цепи якоря и цепи возбуждения машины .
E я t cе Ф t t , где
Ф t - поток цепи возбуждения электромашины;
t - скорость вращения вала ДПТ;
cе - конструктивная константа электромашины.
(138)

4.

Уравнение магнитной цепи электродвигателя
Ф
Ф t
Фнас
-Iв нас
Iв нас
Iв
-Фнас
Iв t
при
Iв t Iв нас
Фнас Sign Iв t при Iв t Iв нас
(139)
Фнас - поток насыщения магнитной цепи ДПТ;
Iв нас - ток возбуждения насыщения магнитной цепи ДПТ;
- тангенс угла наклона линейного участка кривой.
Рис.83 Кривая намагничивания магнитной цепи ДПТ при принятых допущениях
Уравнение моментов на валу электродвигателя
Мэмд t М fд t Мтрд t Мдинд t 0, где
(140)
Мтрд t - момент трения на валу двигателя;
М динд t - динамический момент вала двигателя.
М эм t См Ф t Iя t ,
(141)
М эмд t - электромагнитный момент на валу двигателя;
М fд t - внешний возмущающий момент на валу двигателя;
М тр
Мтрс
д
-Мтрс
См - конструктивная константа ДПТ НВ,
d д t
t
t
,
Jд
Jд
М динд
dt
J д - момент инерции подвижных частей двигателя;
t - угловое ускорение вала двигателя.
(142)
Рис.84 Характеристика сухих трений на валу двигателя.
при д 0
Мтрсд t Sign д
М тр t М эмд t М fд t при д 0 и М эмд t М fд t М трсд
М трсд Sign (М эмд t М fд t ) при д 0 и М эмд t М fд t М трсд
(143)

5.

Математическая модель редуктора и ОУ
Допущения
- Редуктор жесткий и безлюфтовый;
- ОУ уравновешен;
-ОУ имеет сухие и вязкие трения в оси;
-- момент инерции ОУ постоянен.
Уравнения для редуктора
д t i p о t - скоростные соотношения; М д t М fд t
М ро t
i p p
- силовые соотношения.
(144)
Уравнение равновесия моментов на оси объекта управления
где:
(145)
Мuo t Мpo t М fo t Мтрo t Мдинo t
Мдинo t J o d o t dt - динамический момент ОУ ( J o- момент инерции ОУ);
М трo t М тpвo t М трсo t f тро о t M трсо sign o t - вязкие и сухие трения ОУ; (146)
Математическая модель цепей управления САР
Допущения
- усилители имеют широкую полосу пропускания;
- инерционность усилителей пренебрежимо мала;
- УУ реализует уравнение замыкания САР;
- ДС формирует сигнал пропорциональный скорости движения ОУ;
- ВАД имеет коэффициент передачи равный 1.
Уравнение для УУ
Уравнение для УМ
Uя t К ум Uэу t
Уравнение для ЭУ
(147)
U t U з t U о t
(149)
Уравнение для ДС
U o t Uдс t К дс о t
t
U
U
при
t
эу
п
U
К
(148)
Uэу t UпэуSign
U t при U эу t U п
(150)

6. Нелинейная структурная схема исполнительного ДПТ НВ и скоростной САР на его базе.

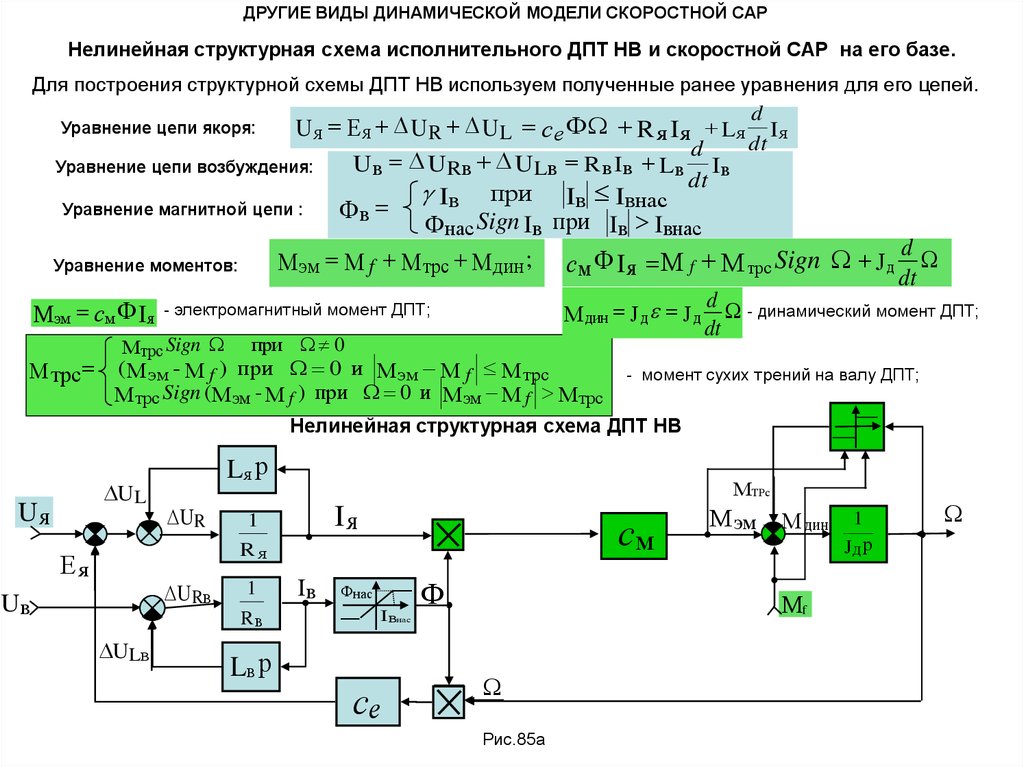
ДРУГИЕ ВИДЫ ДИНАМИЧЕСКОЙ МОДЕЛИ СКОРОСТНОЙ САР
Нелинейная структурная схема исполнительного ДПТ НВ и скоростной САР на его базе.
Для построения структурной схемы ДПТ НВ используем полученные ранее уравнения для его цепей.
d
U я Е я U R U L с е Ф R я I я L я I я
dt
d
Uв
U Rв
U Lв R в Iв Lв Iв
Уравнение цепи возбуждения:
dt
Iв при Iв Iвнас
Уравнение магнитной цепи :
Фв
Фнас Sign Iв при Iв Iвнас
d
М эм М f М трс М дин ; см Ф I я М f М трс Sign J д
Уравнение моментов:
dt
d
М дин J д J д - динамический момент ДПТ;
Мэм см Ф Iя - электромагнитный момент ДПТ;
Уравнение цепи якоря:
М трс
Мтрс Sign
dt
при 0
(Мэм - М f ) при 0 и Мэм М f М трс
М трс Sign (Мэм - М f ) при 0 и Мэм М f М трс
- момент сухих трений на валу ДПТ;
Нелинейная структурная схема ДПТ НВ
UL
Uя
Lя р
UR
МТРс
Iя
1
см
Rя
Ея
URв
Uв
1
Rв
ULв
Lв р
Iв
Фнас
Iвнас
се
Ф
М эм
М дин
Мf
Рис.85а
1
JД р

7.

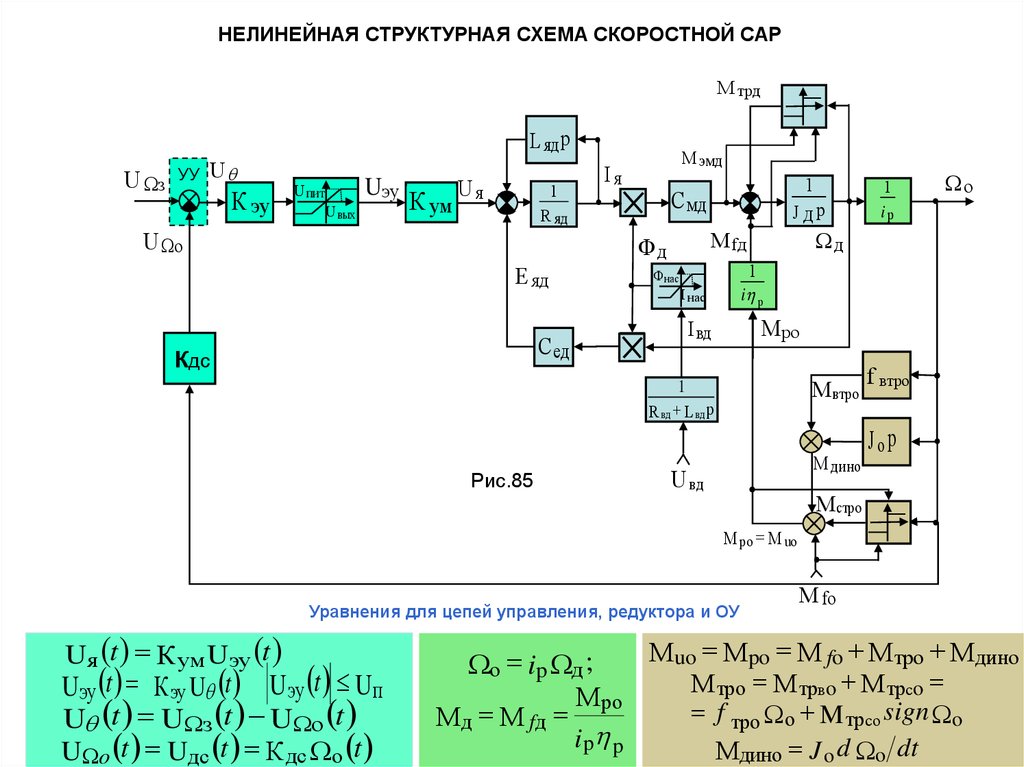
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САР
М трд
L яд р
U з
УУ
U
К эу
Uэу
U пит
U вых
К ум
Uя
1
R яд
U о
М эмд
Iя
С ед
Кдс
JДр
о
1
i р
Ф нас
I нас
Мро
I вд
М втро
1
R вд L вд р
Рис.85
1
iр
д
М fд
Фд
Е яд
1
С мд
М дино
U вд
f втро
Jор
М стро
М ро М uo
М fо
Уравнения для цепей управления, редуктора и ОУ
Uя t К ум Uэу t
Uэу t Кэу U t U эу t Uп
U t U з t U о t
U o t Uдс t К дс о t
Мuo Мpo М fo Мтрo Мдинo
о ip д ;
М трo М тpвo М трсo
М ро
f тро о M трсо sign o
М д М fд
i p p
J d dt
М
динo
o
o

8.

НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САР
М трд
L яд р
U з
УУ
U
К эу
U пит
U вых
К ум
U о
U вд
1
R вд L вд р
Uя
Е яд
I вд
1
R яд
Iя
М эмд
1
С мд
М fд
JДр
д
Фд
Ф нас
I нас
1
iр
1
i р
f
С ед
М дино
М тро
М ро М uo
М fо
К дс
Рис.86
втро
Jор
о

9.

Линеаризованные динамические модели скоростной САР
о
Линеаризацию будем проводить в рабочей точке установившегося режима с воздействиями Uо з ;Uовд ;М fо .
о
Им будут соответствовать выходная переменная о и внутренние переменные в системе, которые также
о о
о
о
о
о
;
обозначим «о»(
т.д.)
;
М
U
I
эмд ;и
я я
д
ос
Будем считать, что отклонения переменных от их значений в выбранной точки малы.
С учетом этого, разложим уравнения 136 – 150 в ряд Тейлора, отбросим члены высшего порядка малости
и запишем в отклонениях:
d Iя t
E я t (136а)
В цепи якоря:
U я t URя t ULя t E я t R я Iя t Lя
U ;U ;
d Iв t dt
В цепи возбуждения: Uв t U Rв t U Lв t R в Iв t Lв
,
dt
о
о
Е я t cе Ф о t се д Ф(t),
о
Ф t Iв t при
Iв Iв
нас
Мэмд t М fд t Мтрд t Мдинд t 0,
о
о
Мэмд t См Ф Iя t См Iя Ф(t),
Мдинд t J д t J д
М трд t f трд д
d д t
,
dt
U t U з t U о t
U o t Uдс t Кдс о t
(137а)
(138а)
(139а)
(140а)
(141а)
(142а)
М ро t
i p p
д t ip о t
Мuo t Мpo t М fo t Мтрo t Мдинo t
М трo t М тpвo t М трсo t f тро о t
Uя t К ум Uэу t
Uэу t Кэу U t
М д t М fд t
(143а)
(144а)
(145а)
(146а)
(147а)
(148а)
(149а)
(150а)

10.

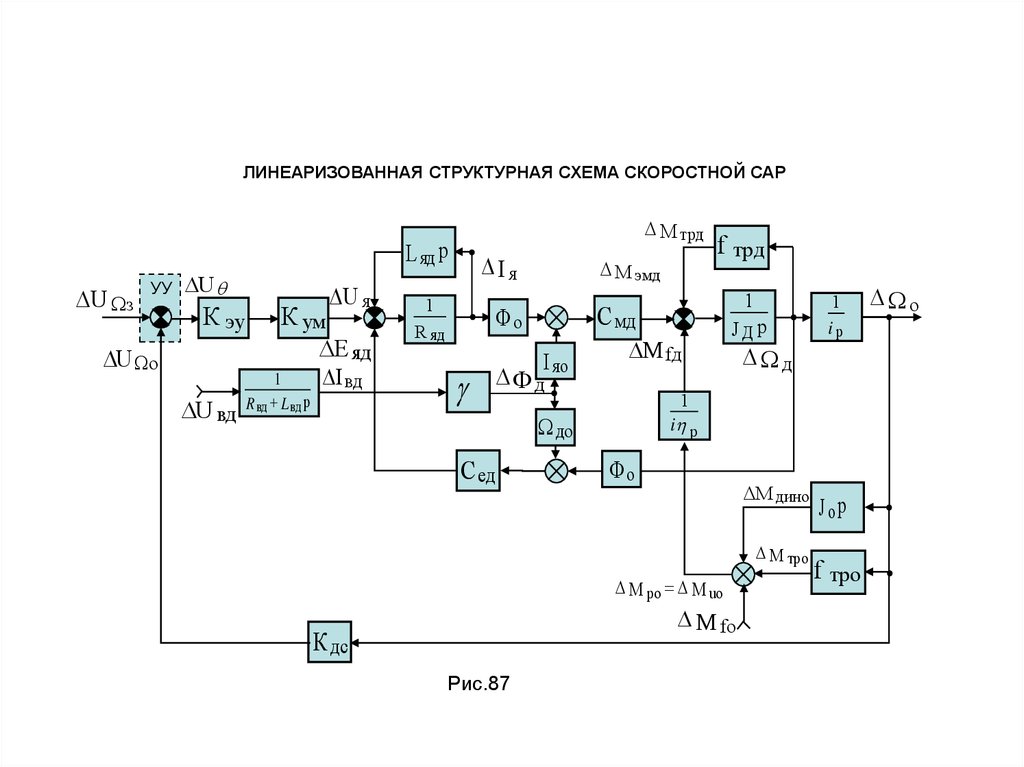
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САР
М трд
L яд р
U з
УУ
U
К эу
U о
U вд
К ум
1
R вд L вд р
U я
Е яд
I вд
Iя
1
R яд
М эмд
I яо
Фд
М fд
JДр
д
i р
Фо
М дино
М тро
М ро М uo
М fо
К дс
Рис.87
1
iр
1
до
С ед
1
С мд
Фо
f трд
Jор
f тро
о

11.

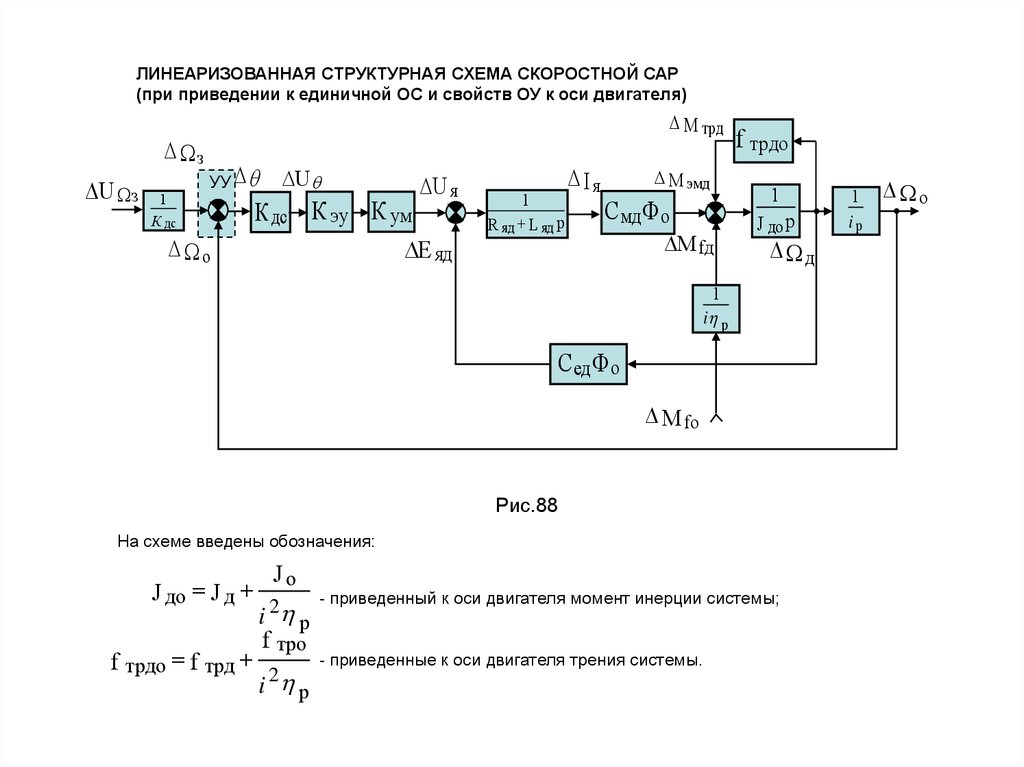
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САР
(при приведении к единичной ОС и свойств ОУ к оси двигателя)
з
U з
1
К дс
М трд
УУ
U
К дс К эу К ум
о
U я
Е яд
1
R яд L яд p
Iя
М эмд
С мд Ф о
М fд
f трдо
1
J до p
д
1
i р
С ед Ф о
М fо
Рис.88
На схеме введены обозначения:
Jо
J до J д 2
i p
f тро
f трдо f трд 2
i p
- приведенный к оси двигателя момент инерции системы;
- приведенные к оси двигателя трения системы.
1
iр
о

12.

Передаточные функции разомкнутой скоростной САР
по управляющему и возмущающему воздействиям
Для получения передаточных функций перейдем в схеме Рис.58 от переменных во времени к их
изображениям по Лапласу. Управляющим воздействием будем считать Зи разорвем обратную связь.
Передаточная функция разомкнутой скоростной САР по управляющему воздействию
Cм Фо /( R яд L яд s)(J до s f трдо )
2
ip
С
С
Ф
о
е м
1
( Lяд s R яд)(J до s f трдо )
Cм Ф о
1
i р J до L яд S2 ( J до R яд L яд f трдо ) S Cм Се Фо2 R яд f трдо
W (s) К ДС КЭУ К УМ 1
К ДС К ЭУ К УМ
К ДС КЭУ К УМ См Фо /(См Се Фо2 R яд f трдо ) i P
K
К
2
(J до R яд Lяд f трдо )
b1S 1 T 22 S 2 T 1 S 1
J до Lяд
b
S
2
2
S 1
S
2
2
См Се Фо R яд f трдо
См Се Фо R яд f трдо
(151)
Передаточная функция разомкнутой скоростной САР по возмущающему воздействию
W fс (s)
1 /(J до s f трдо ) i 2p P
2
С
С
Ф
е м о
1
(Lяд s R яд)(J до s f трдо )
(R яд L яд s ) / i 2p P
2
2
J до L яд S (J до R яд L яд f трдо ) S Cм Се Фо R яд f трдо
2
2
K fс (1 T я s ) К fc (1 a1 f s)
R яд (1 Т я s) /(См Се Фо R яд f трдо ) i p P
2 2
(
)
J
R
L
f
S
1
1 b1S b2 S2
J до Lяд
яд
яд
трдо
до
T
T
2
2S
1
S 1
S
2
2
См Се Фо R яд f трдо
См Се Фо R яд f трдо
(152)

13.

Передаточные функции замкнутой скоростной САР по управляющему и
возмущающему воздействиям
Полученные выражения передаточных функций разомкнутой САР позволяют представить структурную схему
системы в виде:
М fо ( s )
К f ( 1 a 1f s)
1 b 1S b 2 S 2
з( s )
(s)
о( s )
К
b 2 S 2 b 1S 1
Рис.90
где: K К ДС К ЭУ К УМ
b1
CмФо
i p ( C м С е Ф 2о R яд f трдо )
J до R яд L яд f трдо
;
b2
;
Кf
R яд / i 2p P
C м С е Ф 2о R яд f трдо
J яд L яд
;
Cм Се Фо2 R яд f трдо
a1
;
L яд
.
R яд
C м С е Ф 2о R яд f трдо
Передаточная функция замкнутой скоростной САР по управляющему воздействию
К
(s )
b 2 S 2 b 1S 1
К
1
b 2 S 2 b1 S 1
К
2
b 2 S b1 S 1 К
К /( К 1 )
b2 2
b1
S 1
S
1
1
K
К
К з
b 2з S 2 b1з S 1
(153)
Передаточная функция замкнутой скоростной САР по возмущающему воздействию
К fc ( 1 a 1 f S)
fс ( s )
1 b 1S b 2 S 2
1
К
b 2 S 2 b1 S 1
- К fс ( 1 а 1 f S)
b 2 S 2 b 1S 1 К
К fc
1 К
(1 а1 f S )
- К f з ( 1 а 1 f S)
2
b2
b1
S 1 b 2з S b 1з S 1
S2
K 1
К 1
(154)

14.

Передаточные функции для ошибки скоростной САР
по управляющему и возмущающему воздействиям
Передаточные функции для ошибки САР могут быть получены из структурной схемы рис.59 или
используя выражения для них через передаточные функции разомкнутой и замкнутой системы.
Передаточная функция для ошибки скоростной САР по управляющему воздействию
Ф (s)
1
1 W (s)
или
1
1
К
b 2 S 2 b 1S 1
b 2 S 2 b 1S 1
b 2S
2
b 1S 1 К
(b 2 S 2 b 1S 1)
1
1 К
b 2з S 2 b 1з S 1
b 2 з S 2 b1з S 1 К з
К
з
Ф (s) 1 - Ф (s) 1
2
2
b2з S b1з S 1
b 2з S b1з S 1
(b 2 S 2 b 1S 1)
1
1 К
b 2з S 2 b 1з S 1
(155)
Передаточная функция для ошибки скоростной САР по возмущающему воздействию
К fc ( 1 a 1s)
Ф fс (s)
- W fc (s)
1 W (s)
1 b 1S b 2 S 2
1
К
b 2 S 2 b 1S 1
К f з (1 а1f S)
Ф fc (s) - Ф fc (s)
b2з S2 b1з S 1
К fc ( 1 а 1f S)
b 2S
2
b 1S 1 К
К f з ( 1 а 1 f S)
b 2з S
2
b 1з S 1
(156)

15.

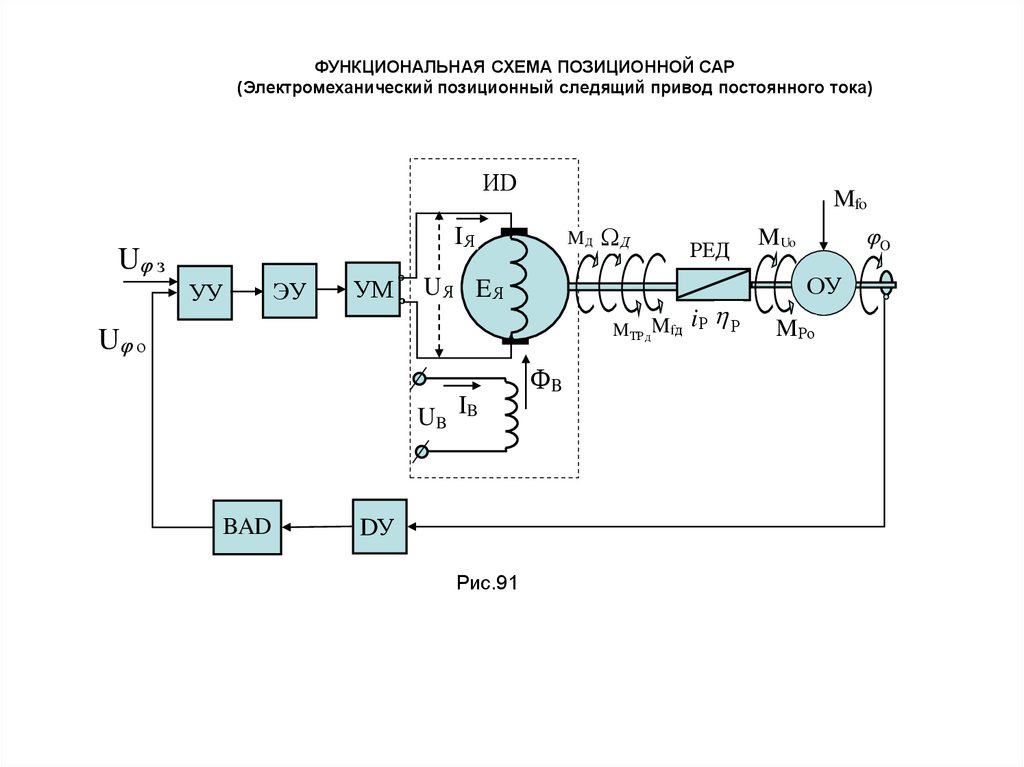
ФУНКЦИОНАЛЬНАЯ СХЕМА ПОЗИЦИОННОЙ САР
(Электромеханический позиционный следящий привод постоянного тока)
ИD
Mfo
IЯ
U з
УУ
ЭУ
УM
MД
Д
РЕД
U Я EЯ
i
MТР Д Mfд Р
U о
ФB
U B IB
BAD
DУ
Рис.91
Р
O
MUo
ОУ
MРo

16.

Математическая модель позиционной САР
При принятых ранее допущениях позиционная САР будет описываться системой уравнений (136) – (149) и
уравнениями:
d o
p o o или о o
р
dt
U 0 K ду o - уравнение датчика угловых перемещений ОУ
(157)
(158)
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ПОЗИЦИОННОЙ САР
М трд
L яд р
U З
УУ
U
К эу
U пит
U вых
К ум
U о
U вд
1
R вд L вд р
Uя
Е яд
I вд
1
R яд
Iя
1
С мд
М fд
Фд
Ф нас
М эмд
I нас
1
iр
JДр
д
1
i р
f
С ед
М дино
М тро
М ро М uo
М fо
К ДУ
Рис.92
втро
Jор
о
1
P
о

17.

ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА ПОЗИЦИОННОЙ САР
(при приведении к единичной ОС и свойств ОУ к оси двигателя)
М трдо
U o
з
УУ
1
К ду
U
Кду
К эу К ум
U я
Е яд
о
1
R яд L яд p
Iя
М эмд
С мд Ф о
М fд
f трдо
1
1
J до p
iр p
д
1
i р
С ед Ф о
М fо
На схеме введены обозначения:
Jо
J до J д 2
i p
f тро
f трдо f трд 2
i p
Рис.93
- приведенный к оси двигателя момент инерции системы;
- приведенные к оси двигателя трения системы.
о

18.

Передаточная функция разомкнутой позиционной САР по управляющему воздействию
Cм Фо /( R яд L яд S)(J до S f трдо )
W (s) К ДУ КЭУ К УМ
2
ip S
Се См Фо
1
(Lяд S R яд)(J до S f трдо )
Cм Ф о
К ДУ К ЭУ К УМ 1
2
2
S
i р J до L яд S ( J до R яд L яд f трдо )S Cм Се Фо R яд f трдо
1
К ДУ КЭУ К УМ См Фо /(См Се Фо2 R яд f трдо ) i P S
K
К
2
S(T 2 S2 T 1S 1) S(b2 S2 b1S 1)
J до Lяд
2 ( J до R яд L яд f трдо )
S 1
S
2
2
См Се Фо R яд f трдо
См Се Фо R яд f трдо
(159)
Передаточная функция разомкнутой позиционной САР по возмущающему воздействию
1 /(J до S f трдо ) i 2p P S
W Mf (s)
2
Се См Фо
1
(Lяд s R яд)(J до s f трдо )
(R яд Lяд s ) / i 2p P S
2
2
J до Lяд S (J до R яд Lяд f трдо )S Cм Се Фо R яд f трдо
2
2
R яд (1 Т я s) /(См Се Фо R яд f трдо ) i p P S
f (1 T я S)
Кf (1 a1S)
(160)
K
2
2
2
J до Lяд
S(T2 S T1S 1) S(1 b1S b2 S )
2 ( J до R яд L яд f трдо )
S 1
S
2
2
См Се Фо R яд f трдо
См Се Фо R яд f трдо

19.

Передаточные функции замкнутой позиционной САР по управляющему и
возмущающему воздействиям
Полученные выражения передаточных функций разомкнутой САР позволяют представить
структурную схему системы в виде:
(s)
М fо
K К ДУ К ЭУ К УМ
з( s )
CмФо
i p ( C м С е Ф 2о R яд f трдо )
(s)
;
К f ( 1 a 1f s)
S(1 b1 S b 2 S 2 )
о( s )
К
S(b 2 S 2 b1 S 1)
Рис.94
Передаточная функция замкнутой позиционной САР по управляющему воздействию
К
К
К / К
S(b 2 S 2 b1 S 1)
1
(
s
)
К
b 2 S 3 b1S 2 S К b 2 S 3 b 1 S 2 1 S 1 b 3 зS 3 b 2 з S 2 b1з S 1
1
S(b 2 S 2 b 1S 1)
K
К
К
(161)
Передаточная функция замкнутой позиционной САР по возмущающему воздействию
К f ( 1 a 1f S)
К
f ( 1 а 1f S )
К
- К f ( 1 а 1f S)
- К f з ( 1 а 1f S)
S(1 b 1S b 2 S 2 )
(162)
fп ( s )
3
2 S
2
3
К
b
b
1
2
1
S
1
b
3
2
b
S
b
S
К
2
1
1
S S S 1 b 3 зS 2 з S b 1 з
K
K
К
S(b 2 S 2 b 1S 1)

20.

Передаточные функции для ошибки позиционной САР
Передаточная функция для ошибки позиционной САР по управляющему воздействию
Ф (s)
1
1 W (s)
1
К
1
Ф (s) 1 - Ф (s) 1
b 3 з S 3 b 2 з S 2 b1 з S
2
b 3 зS 3 b 2 з S b 1з S 1
S(b 2 S 2 b 1S 1)
1
2
b3 зS3 b2 з S
b1з S 1
b 3 з S 3 b 2 з S 2 b1 з S
b 3 зS b 2 з S
3
2
b 1з S 1
или
(163)
Передаточная функция для ошибки позиционной САР по возмущающему воздействию
Ф fп (s)
- W fп (s)
1 W (s)
К f (1 a1S)
S(1 b1S b2 S2)
К
1
S(b 2 S 2 b 1S 1)
Ф fп (s) - Ф fп (s)
- К f з ( 1 а 1f S)
b 3зS b 2з S
3
2
b 1з S 1
К f з ( 1 а 1f S)
b 3зS b 2з S
3
2
b 1з S 1
К f з ( 1 а 1f S)
2
b 3зS 3 b 2з S b 1з S 1
или
(164)

21.

Статические и астатические системы
Сравнивая функциональные схемы скоростной и позиционной САР, мы видим, что они отличаются
лишь регулируемыми переменными и, соответственно, датчиками их измерения. Математическое
описание их элементов тоже идентичны.
Однако передаточные функции этих систем в разомкнутом состоянии отличаются множителем «S»
в знаменателе передаточной функции позиционной системы.
С точки зрения ТАУ, это весьма важное обстоятельство, т.к.:
K
- передаточная функция разомкнутой скоростной системы может
W ( s) 2 2
(T 2 S T 1S 1)
быть представлена произведением только статических звеньев;
- передаточная функция разомкнутой позиционной системы может
быть представлена произведением статических звеньев и
интегрирующего звена.
W ( s)
K
2
S(T 2 S2 T 1S 1)
САР, передаточная функция которых в разомкнутом виде является произведением передаточных
функций только статических звеньев, называются статическими САР.
Структурные схемы таких САР, преобразованные к одноконтурному виду содержат только
статические звенья (идеальное, апериодические, колебательные и т.д.)
САР, передаточная функция которых в разомкнутом состоянии содержит в виде сомножителя
передаточную функцию одного или нескольких интегрирующих звеньев, называются
астатическими САР.
Структурные схемы таких САР, преобразованные к одноконтурному виду содержат статические
звенья и одно или несколько интегрирующих звеньев
Если в передаточной функции разомкнутой системы могут быть выделены «n» интегрирующих
звеньев, то САР называется системой с астатизмом
n-го порядка.

22.

Качество систем автоматического регулирования
и пути его повышения
Качество работы САР оценивается по многим показателям. Показатели качества САР
принято подразделять на группы, основными из которых являются:
- Точность САР в установившихся типовых режимах работы;
- Устойчивость и запасы устойчивости системы;
- Характеристики переходных процессов САР и ее быстродействие.
1
Точность САР в установившихся типовых режимах работы;
Под точностью САР понимают значение ее ошибки регулирования в типовых режимах работы.
К типовым режимам относят следующие виды режимов:
1. Статические режимы, т.е. режимы с постоянными значениями воздействий на систему
x(t ) const ; f (t ) const .
2. Динамические режимы с постоянным значением к-ой производной воздействия.
к
d x(t ) k x(t ) ( k ) const ;
p
x уст
к
dt
к
d f (t ) k f (t ) ( k ) const ;
p
f уст
к
dt
При постоянной к-ой производной сама переменная может быть выражена:
(k )
(k )
f
уст
x уст
f (t ) k .
x(t ) k ;
p
При k=1
x(t )
При k=2
x (t )
p
(1)
x уст t , где
2
t
( 2)
x уст , где
2
(1)
x уст
( 2)
x уст
dx(t )
const - скорость изменения воздействия.
dt
2
x (t )
d 2 const - ускорение изменения воздействия.
dt
3. Динамические гармонические режимы при постоянных значениях амплитуды и частоты.
x(t ) xo Sin t;
f (t ) f o Sin t;

23.

Ошибка линейной САР в установившемся режиме может быть представлена в виде составляющих:
(t ) x (t ) f (t ),
где:
x (t ) - ошибка, вызываемая задающим воздействием;
f (t ) - ошибка, вызываемая возмущающим воздействием;
Если возмущающих воздействий несколько f 1 (t ); f 2 (t ); f 3 (t ) и т.д., то и составляющих в
ошибке системы от возмущающих воздействий будет несколько:
f 1 (t ); f 2 (t ); f 3 (t ) и т.д.
Составляющие ошибки САР могут быть выражены через соответствующие воздействия на нее,
при использовании передаточных функций системы для ошибки по каждому воздействию:
x (t ) Ф x ( p) x(t ) - в операторной форме для функций времени, или
)
x ( s) Ф x ( s) x( s) - в изображениях по Лапласу, через передаточную функцию Ф x ( sдля
ошибки САР по этому воздействию.
f (t ) Ф f ( p) f (t ) - уравнение для ошибки по возмущающему воздействию в
операторном форме,
f ( s) Ф f (s) f ( s) - изображение по Лапласу ошибки САР по возмущающему воздействию.
Ф x ( s)
- передаточная функция замкнутой САР для ошибки по возмущающему воздействию.
Рассмотрим точность различного типа САР в первом типовом режиме.
1. Пусть САР имеет передаточные функции в разомкнутом состоянии:
W x (s)
K x Ax (s)
- передаточная функция разомкнутой САР по управляющему воздействию;
B(s)
K f A f ( s ) - передаточная функция разомкнутой САР по возмущающему воздействию.
W f (s)
B(s)
Такая САР относится к системам статическим, т.к. ее передаточные функции в разомкнутом
состоянии являются произведением передаточных функций только статических звеньев.
Ее передаточные функции в замкнутом состоянии будут соответственно:
W x (s)
(
s
)
Фx
1 W x (s)
и
Ф f (s)
W f ( s)
1 W x ( s)

24.

Передаточные функции замкнутой САР для ошибки по управляющему и возмущающему воздействиям:
Ф x ( s )
1
и
1 W x (s)
Ф f ( s )
W f (s)
1 W x (s)
Выражения для составляющих ошибки САР в изображениях по Лапласу
1
B( s )
x( s )
1 W x (s)
B( s ) K x A x ( s )
W f (s)
K f A f ( s)
(
s
)
Ф
(s) f (s)
f (s)
f ( s)
f
f
1 W x (s)
B(s) K x A x ( s )
x ( s ) Ф x ( s ) x( s )
x( s )
и
Переходя к оригиналам, получим:
x (t ) Ф x ( p ) x(t )
f (t ) Ф f ( p ) f (t )
1
1 W x ( p)
x (t )
B( p )
x (t ) и
B( p ) K x A x ( p )
W f ( p)
K f A f ( p)
f (t )
f (t ), где
1 W x ( p)
B(p) K x A x ( p )
p
d
dt
1.1 В статическом установившемся режиме работы САР по теореме предельного перехода
определим установившиеся ошибки САР, положив все производные равными 0, тогда:
1
x уст
1 W x ( 0)
1 K x
W f (0)
Kf
Ф
f уст
f уст
f уст f (0) f уст
1 W x (0)
1 K x
xуст Ф x (0) x уст
1
x уст
Составляющие ошибки системы не
равны 0, а имеют конечные значения,
зависящие от величины воздействия и
коэффициентов передачи разомкнутой
САР.
Об этом говорит и отличие от идеала передаточных функций замкнутой САР для статических режимов :
Ф x ( 0)
W x ( 0) K x 1 ;
1 W x ( 0) 1 K x
Ф f (0)
W f (0)
Kf
0
1 W x (0) 1 K x

25.

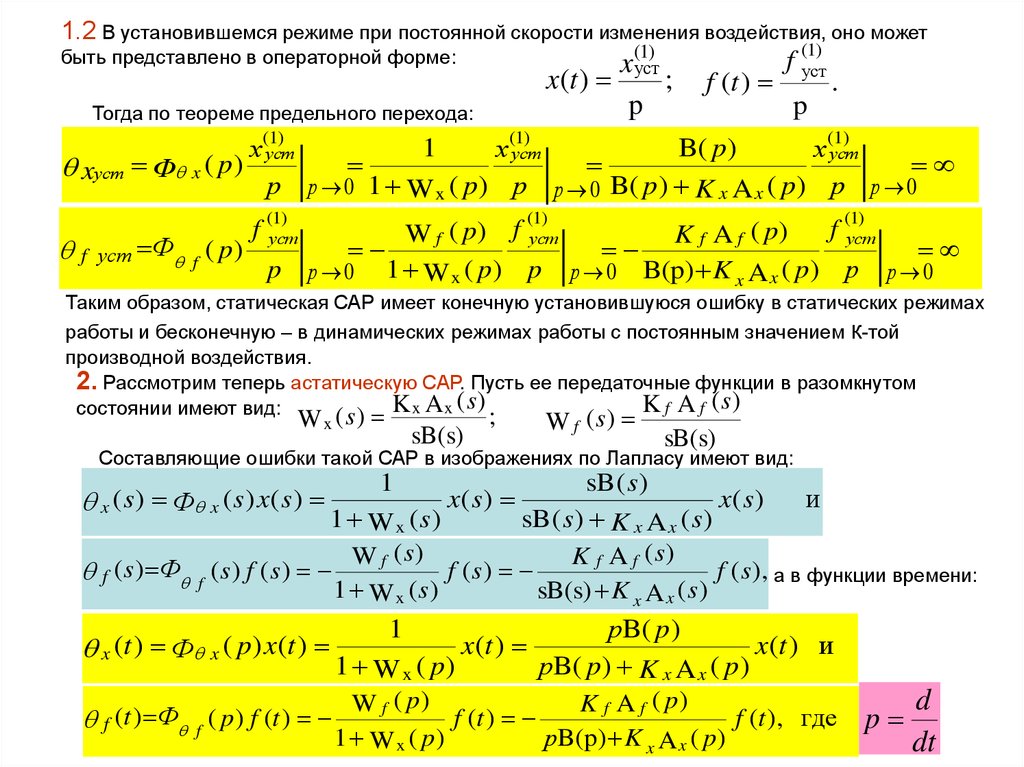
1.2 В установившемся режиме при постоянной скорости изменения воздействия, оно может
(1)
(1)
быть представлено в операторной форме:
Тогда по теореме предельного перехода:
x уст
x(t )
;
p
f (t )
f уст
p
.
(1)
(1)
(1)
1
B( p )
х уст
х уст
х уст
xуст Ф x ( p )
р р 0 1 W x ( p ) р р 0 B( p ) K x A x ( p ) р р 0
(1)
(1)
(1)
f уст
f уст
W f ( p) f уст
K f A f ( p)
f уст Ф f ( p)
p р 0 1 W x ( p) p р 0 B(p) K x A x ( p) р р 0
Таким образом, статическая САР имеет конечную установившуюся ошибку в статических режимах
работы и бесконечную – в динамических режимах работы с постоянным значением к-той
производной воздействия.
2. Рассмотрим теперь астатическую САР. Пусть ее передаточные функции в разомкнутом
(s)
K f A f ( s)
состоянии имеют вид:
(s) K x A x ;
Wx
sB(s)
W f (s)
sB(s)
Составляющие ошибки такой САР в изображениях по Лапласу имеют вид:
sB ( s )
x( s)
и
1 W x (s)
sB ( s ) K x A x ( s )
W f ( s)
K f A f (s)
f (s)
f ( s ), а в функции времени:
f ( s ) Ф f ( s ) f ( s )
1 W x (s)
sB(s) K x A x ( s )
x ( s ) Ф x ( s ) x( s )
x (t ) Ф x ( p ) x(t )
f (t ) Ф f ( p ) f (t )
1
x( s)
1
1 W x ( p)
x (t )
рB( p )
x (t ) и
рB( p ) K x A x ( p )
W f ( p)
K f A f ( p)
f (t )
f (t ), где
1 W x ( p)
рB(p) K x A x ( p )
p
d
dt

26.

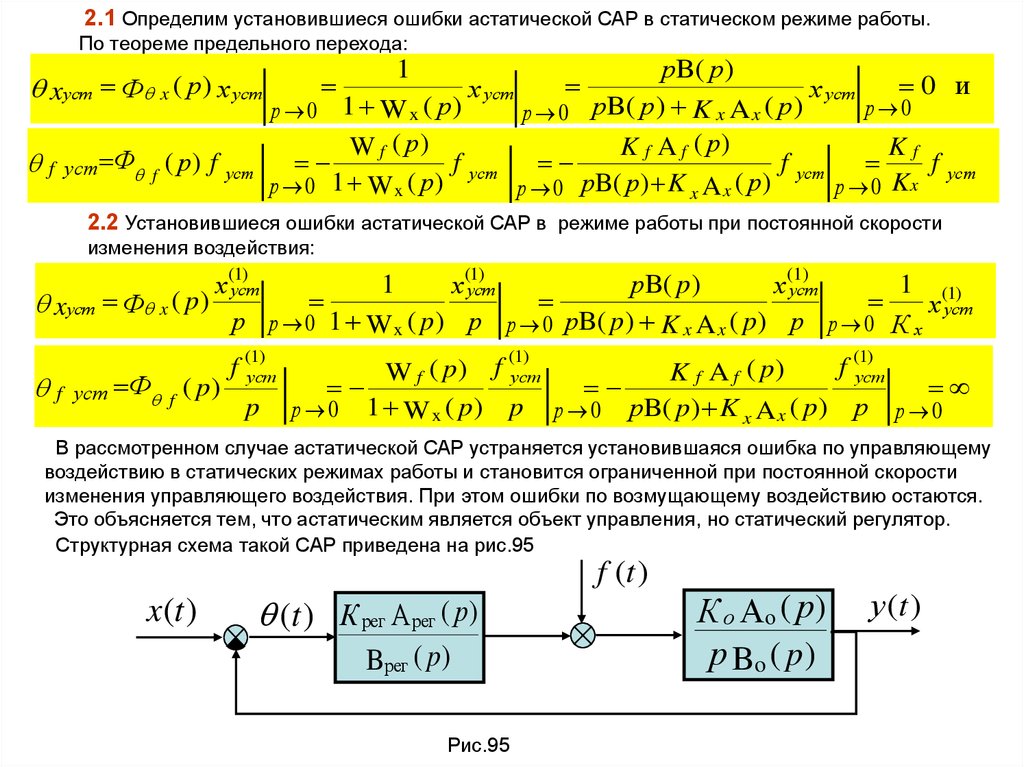
2.1 Определим установившиеся ошибки астатической САР в статическом режиме работы.
По теореме предельного перехода:
xуст Ф x ( р ) х уст
f
уст Ф f
( р) f
уст
рB( р )
0 и
х уст
х уст
р 0
р 0 1 W x ( р)
р 0 рB( р ) K x A x ( р )
W f ( р)
K f A f ( р)
Kf
f уст
f уст
f уст
1
(
р
)
(
р
)
K
x
р
B(
р
)
K
р 0
Wx
р 0
р 0
x Ax
1
2.2 Установившиеся ошибки астатической САР в режиме работы при постоянной скорости
изменения воздействия:
(1)
(1)
(1)
1
рB( p )
1 (1)
х уст
х уст
х уст
(
p
)
xуст Ф x
х уст
р р 0 1 W x ( p ) р р 0 рB( p ) K x A x ( p ) р р 0 К х
f
уст Ф f
( p)
f
(1)
уст
p
(1)
(1)
f уст
W f ( p) f уст
K f A f ( p)
р 0 1 W x ( p ) p р 0 рB( p ) K x A x ( p ) р р 0
В рассмотренном случае астатической САР устраняется установившаяся ошибка по управляющему
воздействию в статических режимах работы и становится ограниченной при постоянной скорости
изменения управляющего воздействия. При этом ошибки по возмущающему воздействию остаются.
Это объясняется тем, что астатическим является объект управления, но статический регулятор.
Структурная схема такой САР приведена на рис.95
f (t )
x(t )
(t ) К рег Арег ( р)
Bрег ( p)
Рис.95
К о Ао ( р )
р Bo ( p )
у (t )

27.

При астатическом регуляторе и статическом объекте
f (t )
(t ) К рег Арег ( р)
x(t )
рBрег ( p)
К о Ао ( р )
Bo ( p )
у (t )
Рис.96
Передаточные функции разомкнутой САР по управляющему и возмущающему воздействиям в
операторном виде:
K f A f ( р)
K x A x ( р)
W x ( р)
рB( р )
;
W f ( р)
B( р )
.
2.1а Составляющие ошибки такой астатической системы по управляющему и возмущающему
воздействиям в статическом режиме работы:
рB( р )
0 и
х уст
р 0
р 0 1 W x ( р)
р 0 рB( р ) K x A x ( р )
W f ( р)
K f р A f ( р)
0.
f уст
f уст
f уст Ф f ( р ) f уст
1
(
р
)
(
р
)
р 0
р 0
Wx
р 0 рB( р ) K x A x
xуст Ф x ( р ) х уст
1
х уст
2.2а Установившиеся ошибки астатической САР в режиме работы при постоянной скорости
изменения воздействия:
(1)
(1)
(1)
1
рB( p )
1 (1)
х уст
х уст
х уст
(
p
)
xуст Ф x
х уст
р р 0 1 W x ( p ) р р 0 рB( p ) K x A x ( p ) р р 0 К х
(1)
f
уст Ф f
( p)
f уст
p
(1)
(1)
f уст
K f рA f ( p)
W f ( p) f уст
К f (1)
f уст
р 0 1 W x ( p) p р 0 рB( p) K x A x ( p) р р 0 К х

28.

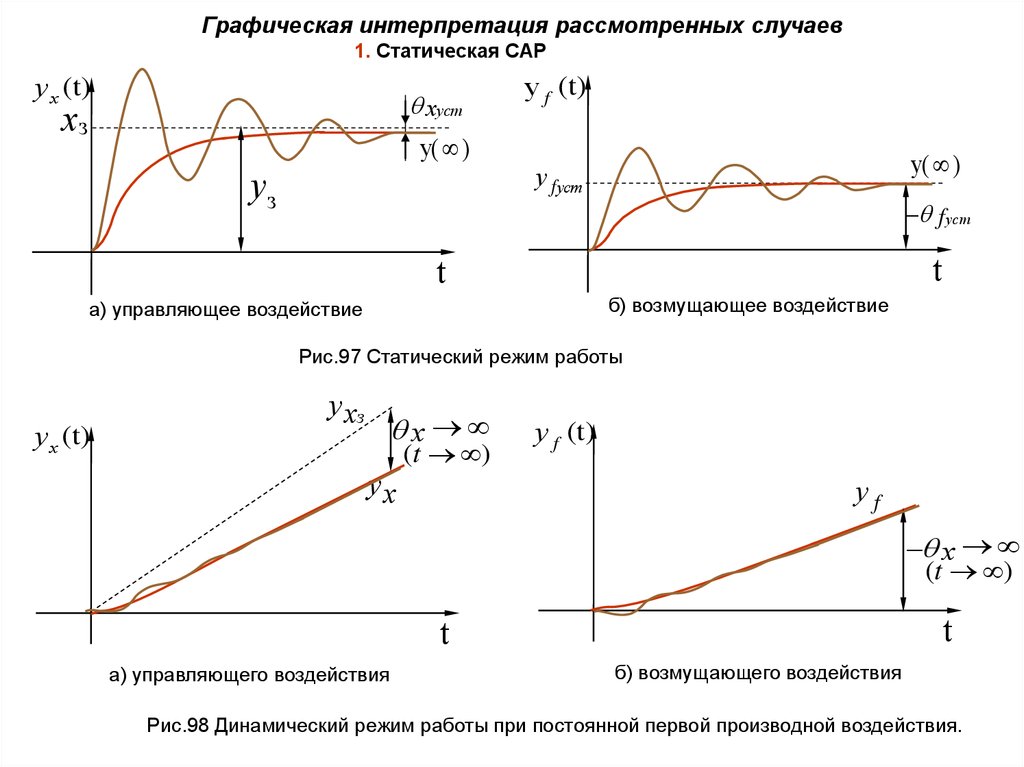
Графическая интерпретация рассмотренных случаев
1. Статическая САР
у х (t)
хуст
хз
у f (t)
y( )
y( )
у fуст
уз
fуст
t
t
б) возмущающее воздействие
а) управляющее воздействие
Рис.97 Статический режим работы
у х (t)
у хз
х
(t )
ух
у f (t)
уf
х
(t )
t
t
а) управляющего воздействия
б) возмущающего воздействия
Рис.98 Динамический режим работы при постоянной первой производной воздействия.

29.

2. Астатическая САР
у х (t)
хуст 0
хз
у f (t)
(2-астатический объект)
y( )
y( )
у fуст
уз
fуст
t
t
(2а -астатический регулятор)
б) возмущающее воздействие
а) управляющее воздействие
Рис.99 Статический режим работы
у х (t)
у хз
ух
у f (t)
хуст
у fуст
а) управляющего воздействия
t
(2а -астатический регулятор)
х у f
(t )
y( )
fуст
(2-астатический объект)
t
б) возмущающего воздействия
Рис.100 Динамический режим работы при постоянной первой производной воздействия.

30.

В общем случае САР может иметь разные порядки астатизма по управляющему и возмущающему
воздействиям и разные характеристические полиномы передаточных функций в разомкнутом
состоянии, т. е.:
K f A f ( s)
K x A x (s)
W x (s)
или в операторной форме:
l
;
s Bx ( s)
K x A x ( р) ;
(
р
)
Wx
l
р Bx ( р)
W f (s)
r
s B f (s)
K f A f ( р)
.
W f ( р) r
(
р
)
р Bf
Тогда составляющие ошибки САР по управляющему и возмущающему воздействиям можно
l
представить:
x (t ) Ф x ( p ) x(t )
1
1 W x ( p)
x(t )
р Bx ( p )
x(t ) и
l
р Bx ( p ) K x A x ( p )
l r
W f ( p)
K f р A f ( p ) Bx ( p )
f (t )
f (t ).
f (t ) Ф f ( p ) f (t )
l
1 W x ( p)
B f ( p )[ p Bx (p) K x A x ( p )]
Выражая воздействия через постоянную к-ую производную
и устремляя Р к нулю, получим выражения для установившихся
ошибок по управляющему и возмущающему воздействиям:
(k )
(k )
f уст
x уст
x(t ) k ; f (t ) k
p
p
l к
(к )
р Bx ( p )
х уст
(к )
l
xуст
х уст
к
1 W x ( p ) р р 0 p Вх ( p ) K x A x ( p )
р 0
1
(165)
(к )
l r к
W f ( p ) f уст
Kf р
A f ( p ) Bx ( p)
(к )
.
f
fуст
уст
к
l
1 W x ( p) p
(
p
)]
B f ( p )[ p Bx (p) K x A x
р 0
р 0
(к )
х уст
к)
к l xуст 0 , а при к l r fуст 0. При к l xуст 1 х(уст
Кх
добротность
САР
по
скорости;
К
(
к
l
1
х
К х - добротность САР .
к l 2 К х - добротность САР по ускорению и т.д.)
При
хуст
(166)

31.

Комбинированное управление и инвариантность системы к воздействиям
Рассмотренные системы реализуют принцип управления по отклонению. Повысить точность таких
систем можно за счет увеличения коэффициента передачи разомкнутой САР или повышения
порядка астатизма САР, т. е. введения интегрирующих звеньев в прямой канал регулятора.
Как будет показано ниже, эти пути ограничены «сверху», т.к. высокое значение Кх и высокий
порядок астатизма приводят к потере запаса устойчивости системы.
Существуют и другие пути, в частности применение комбинированного управления, т.е.
управления по отклонению и возмущению. При этом задающее воздействие тоже рассматривается
как возмущение, т.к. вызывает одну из составляющих ошибки САР (t ) x (t ) f (t ).
Под комбинированным управлением понимается управление по отклонению с одновременным
использованием управления по возмущающему и (или) задающему воздействиям, т.е. когда для
формирования управляющего воздействия на объект управления используется не только
2
2
информация о х(t ) и у (t ) , но и информация о px (t ); p x (t );....; f (t ); pf (t ); p f (t );...
Обобщенная схема системы комбинированного управления
f (p)
х (p)
W f (p)
х(t)
(t)
W х (p)
Рис.101
где:
f (t)
у(t)
f (p) - операторная передаточная функция канала управления по возмущающему воздействию;
х (p) - операторная передаточная функция канала управления по задающему воздействию;

32.

Каналы с операторами х (p) и f (p) управления по соответствующему воздействию вводятся
для компенсации влияния воздействий на ошибку системы (снижения х (t) и f (t) ).
Использование методов теории инвариантности для формирования операторных передаточных
функций х (p) и f (p) позволяет достичь высокой точности САР.
Инвариантность САР.
САР называется инвариантной по отношению к воздействию, если после окончания переходного
процесса, вызванного начальными условиями ошибка системы не зависит от этого воздействия
(управляющего или возмущающего).
Рассмотрим это понятие подробнее.
Пусть на систему действует одно воздействие, например, управляющее (для возмущающего
воздействия аналогично) и дифференциальное уравнение системы для ошибки по этому
воздействию в операторной форме имеет вид:
n
n 1
m
(bn p bn 1 p ... b1 p 1) х t К х (am p ... a1 p 1) х t
или
Bх p х (t ) К х A х p х t
Решение уравнения (167) имеет две составляющих
(167)
(168)
х (t) хп (t ) xв (t ), где:
хп (t ) - общее решение, переходная составляющая (решение уравнения с правой частью =0);
xв (t ) - частное решение, вынужденная составляющая (решение уравнения с правой частью.
K
x A x ( р )
При нулевых начальных условиях
х (t ).
xв (t )
(
р
)
Вх
xв (t ) 0 при х(t ) 0, т.е. при отсутствии воздействия, или при А x ( р) 0 ,т.е. при
равной 0 передаточной функции для ошибки САР по этому воздействию.
Обеспечить полную инвариантность САР к воздействию не всегда удается, но к определенному
классу воздействий, например, в виде степенных функций можно.
В этом случае инвариантность называется частичной.

33.

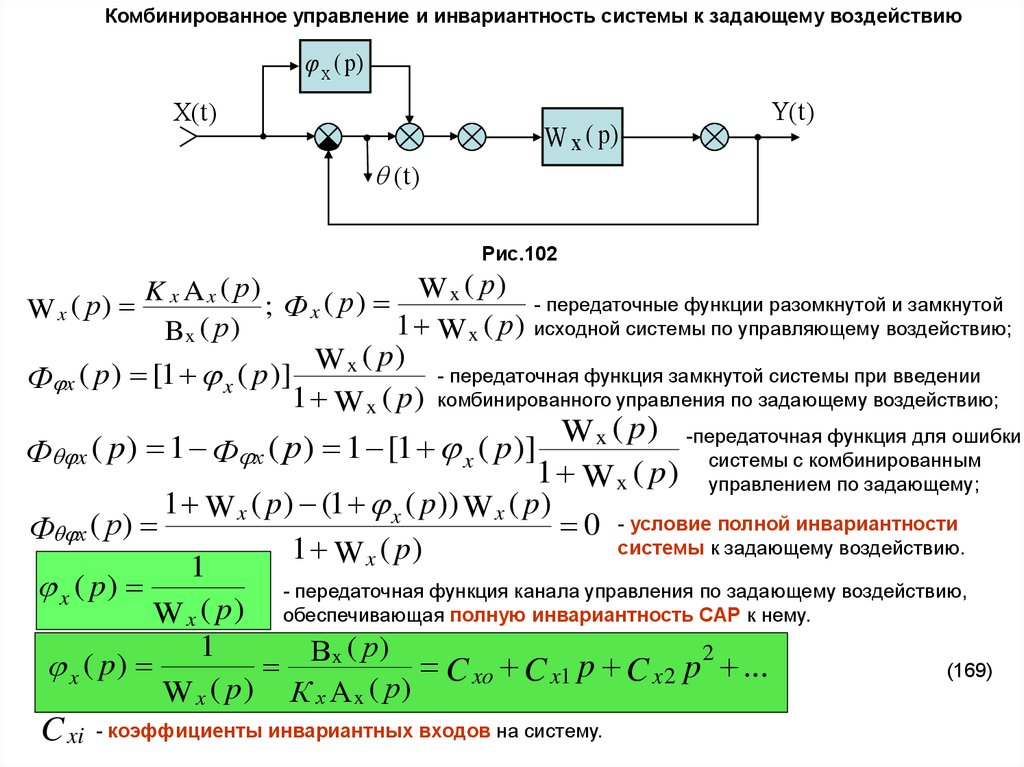
Комбинированное управление и инвариантность системы к задающему воздействию
x ( p)
Х(t)
W x ( p)
Y(t)
(t)
Рис.102
W
x ( р)
K
x A x ( р)
- передаточные функции разомкнутой и замкнутой
; Ф x ( р)
W x ( р)
1 W x ( р ) исходной системы по управляющему воздействию;
Bx ( р )
W x ( p)
(
p
)
[
1
(
p
)]
Ф x
x
1 W x ( p)
- передаточная функция замкнутой системы при введении
комбинированного управления по задающему воздействию;
W
x ( p ) -передаточная функция для ошибки
Ф x ( p ) 1 Ф х ( р ) 1 [1 x ( p )]
с комбинированным
1 W x ( p ) системы
управлением по задающему;
1 W x ( p) (1 x ( p)) W x ( p)
(
р
)
0 - условие полной инвариантности
Ф х
системы к задающему воздействию.
1 W x ( p)
1
x ( p)
- передаточная функция канала управления по задающему воздействию,
W x ( p ) обеспечивающая полную инвариантность САР к нему.
1
( р)
Вx
x ( p)
C xo C x1 p C x 2 p 2 ...
W x ( p) К х А x ( р)
C xi
- коэффициенты инвариантных входов на систему.
(169)

34.

1
Коэффициенты C xi находятся путем разложения x ( p )
1
или при делении Bх p на А х p и умножении на К х . W x ( p )
в ряд по степеням
р
1
1 1 b х1 p b х 2 p 2 ... b хn p n
x ( p)
(
)
2
m
W x ( p ) К х 1 a х1 p a х 2 p ... a хm p
1 b х1 a х1
( )
p b х 2 a х 2 b х1 a х1 a х1 p 2 ...
Кх
Kx
Kx
Этот ряд может быть конечным или бесконечным.
K x A x ( р)
(
р
)
Wx
l
р Bx ( р)
1
и коэффициент C xl
1 l Кх
р ...
(C xо; С х1;... С х (l 1) 0) ,т.е.ряд будет начинаться с члена х ( р )
Кх
Для астатических систем:
,а предыдущие равны 0
.
Определим условие инвариантности к управляющему воздействию для наших примеров.
1. Скоростная САР:
1
х(t ) з (t ); у (t ) о (t ); W xсс ( p)
1
b1 р b2 р 2
xсс ( p )
W xсс ( p ) К К
К
2. Позиционная САР:
1
- операторная передаточная функция канала
управления по задающему воздействию,
обеспечивающая инвариантность к нему
скоростной САР.
х(t ) з (t ); у(t ) о (t ); W xпс ( p)
1
р b1 р 2 b2 р3
xпс ( p )
W xпс ( p ) К
К
К
К
2
b2 p b1 p 1
К
2
р (b2 p b1 p 1)
- операторная передаточная функция канала
управления по задающему воздействию,
обеспечивающая инвариантность к нему
позиционной САР.

35.

1. Скоростная САР, инвариантная к задающему воздействию
b2 2
р
К
М fо (t )
b1 р
К
К f (1 a1 f p )
1
К
1 b1 p b2 p 2
(t )
з (t )
К
b2 p b1 p 1
о (t )
2
Рис.103
2.Позиционная САР, инвариантная к задающему воздействию
b2 3
p
К
М fо (t )
b1 2
p
К
1
p
К
з (t )
К f (1 a1 f p )
p (1 b1 p b2 p 2)
(t )
К
2
p (b2 p b1 p 1)
Рис.104
о (t )

36.

Комбинированное управление и инвариантность системы к возмущающему воздействию
f (p)
f(t)
W f ( p)
Х(t)
(t)
W x ( p)
Y(t)
Рис.105
K f A f ( р)
K
x A x ( р)
; W f ( р)
W x ( р)
B f ( р)
Bx ( р )
Ф f ( p)
W f ( p)
; Ф f ( p )
1 W x ( p)
- передаточные функции разомкнутой исходной
САР по управляющему и возмущающему
воздействиям.
W f ( p ) - передаточные функции замкнутой исходной
САР и для ошибки по возмущающему
1 W x ( p ) воздействию.
При введении канала управления по возмущению с передаточной функцией в операторном виде
ошибка САР по возмущающему воздействию:
f (t ) Ф
откуда:
W f ( p) W x ( p) f ( p)
f (t )
1 W x ( p)
W f ( p) W x ( p) f ( p)
0,
f (t ) : Ф f ( p)
1 W x ( p)
( p) f (t )
f
Условие полной инвариантности САР к
f ( p)
х ( р)
W f ( p)
K f A f ( р) Вх ( р)
C fo C f 1 p C f 2 p 2 ...
W x ( p)
К х B f ( р) А х ( р)
(170)

37.

Комбинированное управление и инвариантность скоростной и позиционной систем
к возмущающему воздействию
К fcc (1 a1 fсс p)
К
(
p
)
(
p
)
;
W
1. Скоростная САР:
xсс
W fcc
2
1 b1 p b2 p 2
b2 p b1 p 1
fсс ( p )
W fсс ( p ) K fсс (1 а1 fcc р )
W xсс ( p )
К
- передаточная функция канала управления по
возмущению скоростной САР.
2
L яд
R яд / i p P
.
a
T
;
;
я
1
f
cc
К
K К ДС К ЭУ К УМ
fcc
2
R яд
Cм Се Фо R яд f трдо
i p ( C м С е Ф 2о R яд f трдо )
CмФо
2. Позиционная САР:
W fпс ( р)
К fпс (1 a1 fпс p)
W xпс ( p )
К
2
р (b2 p b1 p 1)
p(1 b1 p b2 p 2)
W fпс ( p ) K fпс (1 а1 fпc р ) - передаточная функция канала управления по
(
p
)
fпс
возмущению позиционной САР.
W xпс ( p )
К
2
L яд
R яд / i p P
C
м Фо
.
;
a
T
;
я
1
f
пc
К
fпc
K К ДУ К ЭУ К УМ
2
2
R яд
Cм Се Фо R яд f трдо
i p (Cм Се Фо R яд f трдо )
При
и
Кду Кдс К К
fпс ( р) fcс ( р)
f (t ) 0
з (t )/ з (t )
М f (t)
Кf
К
Кf
Тя p
К
W f ( p)
W x ( p)
(t )/ (t )
Рис.98 Обобщенная схема скоростной и позиционной САР, инвариантных к возмущающему воздействию

38.

Неединичные обратные связи и инвариантность системы к задающему воздействию.
f(t)
W f ( p)
Х(t)
(t)
Y(t)
W x ( p)
K x A x ( р) ;
(
р
)
Wx
Bx ( р )
K f A f ( р)
(
р
)
Wf
B f ( р)
ос (p)
Рис.107
Передаточная функция разомкнутой системы по задающему воздействию с введенным
каналом ос ( p) :
W x ( p)
W x ( p )
1 W x ( p ) oc ( p )
.
Передаточная функция для ошибки замкнутой системы по задающему воздействию с введенным
каналом ос ( p) :
1 W x ( p ) oc ( p )
1
.
Ф х ( p)
1 W x ( p ) 1 W x ( p ) oc ( p ) W x ( p )
Условие полной инвариантности системы
к задающему воздействию выполняется при:
Разложив ее в ряд по
степеням Р, получим:
ос ( р) 1
W x ( p)
х ( р).
1
( р)
ос ( p )
Вx
C ос0 C ос1 p C ос 2 p 2 ... (171)
W x ( p) К х А x ( р)

39.

Коэффициенты ошибок САР
Этот метод оценки точности САР применим как для задающего, так и для возмущающего воздействий.
Если воздействие (управляющее х(t ) или возмущающее f (t ) ) изменяется в установившемся
процессе достаточно плавно и имеет конечное число производных, то ошибку системы можно
представить в виде ряда. Изображение по Лапласу ошибки САР по воздействию можно представить:
( s ) Ф ( s ) ( s ),
передаточная функция для ошибки САР по
Ф ( s) -воздействию
(t ) ;
(s ) - изображение по Лапласу воздействия (t )
(управляющего х(t ) или возмущающего f (t ) ).
Разложив передаточную функцию Ф ( s ) в ряд по степеням s , получим:
i
- ряд, сходящийся при малых s , т. е. в установившемся
( s ) ( 0 si ) ( s ), процессе
изменения y (t ) при заданном (t ) .
i 1 i!
где:
2
d (t )
(t )
d
d 2
....
уст (t ) ( 0 p ) (t ) d o d 1
2
dt
dt
i 1 i!
Переходя к оригиналу, получим:
Величины
i
i
i и называют коэффициентами ошибок системы по соответствующему воздействию.
Они могут быть найдены как коэффициенты разложения передаточной функции для ошибки САР
m
в ряд Тейлора при
0:
s
о [Ф ( s)]s o ,
d Ф ( s )
] s o .
m [
m
ds
Часто удобнее находить коэффициенты d i , которые можно получить в результате деления
полинома числителя на полином знаменателя передаточной функции для ошибки САР.
m
А ( s ) a o a 1 s .... a m s
2
s
Ф ( s )
d o d 1 d 2 s ....
n
b o b 1 s .... b n s
B ( s )
Для САР с астатизмом порядка к
Коэффициенты ошибок: о d o ; i d i i!
0
dФ ( s )
] s o , .....,
1 [
ds
о 1 .... (к 1)

40.

Связь коэффициентов ошибок с коэффициентами инвариантных входов
Коэффициенты i инвариантных входов могут быть получены из коэффициентов ошибок САР
i или d i
сi
.
i!
Они и вводятся для исключения соответствующих составляющих ошибки,
представленной в форме ряда производных от воздействия.
Для управляющего воздействия
До введения комбинированного управления передаточная функция замкнутой САР по задающему
1
воздействию:
W
x (s)
1 Ф x ( s ) 1
1 d хi si
Ф x (s)
1 W x (s)
1 W x (s)
i o
При введении комбинированного управления передаточная функция замкнутой САР по
задающему воздействию: Ф x ( s ) [1
x ( s )]Ф x ( s ) [1 x ( s )](1 Ф x ( s )),
а передаточная функция для ошибки от задающего воздействия:
Ф x ( s) 1 Ф x ( s) 1 [1 x ( s)](1 Ф x ( s)) 1 [1 x ( s )](1 d xi si )
Условие инвариантности САР к воздействию
:
i 0
i
Ф
i
x (s ) 1 [1 x ( s )](1 d xi s ) 0
d xi s
i 0
1
2
i
0
, из которого:
x (s )
xo
x1
x2
(
s
)
i
W
x
1 d xi s
i 0
Для возмущающего воздействия
W f (s)
Передаточная функция САР для ошибки по f (t ) :
d fi si
Ф f ( s )
1 W x ( s ) i o
При введении комбинированного управления по возмущению:
f (s) W x (s) W f ( s )
i
f ( s )(1 d xi s ) d fi si
Ф f ( s )
1 W x ( s)
d fi si
i 0
i o
W f (s)
C fo C f 1 s C f 2 s2 C f 3 s3... i 0
Приравнивая ее 0, получим: f ( s )
W x (s)
1 d xi si
i 0
х(t )
C C s C s ...

41.

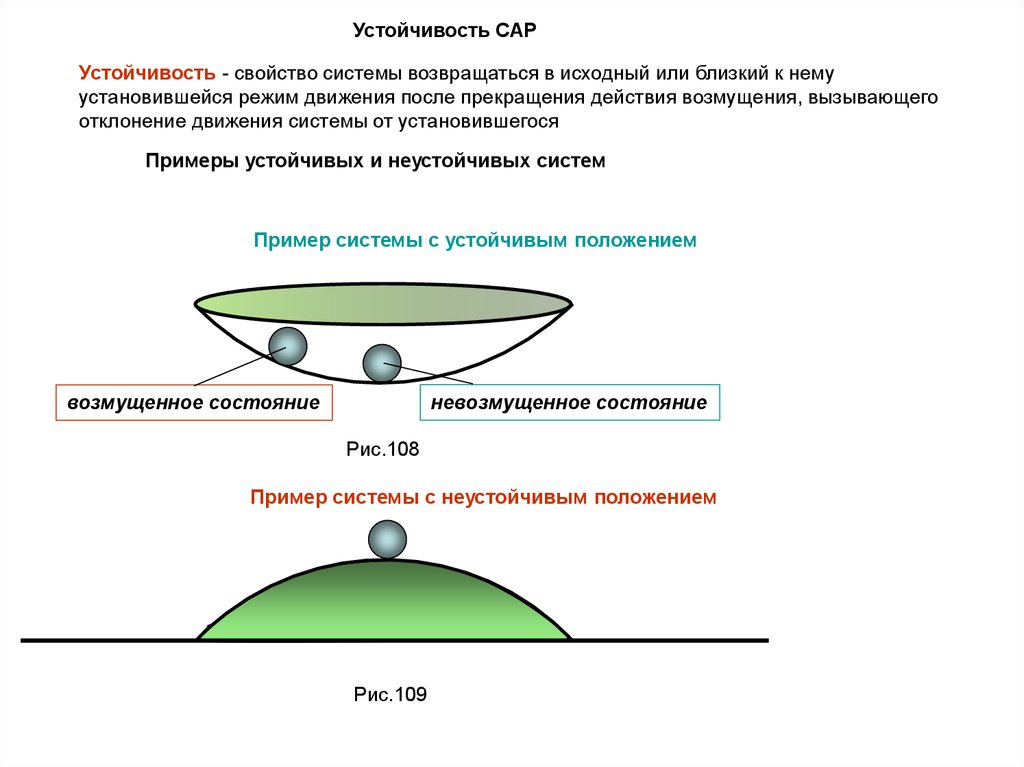
Устойчивость САР
Устойчивость - свойство системы возвращаться в исходный или близкий к нему
установившейся режим движения после прекращения действия возмущения, вызывающего
отклонение движения системы от установившегося
Примеры устойчивых и неустойчивых систем
Пример системы с устойчивым положением
невозмущенное состояние
возмущенное состояние
Рис.108
Пример системы с неустойчивым положением
Рис.109

42.

Система с устойчивым движением
Система с неустойчивым движением
Рис.101
Рис.102

43.

Определение устойчивости на случаи движения систем было введено А.М.Ляпуновым, поэтому
такое понятие называют устойчивостью по Ляпунову.
Систему уравнений, описывающих процессы в оригинале (его математическую модель) можно
представить в форме Каши:
i
(172)
i
d y (t )
F ( y1,....... y n, t ); (i 1,2,.....n) ,
dt
где: yi (t ) - переменные состояния; n- порядок системы;{ y (t ),.., y (t )} Y (t ) - вектор состояния.
1
n
Заданное движение системы характеризуется законом изменения координат y1o (t ),...., y no (t )
и называется невозмущенным движением системы.
Уравнение (172) можно переписать для отклонений
yi (t ) yi (t ) yio (t )
d yi (t )
f i ( y1,......, y n, t ); (i 1,2,.....n) ,
dt
(173)
Уравнения (173) называют уравнениями возмущенного движения, а начальные значения
отклонений yi 0 - возмущениями. При y 0 - невозмущенное движение системы.
i0
Невозмущенное движение системы называется устойчивым, если при всех возмущениях меньших
некоторого значения , отклонения переменных состояния | yi (t ) |будут меньше значений
при t . Обычно это условие записывается так: | y (t ) | при | y | и t .
i
i0
i
i
(
весовые
коэффициенты
для
выравнивания
размерностей
переменных).
i
(i 1,...., n), система называется асимптотически устойчивой.
Если lim yi (t ) 0
t
Графическая иллюстрация для системы второго порядка:
y2
y 20
y10 y
1
устойчивая
y2
y 20
y10 y
1
асимптотически устойчивая
y2
y 20
y10 y
1
неустойчивая

44.

Рассмотрим от чего зависит устойчивость линейной САР
y x (t ) Ф x ( p) x(t ) y f (t ) Ф f ( p) f (t )
A f ( р)
A
x ( р)
(
р
)
.
; Фf
Ф x ( р)
B( р )
В( р )
- передаточные функции системы по
управляющему и возмущающему воздействиям
Раскрывая полиномы, получим уравнения движения САР в операторной форме
где:
n
n 1
m
(bn p bn 1 p ... b1 p 1) y x t (amх p ... a1х p a0 х) х t
n
n 1
r
(bn p bn 1 p ... b1 p 1) y f t (arf p ... а1 f p a0 f ) f t
Решение каждого из этих уравнений можно представить в виде двух составляющих: частного
решения неоднородного уравнения с правой частью, описывающего вынужденный установившийся
процесс в системе, и общего решения однородного уравнения, описывающего переходный процесс в
системе:
y(t) yч (t ) yоб (t ) y уст (t ) yп (t )
Система будет устойчива, когда при
t yп (t ) 0
Найдем эту составляющую, решая уравнение:
n
Его решением является:
n 1
(bn p bn 1 p ... b1 p 1) y x t 0
y п (t ) C i esit
n
, где:
i 1
начальных условий;
Ci - постоянные интегрирования, определяемые из
n
si - корни характеристического уравнения bn s bn 1 sn 1 ... b1 s 1 0 ;
s - комплексная переменная.
Чтобы определить устойчивость САР нет необходимости строить переходный процесс,

45.

Корневой критерий устойчивости
Выясним, какими свойствами должны обладать корни характеристического уравнения (ХУ)
системы, чтобы она была устойчивой.
Корни могут быть вещественными, комплексно-сопряженными или комплексными.
1. Пусть один из корней ХУ системы является:
1.1. Вещественный отрицательный
1 1 , он даст в решении дифф. уравнения
1 , которая при t будет стремиться к 0, т.е. затухать.
составляющую
С1 е
t
С1 е
t
s
1.2. Вещественный положительный 1
1 , которая при
составляющую
С1 еs1t
s
1
t
, даст в решении дифф. уравнения
будет неограниченно возрастать.
С1
t
Рис.103
2. Пусть два корня ХУ системы является комплексно-сопряженными:
2.1. Корни с отрицательной вещественной частью, т.е. 1, 2 1 j .
( j )t
( j )
Они дадут в решении дифф. уравнения две составляющие С1 е 1
С 2 е 1 t , которые,
используя формулы Эйлера и преобразования тригонометрических функций, можно привести к виду:
s
( 1 j )t
С1 е
( 1 j )t
С 2 е
e 1t (C12 sin cos t C12 j cos sin t )]1(t )
e 1t C12 sin( t ),
где введены обозначения:
C1 C 2 C12sin , C1 C 2 C12cos , C12
2 ( C12 C 22 ) ,
arctg C1 C2 ,
C1 C2

46.

Такие две составляющие дают в решении дифф. уравнения гармонику с начальной фазой
1 , которая при
амплитудой
t будет стремиться к 0 (Рис.104).
С1, 2 е
t
2.2. Корни с положительной вещественной частью
дифф. уравнения составляющие
( j )t
С1 е 1
s1,2 1 j
и
дадут в решении
e 1t C12 sin( t ),
и амплитудой С1, 2 е 1t , которая при t
( j )t
С 2 е 1
т.е. гармонику с начальной фазой
будет неограниченно возрастать (Рис.105).
t
Рис.104
Рис.105
2.3. Пара чисто мнимых корней
С1 е
j t
С 2 е
t
j t
s1,2 j дадут в решении дифф. уравнения составляющие
C12 sin( t ),
т.е. незатухающие гармонические колебания.

47.

Система устойчива, если при t переходная составляющая y п (t ) (общее
решение дифференциального
уравнения движения системы) стремиться к 0, т.е. все
n
составляющие
C i esit затухают.
i 1
Проведенный анализ показывает, что необходимым и достаточным условием этого является
отрицательность вещественных частей всех корней характеристического уравнения системы.
Отображая корни ХУ на комплексной плоскости, легко убедиться, что корни с отрицательной
вещественной частью будут находиться слева от оси мнимых.
Корневой критерий устойчивости
Im
можно сформулировать так:
Система устойчива, если все корни ее характеристического
уравнения лежат на комплексной плоскости слева от оси
мнимых, т.е. имеют отрицательные вещественные части.
0
Рис.106
Re
Если хотя бы один вещественный корень или пара
комплексных корней лежат в правой полуплоскости,
система неустойчива.
Границей устойчивости является ось мнимых
Система будет на границе устойчивости, например, при чисто мнимых корнях.
В этом случае в ней будут протекать незатухающие колебания, поэтому ось мнимых называют
колебательной границей устойчивости.
Если вещественный корень равен 0, система тоже находится на границе устойчивости.
Она будет устойчива не относительно регулируемой переменной, а относительно скорости ее
изменения. Такие системы называют нейтрально устойчивыми.

48.

Критерий устойчивости Михайлова
B( p) (bn pn bn 1 pn 1 ... b1 p b0)
Подставляя в полином
где
р j ,
- угловая частота, получим B( j ) U ( ) jV( ) М b ( ) e j ( )
При фиксированной частоте это вектор на комплексной плоскости, а при изменении частоты от 0 до
конец вектора начертит кривую, которая называется кривой или годографом Михайлова.
По виду этой кривой и можно судить об устойчивости системы.
Если при изменении
от 0 до
полное приращение аргумента ( фазы)
( ) n ,
2
характеристический полином B( р ) не имеет корней в правой полуплоскости, и
следовательно система устойчива.
n
Докажем это. Представим характеристический полином в виде:
n
i
n
где: pi - корни уравнения
i 1
B ( j ) b n ( j p i )
Подставляя р j , получим:
i 1
Рассмотрим каждый сомножитель на комплексной плоскости при изменении частоты от 0 до
.
2. pi i
1. pi i
B( p) b ( p p )
B( p) 0
Vi
2
1
V
i
1
2
( 1)
0
( 1)
0
i
Рис.103
Ui
i
Ui
Рис.104

49.

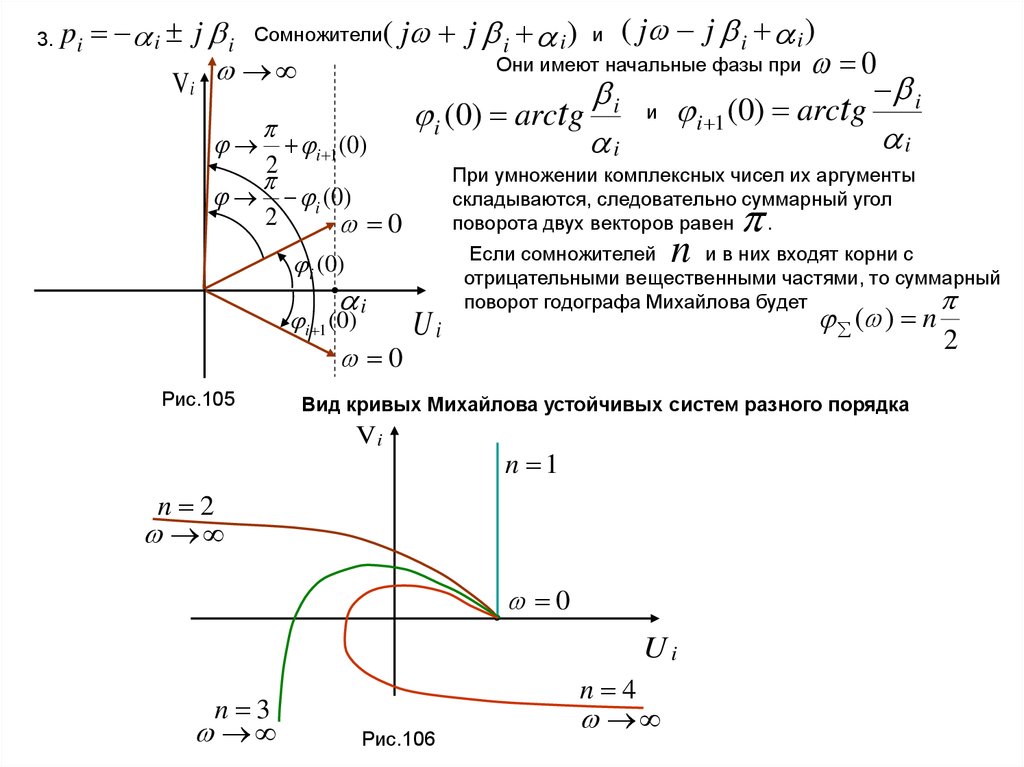
3.
pi i j i Сомножители( j j i i ) и ( j j i .i )
Они имеют начальные фазы при 0
Vi
i 1 (0)
2
i (0)
2
0
i
i (0) arctg
i
i
0
Рис.105
i 1 (0) arctg
n
Ui
Если сомножителей
и в них входят корни с
отрицательными вещественными частями, то суммарный
поворот годографа Михайлова будет
( ) n
2
Вид кривых Михайлова устойчивых систем разного порядка
Vi
n 1
n 2
0
Ui
n 3
i
При умножении комплексных чисел их аргументы
складываются, следовательно суммарный угол
поворота двух векторов равен
.
i (0)
i 1 (0)
и
i
Рис.106
n 4

50.

Вид кривых Михайлова неустойчивых систем разного порядка.
(при различном числе корней с положительной вещественной частью)
При наличие корней характеристического уравнения с положительной вещественной частью
приращение аргумента при изменении частоты от 0 до
будет ( ) 0.5n
Если корней
и среди них
корней с положительной вещественной частью, то суммарный
поворот годографа Михайлова будет:
(n m) m n m
n
m
2
2
2
При четном количестве корней с положительной вещественной частью кривая будет начинаться (
)
справа
0 от оси мнимых на nвещественной оси, т.к. свободный член характеристического комплекса
будет положительным.
B ( j ) b n ( j p i )
i 1
При нечетном количестве корней с положительной вещественной частью кривая будет начинаться (
)
слева
0от оси мнимых на вещественной оси, т.к. свободный член характеристического комплекса
будет отрицательным.
Рассмотрим различные случаи:
Vi
1. n 2, m 1 2 0.5 1 0
2. n 3, m 1 3 0.5 1 0.5
1
3. n 3, m 2 3 0.5 2 0.5
4. n 4, m 2 4 0.5 2 0
0
0
г
Ui
Для систем на границе устойчивости
5. n 4, pi ,i 1 j г
6. n 4, pi 0
4
2
Рис.107
3
6
5

51.

Можно не строить кривую, а искать частоты, соответствующие точкам пересечения с осями,
т.е. корни приравненных нулю вещественной и мнимой частей характеристического комплекса.
B( j ) U ( ) jV( )
Ui - частоты, соответствующие пересечению кривой с осью мнимых;
Vi - частоты, соответствующие пересечению кривой с осью вещественных.
V( ) 0
Для устойчивых систем частоты Ui и Vi должны чередоваться, т.е.
0 V1 U1 V2 U2 V3 U1 ....
U ( ) 0
Например, для систем 3-го порядка характеристический комплекс:
3
2
(
j
(
j
b1 j b0 U ( ) jV( )
)
)
b2
B( j ) b3
U ( ) b0 b2 2 0
Корни:
Отсюда
V1 o;
b0
U1
b2
Для устойчивой САР
b0 b3
V( ) b1 b3 3 0
b0
U1
b2
b1
V2
b3
b1
V2
b3
b1 b2
Это соответствует основному условию устойчивости САР по критерию Гурвица.

52.

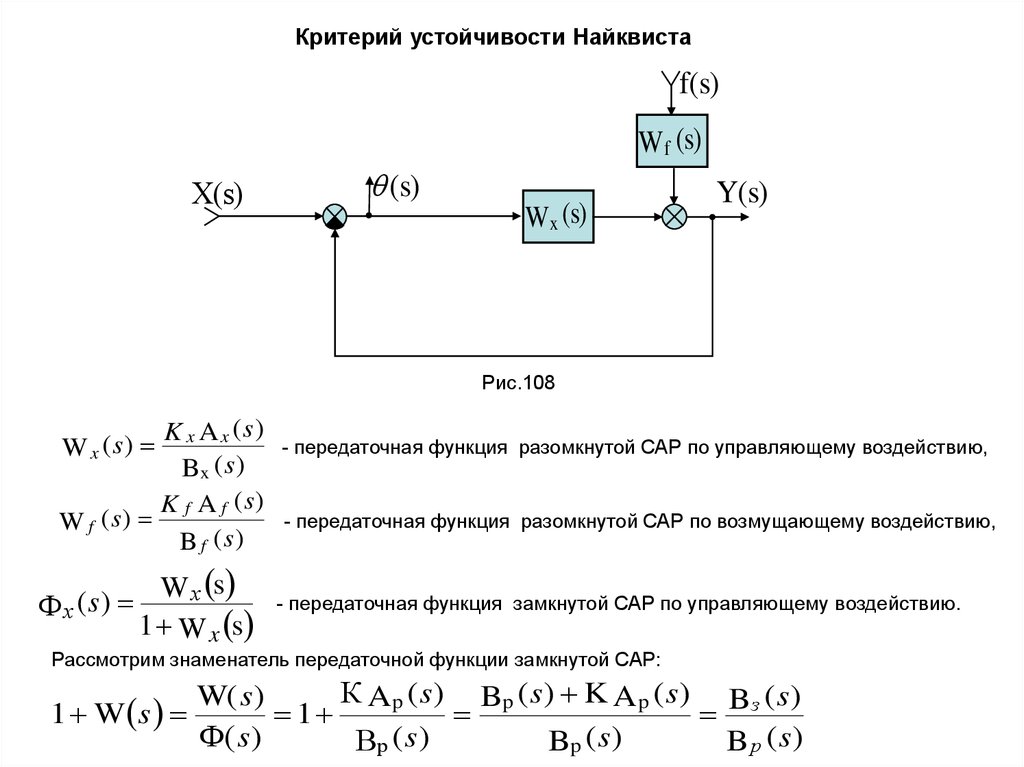
Критерий устойчивости Найквиста
f(s)
Wf (s)
Х(s)
(s)
Wx (s)
Y(s)
Рис.108
K x A x (s)
(
s
)
Wx
Bx ( s )
K f A f (s)
(
s
)
Wf
B f (s)
W х s
(
s
)
х
1 W x s
- передаточная функция разомкнутой САР по управляющему воздействию,
- передаточная функция разомкнутой САР по возмущающему воздействию,
- передаточная функция замкнутой САР по управляющему воздействию.
Рассмотрим знаменатель передаточной функции замкнутой САР:
К A p ( s ) Bp ( s ) K A p ( s ) Bз ( s )
W( s )
1 W s
1
Ф( s )
Вр ( s )
Bp ( s )
B р (s)

53.

j , получим характеристический комплекс замкнутой САР в виде:
К х A хp ( j ) Bхp ( j ) К х A хp ( j ) Bз ( j )
W
x ( j )
1 W x j
1
Ф х ( j )
Вхр ( j )
Bхp ( j )
B р ( j )
Построим АФЧХ разомкнутой САР с W x ( j ) и АФЧХ комплекса 1 W x j .
Заменяя S на
Для этого представим частотную передаточную функцию разомкнутой САР в виде мнимой и
действительной части или в виде модуля и аргумента:
Wx ( j ) U ( ) jV( ) M( ) e j ( )
1 Wx j 1 U( ) jV( ) 1 M( ) e j ( )
При изменении частоты от 0 до нанесем на комплексной плоскости точки в соответствии
Аналогично представим комплекс
с этими выражениями. Их совокупность и будет представлять АФЧХ разомкнутой САР и комплекса.
АФЧХ комплекса это АФЧХ разомкнутой САР, смещенная на 1 вдоль оси действительных.
Im
1
Im
0
0
( )
М( )
К
Рис.109 АФЧХ разомкнутой САР
Re
0
0
К 1
1
Re
Рис.110 АФЧХ комплекса 1 W x
j .
Используя критерий Михайлова, сформулируем необходимые и достаточные условия устойчивости
замкнутой САР по виду АФЧХ разомкнутой САР.

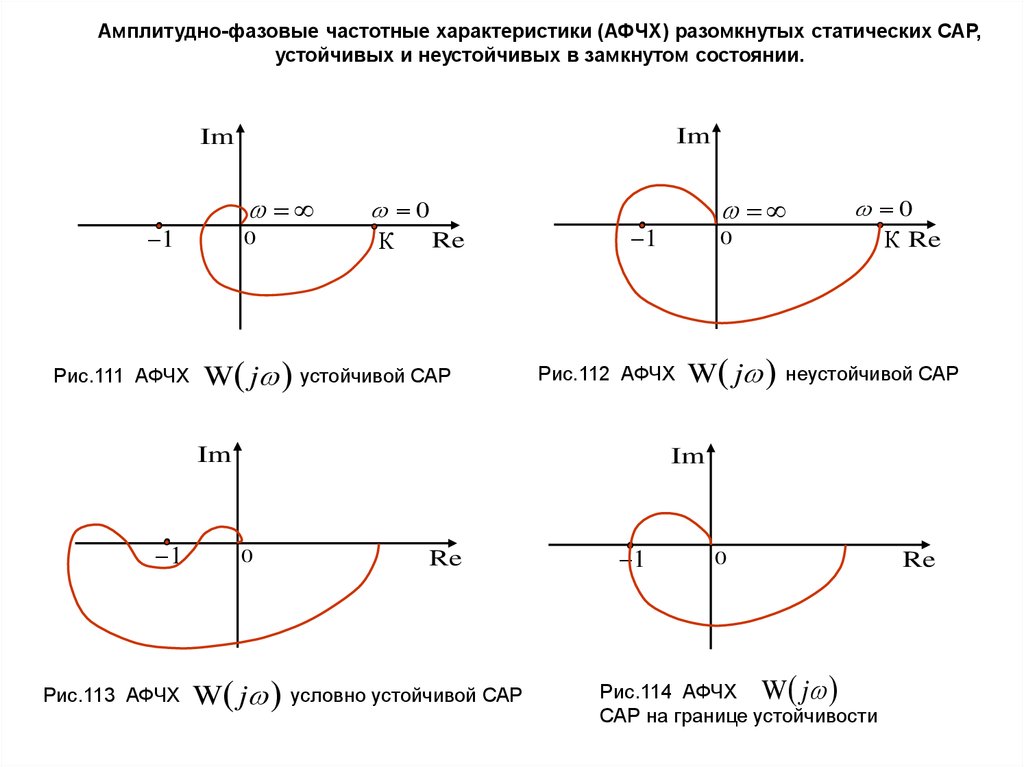
54.

Амплитудно-фазовые частотные характеристики (АФЧХ) разомкнутых статических САР,
устойчивых и неустойчивых в замкнутом состоянии.
Im
Im
1
Рис.111 АФЧХ
0
0
Re
К
W j устойчивой САР
1
Рис.113 АФЧХ
0
К Re
0
Рис.112 АФЧХ
Im
1
W j
неустойчивой САР
Im
0
W j
Re
условно устойчивой САР
1
0
Re
Рис.114 АФЧХ W j
САР на границе устойчивости

55.

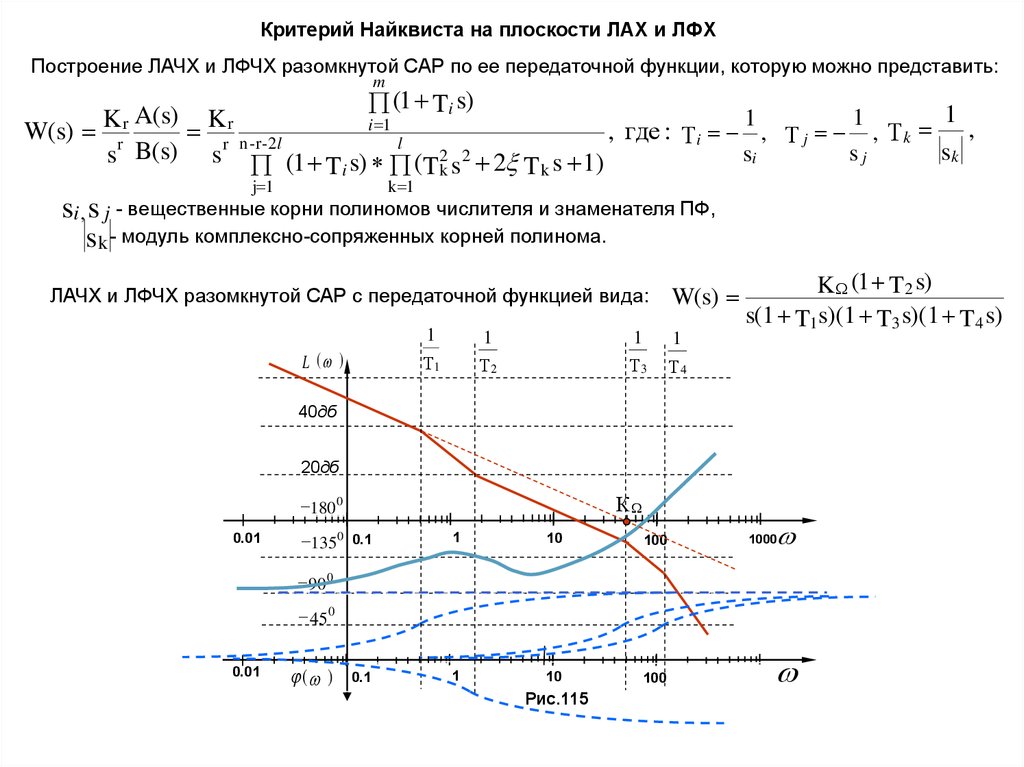
Критерий Найквиста на плоскости ЛАХ и ЛФХ
Построение ЛАЧХ и ЛФЧХ разомкнутой САР по ее передаточной функции, которую можно представить:
m
(1 Ti s)
1
1
1
K
K
r A(s)
r
i 1
,
W(s) r
r n -r -2l
,
где
:
,
,
Т
k
Тj
Тi
l
sk
sj
si
s B(s) s (1 T s) (T 2 s2 2 T s 1)
i
k
k
j 1
k 1
si , s j - вещественные корни полиномов числителя и знаменателя ПФ,
sk - модуль комплексно-сопряженных корней полинома.
ЛАЧХ и ЛФЧХ разомкнутой САР с передаточной функцией вида:
L ( )
W(s)
1
1
1
1
Т1
Т2
Т3
Т4
K (1 T 2 s)
s(1 T1 s)(1 T3 s)(1 T 4 s)
40дб
20дб
К
180 0
0.01
1350 0.1
1
10
100
1
10
100
1000
90 0
45 0
0.01
( )
0.1
Рис.115

56.

Использование для формирования критериев качества
функционалов на переходной характеристике САР.
у х (t) 3
2
хз
п
y( )
1 у max
Тн3Т н2
Т п1 Т п2
t
Тп3
Рис.116
Быстродействие САР определяется временем переходного процесса Т п .
Т п - время от начала действия воздействия до значения времени, после которого ошибка САР
| х (t ) | | y(t ) y( ) | п при t Tп
Обычно назначают п 0,05 y ( )
Запас устойчивости САР характеризуют величиной перерегулирования, отношением соседних
перерегулирований или их числом до достижения значения 0,05%.
Перерегулированием называется величина:
| y max y ( ) |
%
100%
y ( )
Если % (10 30)%, а число перерегулирований 2-3, в большинстве случаев запас
устойчивости достаточен. Иногда допускают % (40 50)%, а число перерегулирований 4.
Используются также интегральные критерии, например:
I | y (t ) y ( ) |dt
0

57.

Корневые критерии качества
Im
Im
i
i
0
Рис.117
Ближайший к оси мнимых корень
рi i
Составляющая в переходном процессе этого
i t
корня:
yi (t ) C i e
yi (Т п) C i ( 0,05) ,
1 1
Т п lп
i
При 0,05
1
1
3
lп
Тп
i 0,05 i
Назначив
найдем:
0
Re
Re
Рис.118
Ближайший к оси мнимых корень
рi i j
Составляющая в переходном процессе этих корней:
yi (t ) C i e it sin( t )
Положив
yi (Т п) C i ( 0,05)
sin( t ) 1
Тп
При
1
i
0,05
и
, получим:
1
1
1
3
lп
Тп
i 0,05 i
lп
Величина
называется степенью устойчивости, которая определяет быстроту затухания
переходного процесса в САР.

58.

i
i
Отношение
называется колебательностью.
yi (t ) C i e it sin( t )
t t1 амплитуда равна:
Пара комплексно сопряженных корней дают составляющую
Оценим зетухание амплитуды колебаний за период. При
Через период
Величину
Т
t
С1 C e i 2
2
2
i (t1 )
С2 C e
C1 e C1 e
2
C
1 C2
1 C 2
C1
C1
Подставляя выражения для
С1
и
называют затуханием за период.
С 2 , получим:
1 e
В САР затухание за период должно быть не менее 90%. При
2
, откуда:
0,9 2,72
2
1
ln
1
При заданной колебательности на плоскости корней характеристического уравнения возникает
запретная область, границей которой являются два луча с углом наклона:
i
arctg arctg
i
Im
i
0
Re

59.

Запас по фазе и амплитуде
М 2
1
М 1
Запретная
-1
2
-1
область
Рис.116
L1 20 lg
1
М 1
м 1
L 2 20 lg М 2
Амплитудно - частотная характеристика замкнутой системы
Ф(j )
а
1
0,707
1
2
0
Мmax
М
р с п э
Рис.117
Показатель колебательности – отношение максимального значения модуля частотной передаточной
функции замкнутой системы к модулю на частоте равной 0
M
Ф(j ) max
Ф(0)
M max
1

60.

Отображение показателя колебательности на плоскости АФЧХ разомкнутой системы
W( j )
| const
M | Ф j | |
1 W( j )
W j U( ) jV( ) M( ) e j ( )
2
V2
U
M
1 U( ) 2 V2
2
V2 M 2 U2 V2
1
U
М
2
2
2
2
2
2
M 2U M U (M 1) V (M 1) 0
2
4
4
2
2 U M 2
M
M
M
2
V
2
U
2
2
2
M 1
M2 1
M2 1 M 1
2
U C 2 V2 R 2
R M
2
M 1
2
C M
2
M 1
- уравнение окружности с радиусом R
и смещением по оси вещественных на
C

61.

Отображение показателя колебательности на плоскости АФЧХ
М=1
Im
М=0.83
М=1.2
М=0.77
М=1.3
М=0.67
М=1.5
М=0.5
М=0.25
М=2
М=4
0
-1
W(j )
Рис.118
Re

62.

Cвязь показателя колебательности с запасами устойчивости
системы по амплитуде и фазе
М
М -1
Im
R
М
М 1
М=const
M
M 2 1
2
М
С
M 2 1
C
01
-1
R
0
Re
Мр
D
90
arcCos
M 2p C
Рис.119
о
60 о
М=1.2
2M pC
M 2 1
1
arcCos
max arcCos
M
C
M
M p max C
M 2 1
М=1.5
М=1.3
М=2
30 о
-4
0
8
4
Рис.120
12
16 дб

63.

Отображение требуемого запаса по фазе на плоскости
логарифмических характеристик
При каждом показателе колебательности M Const , запретная область может быть нанесена
на плоскости логарифмических характеристик разомкнутой системы.
К
W(s)
Пусть разомкнутая САР имеет, например, передаточную функцию
2
S(b2 S b1S 1)
Ее характеристики построены на Рис.141.
М
M
Для диапазона модуля
М р М 1 найдем границы в логарифмическом масштабе:
М 1
М
М
L1 (M) 20 lg М - 1 и L2 (M) 20 lg М 1 - границы диапазона в дб.
Используя
кривые, построим запретную область для фазовой характеристики.
L ( )
1
1
Т1
Т2
40дб
20дб
L1 (М)
180 0
0.01
1350
0.1
1
10
L2 (М)100
0.1
1
10
100
1000
90 0
45 0
0.01
( )
Рис.141

64.

Отображение показателей качества САР на
плоскости логарифмических характеристик
Основные показатели качества САР: точность в установившихся типовых режимах работы, запасы
по амплитуде и фазе, быстродействие, могут быть отображены на плоскости логарифмических
характеристик разомкнутой системы. Это позволяет сформулировать требования к ЛАХ и ЛФХ
разомкнутой системы, обеспечивающих после замыкания требуемые показатели САР.
Рассмотрим точность в типовых установившихся режимах.
Обычно она задается в виде ошибки m САР при воспроизведении ею заданных максимальных
скоростей m и ускорений m или заданного гармонического воздействия с амплитудой Х m и
эквивалентной частотой к. Последний может быть представлен: Х (t ) X m
к
Sin
Xm
Ошибку САР при гармонического воздействии представим: m Ф ( j к ) X m
1 W(j k )
Xm
X
m
Т.к. m X m , то W( j к ) 1 и m
W( j к )
W(j k )
m
х
Это выражение позволяет отобразить требования по
точности на плоскость ЛАХ.
L ( )
L( k ) 20lg W( j к ) 20lg Xm
Ордината контрольной точки Ак, ниже которой не
должна проходить ЛАХ при к
40дб
m
m
m
С другой стороны для гармоники к
,а Хm
m
m
Если m const, а m уменьшать, то к , а Х m ,
2
получим для Ак прямую с наклоном -20дб/дек,
Если m const , а m уменьшать, то к , а Х m
2
пропорционально m, для Ак получим прямую -40дб/дек
К m m - добротность САР по скорости.
К m m - добротность САР по ускорению.
о К - называется базовой частотой.
L ( k )
20дб
180 0
Ак
Запретная
область по
точности
1350 0.1
1
к
10 о
К
100
К
90 0
45 0
( )
0.1
1
10
Рис.142
100

65.

Отображение требуемых запасов устойчивости
Запасы устойчивости удобно задавать в виде показателя колебательности М.
Для обеспечения запасов устойчивости при начальном наклоне ЛАХ -40дб/дек пересечение оси частот
должно проходить под наклоном -20дб/дек., а после пересечения наклон ЛАХ может быть и больше.
В ТАУ показано, что при заданном М можно рассчитать Т2 и Т3 для ЛАХ такие, что фазовая АФЧХ не
будет заходить в окружность, соответствующую М, а ЛФХ в запретную область для такого М.
1 М(М - 1)
1
М
Т
3
Т
2
- При привязке к базовой частоте
о М 1
о М -1
ср
- При привязке к частоте среза (
L ( )
2
о
Т 2)
М
Т2
ср М - 1
Т3
1
1
1
1
Т1
Т2
Т3
М
ср М 1
1
1
Т4
Границы диапазона
изменения модуля при
заданном М в дб.
М
40дб
20дб
180 0
0.01
1350
L1 (M) 20 lg М - 1 и
Ак
Запретная
область по
точности
0.1
1
0.1
1
М
L2 (M) 20 lg М 1
L1 (М)
к
о
СР
10
100
L2 (М) 1000
10
100
90 0
45 0
0.01
( )
Рис.143

66.

Желаемые ЛАХ разомкнутой системы
Отображая показатели качества на плоскости логарифмических характеристик разомкнутой САР,
мы формируем требования к ЛАХ разомкнутой системы, которая при замыкании обеспечит
требуемые показатели качества замкнутой САР.
Построенные с учетом требуемых показателей качества логарифмические характеристики
разомкнутой САР называются желаемыми.
Их различают по виду: 1-2; 2-1-2; 1-2-1-2; 2-1-2-3 (1- наклон ЛАХ -20дб/дек; 2- наклон -40дб/дек и т.д.)
L ( )
1
1
1
1
Т1
Т2
Т3
Т4
40дб
Ак
20дб
180 0
0.01
1350
0.1
1
0.1
1
к
СР К
10
100
1000
10
100
1000
о СР
90 0
45 0
0.01
45
0
( )
Рис.144
К

67.

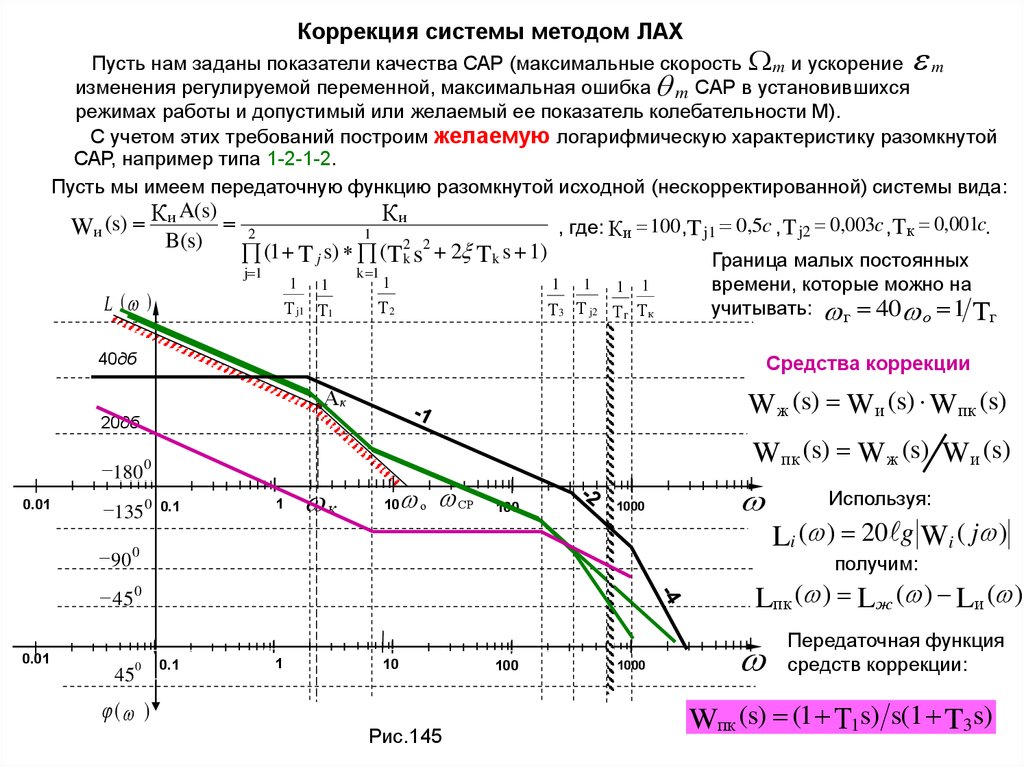
Коррекция системы методом ЛАХ
Пусть нам заданы показатели качества САР (максимальные скорость m и ускорение m
изменения регулируемой переменной, максимальная ошибка m САР в установившихся
режимах работы и допустимый или желаемый ее показатель колебательности М).
С учетом этих требований построим желаемую логарифмическую характеристику разомкнутой
САР, например типа 1-2-1-2.
Пусть мы имеем передаточную функцию разомкнутой исходной (нескорректированной) системы вида:
W и (s)
Ки A(s)
B(s)
Ки
2
1
j 1
k 1
2 2
2
k
(1 T j s) (T s
1
L ( )
1
Т j1 Т1
T k s 1)
, где: К и 100,T j1 0,5c , T j2 0,003c , Tк 0,001c.
1
1
Т2
Т 3 Т j2 Т г Тк
1
1
1
Граница малых постоянных
времени, которые можно на
учитывать: г 40 о 1 Тг
Средства коррекции
40дб
Wж (s) Wи (s) Wпк (s)
Ак
20дб
Wпк (s) W ж (s) Wи (s)
180 0
0.01
1350
0.1
1
к
10
о СР
100
1000
90 0
45
0
( )
Li ( ) 20 g Wi ( j )
получим:
Lпк ( ) Lж ( ) Lи ( )
45 0
0.01
Используя:
0.1
1
10
Рис.145
100
1000
Передаточная функция
средств коррекции:
Wпк (s) (1 Т1s) s(1 T3 s)