2.55M

Category:

physics

Гауссовский пучок

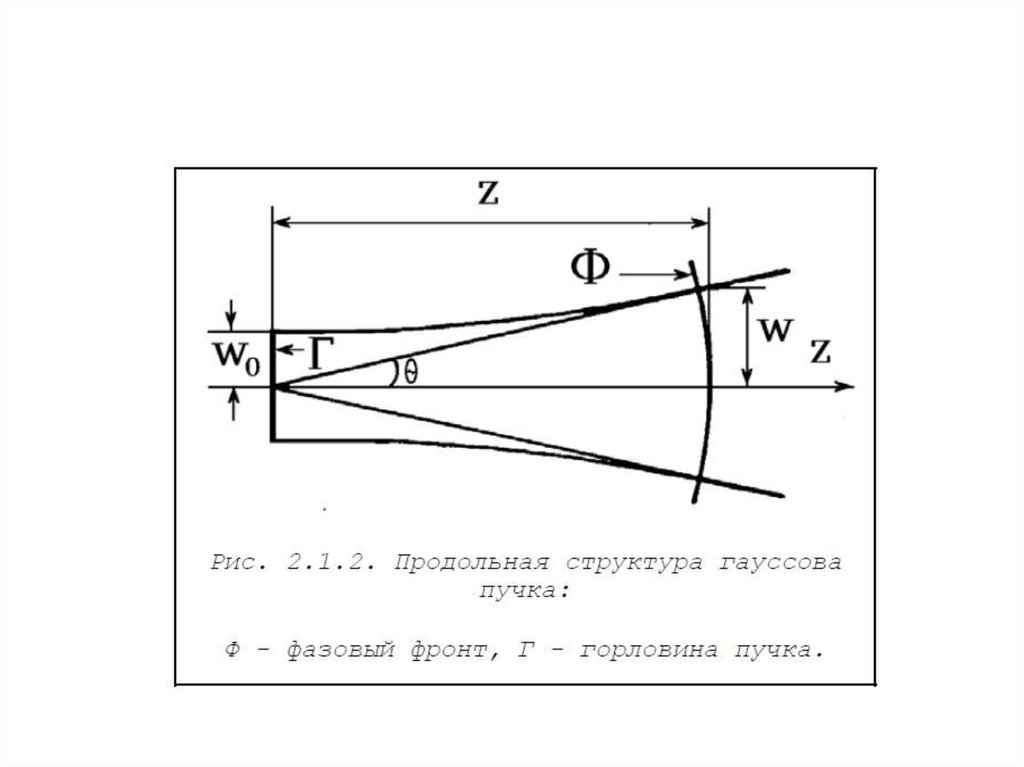
1. Гауссовский пучок

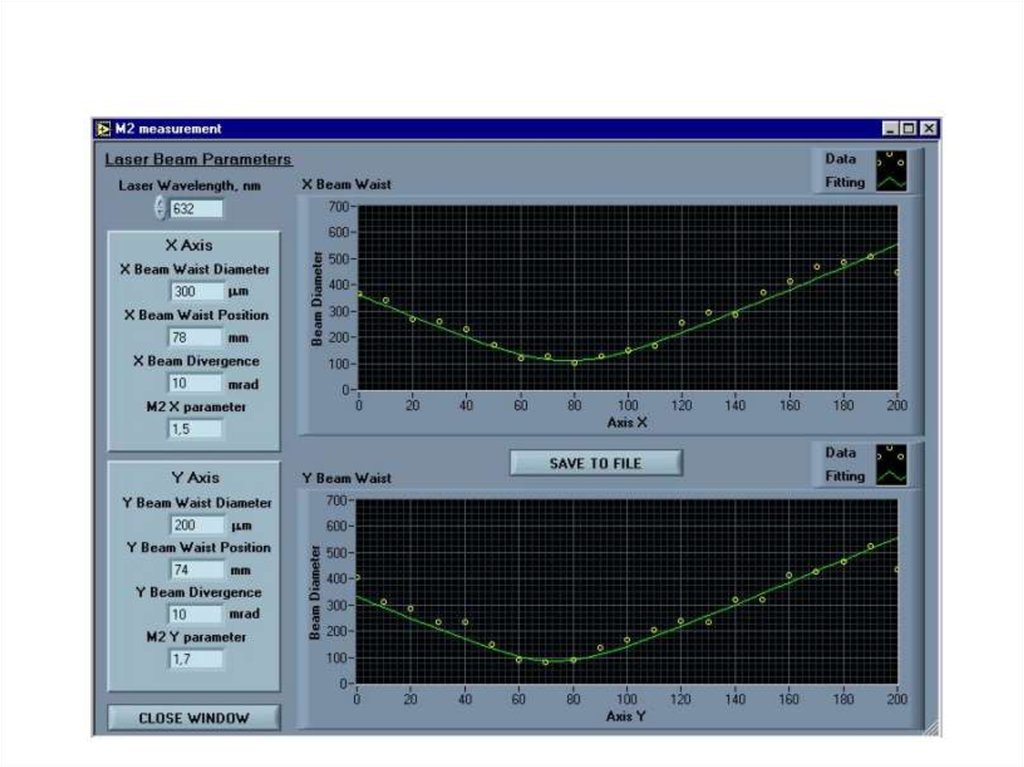
16. Измерения характеристик лазерных пучков

• ГОСТ Р ИСО 11146-1-2008
• М2 - параметр для количественной оценки качества пучка
лазерного луча.
Параметр М2, также называемый параметром качества пучка
или параметром распространения пучка, это общепринятая
величина для определения оптического качества лазерного
пучка. Согласно ISO Standard 11146, она определяется как
отношение BPP к λ / π, последнее является BPP для
дифракционно- ограниченного Гауссова пучка той же длины
волны. Другими словами, половина угла расходимости пучка
это:

17.

• D4σ or second moment width
The D4σ width of a beam in the horizontal or vertical direction is 4
times σ, where σ is the standard deviation of the horizontal or vertical
marginal distribution, respectively. Mathematically, the D4σ beam width
in the x-dimension for the beam profile is expressed as

18.

ВРР ( beam parameter product - произведение параметров пучка),
определяется как произведение диаметра пучка в перетяжке на
полный угол раходимости излучения (мм мрад).

19. Проведение измерений

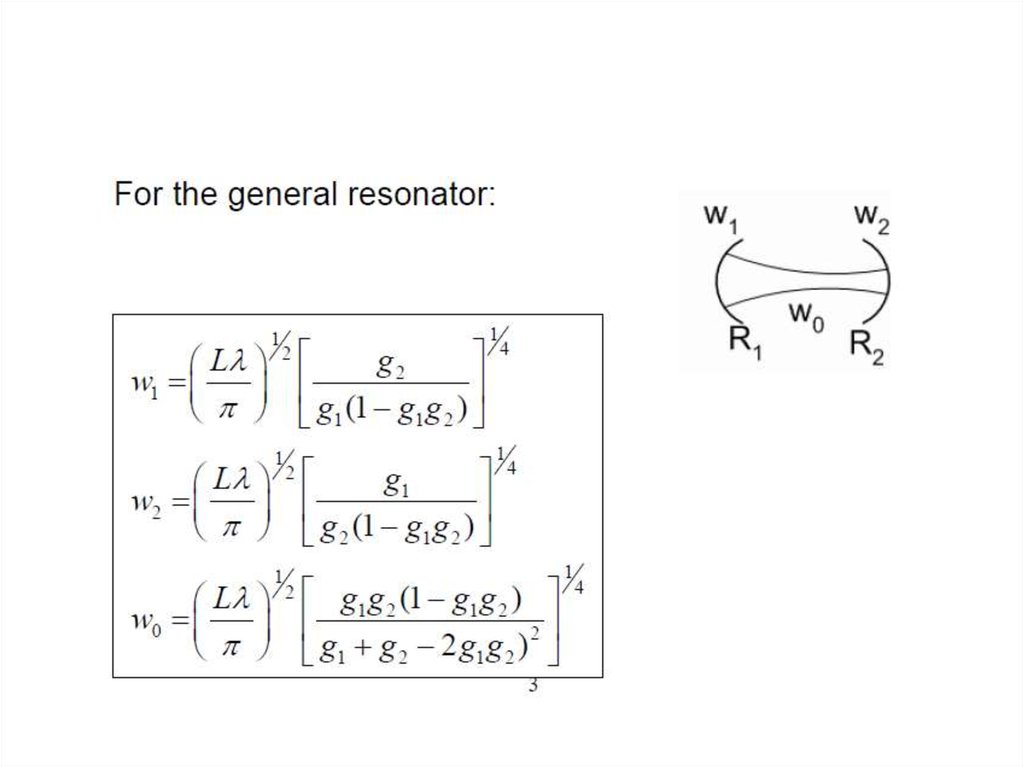
20. 21. Собственные моды резонатора

22.

23.

24.

25.

26.

27.

28.

29. 30. Higher-Order Modes - HG

-4
-4
-4
Higher-Order Modes - HG
2
10
1.5
5
750
500
250
80
60
1
-4
-2
0.5
-2
100
2
4
-5
2
4
-2
20
-4
-10
1
-4
40
-2
2
1
2
0.5
1
4
-250
-500
-750
-4
0.4
-2
2
4
-2
0.6
0.4
0.2
2
4
-4
-2
2
-x /2
2
4
-4
-2
2
4
-2
-4
-2
25
4
15
2
10
1
-4
-2
5
2
3
Hn(x) e
20
3
4
2
30
5
2
2
Hn(x)
2
-1
1.4
1.2
1
0.8
0.6
0.4
0.2
0.8
1
-4
-1
1
-2
4
-0.5
0.2
-2
2
4
Hn(x) e
4
0.8
0.6
2
4
-4
-2
2
4
4
2
-x /2

31. Hermite-Gaussian modes

HG 0,0
0.003
0.003
0.002
0.002
0.001
0.001
HG 1,0
0
-0.001
-0.001
-0.002
-0.002
-0.003
-0.003
-0.002
-0.001 0
0.0010.0020.003
0.003
0.0010.0020.003
0.001
0.001
0
0
-0.001
-0.001
-0.002
-0.002
-0.003
-0.003
-0.002
-0.001 0
-0.003
-0.003
-0.002
-0.001 0
0.003
0.002
0.002
HG 6,1
0
0.0010.0020.003
-0.003
-0.003
-0.002
-0.001 0
0.0010.0020.003

32. Using Gaussian Decomposition

At slit
0.4mm
20cm away
4mm

33. Laguerre-Gaussian modes

34. Resonant Frequency

35. Boundary Conditions in Resonator

Whole number of wavelength in full round
trip i.e. whole number of half wavelengths
between mirrors
2kL=q2π
i.e. fq = q c / (2 L)
For opt freq. modes q ~105, relative spacing is small

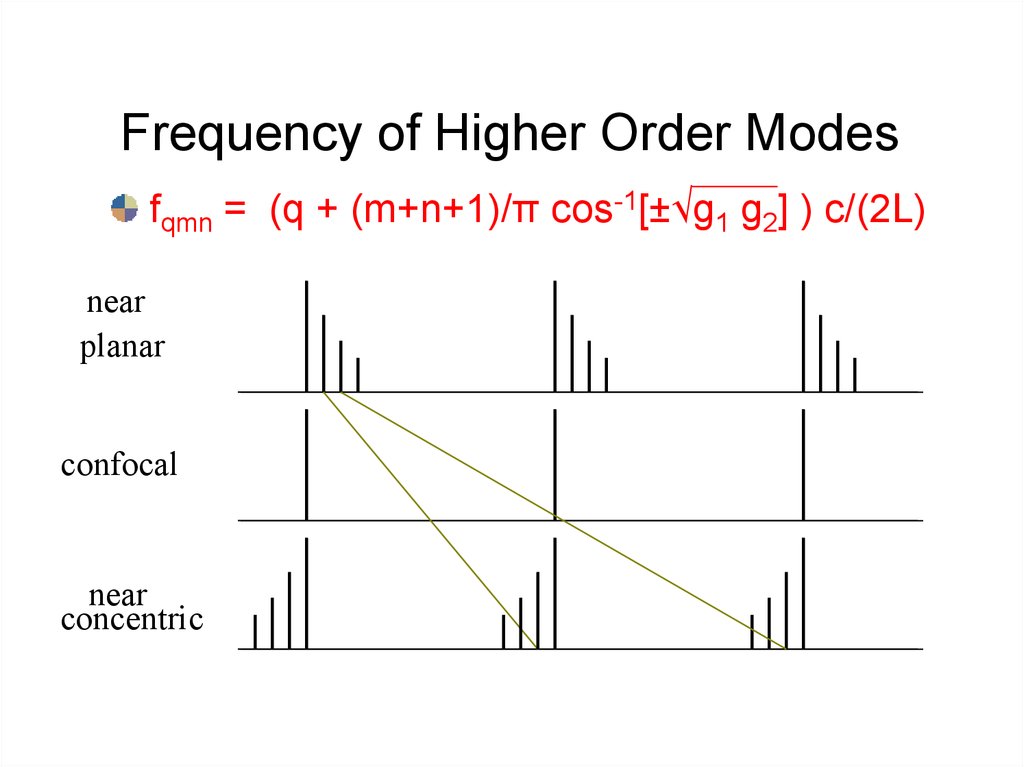
36. Frequency of Higher Order Modes

fqmn = (q + (m+n+1)/π cos-1[±√g1 g2] ) c/(2L)
near
planar
confocal
near
concentric

37. Laguerre-Gaussian modes

38. Frequency of Higher Order Modes