Similar presentations:
Матрицы: элементарные преобразования строк, приведение к ступенчатому виду и виду Гаусса. Ранг матрицы
1.
Лекция N2Тема:
Матрицы: элементарные
преобразования строк, приведение к
ступенчатому виду и виду Гаусса.
Ранг матрицы
1
2.
Опр. 1 Элементарными преобразованиямистрок матрицы называются:
1) Перестановка местами двух строк
2) Замена строки суммой этой строки и
некоторой другой, умноженной на
число
3) Умножение строки на ненулевое
число
2
3.
Аналогично вводятся элементарныепреобразования столбцов.
Опр.2 Опорным элементом строки
называется первый слева ненулевой
элемент этой строки.
3
4.
Пример. 12 3
0
2
3
A
0 0 4
0 0 0
1 2 4 – опорные
элементы
У нулевой строки опорного элемента нет
4
5.
Опр. 3 Матрица называетсяступенчатой, если опорный элемент в
каждой последующей строке
расположен правее, чем в предыдущей.
Если строка нулевая, то все
последующие строки также нулевые.
5
6.
Пример.1
0
A 0
0
0
2 3 4
2 4 5
0 1 4
0 0 3
0 0 0
6
7.
Опр. 4 Матрица имеет вид Гаусса, если1) она ступенчатая
2) все опорные элементы равны
единице
3) над опорными элементами только
нули
7
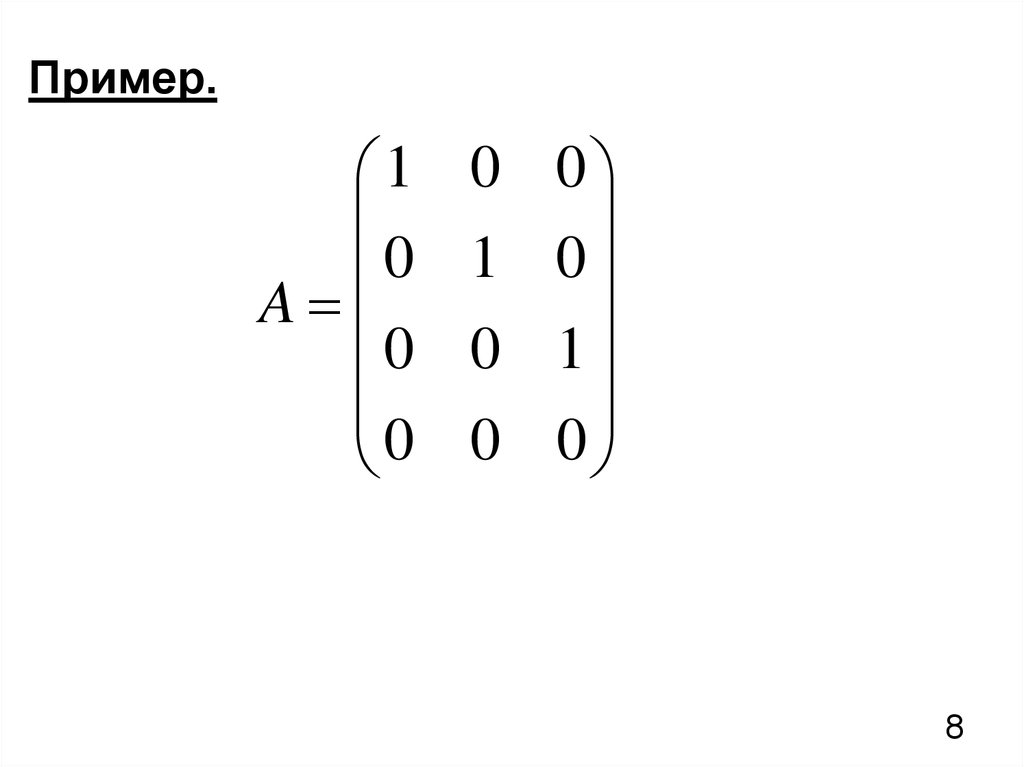
8.
Пример.1
0
A
0
0
0 0
1 0
0 1
0 0
8
9.
Теорема 4 Любая матрица может бытьприведена к ступенчатому виду с
помощью элементарных
преобразований.
Опр. 5 Строки и столбцы матрицы, в
которых расположены ее опорные
элементы, называются базисными.
9
10.
Опр. 6 Рангом матрицы называетсячисло ненулевых строк в ступенчатом
виде матрицы.
Обозначается
r ( A).
Пример.
Привести матрицу к ступенчатому виду
и найти ранг.
10
11.
11
A
3
0
1 2 + -3
1 1 2
2 3
0
3
1
0 2 10
1 4
2 1
0 2 1
1 1 2
0
1
5
0 3 1
0 2 1
1
2
1 1 2
3 2
0
1
5
0 0 16 161
1
0 0 11
11
11
12.
1 1 20
1
5
0 0 1
0 0 1
1 1 2
0 1 5
.
0 0 1
-1
0 0 0
r ( A) 3
12
13.
Решение систем линейных уравнений.Метод Гаусса
Пример.
x y z 3,
2 x y z 1,
x y z 1.
13
14.
1) Составим расширенную матрицысистемы
1 1 1 3
A | b 2 1 1 1 .
1 1 1 1
14
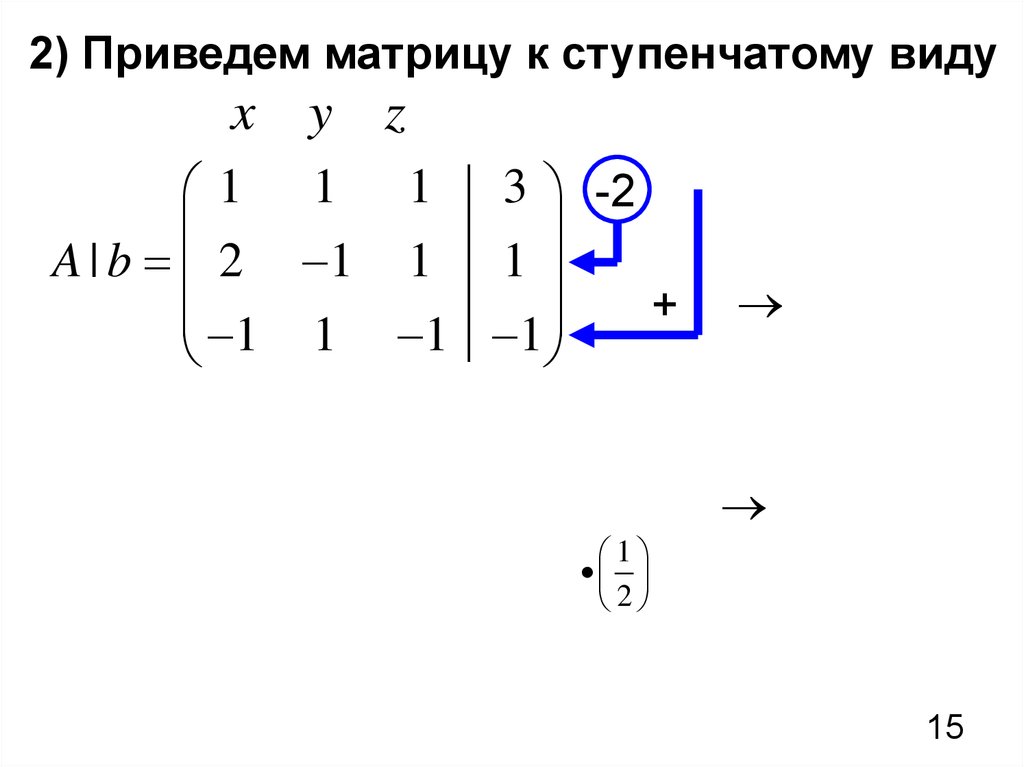
15.
2) Приведем матрицу к ступенчатому видуx
1
A|b 2
1
1
0
0
y z
3 -2
1 1 1
+
1 1 1
1 1 3
3 1 5
1
2 0 2 2
1
1
15
16.
xy z
1 1 1 3
0 3 1 5
0 1 0 1
x z
y
1 1 1 3
0 1 3 5 . r ( A) r ( A | b) 3
0 0 1 1
16
17.
3) Составим новую системуx z y 3,
z 3 y 5,
y 1.
x 0;
z 3 5; z 2;
y 1;
Система имеет единственное решение
Можно было продолжить преобразования,
и привести систему к виду Гаусса.
17
18.
Теорема Кронекера-Капелли.1) Если r ( A)
имеет решения
r ( A | b) , то система не
2) Если r ( A) r ( A | b) n , где n число неизвестных, то система имеет
единственное решение
3) Если r ( A) r ( A | b) n , то система
имеет бесконечное множество решений.
18
19.
ПримерыПример 1. Исследовать на совместность
и решить систему методом Гаусса.
x 2 y 4,
5 x 10 y 20.
1 2 4
1 2 4 -5
A|b
0 0 0
5 10 20
r ( A | b) r ( A) 1 2
n 2
19
20.
Система имеет бесконечное множестворешений. Найдем число свободных
неизвестных k n r 2 1 1.
Базисная неизвестная
x , свободная y .
x 2 y 4.
Обозначим свободную неизвестную y c.
Получим x 4 2c.
Ответ: (4 2c, c) , где c ( , ).
20
21.
В этом примере система имеетбесконечное множество решений.
Запишем некоторые из них:
c 0 (4;0);
c 1 (2;1).
Все решения являются точками прямой
x 2 y 4.
y
2
4
x
21
22.
Пример 2. Исследовать на совместностьи решить систему методом Гаусса.
x 2 y 3 z 2,
x 5 y z 0,
2 x 3 y 2 z 1.
1 2 3 4 -1 -2
A | b 1 5 1 0
2 3 2 1
22
23.
31 2
0 7 4
0 7 4
3
1 2
0 7 4
0 0
0
2
2 -1
5
r ( A) 2;
2
r ( A | b) 3;
2 .
r ( A) r ( A | b)
3
Система несовместна (по теореме
Кронекера-Капелли)
23
24.
Мы рассмотрели два метода решениясистем линейных уравнений:
1) Метод Крамера
2) Метод Гаусса
Метод Крамера предполагает вычисление
определителей. Мы вычисляли
определители 3-его порядка разложением
по элементам первой строки.
24
25.
Пример.Способ 1.
1
2
4
3 -4 5
1 2
5
4
9 10
14
16
1
1
2
3
0 9 10
0 14
16
9 16 10 14 144 140 4.
25
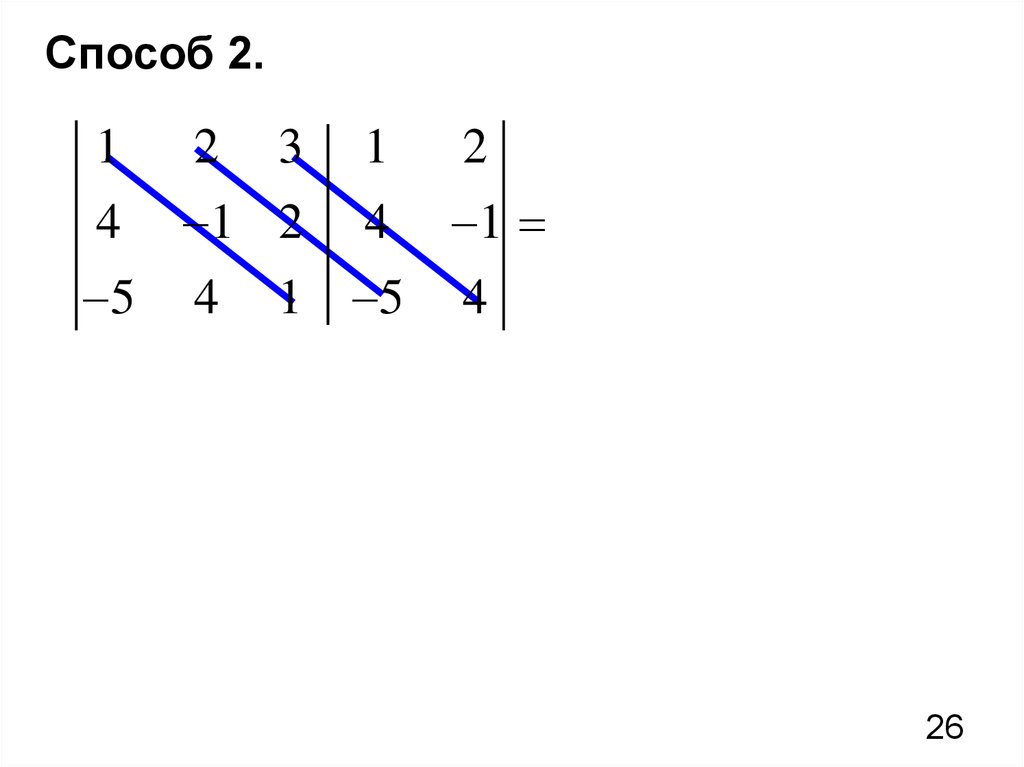
26.
Способ 2.1
2
3
1
2
4
1 2
4
1
5
4
1 5
4
1 20 48 15 8 8
21 48 31 52 48 4.
26
27.
Свойства определителей1) Определитель не изменится, если
поменять строки на соответствующие
столбцы
2) Если у определителя 2 одинаковые
строки или столбца, то он равен нулю.
3) Если у определителя нулевая строка
или столбец, то он равен нулю.
27
28.
Свойства определителей4) Если две строки (столбца) поменять
местами, то знак определителя
изменится на противоположный.
5) Общий множитель строки (столбца)
можно выносить за знак определителя.
6) Определитель не изменится, если к
элементам строки (столбца) прибавить
элементы другой строки (столбца),
умноженные на число.
28
29.
Пример.Вычислить:
2
4
6
2
4
6
4
8
12 2 2
4
6
1 128 2009
0.
1 128 2009
(т.к. две одинаковые строки)
29










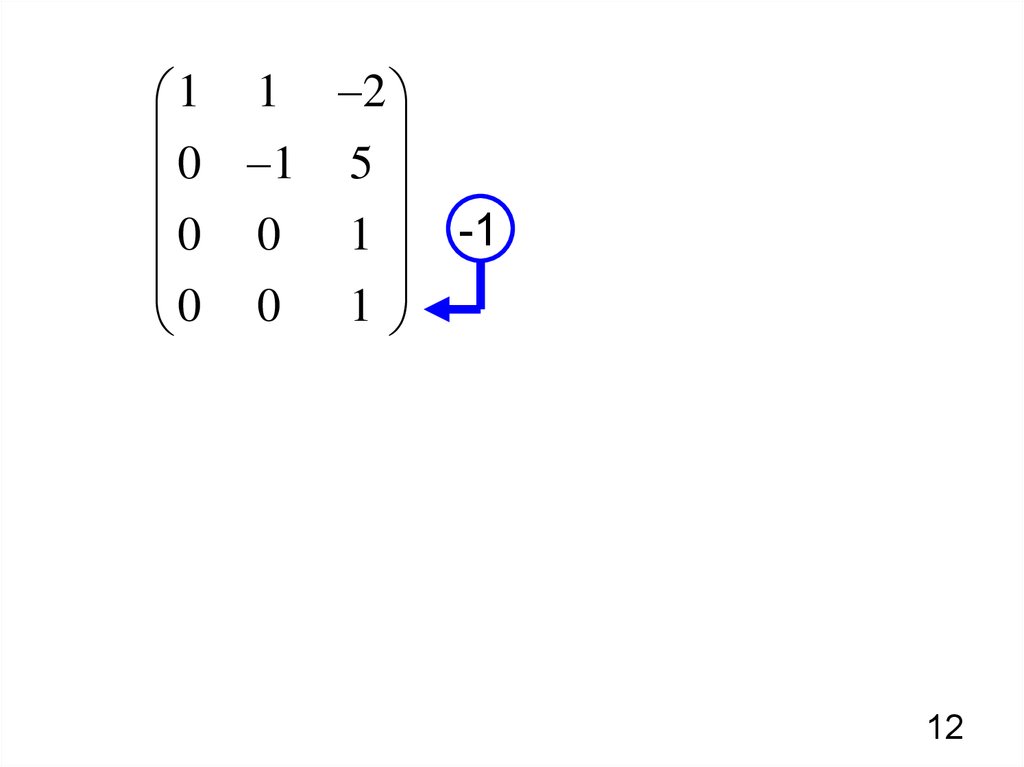















 mathematics
mathematics








