Вычисление ранга матрицы путем приведения её к треугольному виду

1. Дисциплина МАТЕМАТИКА

Лектор: Юлия Абдулловна Ахкамова,
доцент кафедры математики
и методики обучения математике
ЮУрГГПУ
[email protected]

2. Балльно-рейтинговая система 1 курс

Он-лайн 1 лекции 5 баллов (max 1*5=5);
3 лаб. занятия по 5 баллов(max 3*5=15);
Контрольная работа №1 задачи 1,3а,б.в,8 (max 60);
Защита-обсуждение занятий или кр (электронного
варианта) max 10 баллов);
Зачетная работа до 20 баллов .
60 баллов и выше «Зачтено»,

3.

2 Учебный вопрос.
Вычисление ранга матрицы
путем приведения её к
треугольному виду.

4.

Матрица
произвольной
размерности называется трапециевидной
или ступенчатой матрицей, если она имеет
вид
Определение.
a11
0
A 0
0
a12
a13
a22
a23
0
a33
0
0
a1n
a2 n
a3n
0

5.

Определение. Элементарными преобразованиями строк матрицы называются:
1) вычеркивание нулевой строки;
2) умножение строки на любое ненулевое
число;
3) перемена местами двух строк матрицы;
4) прибавление к элементам одной строки
соответствующих
элементов
другой
строки, умноженных на некоторое число;

6.

Ступенчатая матрица получается из
исходной с помощью элементарных
преобразований строк (методом
нулей и единиц).
Определение.
Рангом
матрицы
размерности m×n
называется
количество ненулевых строк
в
эквивалентной
ей
ступенчатой
матрице.

7. Пример. Найти ранг матрицы

1 1 1 3
0
6
2
10
0 6 3 15

8.

1 1 1 3
0 6 2 10 +
0 6 3 15
1 1 1 3
0 6 2 10
0 0 1 1
1 1 1 3
0 6 2 10
0 0 5 5 1/5

9.

10. Теорема

Ранг
матрицы не изменяется при
транспонировании матрицы.

11.

Решение и исследование систем
линейных алгебраических уравнений
(СЛАУ)

12.

Определение. Системой
линейных алгебраических
уравнений (СЛАУ) с неизвестными
х1, х2, ..., хn называется система
уравнений вида
a11x1 a12 x2 a13 x3 a1n x n b1
a21 x1 a22 x 2 a 23x3 a2 n xn b2
am1 x1 am 2 x2 am 3 x3 amn xn bm

13.

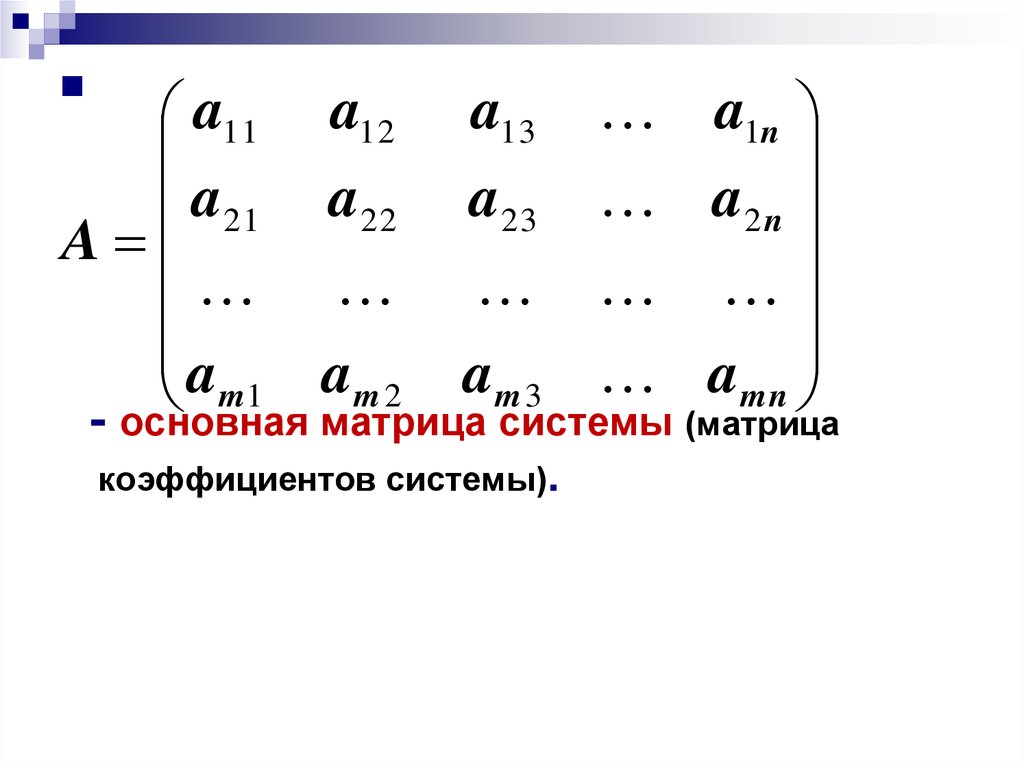
a11 a12 a13 a1n
a21 a22 a23 a 2 n
A
a
am 2 am 3 a mn
m1
- основная матрица системы (матрица
коэффициентов системы).

14.

x1
x2
X x3
- столбец неизвестных.
x
n
b1
b2
B
-столбец свободных членов.
b
m

15.

Напомним, матрица А называется
невырожденной матрицей,
если | A | ≠ 0.

16.

Система
линейных
алгебраических уравнений
(СЛАУ) называется
невырожденной СЛАУ, если ее
основная матрица
невырожденная.

17.

Определение. Решением СЛАУ
системы линейных
алгебраических уравнений
называется совокупность чисел
(С1, С2,…, Сn), которые, при
подстановке их вместо
соответствующих неизвестных,
обращают каждое уравнение в
верное равенство.

18.

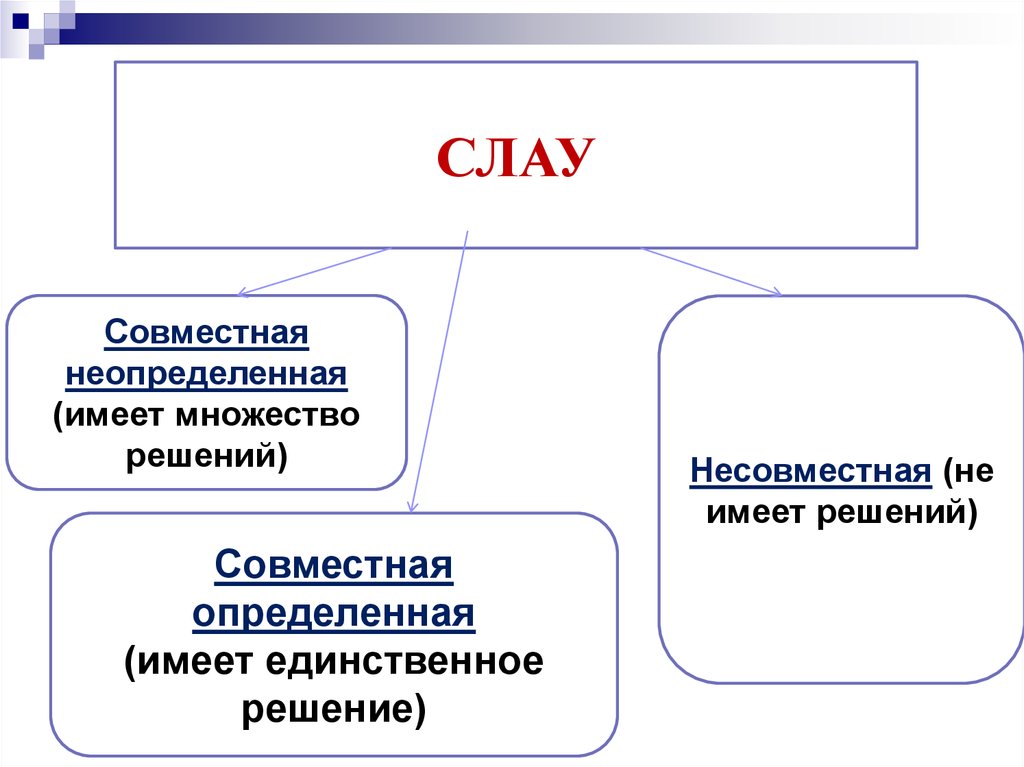
СЛАУ
Совместная
неопределенная
(имеет множество
решений)
Совместная
определенная
(имеет единственное
решение)
Несовместная (не
имеет решений)

19.

Учебный
вопрос .
Матричный метод систем
линейных алгебраических
уравнений.

20.

Рассмотрим
систему n линейных
алгебраических уравнений с n
неизвестными.
Систему линейных
алгебраических уравнений
можно записать в матричном
виде следующим уравнением:
А∙Х=В

21.

Здесь Х - неизвестная матрица.
Пусть матрица А невырожденная,
тогда существует А-1 и
А∙Х=В
А-1∙А∙Х=А-1∙В
Е∙Х=А-1∙В
Х=А-1∙В - решение СЛАУ
матричным методом.

22. Алгоритм решений системы линейных уравнений матричным методом

1) Составить основную матрицу СЛАУ.
2) Вычислить ее определитель.
3) Если определитель не равен нулю,то
находим обратную матрицу.
4)Умножить обратную матрицу на столбец
свободных коэффициентов в указанном
порядке:
Х=А-1∙В

23.

Учебный вопрос.
Метод Крамера систем линейных
алгебраических уравнений.

24.

Габриэль Крамер (31 июля 1704 – 4
января 1752). Швейцарский математик,
ученик и друг Иоганна Бернулли, один из
создателей линейной алгебры.

25.

Рассмотрим
систему n
линейных
алгебраических
уравнений с n
неизвестными.

26.

Теорема. Пусть дана система
линейных алгебраических
уравнений, в которой число
уравнений совпадает с
числом неизвестных, т.е. m=n
и определитель матрицы
системы Δ=detA≠0.
Тогда данная система имеет
единственное решение,
определяемое по формулам:

27.

xj =
j
, j 1,.., n
(1)
где определитель Δj получен
из определителя Δ матрицы
путем замены j-го столбца
столбцом свободных членов.
Формулы (1) называются
формулами Крамера.

28. Алгоритм решений системы линейных уравнений методом Крамера

1) Составить основную матрицу СЛАУ.
2) Вычислить ее определитель Δ.
3) Если определитель не равен нулю, то
находим Δj.
4)Найти значения переменных:
xj =
j
, j 1,.., n

29.

Пример. Решить систему методом
Крамера
2 x1 4 x2 4 x3 10;
3x1 8 x2 10 x3 25;
4 x 3x x 1.
1
2
3
Решение. Найдем определитель
матрицы системы
2
4
3
8
4
3
4
10 12
1

30.

Так
как определитель матрицы
системы не равен нулю, то система
имеет единственное решение.

31.

Вычислим определители Δ1, Δ2, Δ3
10
4
1 25
8
4
10 12
3
1
1
2
10
4
2 3 25 10 12
2
4
10
3 3
8
25 24
4
3
1
4
1
1

32.

По формулам Крамера
1 12
x1
1;
12
2 12
x2
1;
12
3 24
x3
2.
12
Итак, решение системы (–1; –1; 2)