Similar presentations:
Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей. (Лекция 4.1)
1.
Омский государственный техническийуниверситет
Кафедра инженерной геометрии и САПР
Кайгородцева Наталья
Викторовна
Начертательная геометрия
Взаимное расположение
двух прямых, прямой и
плоскости, двух плоскостей
Видеолекция
©ОмГТУ, 2014
1
2. План лекции
1Взаимное расположение двух
прямых. Теорема о прямом угле
2
Взаимное расположение
прямой и плоскости
3
Взаимное расположение
двух плоскостей
1
3.
Взаимное расположение двух прямыхПрямые в пространстве
могут быть:
• пересекающимися;
• скрещивающимися;
• параллельными
(в частном случае совпадать)
• перпендикулярными
(частный случай пересечения)
2
4.
Пересекающиеся прямые3
5.
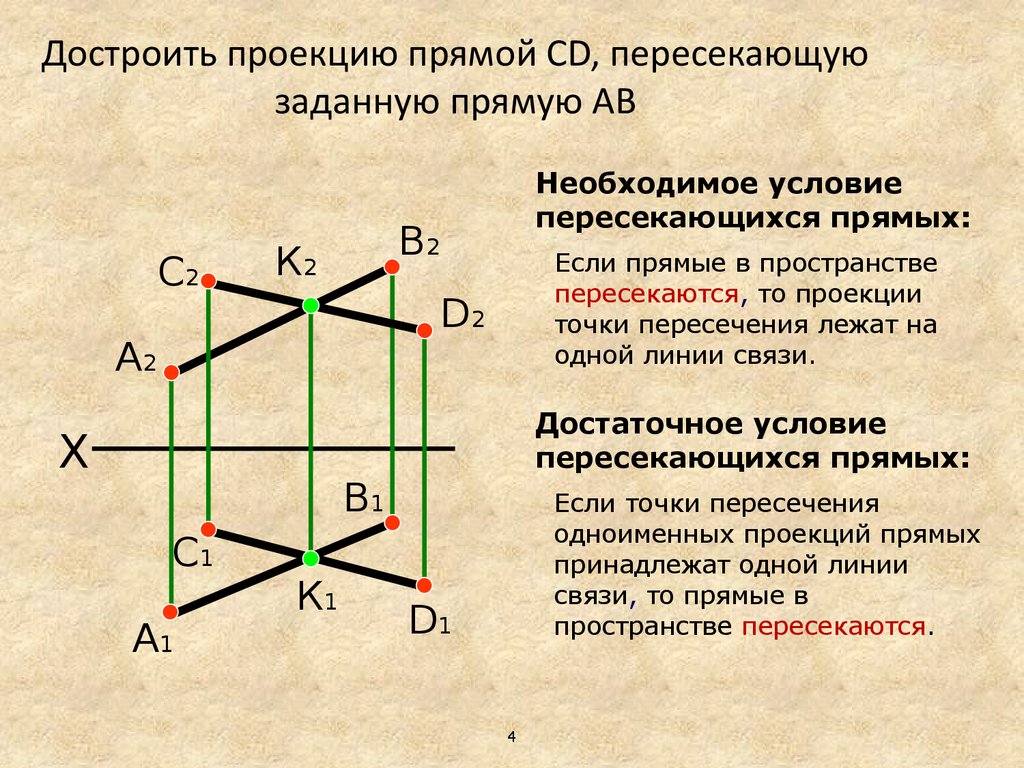
Достроить проекцию прямой СD, пересекающуюзаданную прямую AB
C2
Необходимое условие
пересекающихся прямых:
B2
К2
Если прямые в пространстве
пересекаются, то проекции
точки пересечения лежат на
одной линии связи.
D2
A2
Достаточное условие
пересекающихся прямых:
X
B1
C1
A1
К1
Если точки пересечения
одноименных проекций прямых
принадлежат одной линии
связи, то прямые в
пространстве пересекаются.
D1
4
6.
Скрещивающиеся прямые5
7.
Достроить проекцию прямой EF, скрещивающейсяс заданной прямой AB
E2
12
X
E1
A1
32=42 B2
Если прямые в пространстве
скрещиваются, то точки
пересечения их одноименных
проекций не принадлежат
одной линии связи.
F2
22
A2
Необходимое условие
скрещивающихся прямых:
Достаточное условие
скрещивающихся прямых:
31 B1
41
11=21
Если точки пересечения
одноименных проекций двух
прямых не принадлежат одной
линии связи, то прямые в
пространстве скрещиваются.
F1
6
8.
Параллельные прямые7
9.
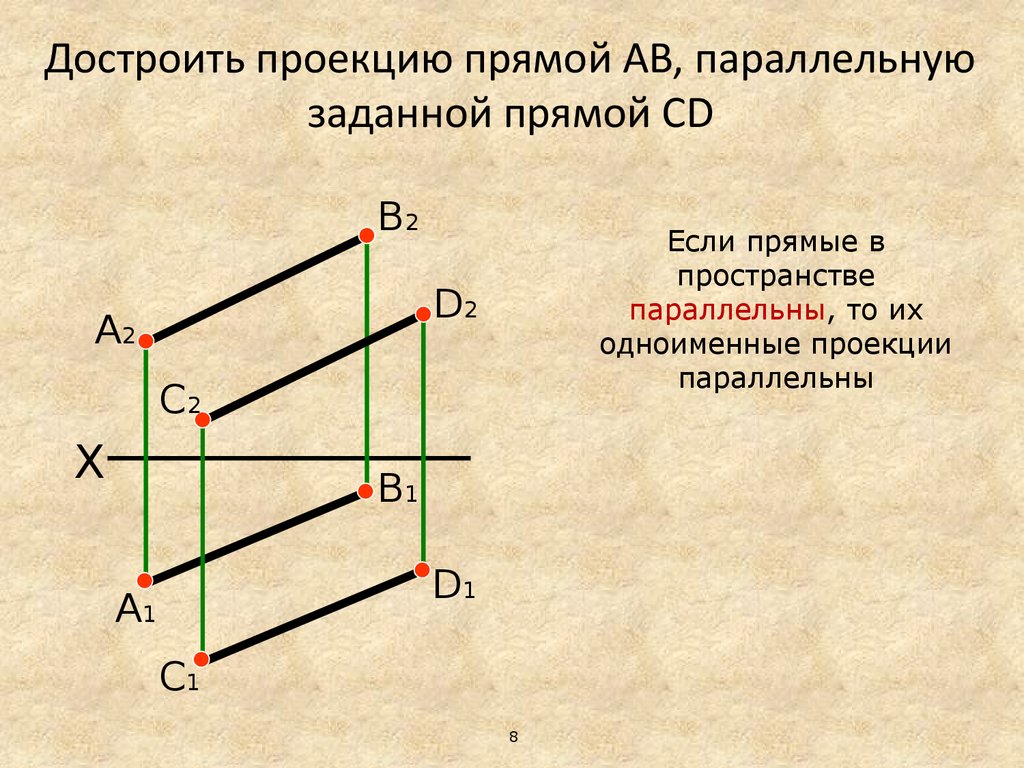
Достроить проекцию прямой AB, параллельнуюзаданной прямой CD
B2
Если прямые в
пространстве
параллельны, то их
одноименные проекции
параллельны
D2
A2
C2
X
B1
D1
A1
C1
8
10.
Параллельны ли заданные прямые?Z
A2
C2
B2
X
B1
A1
D2
A3
C3
B3
D3
C1
D1
Вывод:
Прямые AB и CD не
параллельны.
Y
9
11.
Перпендикулярные прямые.Теорема о проекциях прямого угла
«Прямой угол
проецируется на
плоскость проекций в
натуральную величину,
если одна его сторона
параллельна этой
плоскости проекций, а
вторая ей
не перпендикулярна»
D
Е
90
К
П1
Е1
К1
D1
90
10
12.
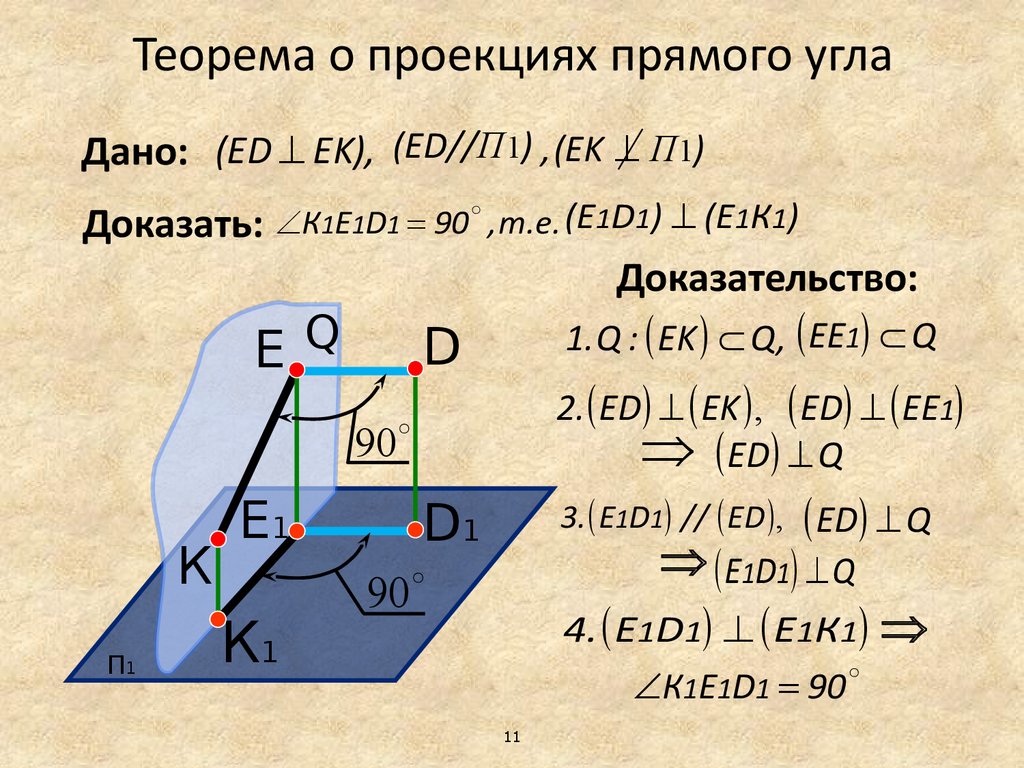
Теорема о проекциях прямого углаДано: (ED EK), (ED//П1) , (EK П1)
Доказать: К1Е1D1 90 , т.е. (Е1D1) (Е1К1)
Доказательство:
ЕQ
1. Q : EK Q, EЕ1 Q
D
2. ED EK , ED EЕ1
ED Q
90
К
П1
Е1
К1
3. Е1D1 // ED , ED Q
D1
90
Е1D1 Q
4. Е1D1 E1К1
К1Е1D1 90
11
13.
Взаимное расположение прямой и плоскостиПрямая и плоскость в
пространстве могут быть:
• параллельными;
• перпендикулярными;
• пересекающимися
12
14.
Параллельность прямой и плоскостиПрямая параллельна плоскости,
если она параллельна какой-либо
прямой, принадлежащей этой
плоскости.
13
15.
Задача. Построить недостающую проекцию прямой МN,параллельной плоскости { АВС}.
В2
А2
N2
12
Алгоритм решения:
1. В плоскости { АВС}
провести прямую (A1)
параллельную заданной
прямой MN;
2. Через точку М провести
прямую (МN), параллельную
прямой (А1);
М2
С2
X
С1
А1
В1
11
М1
N1
14
16.
Перпендикулярность прямой и плоскостиПрямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым, принадлежащим этой плоскости.
15
17.
Пересечение прямой и плоскостиЗадачи на определение
взаимной принадлежности и
пересечения двух и более
геометрических объектов
называются позиционными.
16
18.
Пересечение прямой и плоскостиПересечение прямой и плоскости
Пересечение прямой общего положения и
проецирующей плоскости
Пересечение плоскости общего положения
и проецирующей прямой
17
19.
Определение точки пересечения прямой и плоскостиАлгоритм решения:
1. Через прямую ввести
вспомогательную
проецирующую плоскость ;
2. Найти линию пересечения
вспомогательной плоскости с
заданной;
3. Определить точку
пересечения построенной
линии с заданной;
4. Определить видимость
заданных объектов .
18
20.
Задача. Определить точку пересечения прямой (EF)и плоскости { ABC}.
51
41
А2
E2
X
Р2
В2
F2
К2
22 =32
С2
12
Построить:
К={ АВС}∩(EF)
В1
E1
Решение:
1. Р: P П2, (EF)ϵP;
2. (12)=Р∩{ АВС};
3. К=(12)∩(EF);
21
41=51
К1
А1
31
11
Дано:
{ АВС}: А(110, 70, 40),
В(50, 0, 70),
С(20, 40, 20) ;
(EF): E(90, 10, 20),
F(10, 70, 65);
4. Определить видимость
прямой (EF) с помощью
конкурирующих точек.
С1
F1
19
21.
Пересечение прямой общего положения ипроецирующей плоскости
20
22.
Пересечение плоскости общего положенияи проецирующей прямой
21
23.
Взаимное расположение двух плоскостейПлоскости в пространстве
могут быть:
• параллельными;
• перпендикулярными
(частный случай
пересечения);
• пересекающимися
22
24.
Параллельность двух плоскостейПризнак параллельности:
Если две пересекающиеся прямые одной
плоскости параллельны двум
пересекающимся прямым другой
плоскости, то эти плоскости параллельны.
23
25.
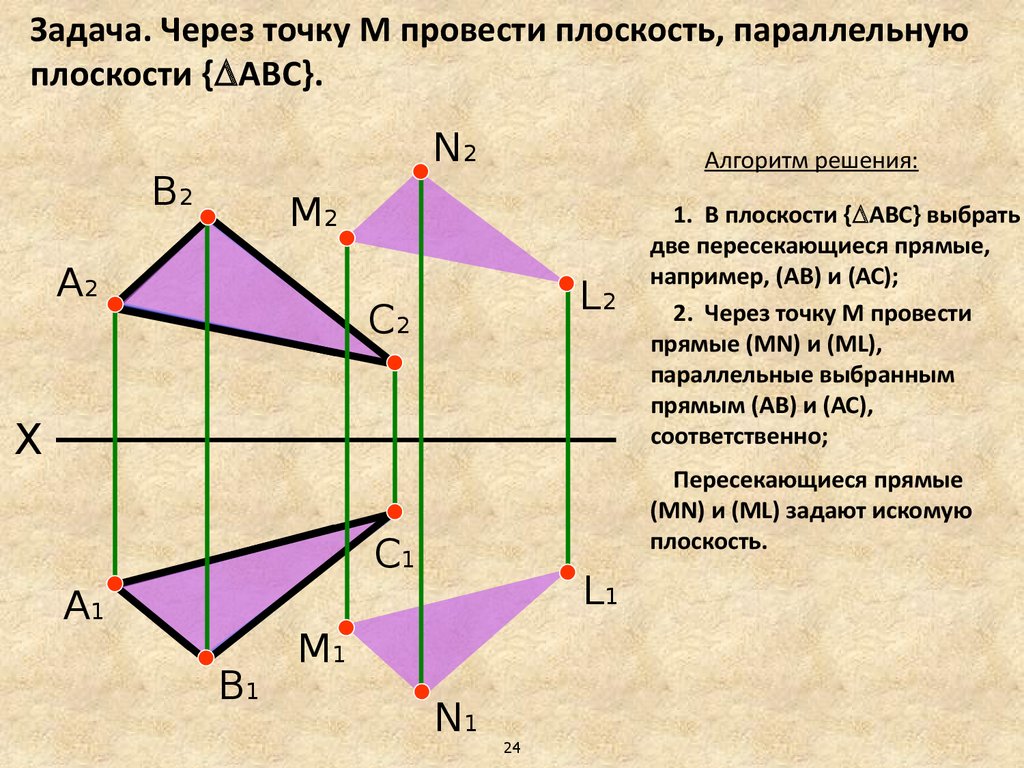
Задача. Через точку М провести плоскость, параллельнуюплоскости { АВС}.
N2
В2
Алгоритм решения:
М2
А2
L2
С2
X
Пересекающиеся прямые
(МN) и (ML) задают искомую
плоскость.
С1
А1
В1
1. В плоскости { АВС} выбрать
две пересекающиеся прямые,
например, (АВ) и (АС);
2. Через точку М провести
прямые (МN) и (ML),
параллельные выбранным
прямым (АВ) и (АС),
соответственно;
L1
М1
N1
24
26.
Перпендикулярность двух плоскостейПризнак перпендикулярности:
Если одна из плоскостей проходит через
перпендикуляр к другой плоскости, то эти
плоскости перпендикулярны.
23
27.
Пересечение плоскостейПересечение двух плоскостей
Пересечение плоскости общего положения
и проецирующей плоскости
Пересечение проецирующих плоскостей
26
28.
Определение линии пересечения двух плоскостей27
29.
Определение линии пересечения двух плоскостейДано:
F2
В2
22
E2
А1
12
42
С2
N2
M2
А2
X
Z
E1
Решение:
D2
32
0
F1
31
11
M1
В1
N1
С1
41
D1
21
Р1
Q1
АВС: А(120, 15, 0),
В(70, 70, 50),
С (10, 35, 25);
DEF: D(30, 70, 0)
Е (105, 10, 40),
F (60, 10, 60).
Построить: (MN)= АВС∩ DEF
Y
28
1. {Р}: (DE)ϵP, P П1;
2. (12)={Р}∩{ АВС};
3. М=(12)∩(DE);
4. {Q}: (DF)ϵQ, Q П1;
5. (34)={Q}∩{ АВС};
6. N=(34)∩(DF);
7. (MN) – искомая линия
пересечения плоскостей;
8. Определить видимость
плоскостей.
30.
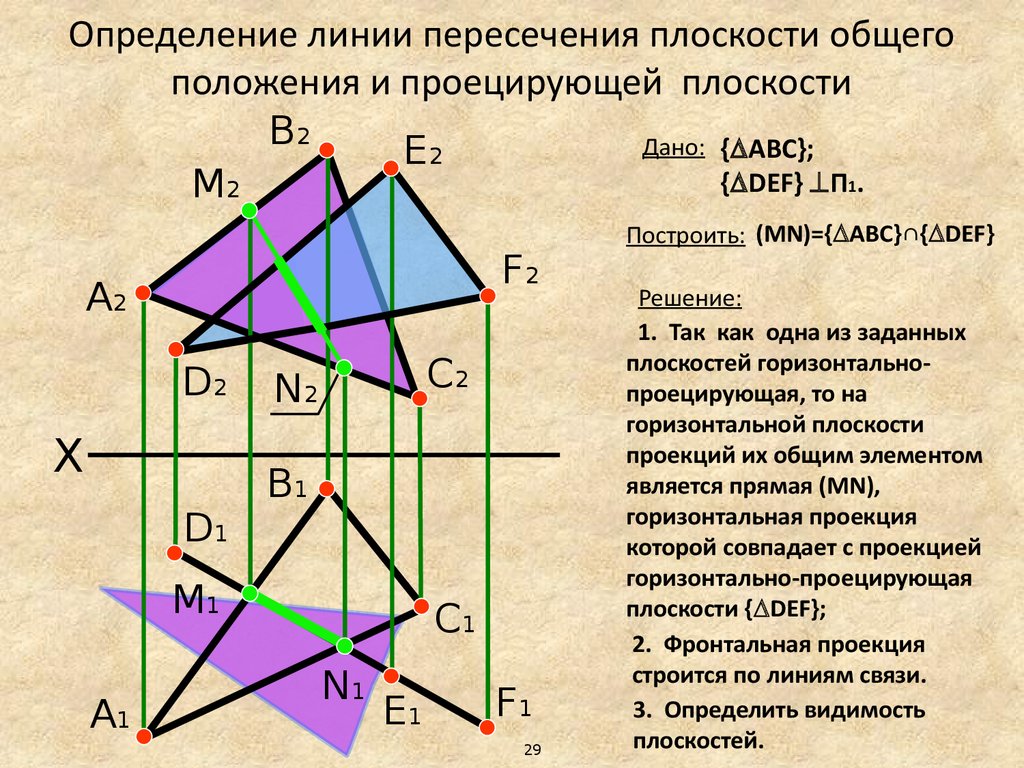
Определение линии пересечения плоскости общегоположения и проецирующей плоскости
В2
Дано: { АВС};
E2
{ DEF} П1.
M2
F2
А2
D2
X
D1
С2
N2
В1
M1
А1
С1
N1
E1
F1
29
Построить:
(MN)={ АВС}∩{ DEF
}
Решение:
1. Так как одна из заданных
плоскостей горизонтальнопроецирующая, то на
горизонтальной плоскости
проекций их общим элементом
является прямая (MN),
горизонтальная проекция
которой совпадает с проекцией
горизонтально-проецирующая
плоскости { DEF};
2. Фронтальная проекция
строится по линиям связи.
3. Определить видимость
плоскостей.
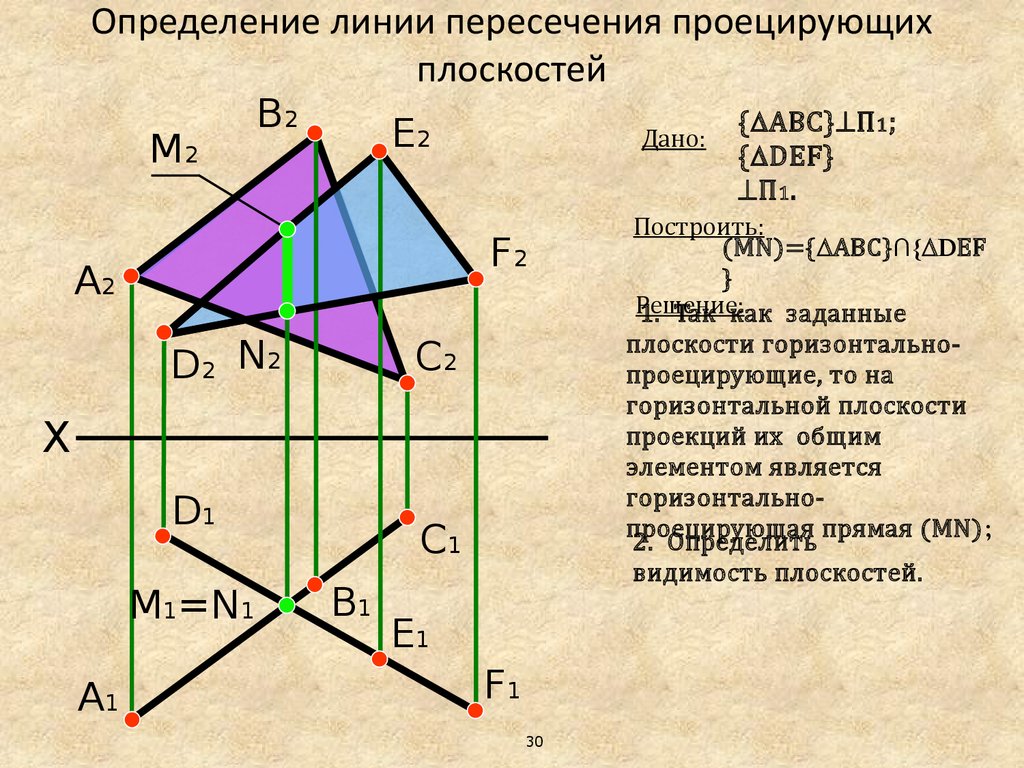
31.
Определение линии пересечения проецирующихплоскостей
В2
{ АВС} П 1;
E
2
Дано:
M2
{ DEF}
F2
А2
D2 N2
С2
X
D1
M1=N1
А1
С1
В1
E1
F1
30
П 1 .
Построить:
(MN)={ АВС}∩{ DEF
}
Решение:
1. Так как заданные
плоскости горизонтальнопроецирующие, то на
горизонтальной плоскости
проекций их общим
элементом является
горизонтальнопроецирующая прямая (MN);
2. Определить
видимость плоскостей.
32.
Контактная информацияЛектор:
Кайгородцева Наталья Викторовна
доцент, к.пед.н.
Кафедра «Инженерная геометрия и САПР»
г. Омск, пр. Мира, 11, корпус 8 кабинет 513
(3812) 65-36-45
igisapr@omgtu.ru
www.omgtu.ru

























 mathematics
mathematics








