Взаимные положения прямой и плоскости, двух плоскостей

1. Лекция 6 «Взаимные положения прямой и плоскости, двух плоскостей»

1

2.

Задача:
Построить
линию
пересечения
двух
треугольников АВС и DEF, как линию соединяющую две
точки встречи прямой с плоскостью.
А(115, 20, 10)
В (75, 75, 70)
С (20,10, 25)
D(130, 65, 30)
E (90, 5, 70)
F (35,55, 5)
2

3.

3

4.

4

5.

5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

12

13.

13

14.

14

15.

15

16.

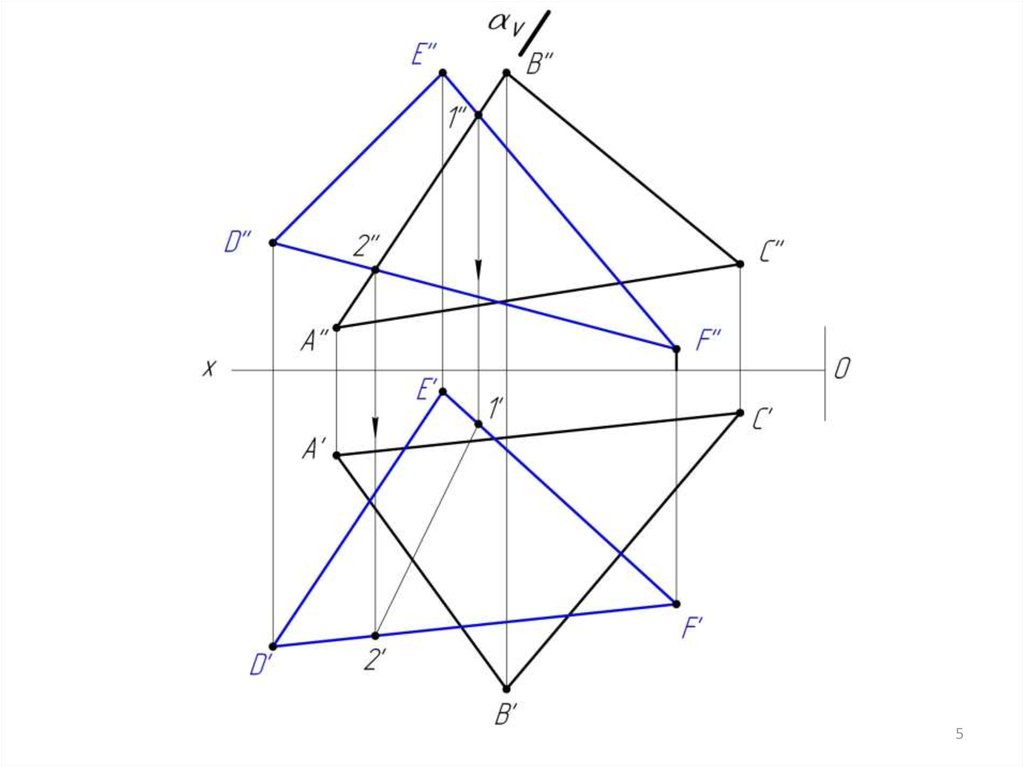
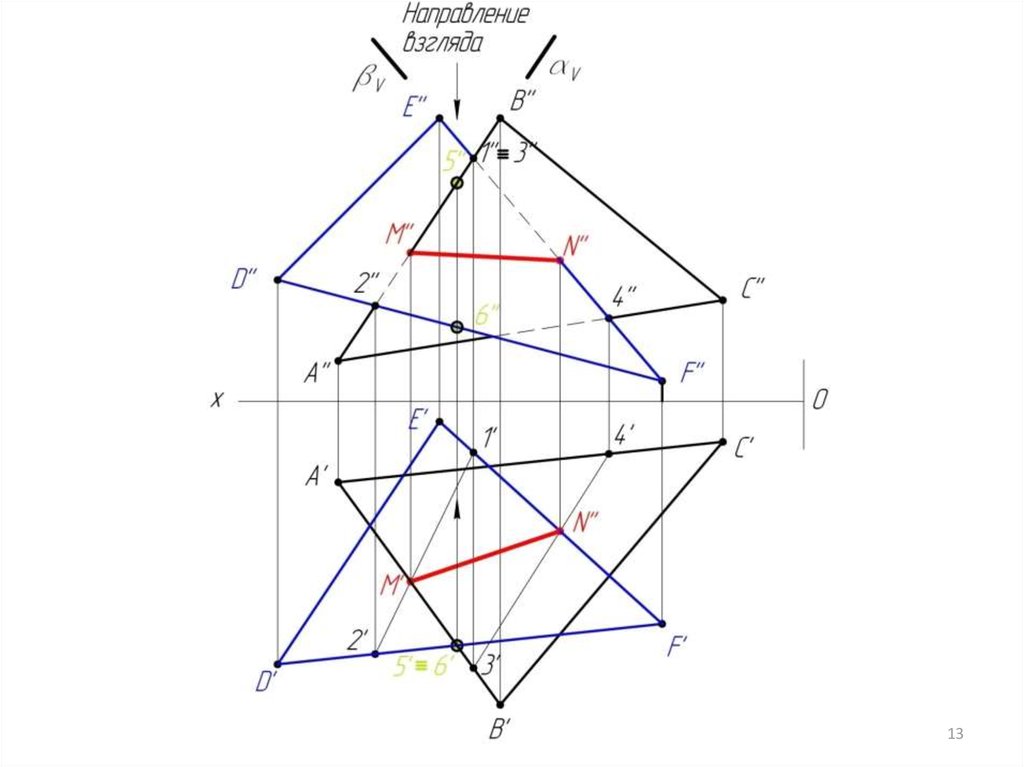
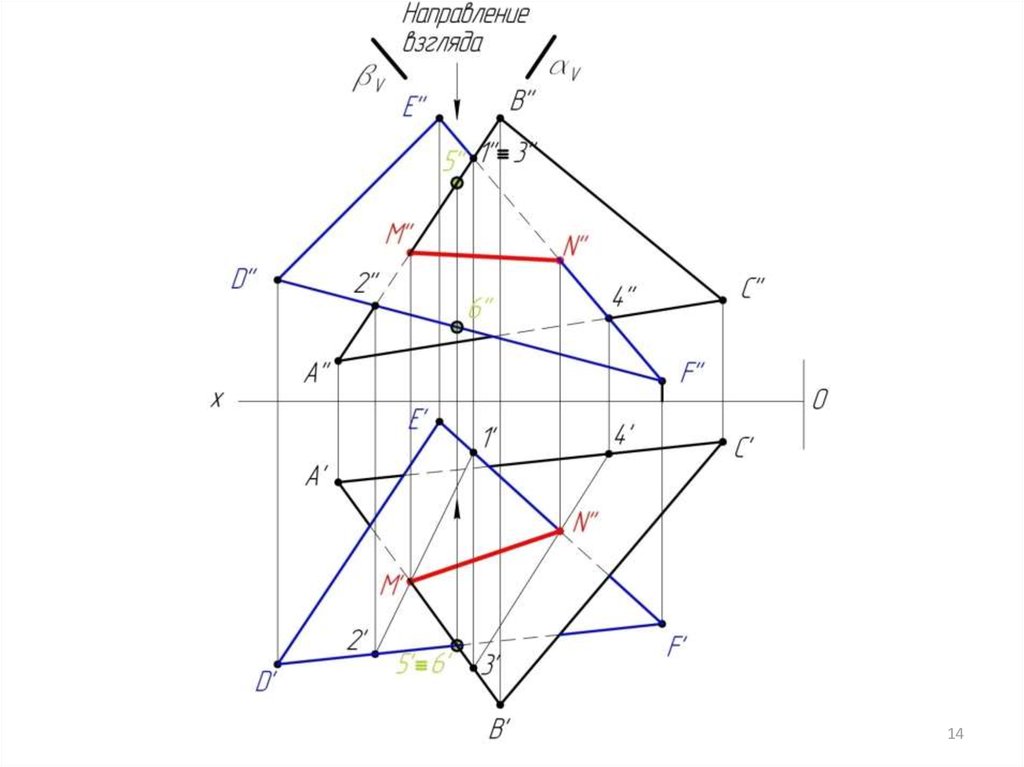
Алгоритм решения задачи
1. Заключаем сторону треугольника АВ в фронтальнопроецирующую плоскость .
АВ ( V); V
2. Строим линию пересечения DEF и плоскости .
DEF = (1-2)
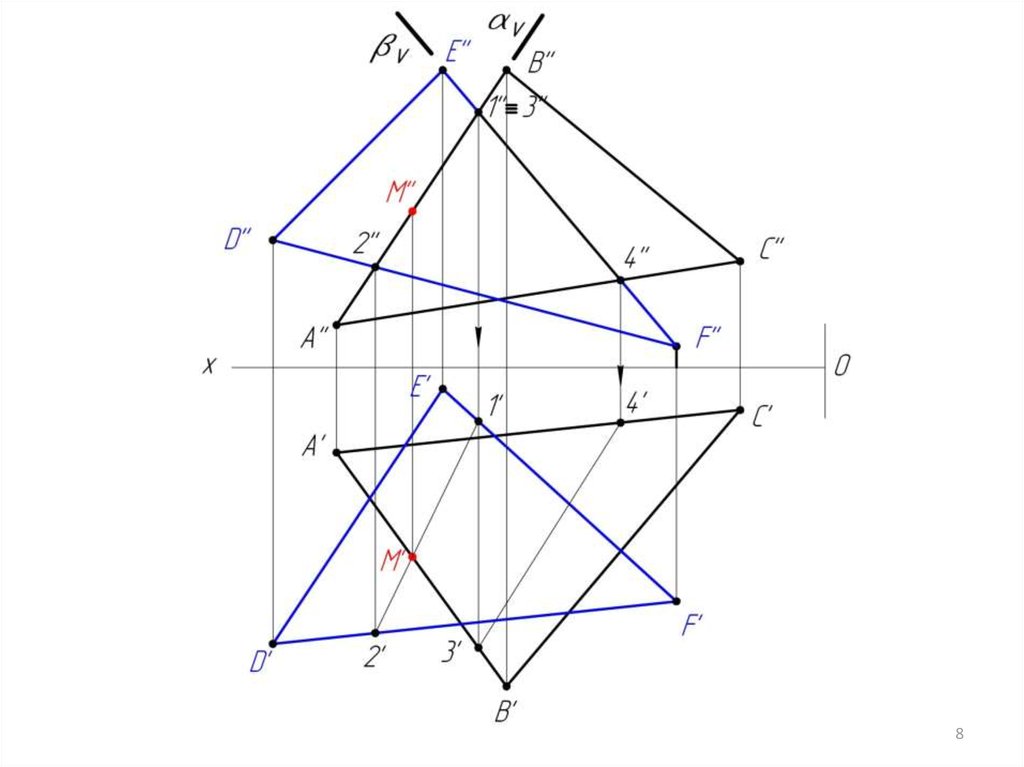
3. Находим точку М пересечения линий АВ и 1-2.
(1-2) АВ = М
4. Заключаем сторону треугольника EF в фронтальнопроецирующую плоскость .
EF ( V); V
5. Строим линию пересечения АВС и плоскости .
АВС = (3-4)
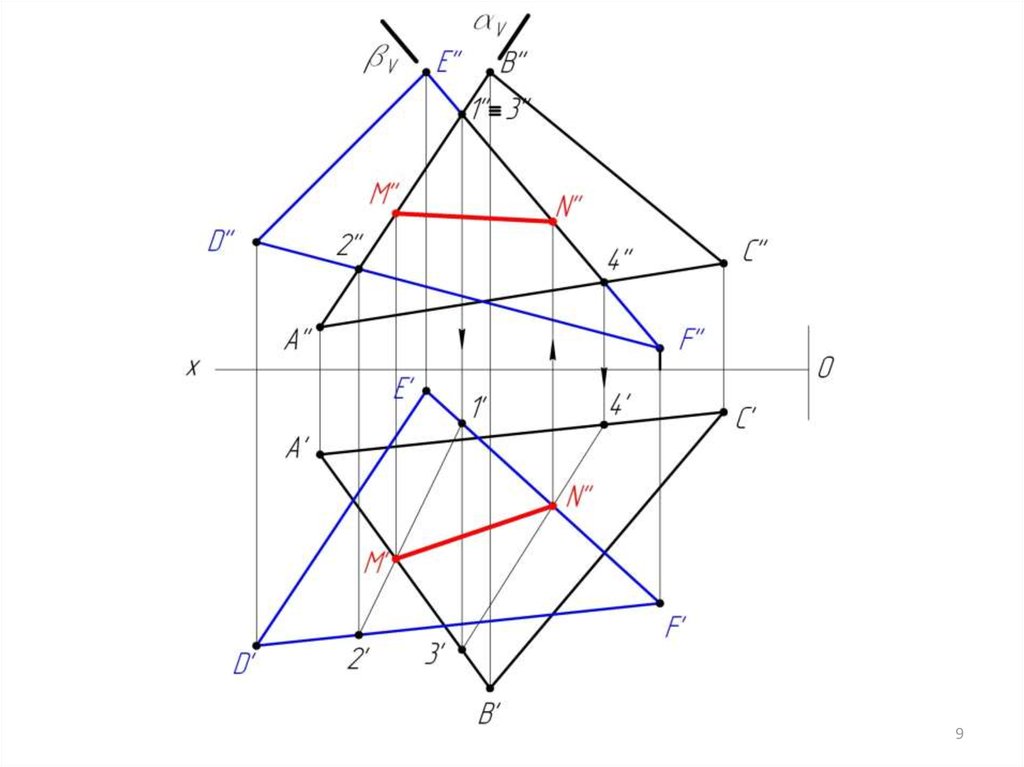
6. Находим точку N пересечения линий EF и 3-4.
(3-4) EF = N
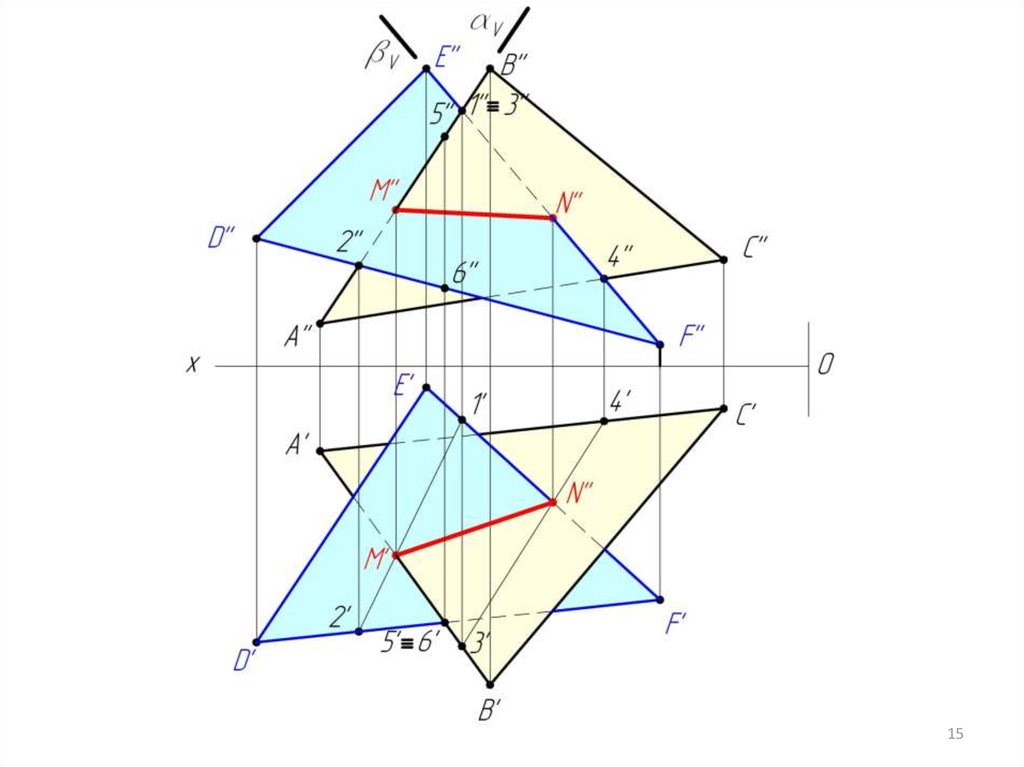
7. Строим линию MN пересечения треугольников АВС и DEF.
[MN] = АВС DEF
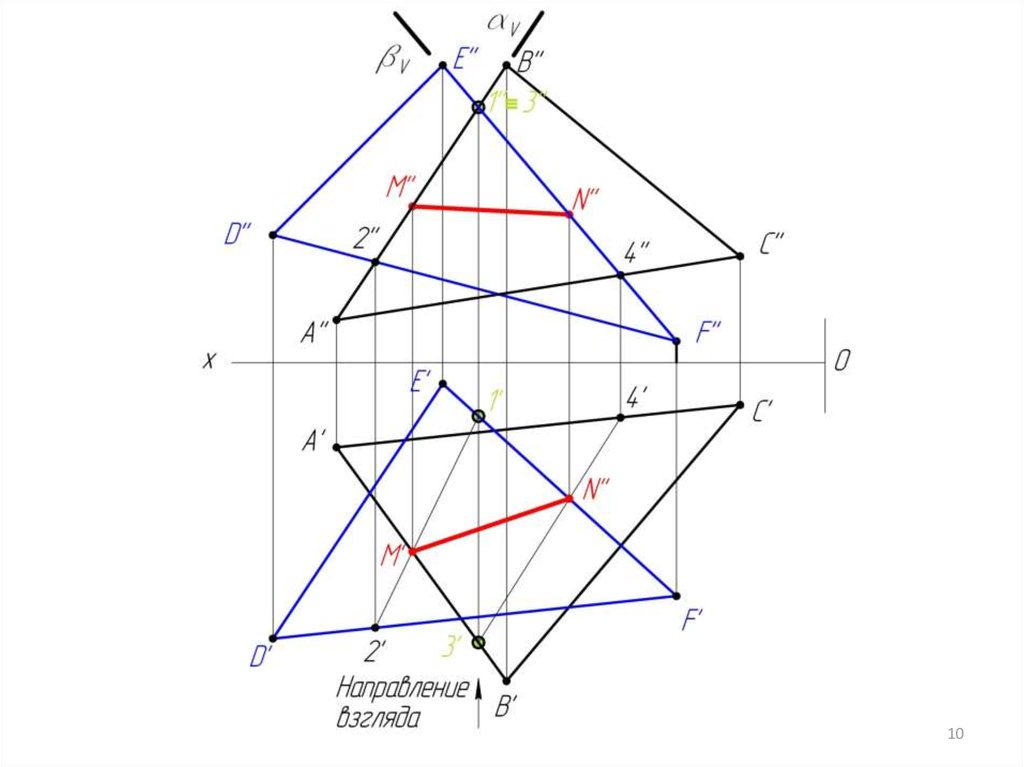
8. Определяем видимость методом конкурирующих точек
16

17.

6.1. Перпендикулярность прямой и
плоскости
Прямая перпендикулярна плоскости, если она
перпендикулярна к двум пересекающимся прямым этой
плоскости.
17

18.

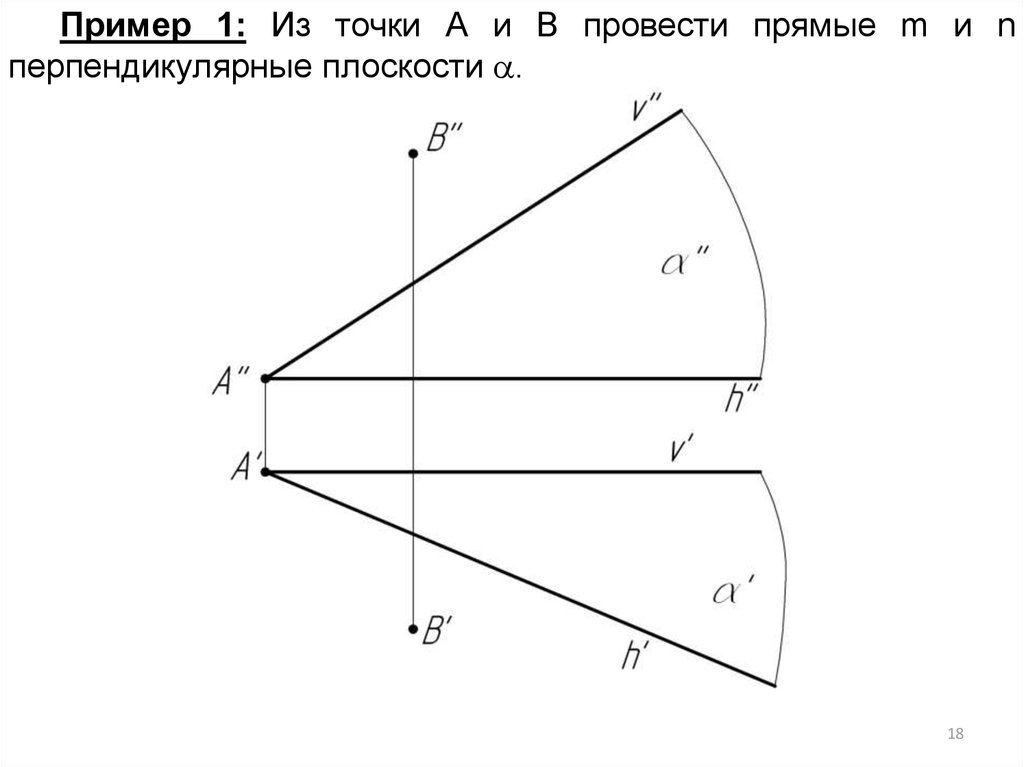
Пример 1: Из точки А и В провести прямые m и n
перпендикулярные плоскости .
18

19.

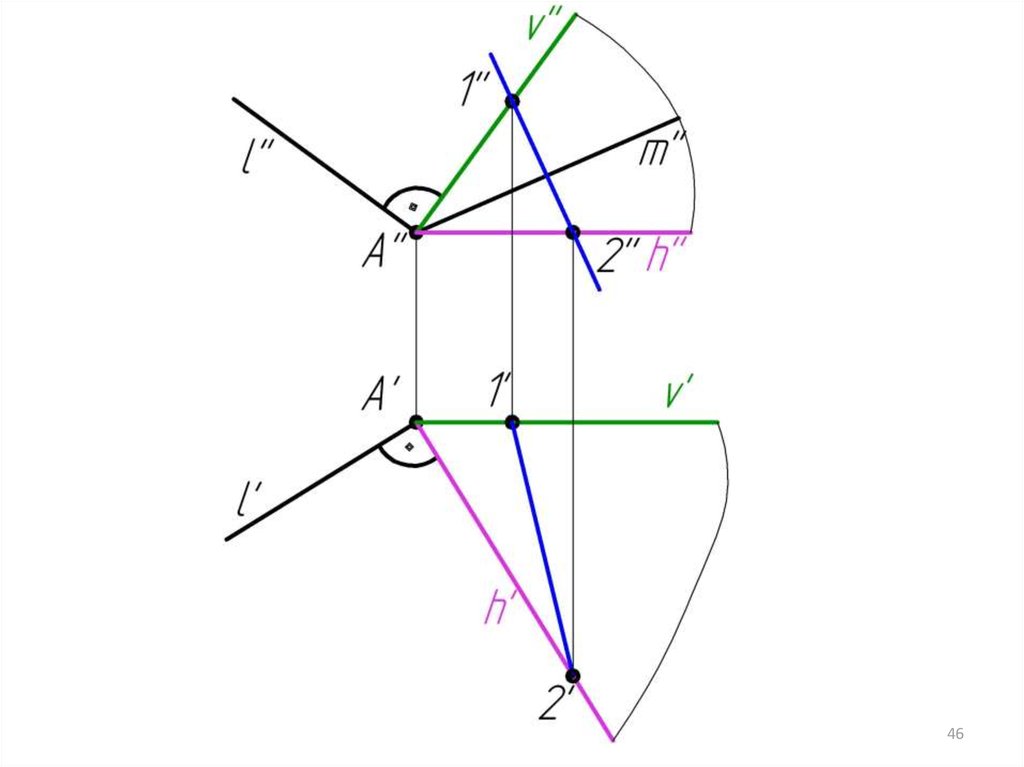
Чтобы
построить
прямую,
перпендикулярную
плоскости, надо иметь на чертеже (или построить)
горизонталь и фронталь этой плоскости. Тогда
горизонтальная
проекция
перпендикуляра
будет
перпендикулярна горизонтали, а фронтальная проекция
перпендикуляра будет перпендикулярна фронтали.
19

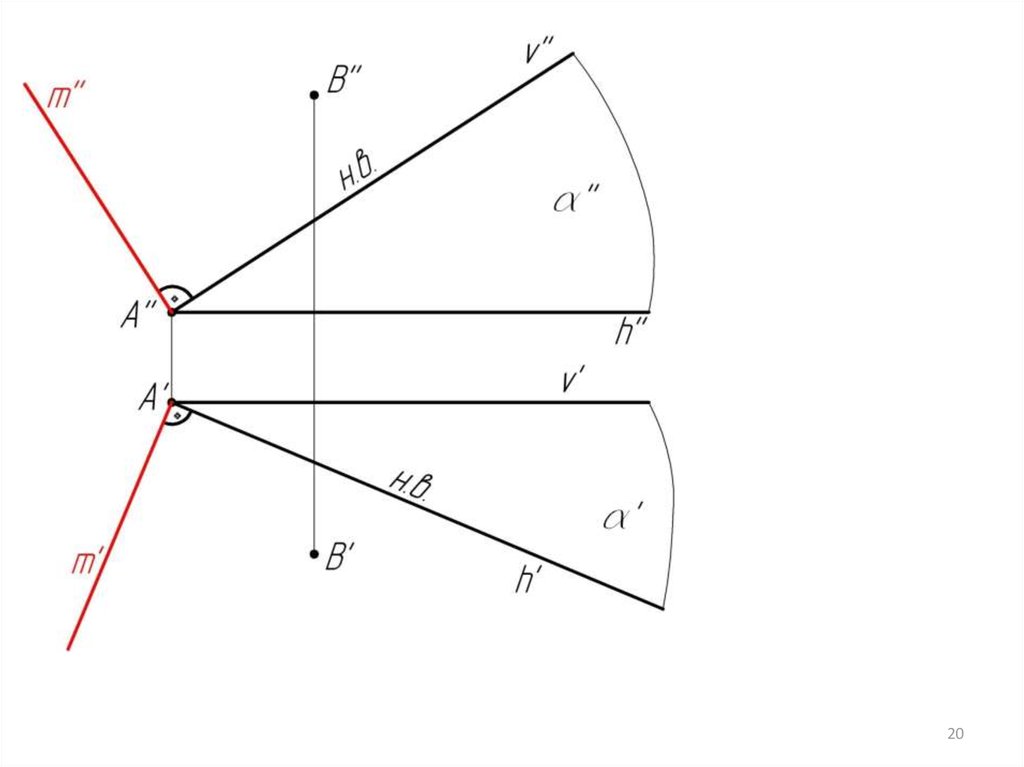
20.

20

21.

m’ h’; m’’ v’’;
m (h v)
n’ h’; n’’ v’’;
n (h v)
21

22.

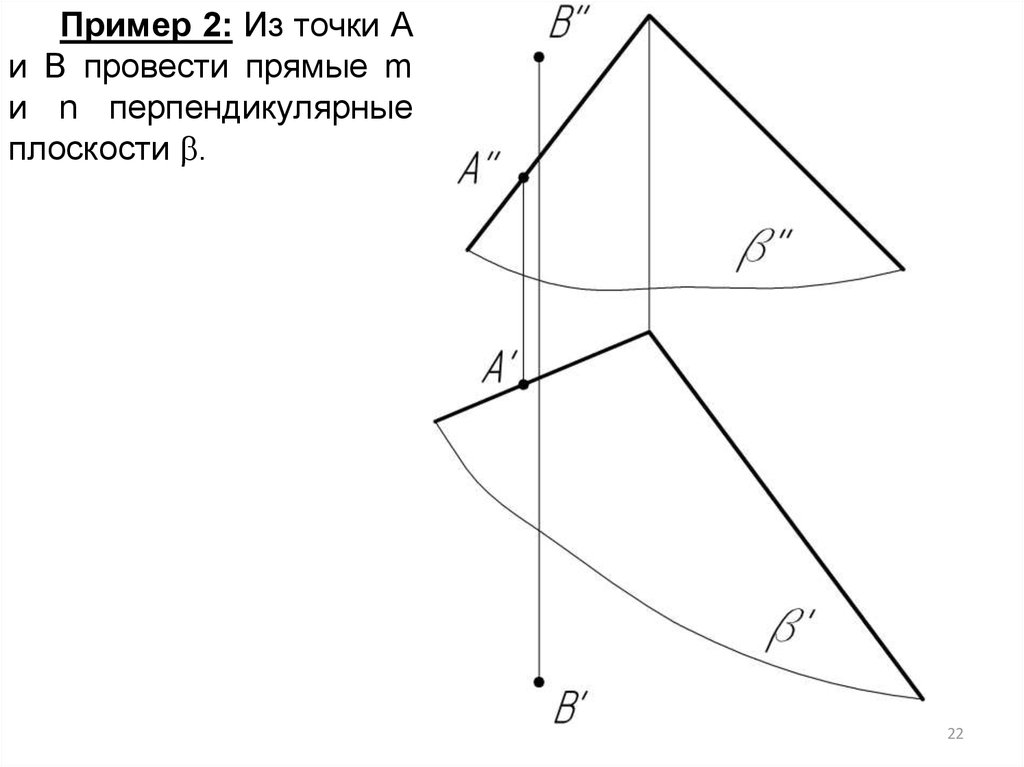
Пример 2: Из точки А
и В провести прямые m
и n перпендикулярные
плоскости .
22

23.

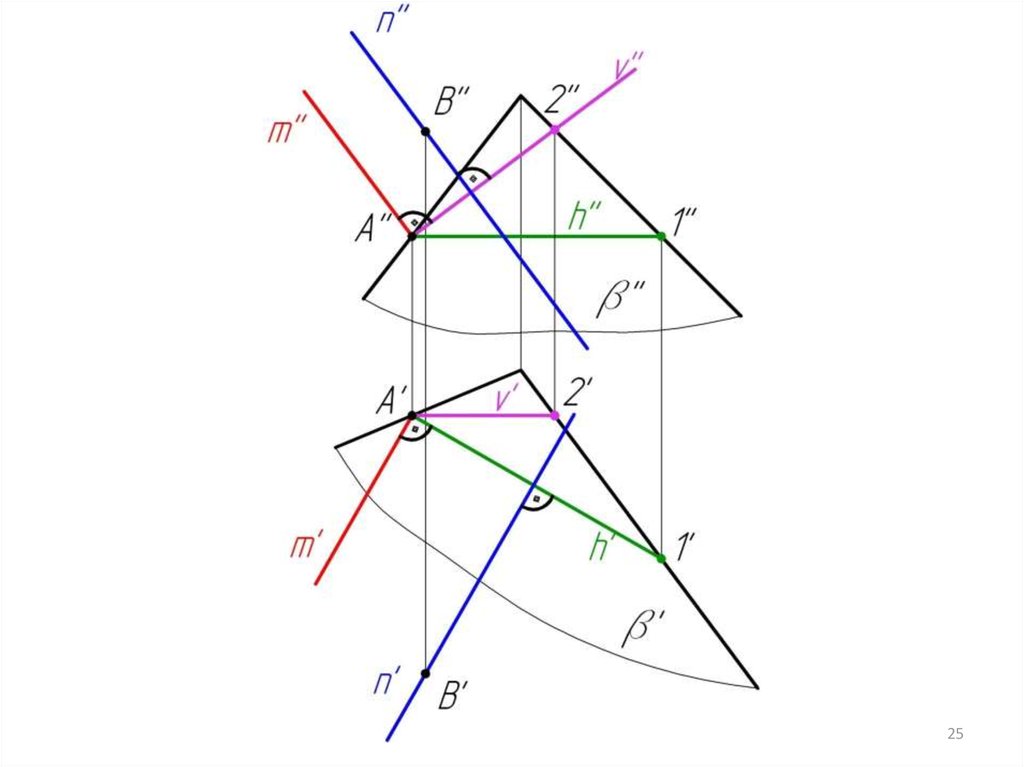
23

24.

24

25.

25

26.

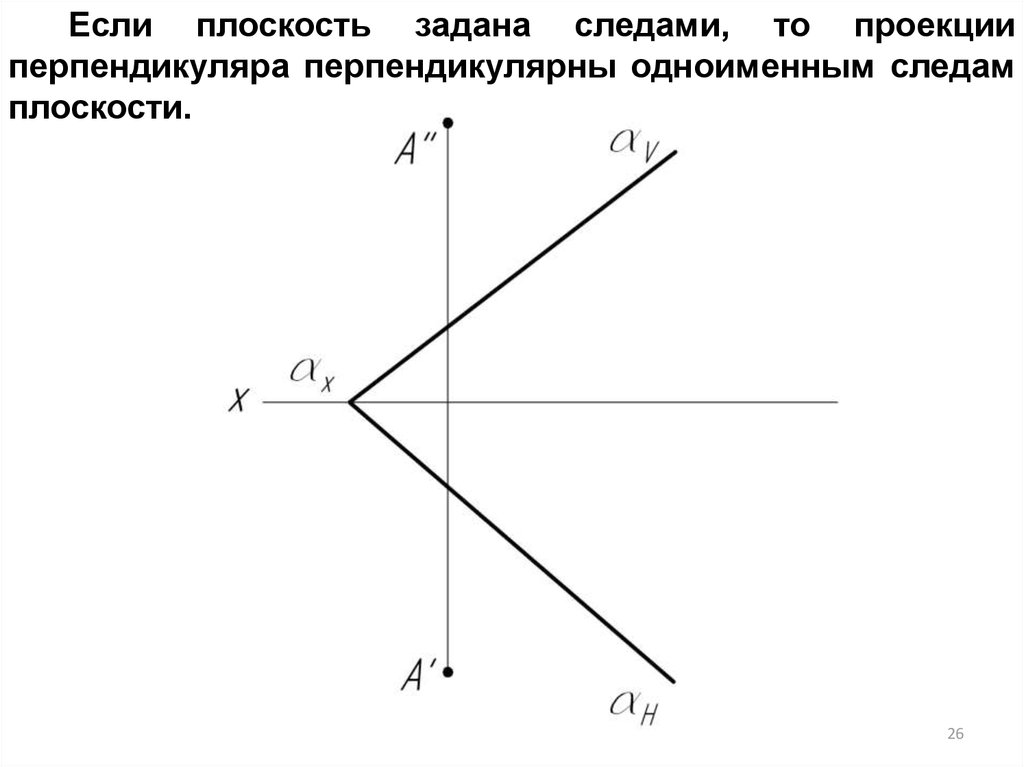
Если плоскость задана следами, то проекции
перпендикуляра перпендикулярны одноименным следам
плоскости.
26

27.

m’ H; m’’ V;
m
27

28.

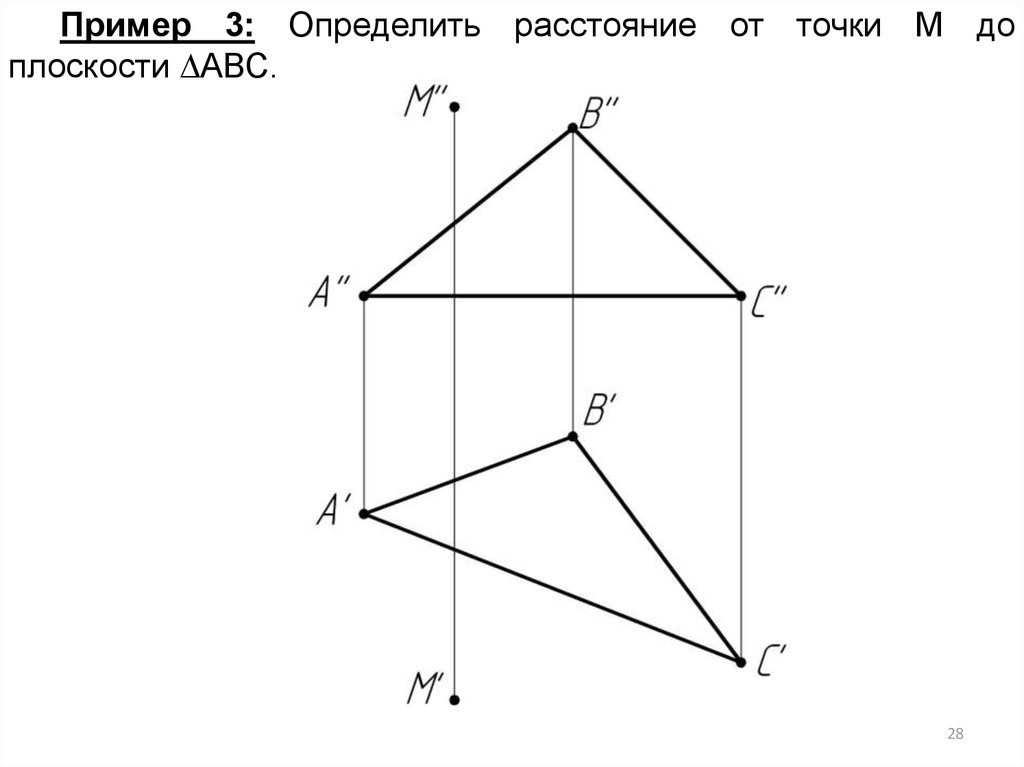
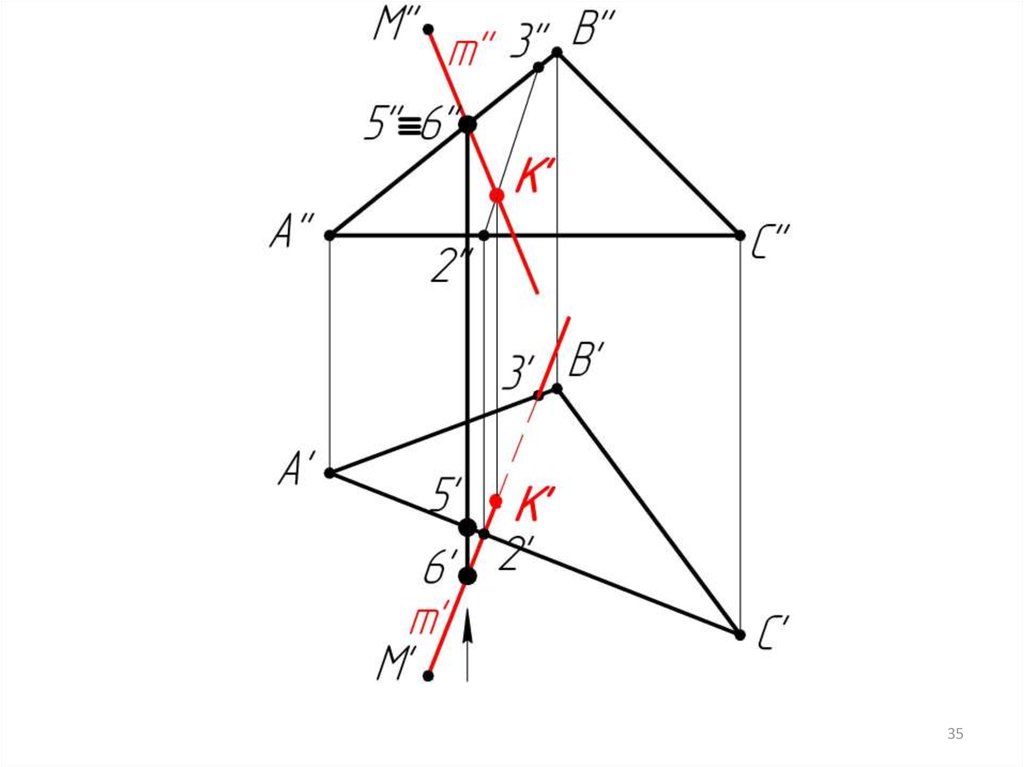
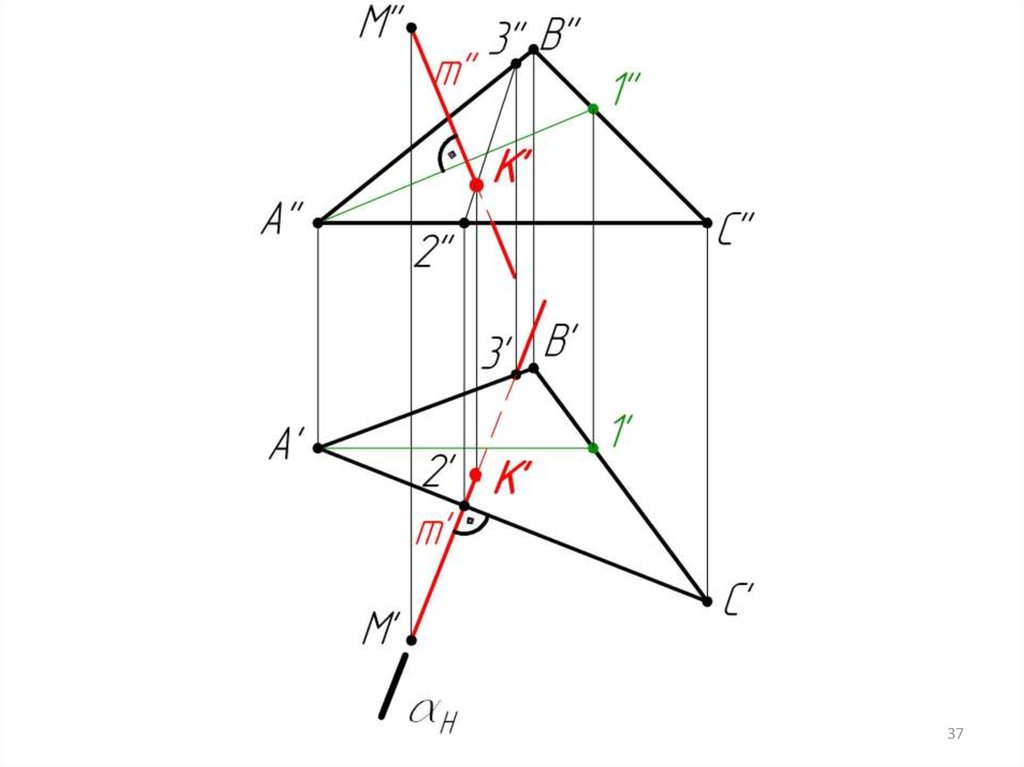
Пример 3: Определить расстояние от точки М до
плоскости АВС.
28

29.

29

30.

30

31.

31

32.

32

33.

33

34.

34

35.

35

36.

36

37.

37

38.

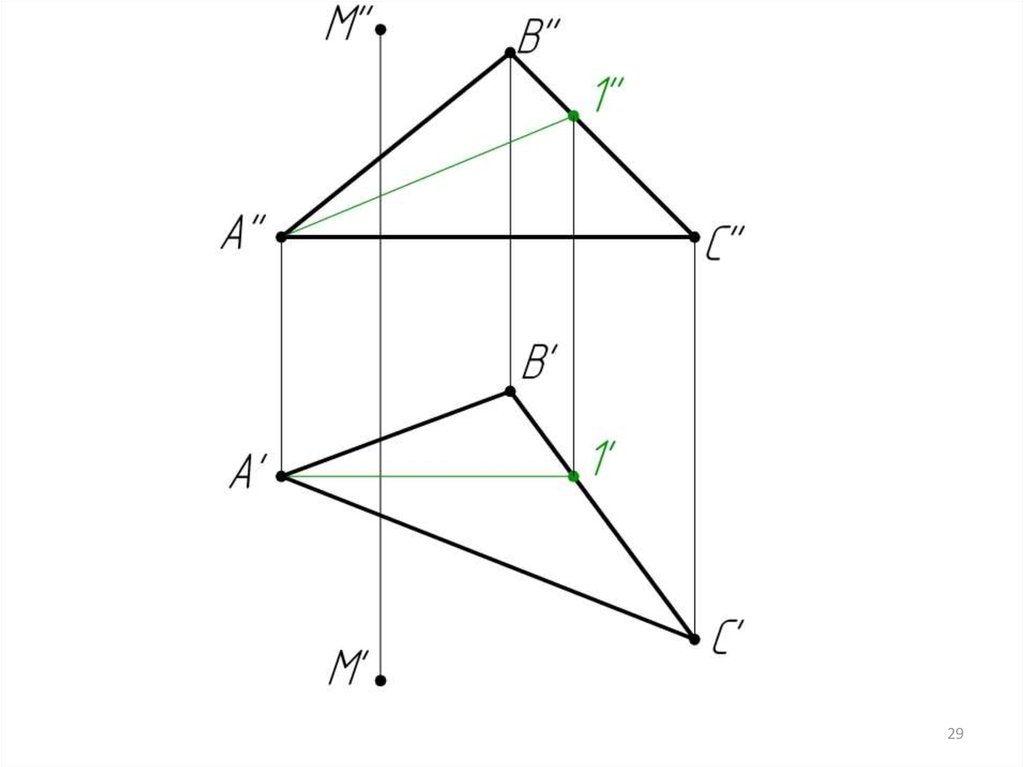
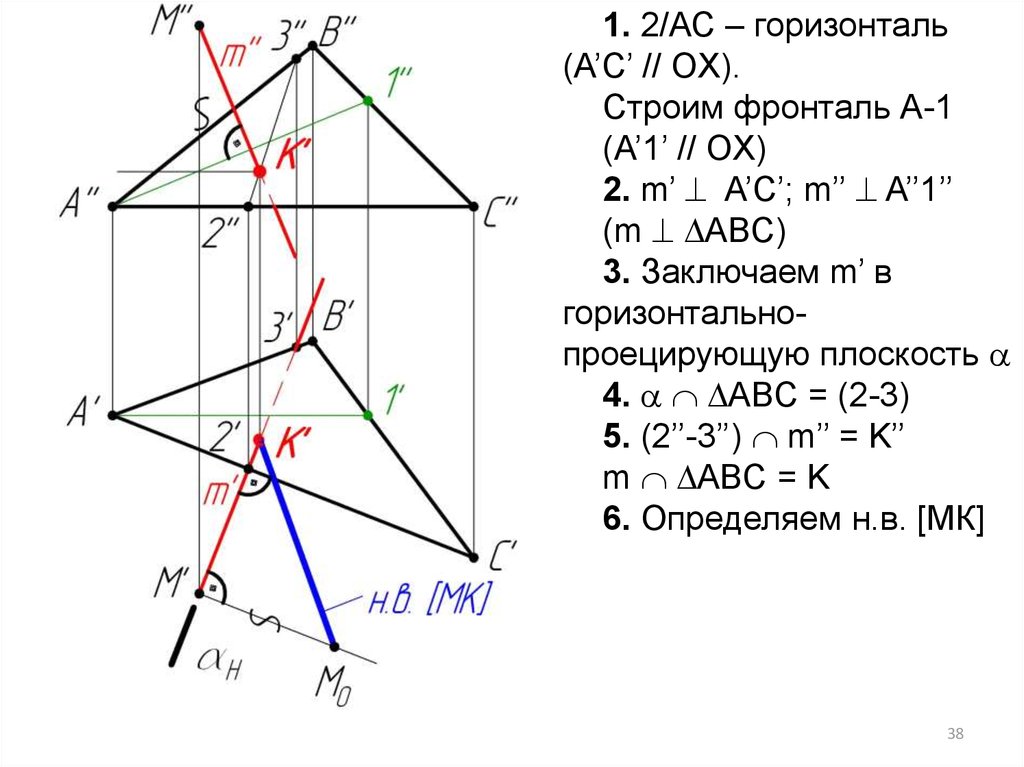
1. 2/АС – горизонталь
(A’C’ // OX).
Строим фронталь А-1
(А’1’ // OX)
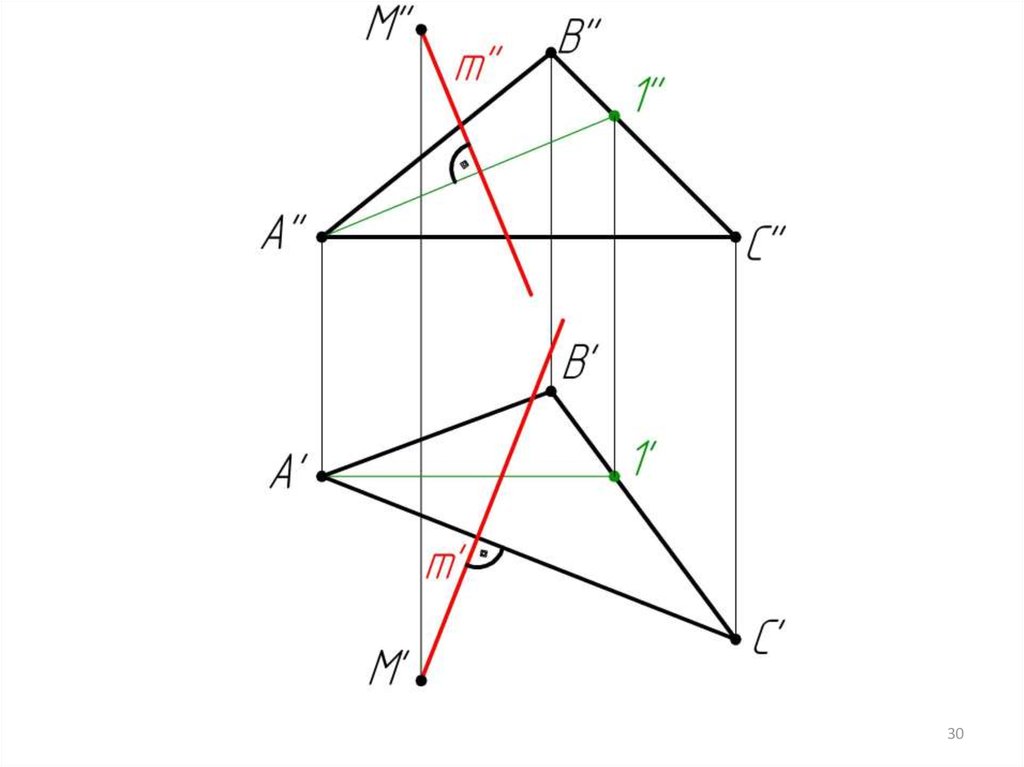
2. m’ A’C’; m’’ A’’1’’
(m ABC)
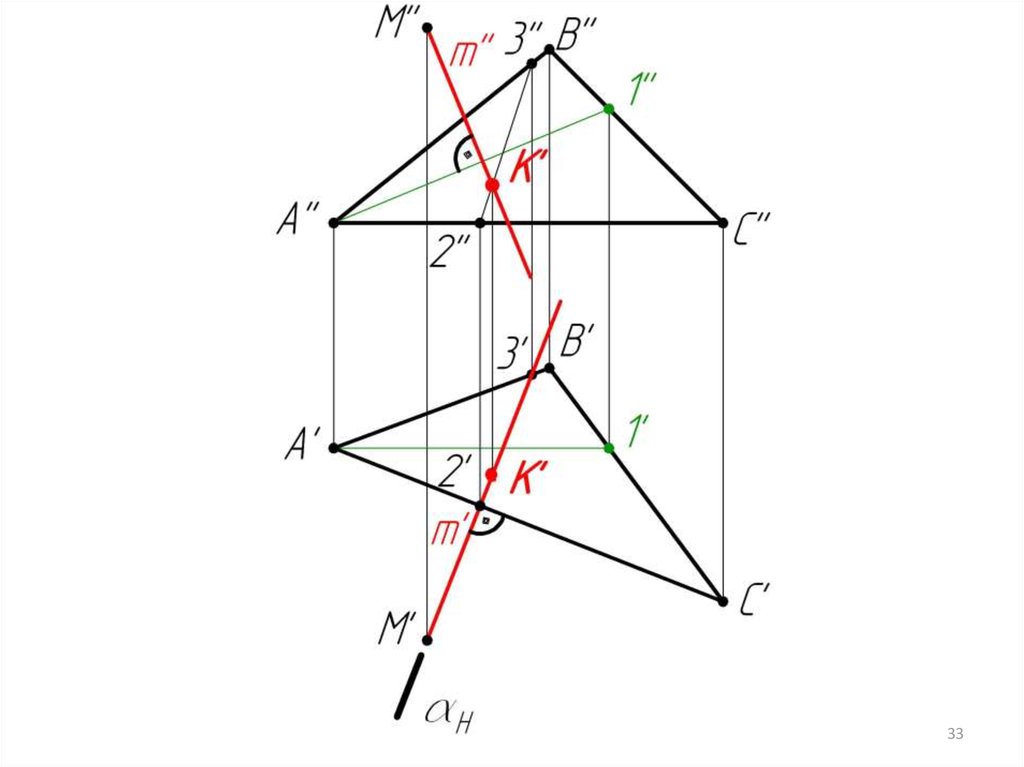
3. Заключаем m’ в
горизонтальнопроецирующую плоскость
4. ABC = (2-3)
5. (2’’-3’’) m’’ = K’’
m ABC = K
6. Определяем н.в. [МК]
38

39.

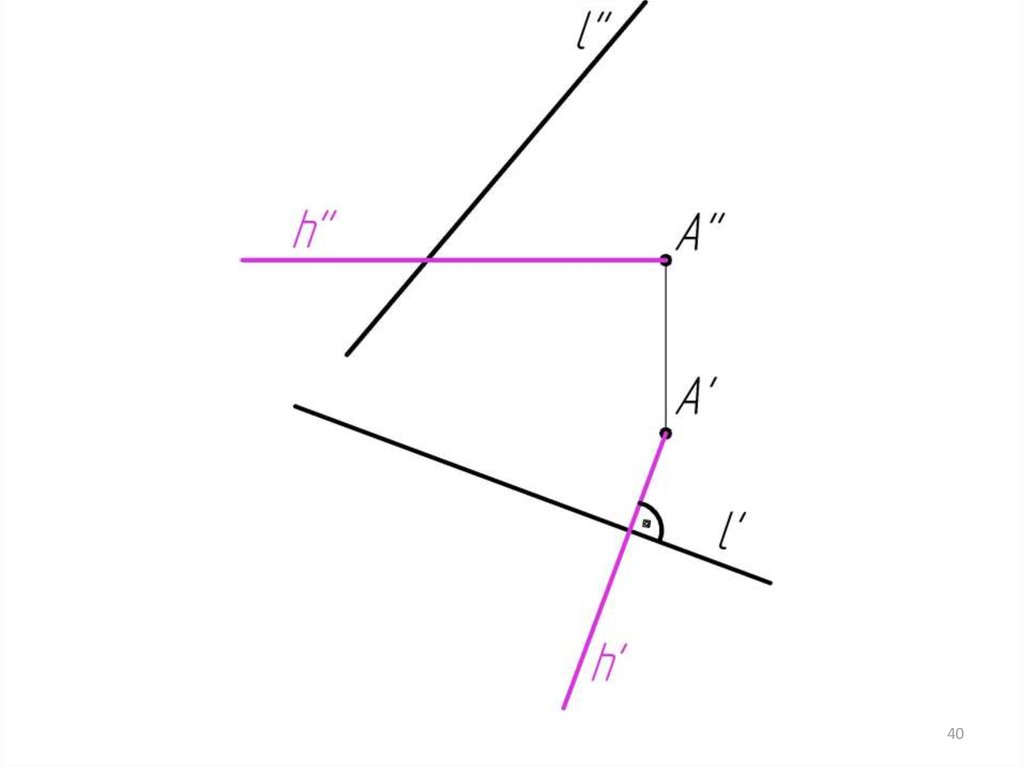
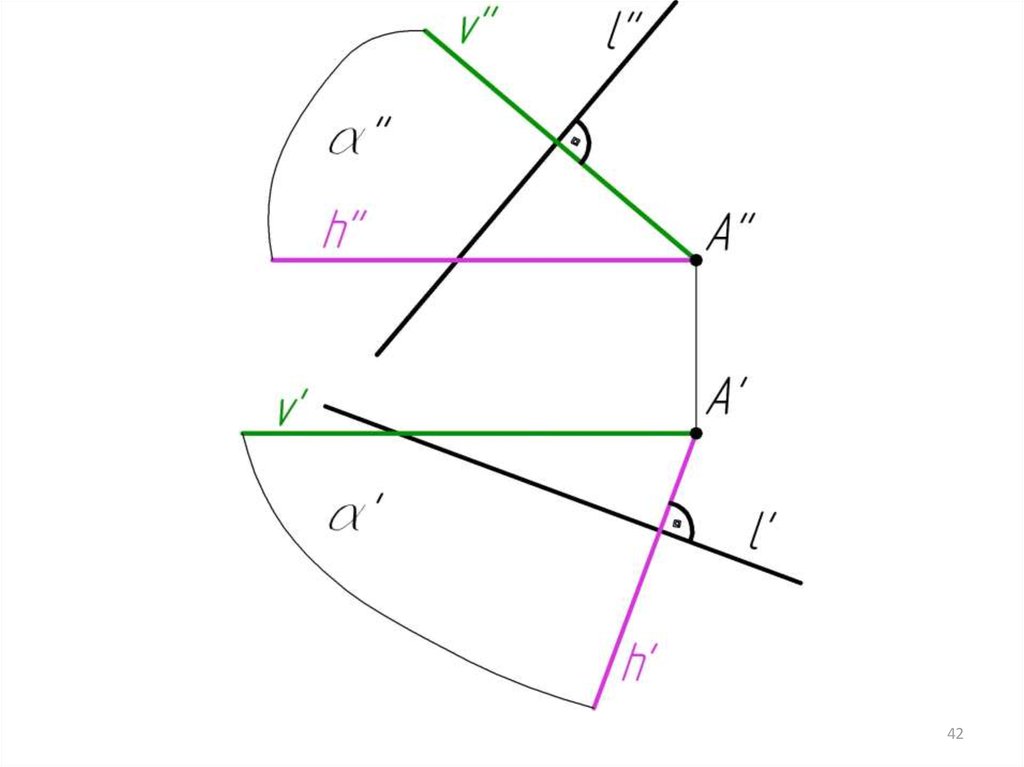
Пример 4: Через точку
перпендикулярную прямой l.
А
провести
плоскость,
39

40.

40

41.

41

42.

42

43.

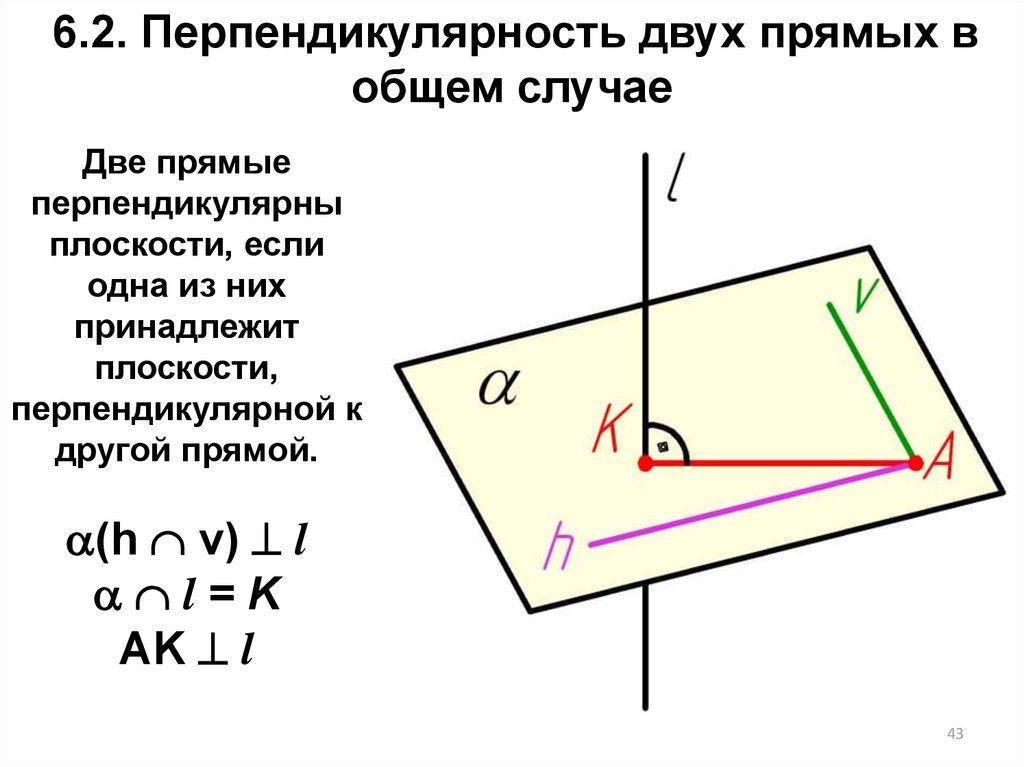
6.2. Перпендикулярность двух прямых в
общем случае
Две прямые
перпендикулярны
плоскости, если
одна из них
принадлежит
плоскости,
перпендикулярной к
другой прямой.
(h v) l
l=K
AK l
43

44.

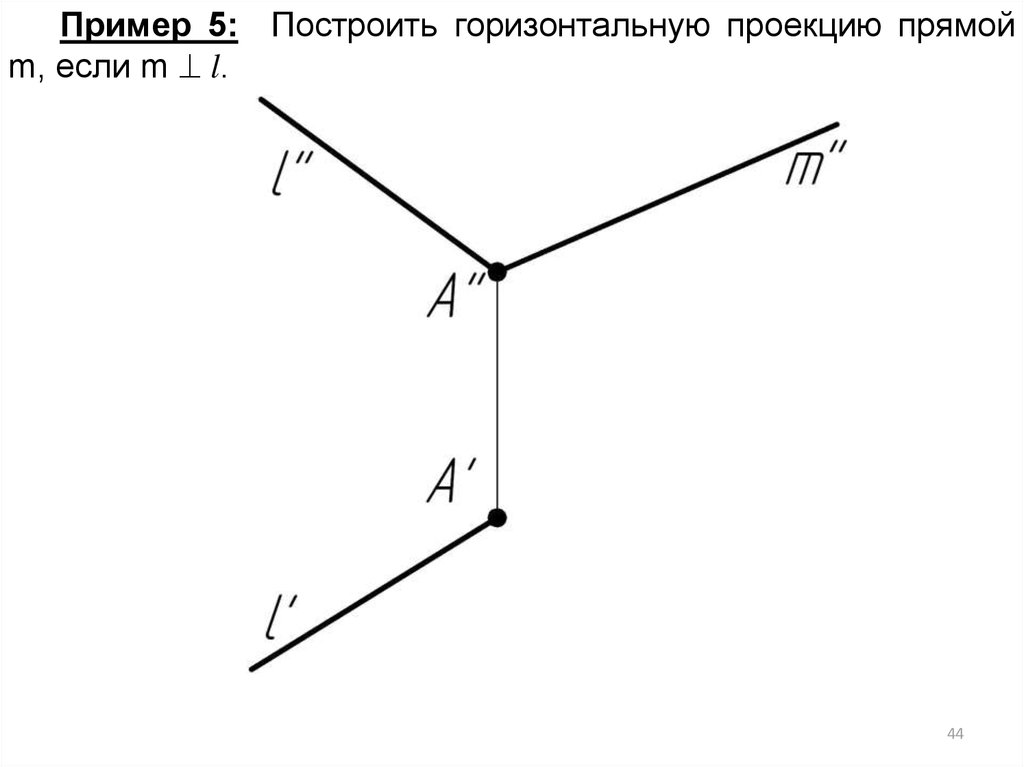
Пример 5: Построить горизонтальную проекцию прямой
m, если m l.
44

45.

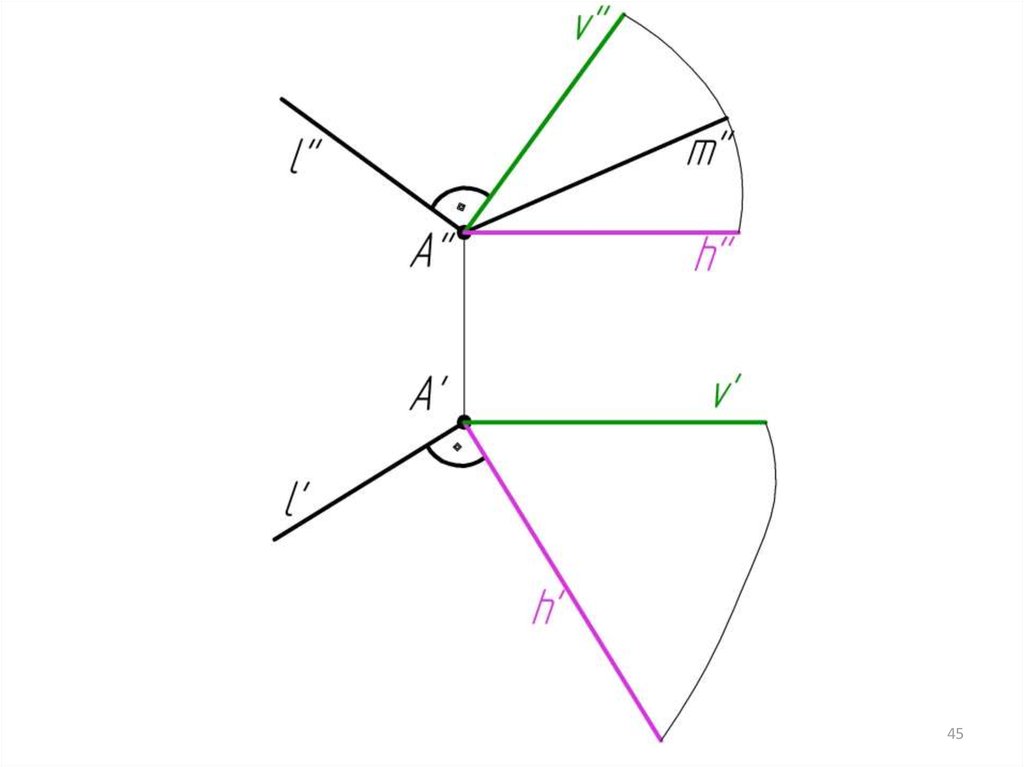
45

46.

46

47.

47

48.

Алгоритм решения:
1. (h v) l; A
2. m ; (1-2) m = M
(1-2)
48

49.

6.3. Перпендикулярность двух плоскостей
Две плоскости перпендикулярны, если одна из них
проходит через прямую, перпендикулярную другой
плоскости.
49

50.

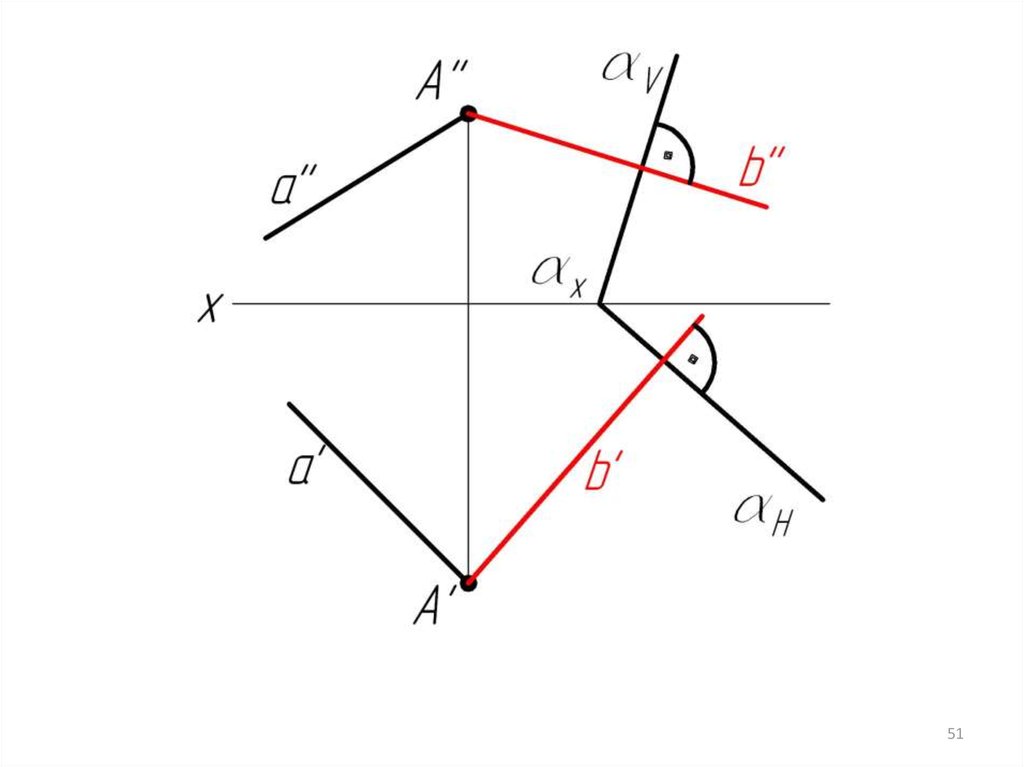
Пример 6: Через прямую а провести плоскость .
Плоскость задана следами.
50

51.

51

52.

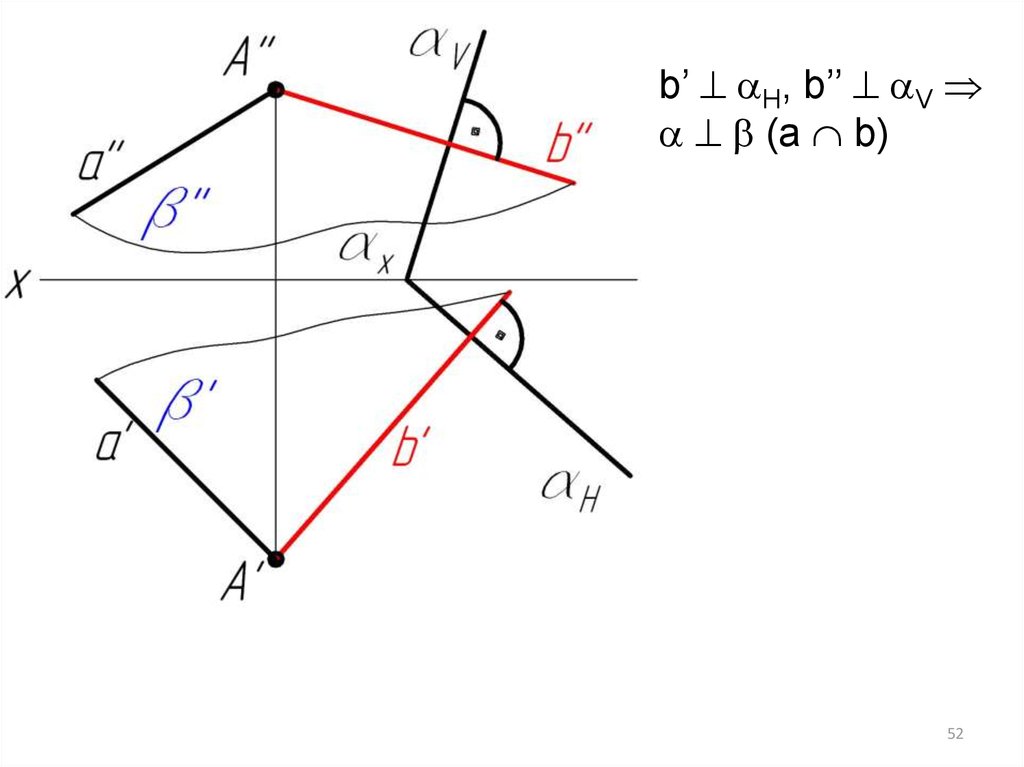
b’ H, b’’ V
(a b)
52

53.

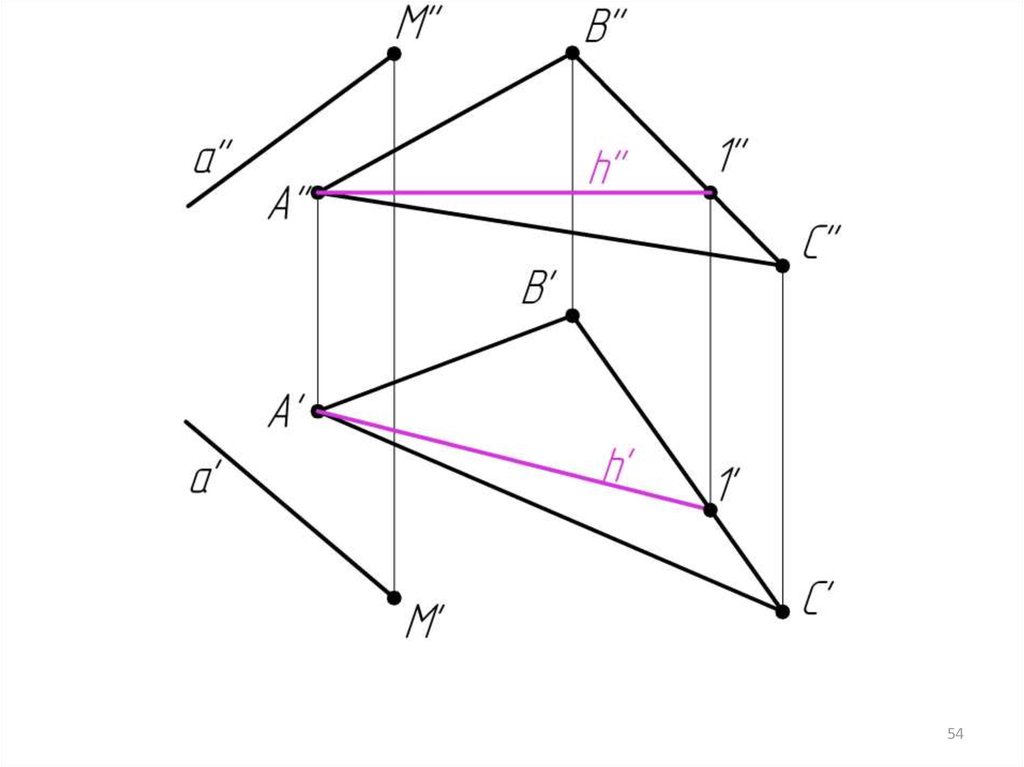
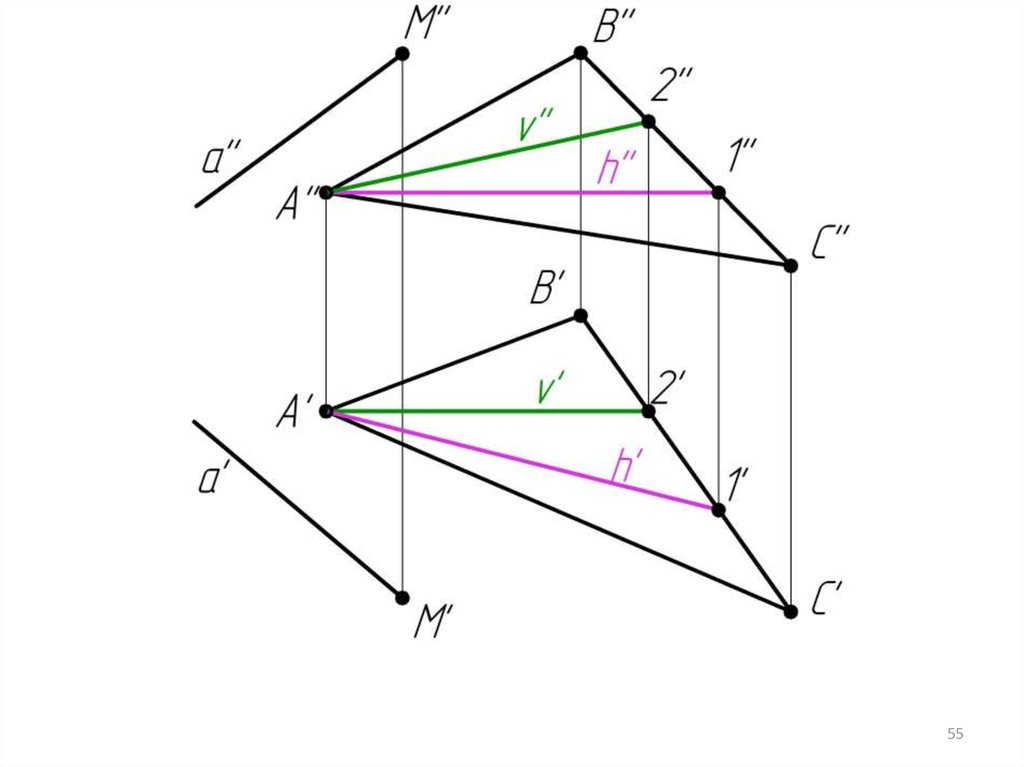
Пример 7: Через прямую а провести плоскость .
53

54.

54

55.

55

56.

56

57.

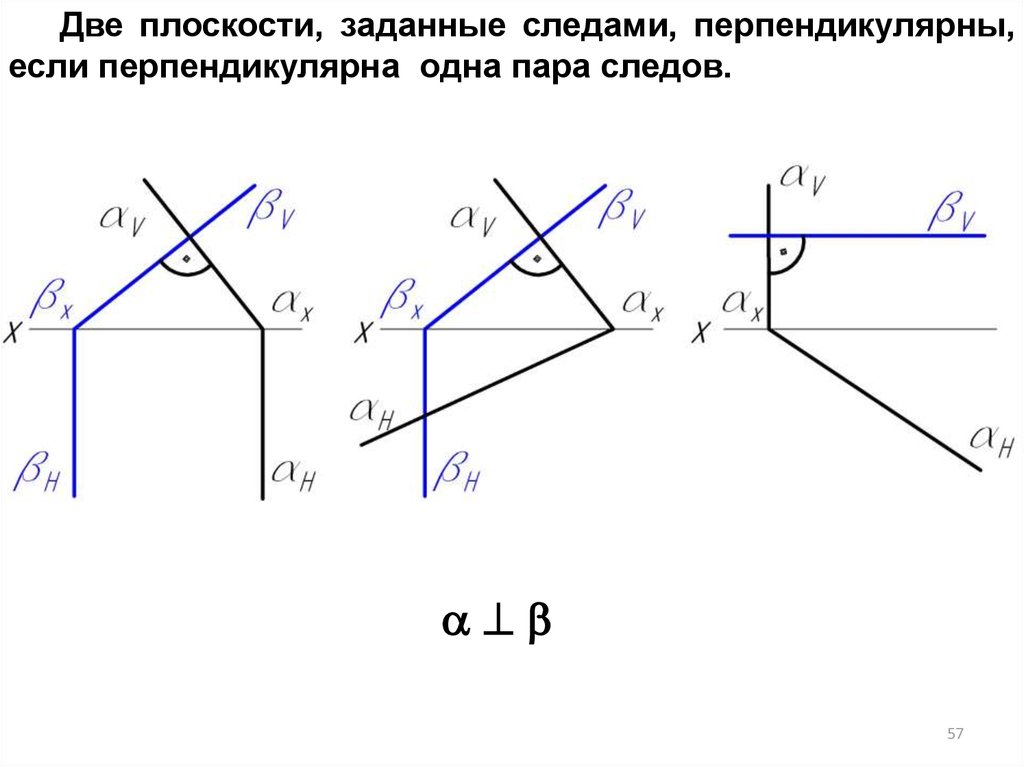
Две плоскости, заданные следами, перпендикулярны,
если перпендикулярна одна пара следов.
57

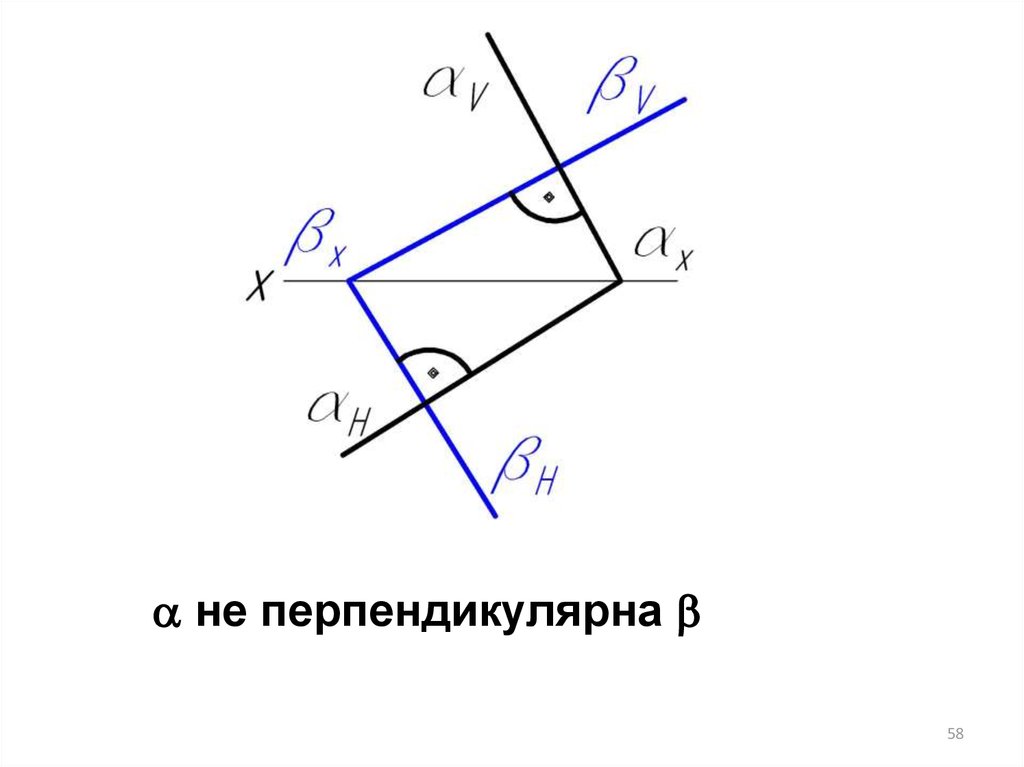
58.

не перпендикулярна
58