Similar presentations:
Интерференция света
1.
Лекция 8ИНТЕРФЕРЕНЦИЯ
СВЕТА
Вопросы:
1. Когерентность и монохроматичность
световых волн. Условия наблюдения интерференции света.
2. Интерференция в тонких пленках.
3. Применение интерференции света.
2.
Интерференция – проявление волновой природы света.Интерференция света – это пространственное перераспределение светового потока при наложении двух (или
нескольких) световых волн, приводящее к образованию
устойчивой по времени картины чередования светлых
полос (максимумов интенсивности) и темных полос
(минимумов интенсивности).
Интерферировать могут только когерентные световые волны.
Условию когерентности удовлетворяют монохроматические
волны – волны одной определенной и строго постоянной частоты:
ω = const. (длины волны: λ = const.), разность фаз которых в
каждой точке Δφ = const.
3.
Реальные источники света не являются строго монохроматическими и когерентными:• излучение всегда имеет статистический характер
(атомы светового источника излучают независимо друг
от друга в случайные моменты времени, и излучение
каждого атома длится очень короткое время 10 8 с);
• через время порядка τ вся совокупность излучающих
атомов обновляется, и поэтому когерентность может
существовать только на интервалах времени порядка τ.
В излученных атомами отдельных
волновых цугах всегда содержится
спектр частот Δω, а их начальные
фазы никак не связаны друг с другом.
2
Таким образом, независимые источники света (кроме лазеров) всегда являются некогерентными и не позволяют
получить интерференционную картину.
4.
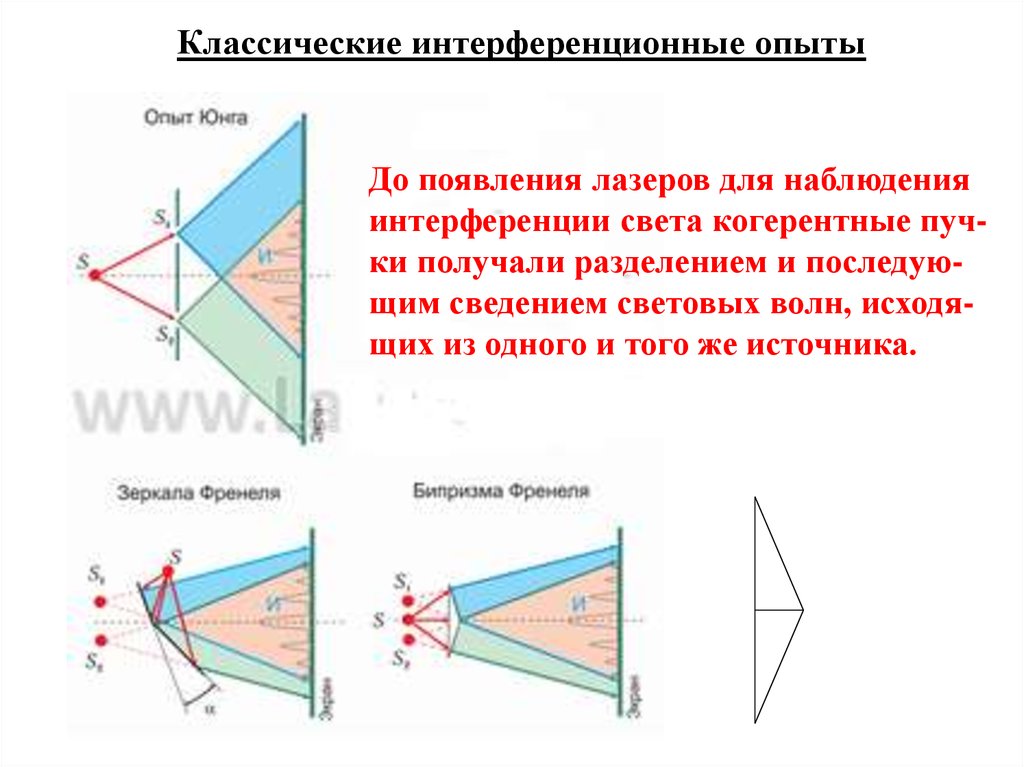
Классические интерференционные опытыДо появления лазеров для наблюдения
интерференции света когерентные пучки получали разделением и последующим сведением световых волн, исходящих из одного и того же источника.
5.
Средняя продолжительность одного цуга принимается завремя когерентности ког , а величина lког с ког называется длиной когерентности.
Условия наблюдения интерференции света:
• условие временной когерентности (определяется степенью
монохроматичности световых волн Δλ/λ): оптическая разность хода интерферирующих волн не может превышать
длину когерентности (Δ < lког). На практике это приводит
к существованию предельного наблюдаемого порядка интерференционных максимумов mпред = λ/Δλ. n(r2 r1 )
• условие пространственной когерентности (определяется
размерами и взаимным расположением источников света):
расстояние между источниками должно быть много меньше
расстояния от источников до точки наблюдения (d << L).
d
L
6.
Задача об интерференции волн сводится к задачео сложении колебаний с одинаковыми частотами,
но с разными фазами.
E A1cos t kr1 A2cos t kr2 Acos t
E – модуль вектора напряженности электрического поля
(светового вектора) волны; k = 2 / – волновое число.
Вместо амплитуды светового вектора А можно пользоваться
величиной интенсивности световой волны I – усредненным
по времени модулем вектора плотности потока энергии (вектора Умова-Пойнтинга):
1 2 0
I E H A
2
0
7.
Результат сложения световых векторов:А А1 А2 2 А1 А2 cos(k геом )
2
или:
где
2
2
I I1 I 2 2 I1I 2 cos(k геом )
геом r2 r1 – геометрическая разность хода
интерферирующих волн.
При интерференции световых волн формируется устойчивая
картина чередования светлых и темных полос:
8.
Если световые волны распространяются в среде с показателем преломления n ≠ 1, то условия максимумов и минимумовформулируются для оптической разности хода Δ = n·Δгеом:
1) условие интерференционных максимумов
(колебания световых векторов происходят в одинаковой фазе)
2m
0
2
т 0 , (m = 0, ± 1, ± 2, ... – порядок максимума)
I1 = I2 = I0 имеем:
Imax = 4I0 (усиление света);
В частном случае при
2) условие интерференционных минимумов
(колебания световых векторов происходят в противофазе)
2m 1
0
2
, (m = 0, ± 1, ±2, ... – порядок минимума)
В частном случае при
I1 = I2 = I0
имеем:
Imin = 0 (гашение света).
9.
Расчет интерференционной картины от двух источниковL22 L2 x d 2
M
2
L1
x
d
0
d/2
L22 L12 2 xd
Так как L >> d, то:
d/2
L2
S2
L12 L2 x d 2
2
S1
L
Э
2 xd
2 xd xd
L2 L1
L2 L1 2 L
L
Применяя условия максимумов и минимумов, находим координаты хmax и хmin:
1 L
L
xmax m 0 ; xmin m 0 m 0, 1, 2, ...
2 d
d
L
L
L
x m m 1 – ширина интерференционd
d
d
ной полосы.
10.
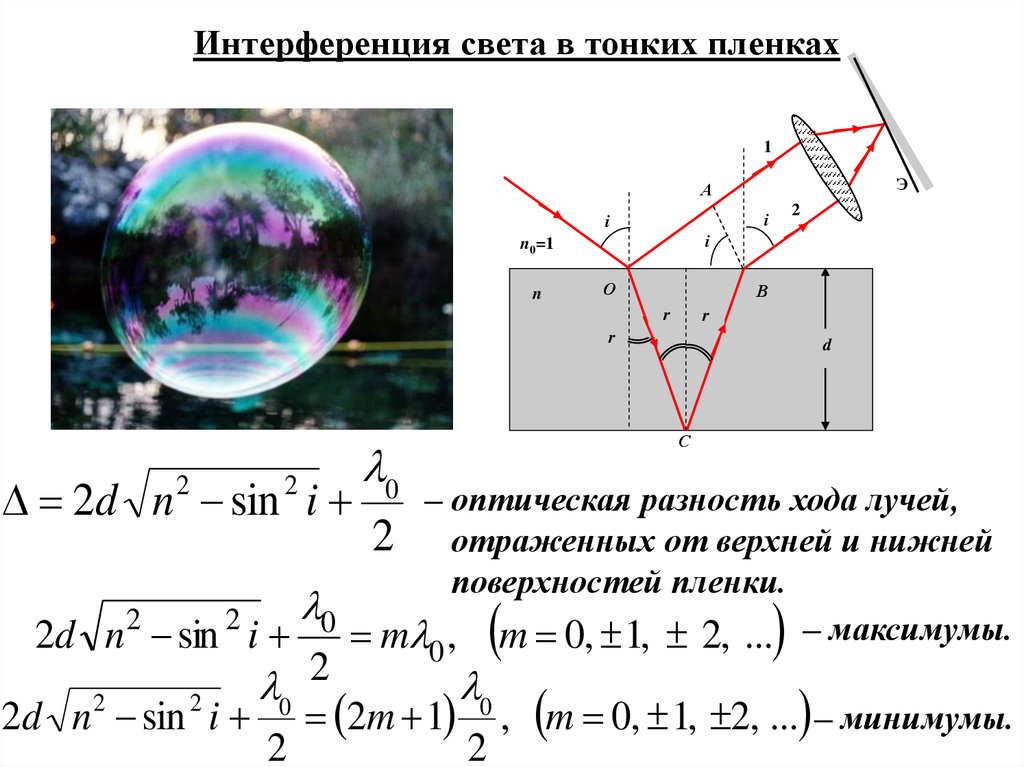
Интерференция света в тонких пленках1
Э
А
i
n0=1
n
2
i
i
О
В
r
r
r
С
0
2d n sin i
2
2
d
2
– оптическая разность хода лучей,
отраженных от верхней и нижней
поверхностей пленки.
0
2
2
2d n sin i m 0 , m 0, 1, 2, ... – максимумы.
2
0
2
2
0
2d n sin i 2m 1 , m 0, 1, 2, ... – минимумы.
2
2
11.
Условия максимумов и минимумов при интерференциив тонких пленках зависят при постоянных значениях n,
0 от угла падения i и толщины пленки d, в зависимости
от этого различают два типа интерференционной
картины: линии равного наклона и линии равной
толщины.
Линиями равного наклона называют интерференционную
картину, возникающую в результате наложения отраженных
лучей, падающих на плоскопараллельную пленку под одинаковыми углами.
Линиями равной толщины называют интерференционную
картину, возникающую в результате наложения лучей,
отраженных пленкой переменной толщины от мест с одинаковой толщиной.
12.
Кольца НьютонаКольца Ньютона классический пример
линий равной толщины.
R
R2 = r2 + (R – d)2
2
2R
d
r
d << R
2
0
r
0
2d
2
R 2
d
r
Условие максимума радиус светлого
кольца в отраженном свете:
1
r 0 R m
2
тем
r m 0 R (m – номер кольца)
св
Условие минимума
радиус темного кольца
в отраженном свете:
13.
Пример применения интерференции светаПросветление оптики –
это нанесение на свободные поверхности линз тонких прозрачных пленок с
показателем преломления
n меньшим, чем у стекла:
1 < nпл < nст.
1,2
1
2
n0=1
d
nпл
nст
2n d 2m 1
пл
0
2
Задачи, решаемые с помощью просветленной оптики:
• устранение многочисленных отражений света в
оптических системах,
содержащих большое количество линз, и, как следствие, – уменьшение потерь светового потока;
• устранение бликов, вызванных отражением от
поверхности линз и приводящих к демаскировке местонахождения оптического прибора.











 physics
physics








