Интерференция света. Лекции 2

1. Лекции 2

Сегодня: вторник, 24 октября 2023 г.
Лекции 2
Интерференция света
Содержание лекции:
• Основные характеристики световых волн
• Принцип Гюйгенса
• Интерференция
• Классические интерференционные опыты
• Интерференция в тонких пленках
• Пространственная когерентность
• Временная когерентность
1

2. Оптическое излучение

Оптика – (от греч. optike – наука о зрительных
восприятиях) – раздел физики, в котором
изучаются оптическое излучение (свет), его
распространение и явления, наблюдаемые при
взаимодействии света и вещества.
Оптическое
излучение
представляет
собой
электромагнитные волны, и поэтому оптика – часть
общего учения об электромагнитном поле.
2

3.

Оптический диапазон длин волн ограничен с
одной стороны рентгеновскими лучами, а с другой –
микроволновым диапазоном радиоизлучения.
Такое ограничение условно и в значительной степени определяется общностью
3
технических средств и методов исследования явлении в указанном диапазоне.

4.

4

5.

Четыре закона геометрической
оптики,
установленные опытным путем:
1. закон прямолинейного
распространения света;
2. закон независимости световых
лучей;
3. закон отражения;
4. закон преломления света.
5

6.

1.Закон прямолинейного распространения света:
свет в оптически однородной
распространяется прямолинейно.
среде
Доказательством этого закона является наличие
тени с резкими границами от непрозрачных
предметов при освещении их источниками малых
размеров.
6

7.

Тщательные эксперименты показали, однако, что этот
закон нарушается, если свет проходит через очень малые
отверстия, причем отклонение от прямолинейности
распространения тем больше, чем меньше отверстия.
Огибание электромагнитными волнами препятствий и проникновение
их в область геометрической тени наиболее отчетливо обнаруживается в
тех случаях, когда размер огибаемых препятствий соизмерим с длиной
7
волны

8.

2. Закон независимости световых пучков:
эффект, производимый отдельным пучком, не
зависит от того, действуют ли одновременно
остальные пучки или они устранены.
Разбивая световой поток на отдельные световые пучки
(например, с помощью диафрагм), можно показать, что действие
выделенных световых пучков независимо.
8
Производимое одним пучком действие не зависит от наличия других пучков

9.

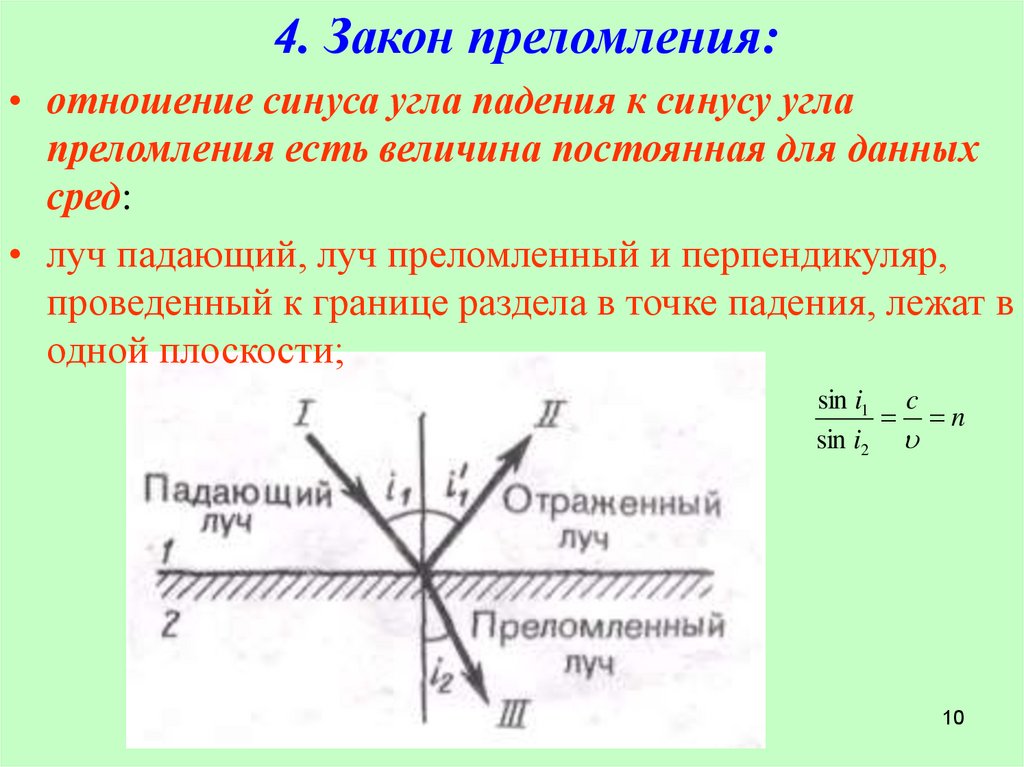
3. Закон отражения
• Угол падения равен углу отражения.
• Отраженный луч лежит в одной плоскости
с падающим лучом и перпендикуляром, к
границе раздела двух сред в точке падения.
S1 - отражаюшая поверхность; S2 - плоскость падения; АО падающий луч; ОВ - отраженный луч; ON - нормаль к отражающей
9
поверхности.

10.

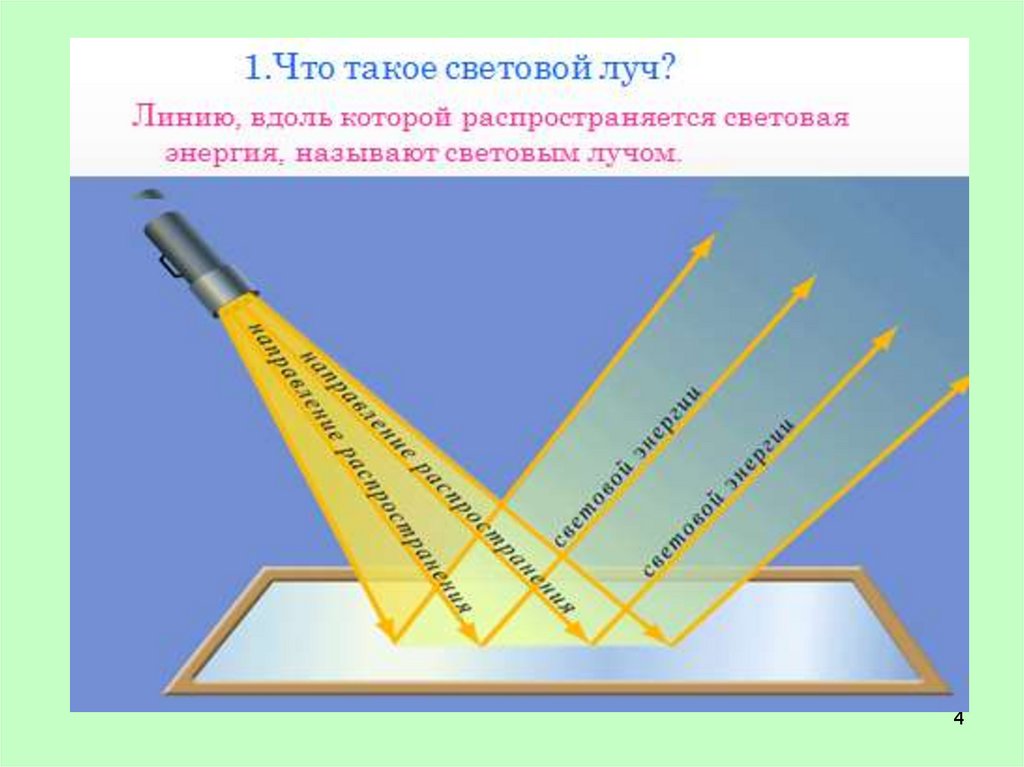
4. Закон преломления:
• отношение синуса угла падения к синусу угла
преломления есть величина постоянная для данных
сред:
• луч падающий, луч преломленный и перпендикуляр,
проведенный к границе раздела в точке падения, лежат в
одной плоскости;
sin i1 c
n
sin i2
10

11.

Начало XIX в. характеризуется интенсивным
развитием математической теории колебаний и
волн и ее приложением к объяснению ряда
оптических явлений. В связи с работами Т. Юнга и
О. Френеля, победа временно перешла к волновой
оптике:
1801 г. Т. Юнг сформулировал принцип
интерференции и объяснил цвета таких пленок;
1818 г. О. Френель получает премию
Парижской Академии за объяснение дифракции;
1840 г. О. Френель и Д. Арго исследуют
интерференцию
поляризованного
света
и
доказывают поперечность световых колебаний; 11

12.

1841 г. О. Френель строит теорию
кристаллооптических колебаний;
1849 г. А. Физо измерил скорость света и
рассчитал по волновой теории коэффициент
преломления воды n 1,33 , что совпало с
экспериментом;
1848 г. М. Фарадей открыл вращение
плоскости поляризации света в магнитном поле
(эффект Фарадея);
1860 г. Дж. Максвелл основываясь на
открытии Фарадея пришел к выводу, что свет
есть электромагнитные, а не упругие волны;
12

13.

1888 г. Г. Герц экспериментально исследовал
электромагнитное поле и подтвердил, что
электромагнитные волны распространяются
со скоростью света с = 3*108 м/с
1899 г. П.Н. Лебедев измерил давление света.
1900 г. Макс Планк показал, что излучение
абсолютно черного тела можно объяснить, если
предложить, что свет излучается не непрерывно,
а порциями, квантами с энергией E0 hν , где
13
ν – частота, h – постоянная Планка.

14. Основные характеристики световых волн

Корпускулярно-волновой дуализм:
свет в некоторых явлениях обладает свойствами,
присущими частицам (корпускулярная теория),
в других явлениях свойствами, присущими волнам
(волновая теория).
В данном разделе будем рассматривать свет
как электромагнитные волны.
14

15.

Световые волны:
Плоская волна:
E E0 cos t kx
Сферическая волна: E E0 cos t kr
r
E - вектор напряженности электрического поля;
Е0 – амплитуда;
r – расстояние до источника ;
k – волновое число;
φ – начальная фаза.
Световой вектор - вектор напряженности
электрического поля.
Его колебаниями обусловлено физиологическое,
фотохимическое и т.д. действие света.
15

16.

Отношение скорости световой волны в вакууме к
фазовой скорости в некоторой среде называется
абсолютным показателем преломления среды:
c
n
v
Поскольку
Получаем
c
v
- для большинства
n прозрачных сред (μ ≈ 1)
Значение n определяет оптическую плотность среды:
оптически более плотная среда – среда с бóльшим n;
оптически менее плотная среда – среда с меньшим n.
16

17.

Интенсивность света – модуль среднего по времени
значения плотности потока энергии, переносимой световой
волной:
I P E, H
P – вектор Пойнтинга
1 0 2
2
I
nE0 ~ nE0
2 0
В случае однородной среды (n = const) интенсивность
пропорциональна квадрату амплитуды световой волны
17

18.

В естественном свете колебания светового вектора
совершаются во всех направлениях, перпендикулярных к
лучу.
Излучение тела обусловлено волнами, испускаемыми его атомами:
длительность излучения атома ~ 10–8 с, за это время образуется цуг
волн (набор горбов и впадин) длиной ~ 3м.
Плоскость колебаний каждого цуга ориентирована случайным образом.
В результирующей волне (суперпозиции цугов от разных атомов) все
направления равновероятны.
18

19.

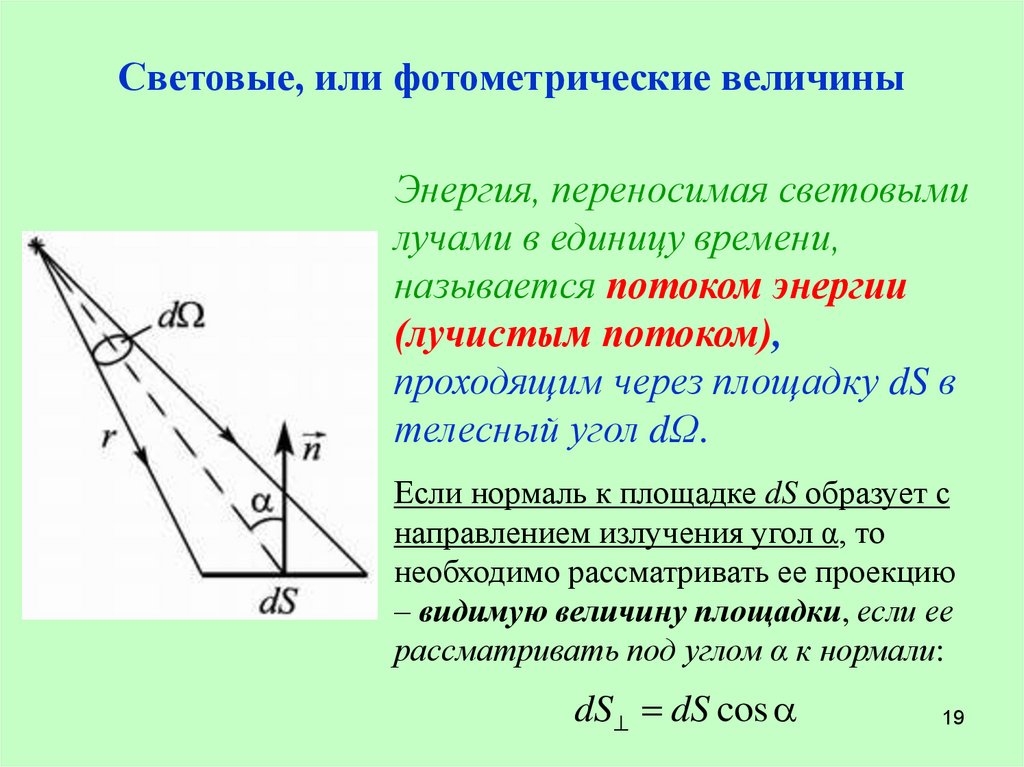
Световые, или фотометрические величины
Энергия, переносимая световыми
лучами в единицу времени,
называется потоком энергии
(лучистым потоком),
проходящим через площадку dS в
телесный угол dΩ.
Если нормаль к площадке dS образует с
направлением излучения угол α, то
необходимо рассматривать ее проекцию
– видимую величину площадки, если ее
рассматривать под углом α к нормали:
dS dS cos
19

20.

Силой света источника I в заданном направлении
называется световой поток, посылаемый им в этом
направлении и отнесенный к единице телесного угла.
Единицы измерения:
[I] = кд (кандела)
Световой поток для точечного источника
I d
1 люмен – это световой поток, посылаемый
источником с силой света в 1 канделу внутрь телесного
угла в 1 стерадиан:
1 лм = 1 кд · 1 ср
20

21.

Освещенностью Е некоторой поверхности называется
световой поток, падающий на единицу площади
освещаемой поверхности:
d
E
dS
1 лм
[E] = лк (люкс): 1 лк =
1 м2
Для точечного источника
I
E 2 cos - закон обратных квадратов:
r
- освещенность, создаваемая точечным источником, обратно
пропорциональна квадрату расстояния до него и прямо
пропорциональна косинусу угла между направлением падающих
лучей и нормалью к освещаемой поверхности.
21

22.

Для протяженных источников вводятся следующие понятия:
• Яркостью L называется световой поток, исходящий из
площадки dS в заданном направлении, отнесенный к единице
телесного угла и к единице ее видимой величины:
d
dI
L
d dS cos dS cos
где
d
dI
d
- сила света площадки dS в том
же направлении
Источники, яркость которых одинакова по всем направлениям,
называются ламбертовскими (косинусными):
dI ~ cos α
22

23.

• Светимостью М называется полный световой поток,
посылаемый единицей светящейся поверхности в одну
сторону (в телесный угол Ω = 2π):
Световой поток с единицы поверхности в телесный угол dΩ
равен
d L cos d
Тогда
/2
M L cos d 2 L cos sin d
0
Для ламбертовских источников (L = const):
M L
23

24.

1. Принцип Гюйгенса
Приближения геометрической оптики неправомерны при
описании процессов, происходящих при падении световой
волны на преграду с отверстиями:
• в приближении геометрической оптики свет за преградой
не проникает в область геометрической тени
• в действительности свет проникает в область
геометрической тени, причем проникновение тем больше,
чем меньше размеры отверстий. Если эти размеры сравнимы
с длиной волны, законы геометрической оптики совершенно
неправомерны.
24

25.

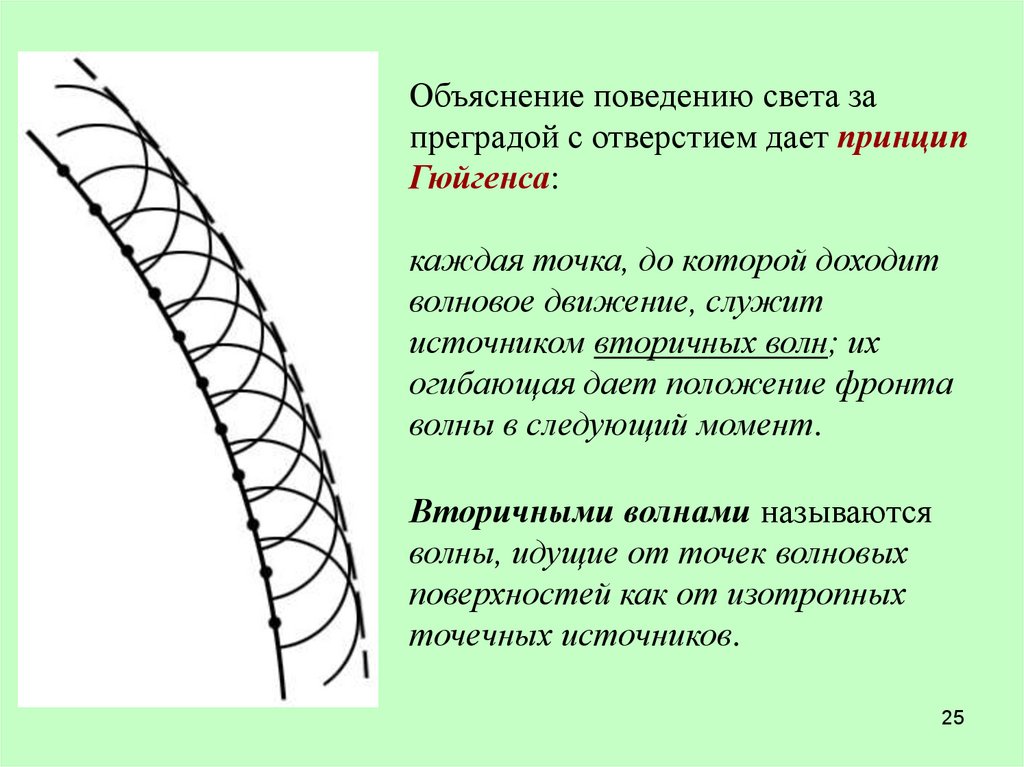
Объяснение поведению света за
преградой с отверстием дает принцип
Гюйгенса:
каждая точка, до которой доходит
волновое движение, служит
источником вторичных волн; их
огибающая дает положение фронта
волны в следующий момент.
Вторичными волнами называются
волны, идущие от точек волновых
поверхностей как от изотропных
точечных источников.
25

26.

2. Интерференция
Рассмотрим две волны одинаковой частоты, накладывающиеся
друг на друга и возбуждающие в некоторой точке пространства
колебания одинакового направления:
x1 A1 cos( t 1 )
x2 A2 cos( ωt φ 2 )
Амплитуда результирующего колебания в данной точке есть
A
2
2
2
A1 A2 2 A1 A2сos( φ 2 φ1 )
Если разность фаз возбуждаемых волнами колебаний остается
постоянной во времени, то такие волны называются
когерентными
26

27.

В случае некогерентных волн:
2 1 const
- разность фаз непрерывно меняется
(вследствие ее среднее по времени
значение равно нулю)
Интенсивность результирующей волны всюду одинакова и
равна сумме интенсивностей, создаваемых каждой из волн в
отдельности:
J J1 J 2
В случае когерентных волн:
2 1 const
- разность фаз постоянна во времени (но
для каждой точки пространства своя)
27

28.

Интенсивность результирующей волны
J J1 J 2 2 J1 J 2 cos(φ 2 φ1 )
2 J1J 2 cos(φ2 φ1 )
- интерференционный член
• Если
cos( φ 2 φ1 ) 0 , интенсивность I > I1 + I2
• Если
cos( φ 2 φ1 ) 0 , интенсивность I < I1 + I2
Таким образом, при наложении когерентных световых волн
происходит перераспределение светового потока в
пространстве с образованием максимумов и минимумов
интенсивности – интерференция.
28

29.

В случае, если интенсивность обоих источников одинакова:
• в максимуме
I = 4I1
• в минимумах I = 0
Естественные источники света некогерентны, поскольку
излучение светящегося тела складывается из волн,
испускаемыми многими атомами (причем фаза нового цуга не
связана с фазой предыдущего цуга).
Когерентные волны можно получить разделением волны,
излучаемой одним источником, на 2 части:
• если полученные волны заставить пройти разные оптические
пути (их разность должна быть небольшой, т.к. складывающиеся
колебания должны принадлежать одному цугу волн)
• далее наложить их друг на друга, - образуется
интерференционная картина.
29

30.

Рассмотрим данный процесс детально:
пусть в т. О происходит разделение волны на 2 когерентные (φ0 = 0):
I волна проходит путь s1 в среде с показателем преломления n1;
II волна проходит путь s2 в среде с показателем преломления n2
В точке Р:
I волна возбудит колебание
s1
x1 A1 cos t
v1
II волна
где v1. v2 – фазовые скорости волн.
s2
x2 A2 cos t
v2
30

31.

Можно показать, что разность фаз двух когерентных волн есть
2
2 1
0
где λ0 – длина волны в вакууме;
Δ n2 s2 n1s1 L2 L1 – оптическая разность
хода
L – оптическая длина пути.
• Если оптическая разность хода равна целому числу длин волн
Δ mλ 0 (m 0, 1, 2, ...) - условие интерференционного
максимума
В этом случае разность фаз кратна 2π, колебания синфазны.
m - порядок интерференции.
31

32.

• Если оптическая разность хода равна полуцелому числу длин
волн:
λ0
Δ (2m 1)
(m 0, 1, 2, ...)
2
- условие
интерференционного
минимума.
В этом случае разность фаз равна ±(2m + 1)π,
колебания находятся в противофазе.
Расстояние между интерференционными полосами – это
расстояние между соседними максимумами.
Ширина интерференционной полосы – расстояние между
соседними минимумами интенсивности.
32

33.

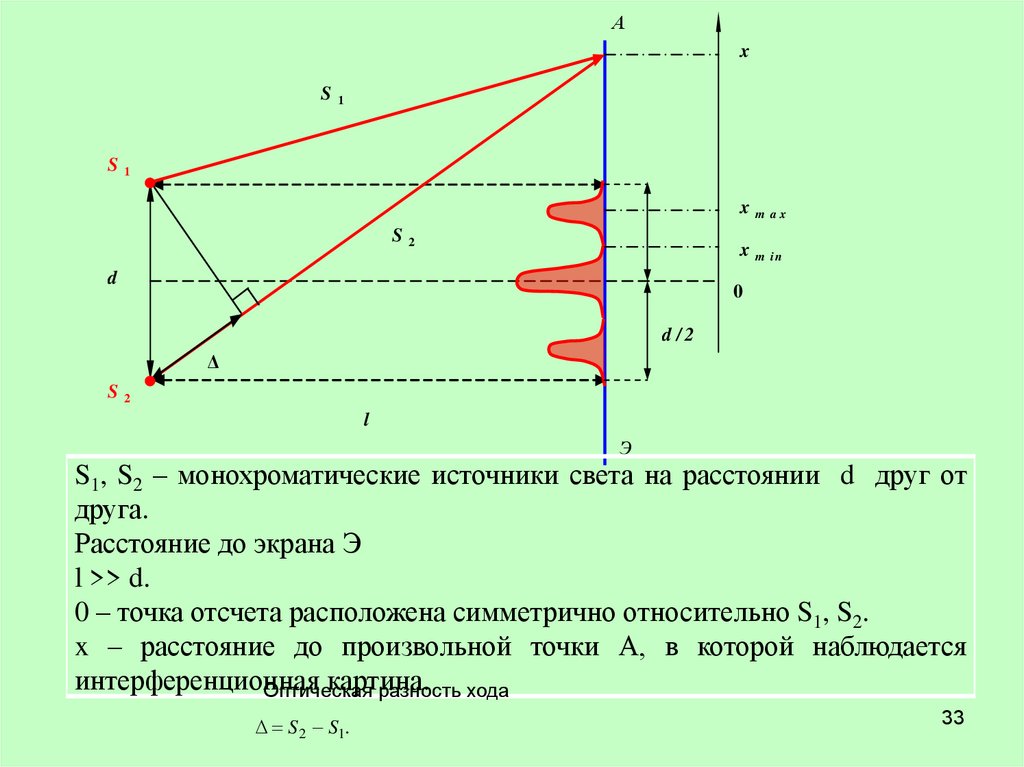
А
x
S1
S1
x m ax
S2
x m in
d
0
d /2
Δ
S2
l
Э
S1, S2 – монохроматические источники света на расстоянии d друг от
друга.
Расстояние до экрана Э
l >> d.
0 – точка отсчета расположена симметрично относительно S1, S2.
x – расстояние до произвольной точки А, в которой наблюдается
интерференционная
картина.
Оптическая
разность хода
S 2 S1.
33

34.

А
x
S1
S1
x m ax
S2
x m in
d
0
d /2
Δ
S2
l
Э
d
S 22 l 2 x
2
,
2
2
d
S12 l 2 x . S 22 S12 2 xd ,
2
S 22 S12 S 2 S1 S 2 S1 S 2 S1
2 xd
,
S 2 S1
если l d S1 S 2 2l
xd
.
l
34

35.

0
l
max 2m xmax m 0 (m 0,1,2....)
2
d
– интерференционный максимум
0
1 l
min 2m 1 xmin m 0
2
2
d
x
– интерференционный минимум
Расстояние между соседними максимумами или минимумами
– ширина интерференционной полосы
l
x 0 const.
d
35

36.

l 0
l 0 l
x xmin( m 1) xmin( m) 2 m 1
2m
0 .
d 2
d 2 d
m = 0 – главный max в точке 0.
m = n – максимум n-го порядка.
!!! Для немонохроматического света (например, белый свет)
только для m = 0 максимум для всех длин волн совпадает
(в середине экрана наблюдается белое пятно или полоса),
а по обе стороны расположены спектрально окрашенные
полосы 1, 2 и т.д. порядков
36

37.

Одной из важных характеристик наблюдаемой интерференционной
картины является видность V, которая характеризует контраст
интерференционных полос:
I max I min
V
I max I min
где Imax и Imin – соответственно максимальное и минимальное
значения интенсивности в интерференционной картине.
При интерференции монохроматических волн видность V зависит
только от соотношения интенсивностей интерферирующих
пучков света :
2 I1 I 2
V
I1 I 2
37

38.

Интерференция двух волн на поверхности жидкости, возбуждаемых
вибрирующими стержнями
Волны распространяются в противоположных направлениях и интерферируют с
образованием стоячей волны. Красный шарик расположен в пучности стоячей
волны и колеблется с максимальной амплитудой. Параллелепипед расположен в
узле интерференционной картины и амплитуда его колебаний равна нулю (он
совершает лишь вращательные движения, следуя наклону волны)
38

39.

Интерференция поверхностных волн от двух точечных источников
В точках, для которых r2 - r1 = λ (1/2+n), поверхность жидкости не колеблется
(узловые точки (линии))
39

40.

Интерференция круговой волны в жидкости
с её отражением от стенки
Расстояние от источника до стенки r кратно целому числу полуволн, исходная
круговая волна интерферирует с волной, отражённой от стенки. Согласно пр.
Гюйгенса, отражённая волна совпадает с той, которая бы возбуждалась
фиктивным точечным источником, расположенным по другую сторону стенки
симметрично реальному источнику. Т.к. r кратно целому числу полуволн, то справа
от источника на оси соединяющей фиктивный и реальный источник разность фаз
будет кратна целому числу волн, и круговая волна накладывается в фазе с волной,
отражённой от стенки, увеличивая высоту гребней в интерференционной картине40

41.

Интерференция круговой волны в жидкости
с её отражением от стенки
Расстояние между точечным источником и стенкой кратно целому числу
полуволн плюс четверть волны. При этом справа от источника круговая
волна накладывается в противофазе с волной, отражённой от стенки. В
результате в широкой полосе справа от источника колебания жидкости
отсутствуют
41

42.

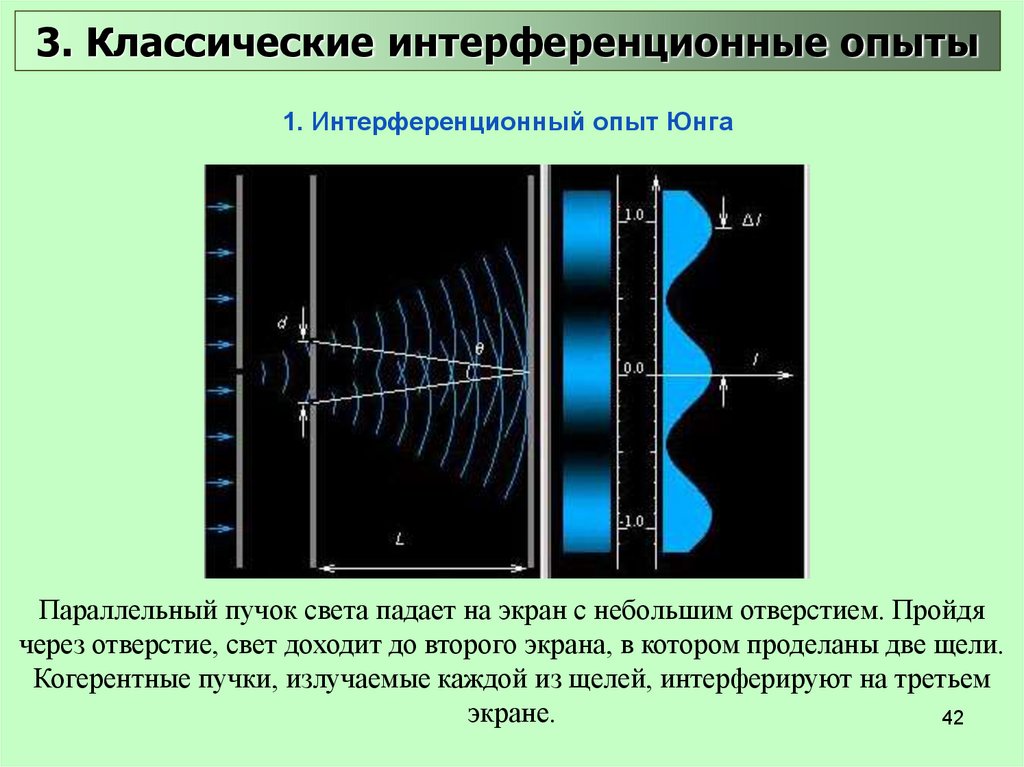
3. Классические интерференционные опыты
1. Интерференционный опыт Юнга
Параллельный пучок света падает на экран с небольшим отверстием. Пройдя
через отверстие, свет доходит до второго экрана, в котором проделаны две щели.
Когерентные пучки, излучаемые каждой из щелей, интерферируют на третьем
экране.
42

43.

l - расстояние от щелей до экрана;
d – расстояние между щелями.
l d
Главный (нулевой) максимум соответствует m = 0 (по центру),
по обе стороны от него располагаются максимумы (минимумы)
1-го порядка (m = 1), 2-го (m = 2) и т.д…
43

44.

2. Зеркала Френеля
Свет от источника S отражается от двух зеркал, расположенных под достаточно
малым углом φ. Волны, падающие на экран, могут рассматриваться как волны
от двух мнимых изображений источника S в обоих зеркалах. Непрозрачный
экран Э1 преграждает свету путь от источника S к экрану Э
44

45.

3. Бипризма Френеля
Состоит из двух стеклянных призм с малыми преломляющими углами,
сложенными основаниями. Источник света – щель S, параллельная ребру
бипризмы. Преломляясь в бипризме, падающий пучок света разделяется на
2 когерентных пучка с вершинами в мнимых изображениях S1 и S2 щели S.
При перекрывании этих пучков на экране образуется система параллельных
45
интерференционных полос

46.

6. Интерференция в тонких пленках
При падении световой волны на тонкую прозрачную пленку
(пластинку) происходит отражение от обеих поверхностей пленки –
возникают 2 световые волны, которые могут интерферировать.
1. Плоскопараллельная пластинка
При падении на пластинку
плоской волны образуются 2
отраженные волны, разность
хода которых есть
0
2h n sin
2
2
2
Наблюдаемая
интерференционная картина полосы равного наклона.
46

47.

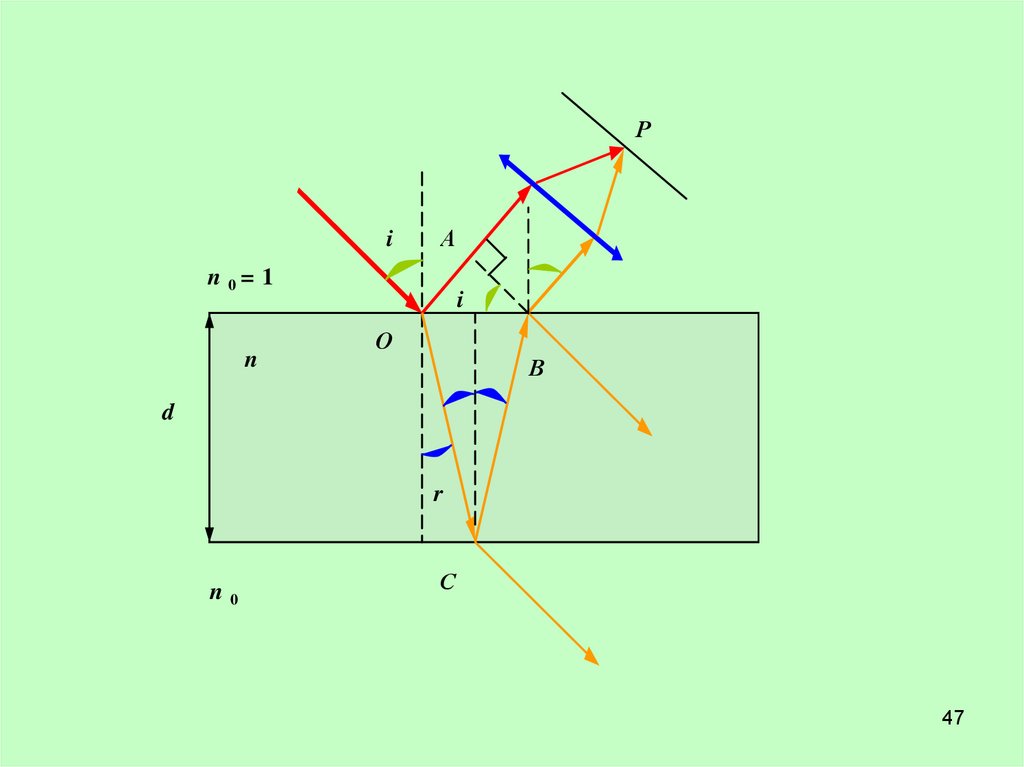
Р
А
i
А
n 0= 1
n
А
d
i
О
В
А
А
А
r
n0
С
47

48.

Р
А
i
А
n 0= 1
n
А
d
i
О
В
А
А
А
r
n0
С
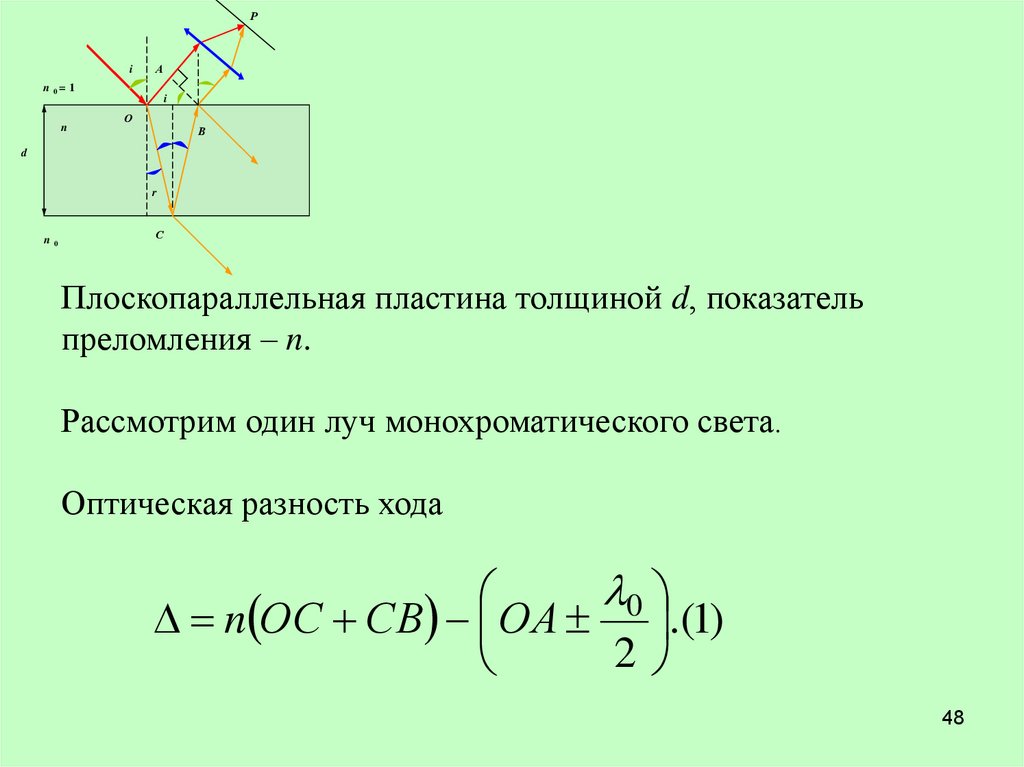
Плоскопараллельная пластина толщиной d, показатель
преломления – n.
Рассмотрим один луч монохроматического света.
Оптическая разность хода
0
n ОС СВ ОА .(1)
2
48

49.

Р
А
i
А
n 0= 1
n
А
d
i
О
В
А
А
А
2
обусловлено потерями полуволны при
отражении света от границы раздела.
r
n0
0
С
Если n > n0, то потеря полуволны происходит в точке О при
отражении от оптически более плотной среды, т.к. вектор Е в
этом случае меняет свою фазу на π.
n > n0 – потеря
0
2
в точке О, в уравнении (1)
0
2
...
0
2
.

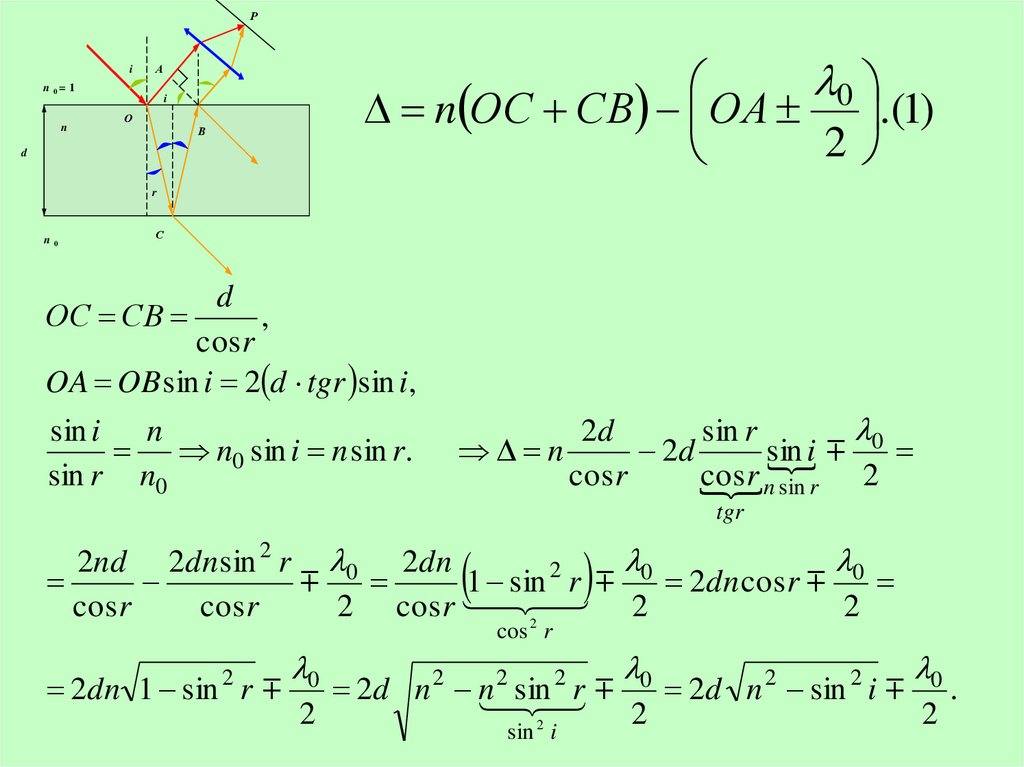
50.

Р
А
i
n
А
d
0
n ОС СВ ОА .(1)
2
А
n 0= 1
i
О
В
А
А
А
r
n0
С
d
,
cos r
OA OB sin i 2 d tgr sin i,
ОС СВ
sin i n
n0 sin i n sin r.
sin r n0
n
0
2d
sin r
2d
sin
i
cos r
cos r n sin r 2
tgr
2nd 2dn sin 2 r 0 2dn
1 sin 2 r 0 2dn cos r 0
cos r
cos r
2 cosr 2 2
2
cos r
2dn 1 sin 2 r
0
2
2
2
2d n 2 n
sin
r
sin 2 i
0
2
2d n 2 sin 2 i
0
2
.

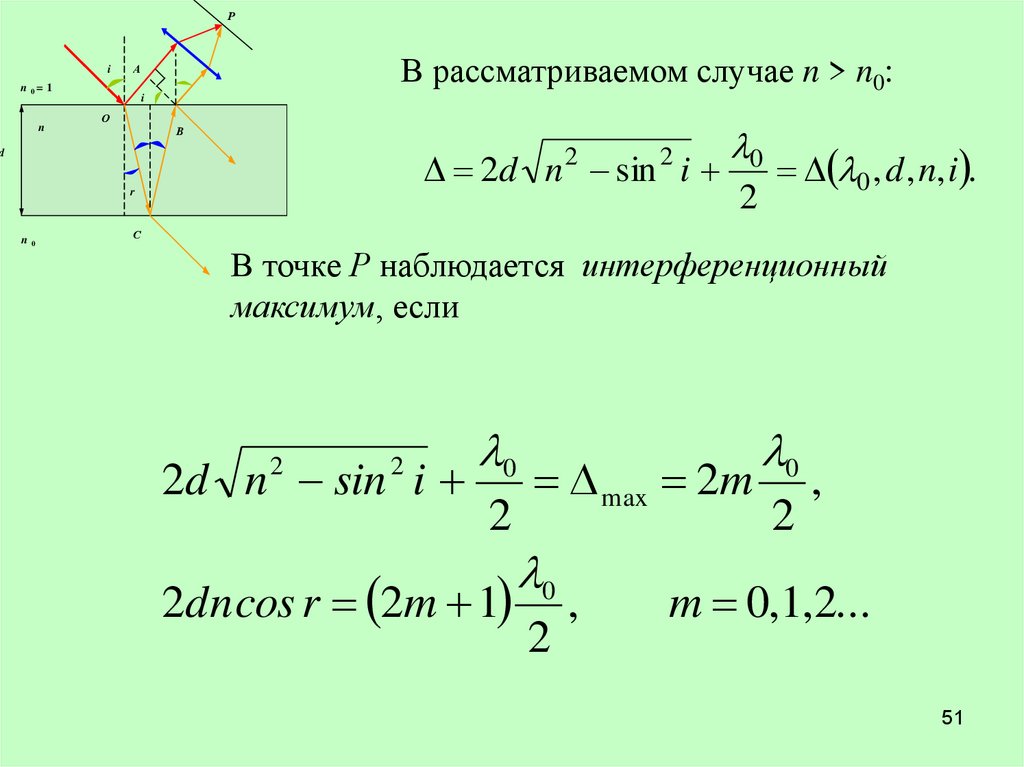
51.

Р
А
i
n
А
d
В рассматриваемом случае n > n0:
А
n 0= 1
i
О
В
А
2d n sin i
А
2
А
r
n0
2
0
2
0 , d , n, i .
С
В точке Р наблюдается интерференционный
максимум, если
2d n sin i
2
2
0
2
2dn cos r 2m 1
max 2m
0
2
,
0
2
,
m 0,1,2...
51

52.

Р
А
i
А
n 0= 1
n
А
d
i
О
В
А
А
А
В
точке
Р
наблюдается
интерференционный минимум, если
r
n0
С
2d n sin i
0
0
,
2
2
2dn cos r 2m
2
2
min 2m 1
0
2
,
m 1,2...
m – порядок интерференционного max или min.
Интерференционная картина наблюдается, если
2d .
52

53.

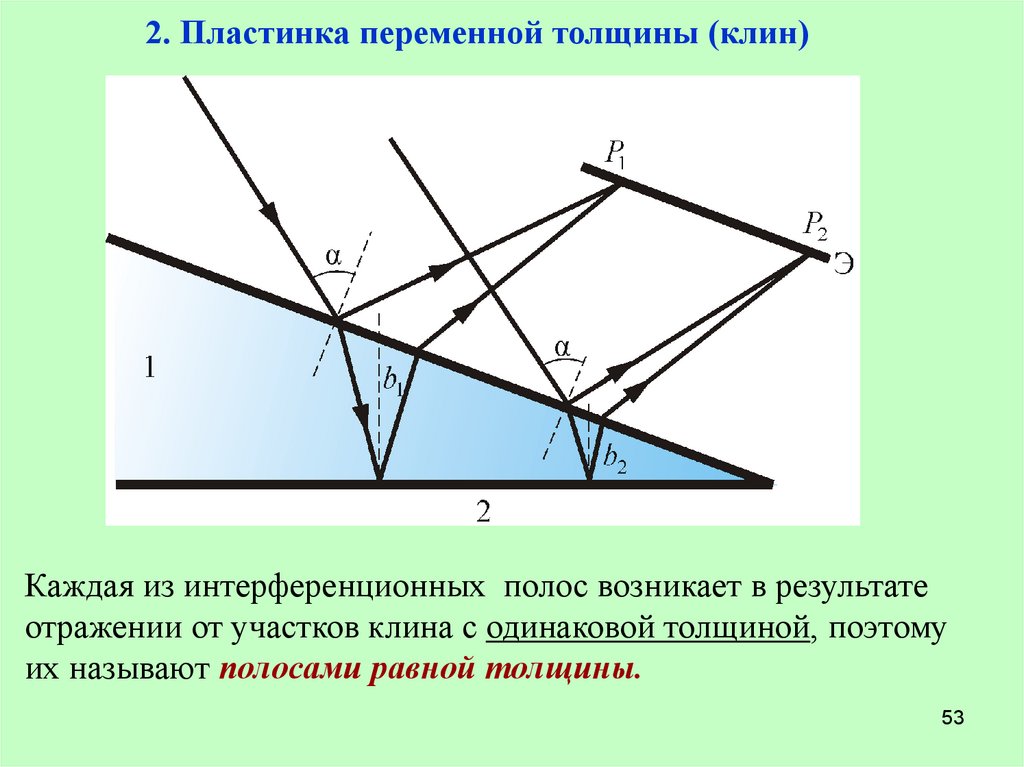
2. Пластинка переменной толщины (клин)
Каждая из интерференционных полос возникает в результате
отражении от участков клина с одинаковой толщиной, поэтому
их называют полосами равной толщины.
53

54.

Кольца Ньютона
Кольцевые полосы равной
толщины, наблюдаемые в
воздушном зазоре между
соприкасающимися выпуклой
сферической поверхностью
линзы малой кривизны и
плоскопараллельной толстой
стеклянной пластнкой,
называют кольцами
Ньютона.
При нормальном падении света полосы равной толщины имеют
вид концентрических окружностей, при наклонном – эллипсов.
54

55.

R
R
r
n 0= 1
d
n
Кольца Ньютона
наблюдаются при
отражении света от
воздушного зазора,
образованного
плоскопараллельной
пластиной и
соприкасающейся с ней
плосковыпуклой линзой
с большим радиусом
кривизны.
Параллельный пучок света падает нормально на плоскую
поверхность линзы, частично отражаясь от верхней и нижней
поверхностей воздушного зазора между линзой и пластиной.
Отраженные лучи накладываются, и возникает интерференционная
картина в виде концентрических окружностей.

56.

R
R
r
n 0= 1
d
n
Показатель преломления воздуха n0 = 1,
i = 0.
R – радиус кривизны линзы,
r – радиус окружности, для которой зазор d
одинаков.
R 2 R d 2 r 2 ,
2
r
R 2 R 2 2 Rd d 2 r 2 d
.
2R
d мал
0
Оптическая разность хода:
0
r 2 0 r 2 0
2d
2
.
2
2R 2
R
2
0
В выражении для оптической разности хода член
2
учитывает изменение фазы на π при отражении от пластины.
56

57.

R
R
r
n 0= 1
d
n
max 2m
0
R 0
1
2m 1
m 0 rmax 0 R m
2
2
2
– радиус светлого кольца,
m = 1, 2 …, т.к. r не может быть отрицательным.
0
1
min 2m 1 m 0 rmin 0 Rm
2
2
– радиус темного кольца,
m = 0, 1, 2 …, m = 0 соответствует r = 0, т.е. это точка в месте касания
пластины и линзы. В этой точке наблюдается минимум интенсивности,
обусловленный изменением фазы на π при отражении от пластины.
57

58.

R
R
r
n 0= 1
d
n
В проходящем свете луч 2 раза отражается от оптически более
плотной среды, поэтому оптическая разность хода для
отраженного и проходящего лучей отличаются на 0
2
Следовательно, уравнению для интерференционного max
отраженного света соответствует уравнение для min
проходящего света, а для min отраженного – max проходящего.
58

59.

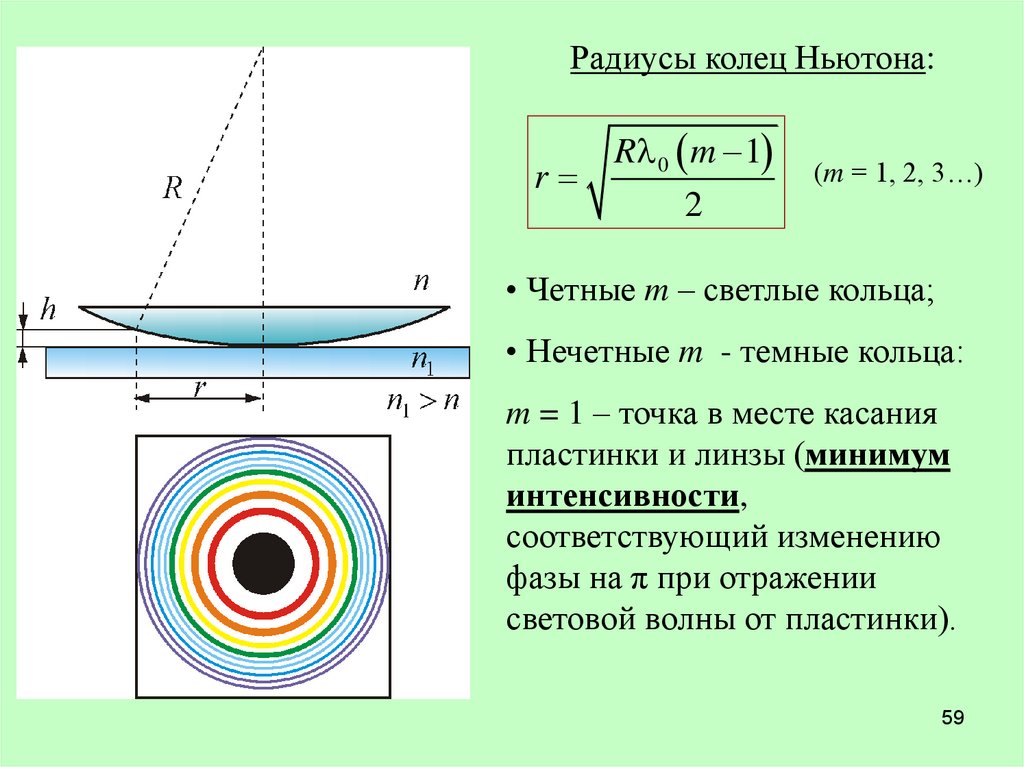
Радиусы колец Ньютона:
r
R 0 m 1
2
(m = 1, 2, 3…)
• Четные m – светлые кольца;
• Нечетные m - темные кольца:
m = 1 – точка в месте касания
пластинки и линзы (минимум
интенсивности,
соответствующий изменению
фазы на π при отражении
световой волны от пластинки).
59

60. 4. Пространственная когерентность

Когерентностью называется согласованное протекание
нескольких колебательных или волновых процессов.
Термином «пространственная когерентность» объединяется
круг вопросов, возникающих при использовании в
интерференционных опытах протяженных источников.
Протяженный источник света можно рассматривать как
совокупность точечных некогерентных источников, в
этом случае интерференционная картина, возникающая на
экране, будет наложением интерференционных картин,
создаваемых каждым из участков в отдельности.
Таким образом, увеличение размеров источника приводит к
ухудшению контрастности интерференционных полос и
даже к их полному исчезновению.
60

61.

Критерий наблюдения интерференции при протяженном
источнике:
b bmax
- интерференционные схемы с
большой апертурой требуют
источников малых размеров.
b - допустимый размер источника;
λ – длина волны;
Ω - апертура интерференции – угол между выходящими из
источника интерферирующими лучами.
Введем понятие радиуса пространственной когерентности
(длины пространственной когерентности):
- это максимальное поперечное направлению распространения
волны расстояние, на котором возможно проявление
интерференции.
61

62.

k
ρк – радиус пространственной когерентности;
λ – длина волны;
θ – угловой размер источника.
Физический смысл понятия радиуса пространственной
когерентности протяжённого источника состоит в
представлении о возможности наблюдения интерференционной
картины от протяжённого источника, если он размещается
внутри круга, диаметр которого равен 2ρк.
Пространственно когерентными источниками называются
источники, размеры и взаимное расположение которых
позволяют (при необходимой степени монохроматичности света)
наблюдать интерференцию.
62

63.

Условия пространственной когерентности двух волн (в
фиксированный момент времени):
1) постоянная во времени разность фаз:
откуда следует
ω1t +φ01 – ω2 t – φ02 = const,
(ω1 – ω2)t + φ01 – φ02 = const.
Это справедливо лишь при
ω1 = ω2
Таким образом, условие постоянства во времени разности фаз
эквивалентно условиям одинаковости для когерентных лучей
циклических частот, частот и длин волн в вакууме.
2) соизмеримость амплитуд интерферирующих волн,
3) одинаковое состояние поляризации,
4) лучи, пройдя разные пути, встречаются в некоторой точке
пространства.
63

64. 5. Временная когерентность

Всякий прибор, с помощью которого можно наблюдать
интерференционную картину (человеческий глаз,
фотопластинка, …) обладает инерционностью: усредняет
информацию, полученную в течение некоторого промежутка
времени.
• Если за это время среднее значение интерференционного члена
равно нулю, интерференция отсутствует;
• Если отлично от нуля, прибор обнаружит интерференцию.
Атом излучает цуг в течение 10 8 с, а по истечении этого
времени первое условие когерентности нарушается за счет
хаотичного изменения начальной фазы каждого из цугов,
полученных при излучении естественных источников.
64

65.

Инерционность человеческого глаза составляет 0,1 с,
и в результате глаз видит равномерно освещенное поле вместо
интерференционной картины
Фаза реальной волны за счет хаотичного изменения
начальной фазы каждого из цугов непрерывно меняется:
Время, за которое случайное изменение фазы волны достигает
значения порядка π, называется временем когерентности
(длительность цуга) (за это время колебание «забывает»
первоначальную фазу и становится некогерентным по
отношению к самому себе).
Расстояние, на которое сместится волна за это время,
называется длиной когерентности.
Для получения интерференционной картины путем деления
естественной волны на 2 части необходимо, чтобы оптическая
разность хода была меньше длины когерентности.
65

66.

Влияние немонохроматичности:
Когерентными являются монохроматические волны неограниченные в пространстве волны одной определенной и
строго постоянной частоты.
Ни один реальный источник не дает строго монохроматического
света, немонохроматичность света (как и увеличение размеров
источника) ведет к ухудшению контрастности
интерференционных полос, а затем к их полному
исчезновению.
Когерентность колебаний, которые совершаются в одной и той
же точке пространства, определяемая степенью
монохроматичности волн, называется временнóй
когерентностью.
66

67.

Можно показать ,что
2
ког
- чем шире интервал частот, представленных в данной волне,
тем меньше время когерентности.
Предельный наблюдаемый порядок интерференции
mпред
- число наблюдаемых интерференционных полос возрастает
при уменьшении спектрального интервала.
67