Similar presentations:
Интерференция света. Лекция 25
1.
Часть 4. ОптикаЛекция 25. Интерференция света
2.
1. Развитие представлений о природесвета
2. Интерференция света. Когерентность
волн. Время и длина когерентности
3. Условия усиления и ослабления света
при интерференции
4. Интерференционный опыт Юнга
5. Интерференция света в тонких
плёнках. Кольца Ньютона
6. Применение интерференции света
3.
В конце 17 века сформировались две теории света:корпускулярная (И. Ньютон) и волновая (Х.
Гюйгенс и Р. Гук).
Корпускулярная теория: свет — поток мельчайших
частиц (корпускул), испускаемых светящимися
телами.
«За»: прямолинейность светового луча, равенство
углов падения и отражения света.
«Против»: v > c (должно быть по теории); проявление
волновых свойств света; пересекающиеся пучки
корпускул не влияют друг на друга.
4.
Волновая теория: свет — волновой процесс,подобный
механическим
волнам,
распространяющийся в упругом эфире. Волновая
теория основывалась на принципе Гюйгенса:
каждая точка, до которой
доходит
волна,
служит
центром вторичных волн, а
огибающая этих волн, даёт
положение волнового фронта в
следующий момент времени.
Христиан Гюйгенс
5.
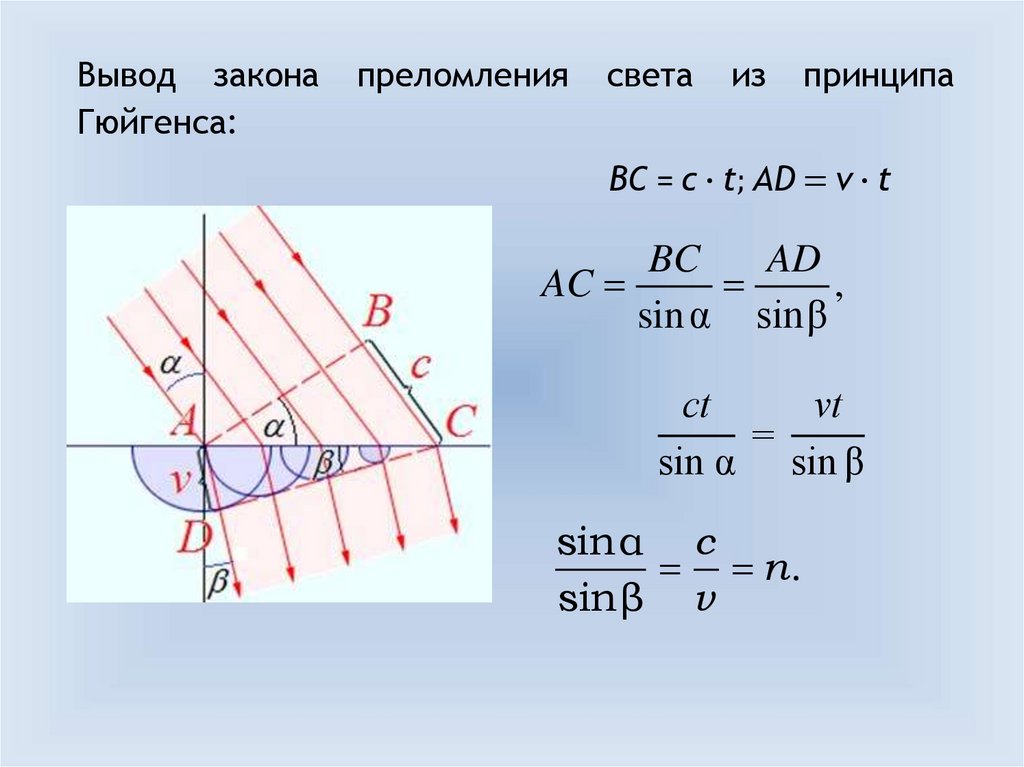
Вывод законаГюйгенса:
преломления
света
из
принципа
BC = c ∙ t; AD = v ∙ t
BC
AD
AC
,
sin α sinβ
ct
vt
=
sin α sin β
sinα c
n.
sinβ v
6.
«За»: v < c (подтверждение на опыте!); объяснениеявлений интерференции и дифракции света, законов
отражения и преломления света.
• «Против»: невозможность объяснить прямолинейное
распространение света в неограниченном однородном
и изотропном пространстве;
• трудность в объяснении различия скорости света в
различных средах;
• трудность в объяснении физической природы наличия
разных цветов.
7.
Конец 19Максвелла
века:
электромагнитная
теория
света
c
v
.
εμ
электронная теория дисперсии света Лоренца:
Трудности:
n f v .
• невозможность объяснения: процессов испускания и
поглощения света;
• фотоэлектрического эффекта;
• эффекта Комптона;
• распределения энергии по длинам волн при тепловом
излучении нагретых тел.
8.
Начало 20 века: М. Планк, А. Эйнштейн. Квантоваятеория света. Свет — это поток световых квантов —
фотонов.
h
ε ф h ; mф 2 .
с
Середина 20 века: А. М. Прохоров, Н. Г. Басов, Ч.
Таунс) — открытие вынужденного излучения атомов и
молекул. Создание оптического квантового генератора
(лазера)
9.
Современные представления о свете:• свет имеет сложную природу —
одновременно
как
волновыми,
корпускулярными свойствами;
обладает
так
и
• чем больше длина волны света, тем больше
проявляются его волновые свойства и в меньшей
степени корпускулярные;
• чем меньше длина волны — тем труднее
обнаруживаются волновые свойства и легче
корпускулярные.
• современная оптика успешно развивается на стыке
квантовой
электроники
и
квантовой
электродинамики.
10.
Интерференция света. Когерентность волн.Время и длина когерентности
Необходимым условием интерференции волн является
их когерентность, т. е. согласованное протекание
во времени и пространстве двух или более волновых
процессов.
Этому условию удовлетворяют волны: одинаковой
частоты
(монохроматические
волны);
имеющие
постоянную разность начальных фаз.
Излучение света атомами в виде отдельных коротких
импульсов
(«оборванных»
синусоид)
называется
волновым цугом.
11.
Продолжительность одного цуга называется временемкогерентности.
Длина когерентности — путь проходимый волной за
время когерентности:
lког с ког .
Вывод: наблюдение интерференции света возможно
лишь при оптических разностях хода двух волн меньших
длины когерентности используемого источника света.
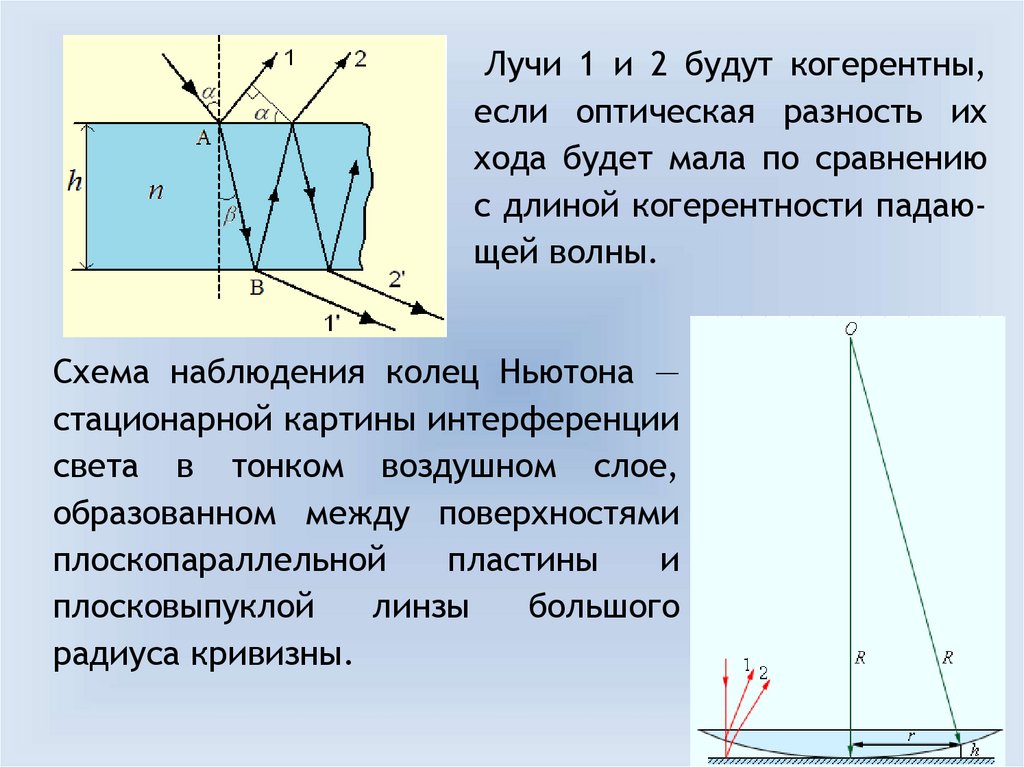
12.
Условия усиления и ослабления света приинтерференции
Для получения когерентных световых волн применим
метод
разделения
волны,
излучаемой
одним
источником, на две части, которые после прохождения
разных оптических путей накладываются друг на друга
и происходит интерференция света.
13.
s1ξ1 x, t A1 cos ω t A1 cosφ1;
v1
s2
ξ 2 x, t A2 cos ω t A2 cosφ 2 .
v 2
Здесь ξ1 x, t и ξ 2 x, t — напряжённость электрического
или магнитного полей электромагнитной волны;
v1 и v 2 — фазовые скорости первой и второй волны;
s1 и s2 — пути, которые прошли первая и вторая волны от
источника колебаний до точки, в которой наблюдается
интерференционная картина.
14.
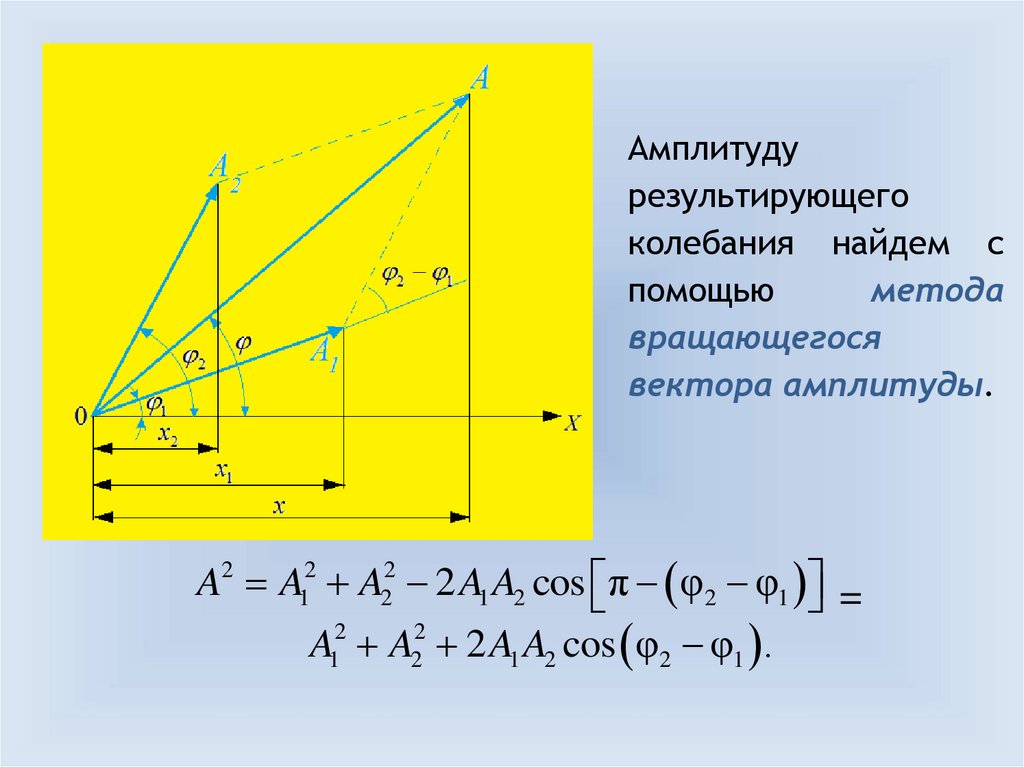
Амплитудурезультирующего
колебания найдем с
помощью
метода
вращающегося
вектора амплитуды.
A2 A12 A22 2 A1 A2 cos π φ2 φ1 =
A12 A22 2 A1 A2 cos φ2 φ1 .
15.
s1 s2A A A 2A1A2 cos ω
v1 v 2
2
2
1
2
2
A12 A22 2A1A2 cos δ I1 I 2 2 I1I 2 cos δ.
Здесь I — интенсивность света: I ~ A2.
s1 s2
s1
s
δ ω ω
c
c
v1 v 2
n2
n1
s1n1 s2n 2 ω
ω
s1n1 s2n 2
c c
c
2π
2π
s1n1 s2n 2 .
Tc
λ
оптическая разность хода
16.
Если оптическая разность хода равна целому числуволн в вакууме: mλ 0 m 0,1,2,... ,
то δ 2mπ , и cosδ 0 колебания обеих волн будут
происходить в одинаковой фазе, и колебания будут
усиливать друг друга.
Тогда I I1 I 2 , а равенство
mλ 0
m 0,1,2,... ,
является условием интерференционного максимума.
17.
Если оптическая разность хода равнаλ0
2m 1
m 0,1,2,... ,
2
то δ 2m 1 π , cosδ 0.
В этом случае колебания обеих волн будут
происходить в противофазе и I I1 I 2 , а равенство
λ0
2m 1
2
m 0,1,2,... ,
является условием интерференционного минимума.
18.
Для некогерентных источников разность фаз δнепрерывно
изменяется,
а
интенсивность
результирующей волны всюду одинакова и равна сумме
интенсивностей каждой из волн в отдельности:
I I1 I 2 .
Распределение интенсивности света в
интерференционной картине. m — порядок
интерференционного максимума.
19.
Интерференционный опыт Юнга2
2
d
d
2
2
s2 L x ; s1 L x .
2
2
2 xd
xd
2
2
.
и s2 s1
s2 s1 2 xd
s1 s2
L
2
2
20.
Это приближенное равенство следует из условияопыта Юнга: L >> d => s1 + s2 ≈ 2L.
Отсюда максимум интенсивности света (светлая
полоса) будет наблюдаться при:
xmax d
L
mλ 0 xmax m λ 0 ;
L
d
а минимум (темная полоса) — при
xmin d
λ0
1 L
2m 1 xmin m λ 0 ;
L
2
2 d
Ширина интерференционной полосы:





















 physics
physics








