Similar presentations:
Интерференция света
1. Интерференция света
Интерференция светаЯвление интерференции. Интенсивность
суммарной волны
Положение максимумов и минимумов при
интерференции от двух источников
Интерференция при отражении от
прозрачных пластинок
Кольца Ньютона
Способы наблюдения интерференции:
опыт Юнга, бизеркало Френеля, бипризма
Френеля, интерферометр Майкельсона
Применения интерференции
2. Интенсивность суммарной волны
Если две волны одинаковой частоты накладываются другна друга, то они могут возбуждать в некоторой точке
пространства колебания одинакового направления:
А1 cos( t 1 ) А2 cos( t 2 )
Амплитуда такого колебания будет равна
A2 A12 A22 2 A1 A2 cos где 2 1
Если разность фаз δ постоянна во времени, то волны
называют когерентными. Когерентностью вообще
называется явление согласованного протекания процессов.
В случае некогерентных волн δ непрерывно меняется,
принимая с равной вероятностью любые значения,
вследствие чего среднее по времени значение cosδ равно
нулю. Поэтому A2 A12 A22 Отсюда
I I1 I 2
В случае когерентных волн cosδ имеет постоянное
значение во времени, так что I I I 2 I I cos
1
2
1 2
3. Явление интерференции
В тех точках пространства, где cos δ>0, там I I1 I 2в точках, где cos δ<0, там I I1 I 2 . Таким
образом, при наложении когерентных световых
волн происходит перераспределение светового
потока в пространстве, в результате чего в одних
местах возникают максимумы, а в других
минимумы интенсивности. Это явление называется
интерференцией волн.
Особенно отчетливо проявляется интерференция,
когда интенсивность обеих интерферирующих волн
одинакова. Тогда в максимумах I = 4I1, в минимумах
I = 0. Для некогерентных волн при том же условии
получается всюду одинаковая интенсивность I = 2I1.
4. Описание интерференции
Из повседневного опыта известно, что при освещении какойлибо поверхности несколькими источниками света
интерференция не наблюдается, вместо неё освещённость,
как правило, монотонно убывает по мере удаления от
источников света. Это объясняется тем, что естественные
источники света не когерентны. Их излучение складывается
из волн испущенных многими атомами и фаза
результирующей волны претерпевает случайные изменения.
Пусть в точке О волна
разделяется на две части. До
точки сложения P первая волна
проходит путь s1 в среде с
показателем преломления n1 , а
вторая волна проходит путь s2 c
показателем n2. В точке Р первая
волна возбудит колебание
1 А1 cos( t
s1
)
1
s2
)
а вторая 2 А2 cos( t
2
5. Описание интерференции
Разность фаз будет равнаs2 s1
2 v
2
2
s2 n2 s1n1 s2 n2 s1n1
s2 n2 s1n1
c
0
0
2 1 c
оптической разностью хода называется величина
s2 n2 s1n1 L2 L1
Из предыдущей формулы видно, что если оптическая
разность хода равна целому числу длин волн в вакууме,
m 0
то разность фаз δ оказывается кратной 2π и колебания,
возбуждаемые в точке Р будут приходить с одинаковой
фазой. Это есть условие интерференционного максимума.
Если ∆ равна полуцелому числу длин волн в вакууме,
1
m 0
2
то в точке Р колебания будут в противофазе, это условие
интерференционного минимум.
6. Схема Юнга
Рассмотрим две цилиндрические когерентные световыеволны, исходящие от источников S1 и S2 , имеющих вид
параллельных светящихся нитей или узких щелей.
Область, в которой эти волны перекрываются, называется
областью интерференции. Во всей этой области
наблюдается чередование максимумов и минимумов
интенсивности. Вычислим ширину полос. Положение точки
на экране зададим координатой х. Из рисунка видно, что
d
s l x
2
2
d
s l x
2
2
2
1
2
2
2
2
7. Схема Юнга (продолжение)
22
Следовательно,
d 2
d
2
2
2
s 2 s1 ( s 2 s1 )( s 2 s1 ) l x l x 2 xd
2
2
Так как d << l, то s2 s1 2l
2 xd
2 xd xd
s
s
1
Тогда 2
s 2 s1
2l
l
Умножив эту разность на показатель среды, получим
оптическую
разность хода:
xd
n
m 0
l
l
x
m
max
Тогда максимумы будут при
d
1 l
xmax m
а минимумы при
2 d
Здесь – λ=λ0/n - длина волны в среде, заполняющей
пространство между источниками и экраном. Расстояние между
соседними максимумами называется расстоянием между
интерференционными полосами, а расстояние между
соседними минимумами – шириной интерференционной l
x
полосы. Они равны по величине и
Отсюда видно, что если d сравнимо с l , то ширина полосы d
станет порядка длины волны. Картина будет различимой, если
d << l
8. Интерференция при отражении от прозрачных пластинок
При падении световой волны на тонкуюпрозрачную пластику (или пленку)
происходит отражение от обеих
поверхностей пластики (верхней и
нижней). В результате возникают две
световые волны, которые при
известных условиях могут
интерферировать.
Разность хода в данном интерференционном расположении:
Здесь b – толщина пластинки, n – показатель преломления,
i – угол падения. Дополнительное слагаемое /2 возникает
из-за разных условий отражения света на двух гранях
пластинки. Условия максимумов и минимумов
интерференции было указано ранее
9. Кольца Ньютона
Важный случай интерференцииполучается при отражении света от
соприкасающихся друг с другом
плоскопараллельной толстой
стеклянной пластинки и плосковыпуклой линзой с большим радиусом
кривизны.
Линза кладется на стеклянную пластинку и освещается
сверху параллельным пучком света. Радиус линзы R
намного больше радиуса интерференционных r. Поэтому
можно считать, что угол падения света на внутреннюю
поверхность линзы i ≈ 0. Тогда геометрическая разность
хода с большой точностью равна 2b. При нахождении
оптической разности хода следует учитывать изменение
фазы на противоположную при отражении от оптически
более плотной среды. Связь между b, r и R можно найти из
геометрических соображений.
10. Кольца Ньютона
Если в зазоре между линзой ипластиной n = 1, то для радиуса
интерференционных полос (колец
Ньютона) получается формула:
При четных значениях m кольца
Ньютона темные (в частности при m
= 0, r = 0). В центре наблюдается
темное пятно из-за потери λ0/2 при
отражении от стеклянной пластинки.
Если m нечетное, то кольца светлые.
11. Способы получения когерентных волн.
Создать когерентные источники длянаблюдения и использования явления
интерференции можно следующими
способами:
1) Делением волнового фронта. К
таким устройствам относятся схема
Юнга, бипризма Френеля, бизеркало
Френеля, билинза Бийе, зеркало
Ллойда,.
2) Делением амплитуды волны. К
таким устройствам относится
интерферометр Майкельсона.
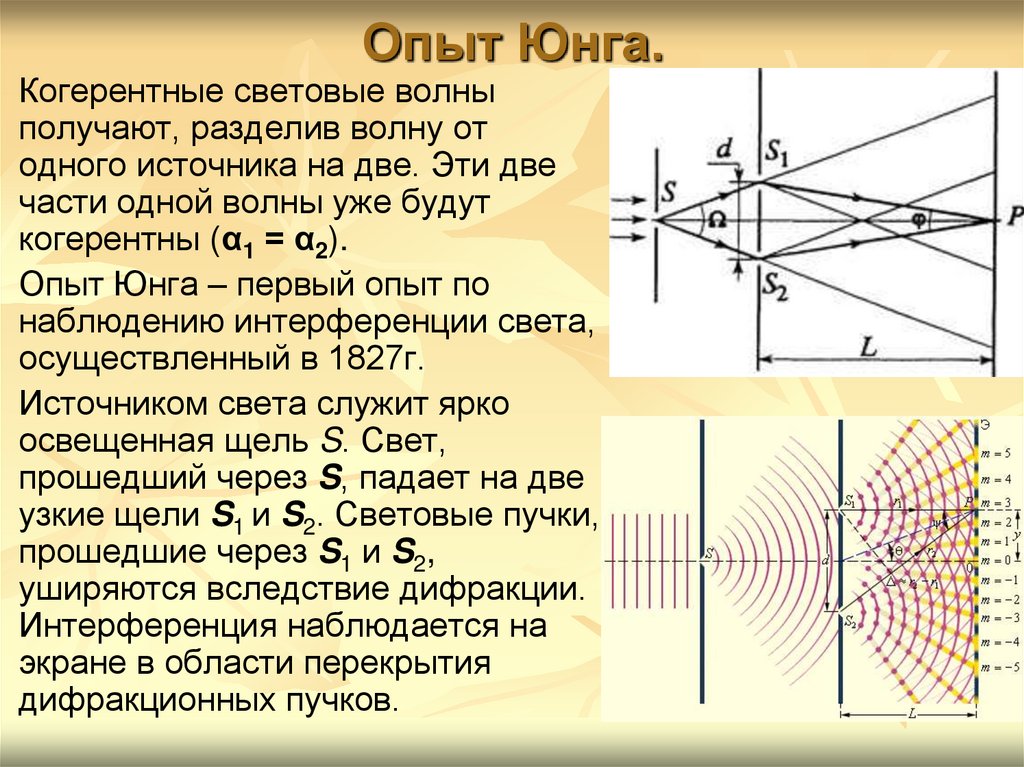
12. Опыт Юнга.
Когерентные световые волныполучают, разделив волну от
одного источника на две. Эти две
части одной волны уже будут
когерентны (α1 = α2).
Опыт Юнга – первый опыт по
наблюдению интерференции света,
осуществленный в 1827г.
Источником света служит ярко
освещенная щель S. Свет,
прошедший через S, падает на две
узкие щели S1 и S2. Световые пучки,
прошедшие через S1 и S2,
уширяются вследствие дифракции.
Интерференция наблюдается на
экране в области перекрытия
дифракционных пучков.
13. Бизеркало Френеля
Бизеркало Френеля (1816 г.). Свет от источника Sотражается от двух зеркал, расположенных под
достаточно малым углом . Волны, падающие на
экран, могут рассматриваться как волны от двух
мнимых изображений источника S в обоих зеркалах.
При изменении положения точки наблюдения P на
экране изменяется разность хода , в результате
чего возникает система интерференционных полос,
ширина которых зависит от угла схождения лучей .
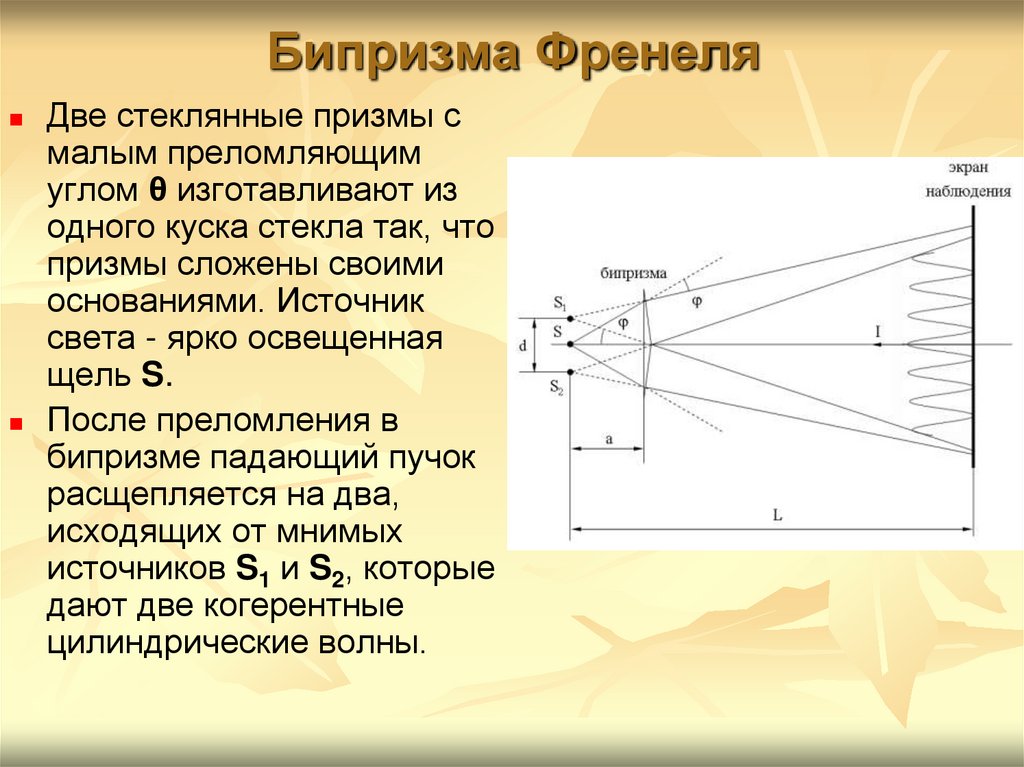
14. Бипризма Френеля
Две стеклянные призмы смалым преломляющим
углом θ изготавливают из
одного куска стекла так, что
призмы сложены своими
основаниями. Источник
света - ярко освещенная
щель S.
После преломления в
бипризме падающий пучок
расщепляется на два,
исходящих от мнимых
источников S1 и S2, которые
дают две когерентные
цилиндрические волны.
15. Интерферометр Майкельсона
Интерферометрами называются приборы,работа которых основана на явлении
интерференции. Классический
интерферометр – это интерферометр
Майкельсона. С помощью этого
интерферометра (и совместно с Морли)
Майкельсон пытался обнаружить движение
Земли относительно эфира.
Луч монохроматического света падает на полупрозрачную
пластинку А, которая разделяет луч падающего света на два
луча 1 и 2. Луч 2 проходит пластинку А, падает на зеркало 2,
отражается от него, проходит снова пластинку А и попадает в
зрительную трубу, в которой наблюдают картину
интерференции лучей 1 и 2 (полосы равной толщины). Луч 1
отражается от пластинки А, проходит пластинку В, отражается
от зеркала 2, проходит пластинки В и А, и - в зрительную
трубу. Пластинка В необходима для того, чтобы создать
одинаковые условия для лучей 1 и 2, а именно, луч 2
проходит пластинку А три раза, и луч 1 соответственно
проходит пластинки три раза - два раза пластинку В и один
раз пластинку А.
16. Интерферометр Майкельсона (продолжение)
Для определения малых измененийрасстояний в зрительную трубу
наблюдают картину интерференции
от излучения определенной длины
волны. Фиксируют положение
светлой полосы с произвольным
номером m. Оптическая разность
хода лучей 2 и 1
Затем смещаем зеркало на расстояние h. Пусть при этом на
интерференционной картине вместо светлой полосы с
номером m встанет светлая полоса с номером (m+1) . В этом
случае для оптической разности хода лучей 2 и 1
Тогда
Если на место светлой полосы становится соседняя с ней
темная полоса, то тогда
. Наименьшее смещение h
зеркала 2, которое можно зафиксировать, составляет 15 нм.
17. Определение качества обработки поверхностей
На исследуемую поверхностькладут плоскопараллельную
пластинку так, чтобы создать
воздушный зазор между
поверхностью и пластинкой (см.
рис.). Перемещая по поверхности
пластинку, по искажению картины
интерференции можно
обнаружить дефекты ее
обработки царапины,
шероховатость), а именно, в
месте нахождения дефекта
правильная картина чередования
светлых и темных полос будет
искажена. При этом можно
выявить неровности размером до
10-8 м.
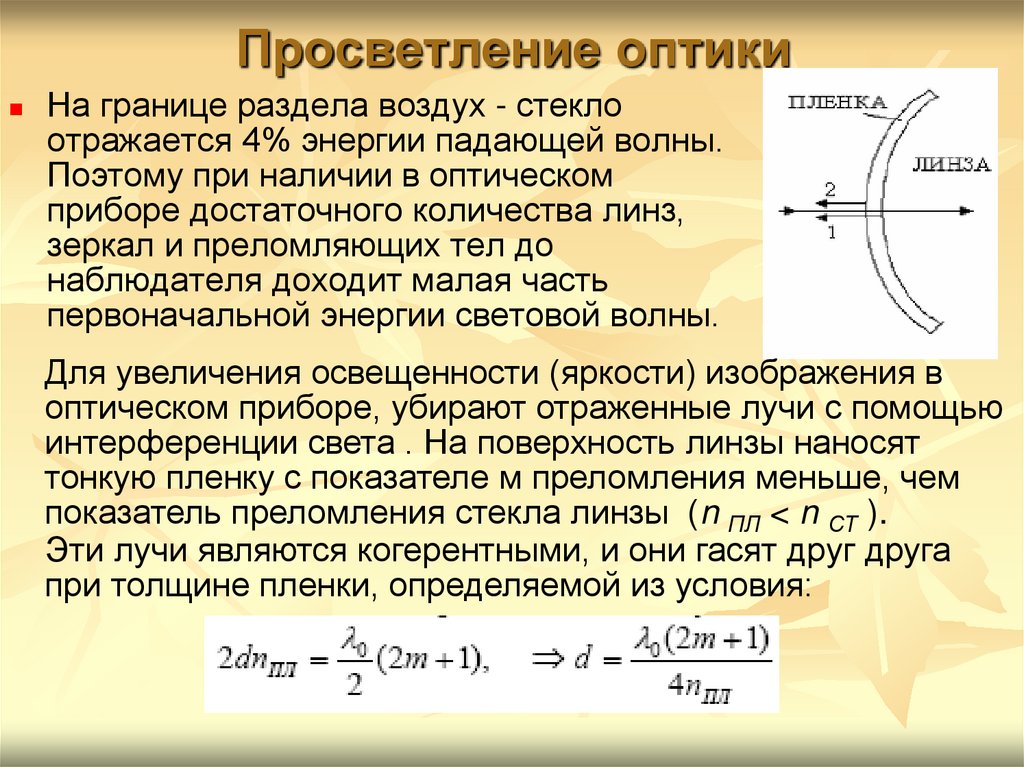
18. Просветление оптики
На границе раздела воздух - стеклоотражается 4% энергии падающей волны.
Поэтому при наличии в оптическом
приборе достаточного количества линз,
зеркал и преломляющих тел до
наблюдателя доходит малая часть
первоначальной энергии световой волны.
Для увеличения освещенности (яркости) изображения в
оптическом приборе, убирают отраженные лучи с помощью
интерференции света . На поверхность линзы наносят
тонкую пленку с показателе м преломления меньше, чем
показатель преломления стекла линзы (n ПЛ < n СТ ).
Эти лучи являются когерентными, и они гасят друг друга
при толщине пленки, определяемой из условия:
19. Многолучевая интерференция
В общем случае при встрече могут интерферировать болеедвух когерентных волн. Такой случай интерференции
называют многолучевой интерференцией. При этом
справедливы основные закономерности, полученные для
двулучевой интерференции. Однако при наложении большого
числа пучков распределение интенсивности в
интерференционной картине существенно иное. Максимумы
и минимумы интенсивности, т.е. светлые и темные полосы, в
двулучевой интерференционной картине имеют одинаковую
ширину. При многолучевой интерференции образуются узкие
максимумы, т.е. резкие светлые полосы, разделенные
широкими темными промежутками. Благодаря этому,
многолучевая интерференция получила важное практическое
применение для изучения тонкой структуры спектральных
линий и в метрологии для сравнения длины стандартного
метра с длинами волн отдельных спектральных линий. Из
других применений многолучевой интерференции отметим
узкополосные оптические фильтры, пропускающие свет
лишь в узком спектральном интервале вблизи заданного
значения длины волны.
















 physics
physics








