Similar presentations:
Fast Frequency and Response Measurements using FFTs
1. Fast Frequency and Response Measurements using FFTs
Alain Moriat,Senior Architect
Fri. 12:45p
Pecan (9B)
www.natinst.com
2. Accurately Detect a Tone
What is the exact frequency and amplitude ofa tone embedded in a complex signal?
How fast can I perform these measurements?
How accurate are the results?
www.natinst.com
3.
Presentation OverviewWhy use the frequency domain?
FFT – a short introduction
Frequency interpolation
Improvements using windowing
Error evaluation
Amplitude/phase response measurements
Demos
www.natinst.com
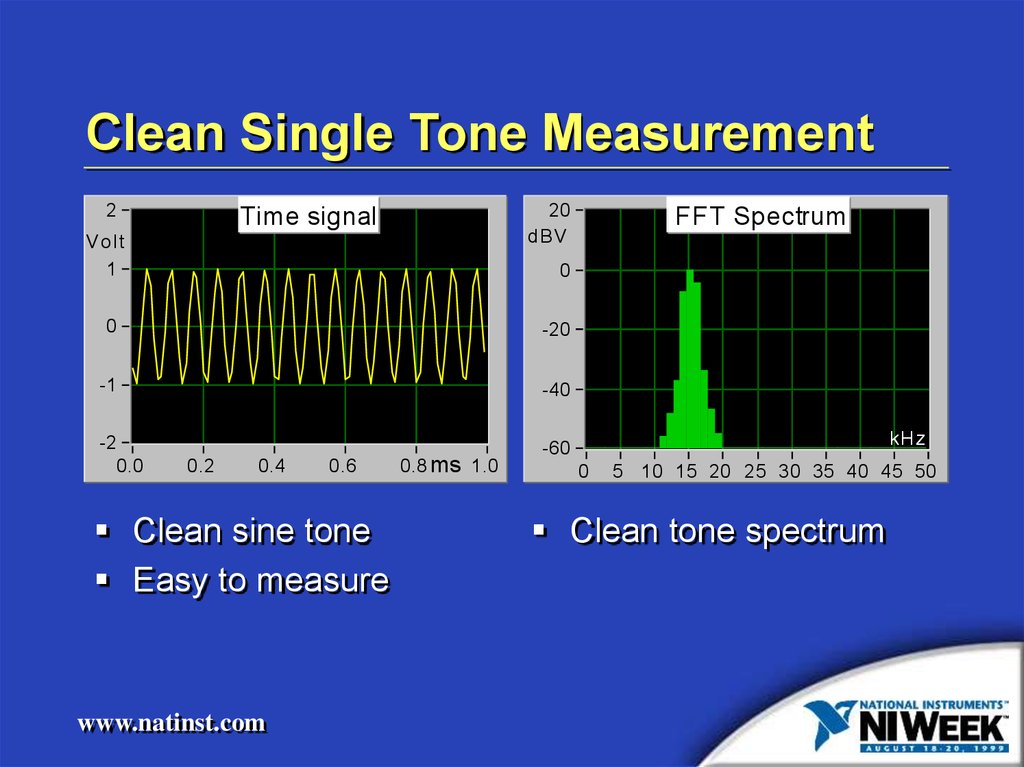
4. Clean Single Tone Measurement
220
d BV
Time signal
Vo lt
1
FFT Spectrum
0
0
-20
-1
-40
-2
0.0
-60
0.2
0.4
0.6
Clean sine tone
Easy to measure
www.natinst.com
0.8 ms 1.0
kHz
0
5 10 15 20 25 30 35 40 45 50
Clean tone spectrum
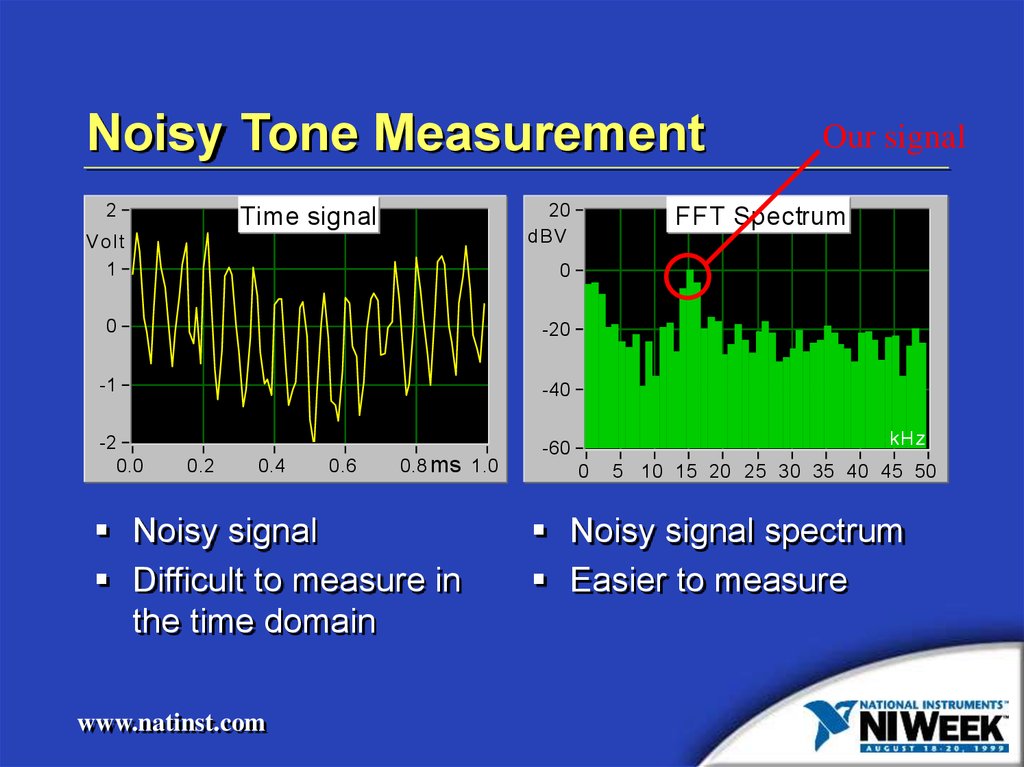
5. Noisy Tone Measurement
220
d BV
Time signal
Vo lt
1
Our signal
FFT Spectrum
0
0
-20
-1
-40
-2
0.0
-60
0.2
0.4
0.6
0.8 ms 1.0
Noisy signal
Difficult to measure in
the time domain
www.natinst.com
kHz
0
5 10 15 20 25 30 35 40 45 50
Noisy signal spectrum
Easier to measure
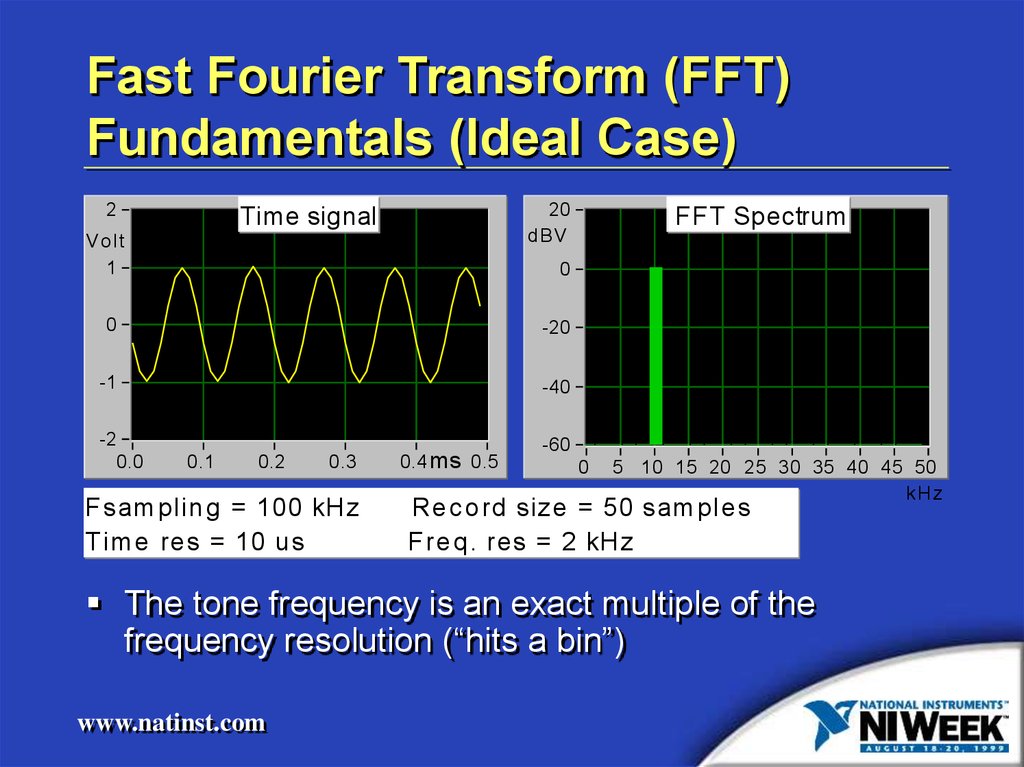
6. Fast Fourier Transform (FFT) Fundamentals (Ideal Case)
220
d BV
Time signal
Vo lt
1
0
0
-20
-1
-40
-2
0.0
FFT Spectrum
0.1
0.2
0.3
F sam p lin g = 100 kH z
T im e re s = 10 u s
0.4 ms 0.5
-60
0
5 10 15 20 25 30 35 40 45 50
kHz
Re c o rd size = 50 sam p le s
F re q . re s = 2 kH z
The tone frequency is an exact multiple of the
frequency resolution (“hits a bin”)
www.natinst.com
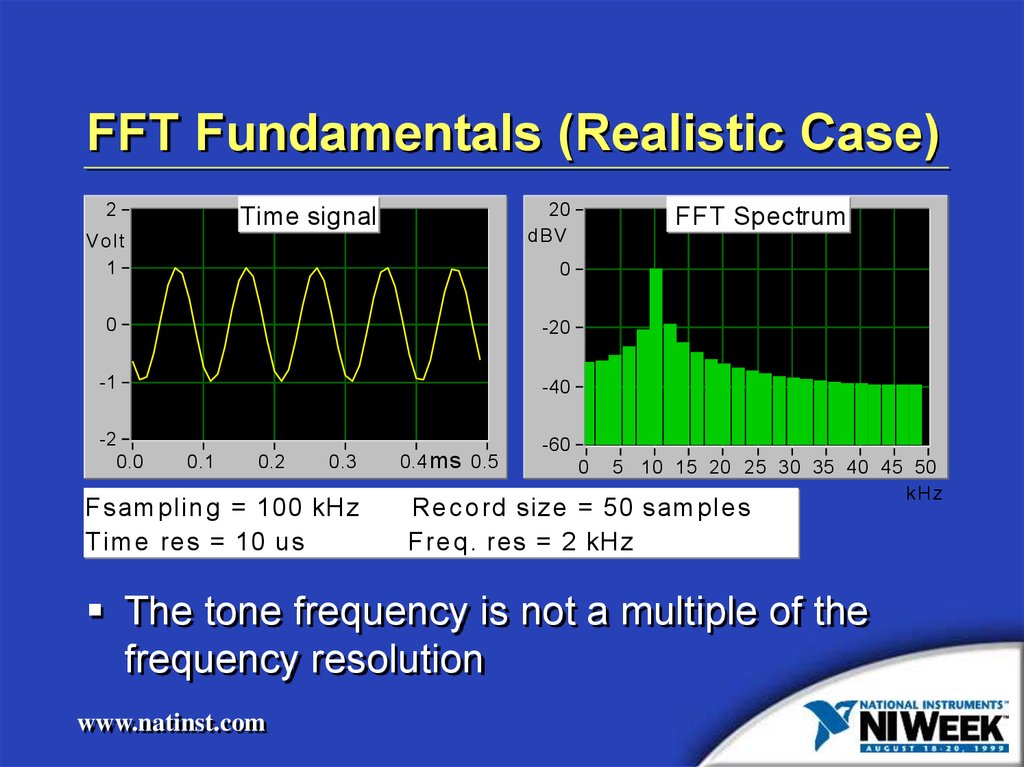
7. FFT Fundamentals (Realistic Case)
220
d BV
Time signal
Vo lt
1
0
0
-20
-1
-40
-2
0.0
FFT Spectrum
0.1
0.2
0.3
F sam p lin g = 100 kH z
T im e re s = 10 u s
0.4 ms 0.5
-60
0
5 10 15 20 25 30 35 40 45 50
kHz
Re c o rd size = 50 sam p le s
F re q . re s = 2 kH z
The tone frequency is not a multiple of the
frequency resolution
www.natinst.com
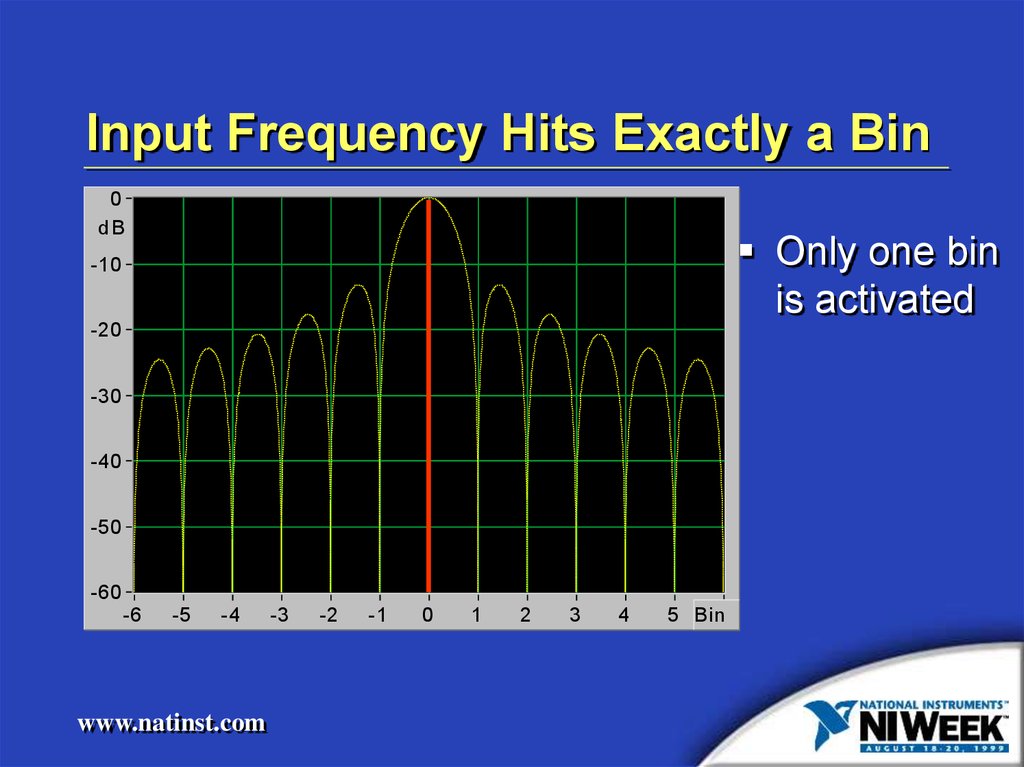
8. Input Frequency Hits Exactly a Bin
0dB
Only one bin
is activated
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
9. Input Frequency is +0.01 Bin “off”
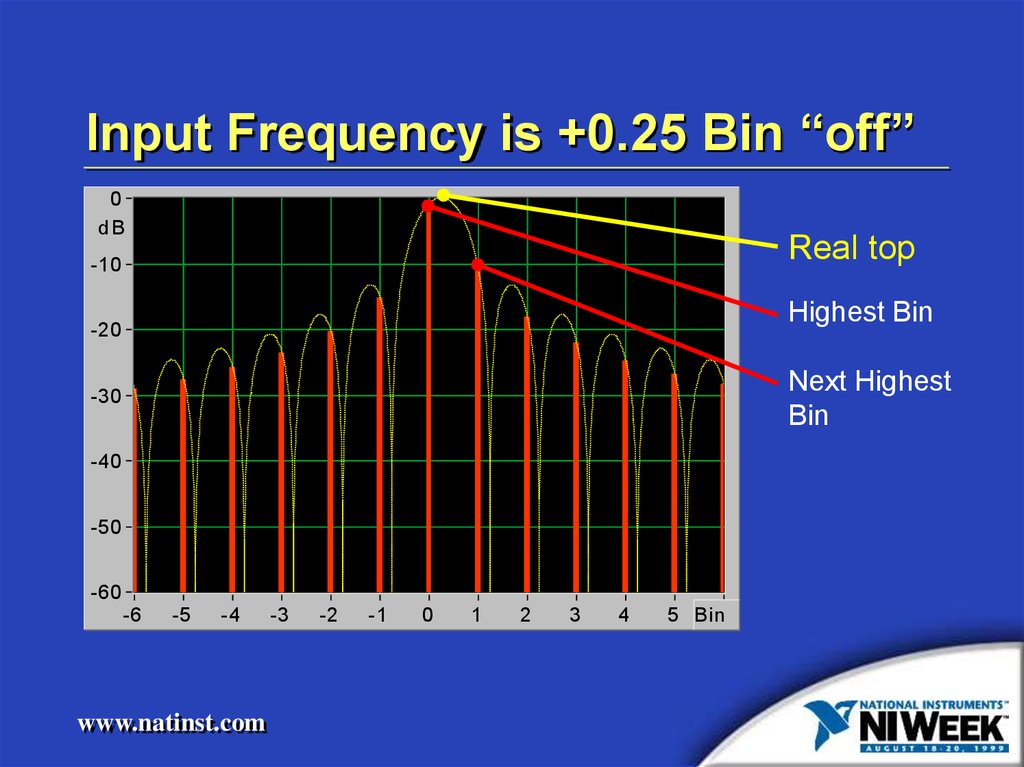
Input Frequency is +0.25 Bin “off”0
dB
Real top
-10
Highest Bin
-20
Next Highest
Bin
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
10. Input Frequency is +0.25 Bin “off”
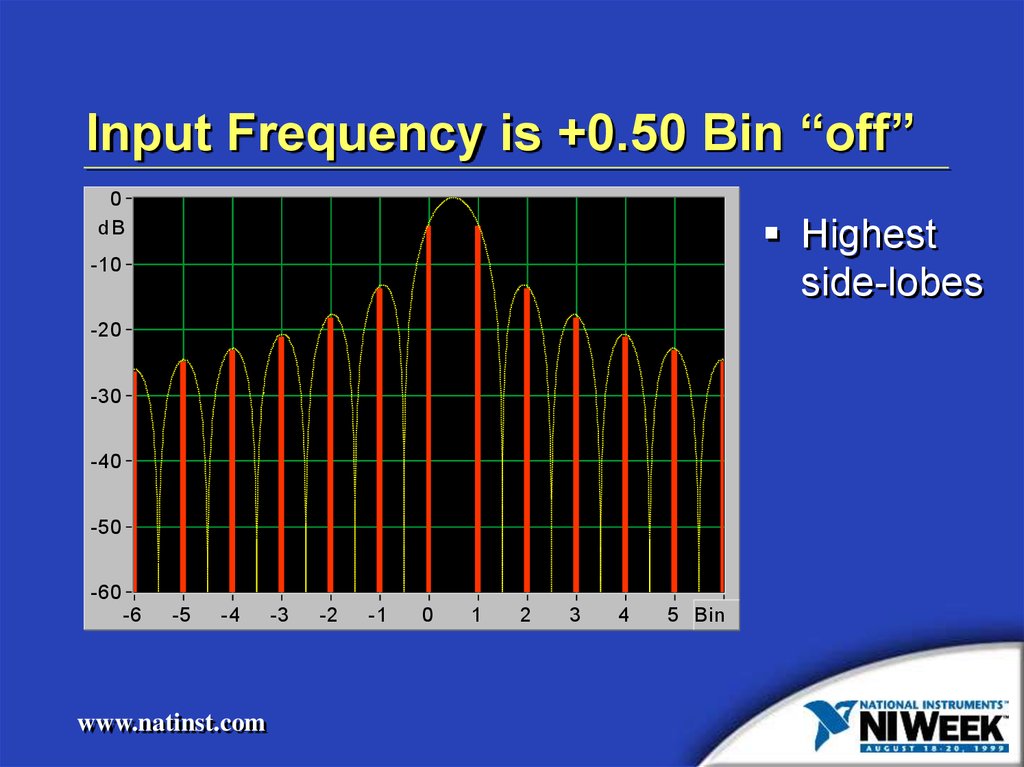
Input Frequency is +0.50 Bin “off”0
dB
Highest
side-lobes
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
11. Input Frequency is +0.50 Bin “off”
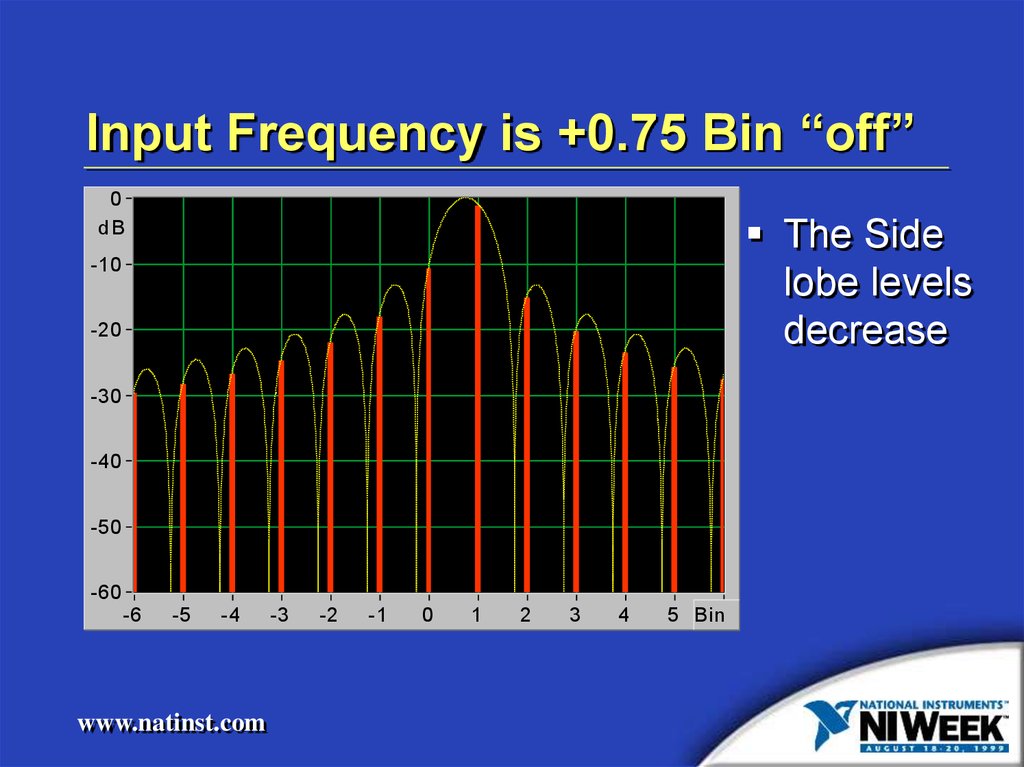
Input Frequency is +0.75 Bin “off”0
dB
The Side
lobe levels
decrease
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
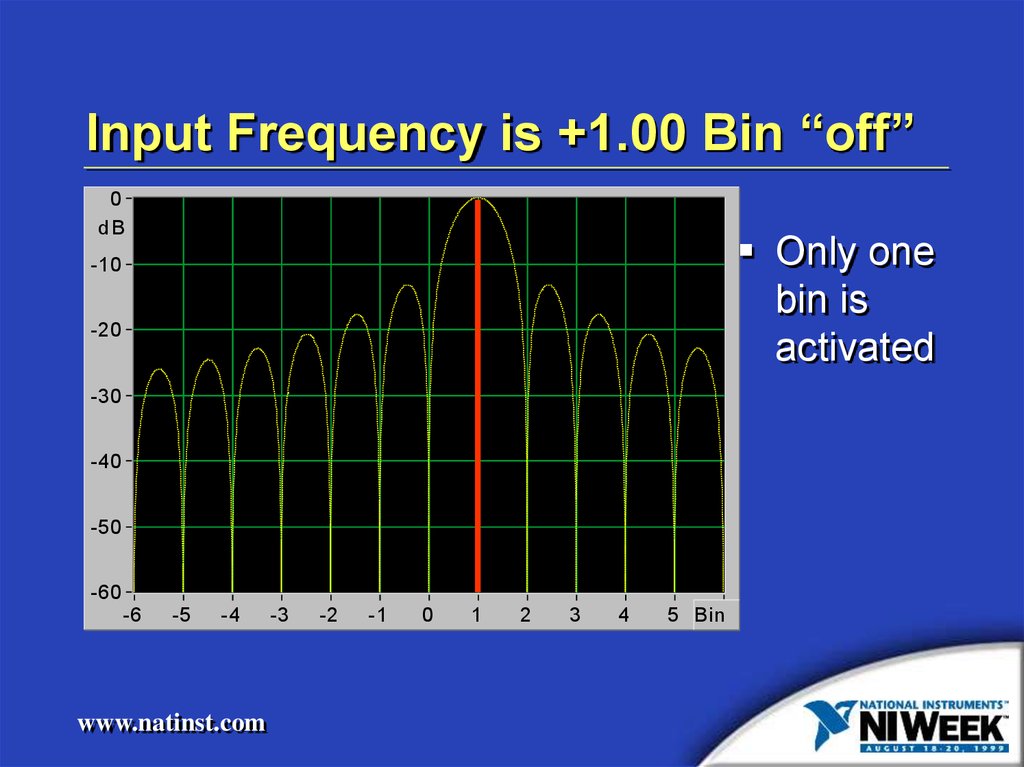
12. Input Frequency is +0.75 Bin “off”
Input Frequency is +1.00 Bin “off”0
dB
Only one
bin is
activated
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
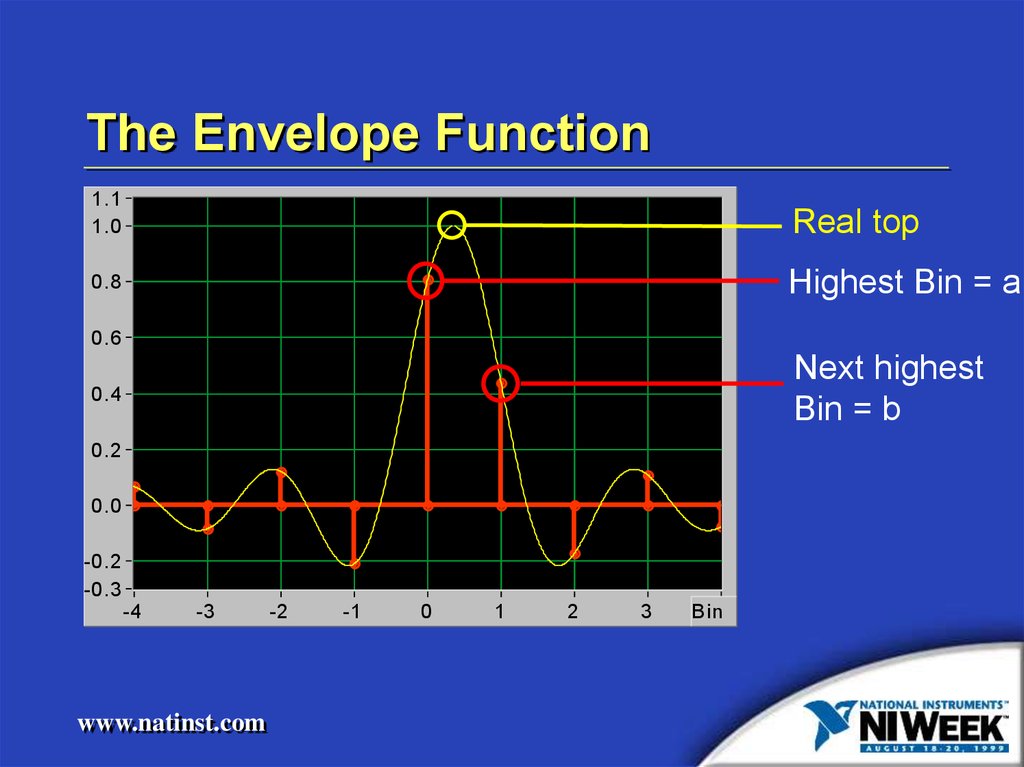
13. Input Frequency is +1.00 Bin “off”
The Envelope Function1.1
1.0
Real top
0.8
Highest Bin = a
0.6
Next highest
Bin = b
0.4
0.2
0.0
-0.2
-0.3
-4
-3
www.natinst.com
-2
-1
0
1
2
3
Bin4
14. The Envelope Function
The MathematicsEnvelope function:
Sin( π bin)
Env
(π bin)
Bin offset:
b
Δbin
(a b)
Real amplitude:
(π Δbin)
Amp a
Sin( π Δbin)
www.natinst.com
15. The Mathematics
DemoAmplitude and frequency detection by
Sin(x) / x interpolation
www.natinst.com
16. Demo
Aliasing of the Side-LobesHighest Bin =
Bin 4
0
dB
-10
-20
Aliased Bin =
“Negative Bin 4”
-30
-40
-50
-60
0
1
2
www.natinst.com
3
4
5
6
7
8
9
Bin
10
17. Aliasing of the Side-Lobes
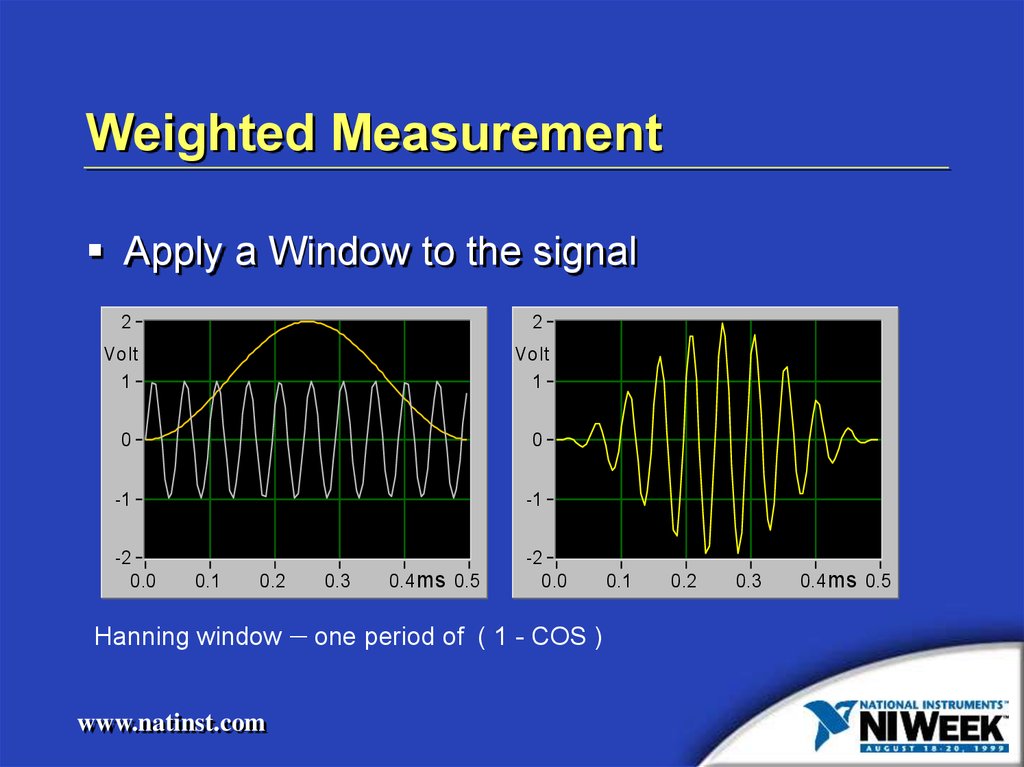
Weighted MeasurementApply a Window to the signal
2
2
Vo lt
1
Vo lt
1
0
0
-1
-1
-2
0.0
-2
0.0
0.1
0.2
0.3
0.4 ms 0.5
Hanning window – one period of ( 1 - COS )
www.natinst.com
0.1
0.2
0.3
0.4 ms 0.5
18. Weighted Measurement
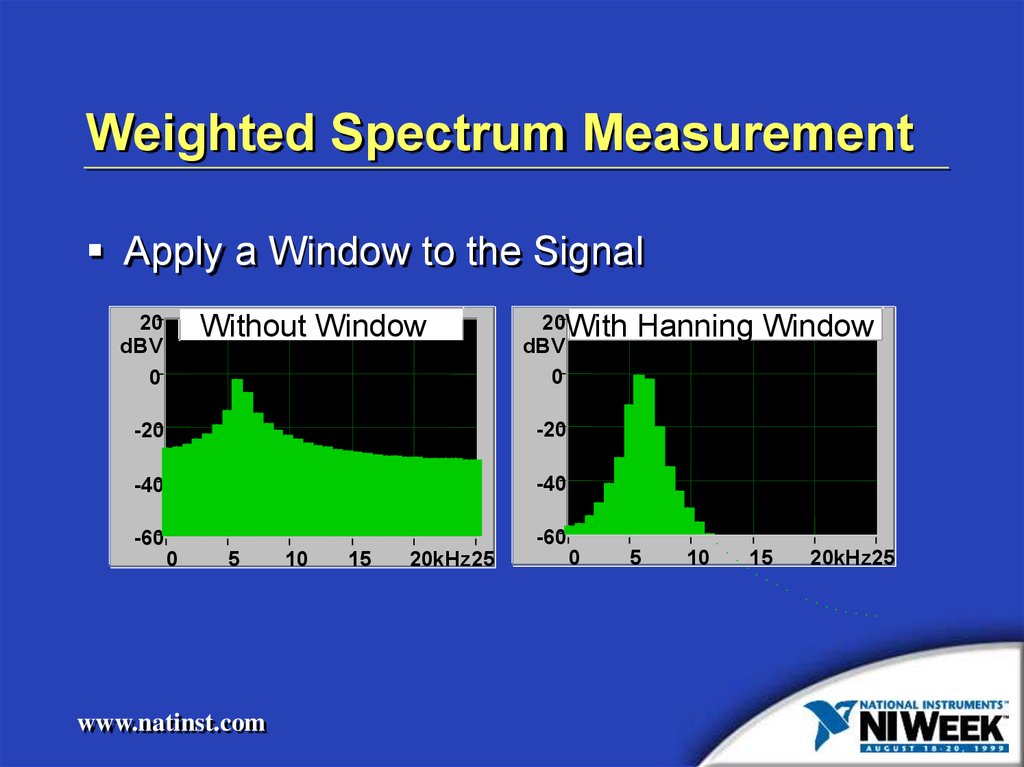
Weighted Spectrum MeasurementApply a Window to the Signal
Without Window
20
dBV
0
20With
dBV
0
-20
-20
-40
-40
-60
-60
0
5
www.natinst.com
10
15
20kHz25
0
Hanning Window
5
10
15
20kHz25
19. Weighted Spectrum Measurement
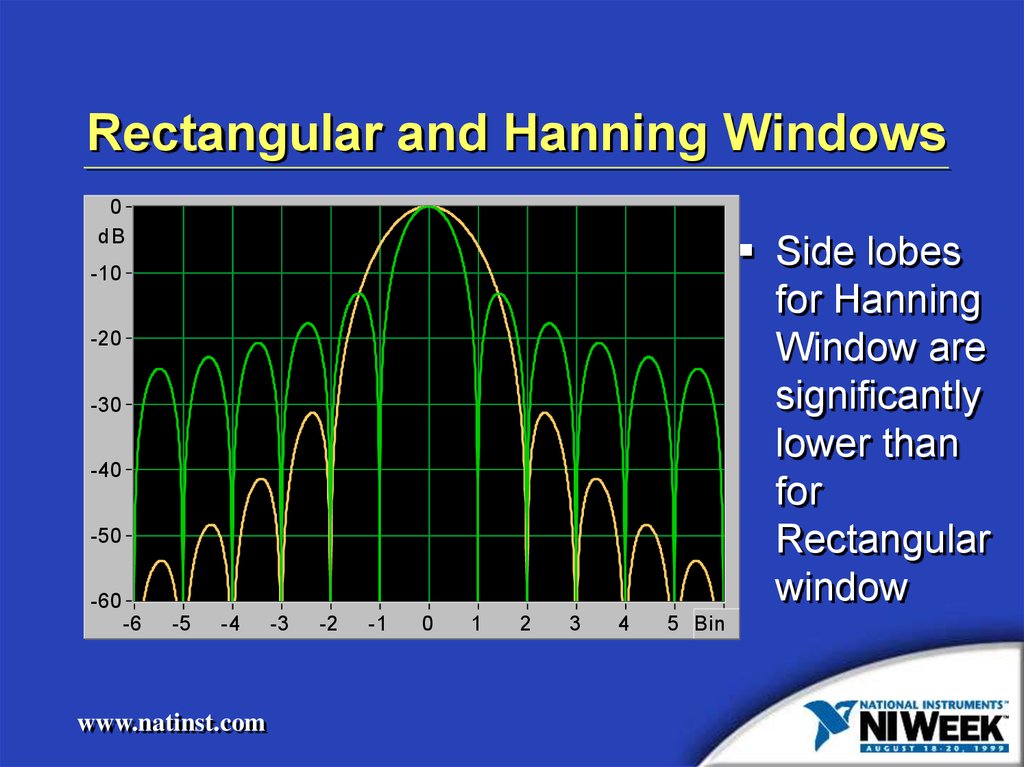
Rectangular and Hanning Windows0
dB
Side lobes
for Hanning
Window are
significantly
lower than
for
Rectangular
window
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
20. Rectangular and Hanning Windows
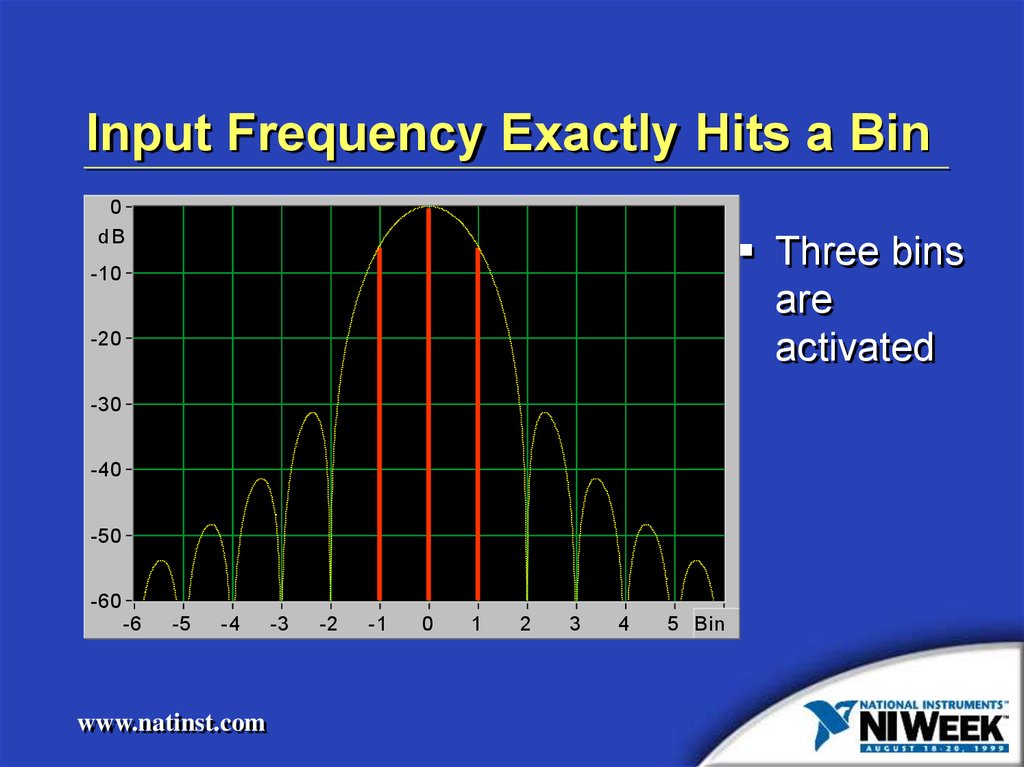
Input Frequency Exactly Hits a Bin0
dB
Three bins
are
activated
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
21. Input Frequency Exactly Hits a Bin
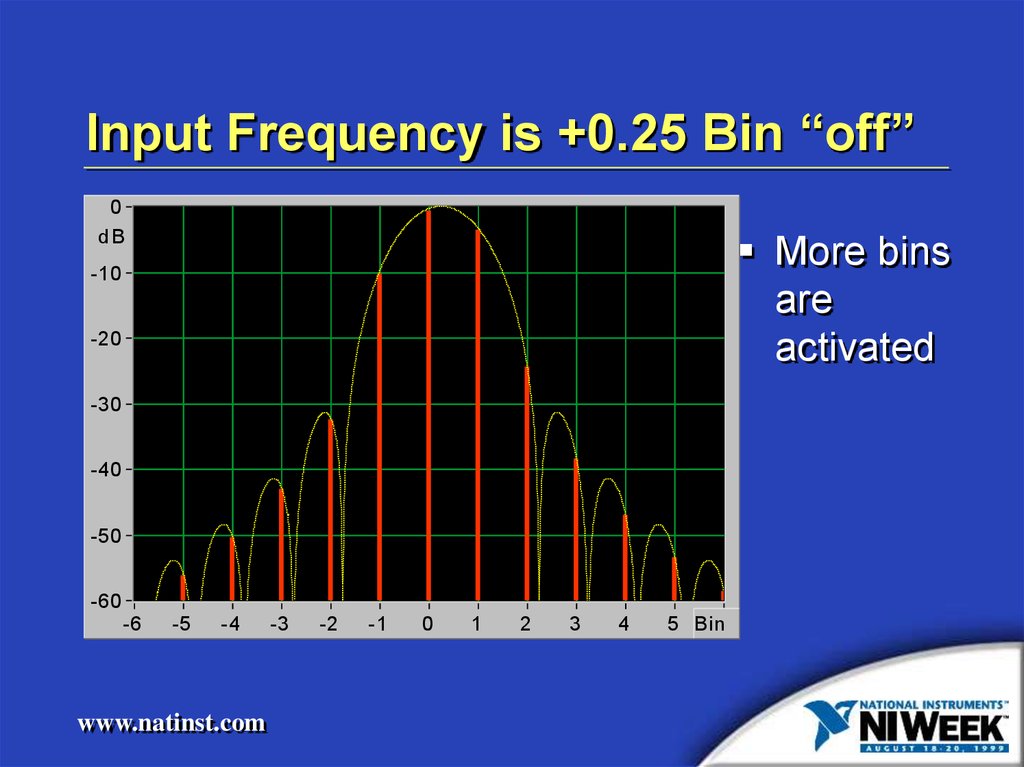
Input Frequency is +0.25 Bin “off”0
dB
More bins
are
activated
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
22. Input Frequency is +0.25 Bin “off”
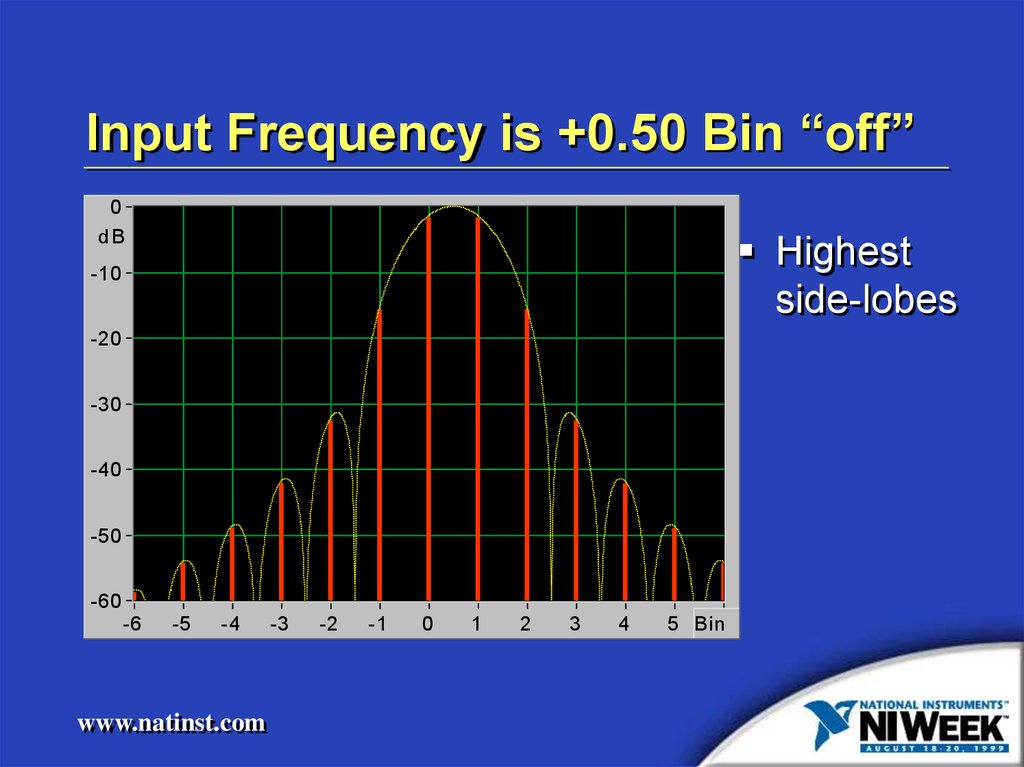
Input Frequency is +0.50 Bin “off”0
dB
Highest
side-lobes
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
23. Input Frequency is +0.50 Bin “off”
Input Frequency is +0.75 Bin “off”0
dB
The Side
lobe levels
decrease
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
24. Input Frequency is +0.75 Bin “off”
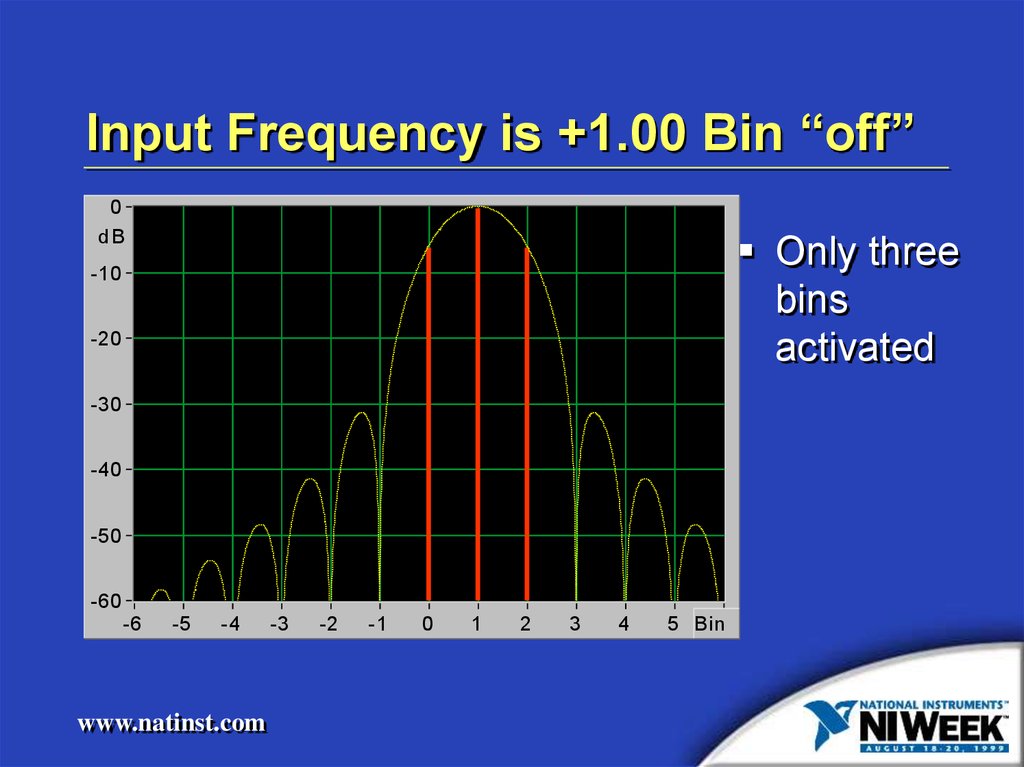
Input Frequency is +1.00 Bin “off”0
dB
Only three
bins
activated
-10
-20
-30
-40
-50
-60
-6
-5
-4
www.natinst.com
-3
-2
-1
0
1
2
3
4
5 Bin6
25. Input Frequency is +1.00 Bin “off”
The Mathematics for Hanning ...Sin( π bin)
Envelope: Env
2
(π bin) (1 bin )
(a - 2b)
Bin Offset: Δbin
(a b)
(π Δbin)
Amplitude: Amp a
(1 Δbin 2 )
Sin( π Δbin)
www.natinst.com
26. The Mathematics for Hanning ...
A LabVIEW ToolTone detector LabVIEW virtual instrument (VI)
www.natinst.com
27. A LabVIEW Tool
DemoAmplitude and frequency detection using a
Hanning Window (named after Von Hann)
Real world demo using:
The NI-5411 ARBitrary Waveform Generator
The NI-5911 FLEXible Resolution Oscilloscope
www.natinst.com
28. Demo
Frequency Detection Resolution1000.00
Freq error (ppm)
ppm
100.00
10.00
1.00
0.10
0.01
1
www.natinst.com
10
Signal periods
100
29. Frequency Detection Resolution
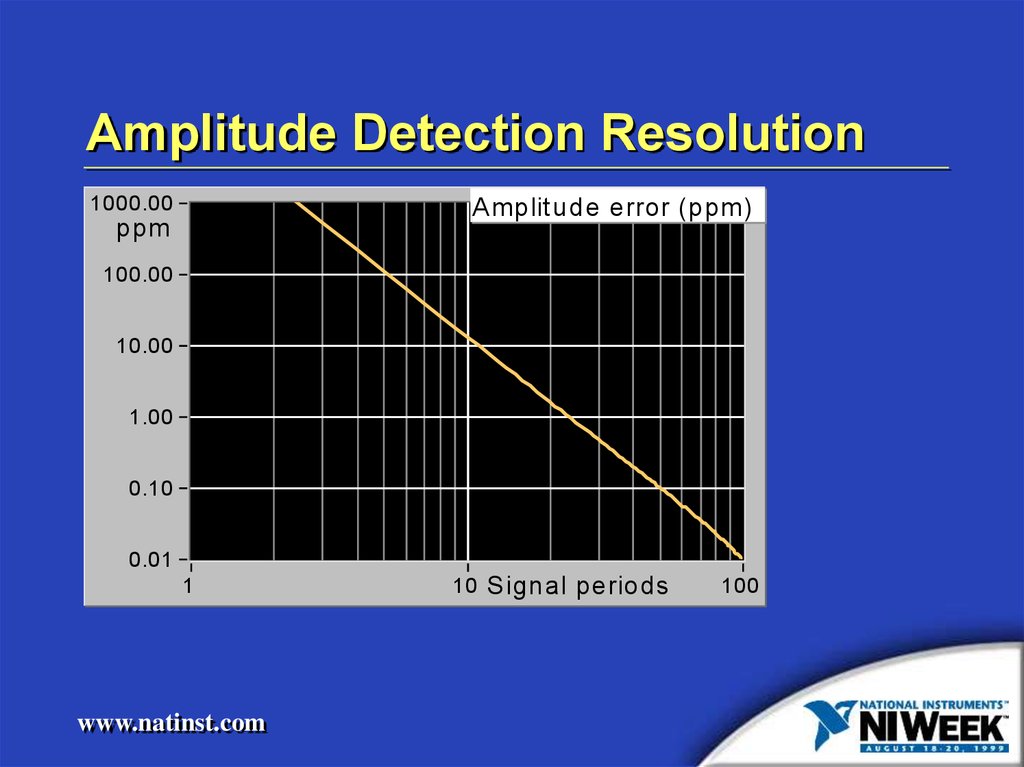
Amplitude Detection Resolution1000.00
Amplitude error (ppm)
ppm
100.00
10.00
1.00
0.10
0.01
1
www.natinst.com
10
Signal periods
100
30. Amplitude Detection Resolution
Phase Detection Resolution1000.00
Phase error (mdeg)
mdeg.
100.00
10.00
1.00
0.10
0.01
1
www.natinst.com
10
Signal periods
100
31. Phase Detection Resolution
ConclusionsTraditional counters resolve 10 digits in one
second
FFT techniques can do this in much less than
100 ms
Another example of 10X for test
Similar improvements apply to amplitude and
phase
www.natinst.com
32. Conclusions
(Notes Page Only)Traditional Counters Resolve 10 digits in one
second
FFT Techniques can do this in much less than
100 ms
Another example of 10X for test
Similar improvements apply to Amplitude and
Phase
www.natinst.com














 electronics
electronics








