Similar presentations:
Частотні характеристики лінійних електричних кіл другого порядку. Частотні властивості послідовного коливального контуру
1. ЛЕКЦІЯ № 8 з навчальної дисципліни Теорія кіл і сигналів в інформаційному та кіберпросторах Тема 4. Частотні характеристики
лінійнихелектричних кіл другого порядку.
Заняття 1. Частотні властивості
послідовного коливального контуру.
2. Л I Т Е Р А Т У Р А 1. Бондаренко В.Н. Основы теории цепей. К.: Институт электродинамики НАН Украины.-2012. с.313-329. 2.
ЛIТЕРАТУРА1. Бондаренко В.Н. Основы теории цепей. К.:
Институт электродинамики НАН Украины.2012. с.313-329.
2. Карташов Р.П., Медведев А.П. Теория
электрорадиоцепей,.
3. 1. Условия и признаки резонанса напряжений.
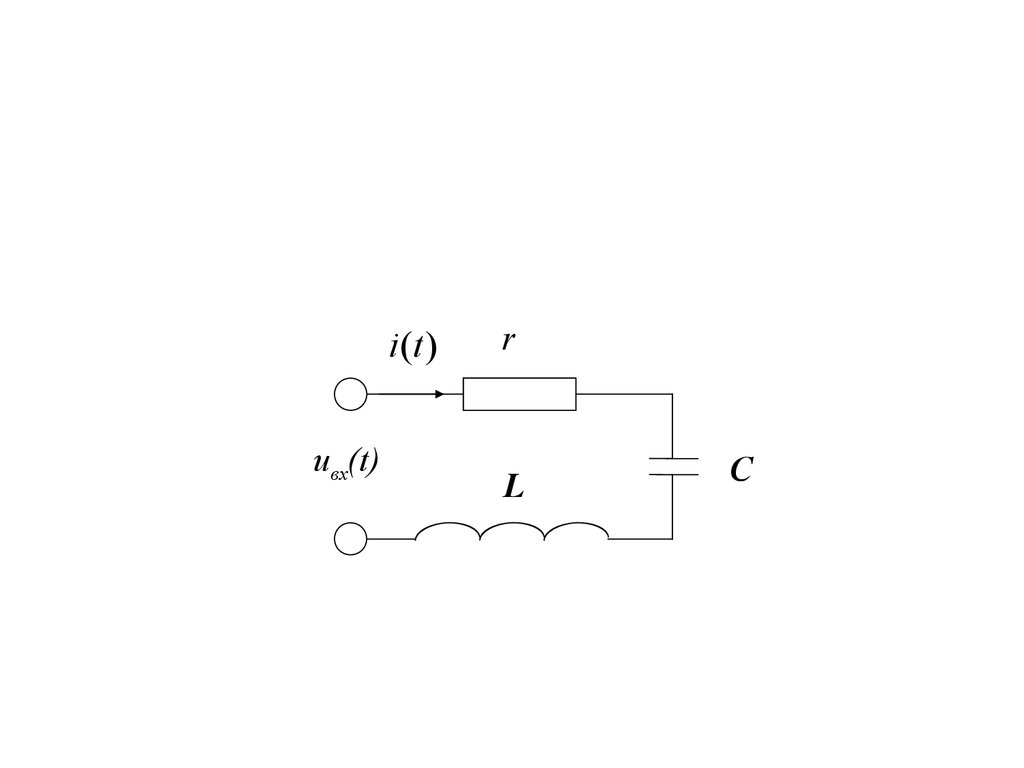
• Последовательным колебательнымконтуром называют цепь, состоящую из
последовательного соединения
индуктивности L и емкости С
4. Элементы электроники
5.
i (t )uвх(t)
r
L
C
6. Пусть напряжение на зажимах контура изменяется по закону
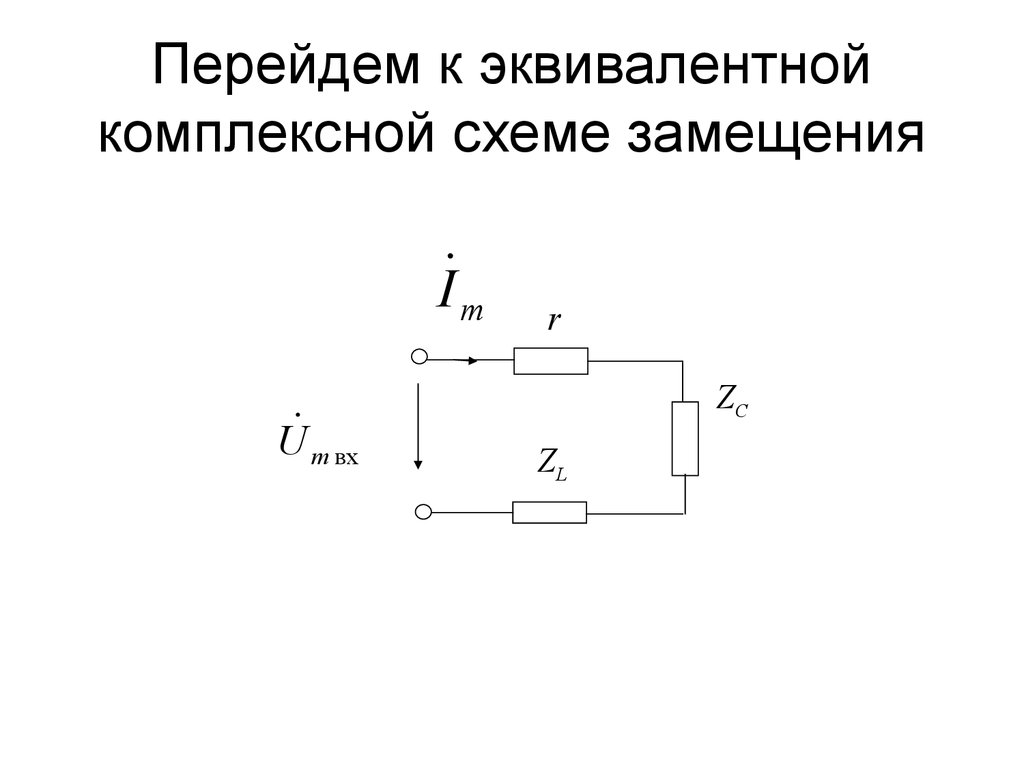
uвх (t ) U m sin t.7. Перейдем к эквивалентной комплексной схеме замещения
I mU m вх
r
ZC
ZL
8. По второму закону Кирхгофа составим уравнение электрического равновесия:
U m âõ U mr U mL U mC1
rI m j L I m j
Im
C
1
I m (r j L j
).
C
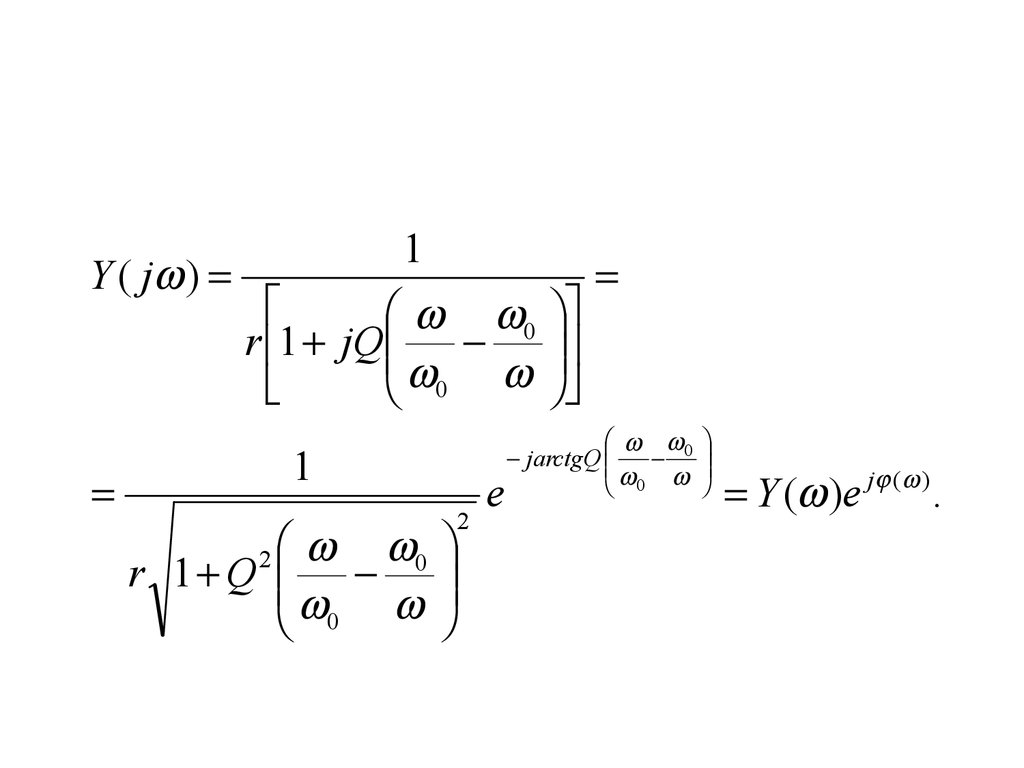
9. Комплексное сопротивление цепи
U m âõ• Zвх=
Im
I (r j L j 1 )
m
C
I m
1
r j L j
C
j
r jx ze ,
10.
• где1
x xL xC L
;
C
x
2
2
arctg ; z r x .
r
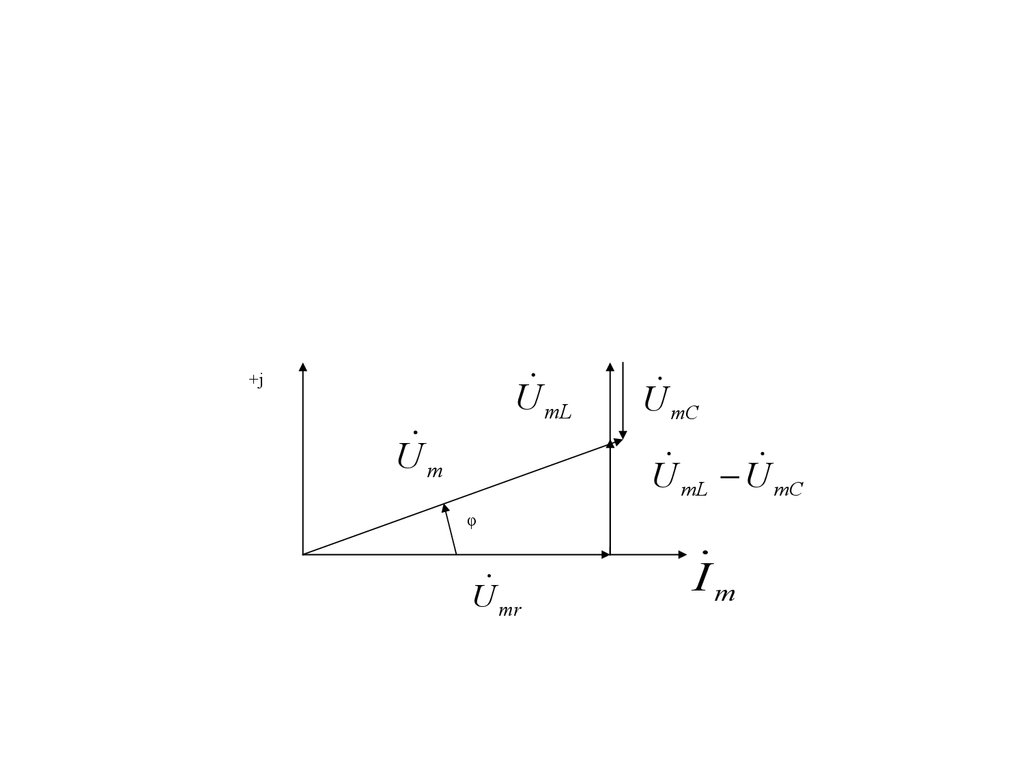
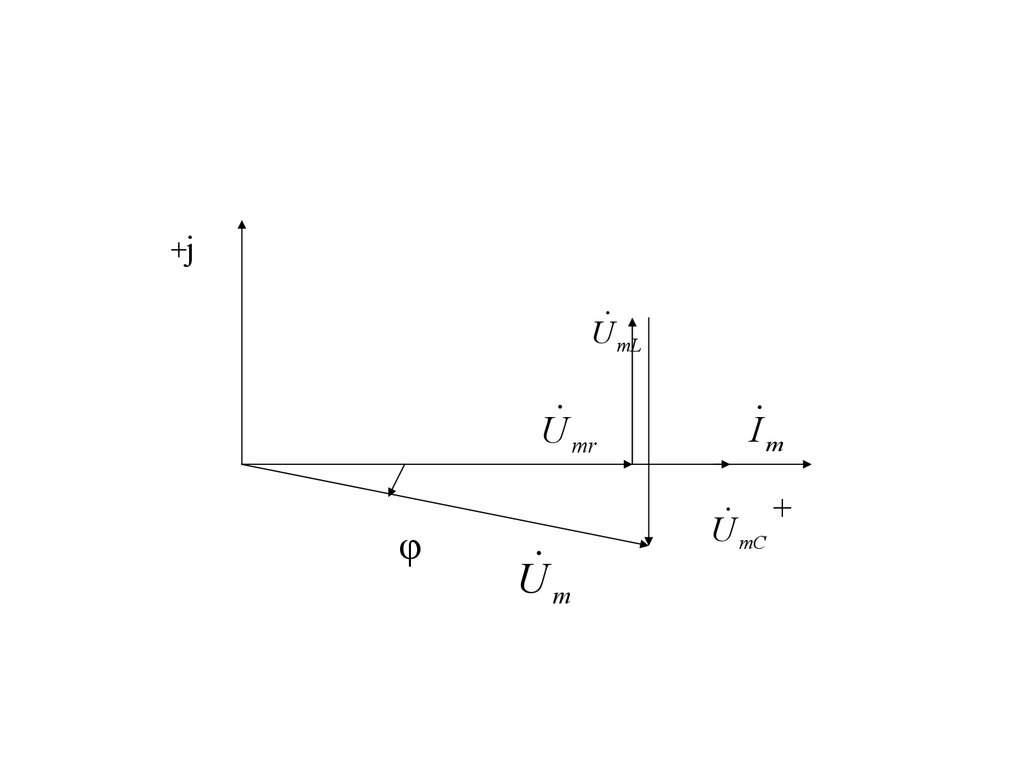
11. При xL>xC сдвиг фаз между приложенным к цепи напряжением и током в цепи φ>0, т.е. будет положительным, ток в цепи отстает от
При xL>xC сдвиг фаз между приложенным кцепи напряжением и током в цепи φ>0, т.е.
будет положительным, ток в цепи отстает от
приложенного напряжения, цепь носит
индуктивный характер (рис. 7.3)
12.
U mL+j
U m
U mC
U mL U mC
φ
U mr
I m
13.
• При xL<xC сдвиг фаз междуприложенным к цепи напряжением и
током в цепи φ<0, т.е. будет
отрицательным, ток в цепи опережает
приложенное к ней напряжение. Цепь
носит емкостной характер
14.
+jU mL
U mr
φ
U m
I m
+
U mC
15.
• Наибольший интерес представляетслучай равенства xL= xC. При этом
реактивное сопротивление контура
равно нулю, комплексное
Z r j ( x L xC ) r ,
сопротивление
цепь носит характер только активного
сопротивления, ток в цепи совпадает по
фазе с приложенным к ней
напряжением.
16.
+jU mL
U mC
U mr
U m
I m
17.
• Уменьшение комплексного сопротивленияконтура до минимального приводит к
возрастанию до максимума тока в контуре,
что свидетельствует о наступлении явления
электрического резонанса. Существуют
различные определения резонанса, взаимно
дополняющие друг друга. Одно из них:
резонансом (от латинского resono –
откликаюсь) называется явление, при
котором сопротивление контура
становится только активным.
18.
• Другое определение: резонансомназывается резкое возрастание
амплитуды вынужденных колебаний
при приближении частоты внешнего
гармонического воздействия к
частоте собственных колебаний
контура. Равенство xL = xC является
условием возникновения резонанса в
последовательном колебательном
контуре.
19.
• При xL= xC сдвиг фаз между током инапряжением φ=0. В этом случае
хL=хLр; хС=хСр. По отношению к входным
зажимам контур при резонансе
эквивалентен цепи, состоящей из
одного активного сопротивления r .
20.
• Первый признак резонанса впоследовательном колебательном
контуре. Амплитуда тока в цепи при
резонансе принимает максимальное
значение Im=Um/r . В остальных случаях
2
2
r
x
амплитуда тока равна Im=Um/
21.
• Второйпризнак
резонанса
напряжений
в
последовательном
колебательном контуре. Напряжения на
реактивных элементах при резонансе
равны по амплитуде и противоположны
по фазе.
22.
U mLjx Lр I m ;
U m C jxCр I m
Учитывая то, что при резонансе xL = Xc,
можно записать, что
j
U m L U mC e
23. 2. Первичные и вторичные параметры последовательного колебательного контура.
• Первичными параметрамипоследовательного колебательного
контура являются величина
индуктивности L, величина емкости С и
величина активного сопротивления r.
Они характеризуют данный контур как
совокупность конкретных элементов и
позволяют отличить его от других
контуров.
24. Рассмотрим, какие параметры относятся к вторичным
Резонансная частота контура - это частота, прикоторой реактивное сопротивление контура равно
нулю. Определим ее из равенства xL = xC :
1
0 L
;
0C
Отсюда
0 LC 1; 0
2
1
.
LC
25.
• Это резонансная частота контура иличастота собственных колебаний,
которая определяется только
параметрами контура.
26. Волновое или характеристическое сопротивление контура.
• Модули реактивных сопротивленийконтура на резонансной частоте равны
и определяются как
x L 0 L
1
xC
0C
1
L
L
;
C
LC
1
L
.
1
C
C
LC
27.
ВеличинаL
C
называется волновым или
характеристическим сопротивлением
контура.
28. Добротность контура
• Резонансные свойства контурахарактеризуются добротностью
контура. Добротностью контура
называют отношение напряжения на
реактивном элементе (индуктивности
или емкости) при резонансе к
напряжению, действующему на
входе контура
29.
QU m Lр
U mвх
U mCр
U mвх
0 L
1
r
0 rC r
отношение волнового сопротивления
контура к активному сопротивлению.
30.
• Добротность определяет эффективность иликачество контура, является безразмерной
величиной.
• Чем меньше активное сопротивление
контура, тем выше его добротность. Для
радиотехнических контуров характерны
значения добротности от 100 до 500.
Свойство контура усиливать приложенное
напряжение широко используется на
практике.
• Величина, обратная добротности, носит
название затухание контура
31.
1 rd .
Q
Это наименование параметра связано с тем,
что оно характеризует скорость затухания колебаний
в контуре при отключении от него источника энергии.
32. 3. Комплексні функції та частотні характеристики ПКК
• Для анализа и описания частотноизбирательных свойств колебательныхконтуров используют комплексные
входные и передаточные функции.
Наибольший интерес при изучении
последовательных контуров
представляют комплексная входная
проводимость и комплексная
передаточная функция по напряжению .
33.
• Комплексной входной функциейцепи называется отношение
комплексных амплитуд тока и
напряжения, действующих на
входных зажимах.
Комплексная входная проводимость:
I mвх
1
Yвх ( j )
U mвх Z вх ( j )
34. 3.1 Комплексная входная проводимость последовательного колебательного контура
• Комплексная входная проводимостьпоследовательного колебательного
контура рассчитывается через его
параметры:
1
1
Yвх ( j )
Z ( j ) r jx
1
x
r (1 j )
r
35.
0x 1
1
1
1 0 L
( L
) ( L
)
r r
C
r
0 C 0 L
0 L
1
0
(
) Q( )
r 0 0 LC
0
36.
Y ( j )1
0
r 1 jQ
0
1
0
r 1 Q
0
2
2
e
0
jarctgQ
0
Y ( )e
j ( )
.
37.
Нормированная комплекснаявходная проводимость получается
Y j
путем отношения
к ее же
значению при 0.
1
Так как Y j 0
, то
r
Yn j
Y j
Y j 0
1
0
1 Q
0
2
2
e
jarctgQ 0
0
Y j
e
.
Y 0
38.
• Нормированная входная АЧХописывается выражением
Y
Yn ( )
Y 0
1
0
1 Q
0
2
2
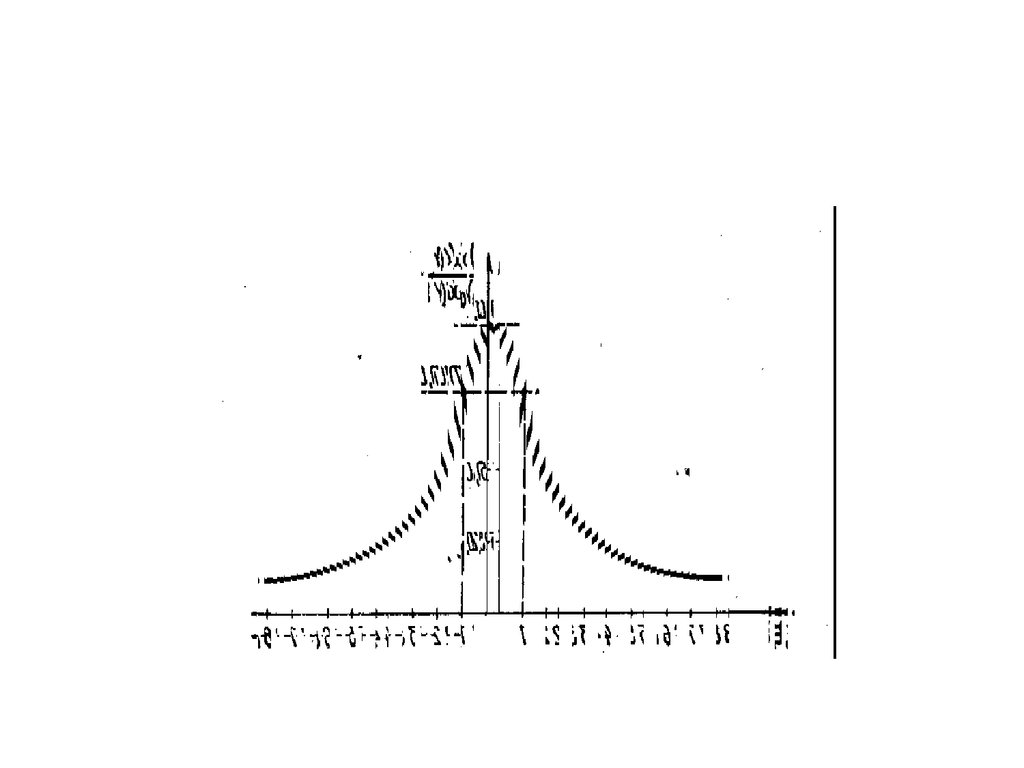
39. График нормированной входной АЧХ имеет следующий вид:
Увеличению добротности контура соответствуютболее острые резонансные кривые или усиление
его частотно-избирательных свойств.
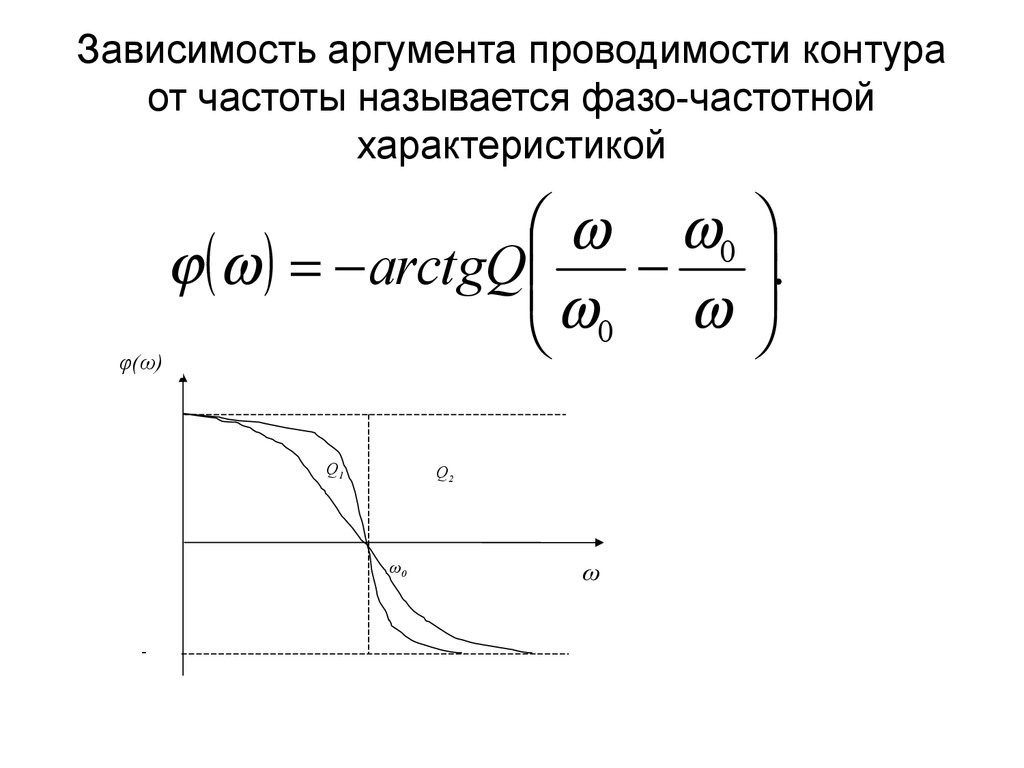
40. Зависимость аргумента проводимости контура от частоты называется фазо-частотной характеристикой
φ(ω)0
arctgQ .
0
Q1
Q2
ω0
-
ω
41.
• Из этого графика следует, что начастотах ниже резонансной контур
имеет емкостной характер, при
резонансе – резистивный, а на частотах
выше резонансной – индуктивный.
42.
При исследовании частотныххарактеристик колебательного контура
в качестве независимой переменной
удобно использовать величину,
характеризующую расстройку контура,
т.е. степень отклонения его
резонансной частоты от частоты
сигнала.
43.
• Разность между частотой сигнала ирезонансной частотой контура
• называют абсолютной расстройкой.
Она может быть как положительной, так
и отрицательной.
0
44.
Отношение абсолютной расстройки крезонансной частоте называется
относительной расстройкой.
0
45.
Фактором расстройки называютвеличину, описываемую выражением
0
0
46.
Обобщенной расстройкой называютпреобразованное отношение
реактивного сопротивления контура к
активному
0
x
Q
Q
r
0
47.
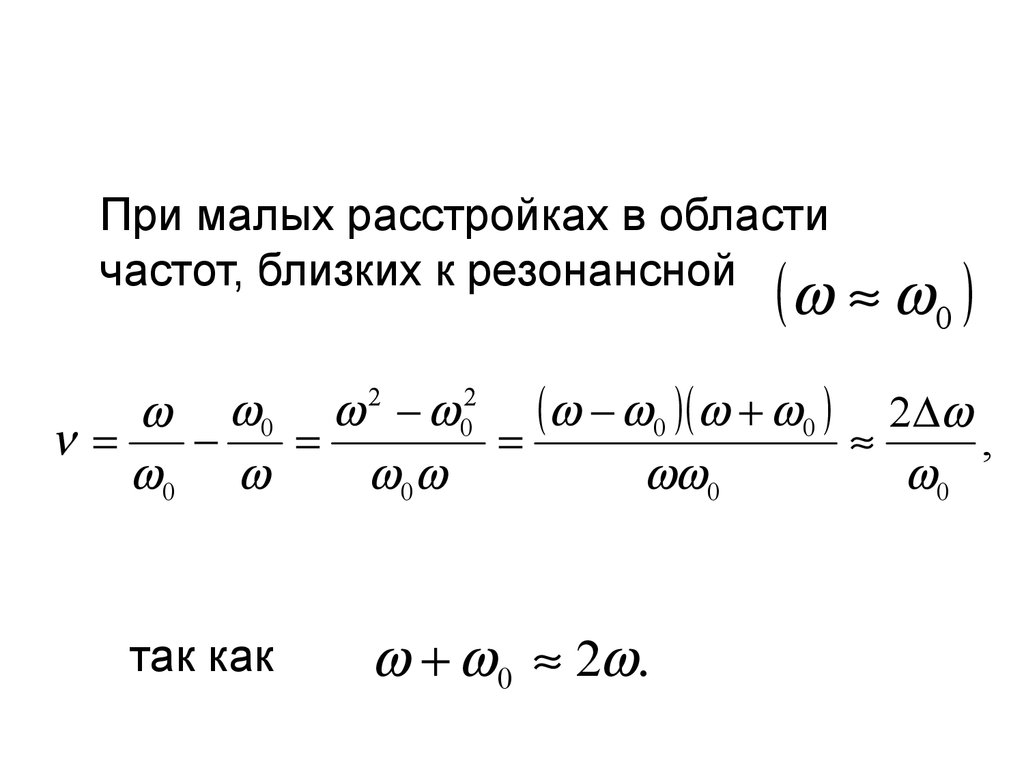
При малых расстройках в областичастот, близких к резонансной
0
2
2
0 0 2
0
0
,
0
0
0
0
так как
0 2 .
48.
• Поэтому вблизи резонанса2
Q 2Q .
49.
• Относительная и обобщенная расстройки, каки фактор расстройки, безразмерные
величины. Все виды расстроек при
резонансе равны нулю.
Преобразуя полученные формулы,
получим выражения для нормированных
частотных характеристик контура в функции
расстройки:
50.
Y j1
Yn ( j )
e arctg ;
Y j 0
1 2
Y
1
Yn ( )
;
Y 0
1 2
arctg
51.
52. 3.2 Комплексная передаточная функция по напряжению .
3.2Комплексная
передаточная
функция
по
• Комплексные передаточные функции по
.
напряжениюнапряжению
последовательного
колебательного контура различают в
зависимости от того, напряжение на
каком из его элементов является
выходным
53.
54.
Для передаточной функции понапряжению на активном
сопротивлении с учетом
1
Y j 0
r
получаем
55.
U mr rI mKUr ( j )
rY ( j )
U m U m
Y ( j )
1
jarctg
e
Y ( j 0 )
1 2
56.
Этому соответствует амплитудночастотная и фазо-частотнаяхарактеристики:
KUr ( )
1
1 2
r ( ) arctg
57. Передаточная функция по напряжению на емкости
U mC1 I m
1
KUC ( j )
Y ( j )
Um
j C U m
j C
1
1
1 0
jarctg
e
j rC 1 2
j 0 rC
0 jarctg ( / 2 arctg )
e
2
1
Q
1
1 2
e arctg
58. Ей соответствуют частотные характеристики:
0KUC ( )
2
1
Q
C ( ) arctg
2
59. Для передаточной функции по напряжению на индуктивности
U mLI m
j L
K UL ( j )
j L
j LY ( j )
e jarctg
U m
U m
r 1 2
j 0 L
jarctg
Q
j ( 2 arctg )
e
e
2
2
r 1
1
0
0
60. Частотные характеристики в этом случае:
KUL ( j )1 2 0
Q
L ( ) arctg
2
61. Покажем графики соответствующих характеристик.
62.
Численно передаточные функции, или коэффициентыпередачи по напряжению, показывают, во сколько раз
напряжение на соответствующем элементе больше
напряжения, действующего на входе контура. Из полученных
соотношений, в частности, следует, что при резонансе
напряжения на реактивных элементах в Q раз превышают
входное напряжение, а напряжение на активном элементе
равно ему.
Напряжение на реактивнх элементах достигает своего
максимального значения в стороне от резонанса, а
максимальные значения этих функций одинаковы.
Из всех комплексных коэффициентов передачи
последовательного колебательного контура практический
интерес представляет передаточная функция по напряжению на
емкости, так как обычно выходное напряжение снимается с
емкости.
63. 4. Резонансні характеристики ПКК
• Резонансными характеристикамиПКК называют зависимость
амплитуды тока в контуре или
напряжений на его элементах от
частоты.
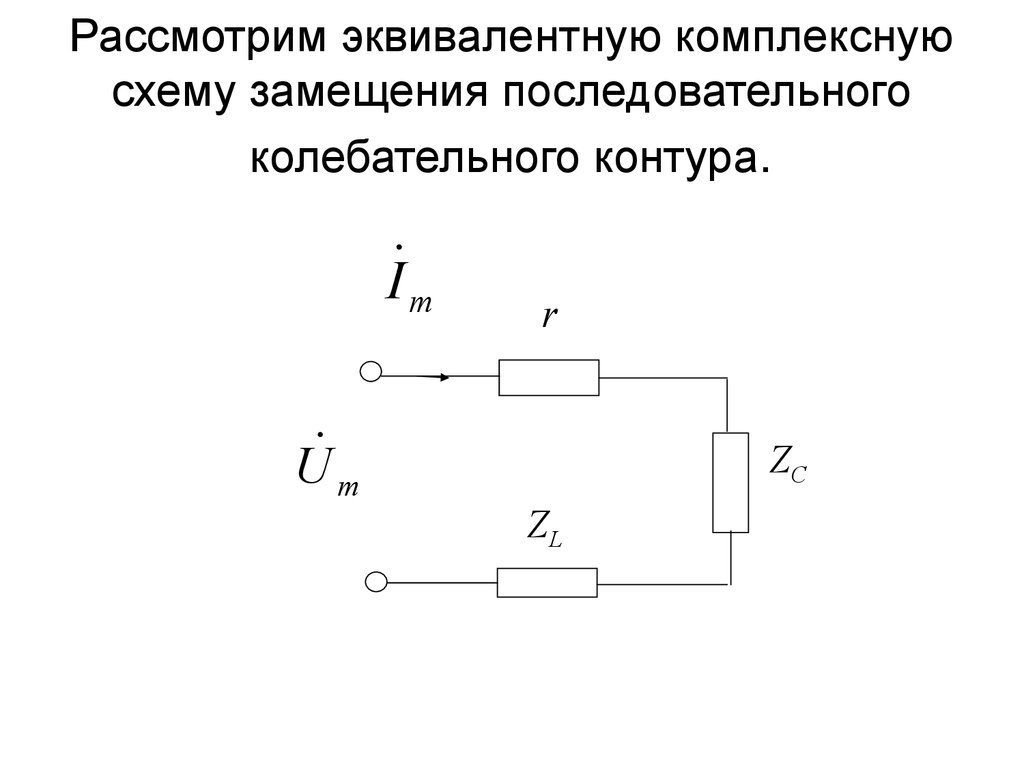
64. Рассмотрим эквивалентную комплексную схему замещения последовательного колебательного контура.
I mU m
r
ZC
ZL
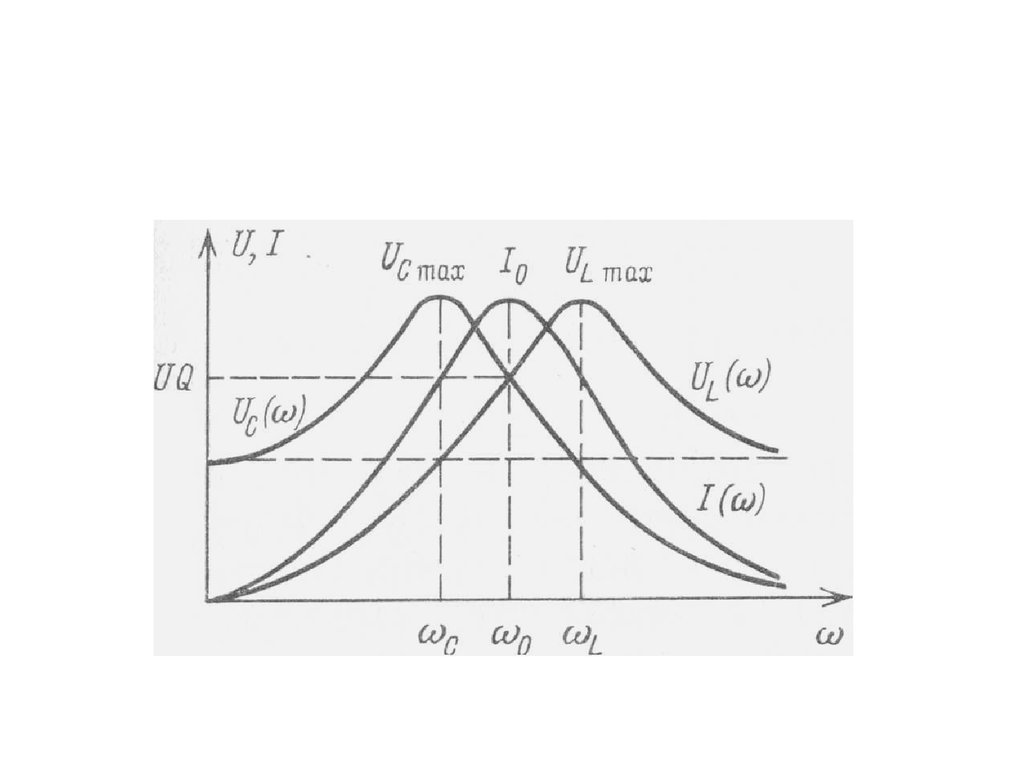
65. Зависимость амплитуды тока от частоты имеет следующий вид:
ImUm
1
r L
C
2
2
66. Проанализируем это уравнение, для чего воспользуемся случаями предельных значений частоты:
0 z Im 0Um
0 z r I m
r
z Im 0
67. Амплитуды напряжений на реактивных элементах можно найти согласно закону Ома:
U m LU m L I m X L
1
r L
C
2
2
U m C I m X C
Um
1
2
C r L
C
2
68.
69.
• При 0 ток в цепи равен нулю инапряжение на активном
сопротивлении также равно нулю.
Учитывая, что X L L , при 0 эта
величина также равна нулю и
амплитуда напряжения U m L 0 =0.
Напряжение, приложенное к контуру,
выделится на емкости, и U m C 0 U mвх .
70.
• При частоте, равной резонансной,наблюдается равенство напряжений на
реактивных элементах, однако эти значения
не максимальны. При изменении частоты в
сторону уменьшения или увеличения от
резонансной происходит незначительное
вначале уменьшение тока, но за счет
увеличения реактивных сопротивлений
происходит рост напряжения на них.
71.
• Приток в цепи также
равен нулю и напряжение на активном
сопротивлении также равно нулю.
1
Учитывая, что X C
, при
эта величина также равна нулю и
амплитуда напряжения U m C 0 =0.
Напряжение, приложенное к контуру,
выделится на индуктивности, и
U m L U mвх
.
С
72. 5. Полоса пропускания ПКК
• Полосой пропусканияпоследовательного колебательного
контура называется диапазон частот
вблизи резонансной, на границах
которого амплитуда тока в контуре
снижается до уровня 0,707 своего
максимального значения.
73.
74.
• Разность граничных частот называетсяабсолютной полосой пропускания:
2 1
75. Отношение разности граничных частот к резонансной частоте называется относительной полосой пропускания:
2 10
0
0
76.
02 1 Q 0 d
2 1
1
0 Q d
0
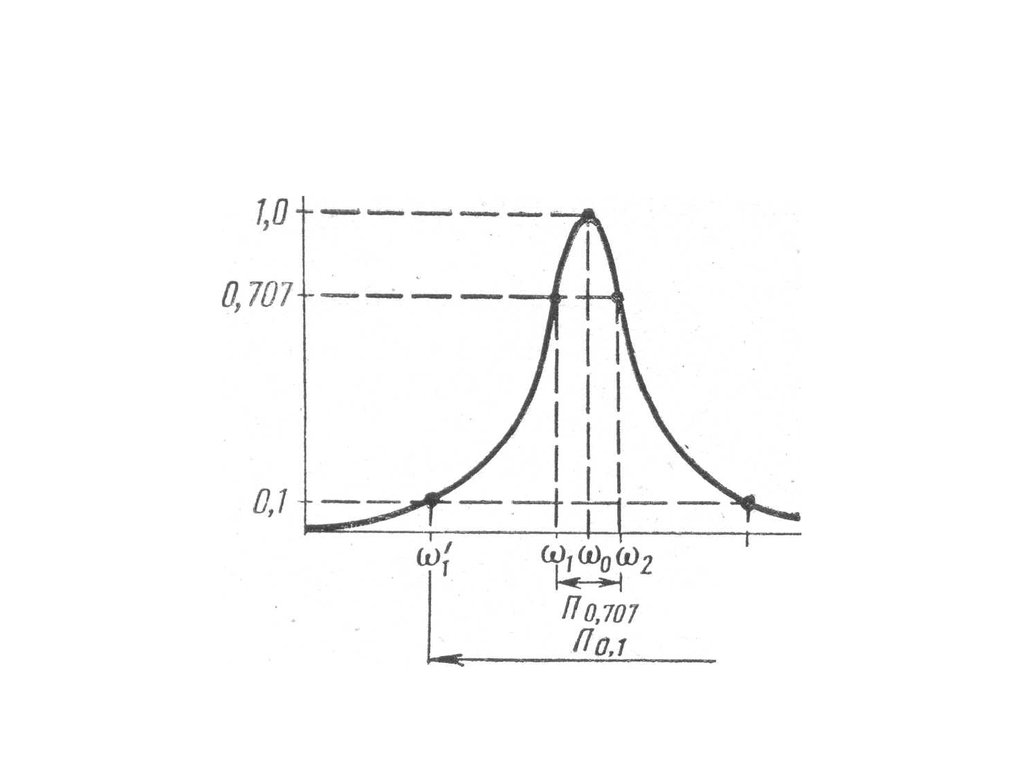
77. 6. Коэффициент прямоугольности амплитудно-частотной характеристики
• Коэффициентом прямоугольностирезонансной кривой контура называется
отношение полосы пропускания
контура, отсчитанной на
1
• уровне 2 0,707 , к полосе пропускания,
отсчитанной на уровне 1 0,1:
КП
10
0 , 707
0 ,1
78.
• коэффициент прямоугольности дляпоследовательного колебательного
контура является постоянной
величиной, не зависящей от его
параметров:
0 d
КП
0,1
10 0 d







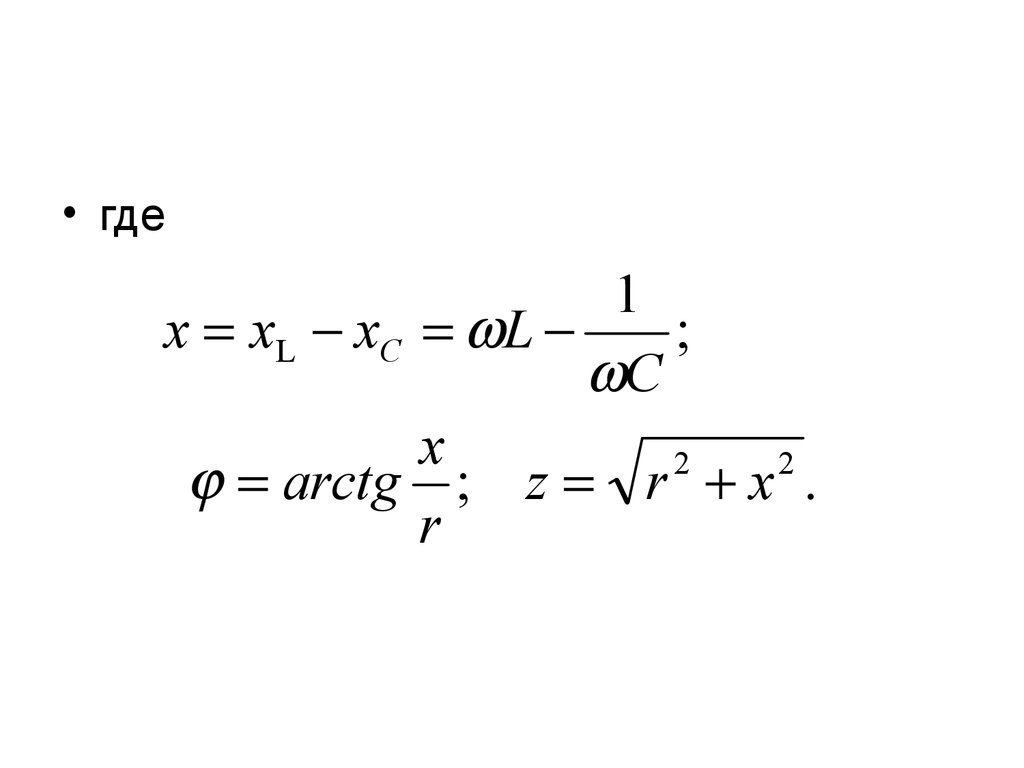






















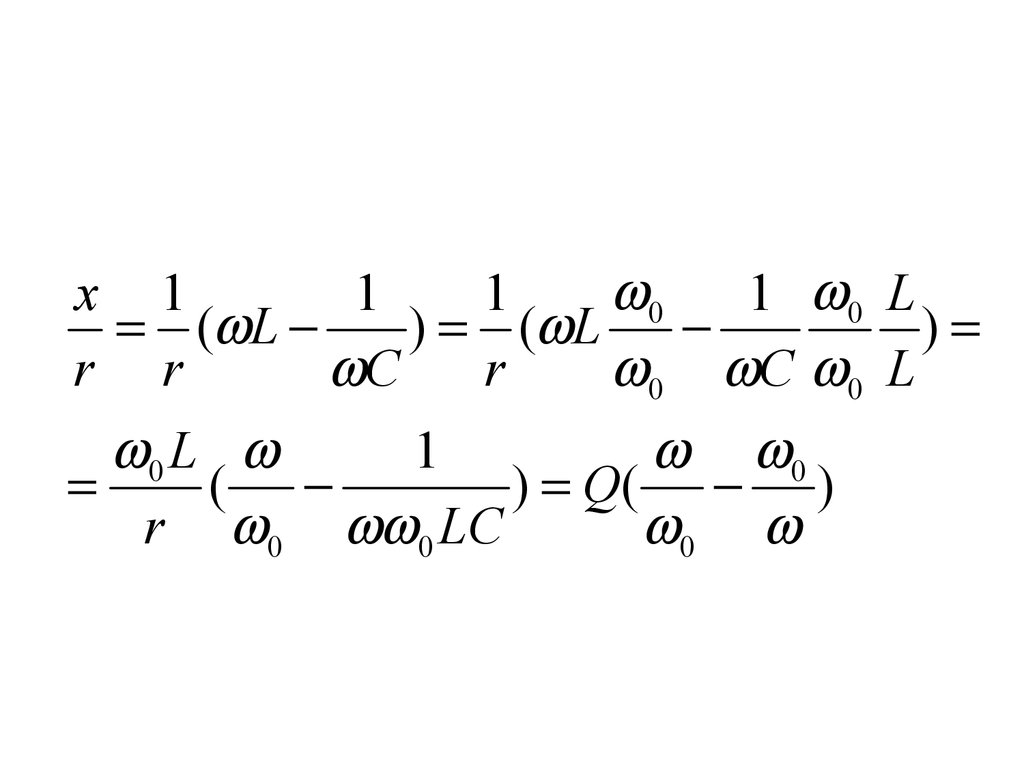









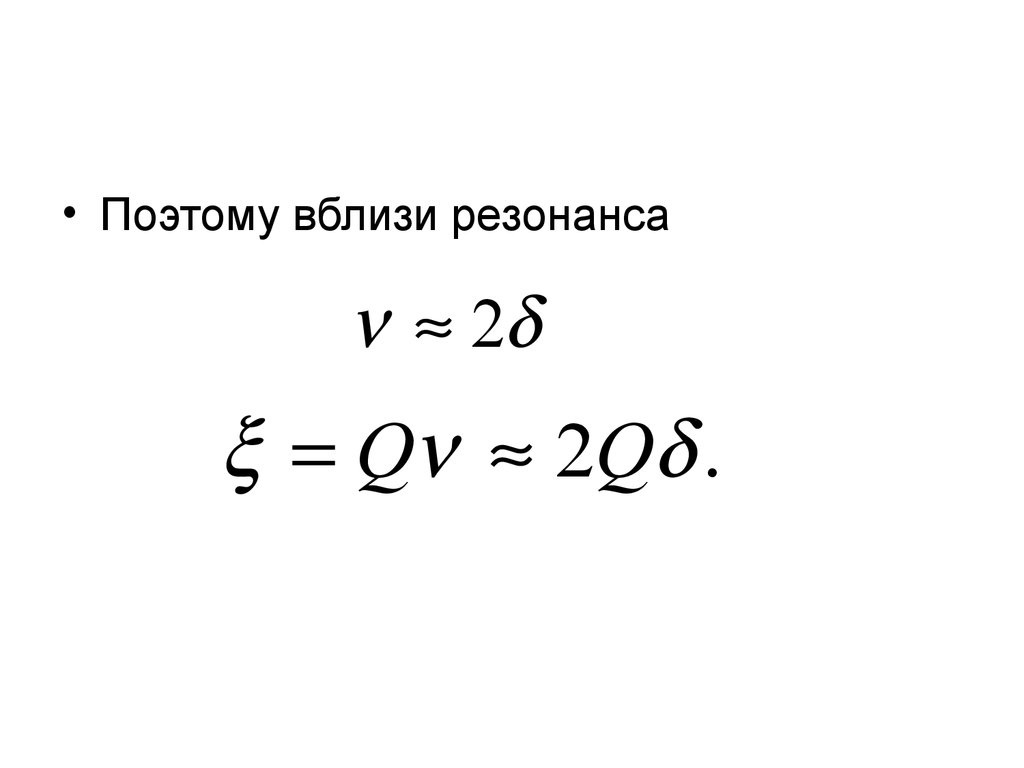

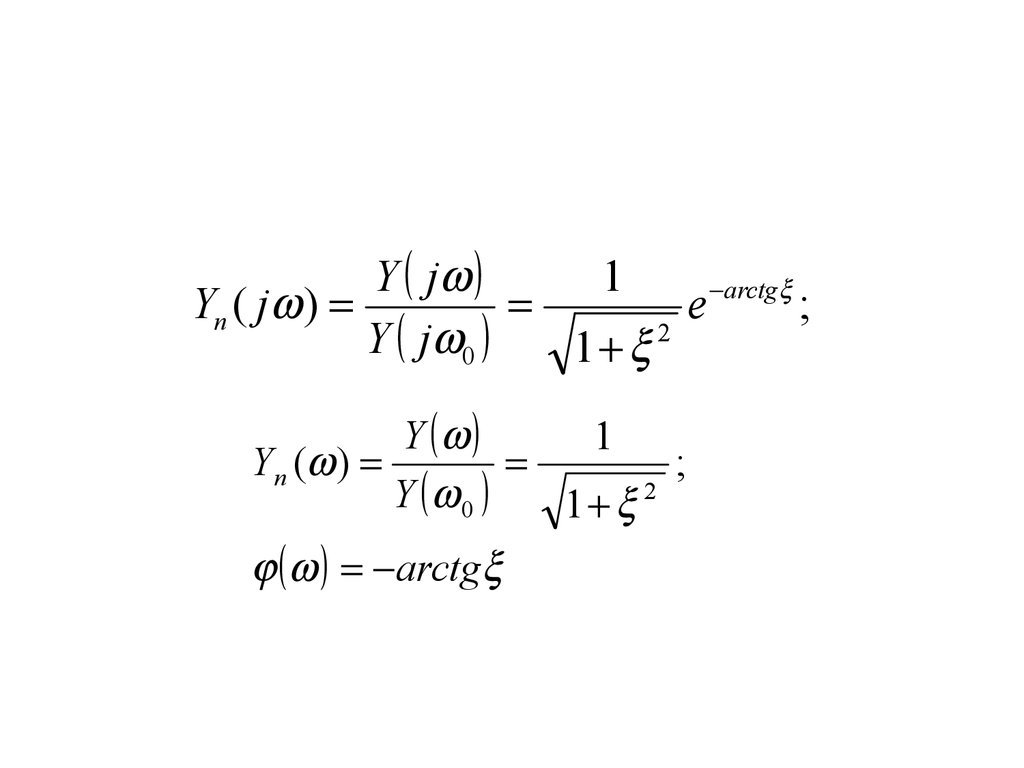



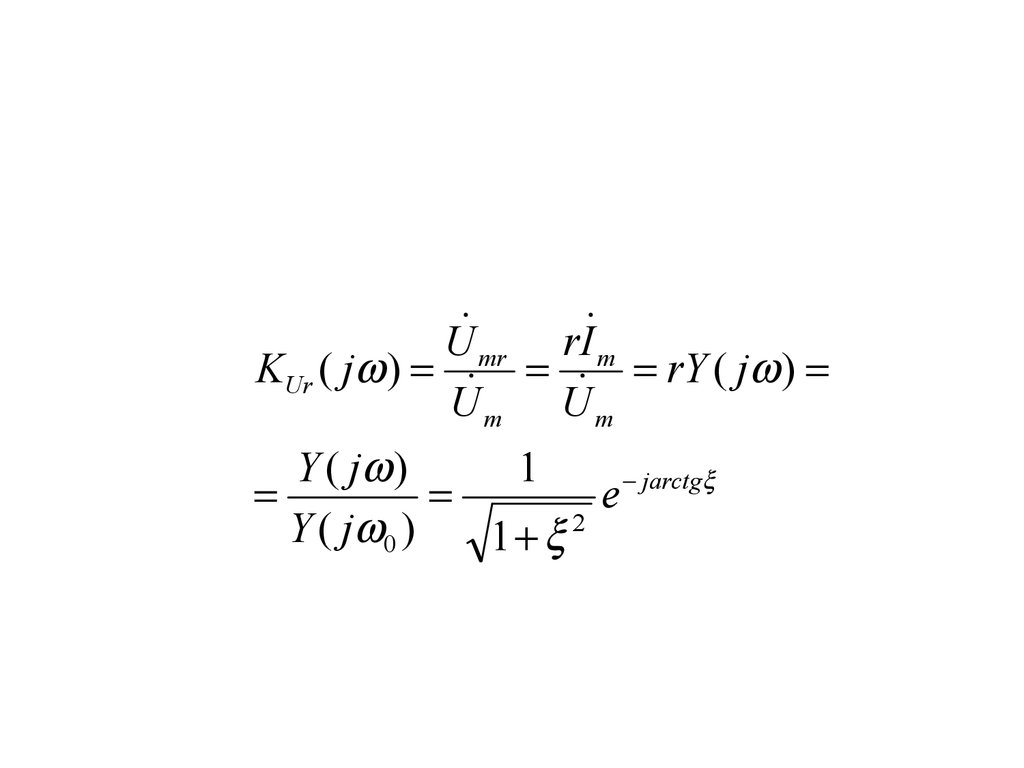

















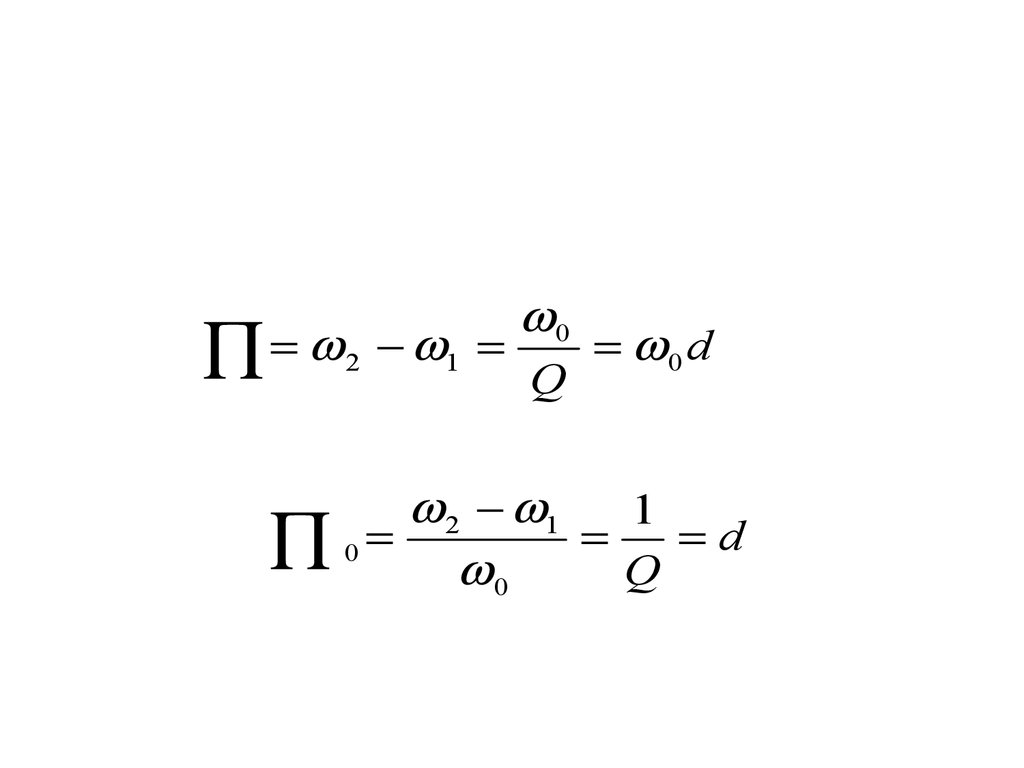


 electronics
electronics








