Представление аналогового сигнала в дискретной форме

1. Оптоэлектроника Лекция 4 Представление аналогового сигнала в дискретной форме

Краснов В.В., Черёмхин П.А.

2. Матричные устройства ввода и регистрации изображений

Модуляторы света
Матричные фотосенсоры

3. Примеры изображений введенных в систему посредством модулятора света

4. Регистрация светового распределения посредством матричного фотосенсора

Матричный фотосенсор с
массивом светофильтров
Байера
Изображение, полученное с матричного
фотосенсора

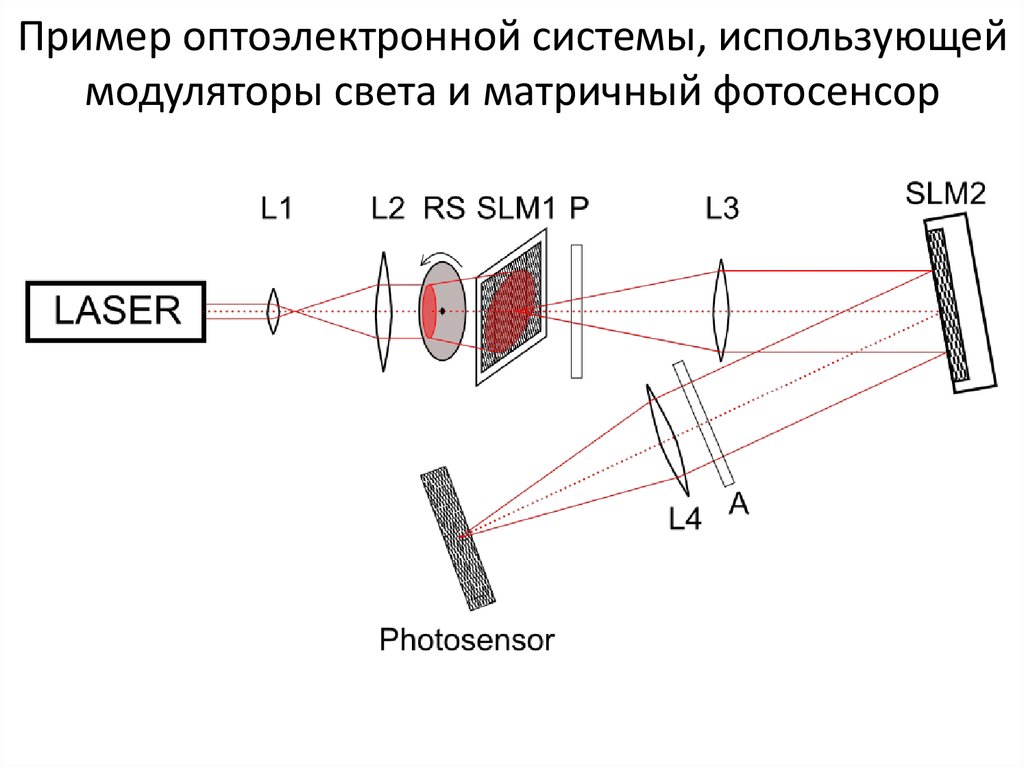
5. Пример оптоэлектронной системы, использующей модуляторы света и матричный фотосенсор

6. Эффект наложения, алайзинг, муар

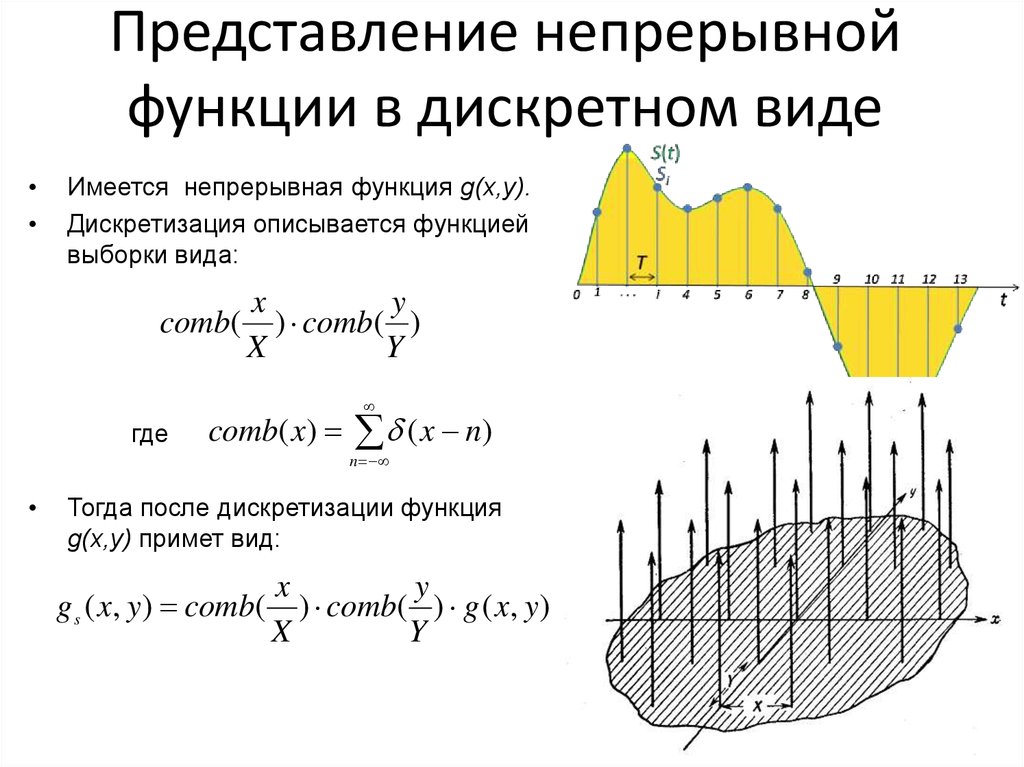
7. Представление непрерывной функции в дискретном виде

Имеется непрерывная функция g(x,y).
Дискретизация описывается функцией
выборки вида:
x
y
comb( ) comb( )
X
Y
где
comb( x)
( x n)
n
Тогда после дискретизации функция
g(x,y) примет вид:
x
y
g s ( x, y ) comb( ) comb( ) g ( x, y )
X
Y

8. Теорема Котельникова (Шеннона-Уиттекера)

• Если спектр функции g ограничен
некоторой частотой R, то, в случае если
частота выборки больше или равна 2R,
исходная функция g может быть точно
восстановлена из дискретной функции gs.
• Частота R называется частотой Найквиста.

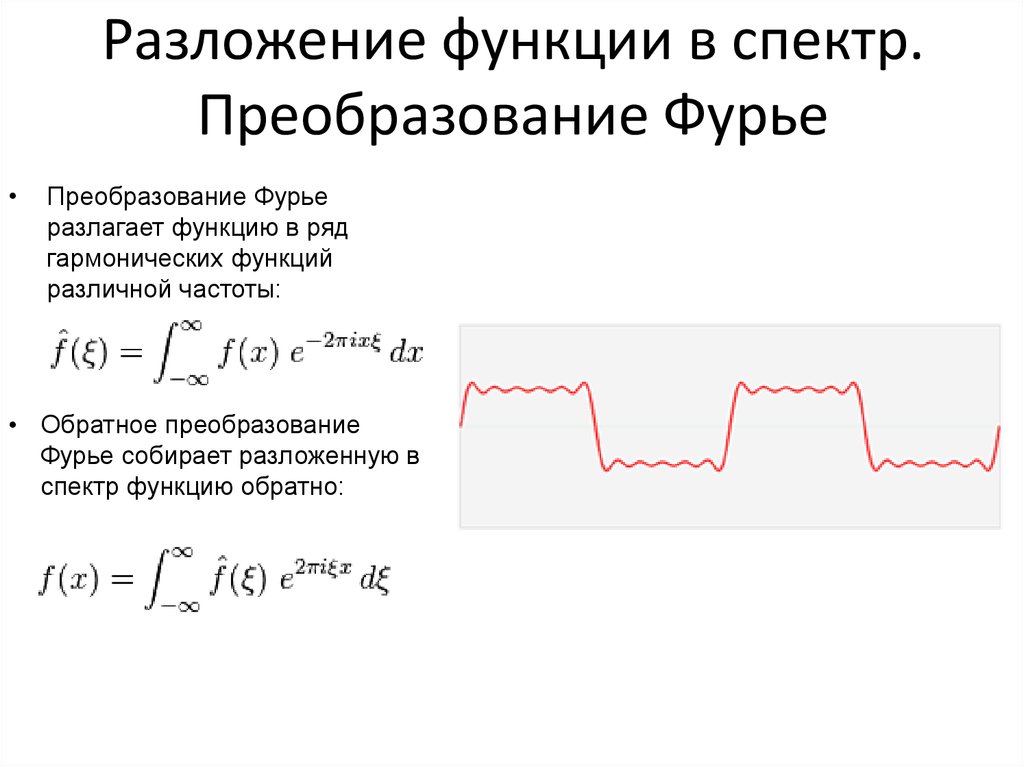
9. Разложение функции в спектр. Преобразование Фурье

Преобразование Фурье
разлагает функцию в ряд
гармонических функций
различной частоты:
• Обратное преобразование
Фурье собирает разложенную в
спектр функцию обратно:

10. Доказательство теоремы Котельникова

x
y
g s ( x, y ) comb( ) comb( ) g ( x, y )
X
Y
Найдем спектр Gs(fx,fy) функции gs(x,y):
x
y
Gs ( f X , fY ) F {comb( ) comb( ) g ( x, y )}
X
Y
Воспользовавшись теоремой свертки, запишем:
x
y
Gs ( f X , fY ) F {comb( ) comb( )} G ( f X , fY )
X
Y
Воспользовавшись теоремой подобия, получаем:
x
y
F {comb( ) comb( )} X Y comb( X f X )comb(Y fY )
X
Y
n
m
X Y ( X f x n) (Y f y m) ( f x , f y )
X
Y
n
m
n m

11.

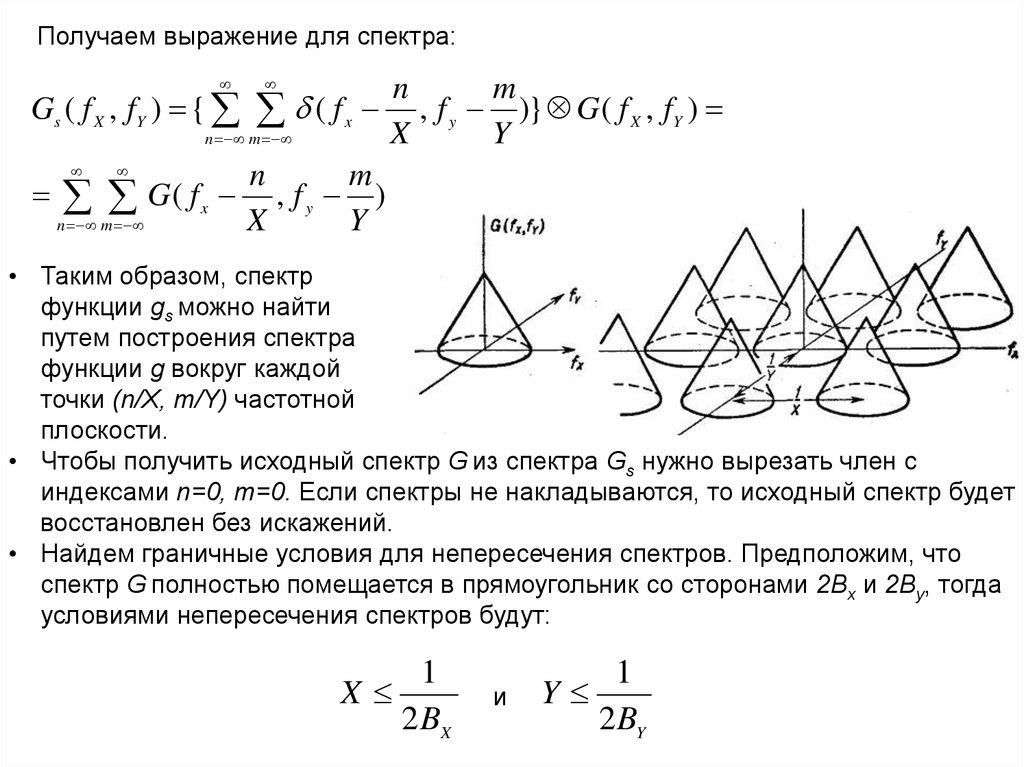
Получаем выражение для спектра:
n
m
Gs ( f X , fY ) { ( f x , f y )} G ( f X , fY )
X
Y
n m
n
m
G( f x , f y )
X
Y
n m
• Таким образом, спектр
функции gs можно найти
путем построения спектра
функции g вокруг каждой
точки (n/X, m/Y) частотной
плоскости.
• Чтобы получить исходный спектр G из спектра Gs нужно вырезать член с
индексами n=0, m=0. Если спектры не накладываются, то исходный спектр будет
восстановлен без искажений.
• Найдем граничные условия для непересечения спектров. Предположим, что
спектр G полностью помещается в прямоугольник со сторонами 2Bx и 2By, тогда
условиями непересечения спектров будут:
1
X
2 BX
и
1
Y
2 BY

12.

Для выделения составляющей спектра G с индексами n=0, m=0 можно
использовать оконный фильтр вида:
fX
fY
H ( f X , fY ) rect (
) rect (
)
2 BX
2 BY
После применения такого фильтра спектр примет вид:
fX
fY
Gs ( f X , fY ) rect (
) rect (
) G ( f X , fY )
2 BX
2 BY
Эквивалентное тождество можно записать в пространстве координат:
x
y
comb( X ) comb( Y ) g ( x, y ) h( x, y ) g ( x, y )
где h(x,y) - импульсный отклик фильтра:
fX
fY
h( x, y ) rect (
) rect (
) exp[ j 2 ( f X x fY y )]df X df y
2 BX
2 BY
4 BX BY sin c(2 BX x) sin c(2 BY y )

13.

Выразив
x
y
comb( ) comb( ) g ( x, y ) XY g (nX , mY ) (x nX , y mY )
X
Y
n m
можно переписать выражение для g:
g ( x, y ) 4 BX BY XY
g (nX , mY ) sin c 2 B
n m
X
( x nX ) sin c 2 BY ( y mY )
Для случая максимально допустимых интервалов выборки получится:
n
m
n
m
g ( x, y ) g (
,
) sin c 2 BX ( x
) sin c 2 BY ( y
)
2 BX 2 BY
2 BX
2 BY
n m
Это выражение называют теоремой выборки Шеннона-Уитеккера.

14. Модуляционная передаточная функция оптической системы

Синусоидальная и
бинарная решетки
переменного периода
до и после регистрации
с объективом Canon
28-70mm f/2.8L
*http://www.normankoren.com/Tutorials/MTF.html
Профиль изображения
решетки (красный) и
модуляционная
передаточная функция
(МПФ) объектива
(синий)*

15. Модуляционная передаточная функция оптической системы

Бинарная решетка
переменного периода
до и после регистрации
камерой
Canon EOS 10D
*http://www.normankoren.com/Tutorials/MTF7.html#Pillars
Профиль изображения
решетки (красный),
МПФ камеры (черный),
МПФ фотосенсора
(синий, точками), МПФ
объектива (синий,
сплошной)*

16. Спасибо за внимание!