Similar presentations:
Комп’ютерне моделювання систем з далекодією
1. Л.8 Комп’ютерне моделювання систем з далекодією
Іонні рідини. Парні потенціали взаємодії Тосі-ФуміU ( rij )
qi q j
rij
Aij e
( i j rij ) /
далекодія
Cij
6
ij
r
Dij
rij8
близькокодія
Через наявність періодичних граничних умов обрізання
потенціалів взаємодії при Rcut< L/2 приводить до
неправильного врахування кулонівських внесків.
U ( rij )
qi q j
rij
qi q j
Rcut
qi q j
2
cut
R
( r Rcut )
rij Rcut
2. Загальний вираз для потенціальної енергії молекулярних систем
Ubond = осциляції навколо довжини молекулярного звязкуUangle = осциляції 3 атомів навколо рівноважного кута
Udihedral = торсійний поворот 4 атомів відносно центрального звязку
Unonbond = не-звязані члени (електростатика та потенціал LJ)
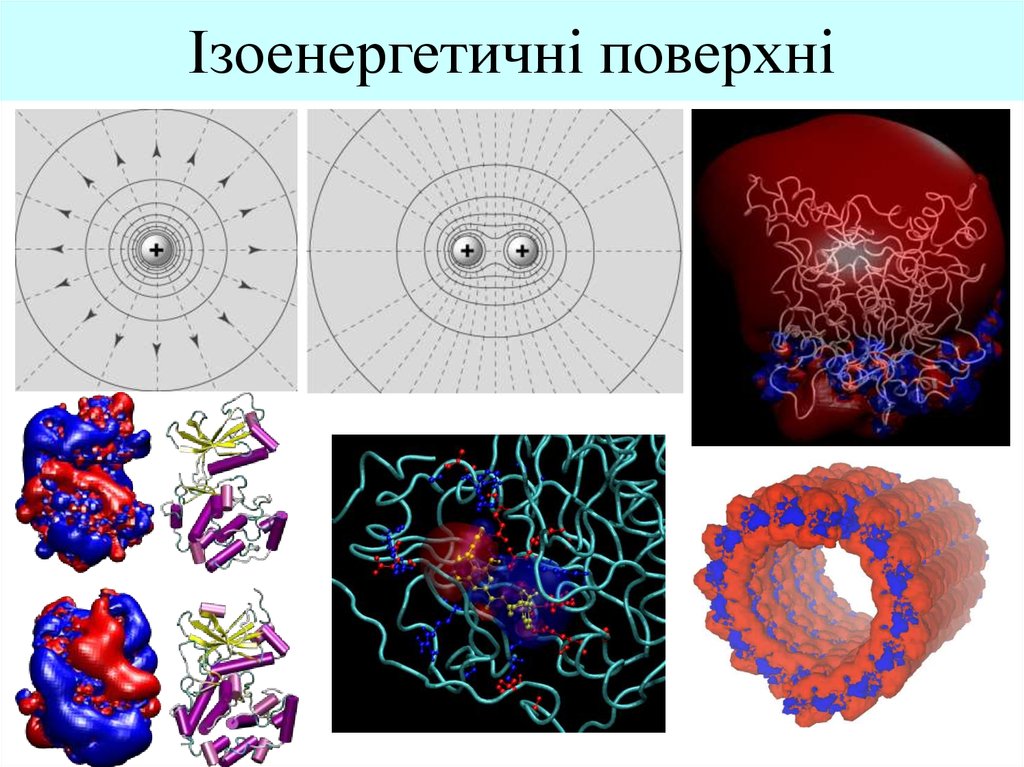
3. Isosurfaces
Ізоенергетичні поверхніIsosurfaces
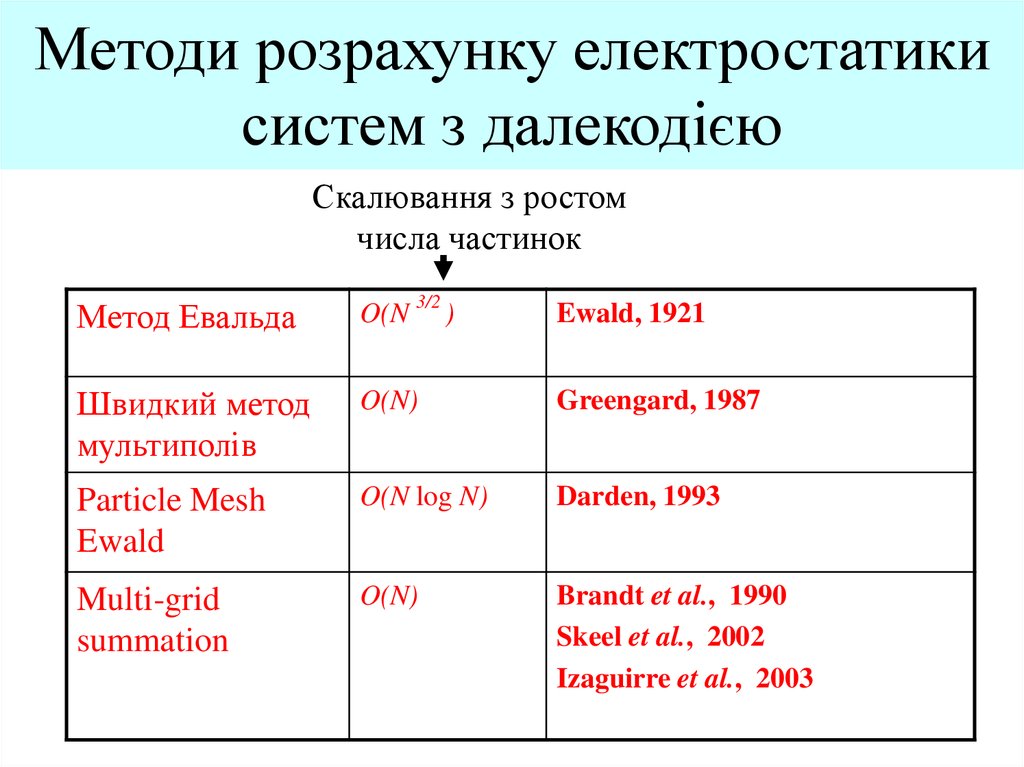
4. Методи розрахунку електростатики систем з далекодією
Скалювання з ростомчисла частинок
Метод Евальда
O(N 3/2 )
Ewald, 1921
Швидкий метод
мультиполів
O(N)
Greengard, 1987
Particle Mesh
Ewald
O(N log N)
Darden, 1993
Multi-grid
summation
O(N)
Brandt et al., 1990
Skeel et al., 2002
Izaguirre et al., 2003
5. Методи розрахунку електростатики систем з далекодією
qi q j1
U (r1 , r2 ,..., rm )
2 n ' i j rj ri nL
Це є умовно збіжна сума. Евальд (1921) показав як
можна обрахувати таку суму через розбиття на дві
швидко збіжні частини:
Точний вираз !!!
Ніяких
наближень !!!
1 f (r ) 1 f (r )
r
r
r
Короткодіюча
частина
Гладка функція
6. Метод Евальда
Евальд запропонував наступну функцію дляутворення короткодіючої частини суми
f (r ) erfc( r )
2
e
x2
dx
r
Короткодіюча частина суми розраховується аналогічно, як у
випадку наприклад Ленард-Джонсівських потенціалів. Сума
по всіх гладких частинах береться у оберненому просторі:
k2
1
1 4 2
e
2
2 k 0 k
2
q e
j
j
ikr j
7. Метод Евальда
Метод Евальд – це техніка для визначення потенціалу періодичноїсистеми точкових зарядів у нейтралізуючому фоні
Ewald (r ) ( r ri R) background
ri , R
Ewald ( r ) 1 ( r ) 2 ( r )
1
1 ( r ) 1
2
( r ri R )
e
i ,R
2
/
2
background
1
2 ( r ) ( r ri R ) 1
i ,R
2
( r ri R )
e
i ,R
2
/
2
8. Метод Евальда
Кулонівський потенціал гладкої частини легко можна обчислитичерез рівняння Пуассона
G 1 (G) 4 1 (G)
2
1 2 G 2 / 4
iGri
e
e
V
1 (G )
,G 0
ri
0
,G 0
2 (r )
R
1 erf ( r ri R / )
r ri R
V
2
9. Метод Евальда
Повний кулонівський потенціал:4 2G 2 / 4
G ( r ri )
Ewald ( r ) 2 e
e
i
G 0 G V
i ,R
1 erf ( r ri R / )
r ri R
2
V
10. Метод “reaction field” для наближеного врахування далекодії у молекулярних системах
У підході “reaction field” постулюється, що кожна молекула єоточена сферичною порожниною кінечного радіусу, в межах якої
електростатична взаємодія розраховується точно. Поза порожниною
система розглядається як діелектричне суцільне середовище. Поява
довільного диполю в порожнині індукує поляризацію в діелектрику,
яка в свою чергу взаємодіє з даною молекулою. Ця модель дозволяє
замінити безмежну кулонівську суму скінченою сумою плюс
“reaction field”. Повна кулонівська взаємодія в такому підході має
форму:
U Coul
2
B
r
1
1
0 ij
qi q j
3
4 0 j i
rij 2 Rc
11. Метод “reaction field”
U Coul2
B
r
1
1
0 ij
qi q j
3
4 0 j i
rij 2 Rc
Другий член є поправкою від “reaction field”, Rc є радіусом
сферичної порожнини. Константа B0 є означена наступним чином:
2( 1 1)
B0
(2 1 1)
ε1 є діелектричною проникністю суцільного середовища поза
порожниною
Щоб позбутись скачку потенціалу на межі порожнини потенціальну
енергію кожної пари зсувають на константу
1 qi q j
4 0 Rc
B0
1 2









 informatics
informatics








