Розрахунок величин за допомогою статистичних усереднень

1. Л.7. Розрахунок величин за допомогою статистичних усереднень

A
1
N conf
N conf
A (r
i 1
i
N
N
,v )
Статистичне усереднення
величин по конфігураціях,
наприклад температура,
кінетична енергія системи, ...
kB T 2
Cv
2
V ( T )
Питома теплоємність при
сталому об’ємі
T (t ) T (t ) T
Флуктуації температури на
протязі МД

2. Розрахунок величин за допомогою статистичних усереднень

Віріал
1
rij Fi ( rij )
3 j i
Тиск в системі
1
P k BT
rij Fi ( rij )
3V j i
В неоднорідній системі (з наявними границями розділу
фаз) компоненти тензору тиску Pii не є однаковими !!!

3. Розрахунок величин за допомогою статистичних усереднень

Компоненти віріала
VIRll (t ) r Fi ( rij )
j i
l
ij
l
j x, y , z
1
Pn Pzz k BT
VIRzz
3V
1
P ( Pxx Pyy Pzz )
3
Поверхневий
натяг
1
1
VIRzz (VIRxx VIRyy )
2 Lx Ly
2

4. Розрахунок величин за допомогою статистичних усереднень

Структурний
фактор
4 N
sin(kr ) 2
S (k ) 1
( g ( r ) 1)
r dr
V 0
kr
Структурний фактор як
середнє “густина-густина”
Просторова Фур’єкомпонента густини
частинок
S (k ) nk n k
1
nk (t )
N
N
e
i 1
ikri ( t )

5. Розрахунок структурного фактора за допомогою статистичних усереднень

Структурний
фактор
4 N
sin(kr ) 2
S (k ) 1
( g ( r ) 1)
r dr
V 0
kr
Структурний фактор як
середнє “густина-густина”
Просторова Фур’єкомпонента густини
частинок
S (k ) nk n k
1
nk (t )
N
N
e
i 1
ikri ( t )

6. Розрахунок структурного фактора за допомогою статистичних усереднень

Структурний
фактор
4 N
sin(kr ) 2
S (k ) 1
( g ( r ) 1)
r dr
V 0
kr
Структурний фактор як
середнє “густина-густина”
Просторова Фур’єкомпонента густини
частинок
S (k ) nk n k
1
nk (t )
N
N
e
i 1
ikri ( t )

7. Розрахунок структурного фактора за допомогою статистичних усереднень

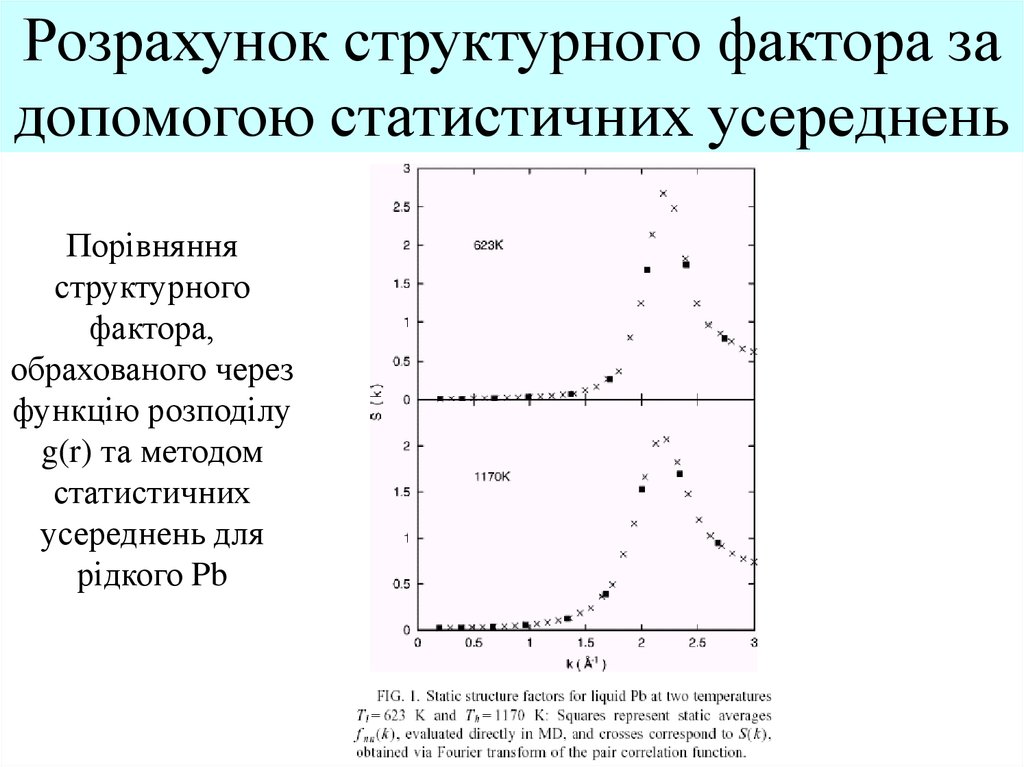
Порівняння
структурного
фактора,
обрахованого через
функцію розподілу
g(r) та методом
статистичних
усереднень для
рідкого Pb

8. Розрахунок структурного фактора за допомогою статистичних усереднень

Алгоритм розрахунку структурного фактора
1. Задається цикл по набору значень |k|
2. Для кожного |k| визначаються різні напрямки вектора k без
врахування дзеркального відображення.
Наприклад, для |k|=1 є три різні напрямки (100), (010),(001)
[дзеркальним відображенням є (-100),(0-10),(00-1)]
3. Для кожного напрямку вектора k розраховується
N
Re( nk ) cos( k x ri x k y ri y k z ri z )
i 1
N
Im( nk ) sin( k x ri x k y ri y k z ri z )
i 1
4. Розраховується внесок у S(k) від даного напрямку k для біжучої
конфігурації

9. Розрахунок структурного фактора за допомогою статистичних усереднень

SN (k ) Re(nk ) Re(nk ) Im(nk ) Im(nk )
5. Внесоки у S(k) від напрямків k і конфігурацій сумуються і
кінцевий вираз ділиться на число напрямків та число
конфігурацій
Для багатосортних систем розраховуються парціальні структурні
фактори
Sij (k ) ni ,k n j , k
Парціальні
густини
Аналогічний
розрахунок
1
Nj
n j ,k ( t )
Nj
Nj
e
i, j A, B
ikri , j ( t )
i 1
Re(n j ,k ) cos(k x ri ,xj k y ri ,yj k z ri ,zj )
i 1

10. Розрахунок залежних від часу (динамічних) властивостей

Часові кореляційні функції
FAB (k , t ) A(k , t ) B (k , t 0)
*
Часові кореляційні функції “густинагустина”, “енергія-густина”, “потікпотік”, автокореляційні функції
швидкостей, ...
Поділяються на:
колективні та одночастинкові
рідина
скло

11. Автокореляційні функції швидкостей

1
(t ) vi (t )vi (t 0)
3
1
[ vix (t )vix (0) viy (t )viy (0) viz (t )viz (0) ]
3
Густина коливних
станів
Z ( ) (t )ei t dt
0
Надлишок
коливних
станів через
колективні
моди типу
“Boson
peak”

12. Автокореляційні функції швидкостей

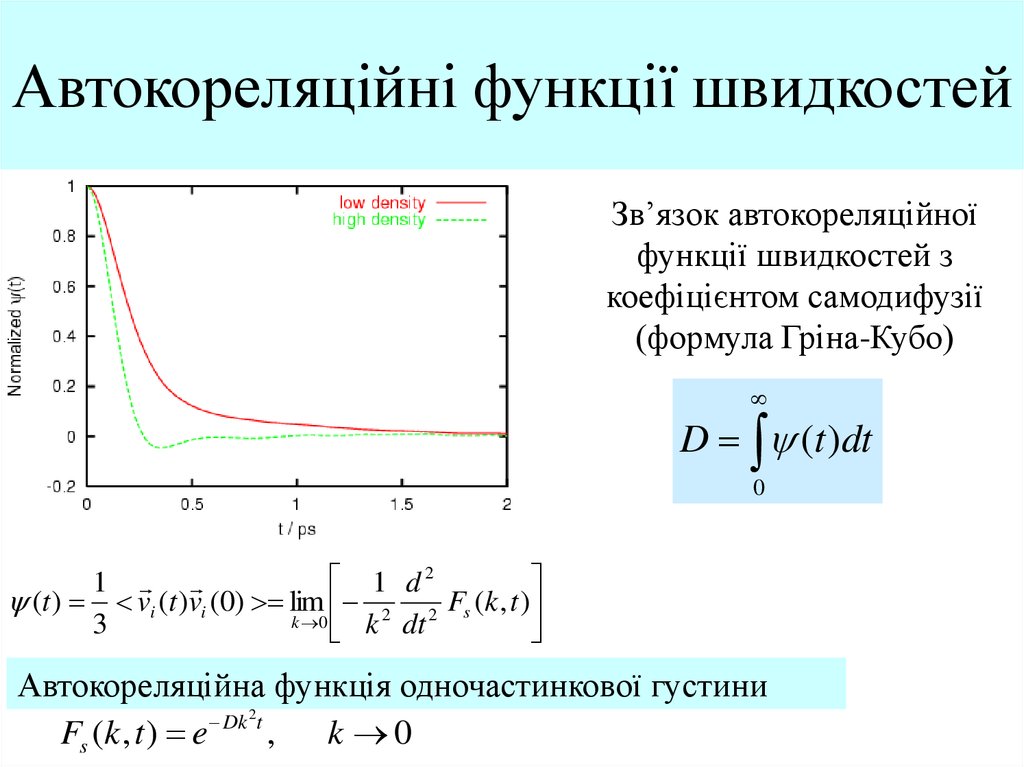
Зв’язок автокореляційної
функції швидкостей з
коефіцієнтом самодифузії
(формула Гріна-Кубо)
D (t )dt
0
1 d2
1
(t ) vi (t )vi (0) lim 2 2 Fs (k , t )
k 0
3
k dt
Автокореляційна функція одночастинкової густини
Dk 2t
Fs (k , t ) e
,
k 0

13. Автокореляційні функції швидкостей

Залежність від різних типів симуляцій: NaCl
класична МД (червона), ab initio МД (зелена)