Similar presentations:
Комп’ютерне моделювання складних систем
1. Комп’ютерне моделювання складних систем
Соловйов Володимир Миколайович,доктор ф.-м. н., проф.
2.
План• Криза сучасної парадигми дослідження складних
систем
• Індустрія 4.0 і мережні технології
• Динамічні системи та сучасні методи їх дослідження
• 1. Фрактальні і мультифрактальні
• 2. Рекурентний аналіз. Кількісні характеристики
• 3. Ентропійні методи
• 4. Мережні міри складності:
- спектральні;
- топологічні.
• 5. Мультиплексні (мультимережні) міри
3. Бібліографія
4. Література
• Хусаінов Д.Я. Введення в моделювання динамічнихсистем: навчальний посібник / Хусаінов Д.Я., Харченко
І.І., Шатирко А.В. –К.: КНУ, 2010. – 132 с.
• Дербенцев В.Д., Сердюк О.А., Соловйов В.М., Шарапов
О.Д. Синергетичні та еконофізичні методи дослідження
динамічних та структурних характеристик економічних
систем – Черкаси: Брама-Україна, 2010. – 300 с.
• Соловйов В.М., Сердюк О.А., Данильчук Г.Б.
Моделювання складних систем– Черкаси: БрамаУкраїна, 2016. – 204 с.
• Vladar T. Complex and Chaotic Nonlinear Dynamics.- 2009,
Springer.- 761 p.
• Lynch S. Dynamical systems with application using Matlab –
2014, Springer.- 519 p.
5. Література
• Николис Г. Познание сложного. Введение. / Г.Николис, И. Пригожин - М.: ЛКИ, 2008.- 354 с.
• Петерс Э. Фрактальный анализ финансовых
рынков.-М.: Интернет- трейдинг, 2004.- 304 с.
• Снарский А.А., Ландэ Д.В. Моделирование
сложных сетей: учебное пособие. — К.: НТУУ
«КПИ», 2015. — 212 с.
• Лоскутов А.Ю., Михайлов А.С. Основы теории
сложных систем. - М.-Ижевск: Институт
компьютерных исследований, 2007. – 620 с.
• Networks of Networks: The Last Frontier of
Complexity. Gregorio D’Agostino, Antonio Scala
Editors, - 2014, Springer.- 342 p.
6.
Дискусія Пола Кругмана• гостра дискусія між старими таборами неокласикою («мейнстрімом») і
кейнсіанством
• два важливих етапи дискусії:
• робота нобелівського лауреата 2007
року Пола Кругмана «Чому економічна
наука безсила?» {Krugman P. How Did
Economists Get It So Wrong?// The New
York Times, September 2, 2009, pp. 3-8}
7.
Нові ініціативиДж.Сороса
• в даний час необхідні нові міждисциплінарні
підходи до економіки, до яких
залучатимуться історія, психологія,
природничі науки (http://www.soros.org;
http://ineteconomics.org/ )
• Ініціатива Дж. Сороса підштовхнула
Євросоюз до активізації робіт у галузі
міждисциплінарного напрямку дослідження
фінансових систем. Сьогодні така діяльність
координується у рамках проекту FuturIcT
8.
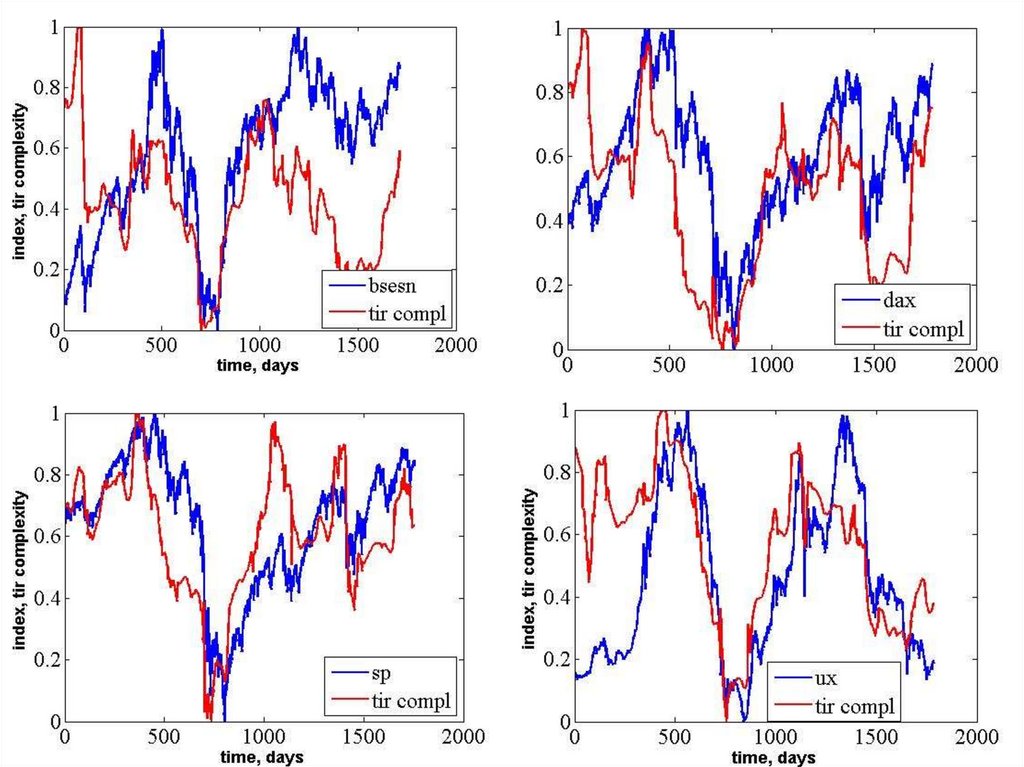
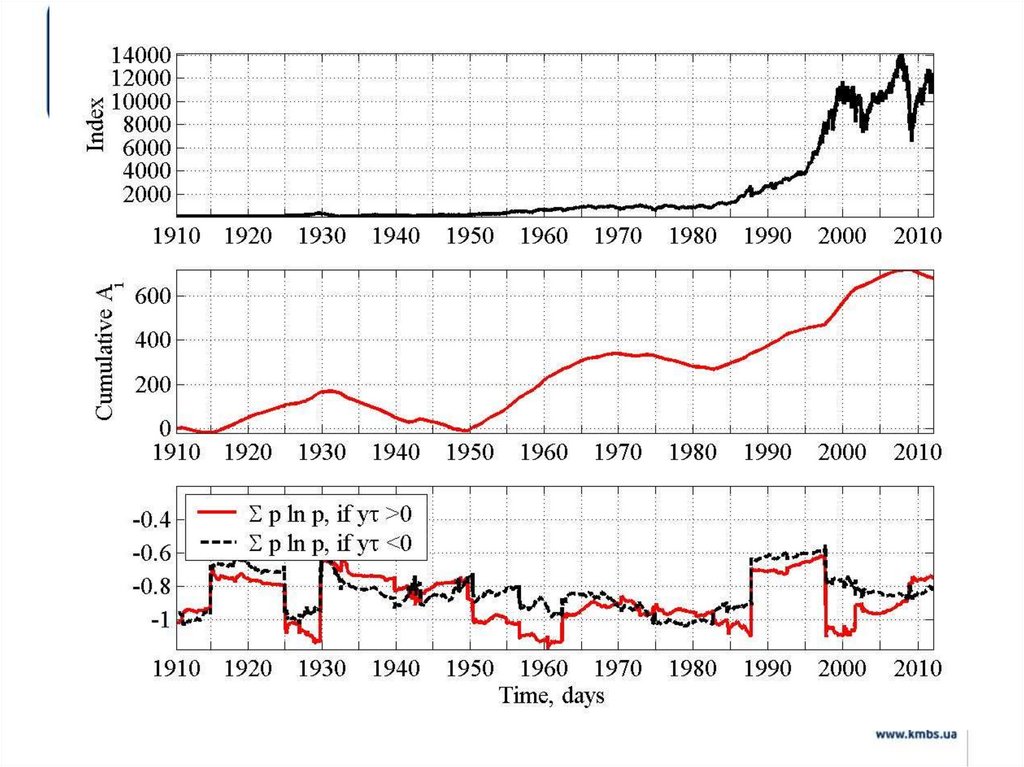
Jean-Philippe Bouchaud. Economics needs a scientificrevolution // Nature. V. 455. P. 1181 (30 October 2008)
Глобальних економічних криз можна
уникнути, якщо застосовувати фізичні
підходи до моделювання економічних
процесів, змінивши при цьому систему
їх мислення і фахової підготовки
І.Ньютон “моделювати безумство людей
значно складніше, аніж рух планет ”
Аксіоми класичної економіки:
- невидима рука ринку;
- раціональність поведінки екон. агентів;
- гіпотеза ефективного ринку тощо
Відсутній здоровий скепсис (як у
фізиків)
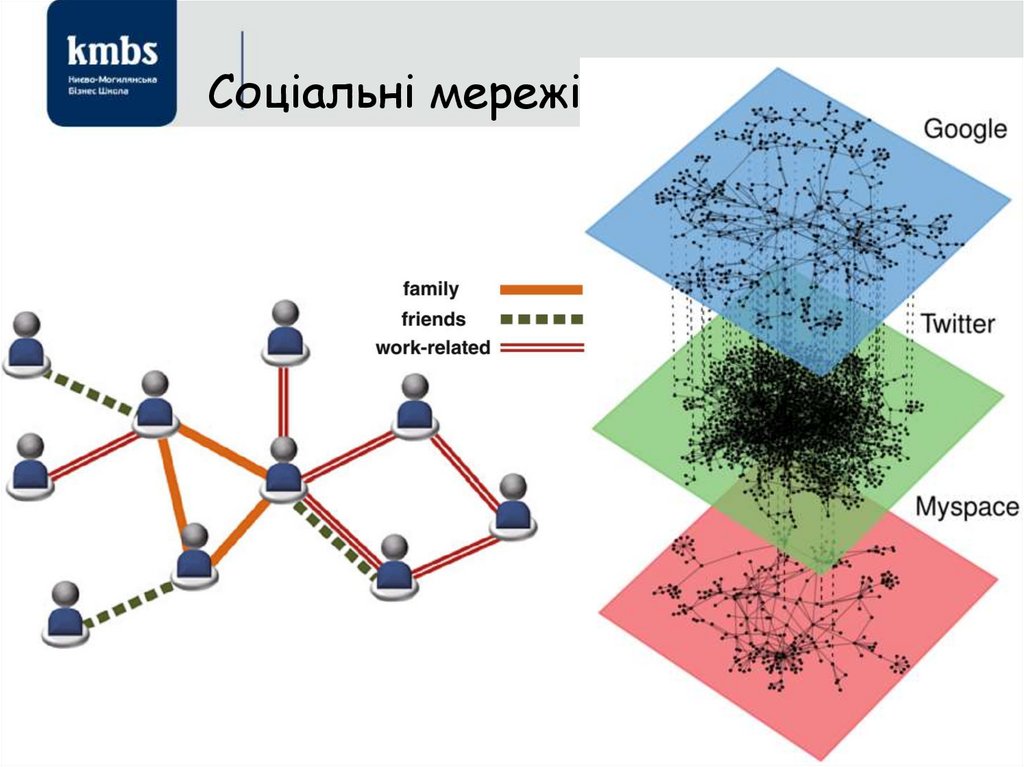
Причина інертності в системі підготовки
економістів
9.
Парадигми синергетикиГ. Г. Малинецкий. Теория самоорганизации. На
пороге IV парадигмы. - КОМПЬЮТЕРНЫЕ
ИССЛЕДОВАНИЯ И МОДЕЛИРОВАНИЕ. 2013. Т.5.
№3, С.315-366
1. Нерівноважна термодинаміка
2. Існування горизонту прогнозу
3. Парадигма складності
4. Мережна парадигма
10.
Століття складності• Я думаю, що наступне століття стане
століттям складності
• Стівен Хокінг, січень 2000
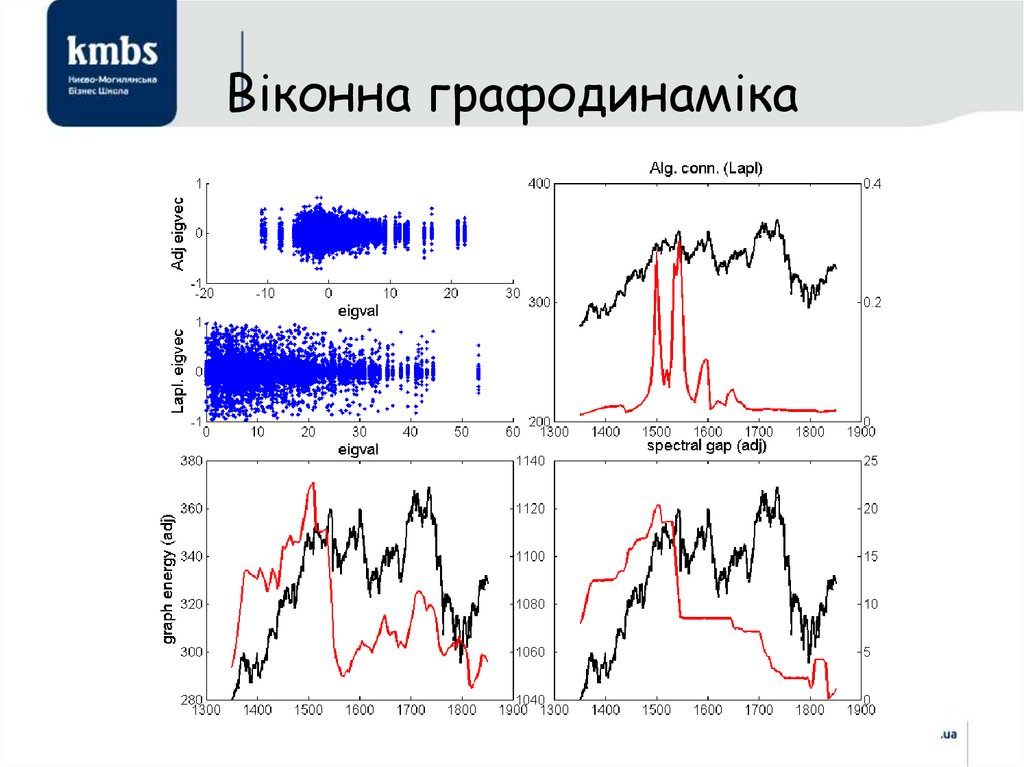
• Що таке складність?
11.
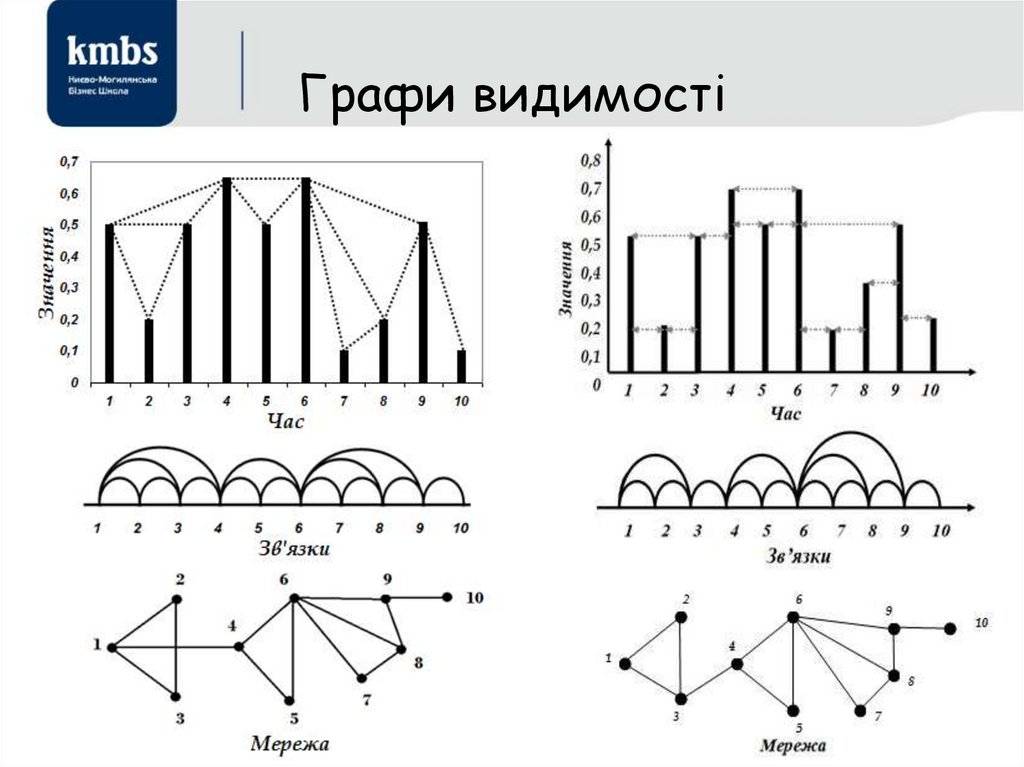
Клаус Мартін Шваб• Schwab K. The Forth Industrial Revolution http://www.amazon.com/dp/B01AIT6SZ8
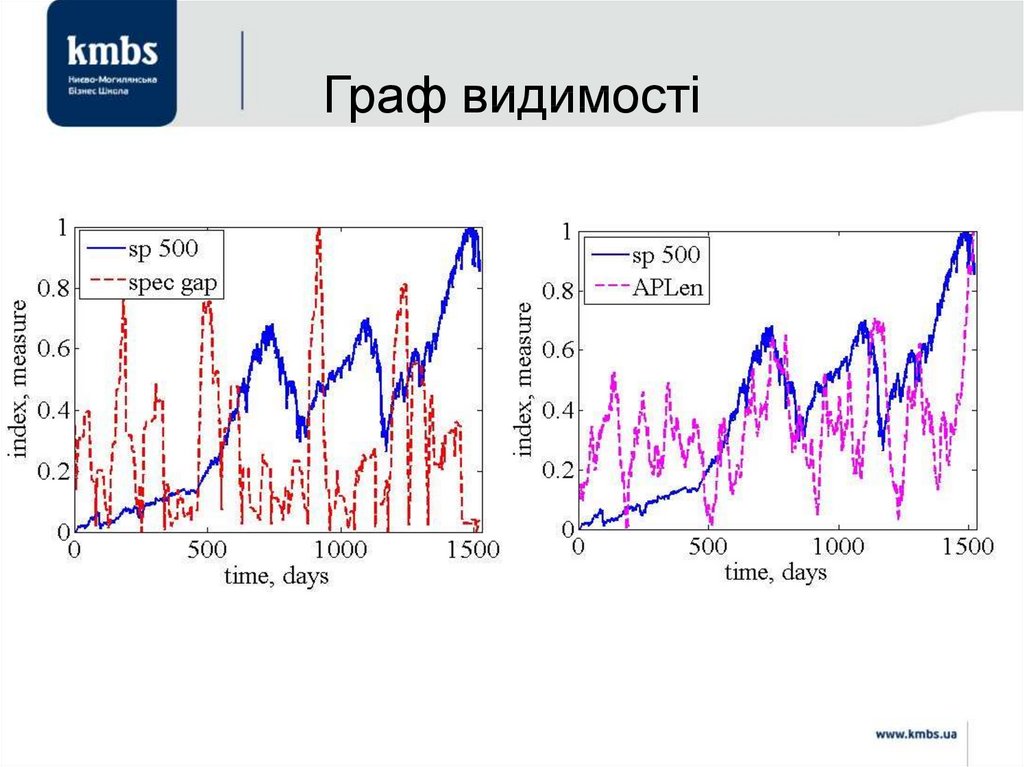
• Рифкин Дж. Третья промышленная революция: Как горизонтальные
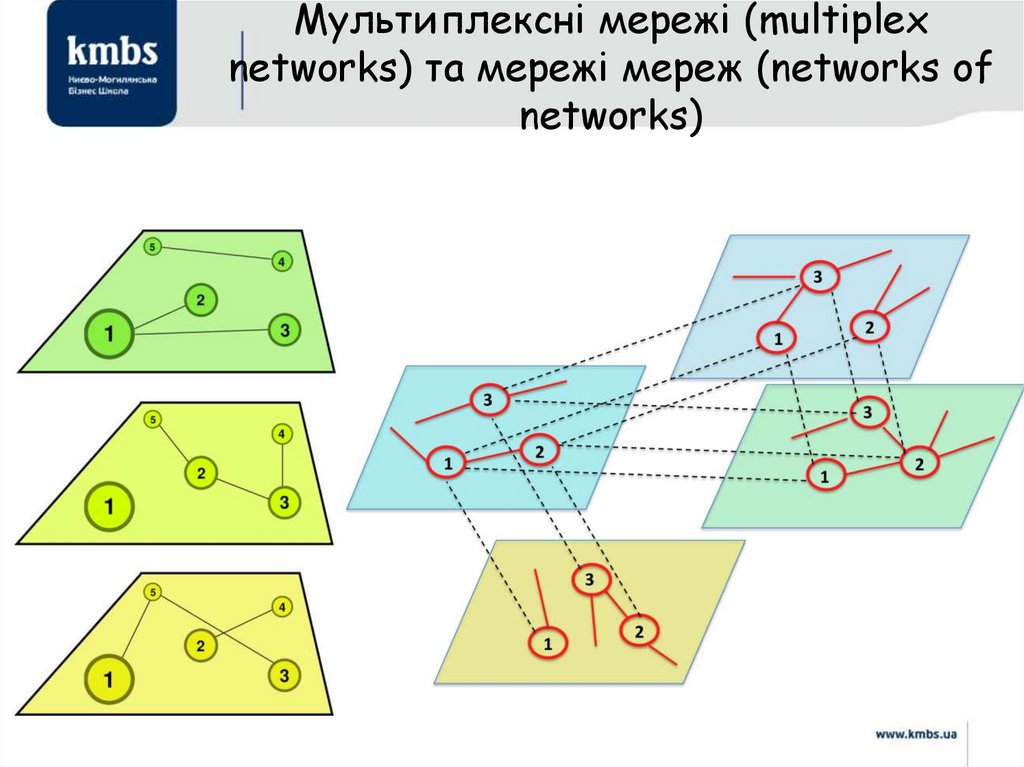
взаимодействия меняют энергетику, экономику и мир в целом /
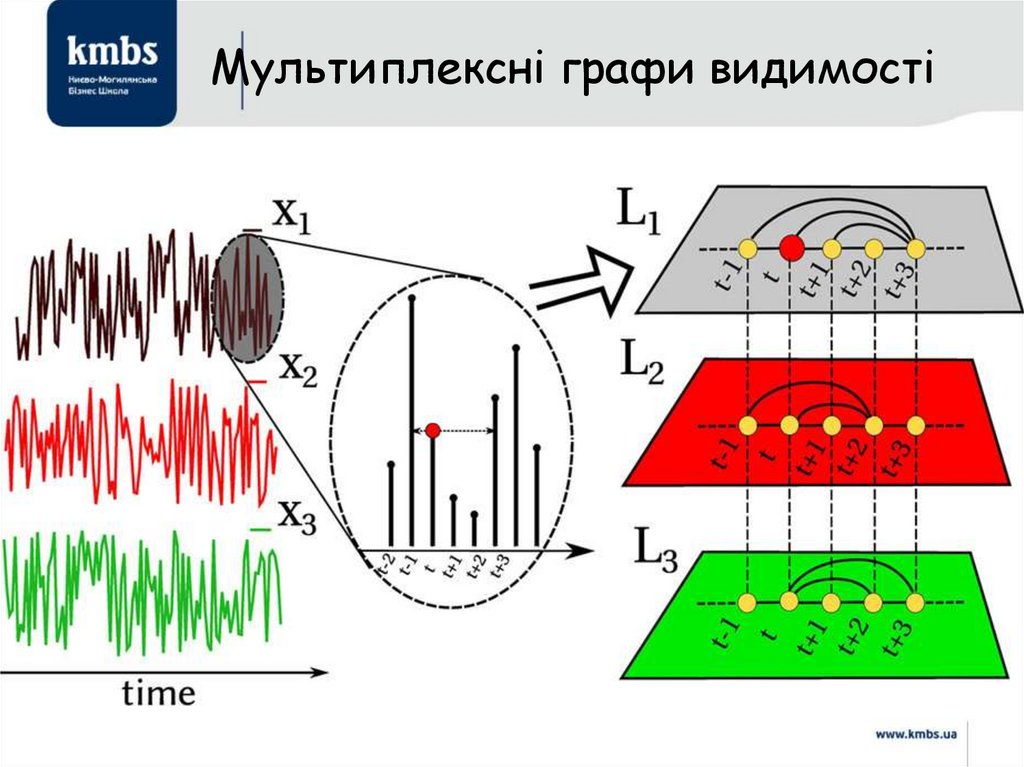
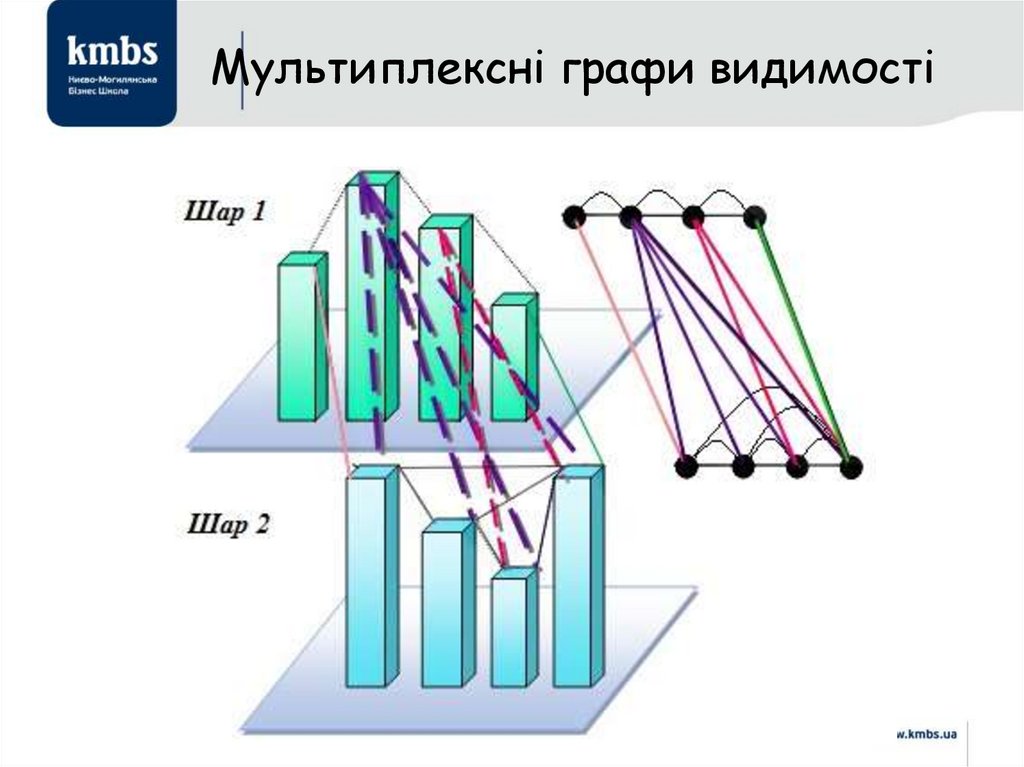
Пер. с англ. — М.: Альпина нон-фикшн, 2014. — 410 с.
• Марш, П. Новая промышленная революция. Потребители,
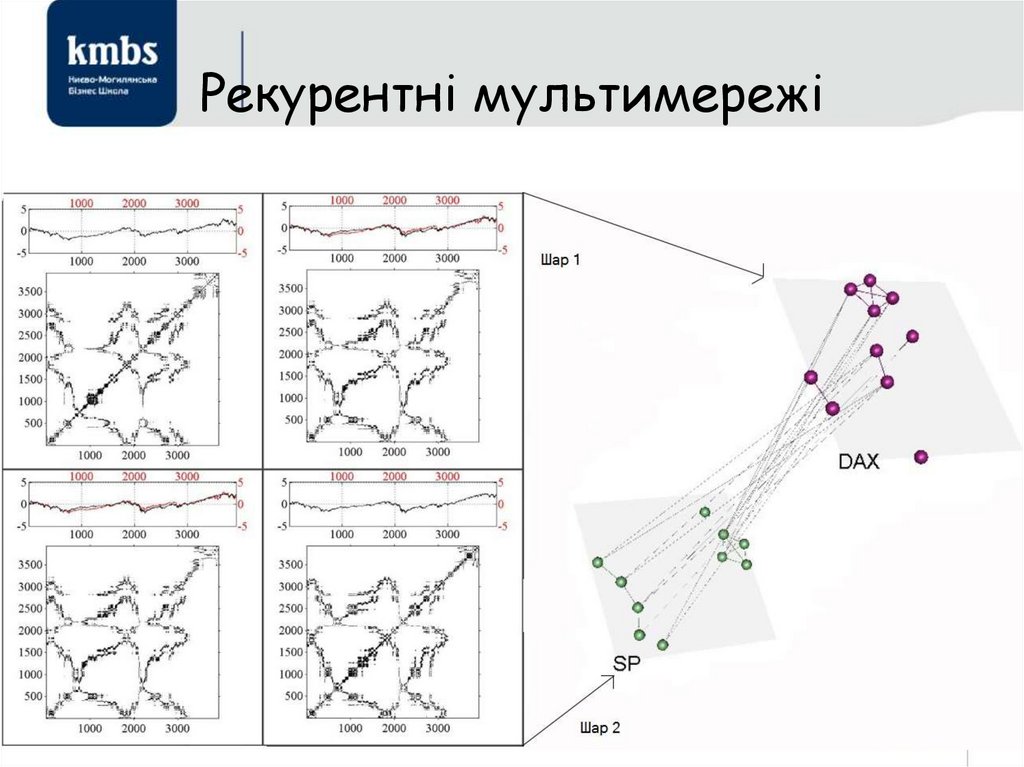
глобализация и конец массового производства / пер. с англ. – М.:
Изд-во Института Гайдара, 2015. – 420 с.
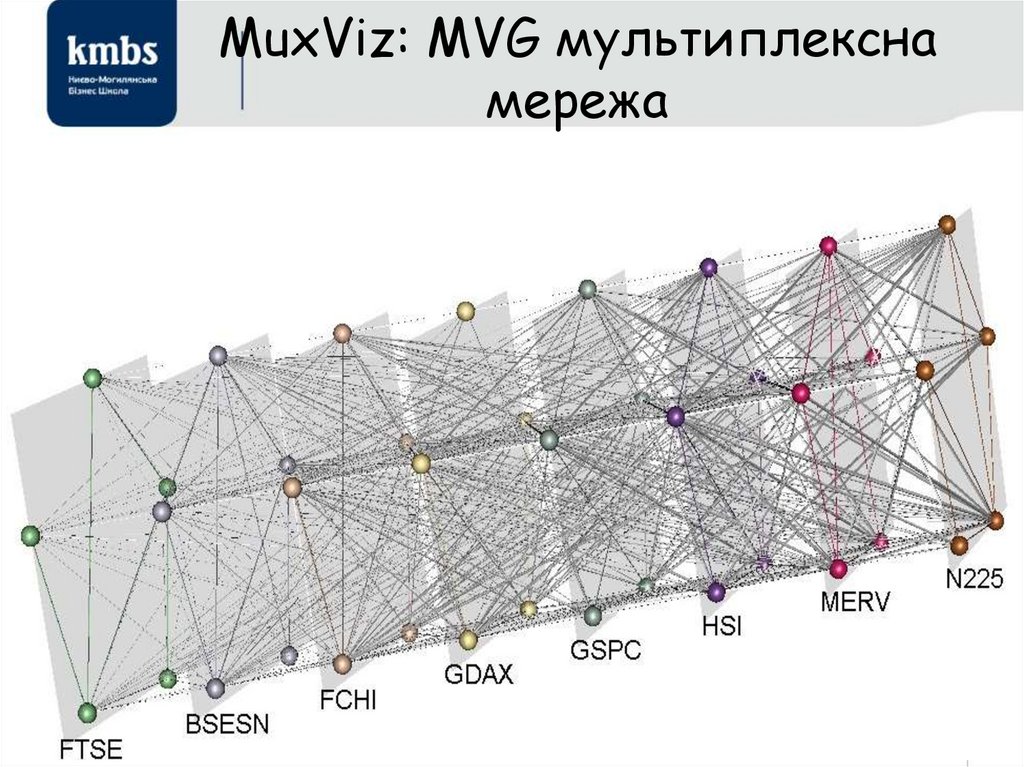
12. Історія І 4.0
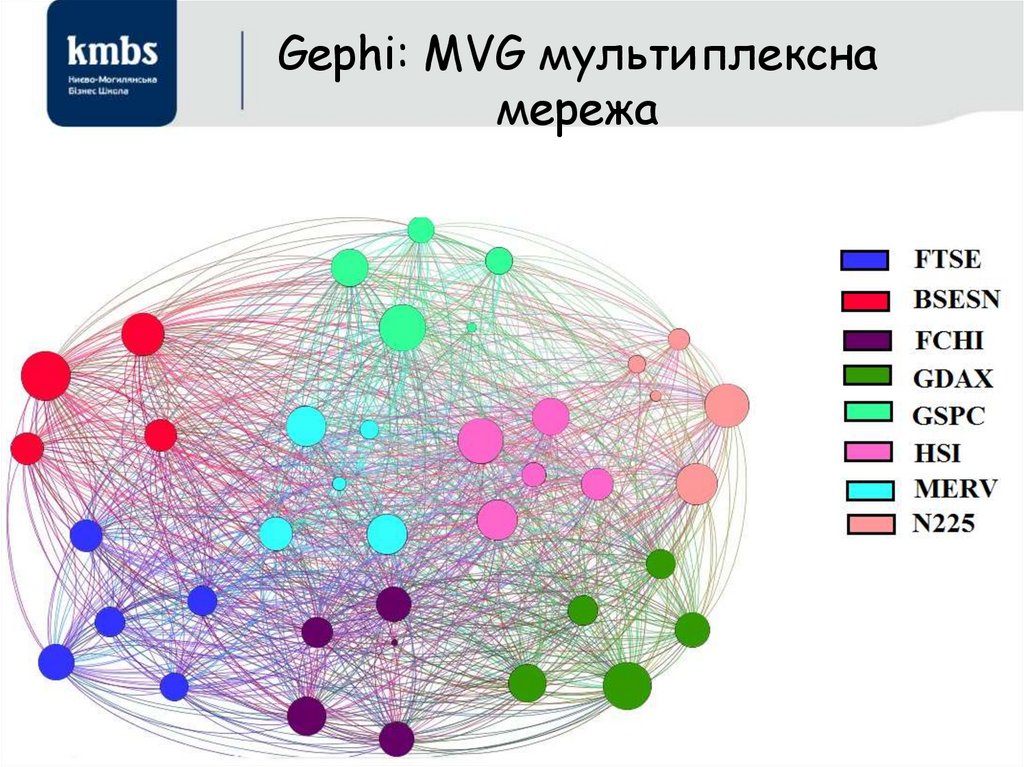
13.
IoT• The Internet of Things (IoT, Інтернет
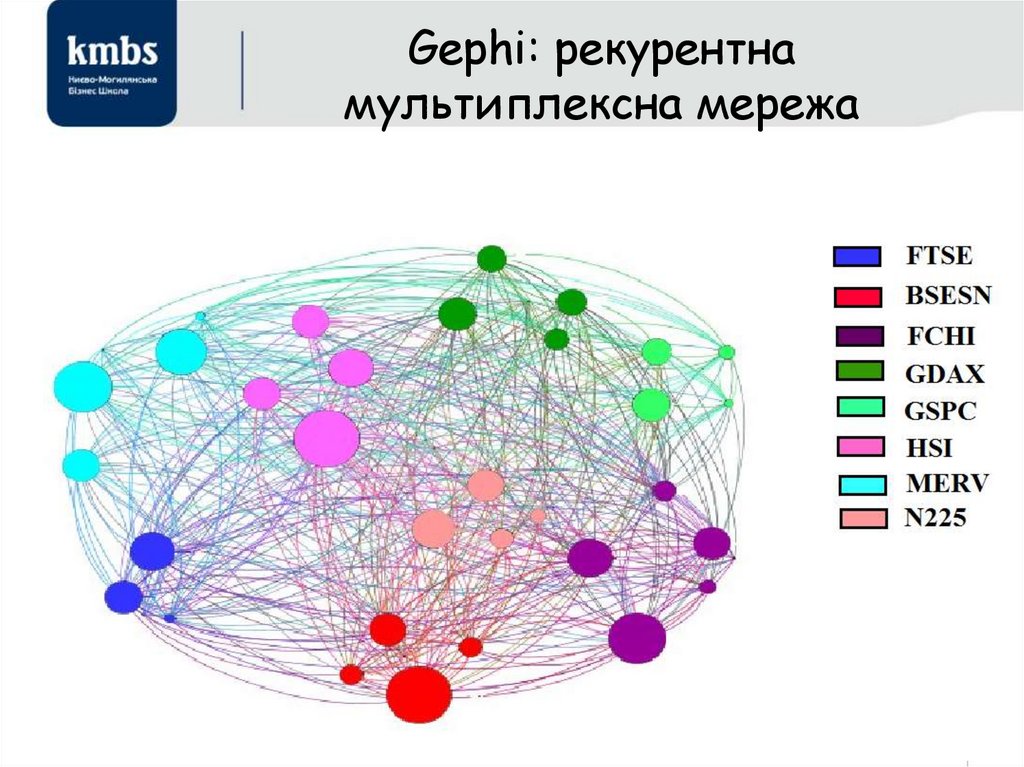
речей) – мережа фізичних об‘єктів,
поєднаних інтернетом
14.
кіберфізичні системи• Під кіберфізичною системою розуміють
поєднання фізичних процесів та
кібернетичних компонентів
15. Базові технології Індустрії 4.0
16. Базові технології Індустрії 4.0
17. Машинне навчання
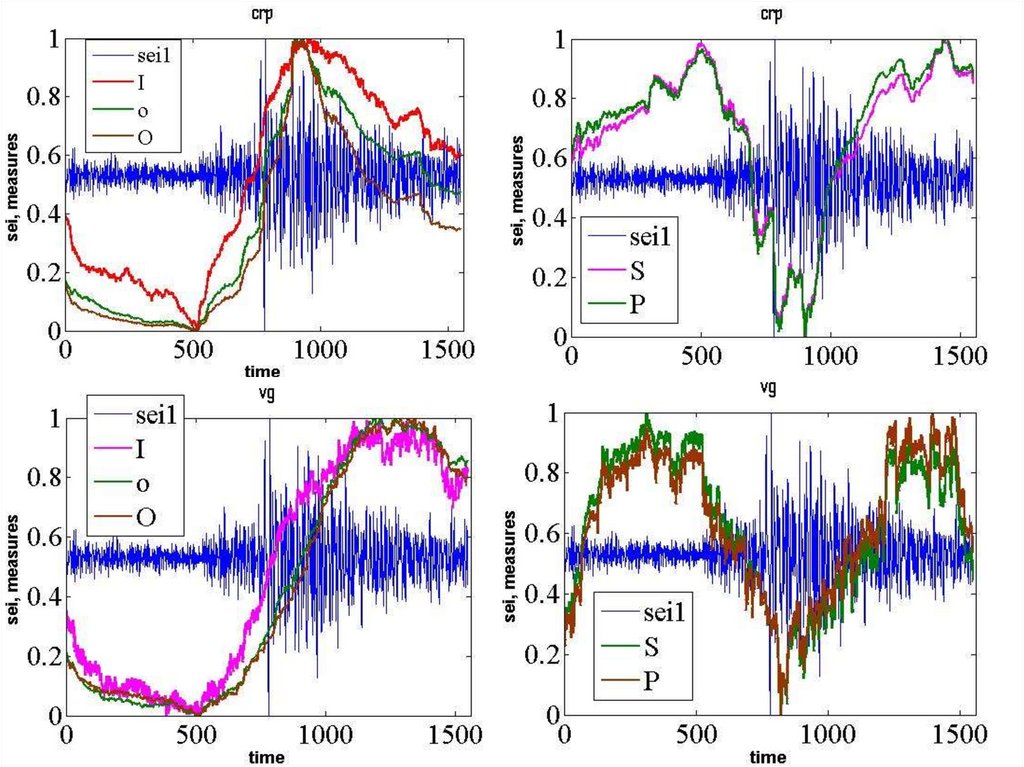
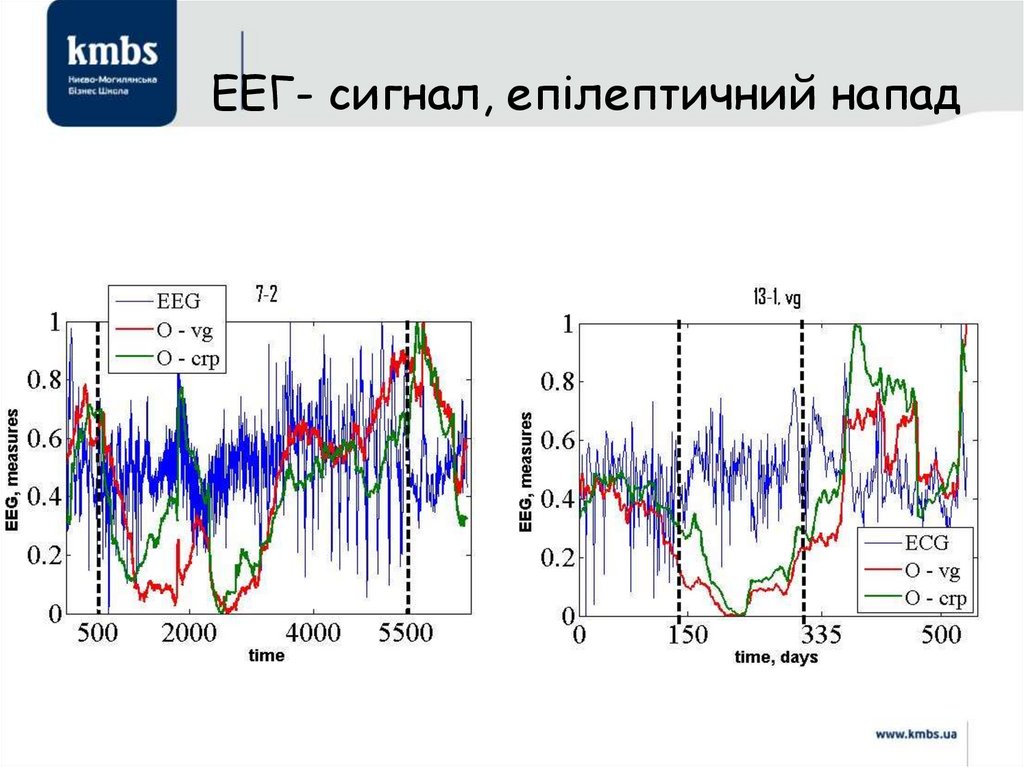
18. Глибоке навчання
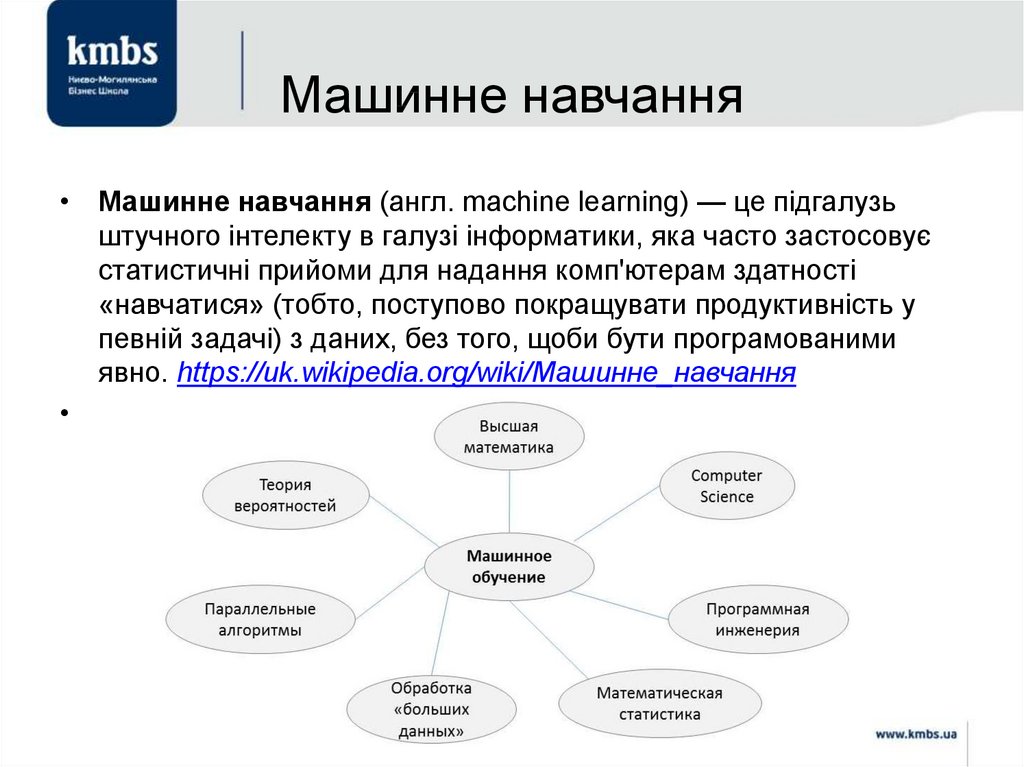
19. Машинне навчання
• Машинне навчання (англ. machine learning) — це підгалузьштучного інтелекту в галузі інформатики, яка часто застосовує
статистичні прийоми для надання комп'ютерам здатності
«навчатися» (тобто, поступово покращувати продуктивність у
певній задачі) з даних, без того, щоби бути програмованими
явно. https://uk.wikipedia.org/wiki/Машинне_навчання
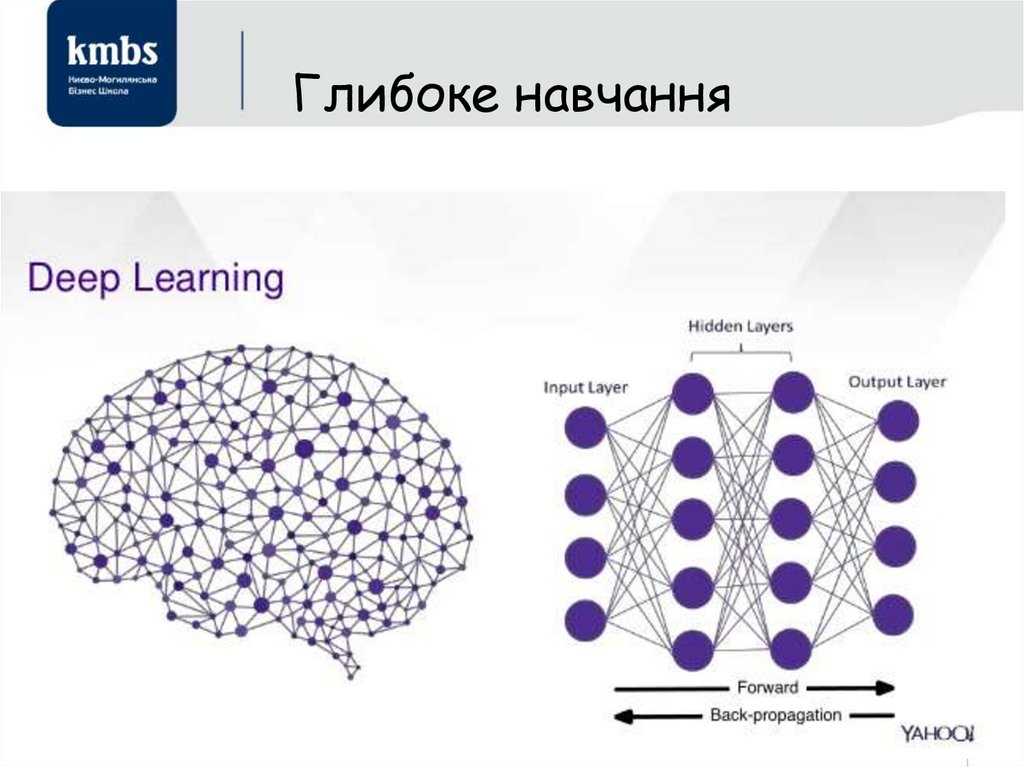
20. Глибинне навчання
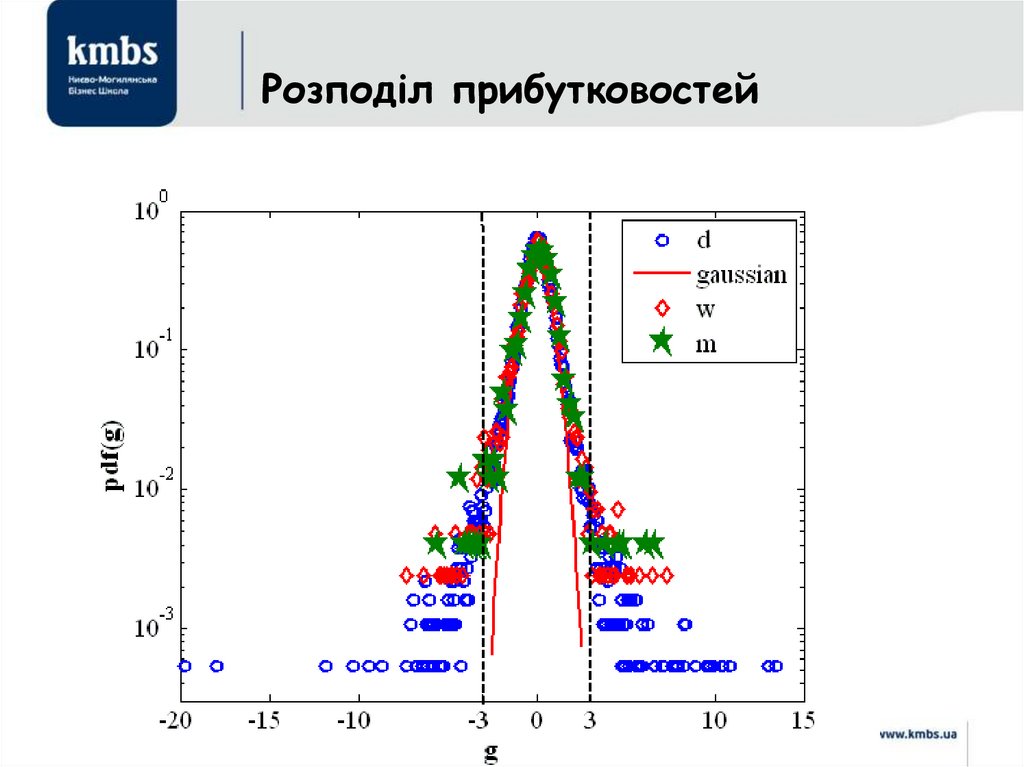
• Глиби́нне навча́ння (також відоме як глибинне структурненавчання, ієрархічне навчання, глибинне машинне навчання,
англ. deep learning, deep structured learning, hierarchical learning,
deep machine learning) — це галузь машинного навчання, що
ґрунтується на наборі алгоритмів, які намагаються моделювати
високорівневі абстракції в даних, застосовуючи глибинний граф
із декількома обробними шарами, що побудовано з кількох
лінійних або нелінійних перетворень.
• https://uk.wikipedia.org/wiki/Глибинне_навчання
21.
22.
Проблеми іможливості I 4.0
• - Штучний інтелект, ризики та можливості;
- Глобальні соціальні мережі і їх вплив на соціальну структуру і
політичні інститути;
- Розвиток технологій замкнутого циклу виробництва,
повторної переробки сировини і поновлюваних джерел енергії,
як це позначиться на ринках сировини;
- Збільшення тривалості життя людей у зв'язку з розвитком
біомедичних технологій, можливо до 120-150 років, як це
відіб'ється на системі соціального страхування, ринку праці і на
споживчих перевагах;
- «Інтернет речей» перетворюється з футуристичного дискурсу
в реальність і починає істотно впливати на наше життя;
- І головна тема - як повсюдна роботизація виробництва і
послуг позначиться на зайнятості людей?
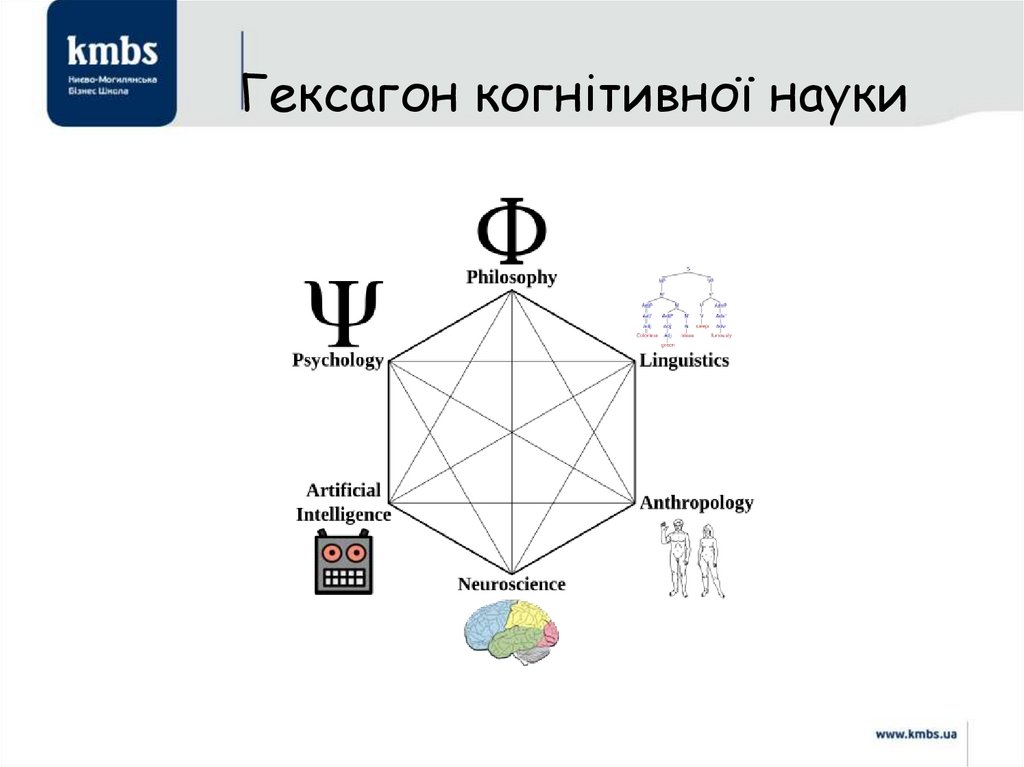
23. Гексагон когнітивної науки
24.
Важливість когнітивноїкомпоненти
• сучасна нейронаука вичерпала можливості парадигми
мозку як молекулярно-хімічної машини для пояснення
механізмів роботи свідомості
• нейронаука немислима без появи нових технічних
засобів візуалізації головного мозку
• Картини активації спеціалізованих зон мозку в
конкретних ситуаціях ухвалення рішень дозволяють
пояснити відхилення їх вибору від раціональної
моделі
25.
Сучасні методи реєстраціїактивності мозку
• Реєстрація ходу обробки інформації:
– електроенцефалографія і визвані потенціали
– магнітоенцефалографія
– регістрація реакцій окремих нейронів
• Функціональне картування:
– позитронно-емісійна томографія (ПЕТ)
– функціональне магнітно-резонансне картування
(fMRI)
• Вплив на мозок: транскраніальна магнітна
стимуляція (ТМС)
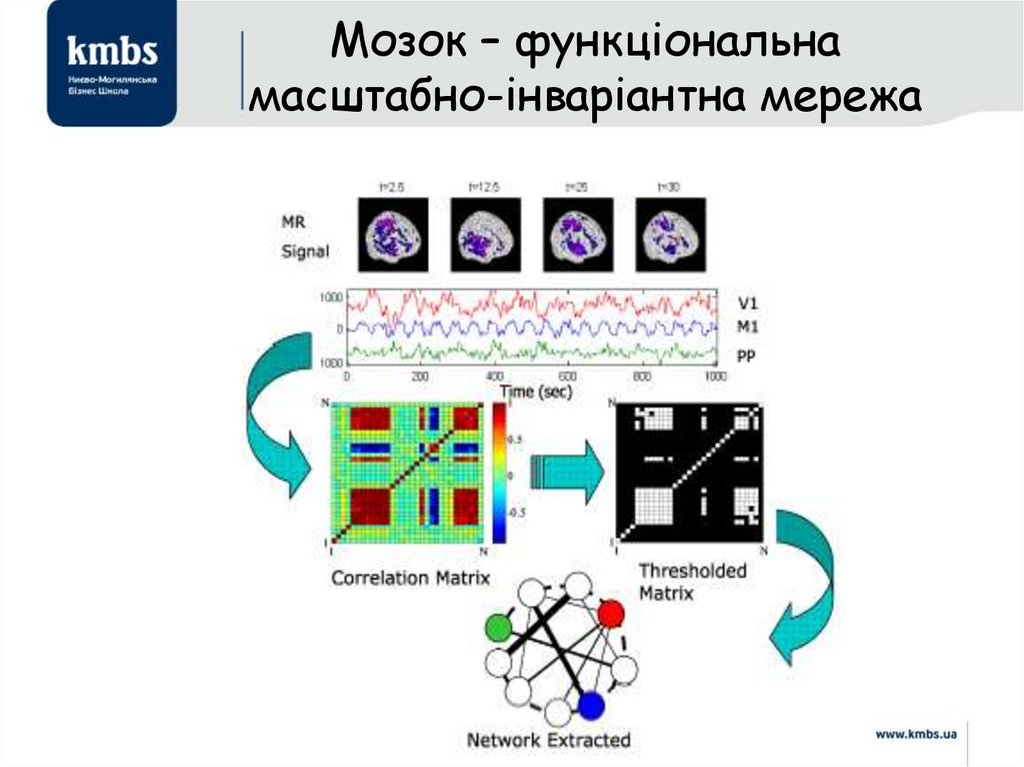
26. Мозок – функціональна масштабно-інваріантна мережа
27.
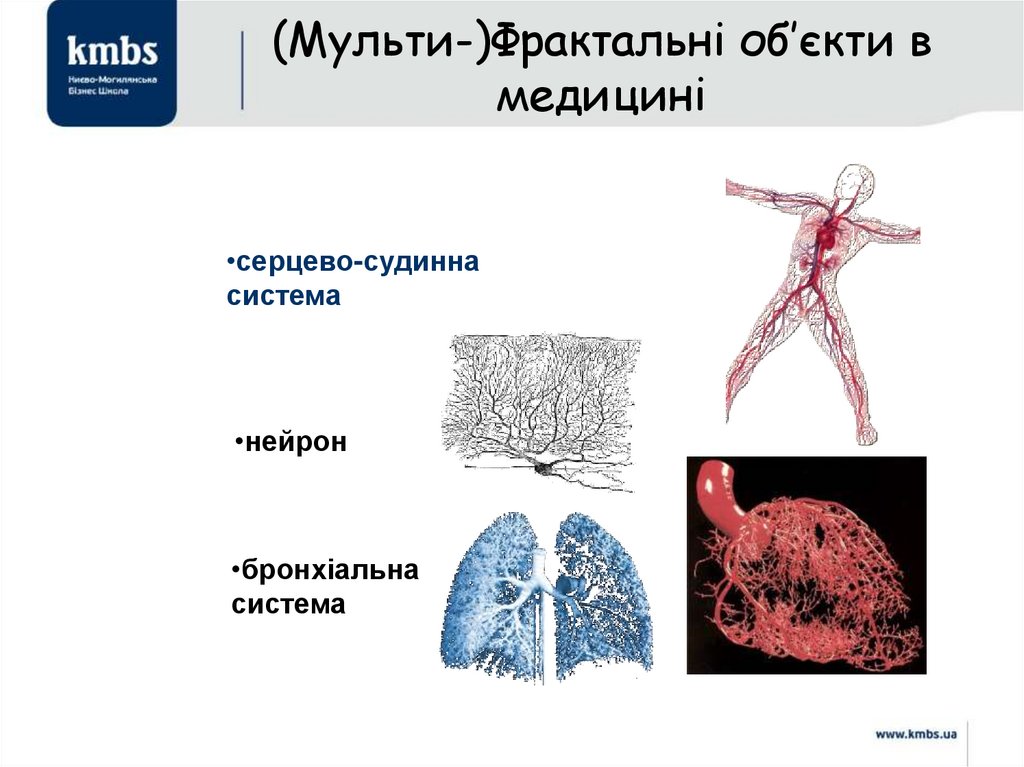
(Мульти-)Фрактальні об’єкти вмедицині
•серцево-судинна
система
•нейрон
•бронхіальна
система
28.
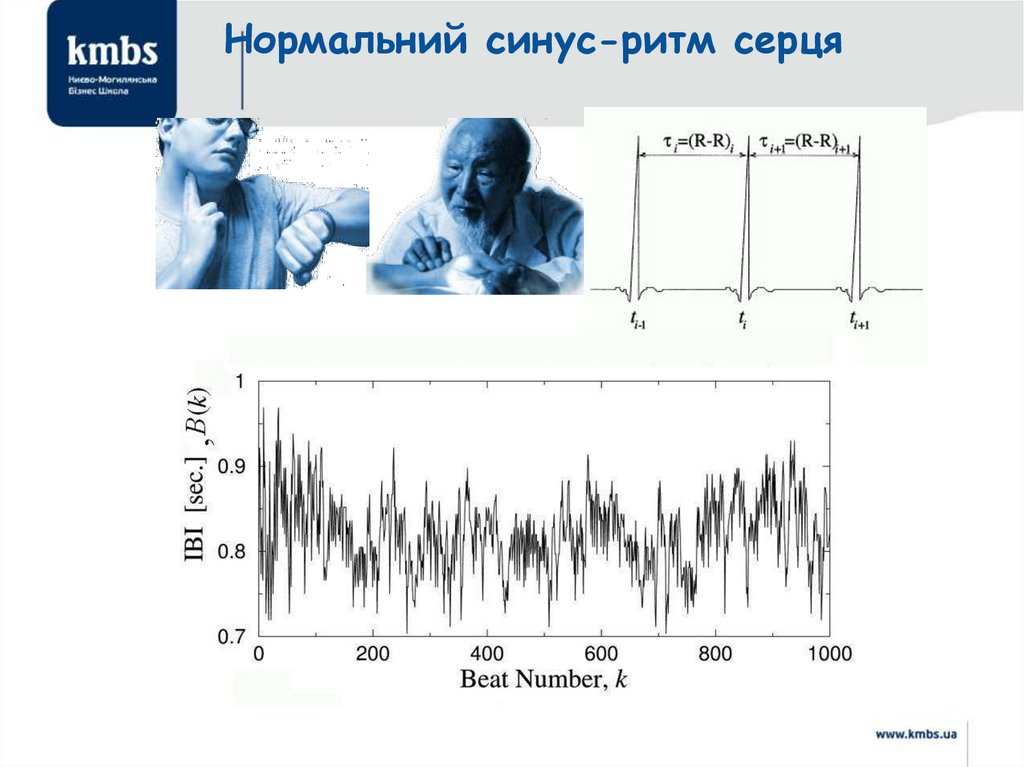
Нормальний синус-ритм серця29.
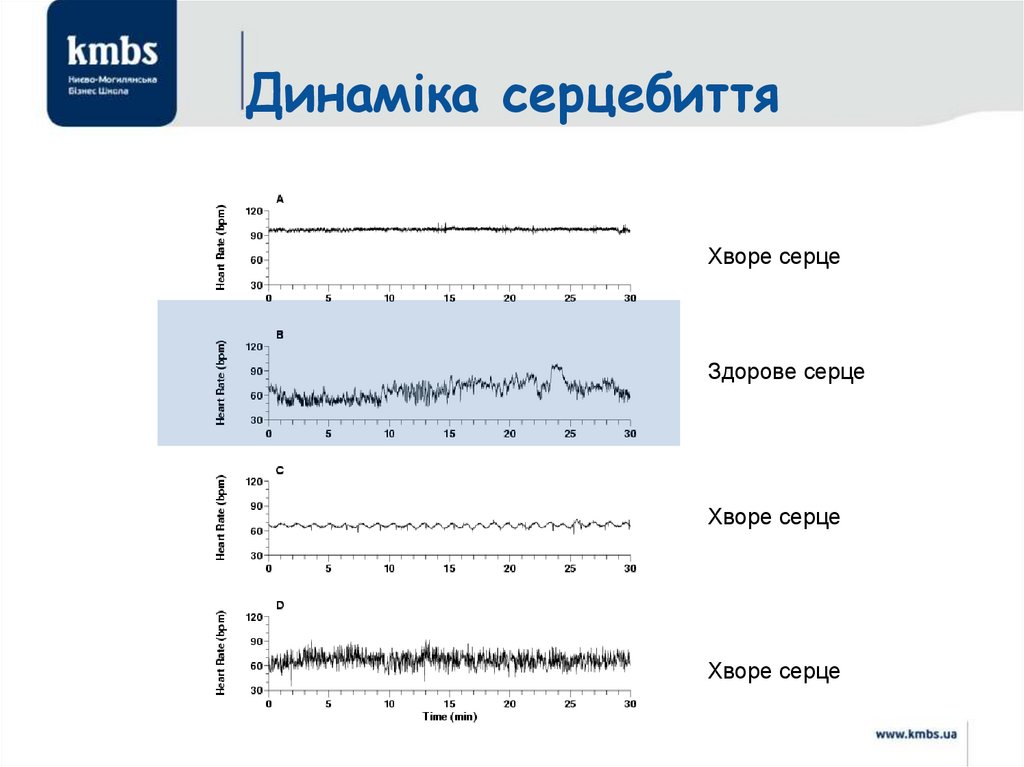
Динаміка серцебиттяХворе серце
Здорове серце
Хворе серце
Хворе серце
30.
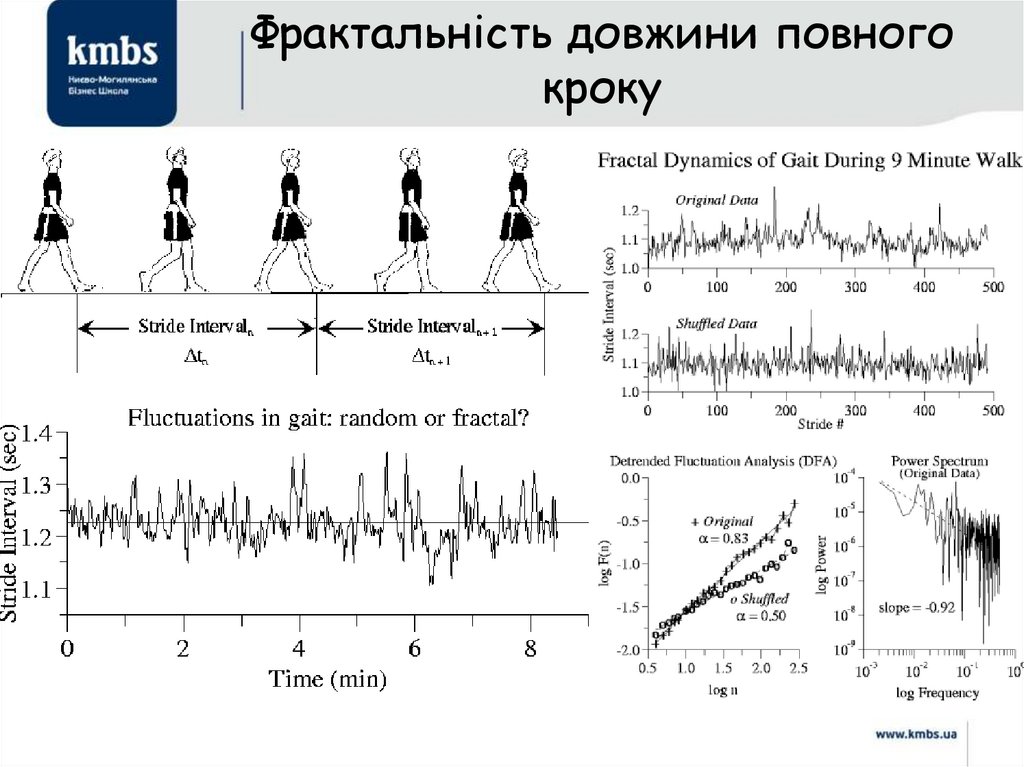
Фрактальність довжини повногокроку
31.
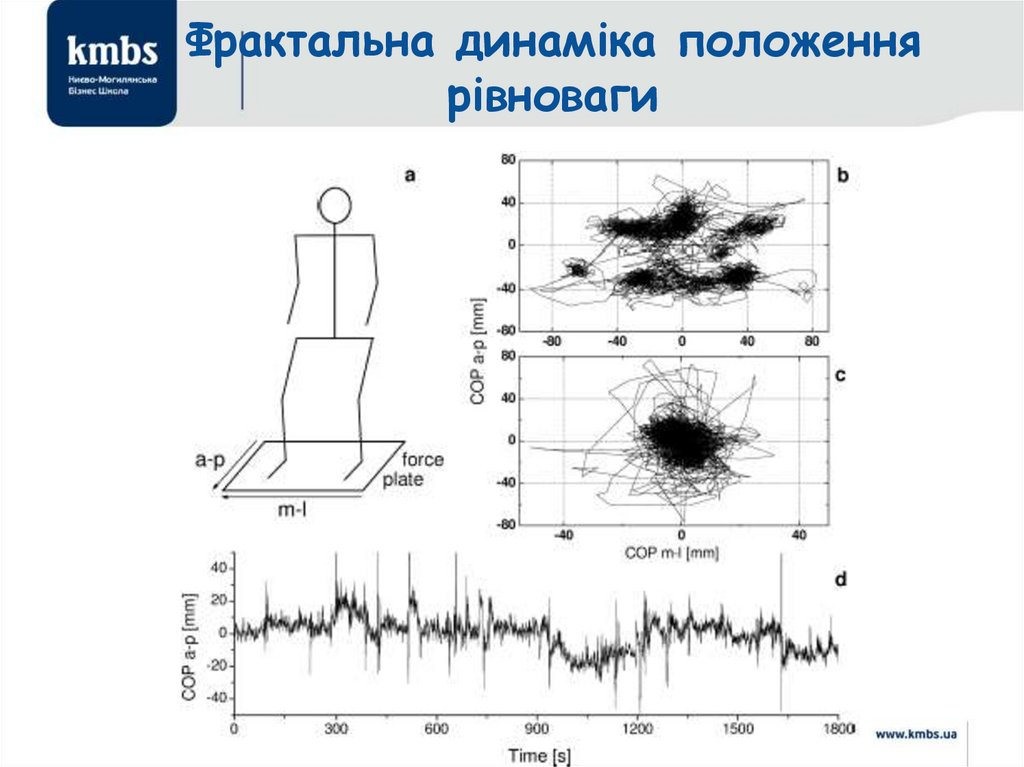
Фрактальна динаміка положеннярівноваги
32.
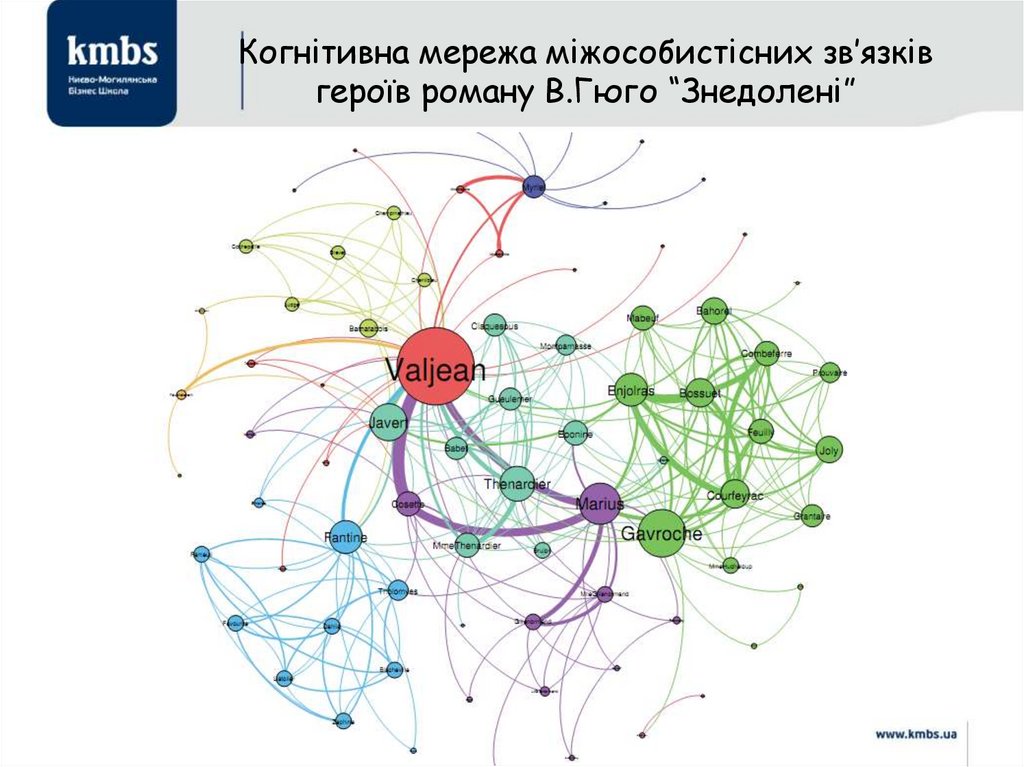
Когнітивна мережа міжособистісних зв’язківгероїв роману В.Гюго “Знедолені”
33. Психодіагностика
34.
Міри складностіІнформаційні міри
• Лемпеля-Зіва;
• ентропії Шеннона, Тсалліса і Реньї, вейвлет-ентропія
Хаос-динамічні
• моно- і мультимасштабні ентропійні міри (ентропії Колмогорова-Сіная,
подібності, шаблонів, перестановок);
• показники Ляпунова, включаючи масштабно-залежну версію;
• фрактальні міри: фрактальна розмірність, декілька модифікацій розрахунку
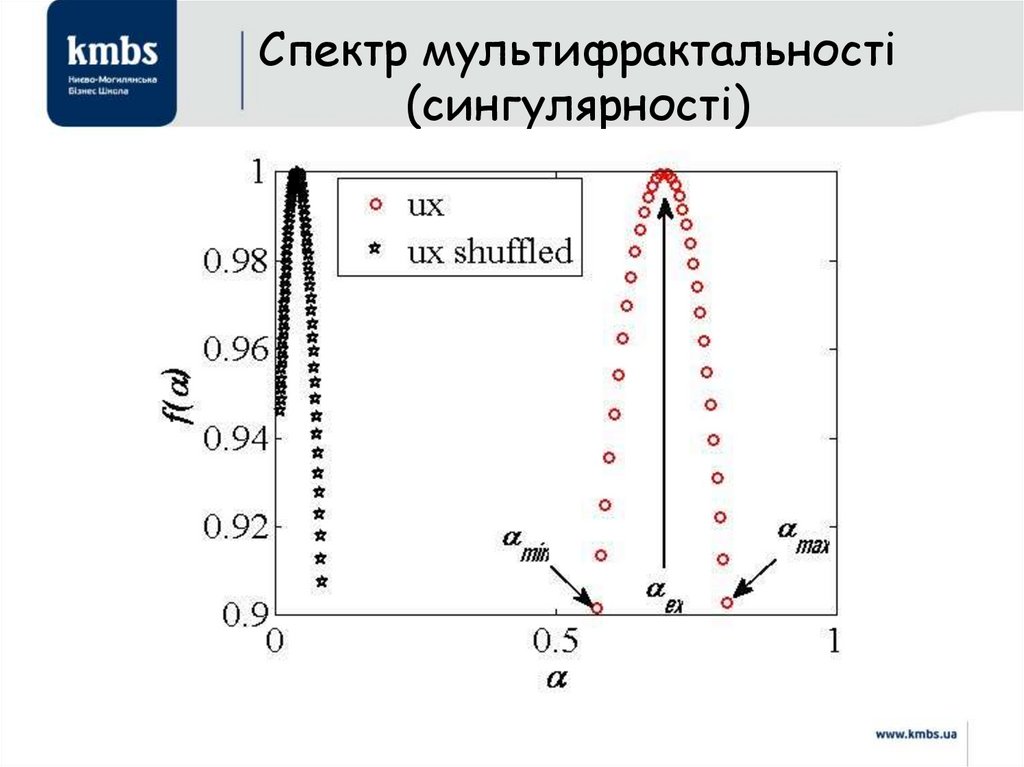
коефіцієнта Херста, спектр сингулярності (мультифрактальності);
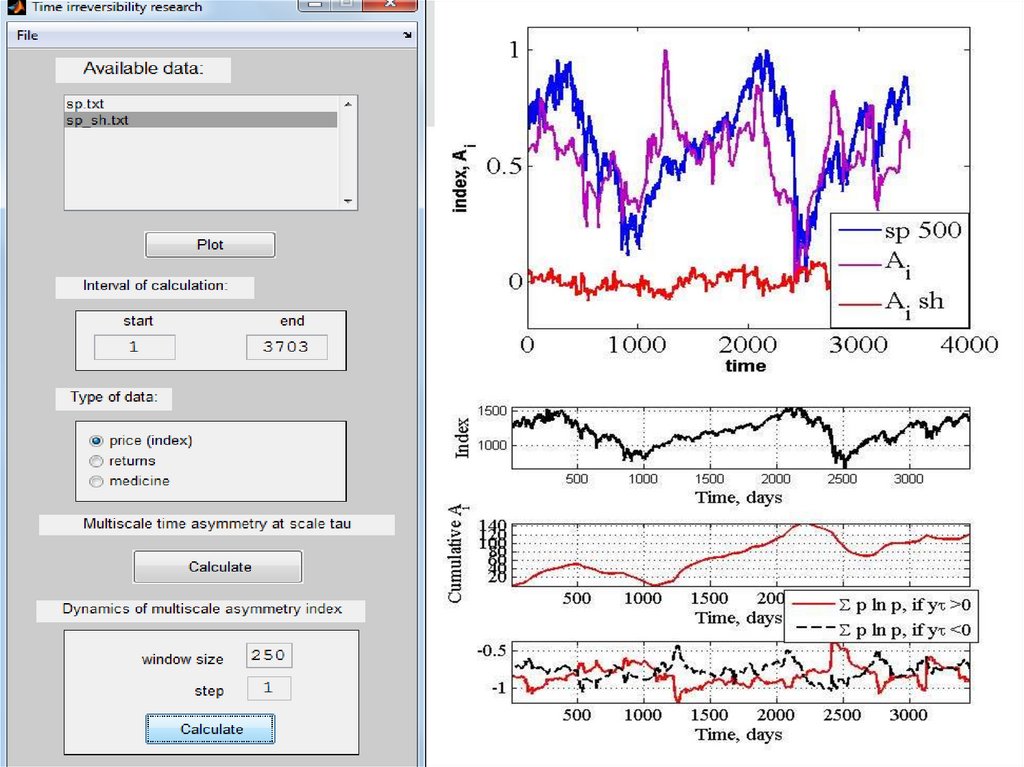
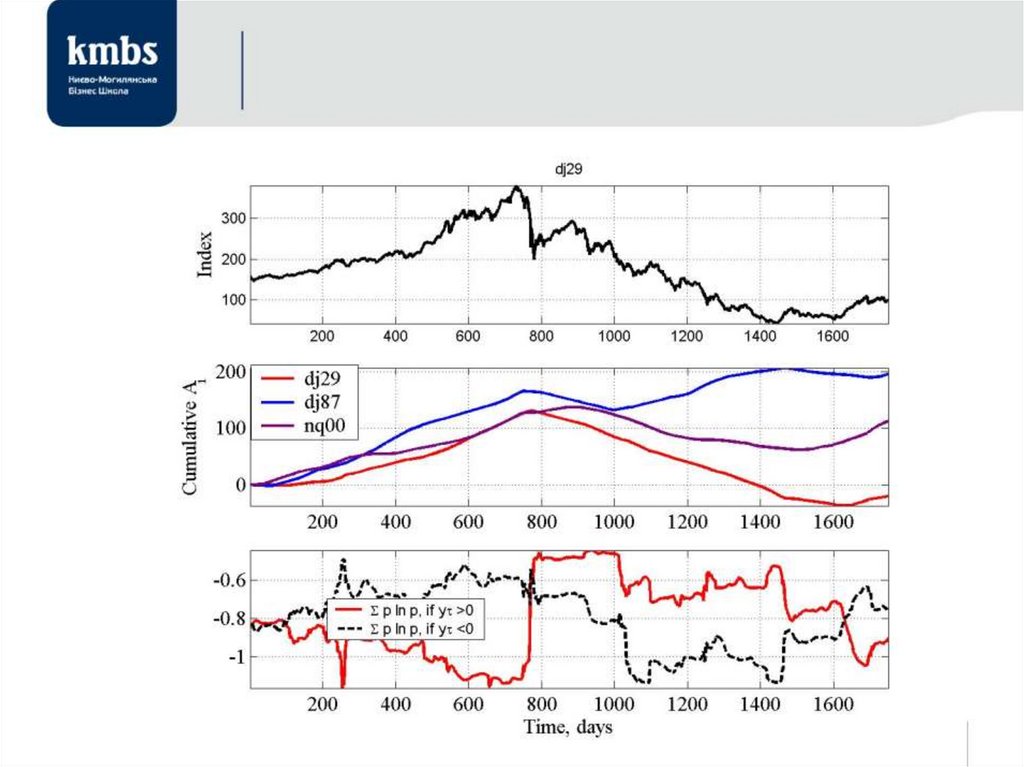
• незворотність процесів;
• рекурентні міри складності, які одержуються в результаті побудови та
кількісного аналізу рекурентних діаграм та інші.
Мережні
- спектральні (спектральний розрив, енергія графа, алгебраїчна зв’язність,..)
- топологічні (ступінь вершини, коефіцієнт кластеризації, середня довжина
шляху, …)
Мульт имережні
- мультиплексні;
- міжмережні.
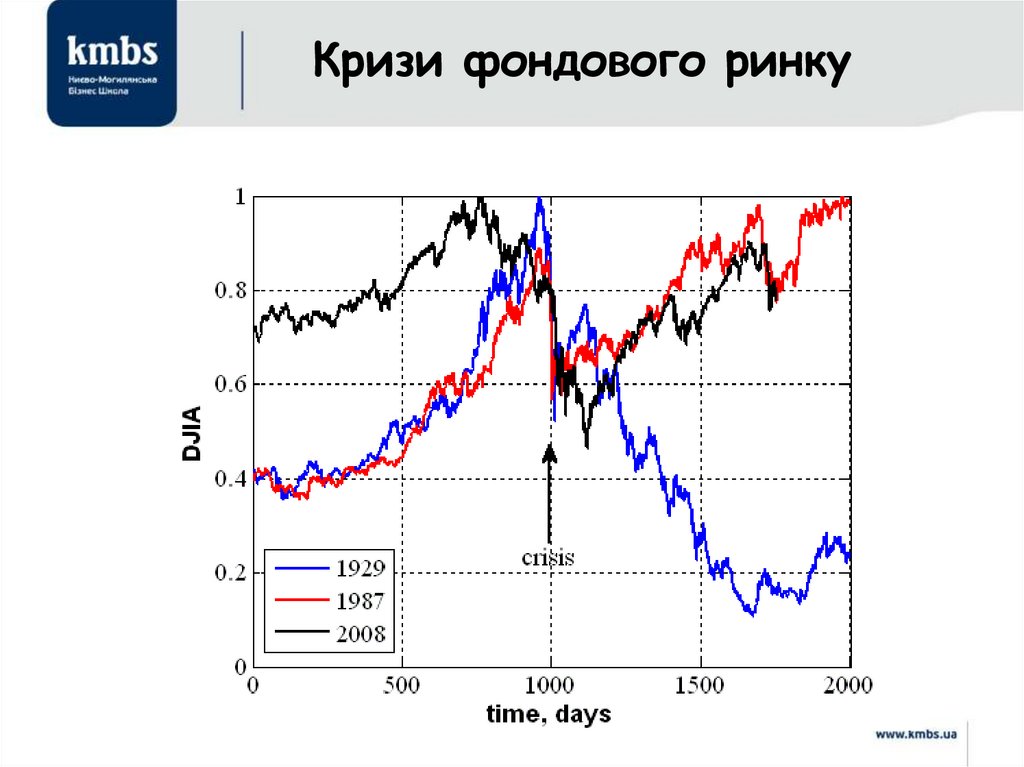
35.
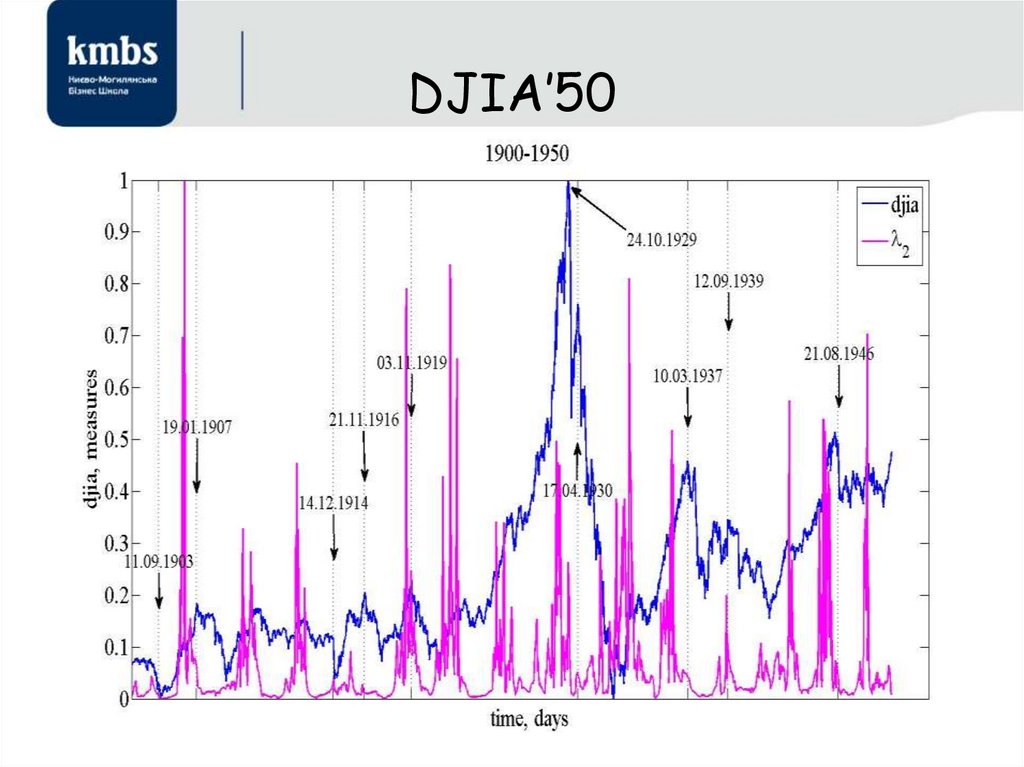
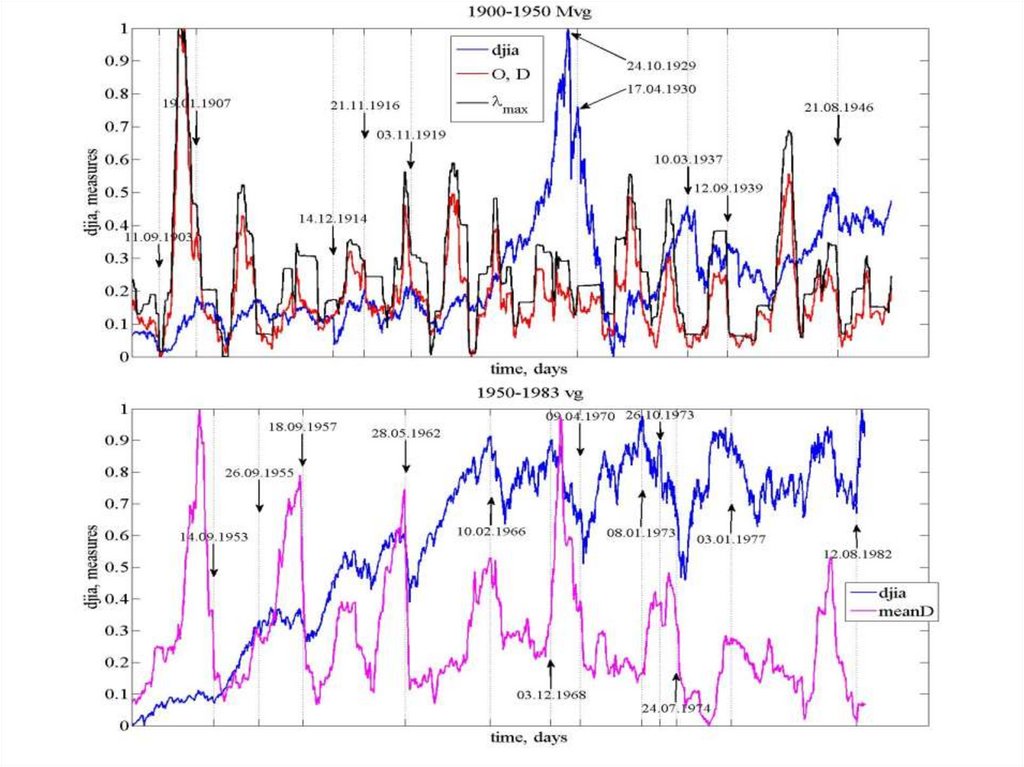
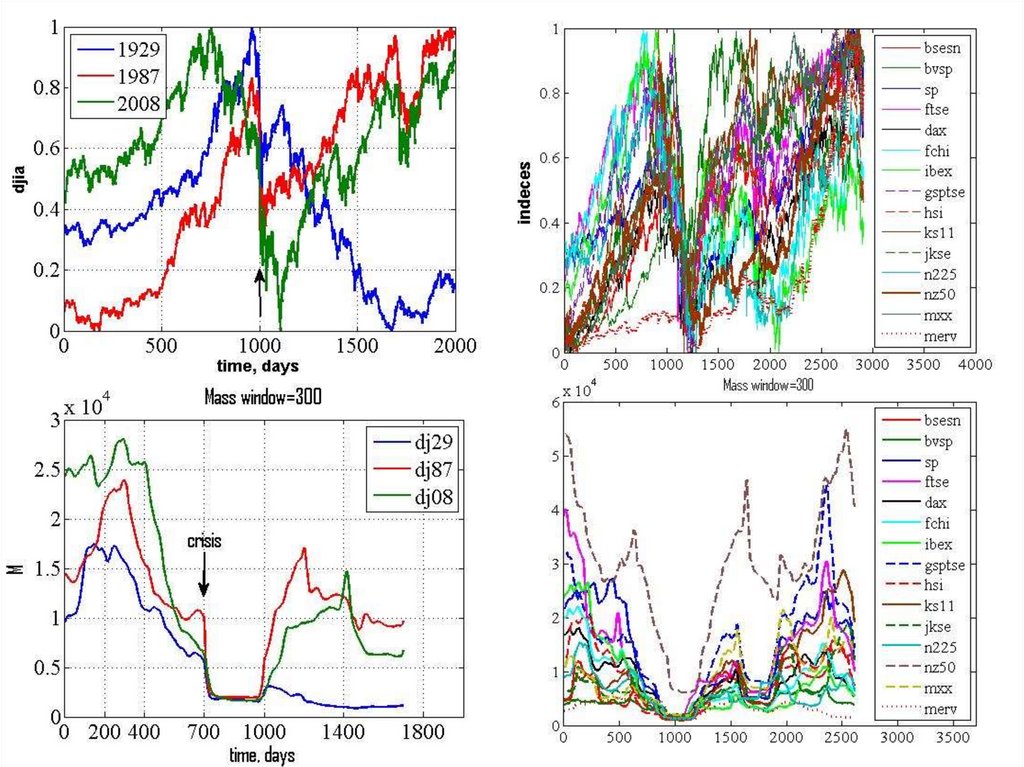
Кризи фондового ринку36. DJIA’50
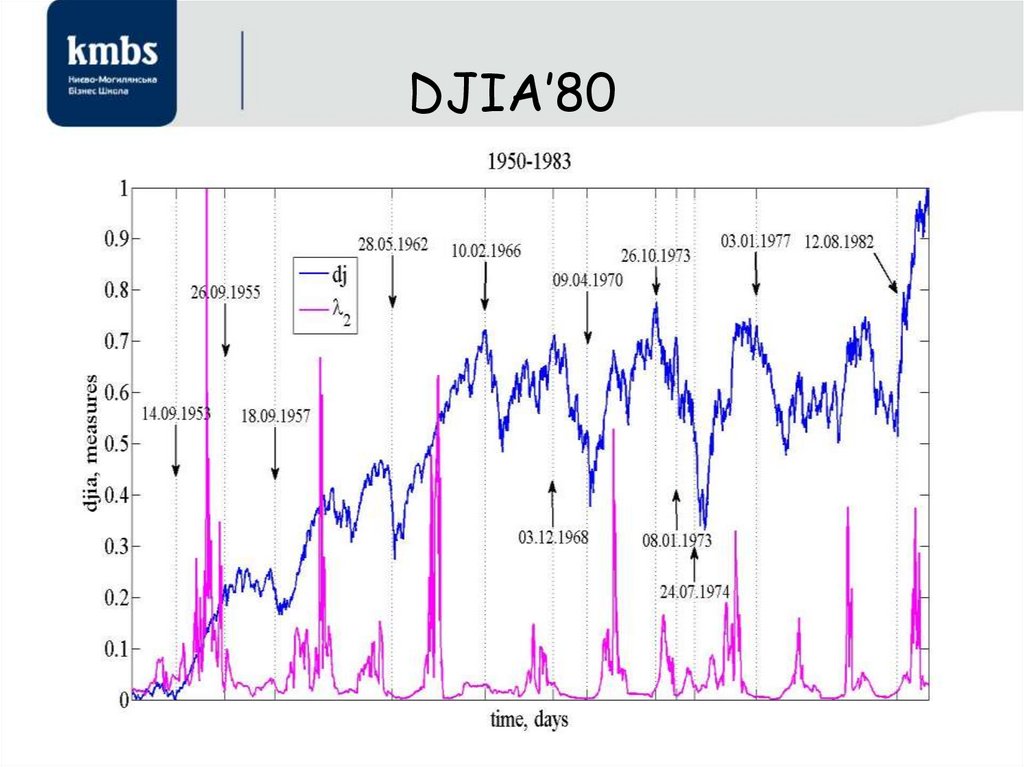
37. DJIA’80
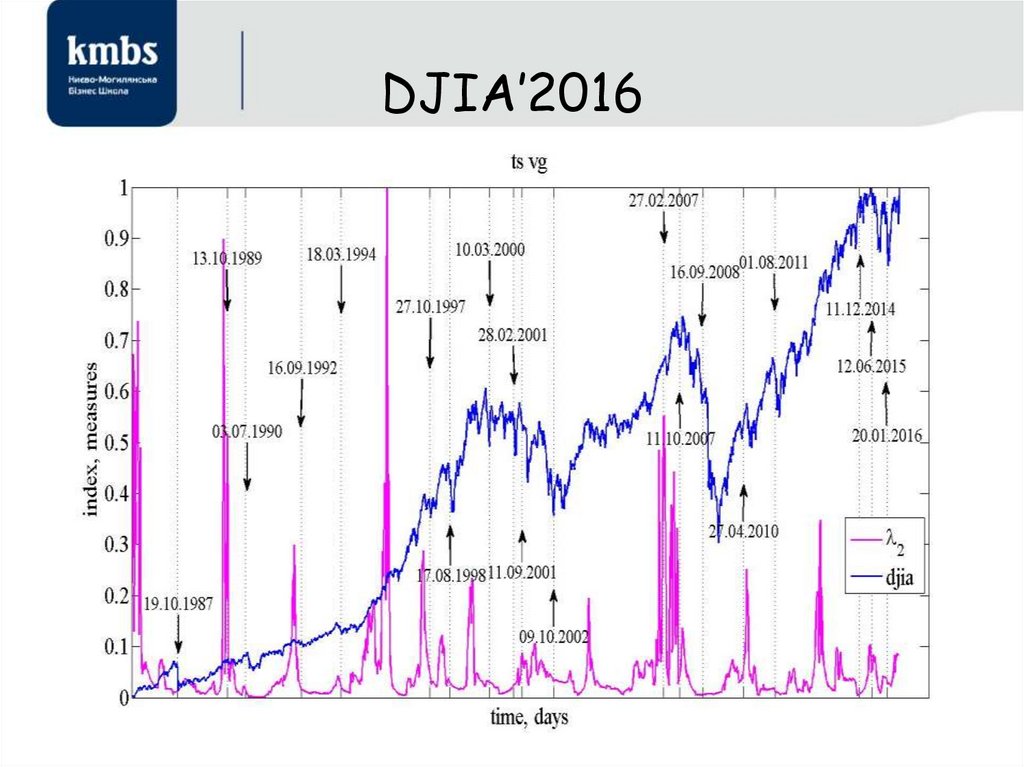
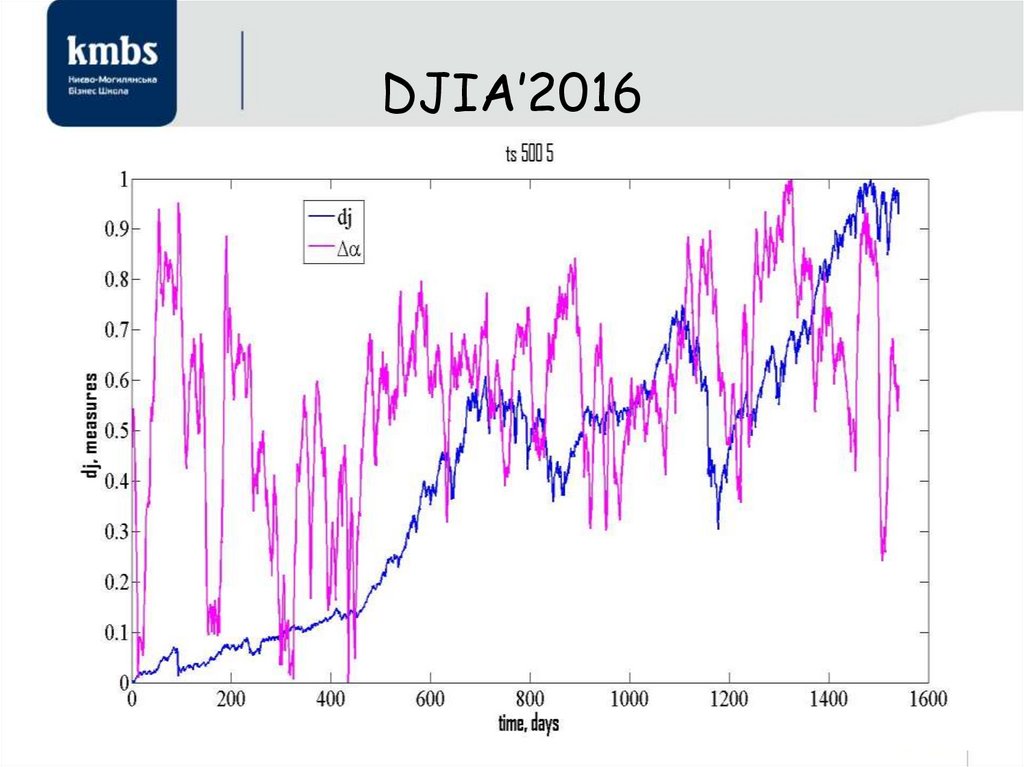
38. DJIA’2016
39.
Визначенняприбутковостей
Обчислюються зміни цін (“прибутковостей”- returns)
активів i 1,..., N
з часом, ( t часовий крок)
Gi t ln Si t t ln Si t ,
Si t - ціна активу i .
Визначаються нормалізовані прибутковості
g i t
i
Gi t Gi
i
.
G Gi є стандартним відхиленням Gi , а ...
2
i
2
означає середнє по часу за вибраний період
Волатильність
1 t n 1
VT t G t '
n t ' t
40.
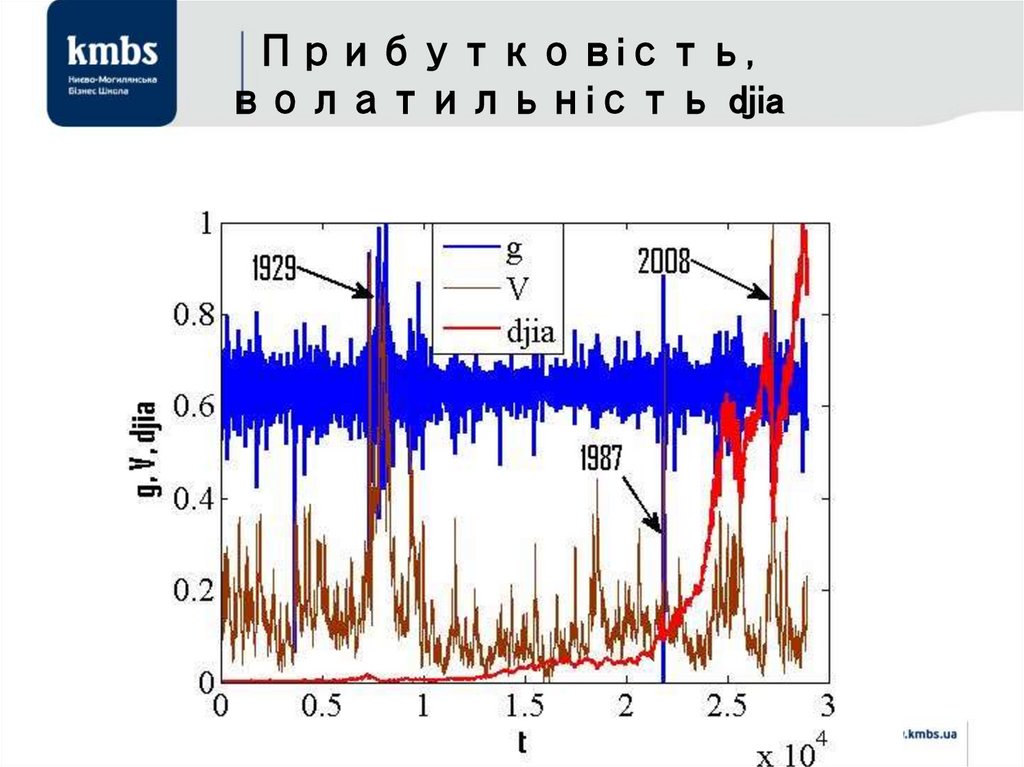
Прибутковість,волатильність djia
41.
Ознака фрактальної поведінки – відсутністьхарактерних часових і просторових масштабів
(scale-free)
Самоподібність
Часовий ряд самоподібний, якщо
d
t
y(t ) a y
a
d
де
означає, що статистичні властивості
обох сторін рівняння ідентичні. Тобто розподіли
часових рядів в координатах вихідних і перетворених
t t/a
y a y
ідентичні
- параметр самоподібності
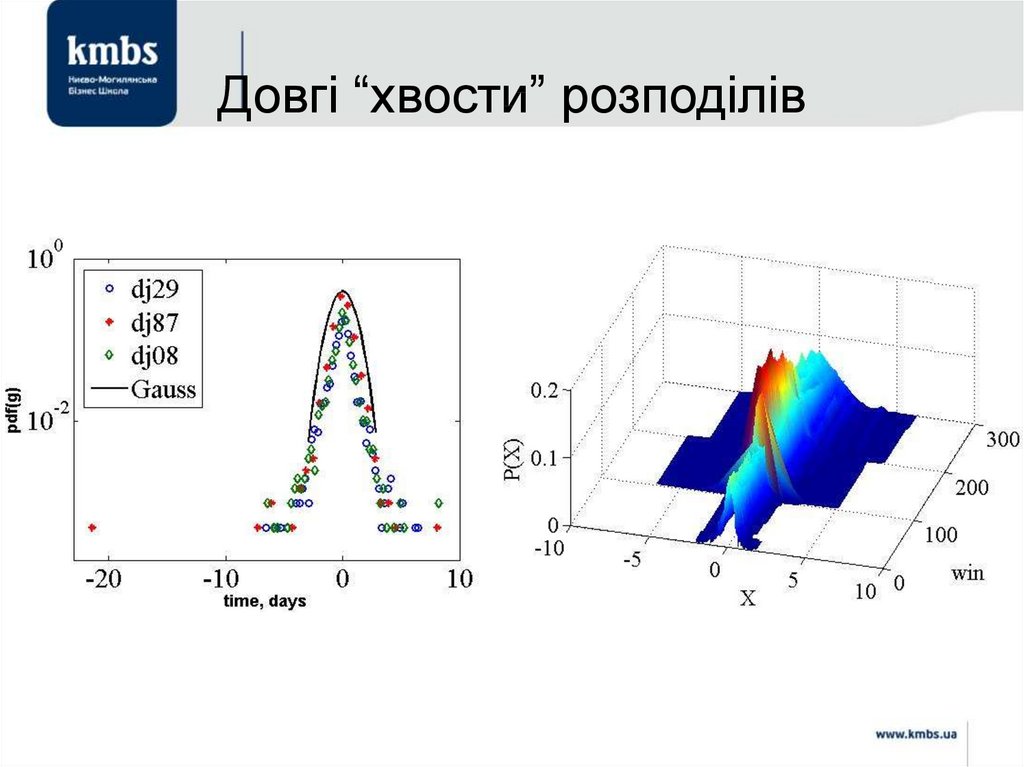
42. Довгі “хвости” розподілів
43.
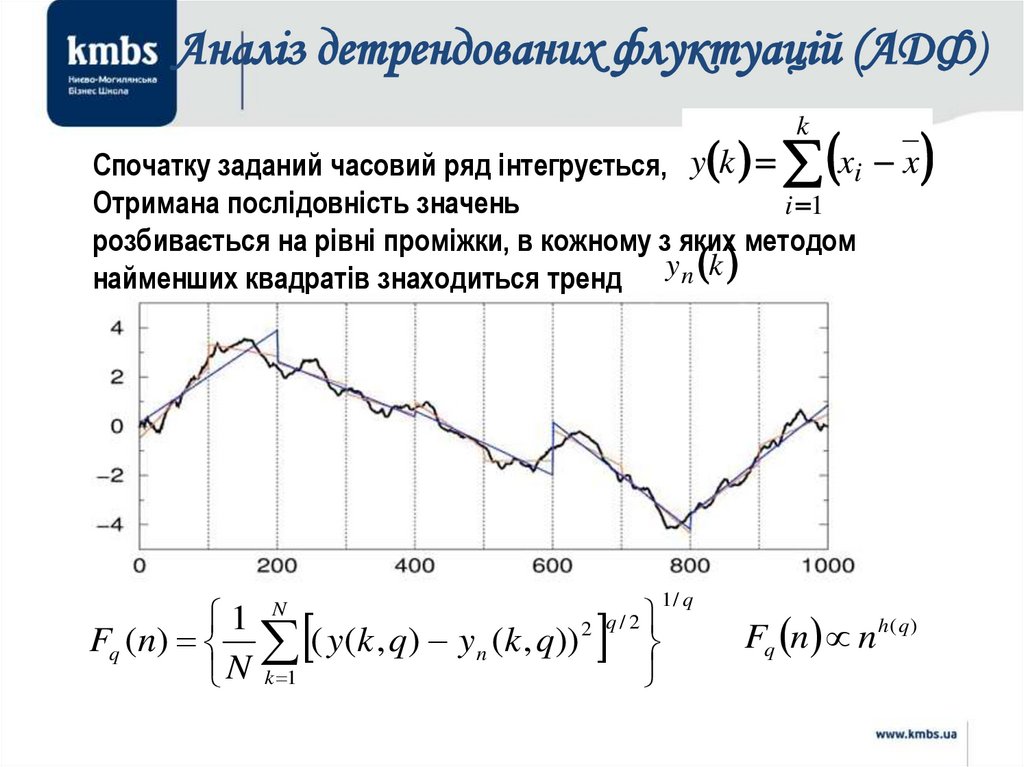
Аналіз детрендованих флуктуацій (АДФ)k
xi x
Спочатку заданий часовий ряд інтегрується, y k
Отримана послідовність значень
i 1
розбивається на рівні проміжки, в кожному з яких методом
найменших квадратів знаходиться тренд y n k
1
Fq (n) ( y(k , q) yn (k , q)) 2
N k 1
N
q/2
1/ q
Fq n n h(q )
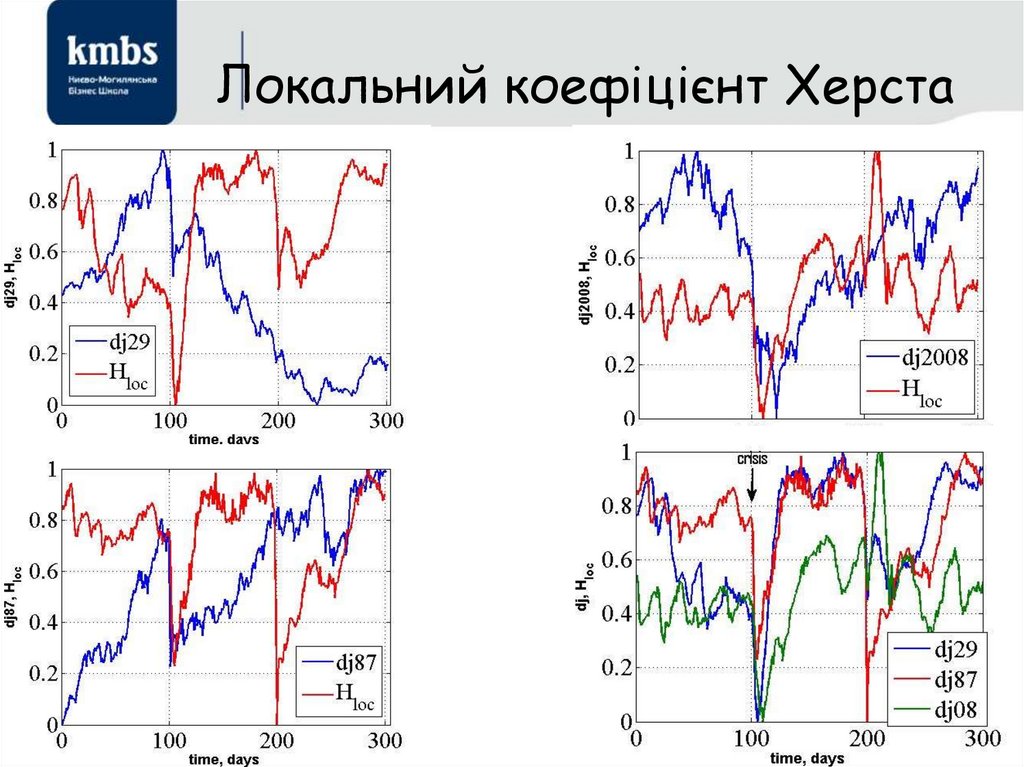
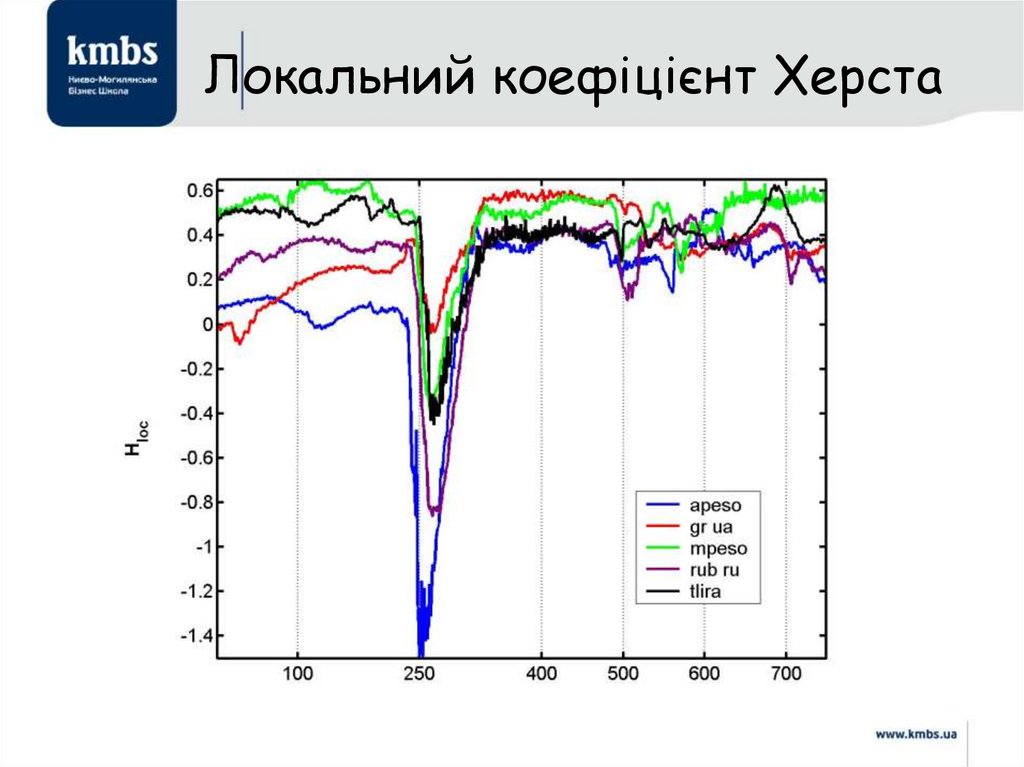
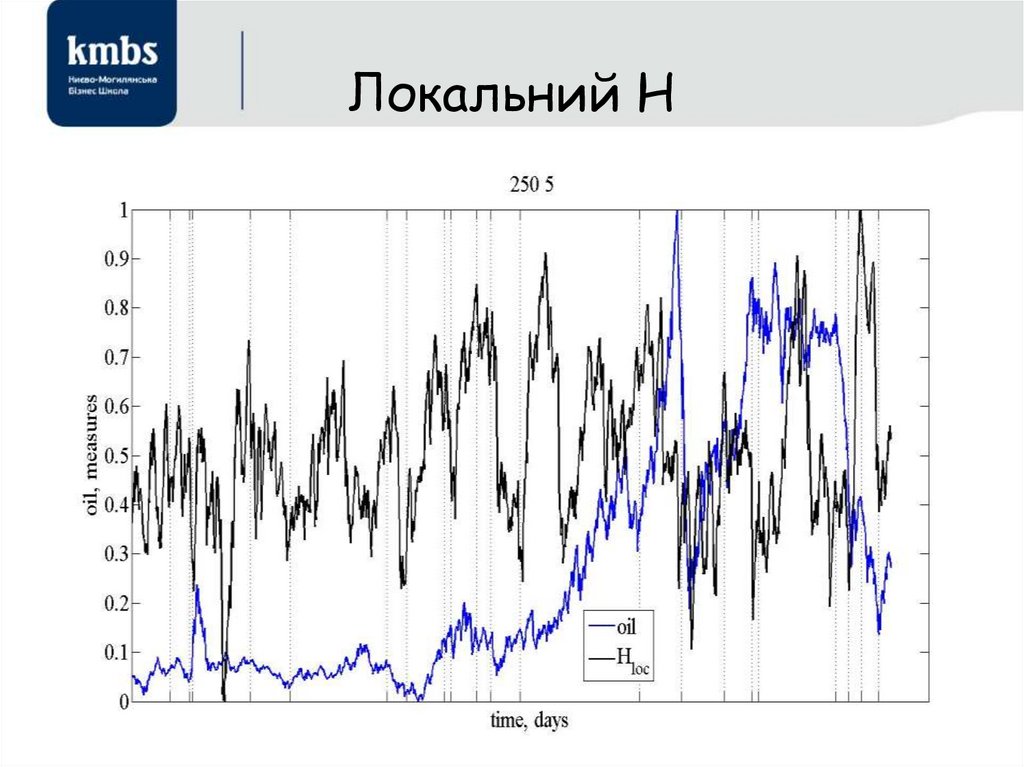
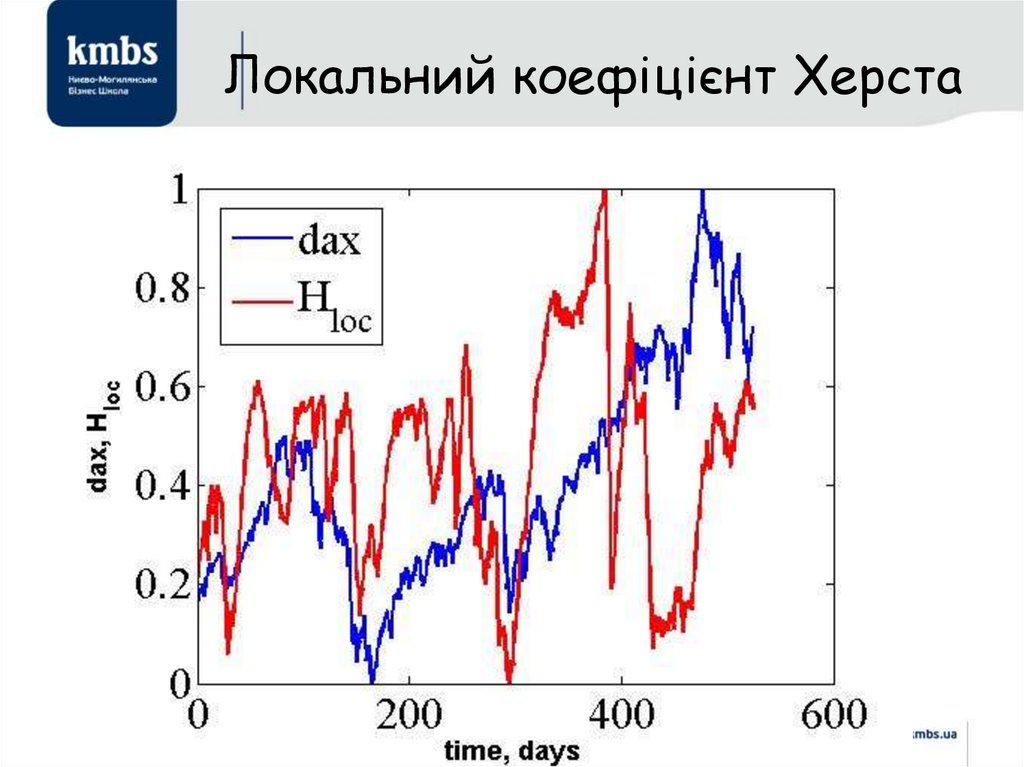
44. Локальний коефіцієнт Херста
45. Локальний коефіцієнт Херста
46. Локальний Н
47. Локальний коефіцієнт Херста
48. Спектр мультифрактальності (сингулярності)
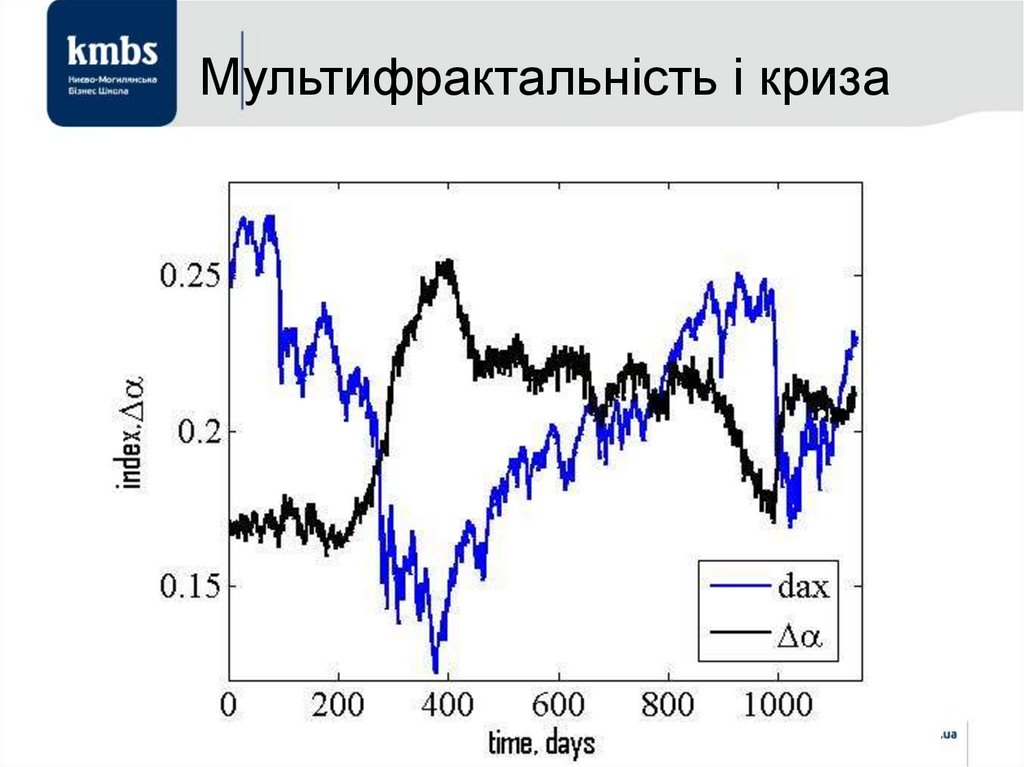
49. Мультифрактальність і криза
50. DJIA’2016
51. Рекурентний аналіз
• Соловйов: 1(с.65-83), 2(92-109)• Реалізує методи, засновані на фундаментальних
властивостях дисипативних динамічних систем.
• Збудження, відхилення, повернення системи до
режиму, близького до попереднього.
• Таку рекурентну поведінку і візуалізують рекурентні
карти
• Ця властивість була відмічена ще в 80-х рр. XIX
століття А.Пуанкаре (Poincare) і згодом
сформульована у вигляді «теореми рекурентності»
(1890 р.):
• Якщо сист ема зводит ь свою динаміку до
обмеженої підмножини фазового прост ору, т о
сист ема майже напевно, скільки завгодно
близько поверт аєт ься до заданого режиму
52.
(Крос-)Рекурентна картаРекурентний графік відображається у вигляді
двовимірної квадратної матриці, заповненої нулями і
одиницями:
i, j 1,..., N
Rij ( i xi x j ),
де N - число станів x i , - гранична відстань,
норма і ( ) - функція Хевісайда.
-
Якщо стан системи у момент часу i рекурентний
іншому її стану в момент j , то значення елемента
матриці з координатами (i, j ) рівне одиниці, у
противному випадку – нулю. Графічно одиниці
відображаються чорними точками, а нулі білими. По
обом осям рекурентного графіка відкладається час
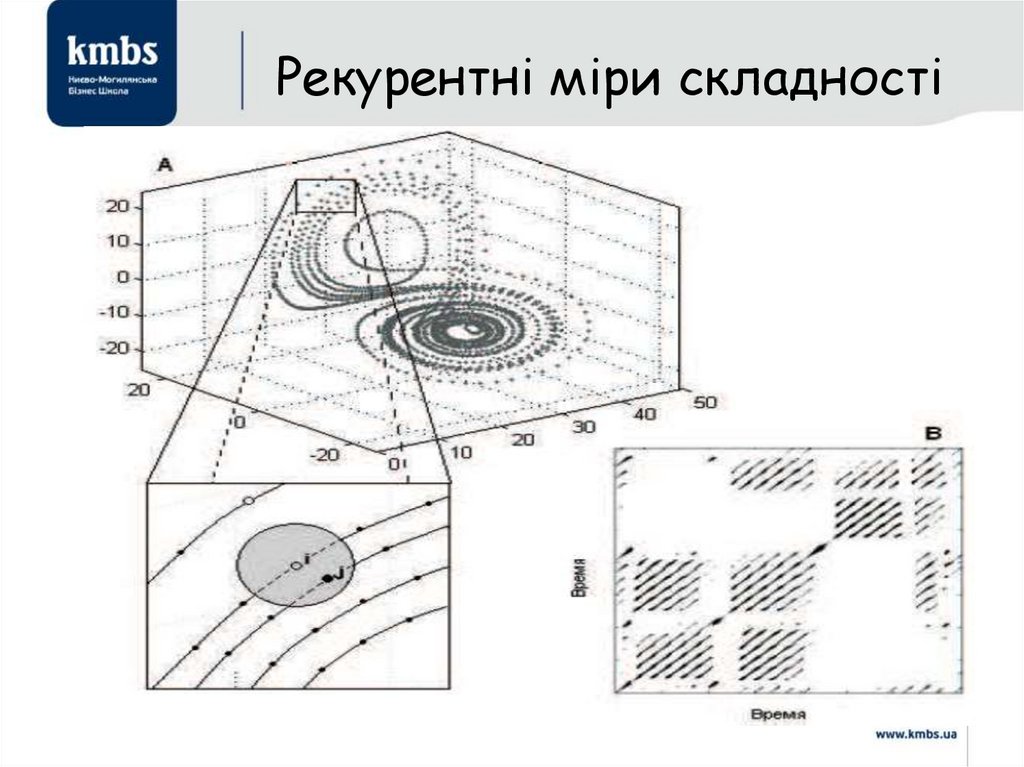
53. Рекурентні міри складності
54.
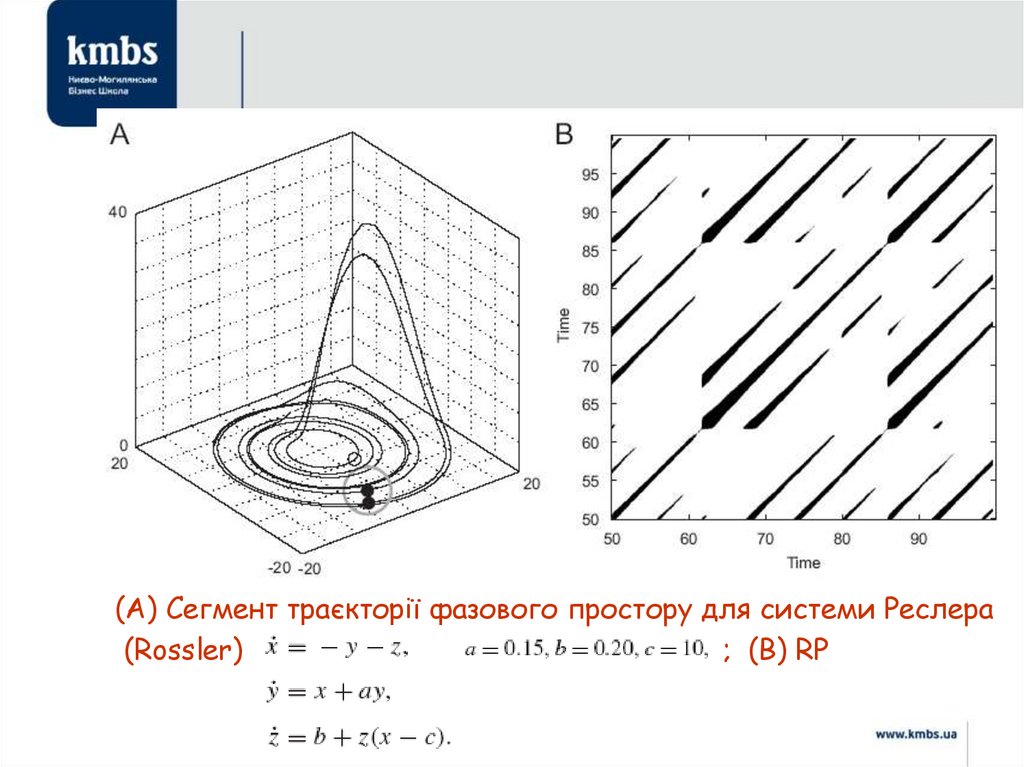
(A) Сегмент траєкторії фазового простору для системи Реслера(Rossler)
; (B) RP
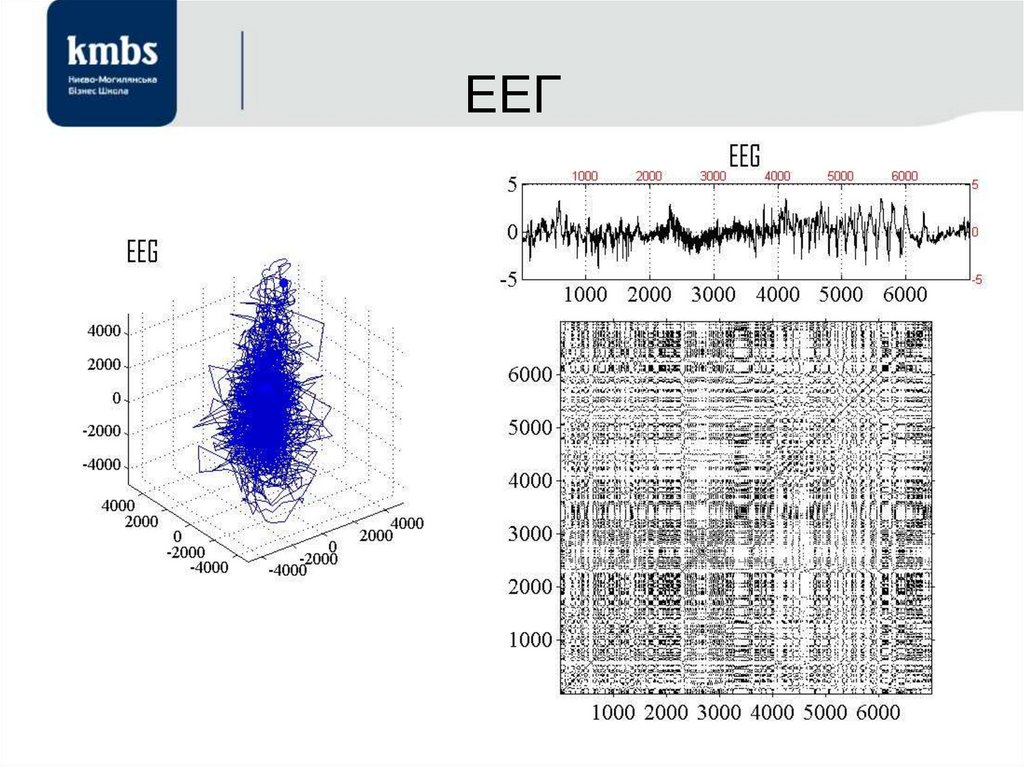
55. ЕЕГ
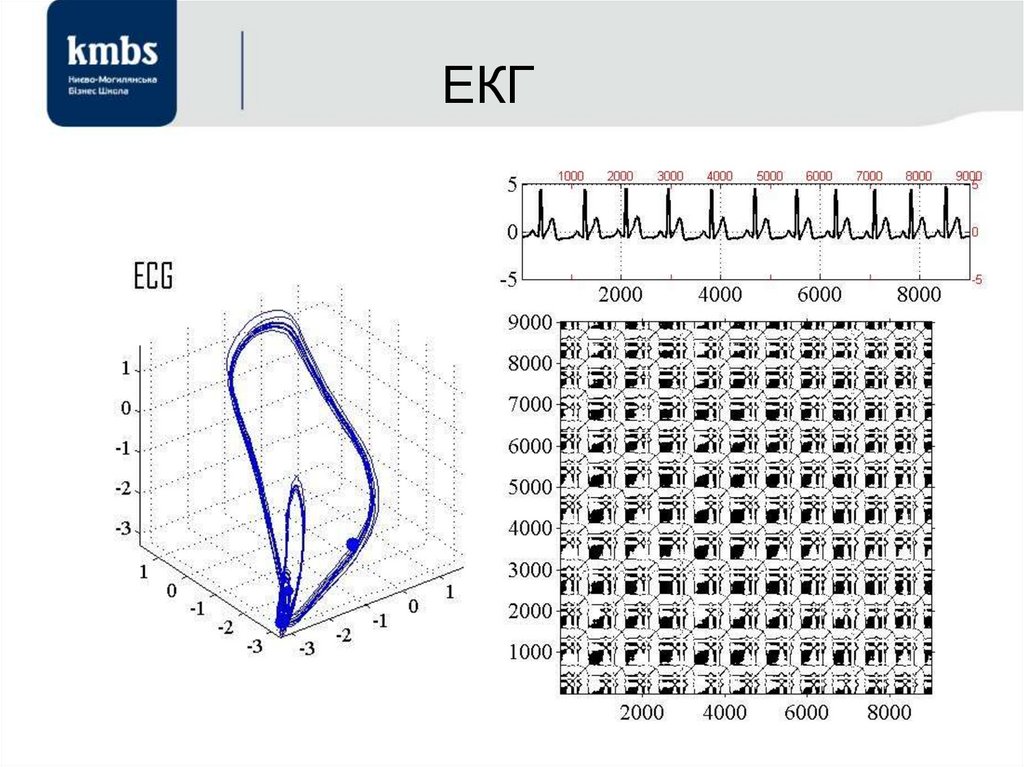
56. ЕКГ
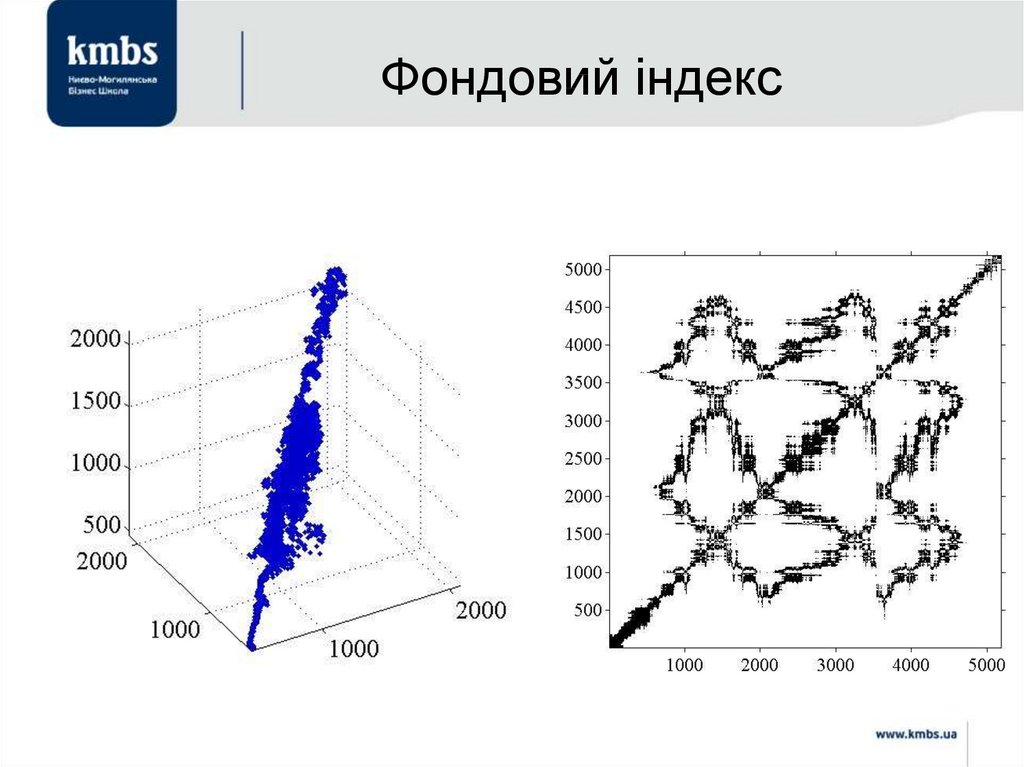
57. Фондовий індекс
58. Побудова атрактора
• Виконується командою phasespace(a), деаргумент - попередньо імпортований у
робочу область часовий ряд
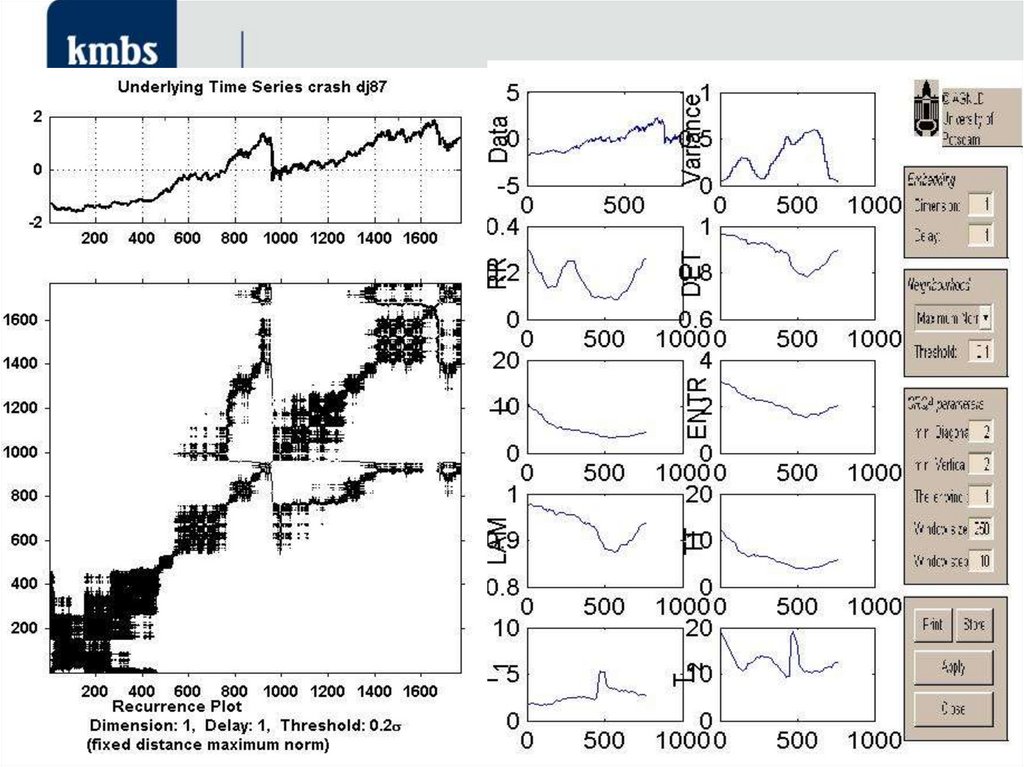
59. Кількісний аналіз рекурентних діаграм (recurrence quantification analysis, RQA)
• Докладний розгляд рекурентних діаграм дозволяєвиявити дрібномасштабні структури – текстуру, яка
складається з простих точок, діагональних,
горизонтальних і вертикальних ліній. Комбінації
вертикальних і горизонтальних ліній формують
прямокутні кластери точок.
• • самот ні, окремо розташовані рекурентні точки
з'являються в тому разі, коли відповідні стани рідкісні,
або нестійкі в часі, або викликані сильною флуктуацією.
При цьому вони не є ознаками випадковості або шуму;
• • діагональні лінії Ri k , j k 1
(при k 1...l де l –
довжина діагональної лінії) з'являються у разі, коли
сегмент траєкторії у фазовому просторі пролягає
паралельно іншому сегменту, тобто траєкторія
повторює саму себе, повертаючись в одну і ту ж область
фазового простору у різний час
60.
Характерна типологіярекурентних карт
A – білий шум
B – періодичний сигнал
C – трендостійкий сигнал
D – броунівський рух
61.
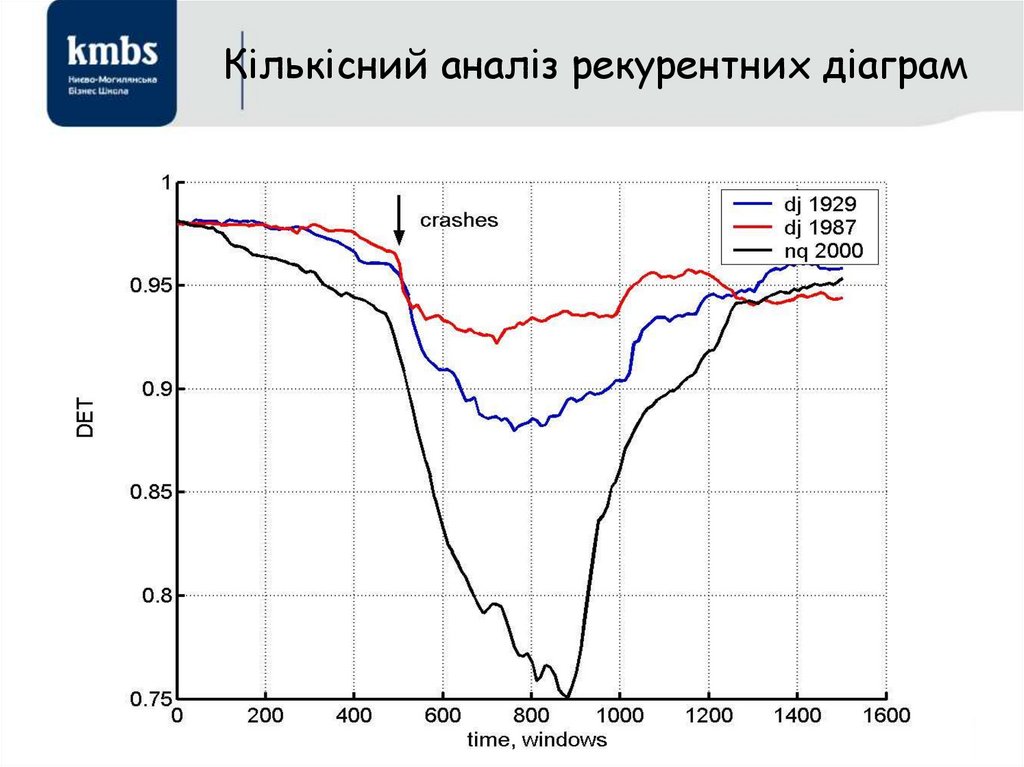
Кількісний аналіз рекурентних діаграм(recurrence quantification analysis, RQA)
• Ці та деякі інші структури використовуються для обчислення
мір кількісного аналізу рекурентних діаграм - RQA.
• Збілут (Zbilut) і Веббер (Webber) розробили інструмент
обчислення ряду мір на основі підрахунку густини
рекурентних точок і побудови частотного розподілу довжин
діагональних ліній: recurrence rate (RR, коефіцієнт
самоподібності), determinism (DET, передбачуваність),
divergence (DIV, зворотна величина максимальної довжини
діагональної лінії), entropy (ENTR, ентропія) і trend (TREND,
тренд). Пізніше були запропоновані міри, що використовують
густину вертикальних (або горизонтальних) структур:
laminarity (LAM, завмирання), trapping time (TT, показник
затримки), дозволяючі виявляти переходи хаос–хаос.
Обчислення цих мір в підматрицях рекурентної діаграми
уздовж лінії ідентичності показує поведінку цих мір у часі
62. Рекурентні міри
Визначимо1 якщо.(i, j ). рекурентні
Rij
0 .інакше
1 . якщо (i, j )and (i 1, j 1)or (i 1, j 1). рекурентні
Dij
0 .інакше
Тепер, наприклад, коефіцієнт самоподібності і
передбачуваність мають вигляд:
1 N
RR 2 Rij
N i , j 1
DET
iN, j 1 Dij
N
i , j 1 Rij
63.
64.
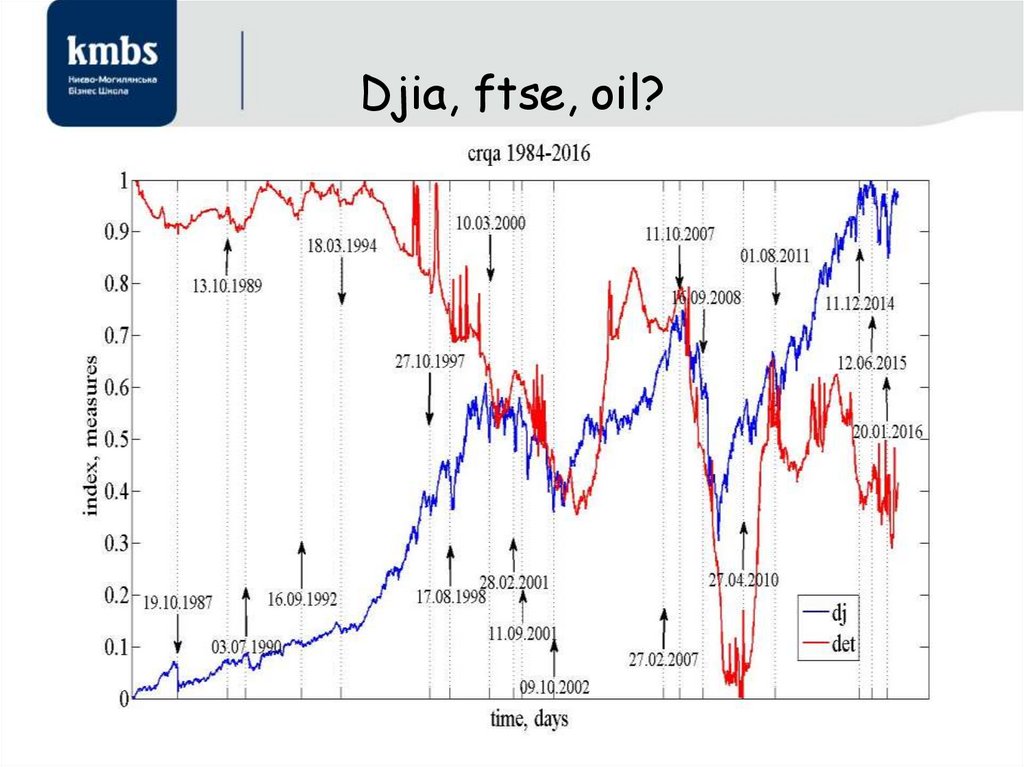
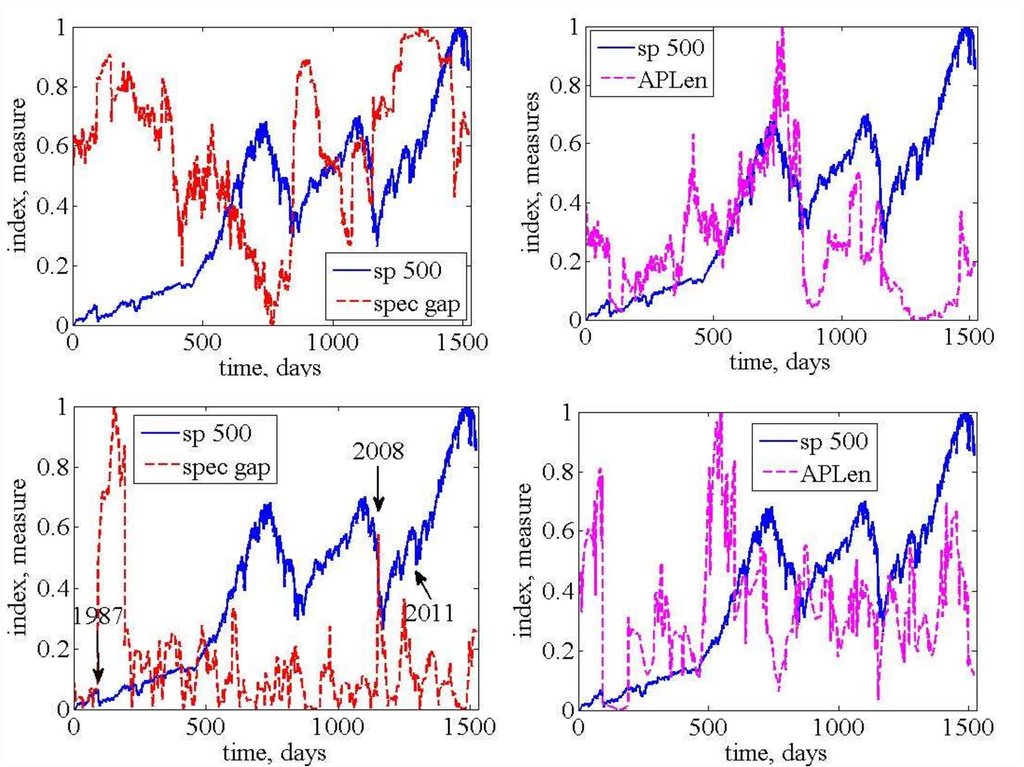
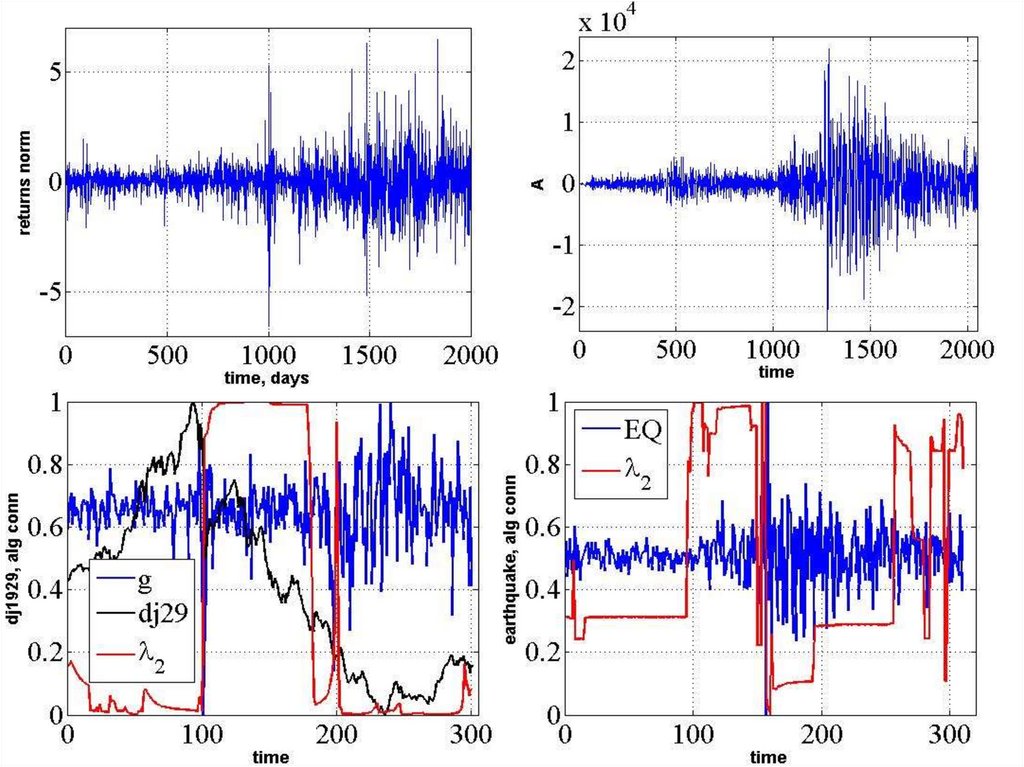
Кількісний аналіз рекурентних діаграм65. Djia, ftse, oil?
66. Ентропійні міри
Соловйов 1 (с.50-64), 2 (с.110-123)
Для всього ряду
Віконна реалізація
Масштабно-залежна
Віконна масштабно залежна
67.
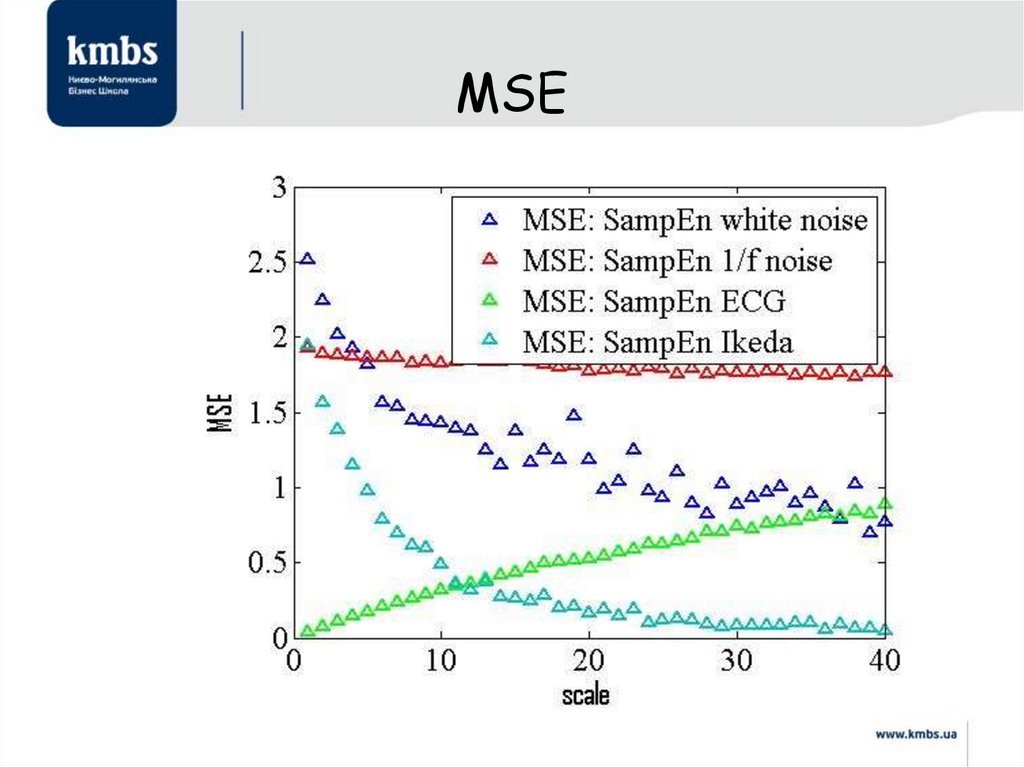
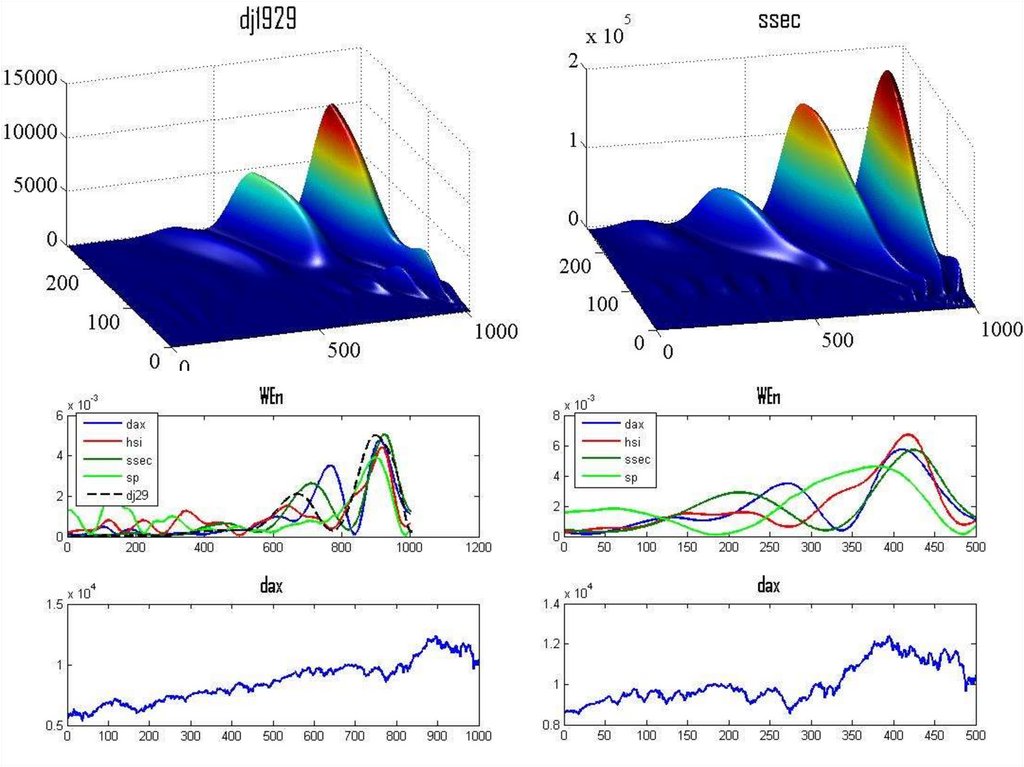
Процедура сoarse-graining68. MSE
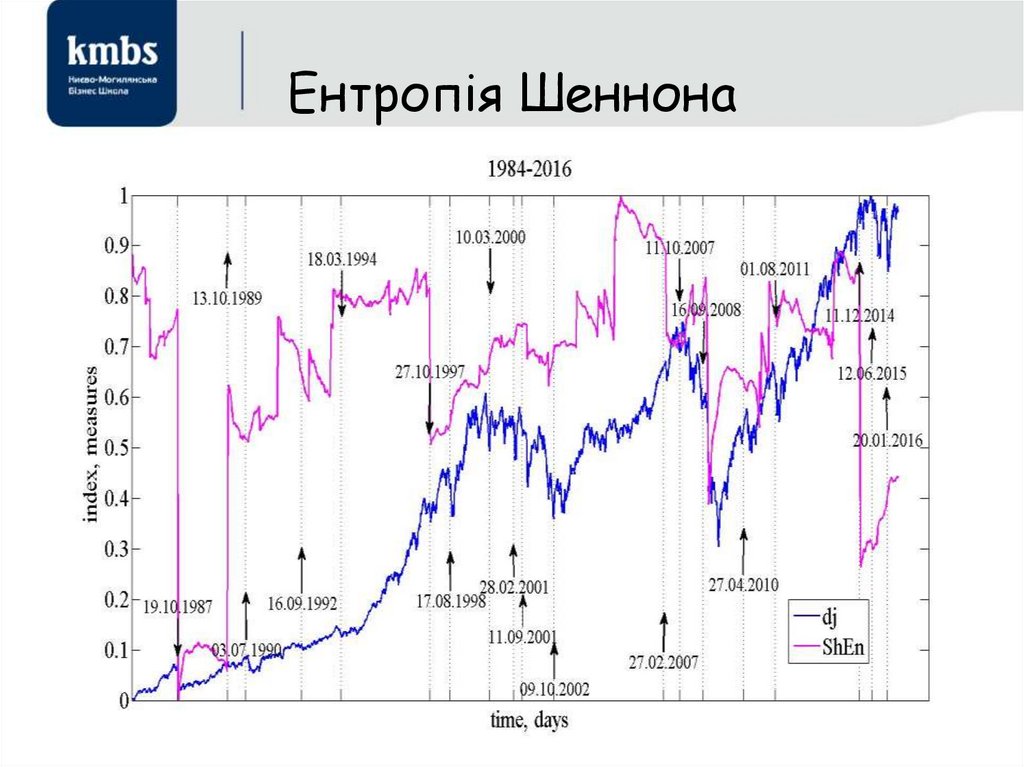
69. Ентропія Шеннона
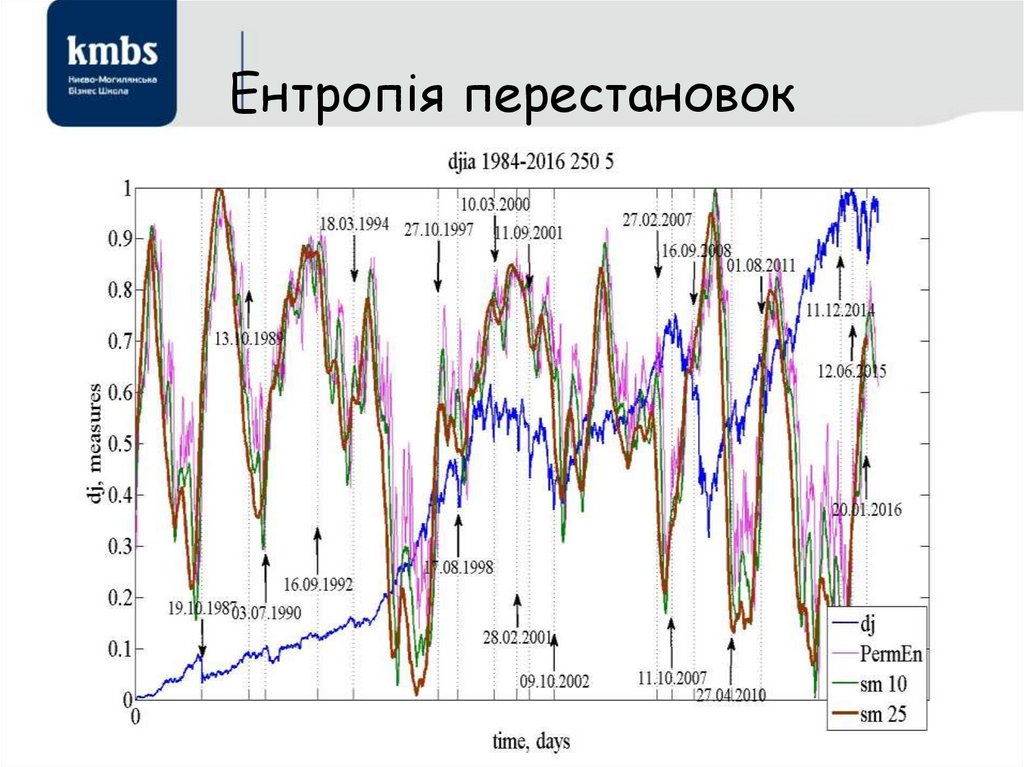
70. Пермутаційна ентропія
• Соловйов (с.116)• Чумак (Maket_Chumak_1.pdf), c. 33
71. Ентропія перестановок
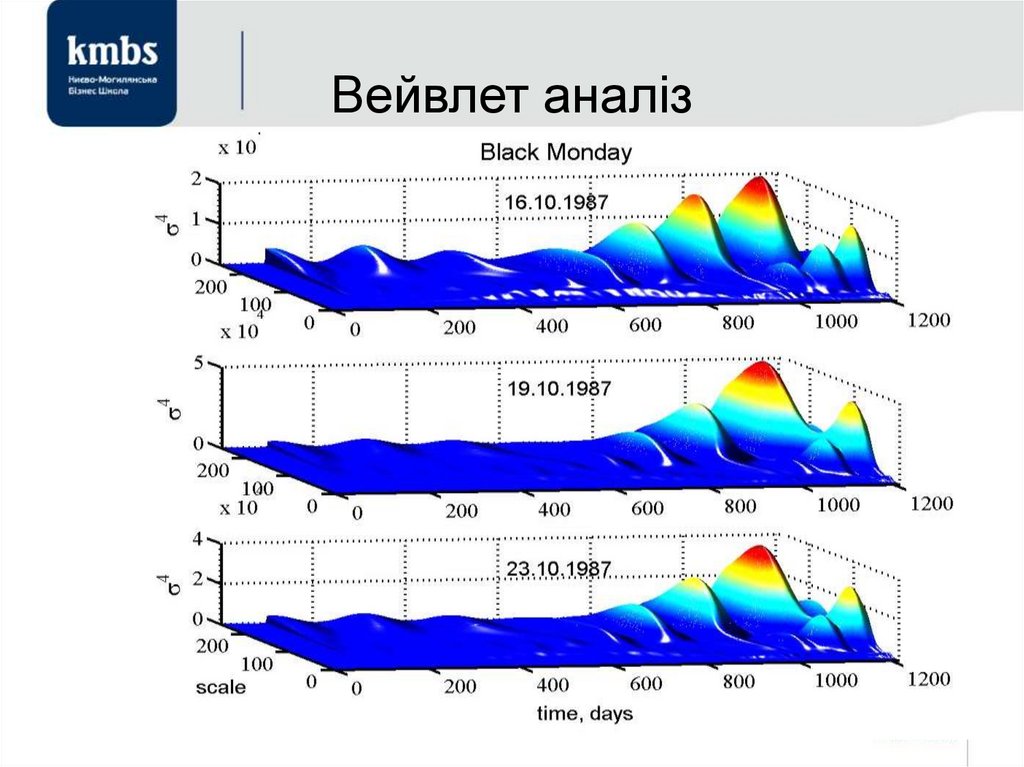
72.
73. Вейвлет аналіз
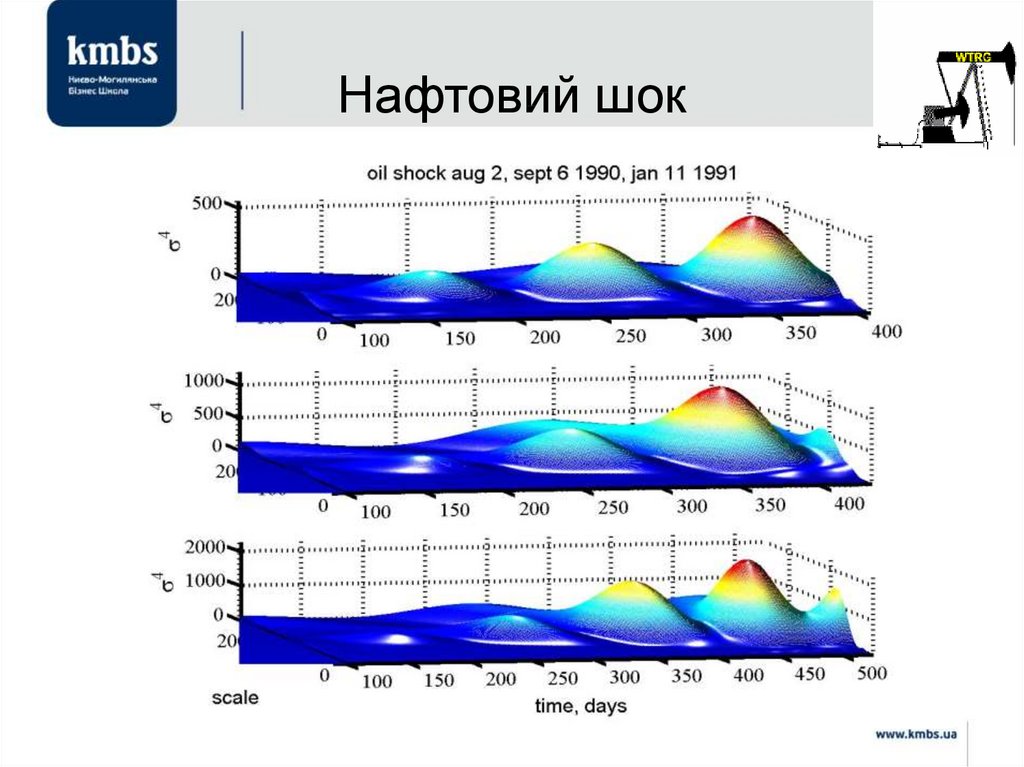
74. Нафтовий шок
75. Мережна парадигма
• Мережа описує колекцію вузлів або вершин (наприклад,фінансові установи, фондові ринки) і зв'язки між ними,
які можуть бути направленими (тобто, дуги) або
ненаправленними (тобто, ребра).
• Вузли задані матрицею різних агентів, кожен з яких має
часовий ряд, динаміку поведінки і зв’язки яких
будуються за певними мірами залежності між часовими
рядами
76. Біологічні мережі
77.
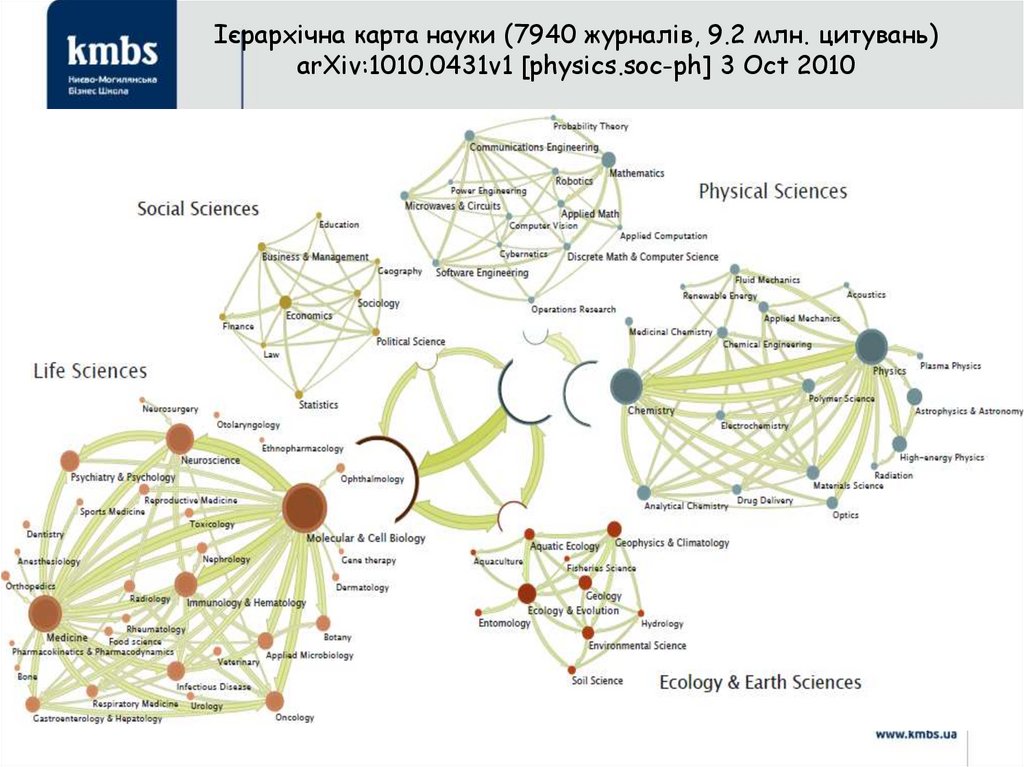
Ієрархічна карта науки (7940 журналів, 9.2 млн. цитувань)arXiv:1010.0431v1 [physics.soc-ph] 3 Oct 2010
78. Транспортні мережі
79. Соціальні мережі
80.
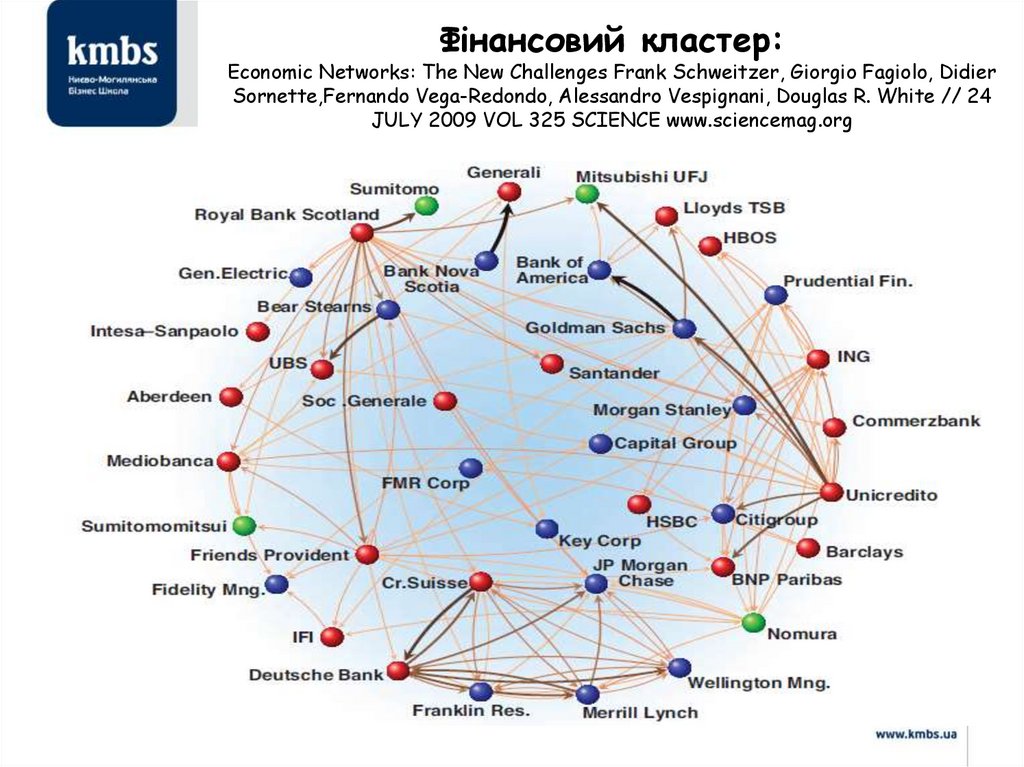
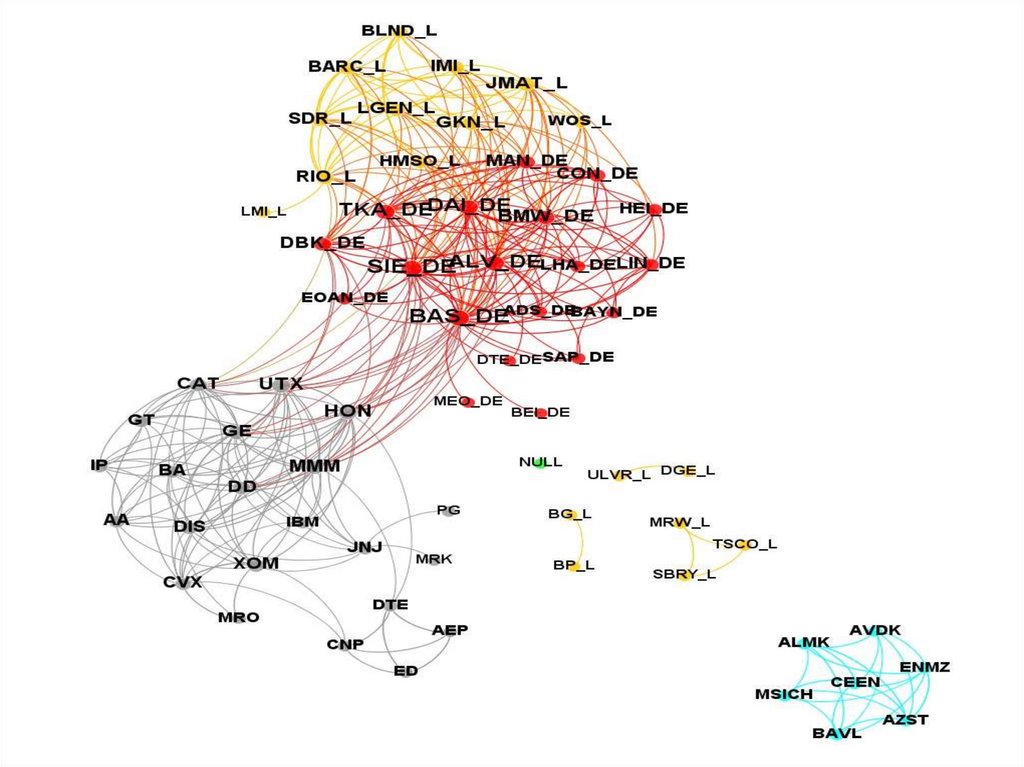
Фінансовий кластер:Economic Networks: The New Challenges Frank Schweitzer, Giorgio Fagiolo, Didier
Sornette,Fernando Vega-Redondo, Alessandro Vespignani, Douglas R. White // 24
JULY 2009 VOL 325 SCIENCE www.sciencemag.org
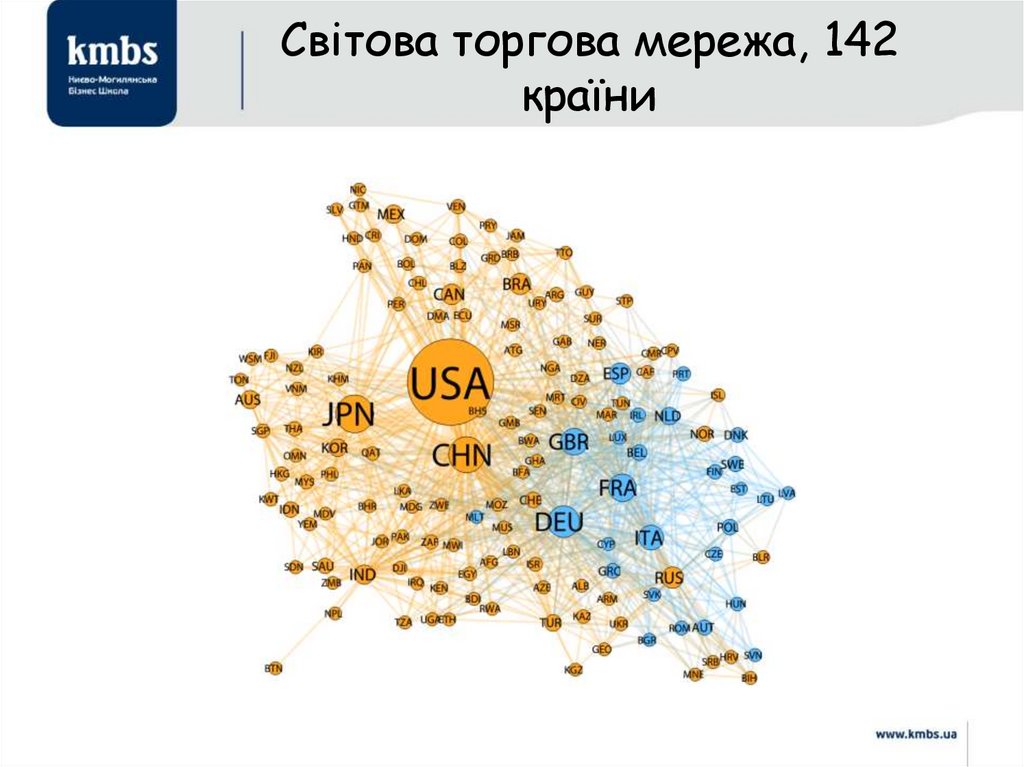
81. Світова торгова мережа, 142 країни
82. Мережа персонажів Біблії
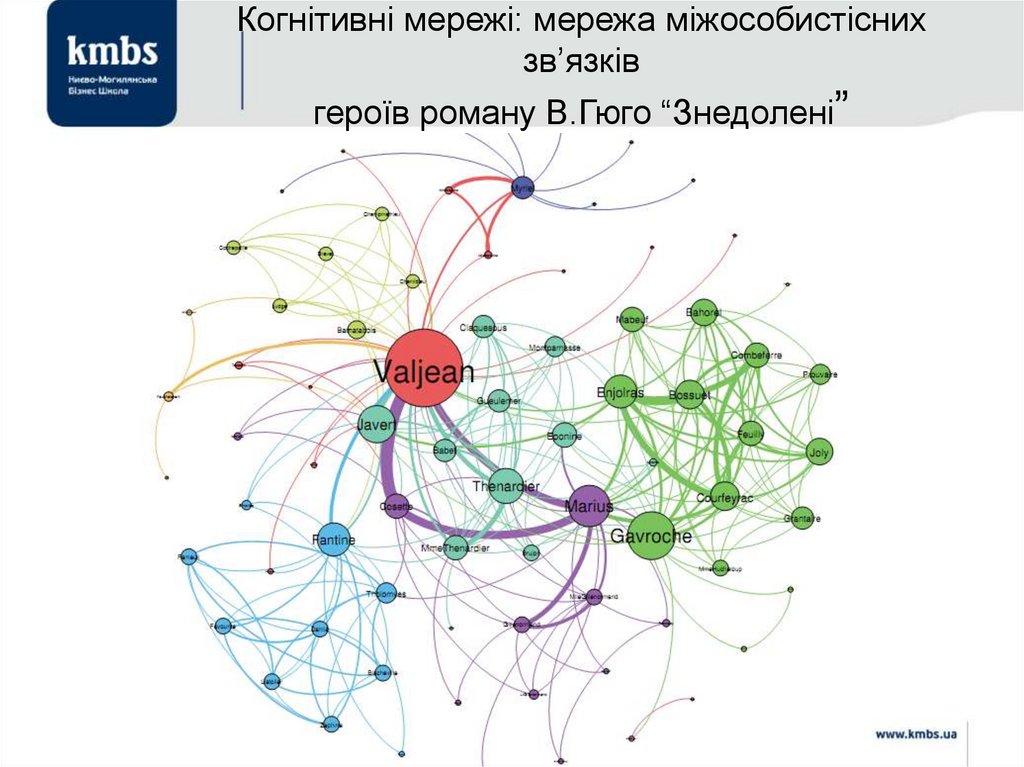
83. Когнітивні мережі: мережа міжособистісних зв’язків героїв роману В.Гюго “Знедолені”
84. Соціальні мережі
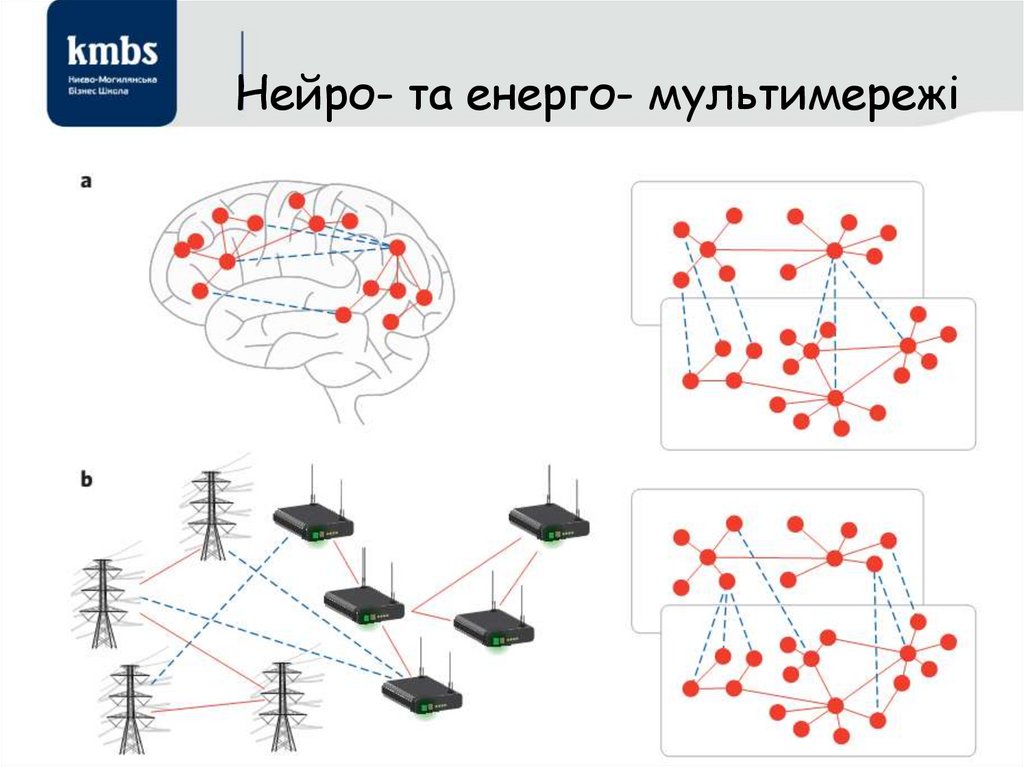
85. Нейро- та енерго- мультимережі
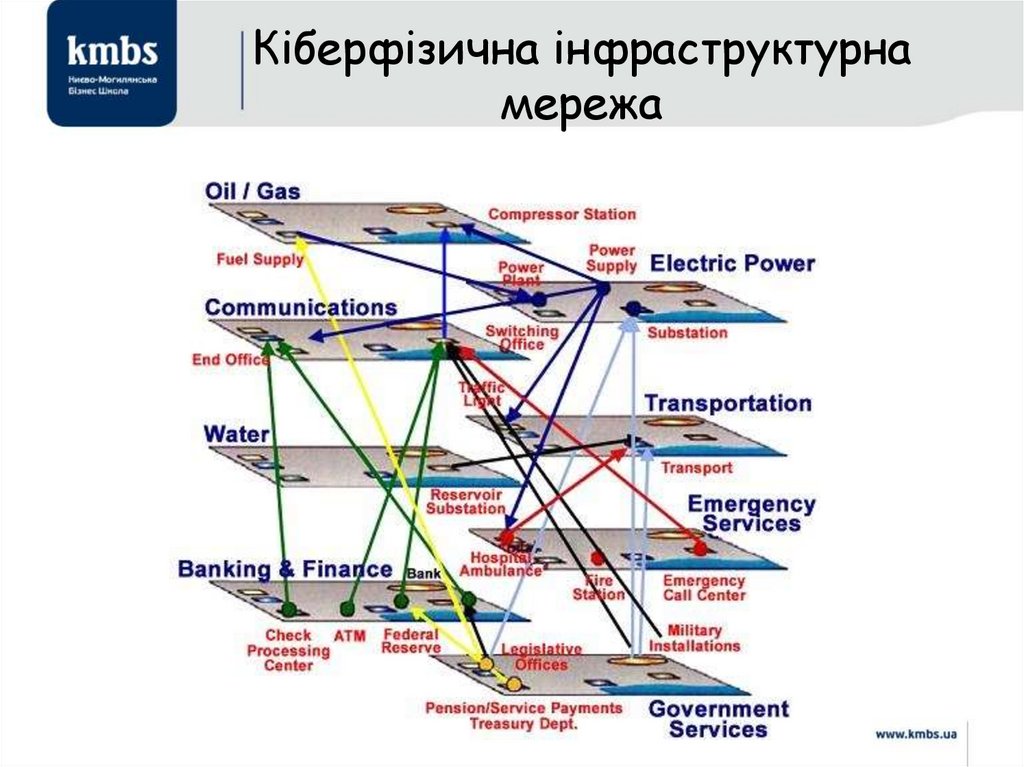
86. Кіберфізична інфраструктурна мережа
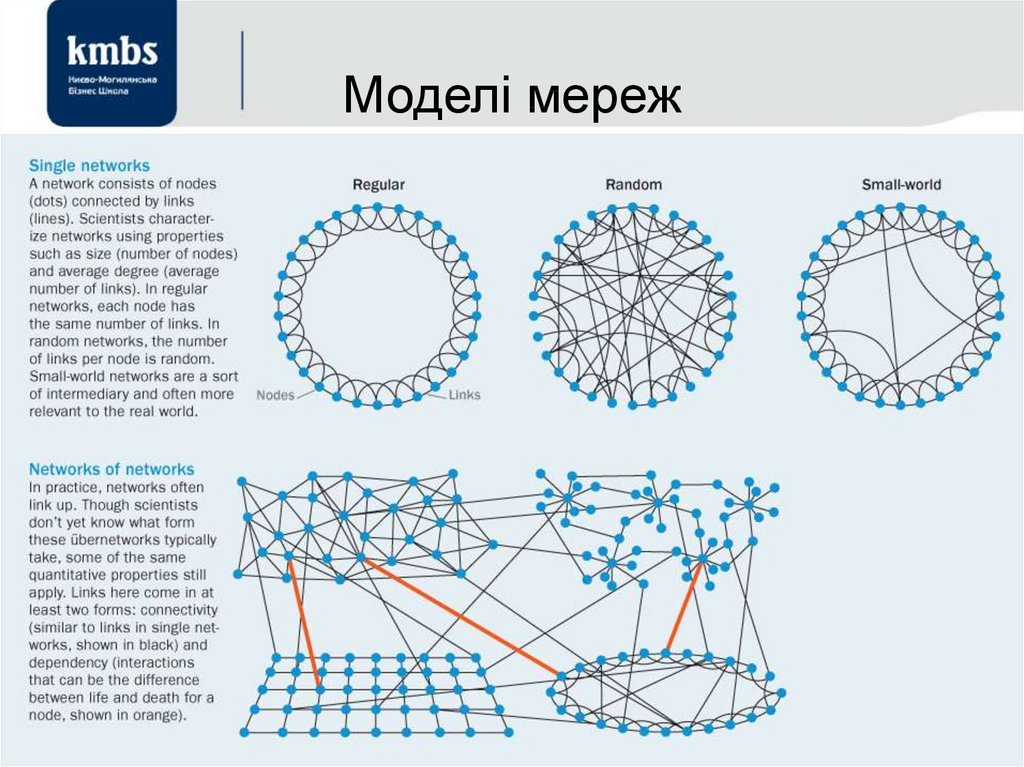
87. Моделі мереж
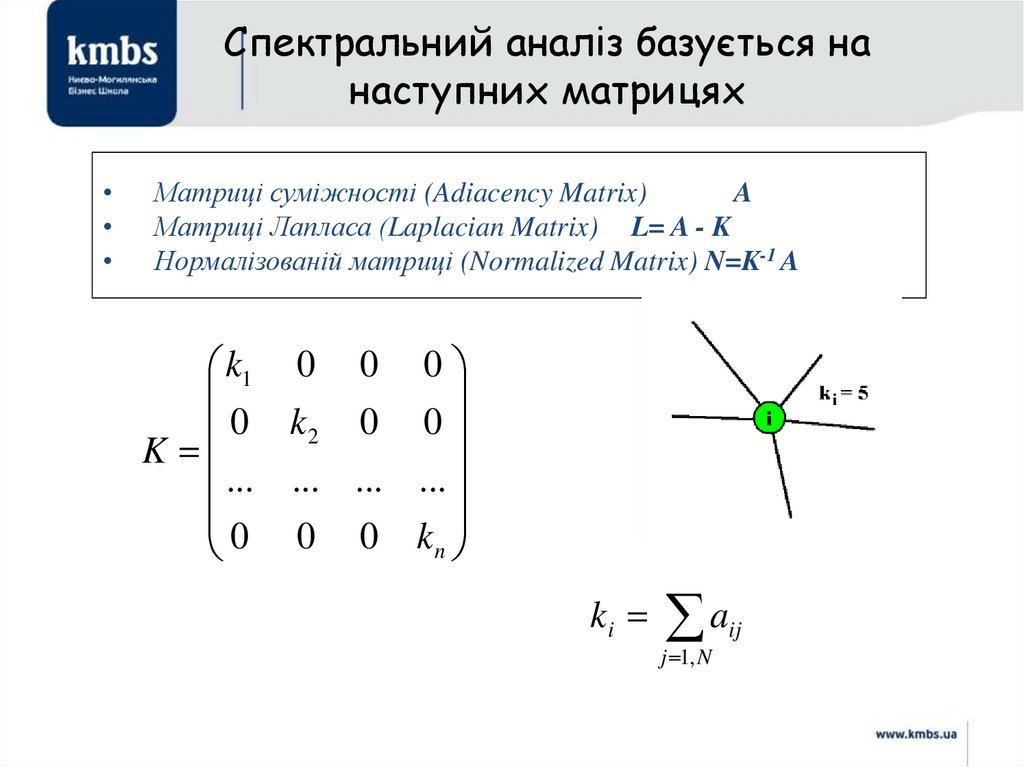
88. Спектральний аналіз базується на наступних матрицях
Матриці суміжності (Adiacency Matrix)
A
Матриці Лапласа (Laplacian Matrix) L= A - K
Нормалізованій матриці (Normalized Matrix) N=K-1 A
k1 0 0 0
0 k2 0 0
K
... ... ... ...
0 0 0 k
n
ki
a
j 1, N
ij
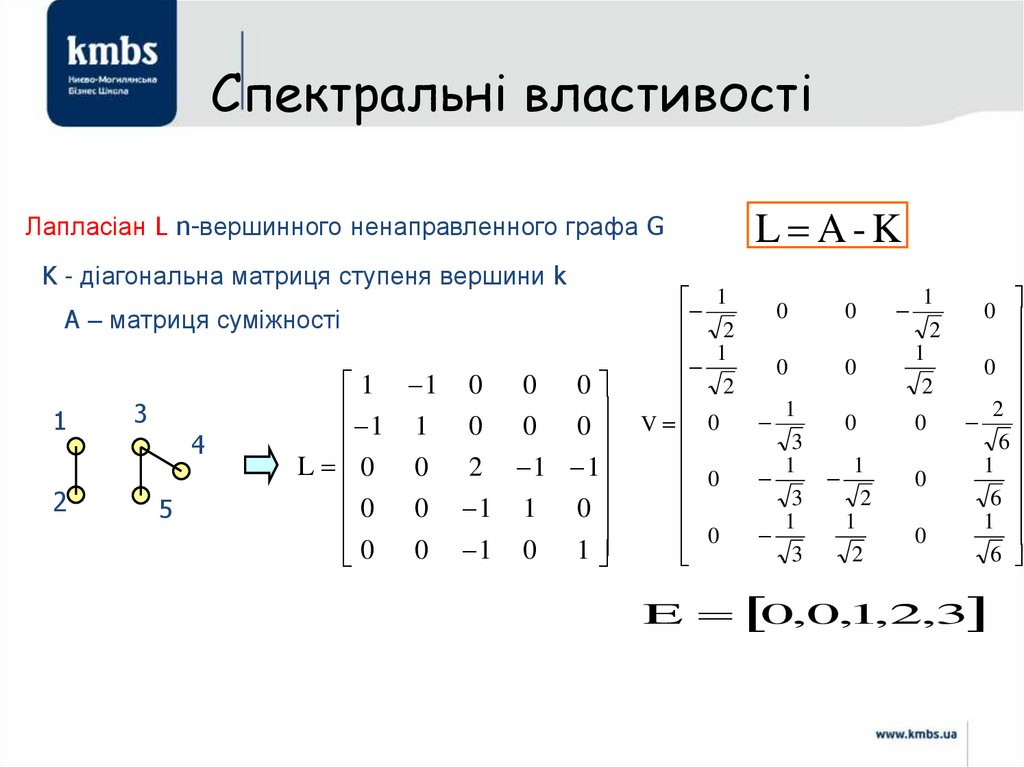
89. Спектральні властивості
Лапласіан L n-вершинного ненаправленного графа GK - діагональна матриця ступеня вершини k
A – матриця суміжності
1
2
3
4
5
1 1 0 0 0
1 1 0 0 0
L 0 0 2 1 1
0
0
1
1
0
0 0 1 0 1
1
2
1
2
V 0
0
0
L A-K
0
0
0
0
1
3
1
3
1
3
0
1
2
1
2
1
2
1
2
0
0
0
0
0
2
6
1
6
1
6
E 0,0,1,2,3
90.
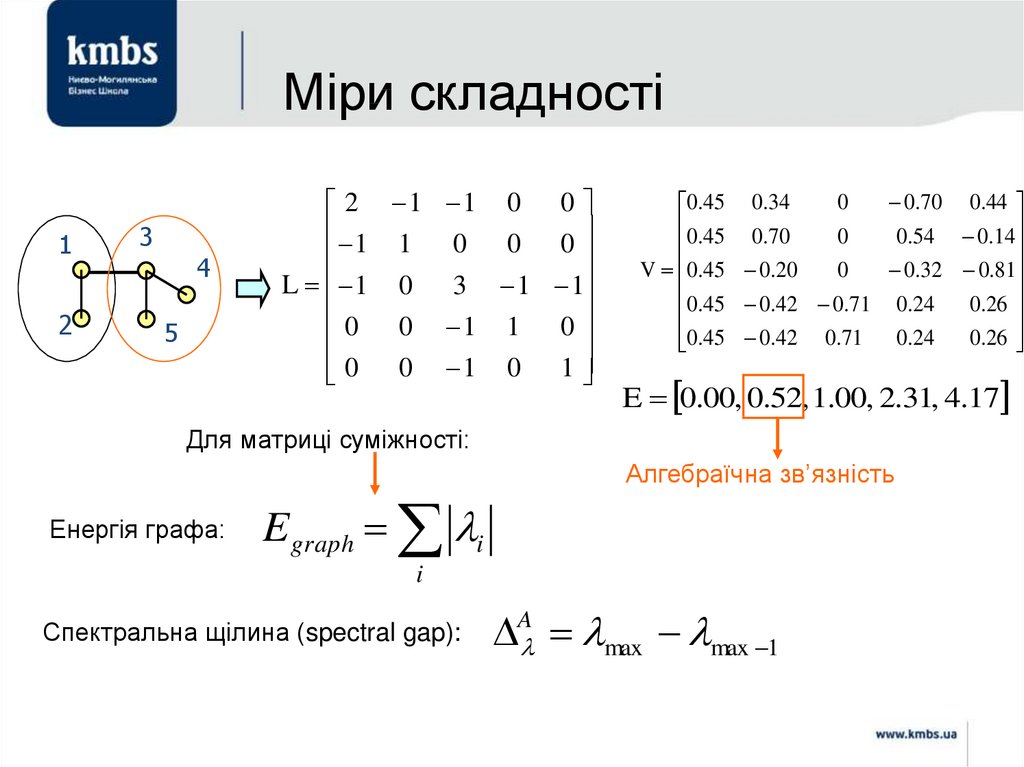
Міри складності1
2
3
4
5
2 1 1 0 0
1 1 0 0 0
L 1 0 3 1 1
0
0
1
1
0
0 0 1 0 1
0
0.70 0.44
0.45 0.34
0.45 0.70
0
0.54 0.14
V 0.45 0.20
0
0.32 0.81
0
.
45
0
.
42
0
.
71
0
.
24
0
.
26
0.45 0.42 0.71 0.24
0.26
E 0.00, 0.52, 1.00, 2.31, 4.17
Для матриці суміжності:
Енергія графа:
Egraph i
Алгебраїчна зв’язність
i
Спектральна щілина (spectral gap):
A max max 1
91.
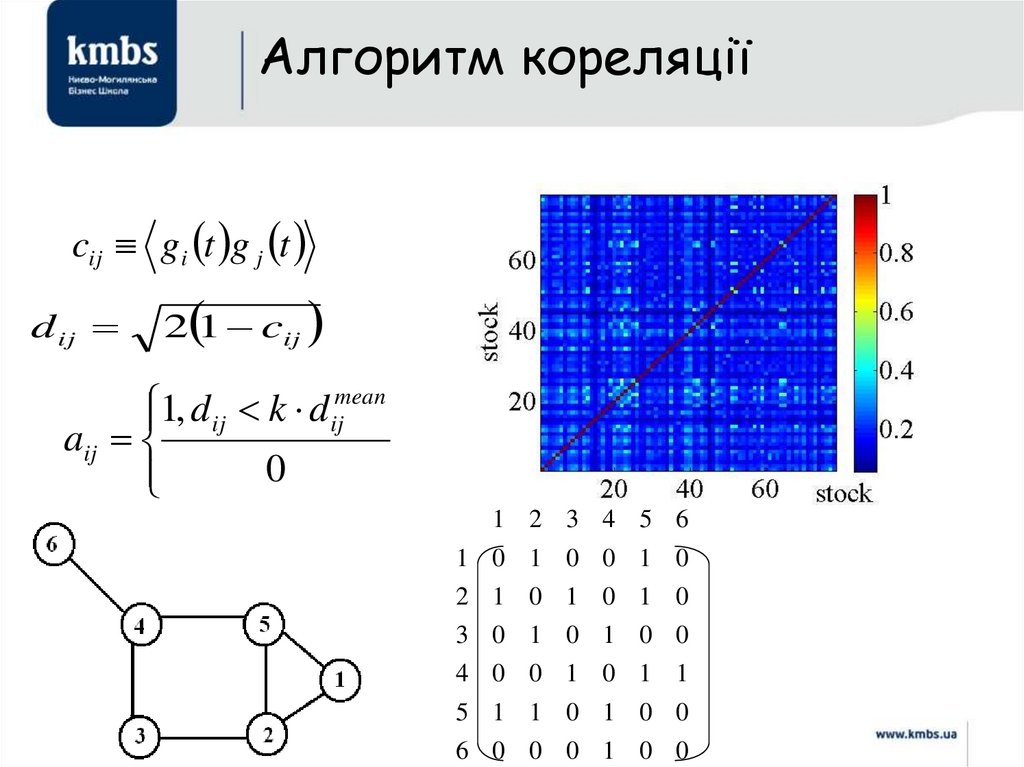
Алгоритм кореляціїcij g i t g j t
d ij
2 1 cij
mean
1
,
d
k
d
ij
ij
aij
0
1 2 3 4 5 6
1 0 1 0 0 1 0
2 1 0 1 0 1 0
3 0 1 0 1 0 0
4 0 0 1 0 1 1
5 1 1 0 1 0 0
6 0 0 0 1 0 0
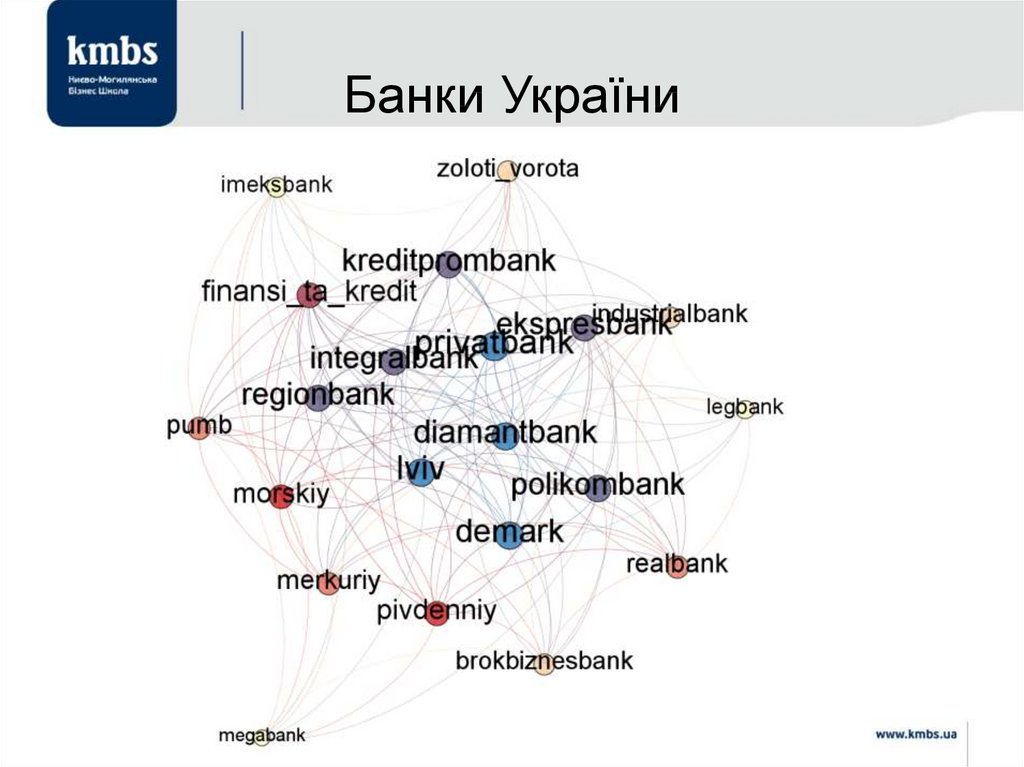
92. Банки України
93.
94. Віконна графодинаміка
95.
96. Графи видимості
97. Граф видимості
98. Мультиплексні мережі (multiplex networks) та мережі мереж (networks of networks)
99. Мультиплексні графи видимості
100. Мультиплексні графи видимості
101. Рекурентні мультимережі
102. Візуалізація: MuxViz
103. MuxViz: MVG мультиплексна мережа
104. Gephi: MVG мультиплексна мережа
105. MuxViz: рекурентна мультиплексна мережа
106. Gephi: рекурентна мультиплексна мережа
107. Мультиплексні міри
• Середнє перекриття зв’язків (average edge[ ]
overlap)
a
M (1
i
i
j i
j i
ij
0,
aij[ ]
)
• визначає число шарів, в яких присутній даний
зв'язок
• високі значення вказують на помітну
кореляцію у структурі сигналів
108. Мультиплексні міри
• Загальне(повне) перекриття (total overlap)O
aij aij
M
oi ki[ ]
• перекриття ст упіня вузла
• міжшарова взаємна інформація
I , P(k , k
[ ]
[ ]
[ ]
1
[ ]
P( k , k )
) log
P(k [ ] ) P(k [ ] )
109. Мультиплексні міри
• ент ропія мультиплексного ступіняM
[ ]
i
[ ]
i
k
k
Si
ln
oi
1 oi
• мультиплексний коефіцієнт участ і
k
M
1
Pi
M 1 1 oi
M
[ ]
i
2
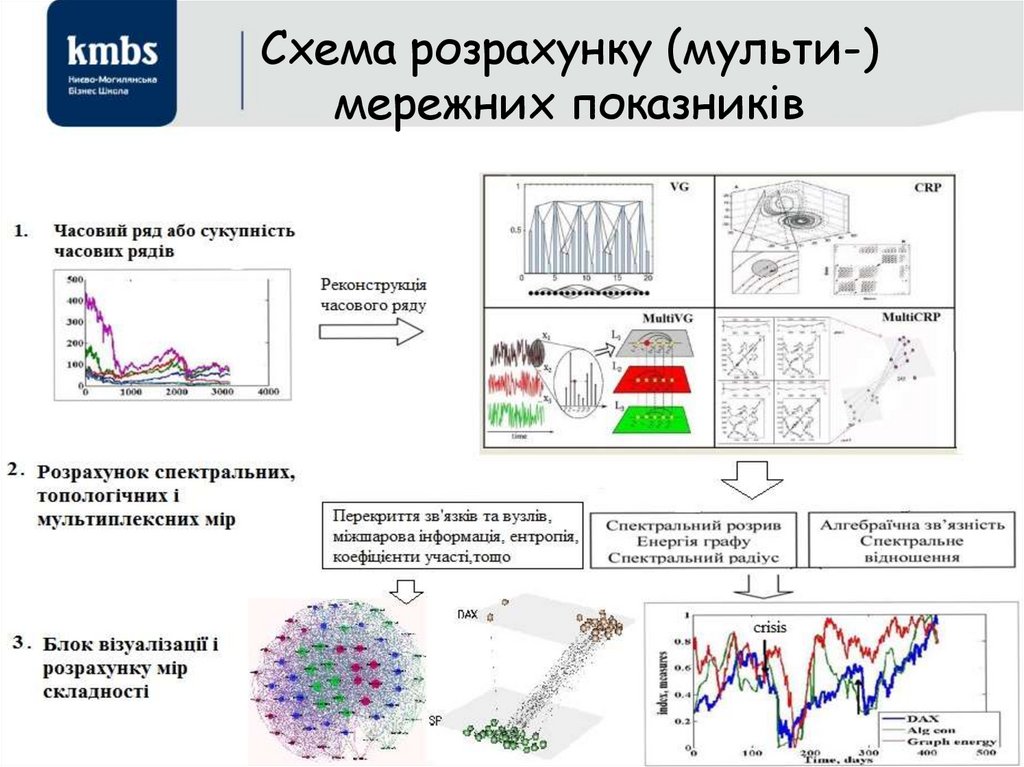
110. Схема розрахунку (мульти-) мережних показників
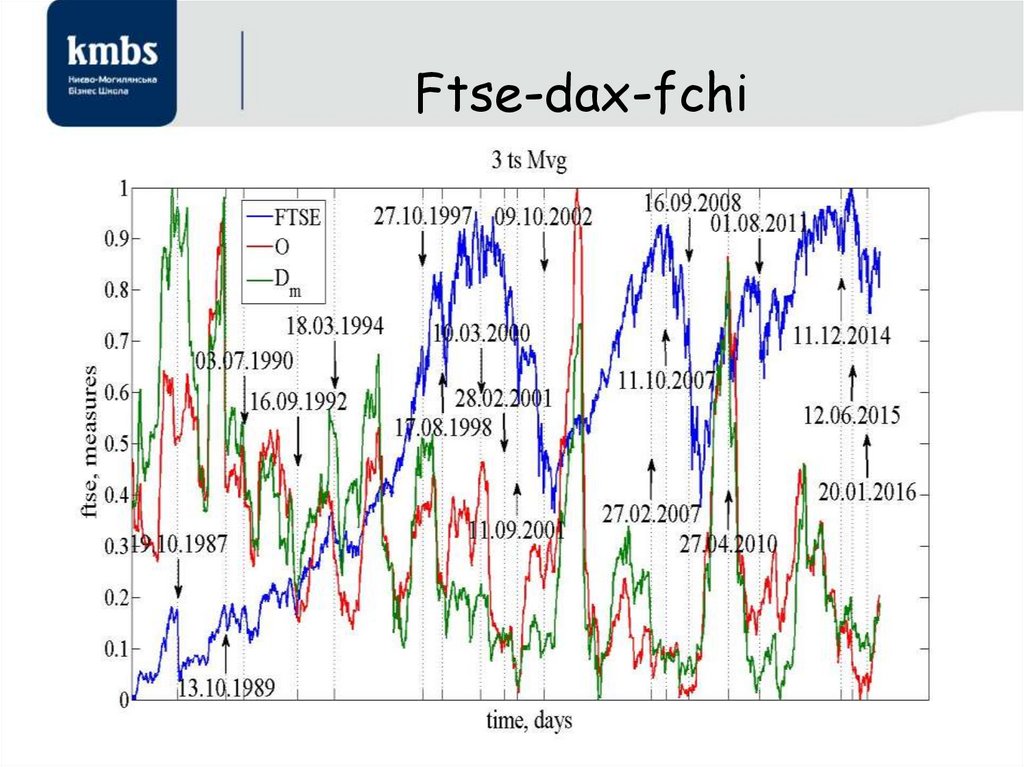
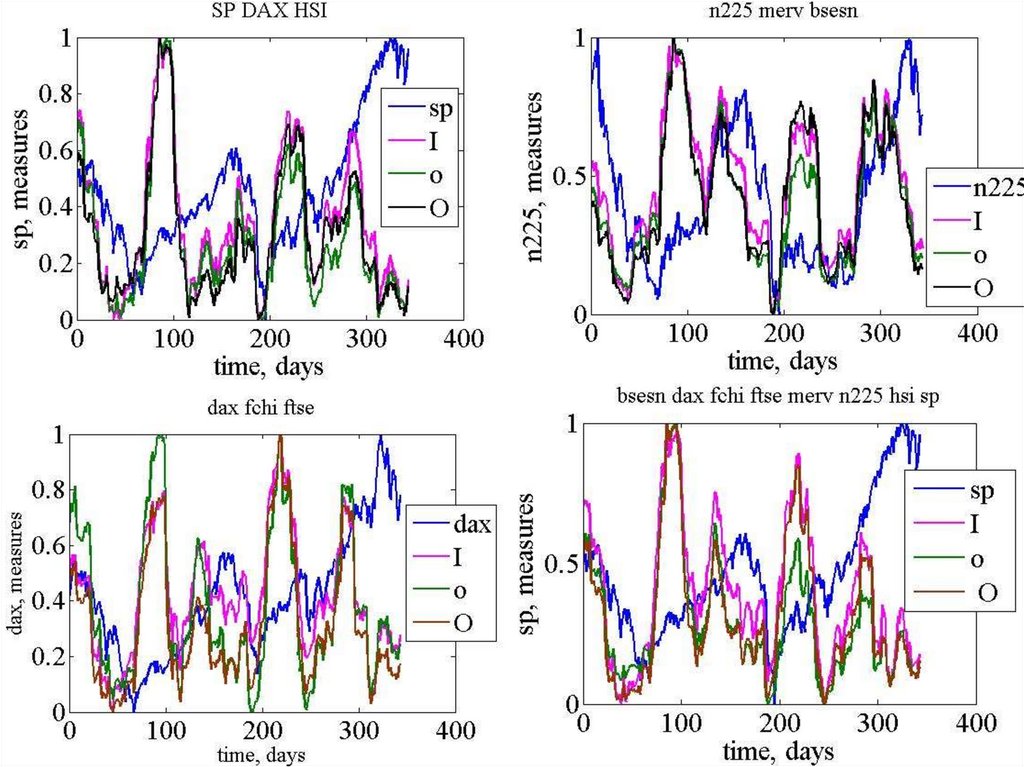
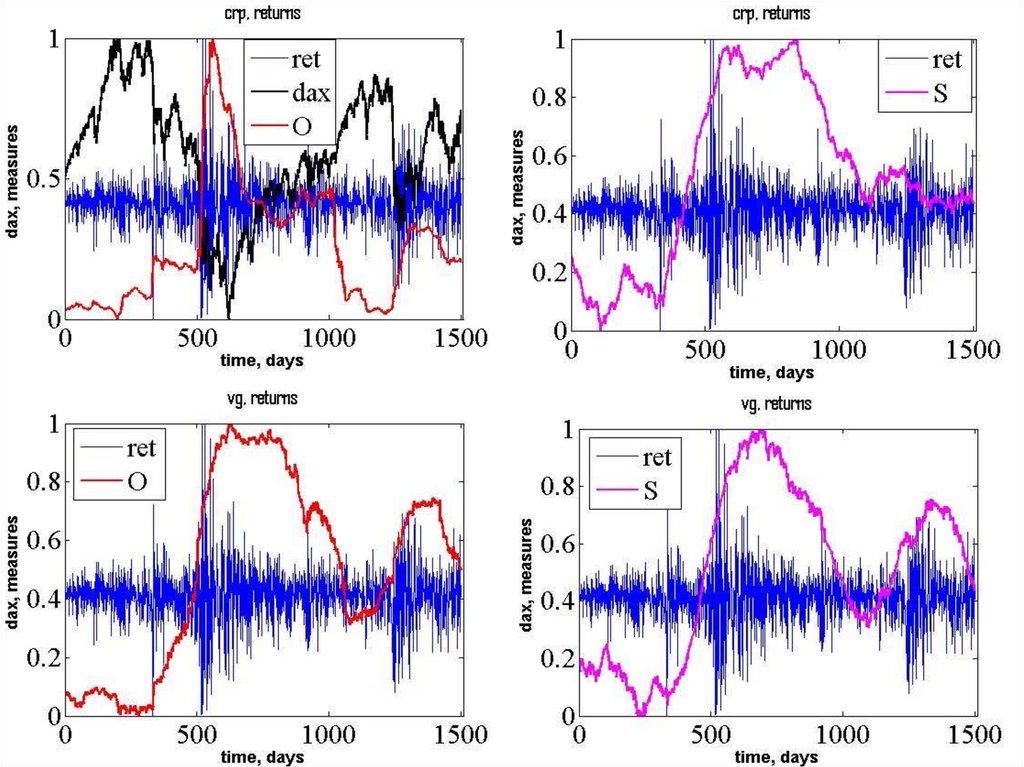
111. Ftse-dax-fchi
112.
113.
114.
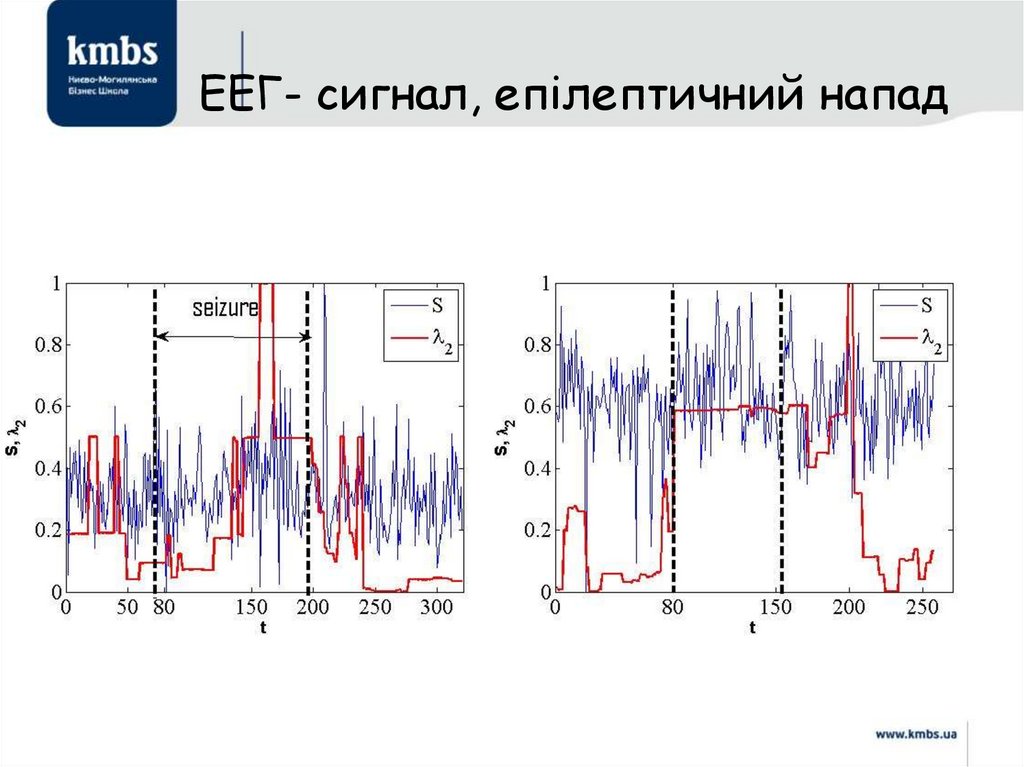
115. ЕЕГ- сигнал, епілептичний напад
116.
117.
118. ЕЕГ- сигнал, епілептичний напад
119.
vnsoloviev@rambler.ruvnsoloviev2016@gmail.com
Запитання?
Дякую за Вашу увагу
120.
Дякую за Вашу увагу!Питання
kafek.at.ua
vnsoloviev@rambler.ru
121.
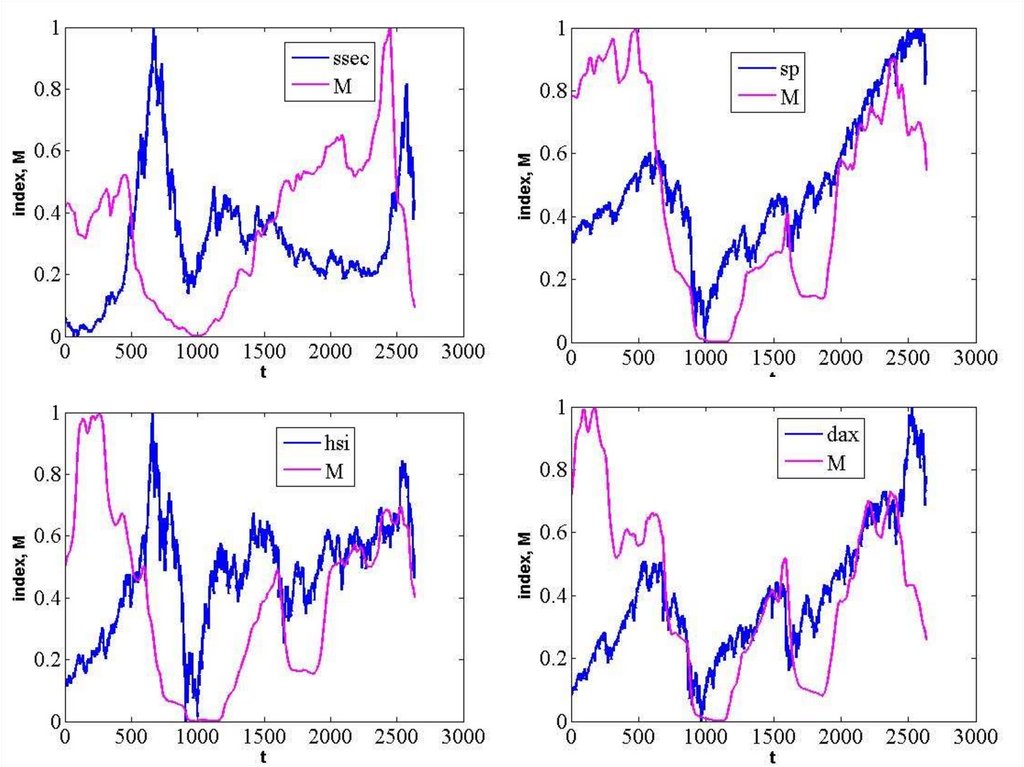
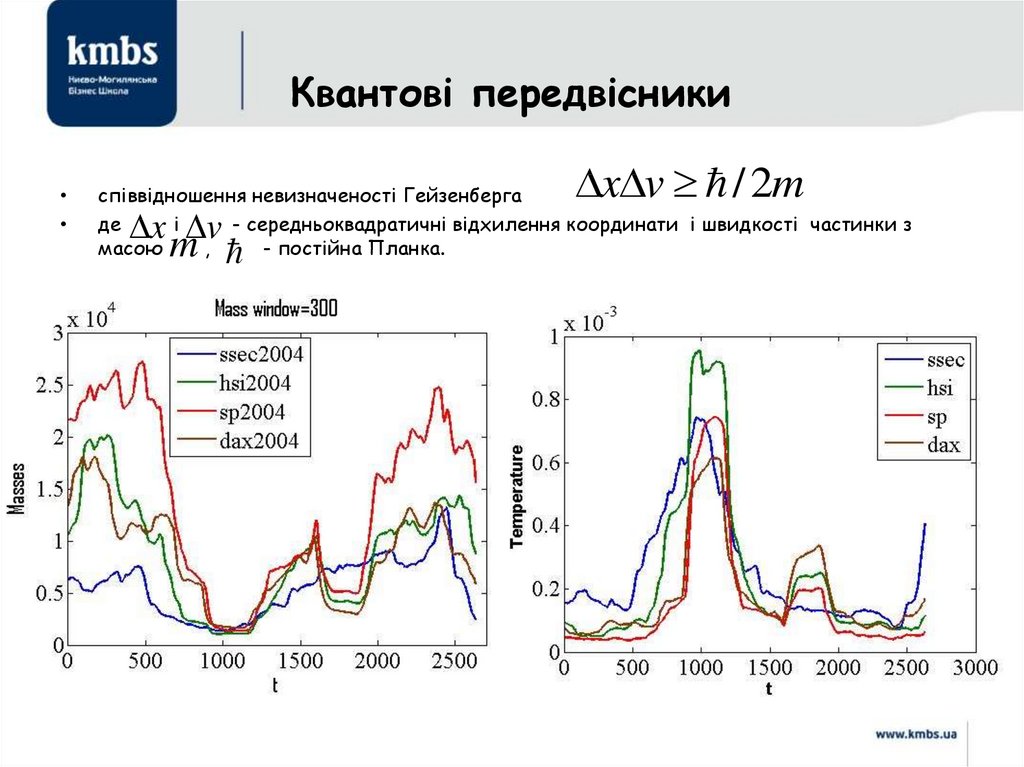
Формалізація принципу Гейзенбергау квантовій механіці
122.
123. Розподіл прибутковостей
124.
125.
126. Квантові передвісники
x v / 2m
співвідношення невизначеності Гейзенберга
де
і
- середньоквадратичні відхилення координати і швидкості частинки з
масою
,
- постійна Планка.
x v
m
127.
Довжина рецесії• Технічна рецесія: ВВП незмінний або
зменшується протягом двох кварталів
• Національне бюро економічних досліджень
(NBER): довжина проміжку між
екстремумами активності і пасивності ринку

















































 informatics
informatics








