Similar presentations:
Комп’ютерна логіка (частина 1)
1.
Комп’ютерна логіка (частина 1)Національний університет «Львівська політехніка»
Lviv Polytechnic National University
17 слайдів
2. Варіанти представлення бітів інформації на фізичному рівні
Lviv, CL.26.03.2014
Комп'ютерна логіка
2 2
3. Структурна схема процесу передачі або оброблення інформації
Джерелоінформації
Кодер
джерела
інформації
Кодер
захисту
інформації
Кодер
каналу /
обчислювача
Джерело
завад
Приймач
інформації
Lviv, CL.
26.03.2014
Декодер
приймача
інформації
Декодер
захисту
інформації
Декодер
каналу /
обчислювача
Комп'ютерна логіка
Модулятор
Канал /
обчислювач
Демодулятор
3 3
4. Функції кодера джерела інформації
Джерелоінформації
1.
Lviv, CL.
26.03.2014
Інформація
Кодер
джерела
інформації
Дані
Код
Кодер
захисту
інформації
Перетворення неелектричних величин в електричні
Перетворення інформації в дані - аналого-цифрове
перетворення
інформації
Усунення
надлишковості
інформації
Комп'ютерна логіка
4 4
5. Кодова таблиця КОИ-7
Lviv, CL.26.03.2014
Комп'ютерна логіка
5 5
6. Кодова таблиця KOI8-U
Lviv, CL.26.03.2014
Комп'ютерна логіка
6 6
7. Кодові таблиці:
Windows1251KOI8-U
KOI8-R
Lviv, CL.
26.03.2014
Комп'ютерна логіка
7 7
8. Послідовний та паралельний спосіб передачі інформації
Lviv, CL.26.03.2014
Комп'ютерна логіка
8 8
9. Кодер захисту інформації
Джерелоінформації
Кодер
джерела
інформації
Кодер
захисту
інформації
Кодер
каналу /
обчислювача
Джерело
завад
Приймач
інформації
Декодер
приймача
інформації
Декодер
захисту
інформації
Декодер
каналу /
обчислювача
Модулятор
Канал /
обчислювач
Демодулятор
Кодер захисту інформації необхідний для інформаційної безпеки
Lviv, CL.
26.03.2014
Комп'ютерна логіка
9 9
10. Перемішування
Lviv, CL.26.03.2014
Комп'ютерна логіка
10 10
11. Загальна схема криптографічної системи
Lviv, CL.26.03.2014
Комп'ютерна логіка
11 11
12.
Lviv, CL.26.03.2014
Комп'ютерна логіка
12 12
13. Семисегментний індикатор
Lviv, CL.26.03.2014
Комп'ютерна логіка
13 13
14.
аб
a
f
g
e
b
c
d
Выход
8
4
2
1
a
b
c
d
e
f
g
Символ
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
1
0
1
1
0
0
0
0
1
0
0
1
0
1
1
0
1
1
0
1
2
0
0
1
1
1
1
1
1
0
0
1
3
0
1
0
0
0
1
1
0
0
1
1
4
0
1
0
1
1
0
1
1
0
1
1
5
0
1
1
0
1
0
1
1
1
1
1
6
0
1
1
1
1
1
1
0
0
0
0
7
1
0
0
0
1
1
1
1
8
0
0
1
1
1
1
1
1
1
1
1
0
1
1
9
DI
Lviv, CL.
26.03.2014
Комп'ютерна логіка
14 14
15. Скручування карти Карно по вертикалі
Lviv, CL.26.03.2014
Комп'ютерна логіка
15 15
16. Позиційні системи числення
Lviv, CL.26.03.2014
Комп'ютерна логіка
16
17. Системи числення з іраціональними основами
Lviv, CL.26.03.2014
Комп'ютерна логіка
17
18. Система залишкових класів
Таблиця 1.5.1Чис- Залишки від Код
ло
ділення на
у
2 3 5 СЗК
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Lviv, CL.
26.03.2014
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
0
1
2
3
4
0
1
2
3
4
0
1
2
3
4
0
1
2
3
4
0
1
2
3
4
0
1
2
3
4
0
0,0,0
1,1,1
0,2,2
1,0,3
0,1,4
1,2,0
0,0,1
1,1,2
0,2,3
1,0,4
0,1,0
1,2,1
0,0,2
1,1,3
0,2,4
1,0,0
0,1,1
1,2,2
0,0,3
1,1,4
0,2,0
1,0,1
0,1,2
1,2,3
0,0,4
1,1,0
0,2,1
1,0,2
0,1,3
1,2,4
0,0,0
Комп'ютерна логіка
18
19. Контроль на парність / непарність
Lviv, CL.26.03.2014
Комп'ютерна логіка
19
20. Код Хеммінга
ii
F
k
==
Лінія зв’язку
F
Код
помилкового
k біта
F – вузол формування кода Геммінга
K1 = i3 i5 i7 i9 i11 i13 i15
K2 = i3 i6 i7 i10 i11 i14 i15
K4 = i5 i6 i7 i12 i13 i14 i15
K8 = i9 i10 i11 i12 i13 i14 i15
K k = (K8 k8)(K4 k4)(K2 k2)(K1 k1)
Lviv, CL.
26.03.2014
Комп'ютерна логіка
20
21. Код Хеммінга
Таблиця 1.6.2n1
n2
n3
n4
n5
n6
n7
n8
n9
n10
n11
n12
n13
n14
n15
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
k1
k2
i3
k4
i5
i6
i7
k8
i9
i10
i11
i12
i13
i14
i15
k1 = i3 i5 i7 i9 i11 i13 i15;
k2 = i3 i6 i7 i10 i11 i14 i15;
k4 = i5 i6 i7 i12 i13 i14 i15;
k8 = i9 i10 i11 i12 i13 i14 i15;
Lviv, CL.
26.03.2014
Комп'ютерна логіка
21
22. SerDes
Lviv, CL.26.03.2014
Комп'ютерна логіка
22
23. Сусідній код (код Грея)
Lviv, CL.26.03.2014
Комп'ютерна логіка
23
24. Сусідні коди
Lviv, CL.26.03.2014
Комп'ютерна логіка
24
25. Властивості алгоритму http://uk.wikipedia.org/wiki/Алгоритм
Скінченність
– алгоритм має завжди завершуватись після виконання скінченної кількості кроків. Процедуру,
яка має решту характеристик алгоритму, без, можливо, скінченності, називають методом
обчислень.
Дискретність
– процес, що визначається алгоритмом, можна розчленувати (розділити) на окремі елементарні
етапи (кроки), кожен з яких називається кроком алгоритмічного процесу чи алгоритму.[31]
Визначеність
– кожен крок алгоритму має бути точно визначений. Дії, які необхідно здійснити, повинні бути
чітко та недвозначно визначені для кожного можливого випадку.
Вхідні дані
– алгоритм має деяку кількість (можливо, нульову) вхідних даних, тобто, величин, заданих до
початку його роботи або значення яких визначають під час роботи алгоритму.
Вихідні дані
– алгоритм має одне або декілька вихідних даних, тобто, величин, що мають досить визначений
зв'язок із вхідними даними.
Ефективність
– Алгоритм вважають ефективним, якщо всі його оператори досить прості для того, аби їх можна
було точно виконати за скінченний проміжок часу з допомогою олівця та аркушу паперу.
Масовість
– властивість алгоритму, яка полягає в тому, що алгоритм повинен забезпечувати розв'язання
будь-якої задачі з класу однотипних задач за будь-якими вхідними даними, що належать до
області застосування алгоритму.
Lviv, CL.
26.03.2014
Комп'ютерна логіка
25
26. Представлення алгоритмів http://uk.wikipedia.org/wiki/Алгоритм
• Блок-схема алгоритму визначеннядієвідміни в дієслові.• У процесі розробки алгоритму можуть використовуватись
різні способи його опису, які відрізняються за простотою,
наочністю, компактністю, мірою формалізації, орієнтації
на машинну реалізацію тощо[31].
• Форми запису алгоритму:
• словесна або вербальна (мовна, формульно-словесна);
• псевдокод (формальні алгоритмічні мови);
• схемна:
– структурограми (схеми Нассі-Шнайдермана);
– графічна (блок-схема, виконується за вимогами стандарту).
Lviv, CL.
26.03.2014
Комп'ютерна логіка
26
27. Блок-схема алгоритму
Lviv, CL.26.03.2014
Комп'ютерна логіка
27
28. Граф автомата Мура та позначки у вершинах графа з двійковим кодуванням станів
Lviv, CL.26.03.2014
Комп'ютерна логіка
28
29. Граф автомата
Lviv, CL.26.03.2014
Комп'ютерна логіка
29
30. Блок-схема алгоритму та граф автомата
Lviv, CL.26.03.2014
Комп'ютерна логіка
30
31. Таблиці переходів та виходів автомата Мура з двійковим кодуванням станів
№0
1
2
3
4
5
6
7
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
1
0
a2
a3
1
1
1
1
a3
Lviv, CL.
26.03.2014
x
0
1
0
1
0
1
0
1
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a0
0
0
1
0
a2
1
0
a2
1
1
a3
1
1
a3
a0
0
0
0
0
a0
Сигнали
збудження
тригерів
D1
D0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
0
Комп'ютерна логіка
№
0
1
2
3
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
0
0
a0
0
1
a1
1
0
a2
1
1
a3
Вихідні
сигнали
автомата
y
1
1
0
0
31
32. Функціональна схема автомата Мура
Lviv, CL.26.03.2014
Комп'ютерна логіка
32
33. Часова діаграма роботи автомата Мура
Lviv, CL.26.03.2014
Комп'ютерна логіка
33
34. Опис автомата формальною мовою
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_arith.all;
use IEEE.std_logic_unsigned.all;
entity fsm1 is
port (
c: in STD_LOGIC;
x: in STD_LOGIC;
y: out STD_LOGIC);
end fsm1;
architecture fsm1_arch of fsm1 is
attribute enum_encoding: string;
type State_type is ( a0, a1, a2, a3);
attribute enum_encoding of State_type: type is
"00 " &
"01 " &
"10 " &
"11" ;
signal State: State_type;
attribute state_vector: string;
attribute state_vector of fsm1_arch: architecture is "State";
begin
State_machine: process (c)
begin
if rising_edge(c) then
case State is
-- a0
-- a1
-- a2
-- a3
when a0 =>
if x='1' then
State <= a0;
elsif x='0' then
State <= a1;
end if;
when a1 =>
State <= a2;
when a2 =>
State <= a3;
when a3 =>
State <= a0;
when others =>
null;
end case;
end if;
end process;
y_assignment:
y <= '1' when (State = a0) else
'1' when (State = a1) else
'0';
end fsm1_arch;
Lviv, CL.
26.03.2014
Комп'ютерна логіка
34
35. Теза Черча
Теза Черча• Теза Черча — твердження, згідно з яким,
клас алгоритмічно-обчислюваних функцій збігається з
класом частково-рекурсивних функцій, функцій
обчислюваних за Тюрінгом та інших формальних
уточнень інтуїтивного поняттяалгоритм. З неї випливає,
що якщо функція належить до класу певної формалізації
алгоритмічно-обчислюваної функції, то вона є
алгоритмічно-обчислювана. Теза не доводиться. А
еквівалентність класів формалізмів підлягає доведенню,
що і було зроблено. Названа на честь американського
математика Алонзо Черча.
• Також виділяють тезу Черча-Тюрінга.
• http://uk.wikipedia.org/wiki/Теза_Черча
Lviv, CL.
26.03.2014
Комп'ютерна логіка
35
36. Формальне визначення
Рекурсивні функції
Машина Тюринга
Нормальні алгорифми Маркова
Скінченні автомати
• http://uk.wikipedia.org/wiki/Алгоритм
Lviv, CL.
26.03.2014
Комп'ютерна логіка
36
37. Загальна структурна схема цифрового автомата
КСхПА
δ
{X}
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
Lviv, CL.
26.03.2014
λ
{A}
{Y}
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Комп'ютерна логіка
37
38. Структурна схема автомата Мура
iКСх
δ
{X} j
ПА
i
{A}
λ
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
j – кількість вхідних сигналів
k – кількість вихідних сигналів
Lviv, CL.
26.03.2014
КСх
k
{Y}
2
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
i – розрядність зворотного зв’язку,
кількість тригерів у пам’яті
автомата
Комп'ютерна логіка
38
39. Структурна схема автомата Мілі
КСх{X}
δ
ПА
{A}
КСх
λ
1
{Y}
2
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
Lviv, CL.
26.03.2014
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Комп'ютерна логіка
39
40. Змінні, набори і функції алгебри логіки
кількістьзмінних
0
кількість
наборів
1
кількість
ФАЛ
2
1
2
3
2
4
8
4
16
256
4
…
n
16
…
65536
…
n
2
2
2n
n
n 1
2
An 2 C n
Lviv, CL.
26.03.2014
n 2
An 1 C n
h!
C h l!(h l )!
l
1
...
Cn
An 2
Комп'ютерна логіка
A A
1
0
40
41. ФАЛ0, ФАЛ1
f0f1
a
f0(a)
f1(a)
f2(a)
f3(a)
0
1
0
1
Фактично є
0
0
ФАЛ0
0
1
1
0
1
1
ФАЛ0
Lviv, CL.
26.03.2014
Комп'ютерна логіка
41
42. Повторювач, інвертор
a1
a
a
a
a
а
a
1
а
a
(a=1)
б
a
a
( a 0)
a
б
Інверсія, інвертор, НЕ
Lviv, CL.
26.03.2014
Комп'ютерна логіка
42
43. Функції алгебри логіки двох змінних
Lviv, CL.26.03.2014
Комп'ютерна логіка
43
44. Кон'юнкція (від латинського conjunctio – сполучник, зв'язок), логічне множення або функція І (И, AND)
a ba
a
&
b
а
ab
b
Зафарбована область - a & b
a
b
ab
б
Кон'юнкція, кон’юнктор, І
Lviv, CL.
26.03.2014
Комп'ютерна логіка
44
45. Диз'юнкція (від латинського disjunctio - роз'єднання), логічне додавання або функція АБО (ИЛИ, OR)
aba
a
1
b
а
a b
a
b
a b
b
Зафарбована область - a v b
б
Диз'юнкція, диз’юнктор,
АБО
Lviv, CL.
26.03.2014
Комп'ютерна логіка
45
46. Функція (штрих) Шеффера або функція І-НЕ (NOT AND, NAND, И-НЕ)
aba
b
Зафарбована область - ab
a
&
b
а
Lviv, CL.
26.03.2014
ab
a
b
ab
б
Комп'ютерна логіка
46
47. Функція (стрілка) Пірса (Вебба) або функція АБО-НЕ (ИЛИ-НЕ, NOT OR, NOR)
a ba
a
1
b
а
Lviv, CL.
26.03.2014
a b
a
Зафарбована область - a b
a b
b
b
б
Комп'ютерна логіка
47
48. Виключне АБО (XOR)
aa
=1 a b
b
а
Lviv, CL.
26.03.2014
a
b
a b
b
Зафарбована область - a b
б
Комп'ютерна логіка
48
49. Рівнозначність (еквівалентність)
aa
b
b
= = a b
Зафарбована область - a b
а
Lviv, CL.
26.03.2014
Комп'ютерна логіка
49
50. Імплікація (пряма)
xa
b
а
Lviv, CL.
26.03.2014
a
b
б
x
a
b
x b
a
в
г
Комп'ютерна логіка
50
51. Імплікація зворотна
xb
a
а
Lviv, CL.
26.03.2014
b
a
б
x
b
a
x a
b
в
г
Комп'ютерна логіка
51
52. Заперечення імплікації (прямої)
Заперечення зворотної імплікаціїLviv, CL.
26.03.2014
Комп'ютерна логіка
52
53. Властивості ФАЛ, монобазиси, базиси
0 1 Л М Сх0 0 0 1 1 Назва ФАЛ
х1 0 1 0 1
* *
f1
0 0 0 1 кон'юнкція, І
*
f7
0 1 1 1 диз'юнкція, АБО х0 v х1
1 1 0 0 інверсія х0
x0
Lviv, CL.
26.03.2014
x
0
x
1
1
1
x
x
x
0
0
0
x
x
x
1
1
x
0
x
1
1
1
x
x
x
1
1
x
1
0
x
x
x
x
x
x
1
x
0
x
1
1
1
x
x
x
1
1
1
0
x
x
0
1
0
0
0
0
0
0
x
x
x
x
x
x
x
Комп'ютерна логіка
1
x
1
x
0
0
x
x
1
1
x
x
1
1
1
x
x
x
1
0
0
x
1
0
0
0
*
1
x
1
0
x
x
1
*
1
* *
x
0
x
1
1
0 1 Л М С
*
1
x
x
Властивості
0
x
1
1
1
x
x
f12
0
x
x
* * *
1
1
0
x
x
x
x
0 1 1 1 диз'юнкція, АБО х0 v х1
1 1 0 0 інверсія х0
x0
x
f7
*
Вираз
ФАЛ
x
х0 0 0 1 1 Назва ФАЛ
х1 0 1 0 1
x
x0 x1
*
Базис АБО, НЕ
0
*
*
Властивості
x0
x
f12 1 1 0 0 інверсія х0
0
x
x
x
x
x
* *
x
х0 ·х1
x
0 0 0 1 кон'юнкція, І
0 1 Л М С
x
f1
Вираз
ФАЛ
0
*
*
*
* * *
1
*
х0 0 0 1 1 Назва ФАЛ
х1 0 1 0 1
x
f14 1 1 1 0 І-НЕ (Шефера)
f15 1 1 1 1 константа "1"
1
x0
f12 1 1 0 0 інверсія х0
f13 1 1 0 1 імплікація пряма x0 x1
f15 1 1 1 1 константа "1"
x0 x1
x0 x1 x0 x1 *
x
f11
x1
0 1 1 0 сума за mod 2
*
Базис І, НЕ
* *
*
f6
x
f10
1 0 1 0 інверсія х1
1 0 1 1 імплікація звор.
x0 x1 x0 x1
х0 ·х1
1
1 0 0 1 рівнозначність
*
* *
0 0 0 1 кон'юнкція, І
0
f9
* *
Властивості
f1
0
f8
0 1 1 1 диз'юнкція, АБО х0 v х1
1 0 0 0 АБО-НЕ (Пірса) x0 x1
*
0 1 Л М С
0
f7
*
Вираз
ФАЛ
0 1 1 0 сума за mod 2
* * * * *
х1
*
x0 x1 x0 x1 *
х0 0 0 1 1 Назва ФАЛ
х1 0 1 0 1
x
f6
f4
*
Властивості
Базис Жегалкіна
0
f5
0 1 0 0 заборона по х0
0 1 0 1 х1
0
* * * * *
0
х0
x0 x1
f3
f12
*
x
x0 x1
*
0
f2
0 0 1 0 заборона по х1
0 0 1 1 х0
* *
0
* *
x
х0 ·х1
*
x
0 0 0 1 кон'юнкція, І
* *
1
f1
х0 ·х1
*
0
x
0 0 0 0 константа "0"
0 1 Л М С
f0
Вираз
ФАЛ
x
Властивості
Базис Буля
Вираз
ФАЛ
0
х0 0 0 1 1 Назва ФАЛ
х1 0 1 0 1
53
*
54. Деякі ФАЛ3
Lviv, CL.26.03.2014
Комп'ютерна логіка
54
55. Сингулярні таблиці
Lviv, CL.26.03.2014
Комп'ютерна логіка
55
56.
Комп’ютерна логіка (частина 2)Національний університет «Львівська політехніка»
Lviv Polytechnic National University
Lviv, CL.
26.03.2014
Комп'ютерна логіка
56
слайдів
57. Виконання навчального плану
Здана курсова робота
Виконано програму практичних занять
Написано усі 16 лекційних контрольних робіт
Дано відповідь на усі 10 питань 1-го модульного
контролю
• Дано відповідь на усі 10 питань 2-го модульного
контролю
• Є конспект лекцій (приблизно 5 сторінок на
лекцію)
Lviv, CL.
26.03.2014
Комп'ютерна логіка
57
58. Державна оцінка (іспит)
• 1. Автоматом за результатами модульнихконтролів
• 2. Оцінка на іспиті
• 3а. Оцінка на комісії
– або
• 3б. Оцінка за результатами повторного
вивчення курсу
Lviv, CL.
26.03.2014
Комп'ютерна логіка
58
59. Стандартні вимоги до відповідей на модулях та іспитах
• Повинна бути дана відповідь на усі питаннябілету
• Під час підготовки до відповіді нічим не
можна користуватися
• Під час підготовки до відповіді ні с ким не
можна перемовлятися та обмінюватися
інформацією
• Для допуску до іспиту потрібно виконати
навчальний план
Lviv, CL.
26.03.2014
Комп'ютерна логіка
59
60. Полегшені умови до 1-го модуля
• Білет на 1-ий модуль видається достроково за умови– До 7-го навчального тижня здано задачі 3-ої частини курсової
роботи і отримано за них більше 30 балів
– За практичні заняття отримано більше 10 балів (з 15)
– Написано усі лекційні контрольні роботи на дану дату
– Правильно дано відповіді на усі питання тестів до 1-ої частини
Комп’ютерної логіки (1-ий курс) у ВНС
– Є конспект лекцій (приблизно 5 сторінок на лекцію)
– Здано академрізницю (в кого вона є)
– Складено іспит за повторне вивчення 1-ої частини Комп’ютерної
логіки (кому це потрібно)
• Під час підготовки до відповіді дозволяється
користуватися чим завгодно
• Повинна бути дана відповідь на усі питання білету
Lviv, CL.
26.03.2014
Комп'ютерна логіка
60
61. Полегшені умови до 2-го модуля, іспту, комісії та повторки
• Білет на 2-ий модуль видається достроково за умови– До 15-го навчального тижня здано усі задачі курсової роботи і
отримано за них більше 60 балів
– В сумі за практичні заняття отримано більше 20 балів (з 30)
– Написано усі лекційні контрольні роботи на дану дату
– Правильно дано відповіді на усі питання тестів до 2-ої частини
Комп’ютерної логіки (2-ий курс) у ВНС
– Є конспект лекцій (приблизно 5 сторінок на лекцію)
– Здано академрізницю (в кого вона є)
– Складено іспит за повторне вивчення 1-ої частини Комп’ютерної
логіки (кому це потрібно)
• Під час підготовки до відповіді дозволяється
користуватися чим завгодно
• Повинна бути дана відповідь на усі питання білету
Lviv, CL.
26.03.2014
Комп'ютерна логіка
61
62. Оцінювання відповідей при стандартному підході
Оцінка Оцінка практичні Оцінка ЛекційніКР Оцінка білетДля модулів:
Оцінка 50; Оцінка практичні 15; Оцінка ЛекційніКР 5; Оцінка білет 30
Для іспиту:
Оцінка 100; Оцінка практичні 30; Оцінка ЛекційніКР 10; Оцінка білет 60
Lviv, CL.
26.03.2014
Комп'ютерна логіка
62
63. Оцінювання відповідей при полегшеному підході
Оцінка Оцінка практичніОцінка ЛекційніКР
5
Оцінка білет * 7
*
6
Для модулів:
Оцінка 50; Оцінка практичні 15; Оцінка ЛекційніКР 5; Оцінка білет 30
Для іспиту:
Оцінка 100; Оцінка практичні 30; Оцінка ЛекційніКР 10; Оцінка білет 60
Lviv, CL.
26.03.2014
Комп'ютерна логіка
63
64. Основні правила виконання операцій у базисі Буля
a vb = b vaab = ba
a v (b v c ) = (a v b ) v c
a (bc ) = (ab )c
Закон комутативності
Закон асоціативності
Закон дистрибутивності
a v bc = (a v b )(a v c )
a = 1, якщо a 0;
Якщо a = 0, то`a = 1
0 v 0 = 0;
0 v1 = 1
1 v1 = 1
`0 = 1
a v0 = a
a v1 = 1
a va = a
a a
a v`a = 1
a b c a b c
Lviv, CL.
26.03.2014
a (b v c ) = ab v ac
a = 0, якщо a 1;
Якщо a = 1, то`a = 0
0 0 = 0;
1 0 = 0;
1 1 = 1;
`1 = 0;
a 1 = a;
a 0 = 0;
a a = a;
a a
`a a = 0;
abc a b c
a (a v b ) = a
a v`ab = a v b
a v ab = a
a (`a v b ) = ab
ab v`ab = b (a v`a ) = b
(a v b )( `a v b ) = b
Комп'ютерна логіка
Правило де Моргана
(закон поглинання)
(закон поглинання)
(закон склеювання)
64
65. Аналітичне представлення функцій алгебри логіки Досконалі нормальні форми
ДДНФ:f(a, b, c) = F0(0, 0, 0) F3(0, 1, 1) F4(1, 0, 0) =`a `b `c `a b c a `b `c.
ДКНФ:
f(a, b, c) = Ф1(0,0,1)& Ф2(0, 1, 0) & Ф5(1, 0, 1) & Ф6(1, 1, 0) & Ф7(1, 1, 1) =
= (a b `c)&(a `b c)&(`a b `c)&(`a `b c) &(`a `b `c).
Lviv, CL.
26.03.2014
Комп'ютерна логіка
65
66. Базис Буля
ab
a
&
a b ... z
...
z
елемент І (AND),
кон'юнктор
Lviv, CL.
26.03.2014
b
1
a b ... z
...
z
елемент АБО (OR),
диз'юнктор
Комп'ютерна логіка
a
1
a
елемент НЕ (NOT),
інвертор
66
67. Кон'юнкція (від латинського conjunctio – сполучник, зв'язок), логічне множення або функція І (И, AND)
a ba
a
&
b
а
ab
b
Зафарбована область - a & b
a
b
ab
б
Кон'юнкція, кон’юнктор, І
Lviv, CL.
26.03.2014
Комп'ютерна логіка
67
68. Диз'юнкція (від латинського disjunctio - роз'єднання), логічне додавання або функція АБО (ИЛИ, OR)
aba
a
1
b
а
a b
a
b
a b
b
Зафарбована область - a v b
б
Диз'юнкція, диз’юнктор,
АБО
Lviv, CL.
26.03.2014
Комп'ютерна логіка
68
69. Повторювач, інвертор
a1
a
a
a
a
а
a
1
а
a
(a=1)
б
a
a
( a 0)
a
б
Інверсія, інвертор, НЕ
Lviv, CL.
26.03.2014
Комп'ютерна логіка
69
70. Синтез логічних схем з одним виходом у базисі Буля на елементах з довільною кількістю входів
МатрицяДиз'юнктор
кон'юнкторів
a
&
1
a b c
b
Входи
a
Матриця
інверторів
a
b
b
1
1
a
b
c
c
1
c
c
a
b
c
&
a
&
a b c
&
a b c
a b c
Вихід
f
b
c
a
b
c
f a b c a b c a b c a b c
Lviv, CL.
26.03.2014
Комп'ютерна логіка
70
71. Двовходові елементи базису Буля
ab
&
a
b
ab
елемент 2І (2AND),
кон'юнктор
a
a
b
&
ab
&
abc
c
a
b
&
c
&
d
ab
&
&
cd
c
d
&
e
ab
&
abc
a
b
1
a b
c
1
a b c
a
b
1
c
1
a b
&
a
1
a
елемент НЕ (NOT),
інвертор
1
abc deh
de
&
1
deh
h
i
j
a b
елемент 2АБО (2OR),
диз'юнктор
b
abcd
1
hi
&
abc deh ijk
ijk
k
1
a b c d
c d
d
Lviv, CL.
26.03.2014
Комп'ютерна логіка
71
72. Основні правила виконання операцій у монобазисах І-НЕ (Шеффера) та АБО-НЕ (Пірса)
Lviv, CL.26.03.2014
Комп'ютерна логіка
72
73. Монобазис І-НЕ (NAND)
aa
&
b
b
a b ... z
...
z
&
a
b
a b ... z
...
z
елемент І-НЕ (NAND)
a
1
a
елемент НЕ-АБО
1
a
a
&
a b ... z
1
ab... z
a
1
a
b
1
b
a b ... z
...
z
елемент І-НЕ (NAND)
...
елемент НЕ (NOT)
z
1
елементи НЕ
Lviv, CL.
26.03.2014
1
z
елемент НЕ-АБО
Комп'ютерна логіка
73
74. Синтез логічних схем з одним виходом у монобазисі І‑НЕ
Синтез логічних схем з одним виходом у монобазисі І-НЕМатриця
Елемент НЕ-АБО
елементів І-НЕ
a
&
1
a b c
b
c
d
Входи
&
e
d e h
f=abc v deh v іjk
Вихід
h
i
j
f
&
i j k
k
Lviv, CL.
26.03.2014
Комп'ютерна логіка
74
75. 2І-НЕ
a2І-НЕ
&
&
a b
a b
1
b
b
елемент 2І-НЕ
a
b
&
ab
a
1
ab
&
&
ab
b
1
ab
&
abc
c
b
c
cd
&
cd
1
a a a
елемент НЕ-2АБО
&
&
a
1
a b
b
a
b
a
b
c
d
&
&
елементи 2І-НЕ
ab
елементи 2І-НЕ
&
a
&
1
a b
елемент НЕ-2АБО
&
b
&
a b
1
a b c
c
abcd
&
d
Lviv, CL.
26.03.2014
1
елемент НЕ-2АБО
c
a
a
елемент 2І-НЕ
a
a
a a a
1
c
&
&
ab cd
cd
d
&
a
1
a b
&
b
c
1
d
c d
&
a b
1
a b c d
c d
елемент НЕ-2АБО
Комп'ютерна логіка
75
76. Синтез логічних схем з одним виходом у монобазисі 2І-НЕ (Шеффера)
a&
ab
f=abc v deh v іjk
1
b
ab
&
c
d
e
h
i
j
&
&
k
Lviv, CL.
26.03.2014
de
ij
abc
1
de
&
deh
ij
&
ijk
1
abc deh
&
abc deh
1
f
1
Комп'ютерна логіка
76
77. Монобазис АБО‑НЕ (NOR)
Монобазис АБО-НЕ (NOR)a
a
1
b
a b ... z
...
z
a
b
a b ... z
...
z
елемент АБО-НЕ (NOR)
a
&
b
1
a
a
елемент НЕ-І
&
a
a
1
a
b
1
b
a b ... z
1
a b ... z
...
z
&
a b ... z
елемент НЕ (NOT)
...
z
1
елемент АБО-НЕ (NOR)
елементи НЕ
Lviv, CL.
26.03.2014
&
z
елемент НЕ-І
Комп'ютерна логіка
77
78. Синтез логічних схем з одним виходом у монобазисі АБО‑НЕ
Синтез логічних схем з одним виходом у монобазисіАБО-НЕ
Матриця
Елемент НЕ-І
елементів АБО-НЕ
a
1
&
a b c
b
f=(avbvc)&(dvevh)&(іvjvk)
c
d
Входи
1
e
d e h
Вихід
h
i
j
f
1
i j k
k
Lviv, CL.
26.03.2014
Комп'ютерна логіка
78
79. 2АБО-НЕ
a1
a
a a a
&
елемент 2АБО-НЕ
a
a b
1
&
a b
a
b
1
a b
1
c d
&
b
елемент 2АБО-НЕ (NOR)
a
1
a
елемент НЕ-2І
c
1
&
a
1
b
c
d
1
елементи 2АБО-НЕ
a
1
b
c
Lviv, CL.
26.03.2014
a b
a
b
b
елементи 2АБО-НЕ
a
1
1
a b c d
&
1
b
ab
&
abc
c
1
c
( a b ) (c d )
c d
a
1
a
b
1
b
&
c
1
c
1
a b c
d
&
ab
елемент НЕ-2І
a b
&
ab
1
елемент НЕ-2І
a b
c d
елемент НЕ-2І
d
ab
b
&
a b
a a a
1
Комп'ютерна логіка
ab
&
abcd
&
cd
d
1
1
cd
79
80. Синтез логічних схем з одним виходом у монобазисі 2АБО-НЕ (Пірса)
Синтез логічних схем з одним виходом у монобазисі 2АБОНЕ (Пірса)f (a b c)( d e h)(i j k )
a
1
a b
&
b
c
d
e
h
i
j
1
1
d e
i j
&
&
(a b c)( d e h)
(a b c)(d e h)
a b
1
a b c
&
1
&
d e
1
d e h
i j
1
i j k
f
k
Lviv, CL.
26.03.2014
Комп'ютерна логіка
80
81. Схеми елементів монобазисів на КМОН-транзисторах
Lviv, CL.26.03.2014
Комп'ютерна логіка
81
82. Основні правила виконання операцій у базисі Жегалкіна
a b = a`b v`ab = (a v b)(`a v`b).Для цієї функції справедливі наступні аксіоми:
a a = 0; a a a = a;
a `a = 1; a 1 =`a; a 0 = a.
На підставі розглянутих аксіом і властивостей
елементарних логічних функцій можна, наприклад,
вивести правила представлення функцій І, АБО, НЕ
через функцію додавання за модулем 2 і навпаки:
a v b = a b ab;
ab = (a b) (a v b).
a a 1
Lviv, CL.
26.03.2014
Комп'ютерна логіка
82
83. Виключне АБО (XOR)
aa
=1 a b
b
а
Lviv, CL.
26.03.2014
a
b
a b
b
Зафарбована область - a b
б
Комп'ютерна логіка
83
84. Реалізація XOR
Матрицяінверторів
Входи
a
&
1-ий ступінь
a
a
b
Входи
Матриця
інверторів
a
1
1-ий ступінь
a
a
b
b
1
b
a
b
a
b
&
&
a b
1
b
a
&
a b
&
1
Вихід
f
a b
b
Вихід
f
Входи
Матриця
інверторів
a
1
a
b
1
b
Lviv, CL.
26.03.2014
b
b
2-ий ступінь
a b
&
a
2-ий ступінь
Комп'ютерна логіка
1-ий ступінь
a
a
1
2-ий ступінь
( a b)
b
a
b
b
1
&
Вихід
f
( a b)
84
85. Порівняння варіантів синтезу комбінаційних логічних схем
cc
0
1
1
4
7
a b d
6
F
9
1
4
1
B
1
A
5
8
C
a b d
8
D
d
1
2
1
7
6
F
E
a b c d
1
1
a
3
1
1
b
E
1
1
1
c
D
1
8
0
1
8
C
a
2
1
5
1
c
3
1
1
9
1
b
1
B
A
a b c d
d
f a b c d a b c d c
f a b d a b d c
( 1 a )( 1 b )c( 1 d ) a b c ( 1 d ) ( 1 c )
.
c
0
1
3
2
0
4
c d
5
7
0
8
C
D
a b c
6
F
0
b
E
f c d a b c a b c (c d ) (a b c) (a b c)
0
a
8
9
B
0
d
Lviv, CL.
26.03.2014
a b c
A
0
Комп'ютерна логіка
85
86. ДНФ
ВходиМатриця
інверторів
a
1
1-ий ступінь
Входи
a
a
b
1
2-ий ступінь
b
b
a
&
a b d
b
1
a
Вихід
d
&
b
a b c
b
&
1-ий ступінь
a
a
f
a
Матриця
інверторів
&
b
b
d
1
c
d
&
a b d
b
d
1
Вихід
f
a
&
a b c
b
d
c
a
2-ий ступінь
d
c
d
d
&
d
c
c
d
Матриця
інверторів
Входи c
1
1-ий ступінь
c
a
d
b
c
1
d
a
&
b
2-ий ступінь
a b d
d
d
Вихід
1
a b d a b d c
a
b
3-ий ступінь
1
&
f
a b d
b
d
c
d
Lviv, CL.
26.03.2014
Комп'ютерна логіка
86
87. КНФ
Матрицяінверторів
Входи a
&
1-ий ступінь
a
a
b
&
b
b
c
&
c
c
d
&
d
d
c
1
c d
d
a
1
b
2-ий ступінь
&
Матриця
інверторів
Вихід
a b c
Входи a
1
f
b
c
1
a
1
b
c
a b c
1
d
&
1-ий ступінь
a
a
b
Lviv, CL.
26.03.2014
&
b
c
1
d
a
c
c
c
Входи a
d
b
b
Матриця
інверторів
c
a
a
1
d
b
1-ий ступінь
2-ий ступінь
c d
1
a b c
1
a b c
b
d
c
1
c d
d
a
2-ий ступінь
1
a b c
1
a b c
b
&
Вихід
f
c
a
b
c
3-ий ступінь
Вихід
&
(c d )(a b c)(a b c)
1
f
c
a
b
c
Комп'ютерна логіка
87
88. Поліном Жегалкіна
Суматори замодулем 2 як
Матриця
інвертори
кон'юнкторів
a
&
a b c d
"1"
b
Входи
a
b
c
d
=1
a
=1
b
=1
c
=1
d
c
d
a
a
b
b
c
d
c
c
Суматори за
модулем 2
=1
=1
&
Вихід
a b c d
f
d
f ( 1 a )( 1 b )c( 1 d ) a b c ( 1 d ) ( 1 c )
Lviv, CL.
26.03.2014
Комп'ютерна логіка
88
89. Форми представлення ФАЛ
• Табличні– Таблиці істинності
– Сингулярні таблиці
Геометричні
Числові
Часові діаграми
Схеми
Аналітичні (формули)
інші
Lviv, CL.
26.03.2014
Комп'ютерна логіка
89
90. Аналітичні форми представлення ФАЛ
• Нормальні– Досконалі
• ДДНФ
• ДКНФ
• інші
– Скорочені (ДНФ, КНФ)
• Мінімальні
• Глухого кута
• Абсолютно мінімальні
• Анормальні
– Дужкові
– Із запереченням більше ніж над однією змінною
Lviv, CL.
26.03.2014
Комп'ютерна логіка
90
91. Терм
• Терм - це група літерал і констант, об'єднаних тим самим знакомлогічного зв'язування: логічного додавання або ж логічного
множення. У термі кожен літерал і кожна константа зустрічається
тільки один раз, тобто в терм може входити або змінна, або її
заперечення.
• Диз'юнктивний терм (макстерм, елементарна диз’юнкція) - це
логічна функція, що зв'язує всі літерали знаком диз'юнкції.
• Наприклад:
• f1 = a `b c d;
f2 = a b.
• Макстерм називають також конституентою нуля, тому що ця логічна
функція дорівнює 0 тільки тоді, коли всі її літерали рівні 0 одночасно.
• Кон'юнктивний терм (мінтерм, елементарна кон’юнкція) - це
логічна функція, що зв'язує літерали знаком кон'юнкції.
• Наприклад:
• f1 =`a & b &`c & d;
f2 = a b c.
• Мінтерм називають також конституентою одиниці, тому що ця
функція дорівнює 1 тільки тоді, коли всі її літерали одночасно
дорівнюють одиниці.
Lviv, CL.
26.03.2014
Комп'ютерна логіка
91
92. Нормальні форми з мінтермами
• Будь-яка таблично задана ФАЛ може бутипредставлена аналітично у вигляді
– диз'юнкції скінченого числа мінтермів, на кожнім з яких
функція дорівнює одиниці (диз’юнктивна нормальна
форма, ДНФ):
f(a, b,..., z) = F1 F2 ... F n,
– суми за модулем 2 скінченого числа мінтермів, на
кожнім з яких функція дорівнює одиниці (поліном
Жегалкіна):
f ( a ,b ,..., z ) F 1 F 2 ... Fn ,
де i - номери наборів, на яких функція дорівнює 1.
Lviv, CL.
26.03.2014
Комп'ютерна логіка
92
93. Нормальні форми з макстермами
• Будь-яка таблично задана ФАЛ може бутипредставлена аналітично у вигляді
– кон'юнкції скінченого числа макстермів, на кожнім з
яких функція дорівнює нулю (кон’юнктивна нормальна
форма, КНФ):
f(a, b,..., z) = Ф1 & Ф2 & ... & Фm,
– результату порівняння скінченого числа макстермів, на
кожнім з яких функція дорівнює нулю (поліном
рівнозначності):
f ( a ,b ,..., z ) 1 2 , , , m ,
де i - номери наборів, на яких функція дорівнює 1.
Lviv, CL.
26.03.2014
Комп'ютерна логіка
93
94. Досконалі нормальні форми
• Кількість термів дорівнює кількостіодиничних (нульових) значень ФАЛ у її
таблиці істиності
• У кожному термі присутні усі змінні
• Немає однакових термів
Lviv, CL.
26.03.2014
Комп'ютерна логіка
94
95. Критерії синтезу схем ФАЛ
• Швидкодія (продуктивність)• Апаратні витрати
Споживана потужність
Надійність
Складність
Однорідність структури
Ціна
інші
Lviv, CL.
26.03.2014
Комп'ютерна логіка
95
96. Методи визначення ціни реалізації ФАЛ
• Грошові одиниці• Негрошові одиниці
– Кількість операцій
• І, АБО, НЕ
• І, АБО
• І (АБО)
– Кількість термін
• В ДНФ
• В КНФ
– Кількість літер
• В нормальних формах
• В анормальних формах
– Кількість входів
• І, АБО, НЕ
• І, АБО
• І (АБО)
– інші
Lviv, CL.
26.03.2014
Комп'ютерна логіка
96
97. Мінімізація ФАЛ
• Канонічна задача мінімізації– У базисі Буля
– Над нормальними формами
– Мета – зменшення кількості літер
• Загальна задача мінімізації
– Усі інші методи
Lviv, CL.
26.03.2014
Комп'ютерна логіка
97
98. Методи розв’язання канонічної задачі мінімізації
• Аналітичні– Квайна-МакКласскі-Петрика
– Інші
• Табличні
• Геометричні
• Графо-аналітичні
– Карти Карно
– Діаграми Вейча
• Алгебро-топологічні
• інші
Lviv, CL.
26.03.2014
Комп'ютерна логіка
98
99. Методи розв’язання загальної задачі мінімізації (аналітичні)
• Еврістичний (Метод спроб і помилок)• Винесення за дужки
• Внесення надлишковості і глобального
винесення за дужки
• Перехід до небулевого базису
• Метод функціональної декомпозиції
• інші
Lviv, CL.
26.03.2014
Комп'ютерна логіка
99
100. Еврістичний
f ab ab ( a b )abLviv, CL.
26.03.2014
Комп'ютерна логіка
100
101. Винесення за дужки
f abc acde abdg degac( b de ) dg( ab e )
Внесення надлишковості і
глобального винесення за дужки
f abc acde abdg deg
aabc acde abdg d deg
ab( ac dg ) de( ac dg )
( ab de )( ac dg )
Lviv, CL.
26.03.2014
Комп'ютерна логіка
101
102. Метод функціональної декомпозиції проста розділова і загальний випадок
X1f a bd bc ac
Ф1
Ф2
X2
f(X1,X2)
1 a b
2 1 d 1 c
X1
Ф1
f(X1,X2,X3 )
X3
X2
Ф2
f ab ade bc d be
1 b de
2 1 a 1 ( c e )
Lviv, CL.
26.03.2014
Комп'ютерна логіка
102
103. Багаторозрядний суматор
Lviv, CL.26.03.2014
Комп'ютерна логіка
103
104. 4-розрядні суматори (у прямому, оберненому і доповняльному кодах)
Lviv, CL.26.03.2014
Комп'ютерна логіка
104
105. Повний однорозрядний суматор
Co ABCi ABCi ABCi ABCi BCi ACi ABS A BCi ABCi AB Ci ABCi
Lviv, CL.
26.03.2014
Комп'ютерна логіка
105
106. Функціональна схема повного однорозрядного двійкового суматора
Lviv, CL.26.03.2014
Комп'ютерна логіка
106
107. Багатозначні логіки. Нечітка логіка
• Тризначна логіка Лукасевича {0,1/2,1}(ні, може бути, так)
• Тризначна логіка Поста {0,1,2}
• N-значна логіка Лукасевича {0/n-1,1/n-1,
…,n-1/n-1}
• N-значна логіка Поста {0,1,2, …,n-1}
Lviv, CL.
26.03.2014
Комп'ютерна логіка
107
108. Небулеві базиси
Базис Жегалкіна
Мажоритарний базис
Пороговий базис
Штучний інтелект
Lviv, CL.
26.03.2014
Комп'ютерна логіка
108
109. БАЗОВІ КОМБІНАЦІЙНІ ВУЗЛИ
дешифратори і демультиплексори;
мультиплексори;
шифратори;
перетворювачі кодів;
постійні запам’ятовуючі пристрої;
програмовані логічні матриці;
програмовані матриці логіки;
суматори і напівсуматори;
вузли порівняння;
арифметично-логічні пристрої;
вузли зсуву;
помножувачі;
інші.
Lviv, CL.
26.03.2014
Комп'ютерна логіка
109
110. Дешифратор “3 у 8”
Матрицякон'юнкторів
Дешифратор “3 у 8”
Виходи
1
&
4 2 1 CS
0
І0
&
4 2 1 CS
1
2
Входи
4
CS
Матриця
інверторів
1
1
1
2
1
2
4
4
1
1
1
2
4
CS
2
4
CS
1
І1
&
4 2 1 CS
2
І2
&
4 2 1 CS
3
2
4
CS
1
2
4
CS
1
2
4
CS
1
1
2
4
CS
1
4 2 1 CS
4
I0
I1
I2
І4
&
4 2 1 CS
5
CS
І5
&
4 2 1 CS
6
I[2:0]
CS
DC O0
O1
O2
O3
O4
O5
O6
O7
в
DC
O[7:0]
г
І6
&
2
4
CS
CS
І3
&
2
4
CS
1
2
4
DC 0
1
2
3
4
5
6
7
б
4 2 1 CS
7
І7
а
Lviv, CL.
26.03.2014
Комп'ютерна логіка
110
111. Матрична схема дешифратора “3 у 8"
Матрична схема дешифратора “3 у 8"Матриця
інверторів
Матриця кон'юнкторів
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
Входи
4
4
2
2
1
1
CS
0 1 2 3 4 5 6 7
Виходи
Lviv, CL.
26.03.2014
Комп'ютерна логіка
111
112. VHDL-опис дешифратора “3 у 8”
library IEEE;
use IEEE.STD_LOGIC_1164.all;
use IEEE.STD_LOGIC_UNSIGNED.all;
entity DC is
port (
O : out STD_LOGIC_VECTOR (7 downto 0);
I : in STD_LOGIC_VECTOR (2 downto 0);
CS : in STD_LOGIC);
end entity;
architecture DC_arch of DC is
begin
O(0) <= CS when (I = 0) else '0';
O(1) <= CS when (I = 1) else '0';
O(2) <= CS when (I = 2) else '0';
O(3) <= CS when (I = 3) else '0';
O(4) <= CS when (I = 4) else '0';
O(5) <= CS when (I = 5) else '0';
O(6) <= CS when (I = 6) else '0';
O(7) <= CS when (I = 7) else '0';
end architecture;
Lviv, CL.
26.03.2014
Комп'ютерна логіка
112
113. Реалізація ФАЛ на дешифраторах
Матрицяінверторів
Матриця кон'юнкторів
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
Входи
c
b
a
"1"
1
2
4
CS
DC 0
1
2
3
4
5
6
7
a b c
a b c
a b c
4
4
2
2
1
1
1
Вихід
f
a b c
a b c
CS
Вихід
f
АБО0
0 1 2 3 4 5 6 7
Виходи дешифратора
Lviv, CL.
26.03.2014
Комп'ютерна логіка
113
114. Нарощування розрядності дешифраторів
12
4
d
c
d
c
b
b
DC 0
8
a
d
c
b
a CS
b
1
2
4
CS
D1 1
Lviv, CL.
26.03.2014
CS
1
d
c
CS
1
2
4
a CS
CS
a b c d CS
DC 0
a b c d CS
1
a b c d CS
2
a b c d CS
3
a b c d CS
4
a b c d CS
5
a b c d CS
6
a b c d CS
D2 7
a b c d CS
DC 0
a b c d CS
1
a b c d CS
2
a b c d CS
3
a b c d CS
4
a b c d CS
5
a b c d CS
6
a b c d CS
D3 7
Комп'ютерна логіка
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
4
8
CS
DC 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
114
115. Демультиплексор DX = Дешифратор DC
Матрицякон'юнкторів
Виходи
1
Дані
Керування
1
2
4
CS
DC 0
1
2
3
4
5
6
7
&
4 2 1 CS
0
І0
&
4 2 1 CS
1
І1
&
4 2 1 CS
2
І2
&
4 2 1 CS
3
І3
&
4 2 1 CS
4
І4
&
4 2 1 CS
5
І5
&
4 2 1 CS
6
І6
&
4 2 1 CS
7
2
4
CS
Матриця
інверторів
1
1
1
1
2
1
4
1
1
2
2
4
CS
4
2
4
CS
1
2
4
CS
1
2
Керування
Дані
1
2
4
CS
DX 0
1
2
3
4
5
6
7
4
CS
1
2
4
CS
1
2
4
CS
1
2
4
CS
1
2
4
CS
Lviv, CL.
26.03.2014
І7
Комп'ютерна логіка
115
116. Класифікація DC та DX
Дешифратор DCДемультиплексор DX
Входів
Виходів
Назва
Входів
Виходів
Назва
1
2
1у2
1
2
1у2
2
4
2у4
2
4
1у4
3
8
3у8
3
8
1у8
4
16
4 у 16
4
16
1 у 16
5
32
5 у 32
5
32
1 у 32
n
2n
n у 2n
n
2n
1 у 2n
Lviv, CL.
26.03.2014
Комп'ютерна логіка
116
117. Мультиплексор 8 в 1
Інформаційнівходи
Входи
управління
Інформаційні
входи
Входи
управління
0
1
2
3
4
5
6
7
1
2
4
Матриця кон'юнкторів
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
Входи управління
а
I0 MUX
I1
I2
I3
I4
I5
I6
I7
S0
S1
S2
б
MUX
Інформаційні входи
Входи управління
Матриця
інверторів
MUX
4
4
2
2
1
1
Інформаційні входи
0
1
2
3
4
5
6
7
Вихід
АБО0
г
I[7:0]
S[2:0]
в
Lviv, CL.
26.03.2014
Комп'ютерна логіка
117
118. VHDL-опис
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_unsigned.all;
entity mux is
port ( I : in std_logic_vector (7 downto 0);
S : in std_logic_vector (2 downto 0);
O : out std_logic);
end entity;
architecture mux_arch of mux is
begin
O <= I(CONV_INTEGER(S));
end architecture;
Lviv, CL.
26.03.2014
Комп'ютерна логіка
118
119. Реалізація ФАЛ на мультиплексорах
"1""0"
Lviv, CL.
26.03.2014
Комп'ютерна логіка
c
b
a
0
1
2
3
4
5
6
7
1
2
4
MUX
f
119
120. Нарощування розрядності мультиплексорів
01
2
3
4
5
6
7
1
1
2
2
4
4
8
9
10
11
12
13
14
15
1
2
4
Lviv, CL.
26.03.2014
0
1
2
3
4
5
6
7
1
2
4
0
1
2
3
4
5
6
7
1
2
4
MUX
0
MUX
D1
MUX
0 MUX
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8
1
1
D2
1
2
4
8
D2
Комп'ютерна логіка
120
121. Класифікація DC, DX, MUX
Дешифратор DCДемультиплексор DX
Мультиплексор MUX
Входів
Виходів
Назва
Входів
Виходів
Назва
Входів
Виходів
Назва
1
2
1у2
1
2
1у2
2
1
2в1
2
4
2у4
2
4
1у4
4
1
4в1
3
8
3у8
3
8
1у8
8
1
8в1
4
16
4 у 16
4
16
1 у 16
16
1
16 в 1
5
32
5 у 32
5
32
1 у 32
32
1
32 в 1
n
2n
n
2n
1 у 2n
2n
1
2n в 1
Lviv, CL.
26.03.2014
Комп'ютерна логіка
121
122. Шифратор Coder CD
Lviv, CL.26.03.2014
Комп'ютерна логіка
122
123. Класифікація DC, CD, DX, MUX
Дешифратор DCШифратор CD
Демультиплексор DX
Мультиплексор MUX
Входів
Виходів
Назва
Входів
Виходів
Назва
Входів
Виходів
Назва
Входів
Виходів
Назва
1
2
1у2
2
1
2у1
1
2
1у2
2
1
2в1
2
4
2у4
4
2
4у2
2
4
1у4
4
1
4в1
3
8
3у8
8
3
8у3
3
8
1у8
8
1
8в1
4
16
4 у 16
16
4
16 у 4
4
16
1 у 16
16
1
16 в 1
5
32
5 у 32
32
5
32 у 5
5
32
1 у 32
32
1
32 в 1
n
2n
n у 2n
2n
n
2n у n
n
2n
1 у 2n
2n
1
2n в 1
Lviv, CL.
26.03.2014
Комп'ютерна логіка
123
124. Пріоритетний шифратор
CD0
1
2
0
1
2
1
3
4
5
6
7
2
4
3
4
5
6
7
CD
1
2
4
RDY
7
6
5
4
3
2
1
0
4
2
1
1
0
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
0
0
1
1
0
0
0
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
Rd
0
1
2
3
4
5
6
7
4
2
1
Lviv, CL.
26.03.2014
7
6
5
4
3
2
1
0
4
2
1
1
X
X
X
X
X
X
X
1
1
1
1
0
1
X
X
X
X
X
X
1
1
0
1
0
0
1
X
X
X
X
X
1
0
1
1
0
0
0
1
X
X
X
X
1
0
0
1
0
0
0
0
1
X
X
X
0
1
1
1
0
0
0
0
0
1
X
X
0
1
0
1
0
0
0
0
0
0
1
X
0
0
1
1
1
1
1
1
1
1
1
1
0
0
0
1
0
0
0
0
0
0
0
0
X
X
X
0
Комп'ютерна логіка
y
124
125. Перетворювач кодів = DC + CD
Lviv, CL.26.03.2014
Комп'ютерна логіка
125
126. Двійково-десяткові коди
Lviv, CL.26.03.2014
Комп'ютерна логіка
126
127. Перетворювач кодів 8421 у 8421+3
‘0’DC
a1
a2
a4
a8
Lviv, CL.
26.03.2014
1
2
4
8
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
a
b
c
d
e
f
‘0’
‘0’
‘0’
0
1
2
3
4
5
6
7
8
9
‘0’
‘0’
‘0’
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
CD
1
2
4
8
b1
b2
b4
b8
Комп'ютерна логіка
a1
a2
a4
a8
1
2
4
8
X/Y
1
2
4
8
b1
b2
b4
b8
127
128. Матрична схема перетворювача коду 8421 у код 8421+3
84
Дешифратор –
набір елементів І,
матриця І
2
1
АБО1
8
АБО2
4
АБО3
2
АБО4
1
Шифратор –
набір елементів
АБО, матриця АБО
I0 I1 I2 I3 I4 I5 I6 I7 I8 I9 I10 I11 I12 I13 I14 I15
Lviv, CL.
26.03.2014
Комп'ютерна логіка
128
129. Перетворювач кодів для семигементного індикатора
Lviv, CL.26.03.2014
Комп'ютерна логіка
129
130. Перетворювач кодів – дешифратор для 7-сегментного індикатора
Перетворювач кодів – дешифратор для 7сегментного індикатораLviv, CL.
26.03.2014
Комп'ютерна логіка
130
131. Постійний запам’ятовуючий пристій
Матриця кон'юнкторів(елементів І)
ROM
A0
A1
D0
D1
D2
D3
A2
Матриця І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
інверторів
Входи
A2
A2
A1
A1
A0
A0
CS
а
ROM
D[3:0]
A[2:0]
CS
б
CS
Виходи
- точки, де завжди
є з'єднання
- точки, де може бути
з'єднання
АБО0
D0
D1
D2
D3
АБО1
АБО2
АБО3
Матриця диз'юнкторів
(елементів АБО)
в
Lviv, CL.
26.03.2014
Комп'ютерна логіка
131
132. Реалізація ФАЛ на ПЗП
Lviv, CL.26.03.2014
Комп'ютерна логіка
132
133. Реалізація ФАЛ на ПЗП
Входиa
b
c
"0"
"1"
A0 ROM D0
D1
A1
D2
A2
D3
A3
A4
A5
A6
A7
CS
Матриця Матриця кон'юнкторів
інверторів
(елементів І)
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7 І 8
A7
A7
A3
A3
A2
A2
A1
A1
A0
A0
І 255
f0
f1
f2
CS
- точки, де є з'єднання
Виходи
АБО0
D0
D1
D2
D3
АБО 1
АБО2
АБО3
Матриця диз'юнкторів
(елементів АБО)
Lviv, CL.
26.03.2014
Комп'ютерна логіка
133
134. Опис ПЗП на мові VHDL
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_unsigned.all;
entity rom is
port (
CS : in STD_LOGIC;
A : in STD_LOGIC_VECTOR(2 downto 0);
D : out STD_LOGIC_VECTOR(3 downto 0));
end entity;
architecture rom_arch of rom is
begin
process(A, CS)
begin
if (CS = '1') then
case (A) is
when "000" => D <= "0100";
when "001" => D <= "0010";
when "010" => D <= "0111";
when "011" => D <= "0100";
when "100" => D <= "0001";
when "101" => D <= "0011";
when "110" => D <= "0101";
when "111" => D <= "0101";
when others => D <= "0000";
end case;
else
D <= "0000";
end if;
end process;
Lviv, CL.
26.03.2014
Комп'ютерна логіка
134
135. Програмовані логічні матриці
PLAD0
D1
D2
D3
A0
A1
A2
Входи
Матриця
інверторів
(елементів
НЕ)
A2
A2
A1
A1
A0
A0
Матриця кон'юнкторів
(елементів І)
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
CS
а
PLA
D[3:0]
A[2:0]
CS
б
CS
- точки, де завжди
є з'єднання
- точки, де може бути
з'єднання
Виходи
АБО0
D0
D1
D2
D3
АБО1
АБО2
АБО3
Матриця диз'юнкторів
(елементів АБО)
в
Lviv, CL.
26.03.2014
Комп'ютерна логіка
135
136. Реалізація ФАЛ на ПЛМ
PLAa
b
c
"1"
A0
A1
A2
D0
D1
D2
D3
f0
f1
f2
Входи
Матриця кон'юнкторів
(елементів І)
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
Матриця
інверторів
(елементів
НЕ)
A0
A0
a
a
A1
b
b
A2
c
c
CS
а
A1
A2
CS
- точки, де є з'єднання
Виходи
АБО0
D0 f0
D1 f1
D2 f2
D3
АБО1
АБО 2
АБО3
b c
a b
c
a c a b c a b
Матриця диз'юнкторів
(елементів АБО)
Lviv, CL.
26.03.2014
Комп'ютерна логіка
f0 b c a c a b
f1 a b a b c
f2 c a b a b
б
136
137. Таблиця прошиття ПЛМ
Lviv, CL.26.03.2014
Комп'ютерна логіка
137
138. Програмовані матриці логіки
PALA0
A1
A2
D0
D1
D2
D3
Входи
Матриця кон'юнкторів
(елементів І)
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
Матриця 1
інверторів
(елементів
НЕ)
A2
A2
A1
A1
A0
A0
CS
а
PAL
D[3:0]
A[2:0]
CS
б
Матриця 2
інверторів
(елементів
НЕ)
CS
- точки, де завжди
є з'єднання
D3
D3
- точки, де може бути
з'єднання
D2
D2
D1
D1
D0
D0
Виходи
АБО0
D0
D1
D2
D3
АБО1
АБО 2
АБО3
Матриця диз'юнкторів
(елементів АБО)
в
Lviv, CL.
26.03.2014
Комп'ютерна логіка
138
139. Реалізація ФАЛ на ПМЛ
PALa
b
c
"1"
D0
D1
D2
D3
A0
A1
A2
f0 Входи
f1
Матриця 1
інверторів
(елементів
НЕ)
Матриця кон'юнкторів
(елементів І)
І 0 І1 І 2 І 3 І 4 І 5 І 6 І 7
A2
a
a
A1
A1
b
b
A0
A0
c
c
A2
CS
а
Матриця 2
інверторів
(елементів
НЕ)
CS
- точки, де є з'єднання
D3
D3
D2
D2
D1
D1
D0
D0
Виходи
АБО0
АБО1
АБО 2
АБО3
b c
a c
D0
D1
c a b
f1
f0
D2
D3
f1
f0 b c a c a b
f1 c a b a b
c
a b
b c a c
a b
a b
c a b
Матриця диз'юнкторів
(елементів АБО)
Lviv, CL.
26.03.2014
b c a c
f0
б
Комп'ютерна логіка
139
140. Таблиця прошиття ПМЛ
Lviv, CL.26.03.2014
Комп'ютерна логіка
140
141. Операційний пристрій на основі ПЗП
S = 2M + 3NA
Адреса
a3
1
a2
1
M
N
Lviv, CL.
26.03.2014
a1
0
m1
a0
1
m0
1
n1
n0
3
Комп'ютерна логіка
141
142. Таблиця прошиття ПЗП
A(адреса
ПЗП)
A10
a2
A2
n0
a3
A3
n1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
a0
A0
m0
a1
A1
m1
N
2M + 3N=S
M
S16
M
N
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Lviv, CL.
26.03.2014
Дані
Розрахунок
Адреса
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
*0
*0
*0
*0
*1
*1
*1
*1
*2
*2
*2
*2
*3
*3
*3
*3
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
0
2
4
6
3
5
7
9
6
8
10
12
9
11
13
15
0
2
4
6
3
5
7
9
6
8
A
С
9
B
D
F
Комп'ютерна логіка
s3
D1
0
0
0
0
0
0
0
1
0
1
1
1
1
1
1
1
s2
D0
0
0
1
1
0
1
1
0
1
0
0
1
0
0
1
1
s1
D1
0
1
0
1
1
0
1
0
1
0
1
0
0
1
0
1
s0
D0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
D
(дані
ПЗП)
0
2
4
6
3
5
7
9
6
8
A
С
9
B
D
F
142
143. Матричний (паралельний, комбінаційний) помножувач
Lviv, CL.26.03.2014
Комп'ютерна логіка
143
144. Логічні операції над числами
145. Зсуви
M=6m2 m1
1
1
m3
0
Co=0
m0
0
Ci=1
1
r3
1
0
r2
r1
R=D
1
r0
m3
0
Co=0
m3
0
m0
0
Ci=1
1
r3
Логічний зсув ліворуч
1
0
r2
r1
R=D
1
r0
1
r3
1
0
r2
r1
R=C
m0
0
0
r0
Циклічний зсув ліворуч
Арифметичний зсув ліворуч
m3
0
M=6
m2 m1
1
1
m0
0
1
r3
0
r2
1
r0
Ci=1
1
r1
R=B
M=6
m2 m1
1
1
M=6
m2 m1
1
1
Co=0
Логічний зсув праворуч
m3
0
M=6
m2 m1
1
1
m0
0
0
r3
0
r2
1
r0
1
r1
R=3
m3
0
M=6
m2 m1
1
1
m0
0
0
r3
0
r2
1
r0
Co=0
1
r1
R=3
Циклічний зсув праворуч
Арифметичний зсув праворуч
Lviv, CL.
26.03.2014
Комп'ютерна логіка
145
146. Арифметико-логічний пристрій
AB
A
B
Fмл
F
AU
MUX
R
A
LU
A
B
B
R
Fмл
F
A
Fмл
A
B
Fмл
Fст
A
Ra
Rл
0
A
B
F
A
B
F
ALU
R
R
1
R
ShU
R
Rз
2
F
Reserve
A
B
R
F
Код операції -КОП
Rр
3
Sel
Fст
00 - арифметичні
01 - логічні
10 - зсуви
11 - резерв
Fмл
147. Арифметичний вузол
00...0A
11...1
F4F3
Код операції - арифметичні
Fст
00 - арифметичні
F4F3
01
01
01
00
01
11
00
11
F2F1
01
10
00
01
11
01
00
00
F0
0
1
1
1
0
0
0
0
(Fмл)
(0A)
(0B)
(09)
(03)
(06)
(1A)
(00)
(18)
A+B+0 =
A+(not B) +1 =
A+0+1=
0+B+1=
A+11...1+0=
11...1+B+0=
0+0+0=
11...1+0+0=
A+B
A-B
A+1
B+1
A-1
B-1
0
11...1
1
MUX
0
1
R
2
3
Sel
1
MUX
0
1
R
2
3
Sel
00...0
B
11...1
F2F1
F0
SUM
OpA
OpB
A
B
Ci
S
Co
Ra
Co
148. Логічний вузол
AB
A
B
A
B
A
B
&
MUX
R
RAND
0
1
R
ROR
1
Rл
A
B
A
B
Fмл
A
B
A
B
=1
R
RXOR
2
==
R
REQ
3
Sel
149. Вузол зсувів
AA
A
A
A
A
A
LSL
RL
ASL
LSR
RR
ASR
R
0
R
1
R
2
R
3
R
4
R
5
MUX
6
7
Fмл
Sel
Rз
150. Структура комп’ютера
Пам'ятьПристрій
вводу
Пристрій
керування
Операційний
пристрій
Процесор
Пристрій
виводу
Дані
Стан
Керування
Команда
151. Загальна структурна схема цифрового автомата
КСхПА
δ
{X}
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
λ
{A}
{Y}
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
152. Структурна схема автомата Мура
iКСх
δ
{X} j
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
j – кількість вхідних сигналів
k – кількість вихідних сигналів
ПА
i
{A}
КСх
λ
k
{Y}
2
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
i – розрядність зворотного зв’язку,
кількість тригерів у пам’яті
автомата
153. Структурна схема автомата Мілі
КСх{X}
δ
ПА
{A}
КСх
λ
1
{Y}
2
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
154. Рекомендована послідовність синтезу цифрових автоматів
•Синтез абстрактного автомата• Синтез алгоритма роботи автомата.
• Вибір структури автомата (Мура або Мілі).
• Фіксація алгоритма у вигляді графа.
•Синтез структурного автомата
• Вибір елементної бази комбінаційної частини.
• Вибір елементної бази пам’яті автомата.
• Вибір способу кодування вхідних та вихідних сигналів.
• Вибір способу кодування внутришніх станів автомата.
• Створення таблиці переходів автомата.
• Створення таблиці виходів автомата.
• Мінімізація формул для сигналів збудження тригерів автомата. Фіксація
результатів у вигляді диз’юнктивної нормальної форми (ДНФ).
• Для деяких структурних автоматів (у яких комбінаційна частина реалізується
на дешифраторах, мультиплексорах, а також для мікропрограмних автоматів, у
яких комбінаційна частина реалізується на ПЗП) даний етап мінімізації
непотрібний.
• Мінімізація формул для виходів автомата. Фіксація результатів у вигляді
диз’юнктивної нормальної форми (ДНФ).
• Для деяких структурних автоматів (у яких комбінаційна частина реалізується
на дешифраторах, мультиплексорах, а також для мікропрограмних автоматів, у
яких комбінаційна частина реалізується на ПЗП) даний етап мінімізації
непотрібний.
• Синтез пам’яті автомата.
• Синтез комбінаційної частини автомата.
155. RS-тригер
№0
1
2
3
R
0
0
1
1
S
0
1
0
1
Qt
Qt-1
1
0
Заборона
RS-тригер
RS
a0
0
R S
RS
a1
1
RS
156. неRнеS-тригер
№0
1
2
3
R
0
0
1
1
S
0
1
0
1
Qt
Заборона
0
1
Qt-1
157. D-тригер, що спрацьовує по тілу
D№
0
1
C
0
1
Qt
Qt-1
D
a0
0
D
D
a1
1
D
158. D-тригер, що спрацьовує по фронту
№0
1
2
3
C
0
1
Qt
Qt-1
Qt-1
Qt-1
D
D
a0
0
D
D
a1
1
D
159. Функціональна схема D-тригера, що спрацьовує по фронту
160. Т-тригер
№0
1
2
3
C
0
1
Qt
Qt-1
Qt-1
Qt-1
Q t 1
a0
0
a1
1
161. T-тригер з входом дозволу роботи
№0
1
2
3
4
C
0
1
X
CE
X
X
X
0
1
Qt
Qt-1
Qt-1
Qt-1
Qt-1
Q t 1
CE
a0
0
CE
CE
a1
1
CE
162. JK-тригер
№0
1
2
3
4
5
6
C
0
1
J
X
X
X
0
0
1
1
K
X
X
X
0
1
0
1
Qt
Qt-1
Qt-1
Qt-1
Qt-1
0
1
Q t 1
K
a0
0
J
K
a1
1
J
163. Тригери з асинхронними входами (R, S) та входом дозволу СІ (CE)
SD
C
CE
R
T
R
0
1
1
0
0
0
0
S
1
0
1
0
0
0
0
0 0
CE
X
X
X
0
1
1
1
C
X
X
X
X
0
1
↓
Qt
1
0
X
Qt-1
Qt-1
Qt-1
Qt-1
1
↑
D
Працюють
асинхронні входи
Заборона
Немає дозволу
Немає потрібного
фронту СІ
Запис даних по
фронту СІ
164. Лічильник на T-тригерах
a0000
a7
111
a1
001
a2
010
a6
110
a5
101
a3
011
a4
100
165. Лічильник на D-тригерах
166. Лічильник на JK-тригерах
167. Регістр зсуву
168. Паралельний регістр
D0D
C
D1
D
C
D2
D
C
D3
C
D
C
T
Q0
D1
T
Q1
D2
T
Q2
RG
D0
D1
D2
D3
C
Q0
Q1
Q2
Q3
RG
D3
T
D4
D(3:0) Q(3:0)
Q3
C
169. Оперативний запам’ятовуючий пристрій (ОЗП)
DIA
m
n
Wr
DC
B
CS
Q
CS0
D
C
CS1
D
C
n
CS 2
RG
RG
Q
Q
Word0
Word1
0
MUX
m
1
DO
RAM
m
CS2^n-1
D
C
RG
2n-1
Q
n
Sel
n
m
DI
Wr
A
DO
170. Кодуванням станів автомата
ii
КСх
ПА
δ
{X} j
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
j – кількість вхідних сигналів
k – кількість вихідних сигналів
КСх
КСх
i
{A}
λ
{Y}
k
ПА
δ
{X} j
i
КСх
{A}
2
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
i – розрядність зворотного зв’язку,
кількість тригерів у пам’яті
автомата
k
λ
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
j – кількість вхідних сигналів
k – кількість вихідних сигналів
{Y}
2
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
i – розрядність зворотного зв’язку,
кількість тригерів у пам’яті
автомата
Кількість тригерів залежить тільки від
кількості станів і способу їх кодування
№
0
1
2
...
8
9
Позначення
ai
a0
a1
a2
Стан автомата
Код
Q9 Q8
Q2
...
0
0
0
...
0
0
0
...
0
0
1
...
...
...
a8
a9
0
1
...
1
0
...
...
...
...
0
0
№
Q1
0
1
0
Q0
1
0
0
...
...
0
0
0
0
0
1
2
...
8
9
Стан автомата
Позначення
Код
ai
Q3 Q2 Q1
0
0
0
a0
0
1
0
a1
a2
1
0
1
...
...
a8
a9
1
1
...
0
0
...
0
0
Q0
0
1
0
...
0
1
171. Синтез автомата Мура
Попередній станавтомата
Позначення
Код
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
1
0
a2
a3
1
1
1
1
a3
№
0
1
2
3
4
5
6
7
№
0
1
2
3
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
0
0
a0
0
1
a1
1
0
a2
1
1
a3
Вихідні
сигнали
автомата
y
1
1
0
0
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a0
0
0
1
0
a2
1
0
a2
1
1
a3
1
1
a3
a0
0
0
0
0
a0
x
0
1
0
1
0
1
0
1
Q0
0
Q1
4
1
1
5
3
1
7
1
2
Q0
0
1
6
x
D1 Q1Q0 Q1Q0
Q1
4
1
1
1
5
1
3
2
7
6
x
D0 Q1Q0 Q0 x
Сигнали
збудження
тригерів
D1
D0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
0
Q0
0
Q1
2
1
1
1
3
y Q1
172. Результат синтезу – схема автомата Мура
173. Сусіднє кодування станів
КСх№
0
1
2
3
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
0
0
a0
0
1
a1
1
0
a3
1
1
a2
Вихідні
сигнали
автомата
y
0
1
1
0
x
0
1
0
1
0
1
0
1
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a1
0
1
1
1
a2
1
1
a2
0
0
a0
0
0
a0
a3
1
0
0
0
a0
Q0
Q1
1
3
4
5
7
1
2
6
{Y}
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a3
1
0
a3
a2
1
1
1
1
a2
0
λ
2
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
0
1
2
3
4
5
6
7
{A}
δ
{X}
№
КСх
ПА
Q0
0
1
1
x
D1 Q0 x Q1Q0
Q1
4
1
1
3
1
5
7
1
2
6
Сигнали
збудеження
тригерів
D1
D0
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
0
Q0
0
1
Q1
2
1
1
1
3
x
D0 Q1
y Q1Q0 Q1Q0
174. Схема автомата
175. Унітарне кодування станів
КСхПА
δ
{X}
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
0
1
2
3
Позначення
ai
a0
a1
a2
a3
Попередній стан автомата
D3 Q2 x
D2 Q1
D1 Q0
D0 Q3 Q2 x
y Q3 Q1
№
0
1
2
3
4
5
6
7
Позначення
ai
a0
a0
a1
a1
a2
a2
a3
a3
Q3
0
0
0
0
0
0
1
1
Код
Q2 Q1
0
0
0
0
0
1
0
1
1
0
1
0
0
0
0
0
Q3
0
0
0
1
λ
{Y}
2
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Попередній стан автомата
№
КСх
{A}
Код
Q2 Q1
0
0
0
1
1
0
0
0
Q0
1
0
0
0
Вихідні
сигнали
автомата
y
0
1
0
1
Наступний стан автомата
x
Q0
1
1
0
0
0
0
0
0
0
1
0
1
0
1
0
1
Позначення
aj
a1
a1
a2
a2
a3
a0
a0
a0
q3
0
0
0
0
1
0
0
0
Код
q2
q1
0
1
0
1
1
0
1
0
0
0
0
0
0
0
0
0
q0
0
0
0
0
0
1
1
1
D3
0
0
0
0
1
0
0
0
Сигнали
збудеження
тригерів
D2 D1
0
1
0
1
1
0
1
0
0
0
0
0
0
0
0
0
D0
0
0
0
0
0
1
1
1
176. Схема автомата
177. Автомат на Т-тригерах
КСхПА
δ
{X}
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
№
0
1
2
3
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
0
0
a0
0
1
a1
1
0
a2
1
1
a3
0
1
2
3
4
5
6
7
Вихідні
сигнали
автомата
y
1
1
0
0
Q0
0
Q1
4
1
1
1
3
5
7
1
1
1
2
6
1
x
CE0 Q1 Q0 x
Q1
0
1
3
4
5
7
x
CE1 Q0
1
1
2
6
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a0
0
0
1
0
a2
1
0
a2
1
1
a3
1
1
a3
a0
0
0
0
0
a0
x
0
1
0
1
0
1
0
1
Q0
0
1
1
Q1
{Y}
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Q0
1
λ
2
Попередній стан
автомата
Позначення
Кодt
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
1
0
a2
a3
1
1
1
1
a3
№
КСх
{A}
2
1
1
1
3
y Q1
Сигнали
збудеження
тригерів
CE1
CE0
0
1
0
0
1
1
1
1
0
1
0
1
1
1
1
1
178. Схема автомата
179. Автомат на JK-тригерах
КСхПА
δ
{X}
1
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
№
№
0
1
2
3
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
0
0
a0
0
1
a1
1
0
a2
1
1
a3
Вихідні
сигнали
автомата
y
1
1
0
0
0
1
2
3
4
5
6
7
Q0
Q1
0
1
3
4
5
7
X
X
1
X
Q0
2
6
1
X
1
3
2
0
4
5
7
6
4
X
Q1
X
X
x
K 1 Q0
1
x
0
1
0
1
0
1
0
1
X
1
Q1
1
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a0
0
0
1
0
a2
1
0
a2
1
1
a3
1
1
a3
a0
0
0
0
0
a0
1
3
2
0
1
3
5
7
6
4
5
7
1
x
J 0 Q1 x
1
Сигнали збудеження
тригерів
J1
0
0
1
1
X
X
X
X
Q0
1
X
X
1
X
Q1
X
{Y}
λ
2
Q0
0
x
J 1 Q0
Попередній стан
автомата
Позначення
Кодt
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
1
0
a2
a3
1
1
1
1
a3
КСх
{A}
X
X
K0 1
1
X
K1
X
X
X
X
0
0
1
1
Q0
2
6
0
1
X
Q1
2
1
1
1
3
x
y Q1
J0
1
0
X
X
1
1
1
1
K0
X
X
1
1
X
X
X
X
180. Схема автомата
181. Синтез автомата Мілі
№КСх
{X}
δ
ПА
{A}
КСх
λ
1
{Y}
0
1
2
3
4
5
6
7
Попередній стан
автомата
Позначення
Код
ai
Q1 Q0
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
1
0
a2
a3
1
1
1
1
a3
Наступний стан
автомата
Позначення
Код
aj
q1
q0
a1
0
1
a0
0
0
1
0
a2
1
0
a2
1
1
a3
1
1
a3
a0
0
0
0
0
a0
x
0
1
0
1
0
1
0
1
Сигнали
збудеження
тригерів
D1
D0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
0
y
1
1
0
0
0
0
1
1
2
КСх - комбінаційна схема
ПА - пам’ять автомата
δ – функція переходів
λ – функція виходів
Q0
{X} – множина вхідних сигналів
{Y} – множина вихідних сигналів
{A} – множина внутришніх станів
0
Q1
4
1
1
5
3
1
7
1
2
Q0
0
1
6
x
D1 Q1Q0 Q1Q0
Q1
4
1
1
1
5
1
3
2
7
6
x
D0 Q1Q0 Q0 x
Q0
0
Q1
4
1
1
5
1
3
7
2
1
6
1
x
y Q1Q0 Q1Q0
182. Схема автомата
183. Мікропрограмний автомат
ROMПА
δ
{X}
{A}
{Y}
λ
ROM - комбінаційна схема мікропрограмного автомата - постійний
запам’ятовуючий пристрій
{X} – множина вхідних сигналів
ПА - пам’ять автомата
δ – функція переходів
{Y} – множина вихідних сигналів
λ – функція виходів
{A} – множина внутришніх станів
A
(адреса №10
ПЗП)
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
Попередній стан
автомата
Код
Позначення
Q1 Q0
ai
A2 A1
a0
0
0
a0
0
0
0
1
a1
0
1
a1
1
0
a2
a2
1
0
a3
1
1
1
1
a3
x
y
A0
0
1
0
1
0
1
0
1
D2
1
1
1
1
0
0
0
0
Сигнали
збудеження
тригерів
D1
D0
D1
D0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
0
Наступний
стан
автомата
aj
a1
a0
a2
a2
a3
a3
a0
a0
D
(дані
ПЗП)
5
4
6
6
3
3
0
0
184. Схема автомата
185. Література. References
http://ru.wikibooks.org/wiki/ Кодирование текста
http://ich.tsu.ru/~ptara/course/network/bis-unit5/Unit5.html Компьютерные сети
http://www.pandia.ru/text/77/132/865.php Типы каналов связи
http://skachate.ru/informatika/22409/index.html?page=2 Представление информации в линиях
связи интерфейсов на физическом уровне
http://www.bestreferat.ru/referat-194986.html Криптографічні методи захисту інформації
http://cozap.com.ua/text/12464/index-1.html?page=2 Методи криптографічного захисту інформації
http://www.znanius.com/3851.html Криптографічний захист інформації
http://uk.wikipedia.org/wiki/%D0%9F%D0%BE%D1%82%D0%BE%D0%BA%D0%BE%D0%B2%
D0%B8%D0%B9_%D1%88%D0%B8%D1%84%D1%80 Потоковий шифр
http://www.bestreferat.ru/referat-141325.html Основи інформаційної безпеки
http://edu.dvgups.ru/METDOC/GDTRAN/NTS/EPS/EPT/METOD/UP/frame/7_1.htm Дешифратор
http://life-prog.ru/ukr/view_arhitektura.php?id=4 Семисегментний індикатор.
http://avrlab.com/node/307 как использовать семисегментный индикатор
http://www.eope.ee/_download/euni_repository/file/1714/DT_4_suntees_ru.zip/DT_4_suntees_ru/43___.html
Минимизация логических функций
Lviv, CL.
26.03.2014
Комп'ютерна логіка
18
185
5

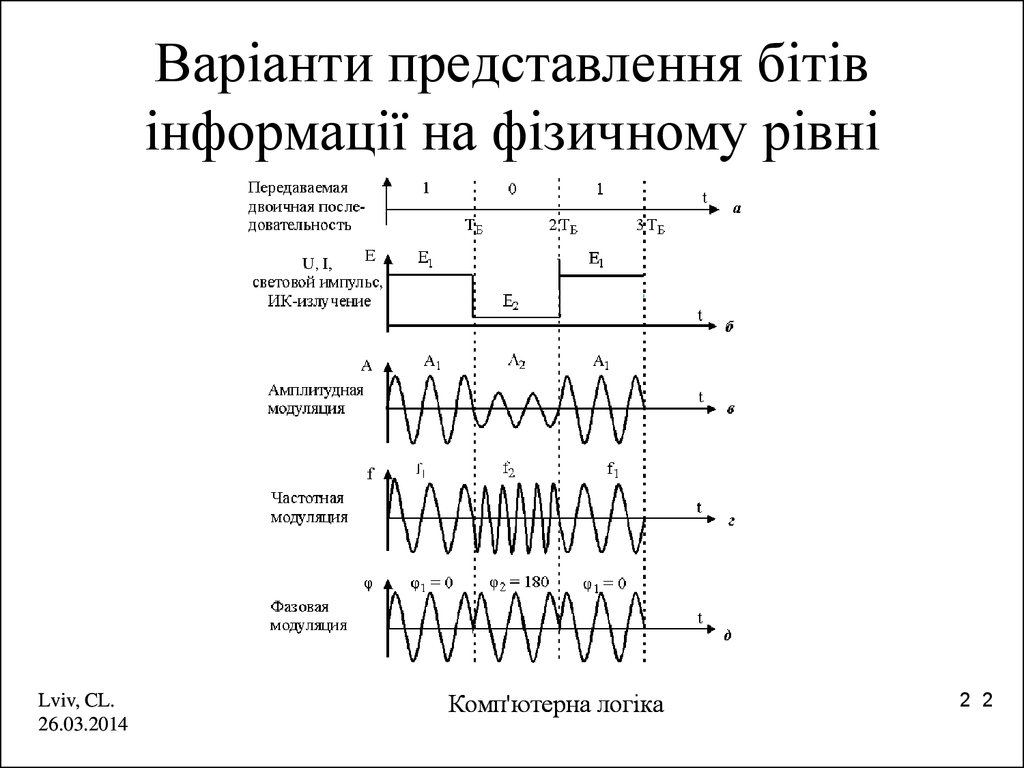
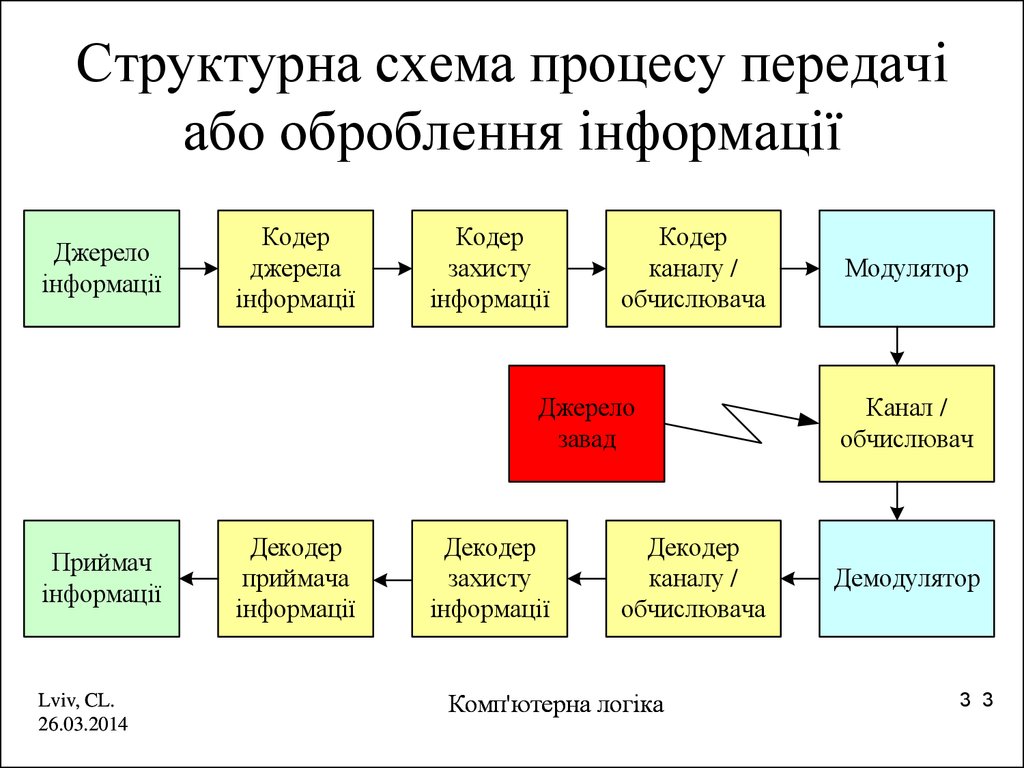
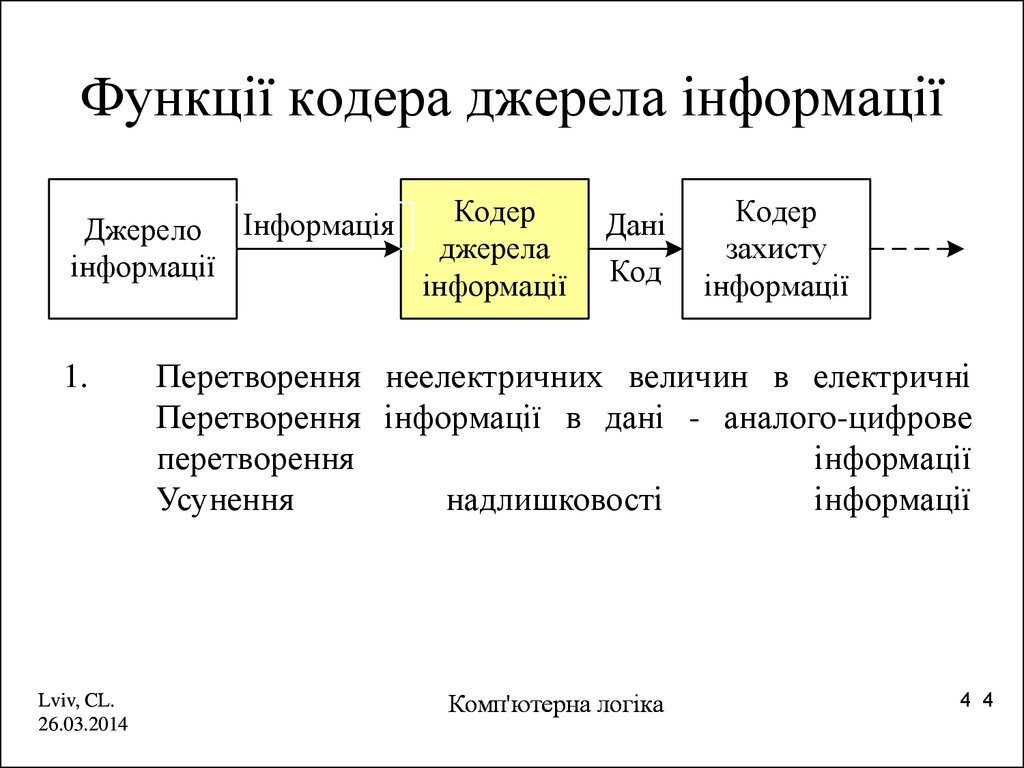

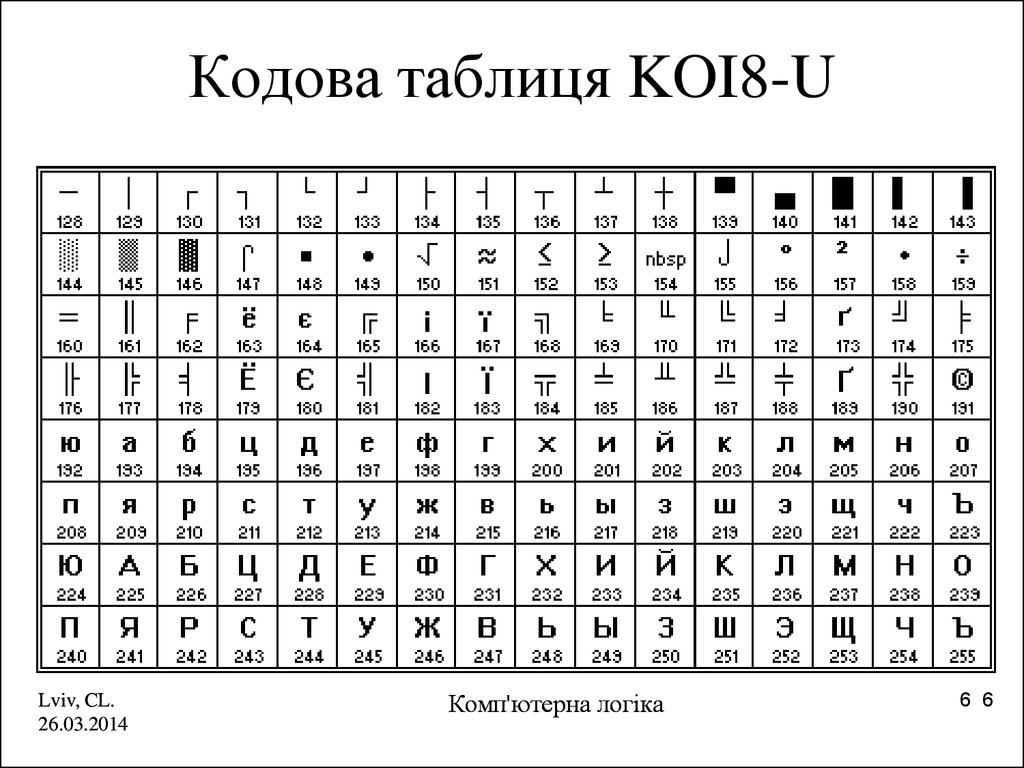

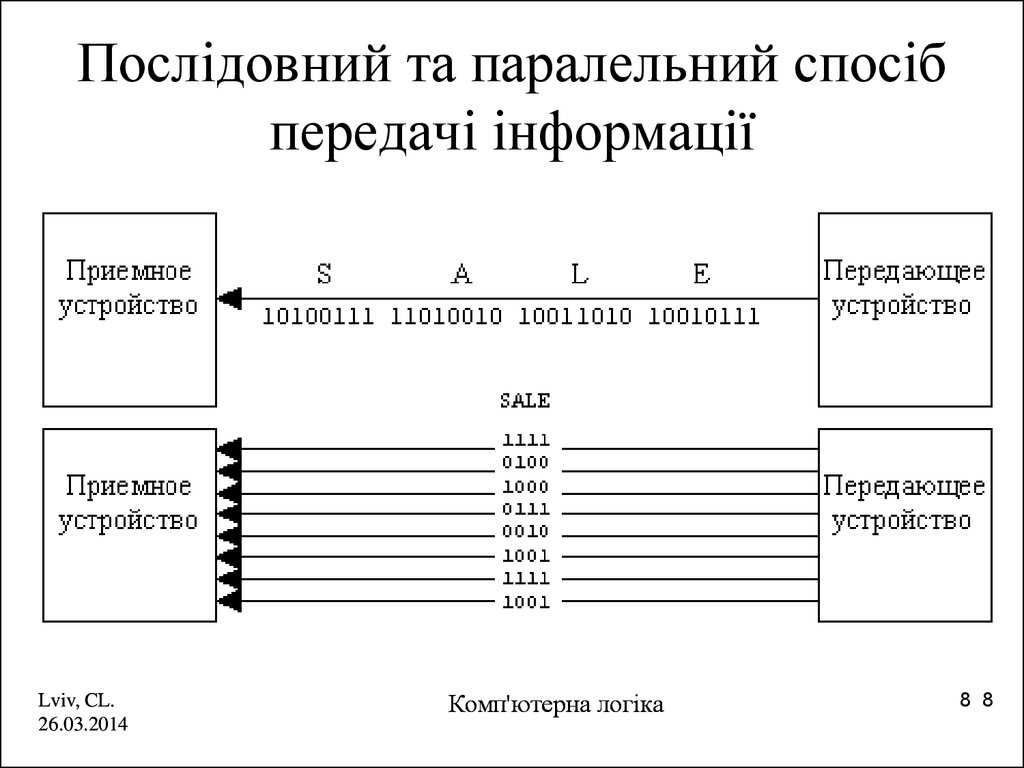
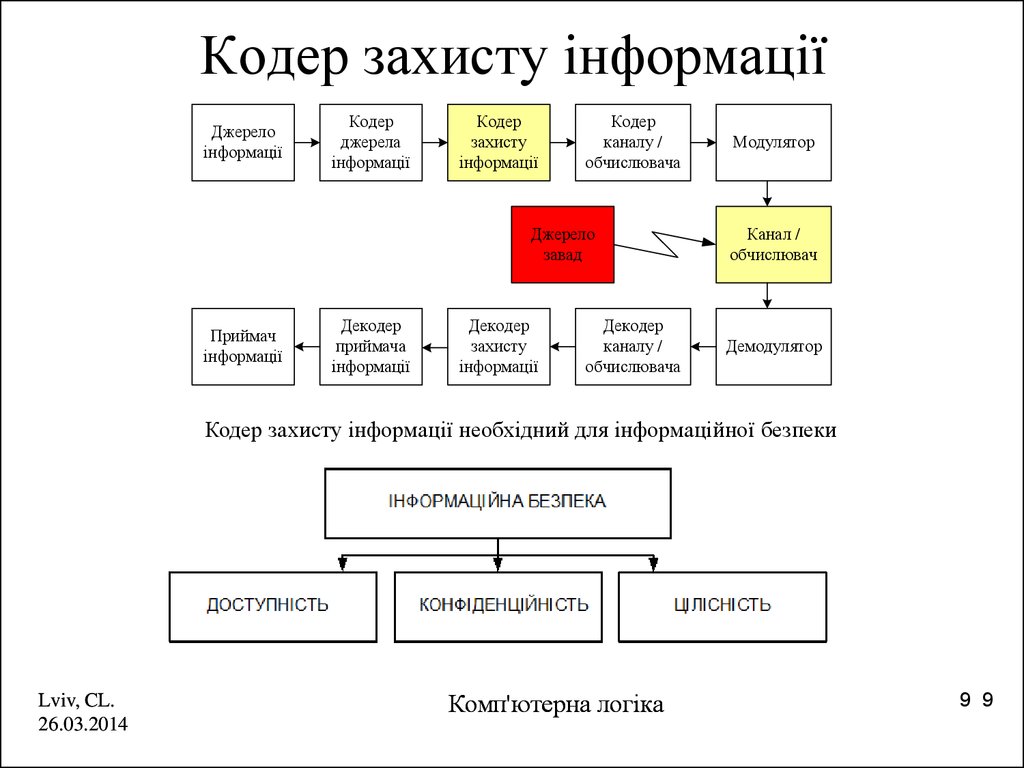


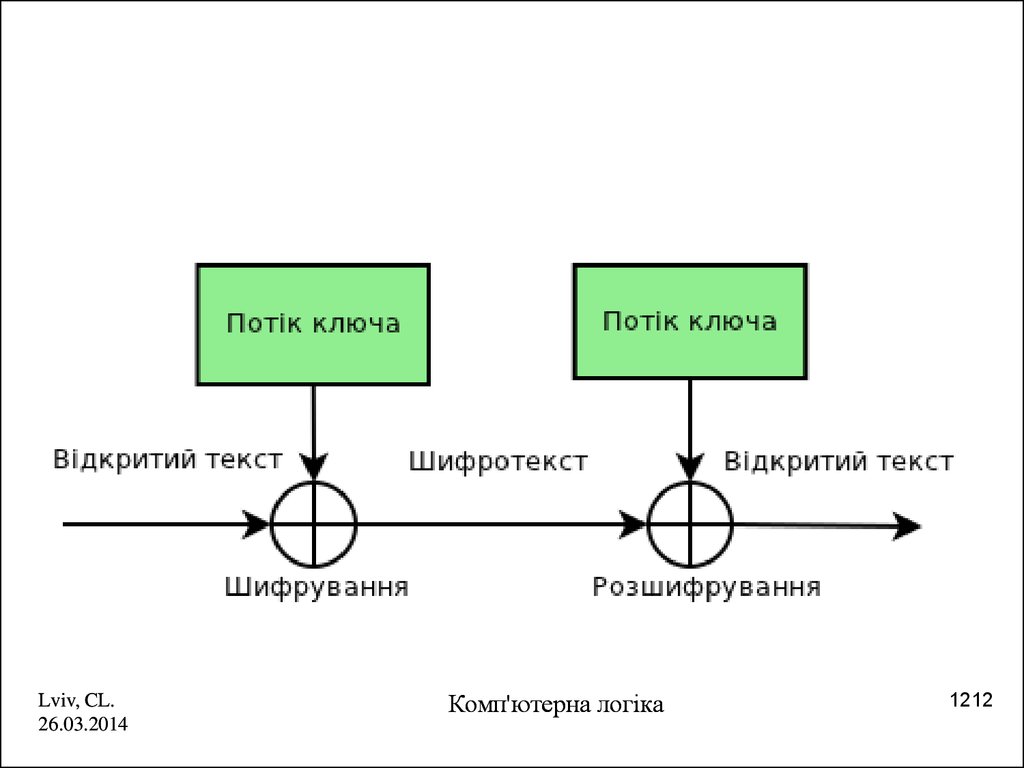
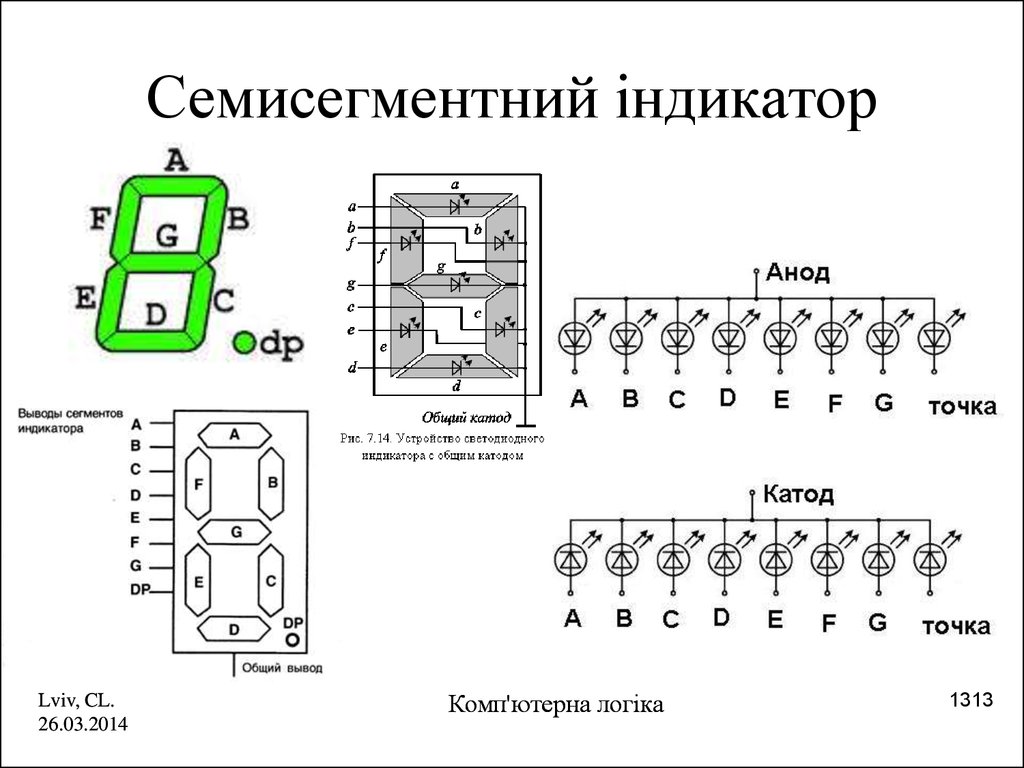
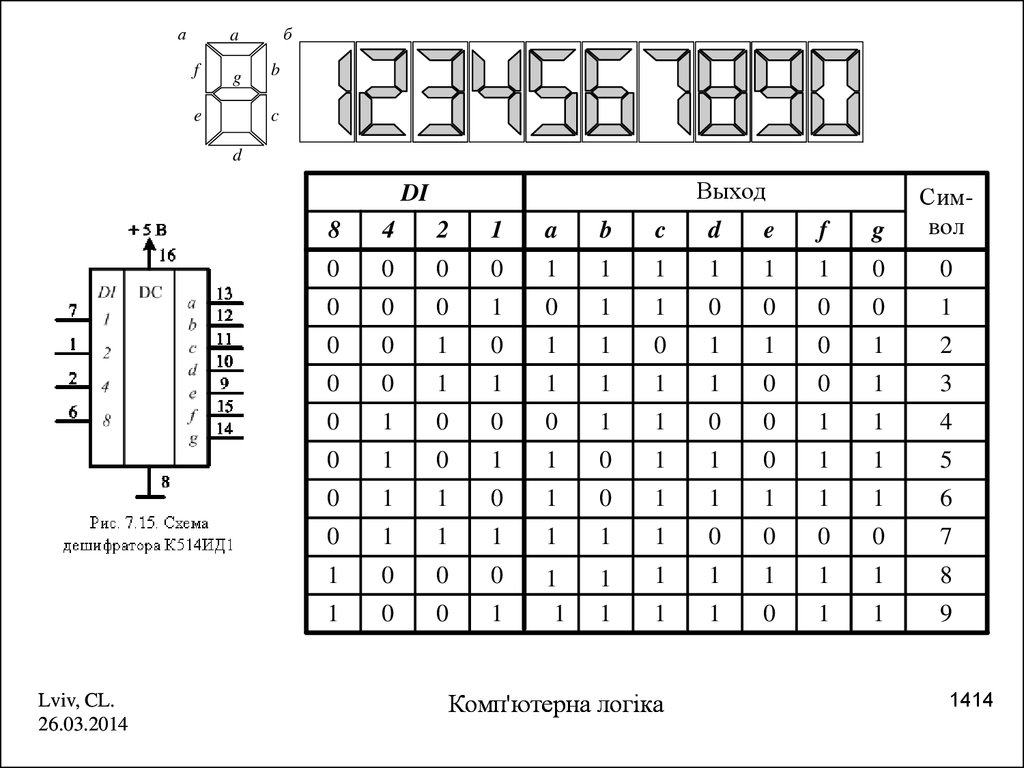
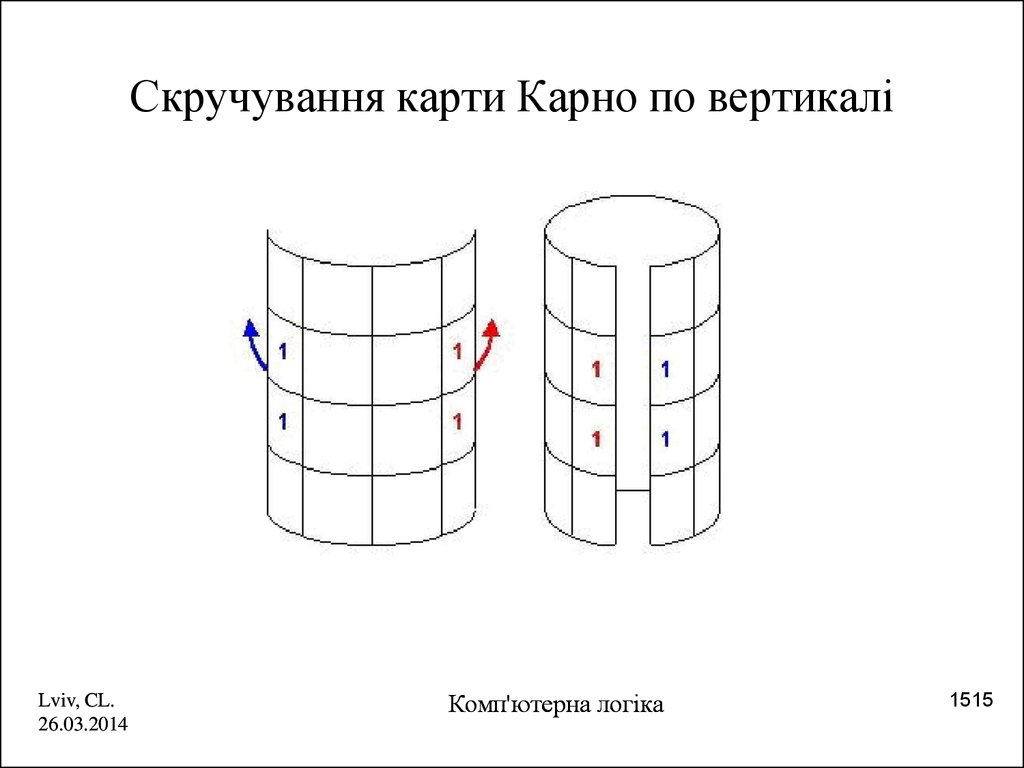
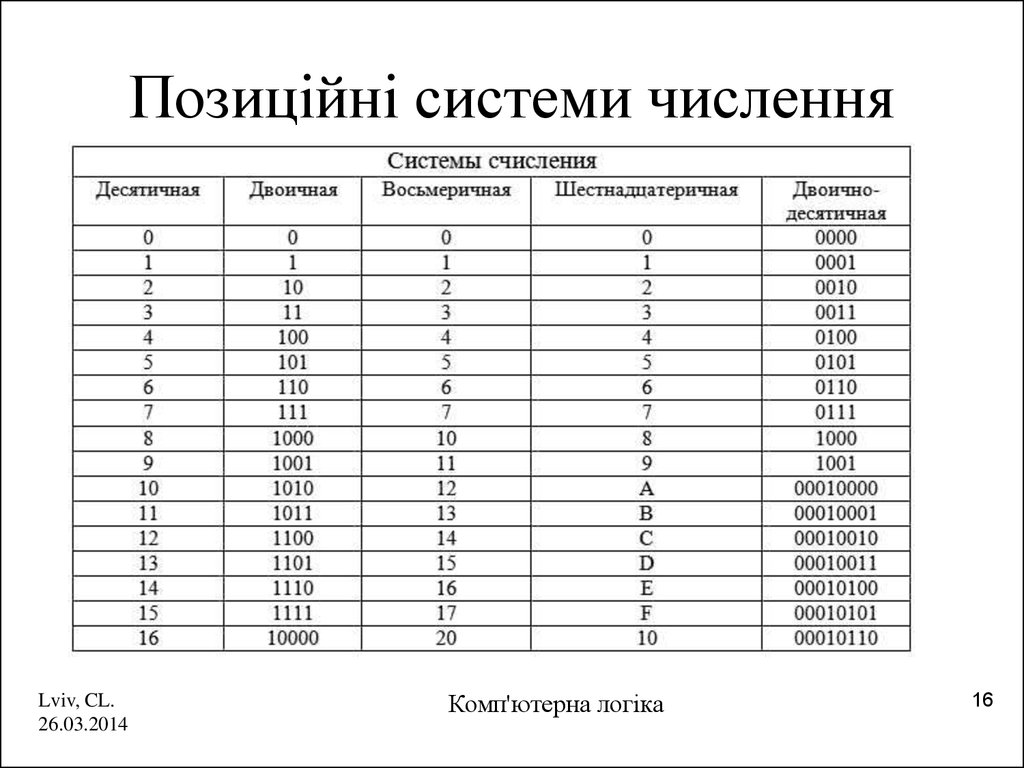


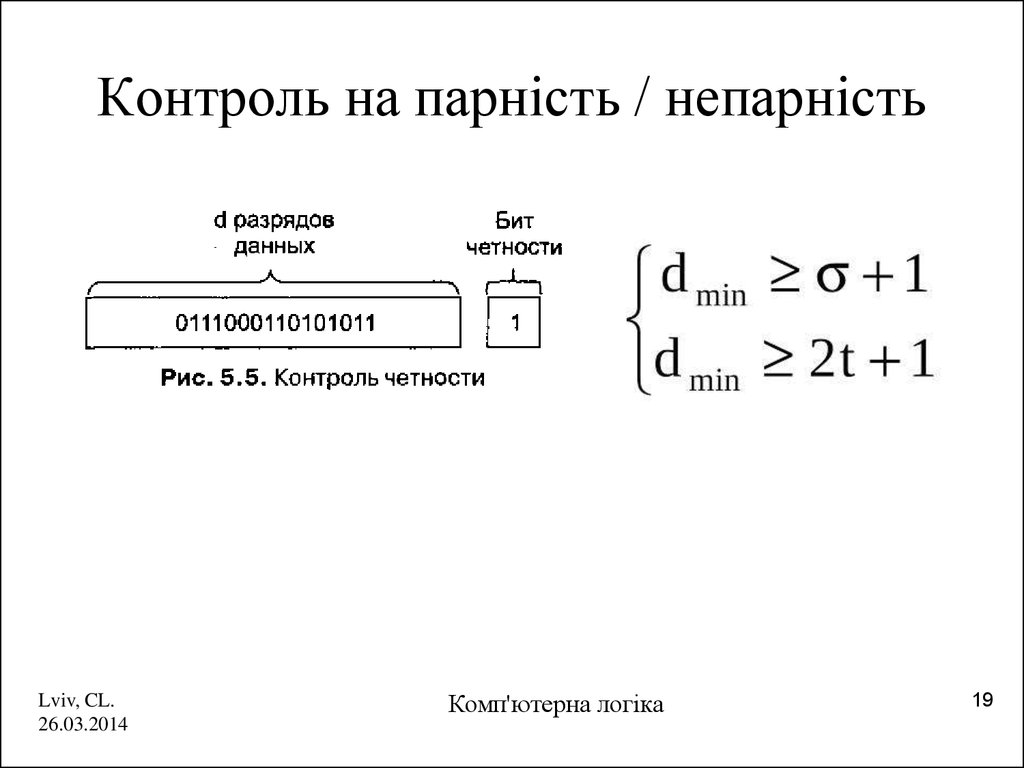
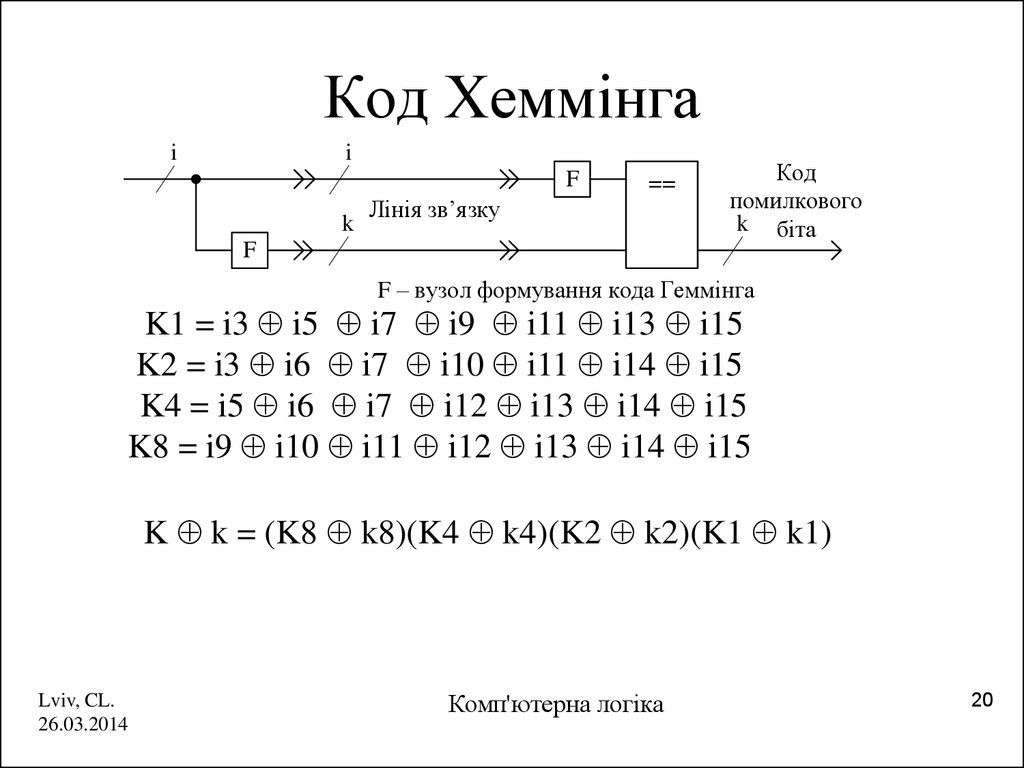
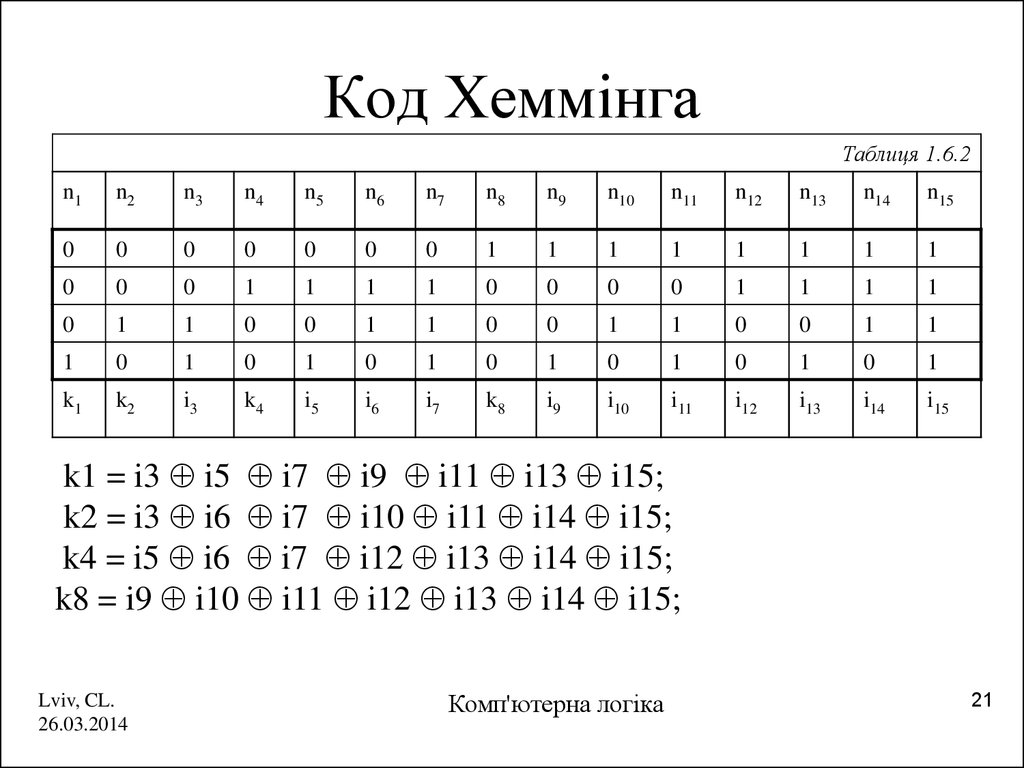
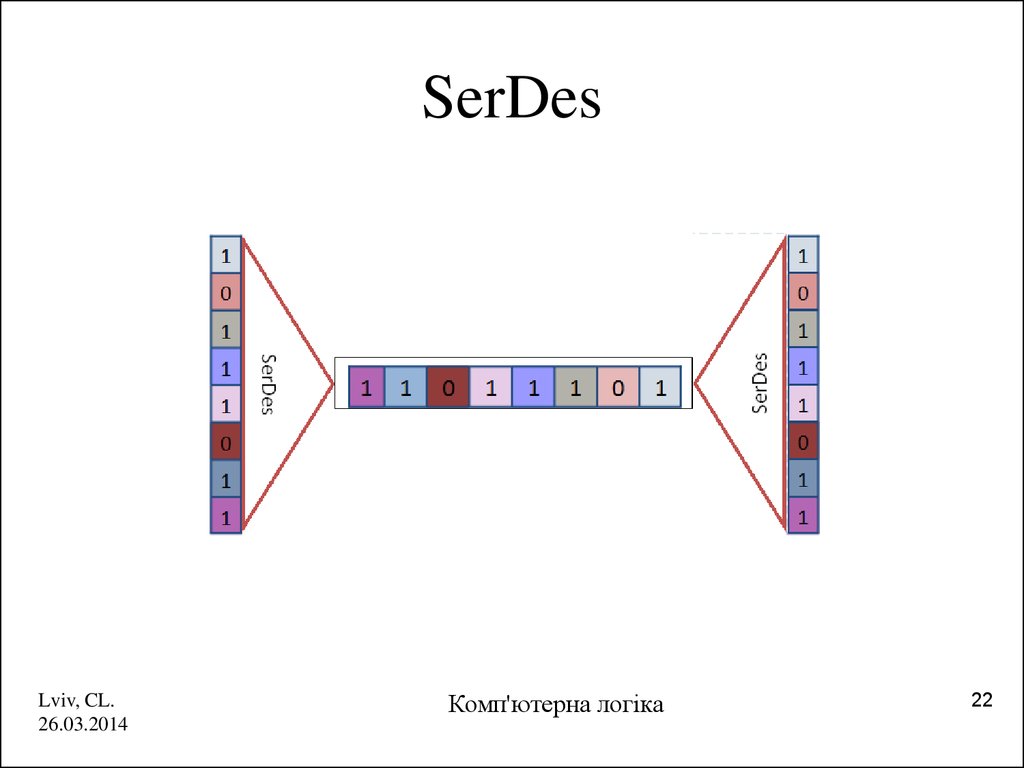





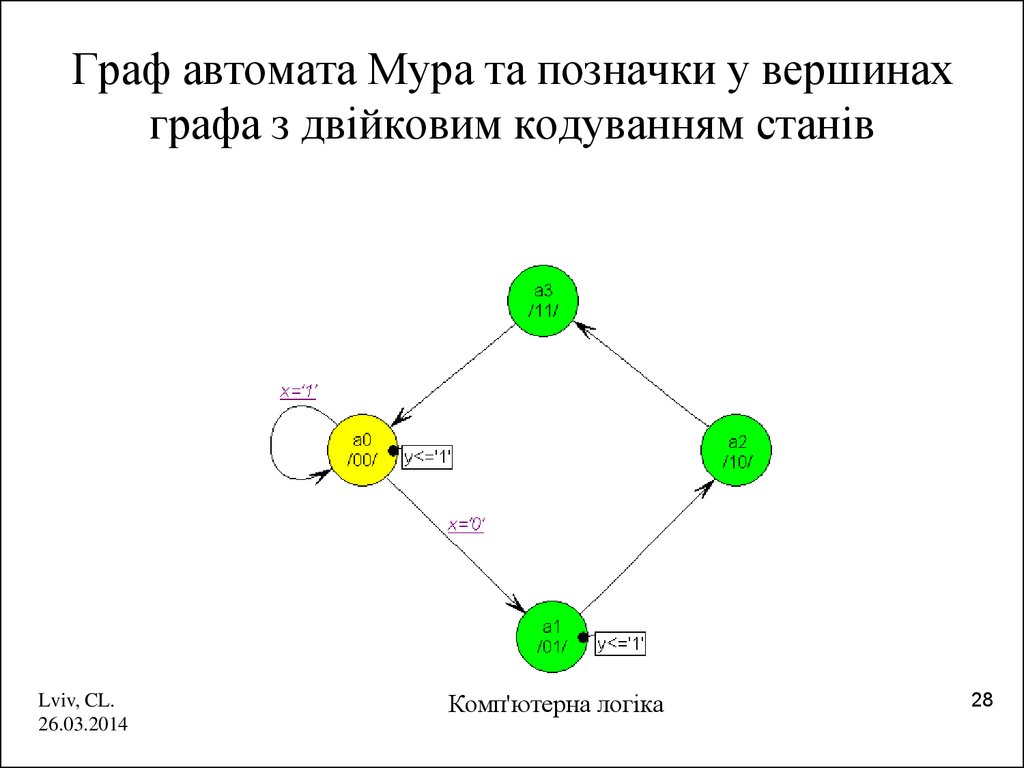
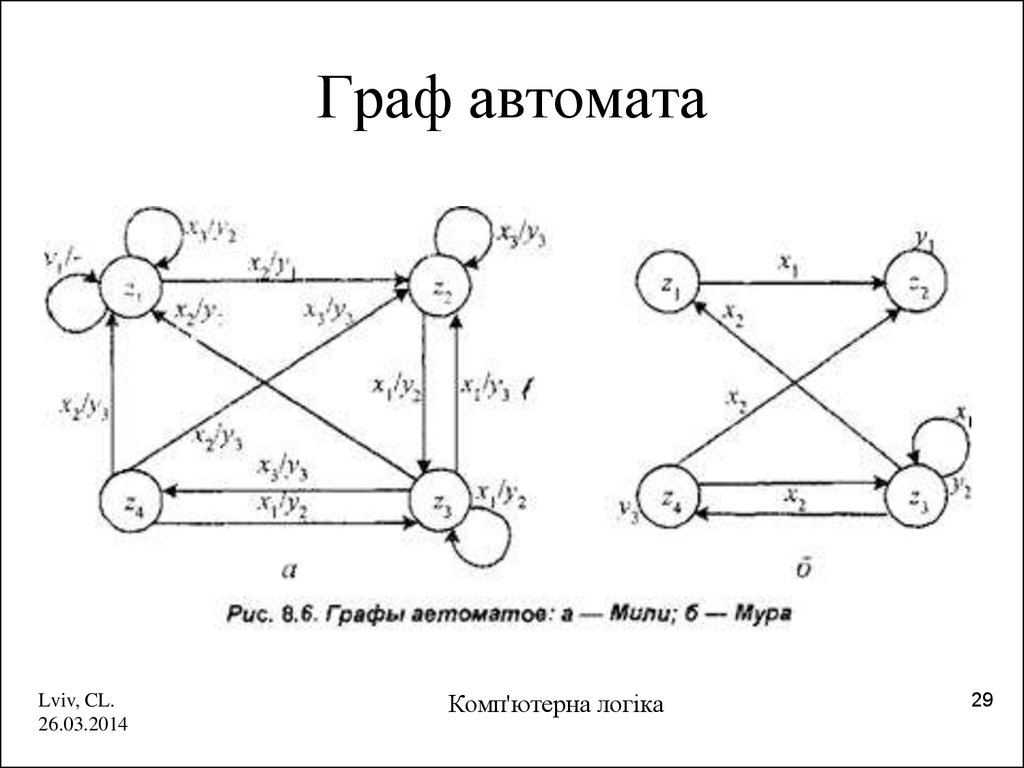
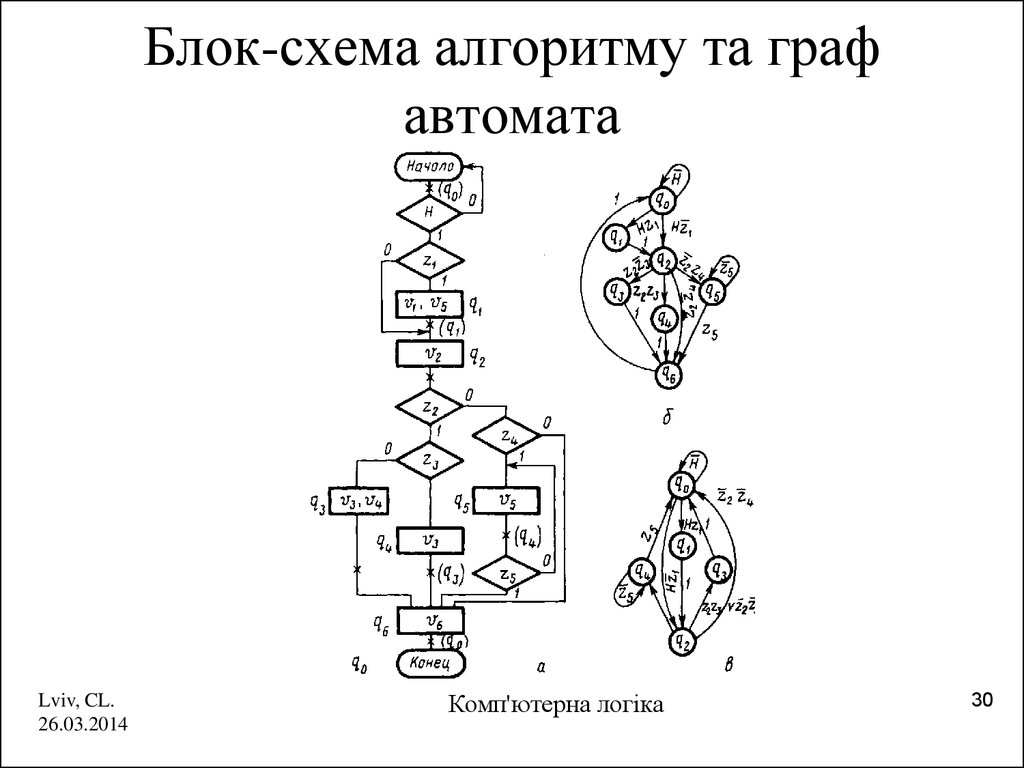
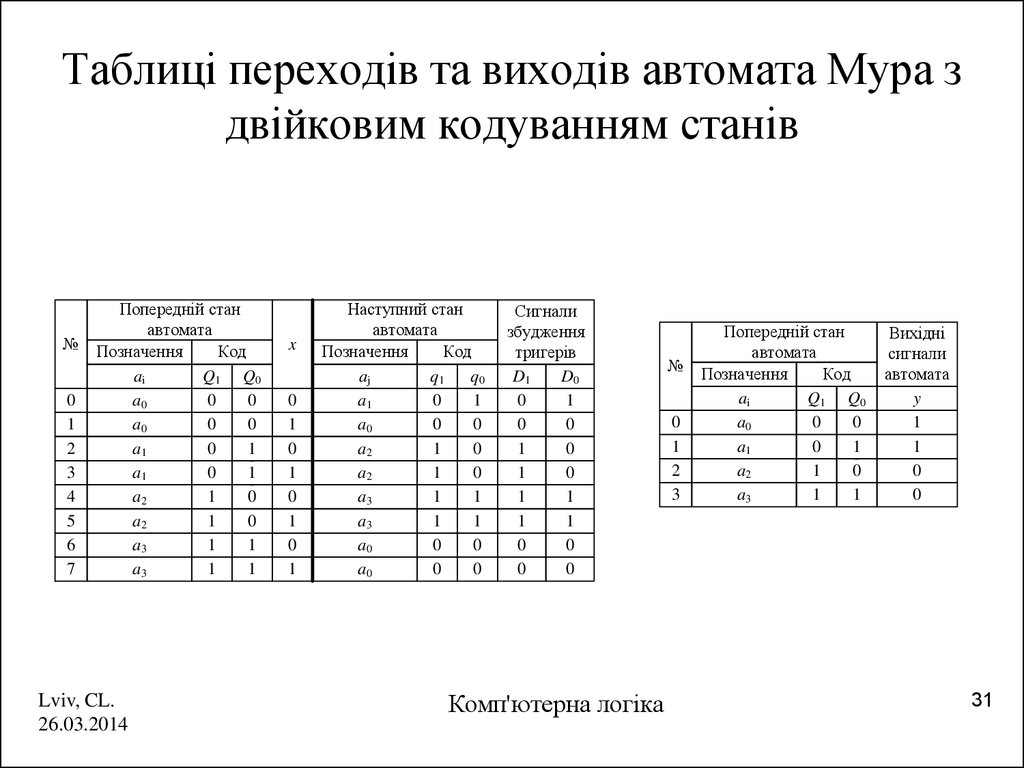
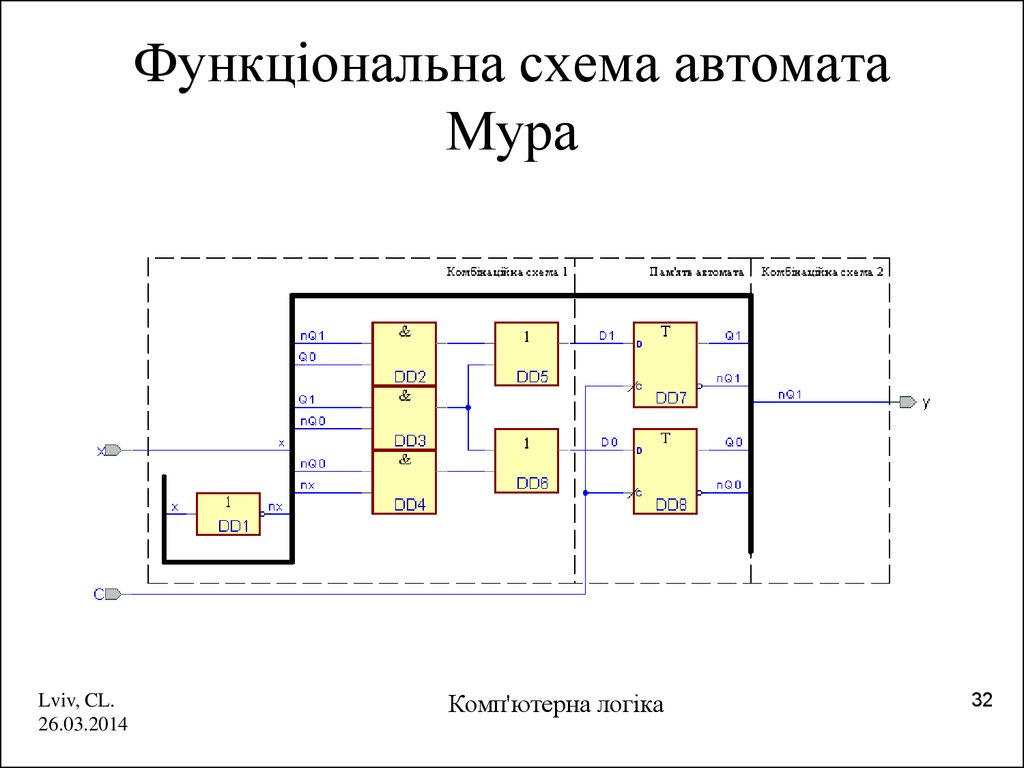




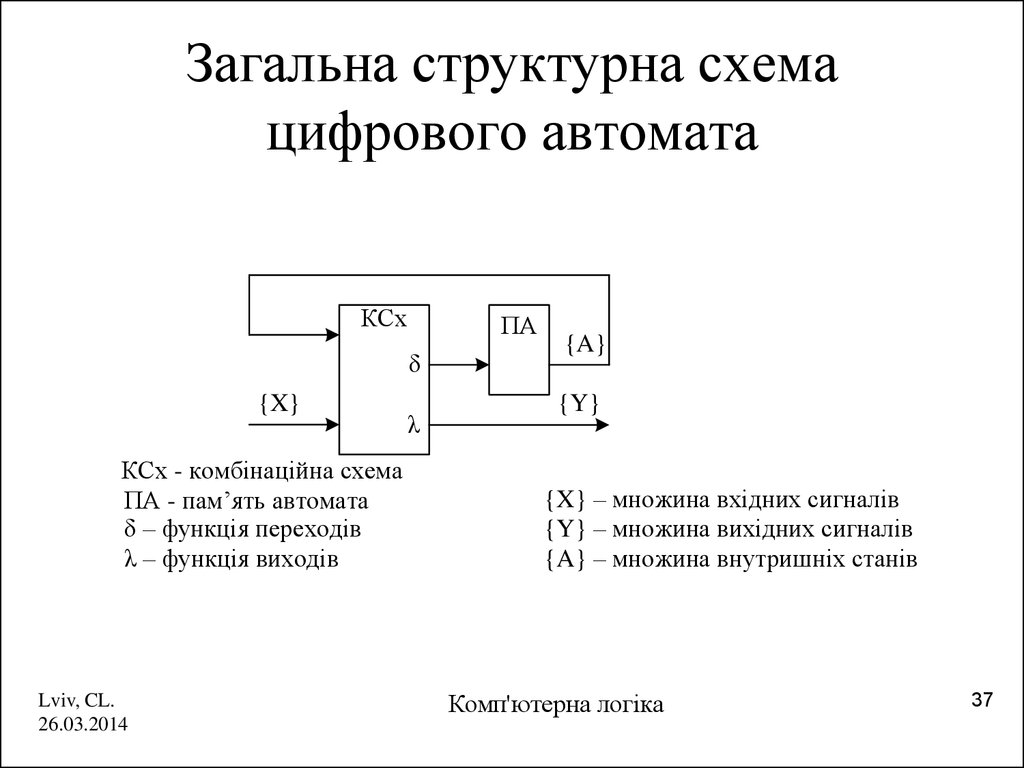
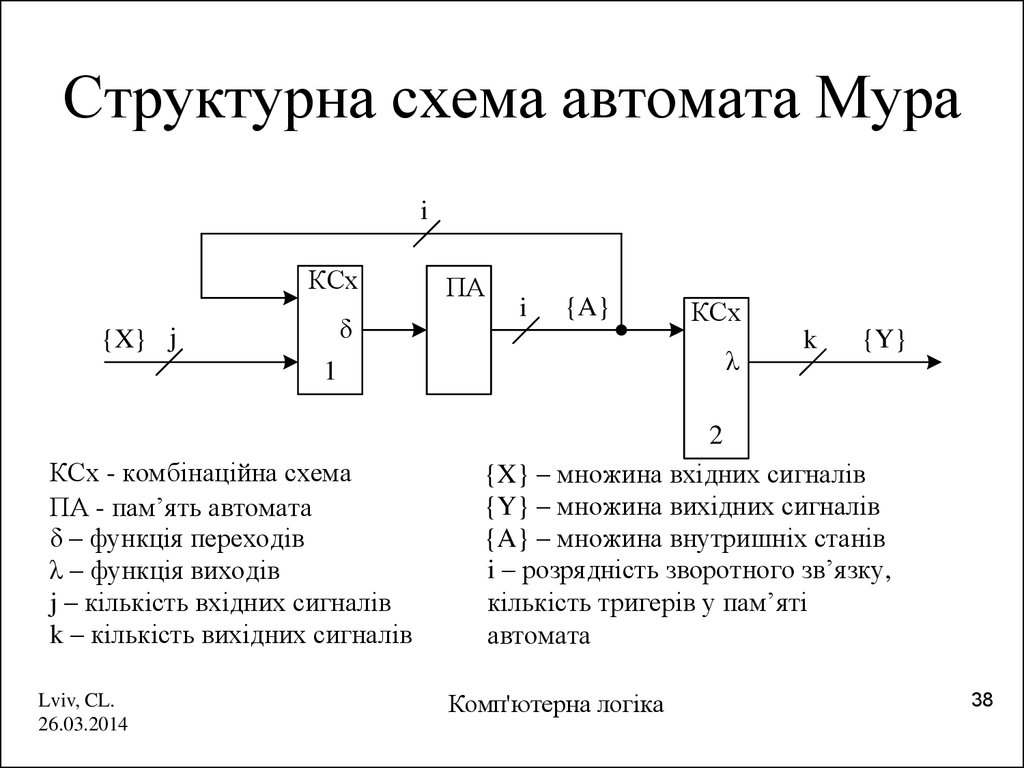
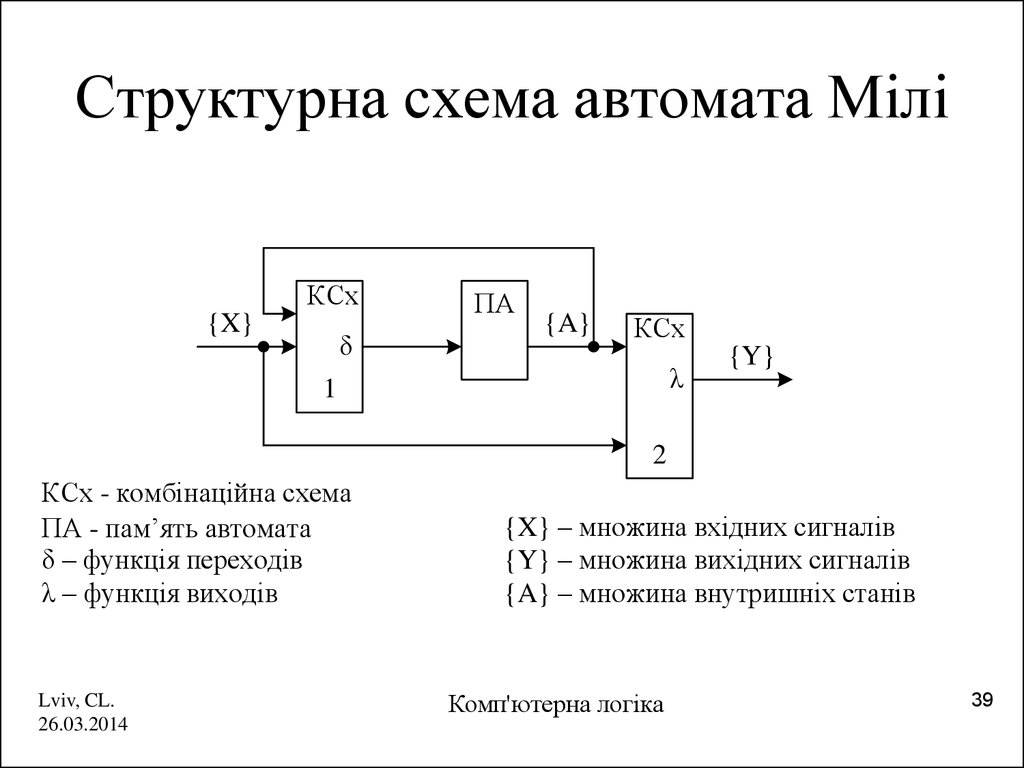

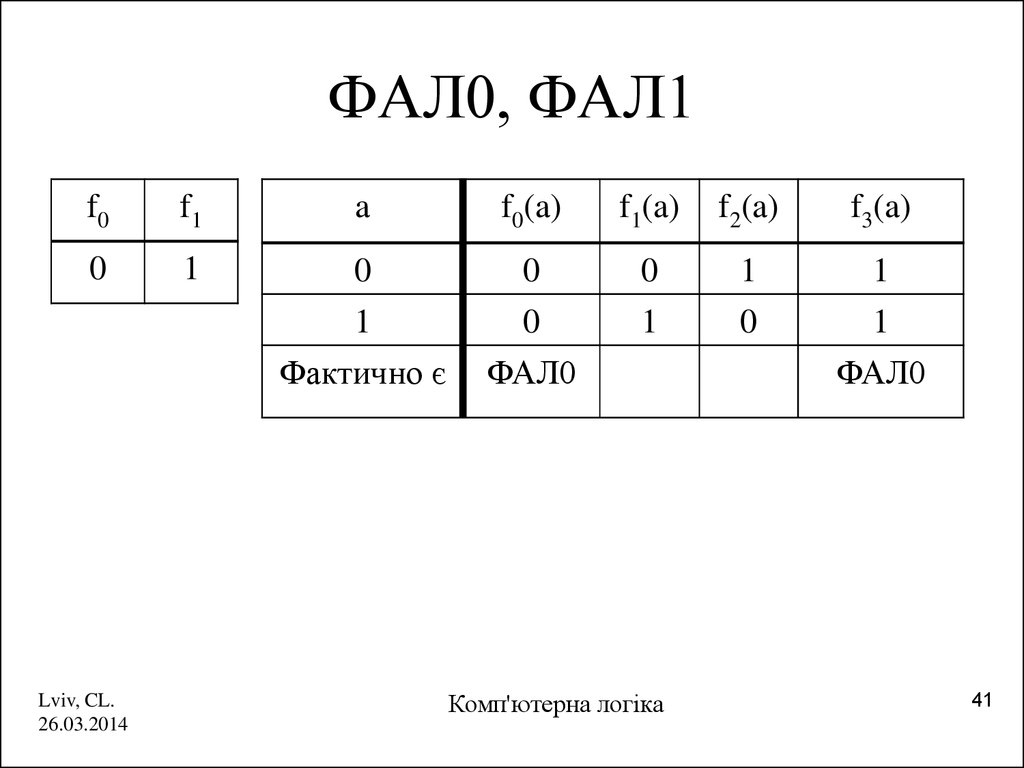
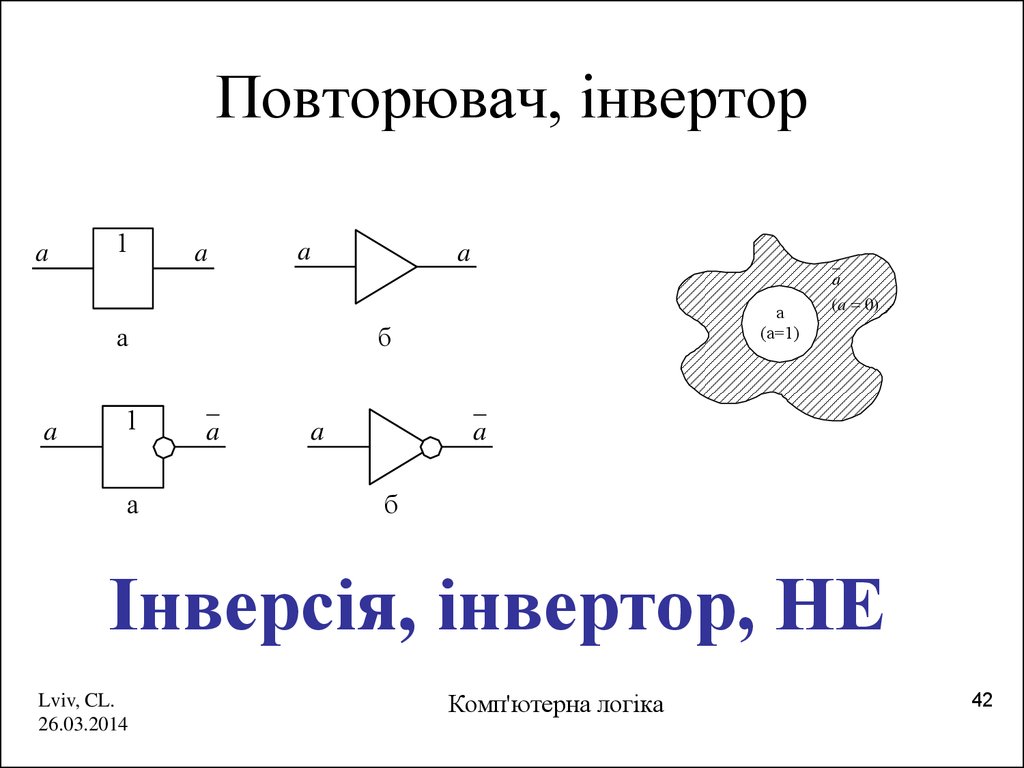
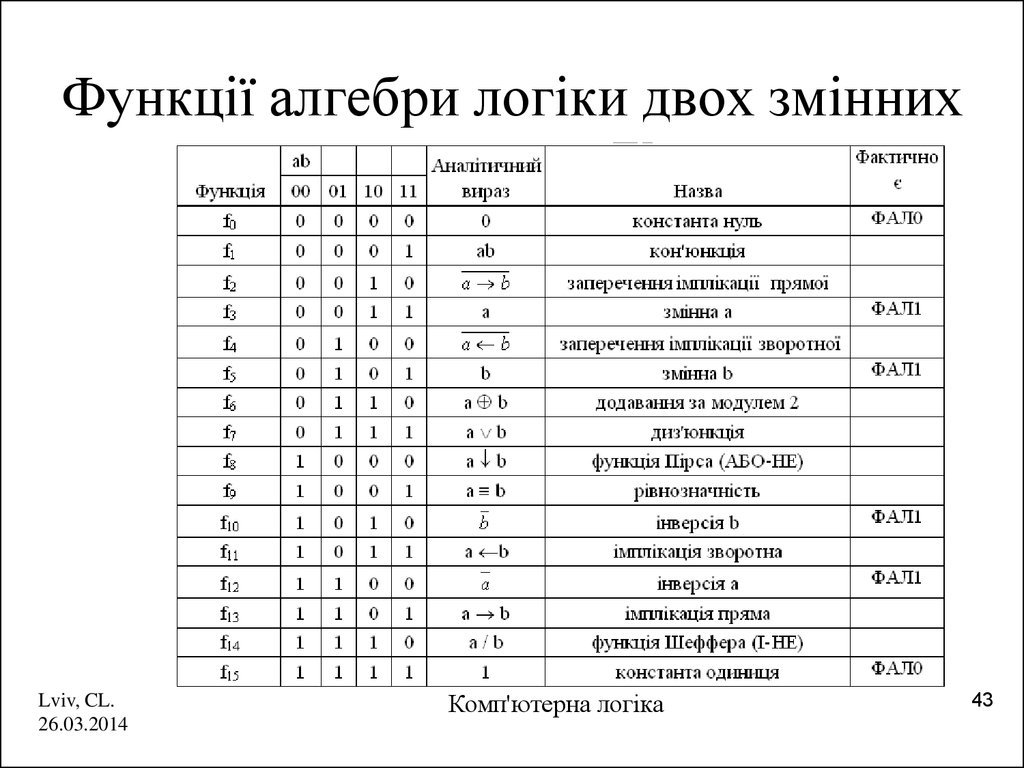

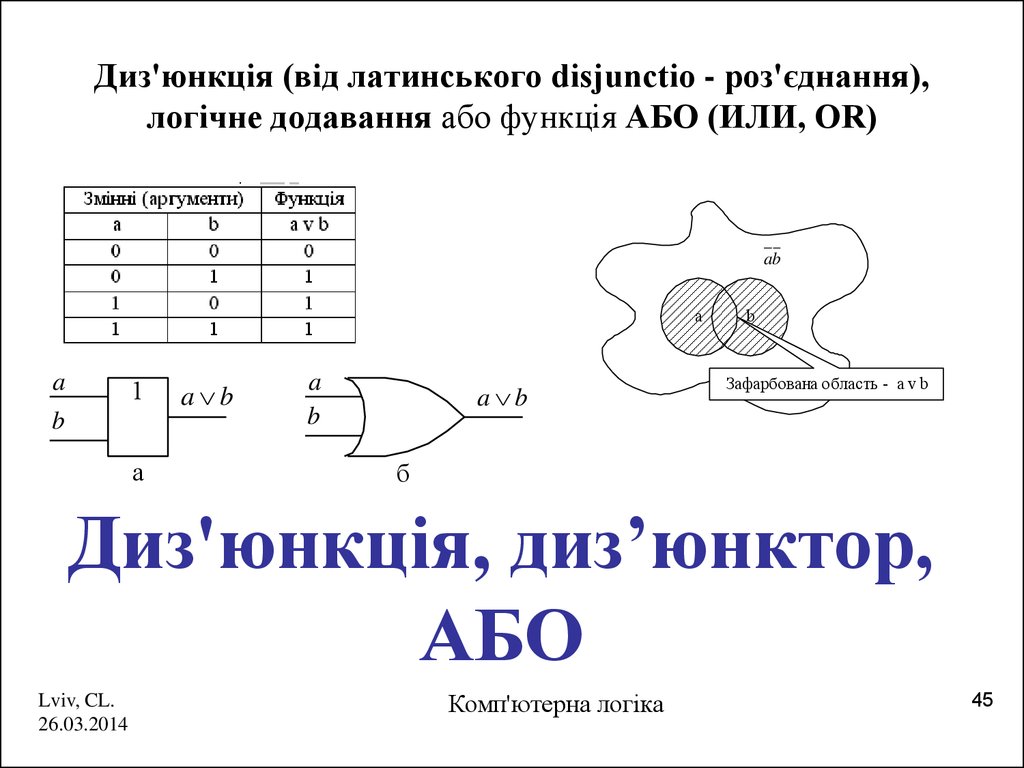
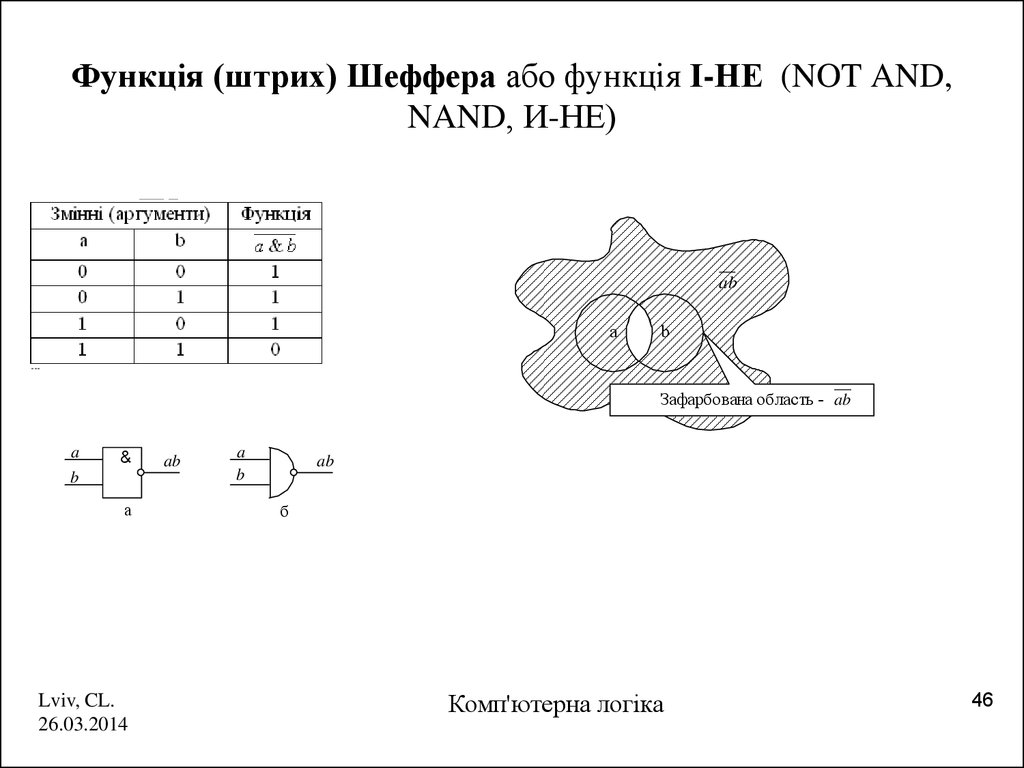



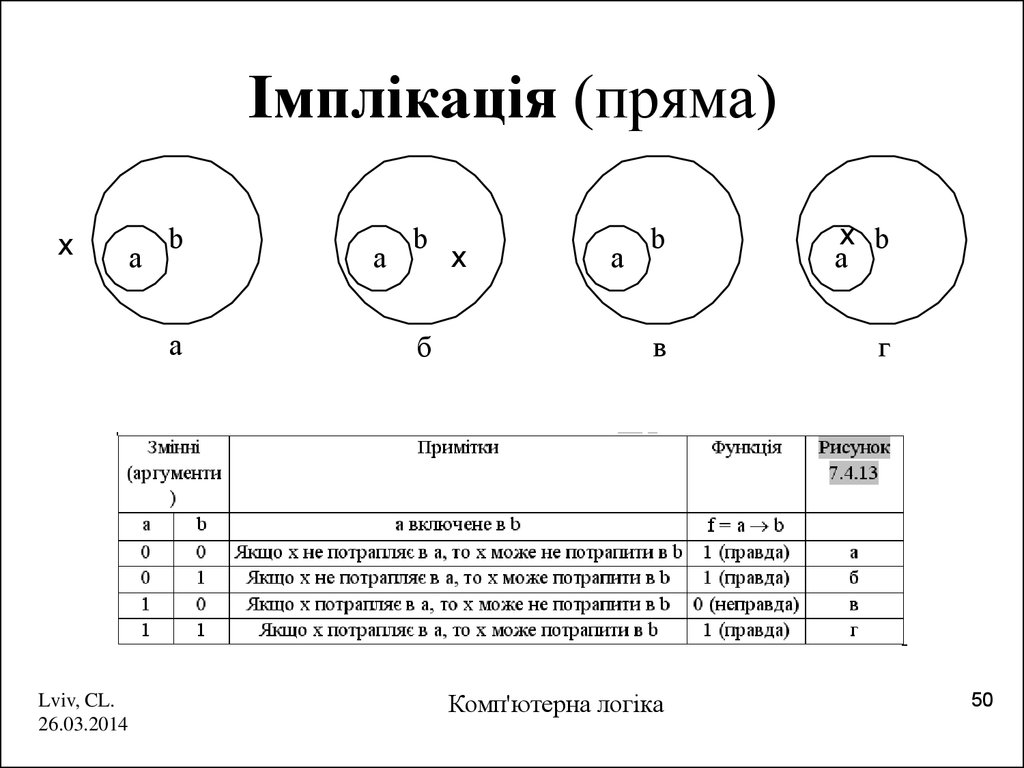
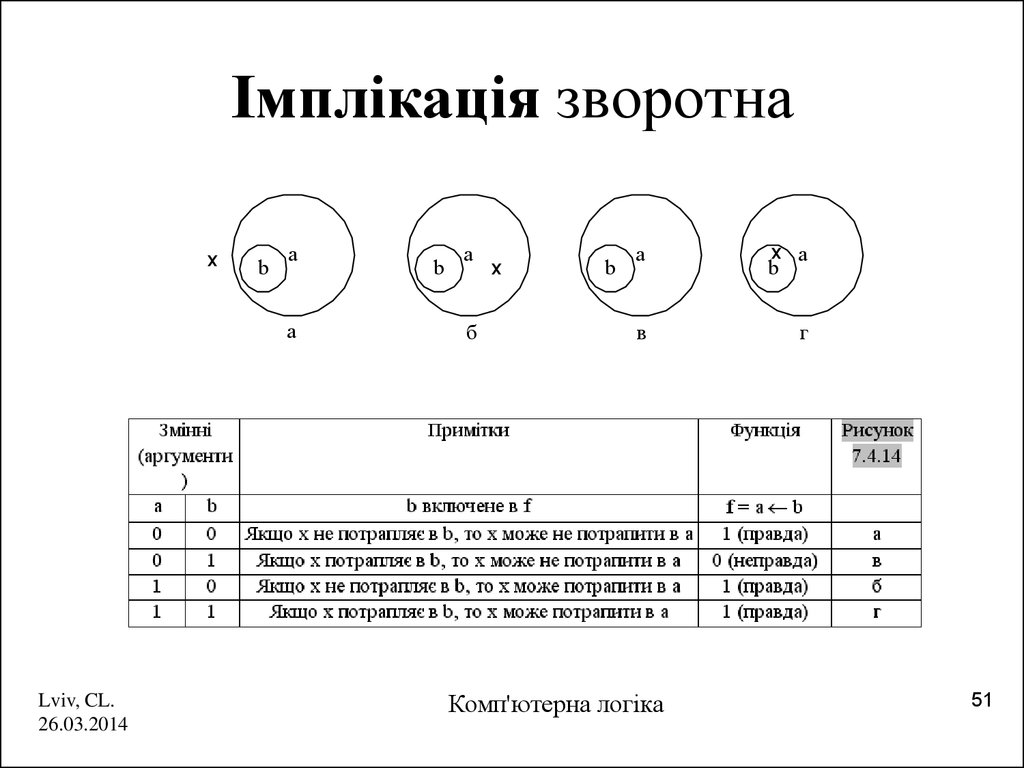

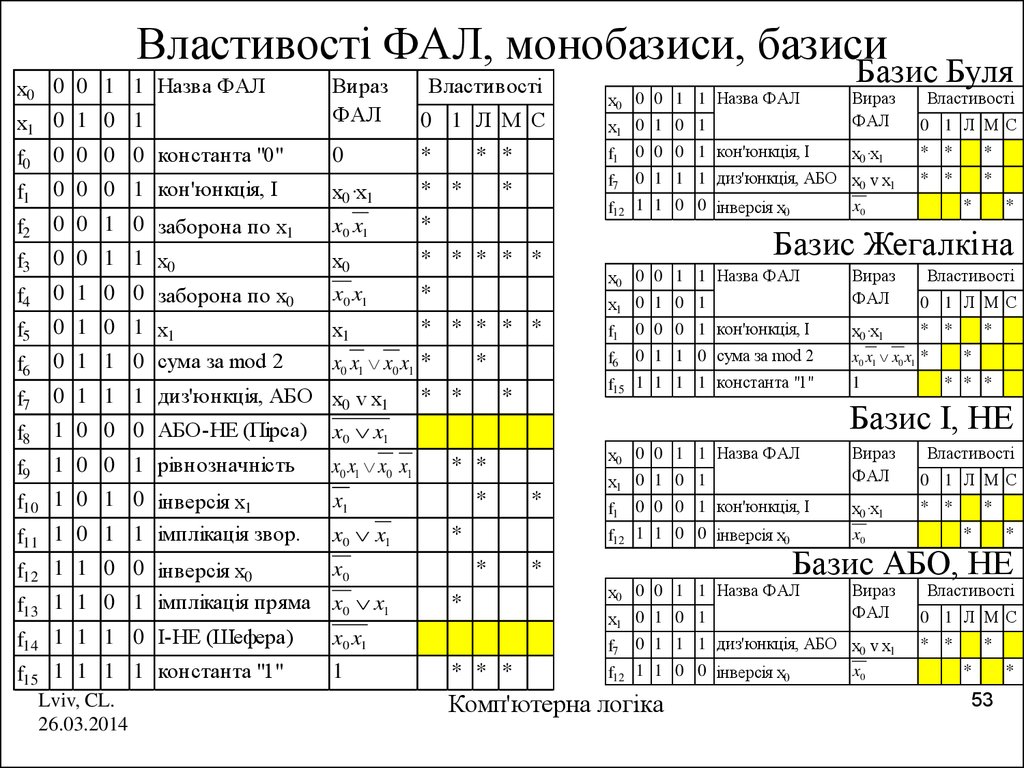

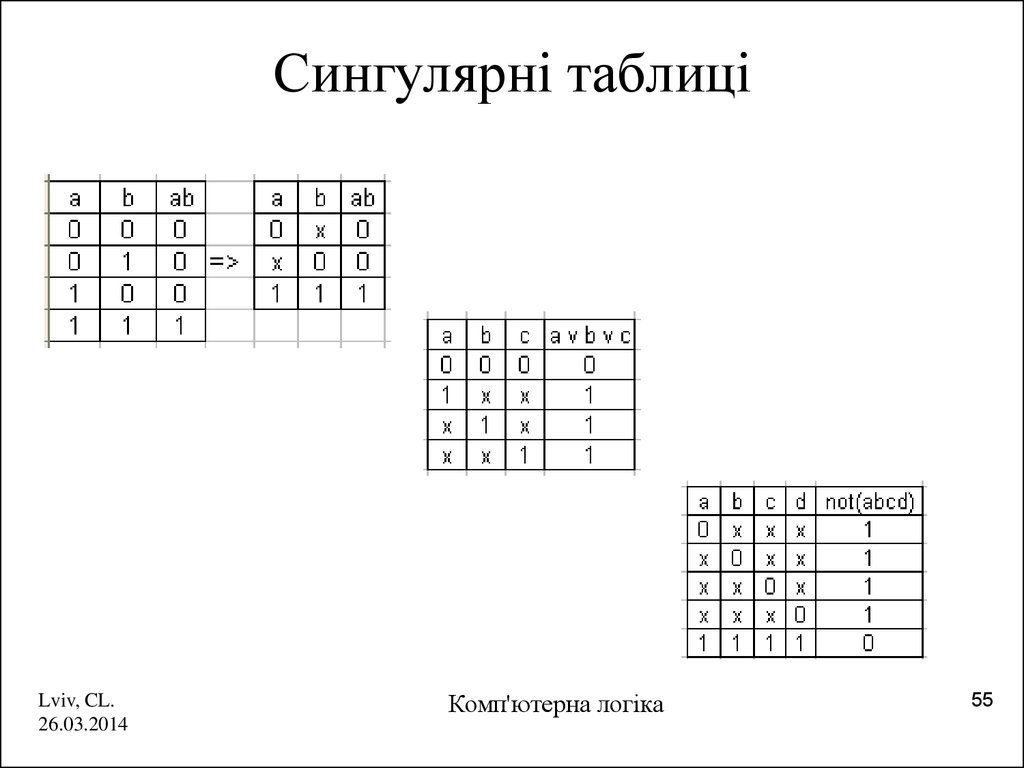








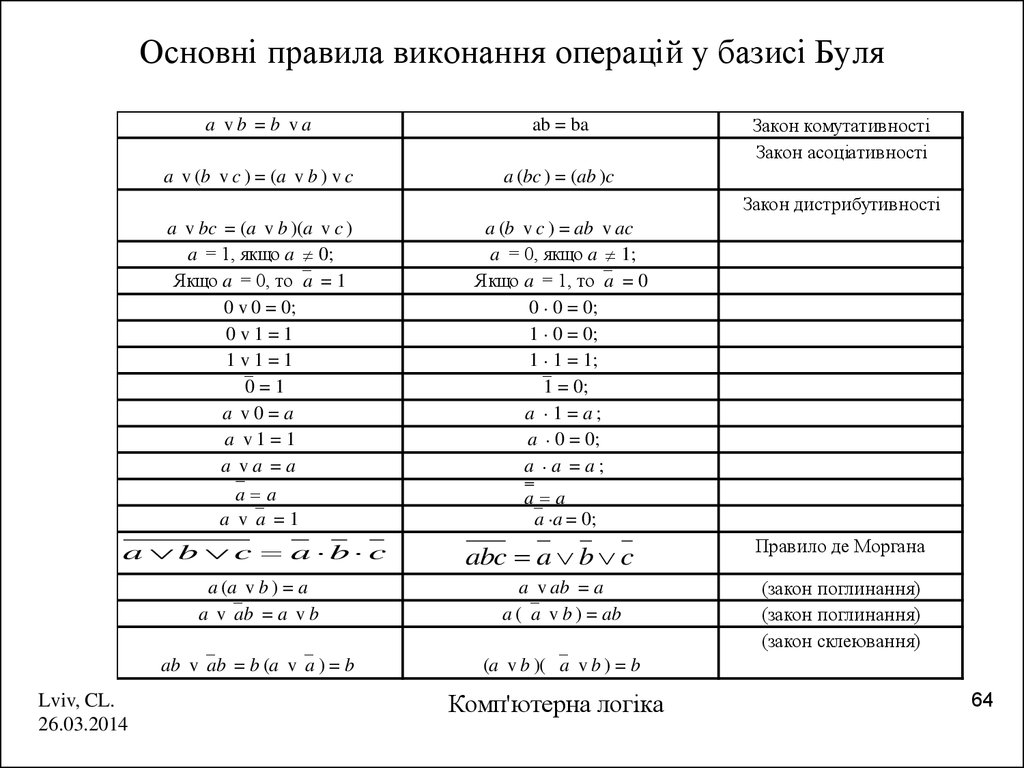
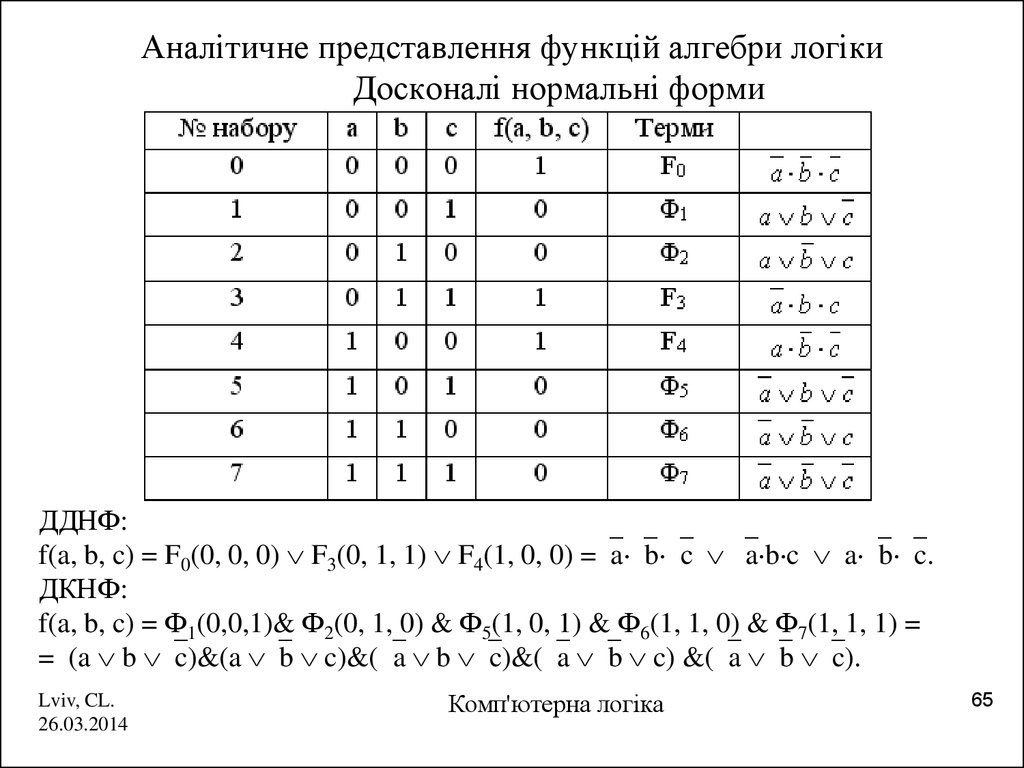


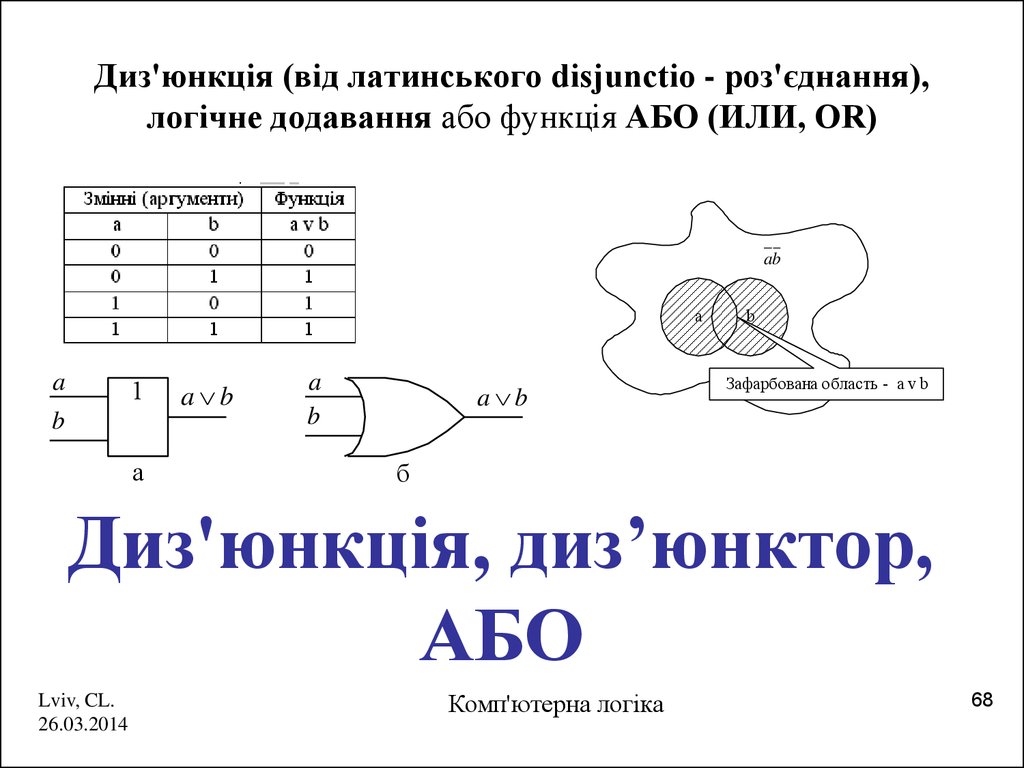
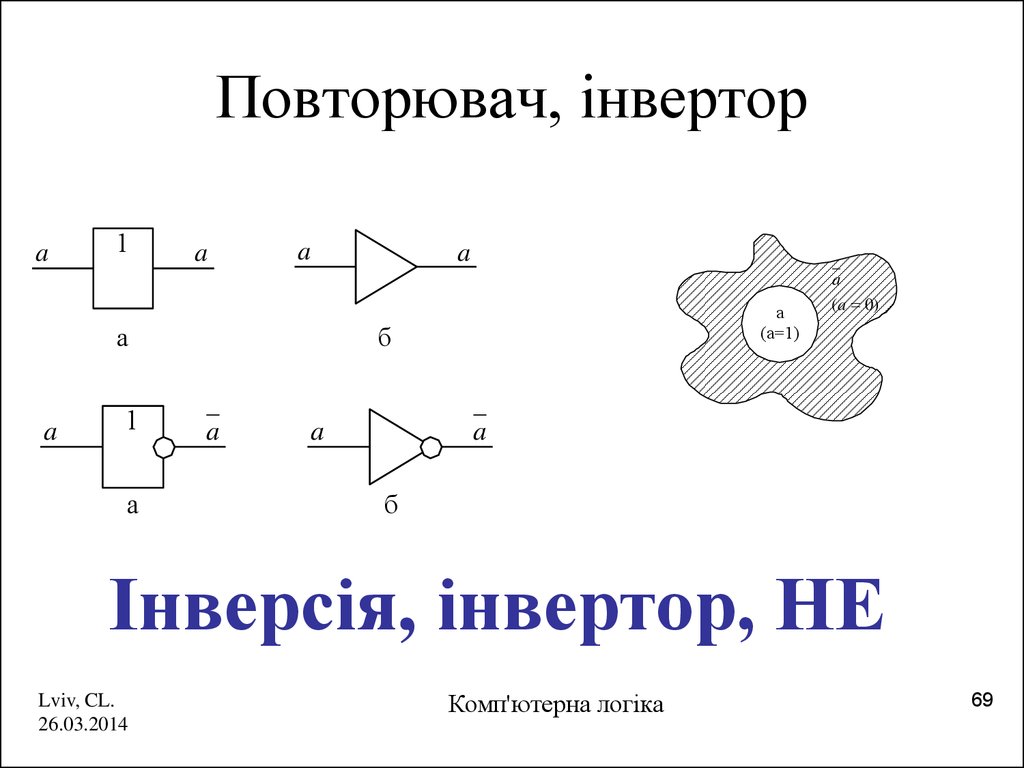

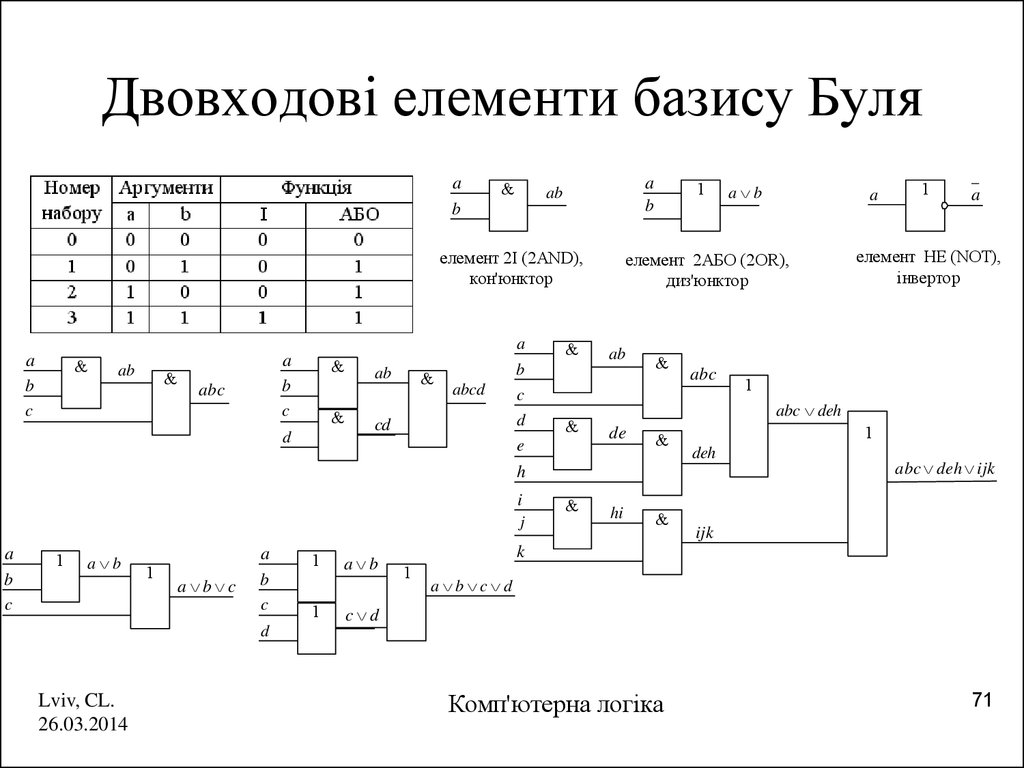


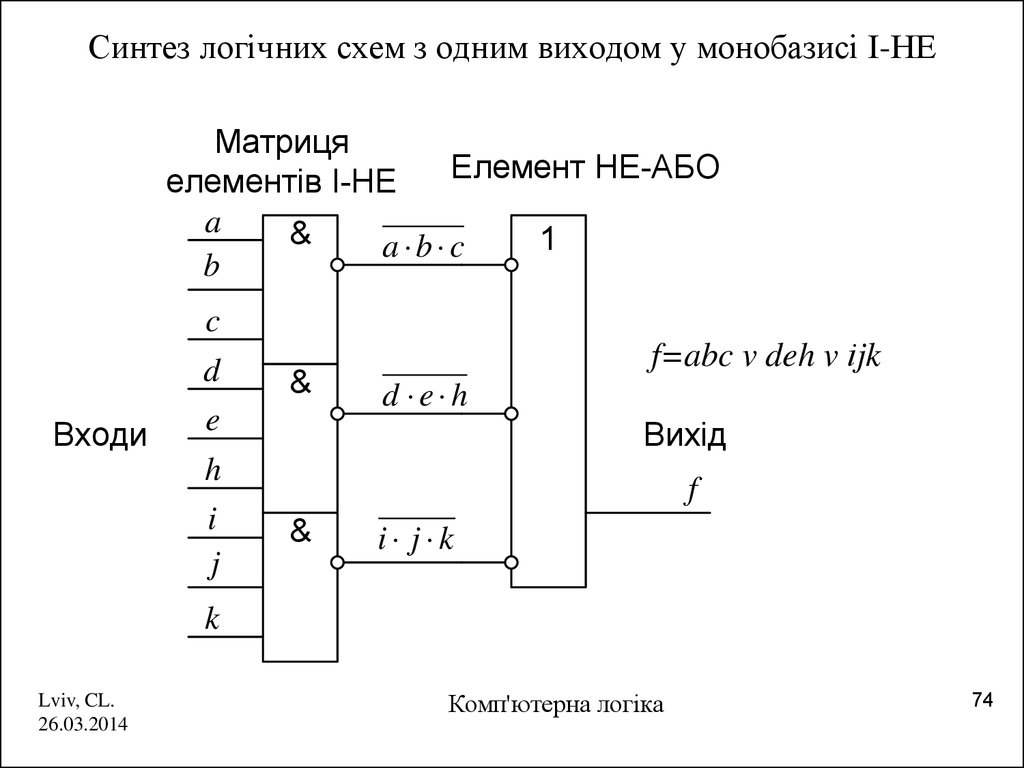

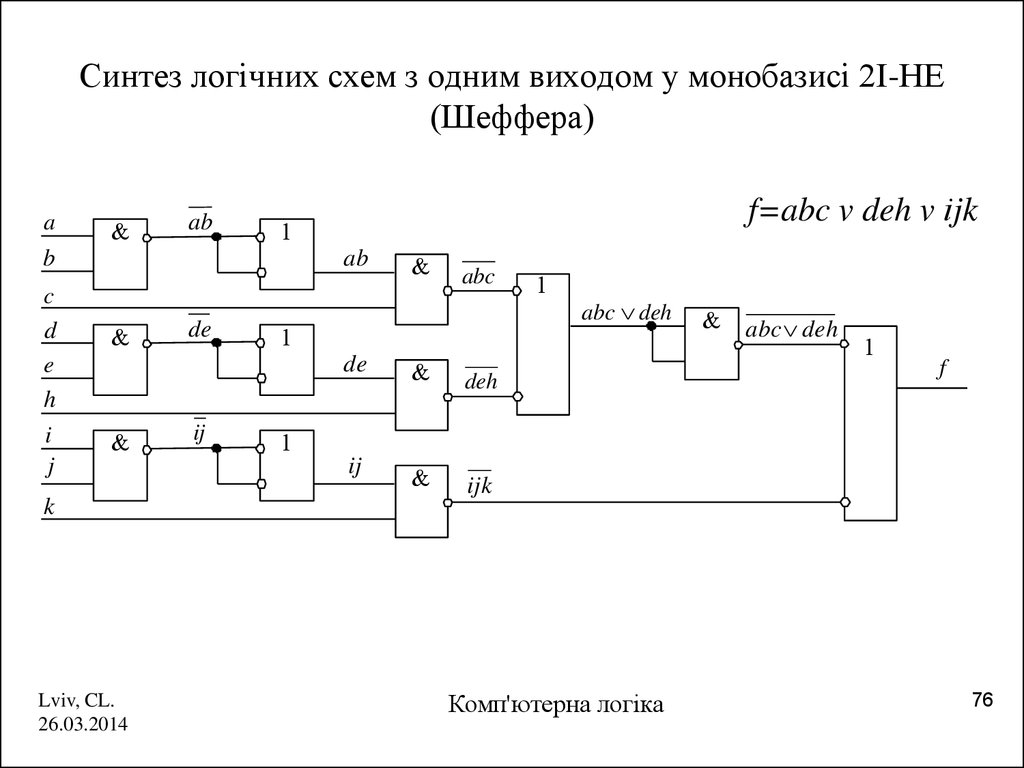

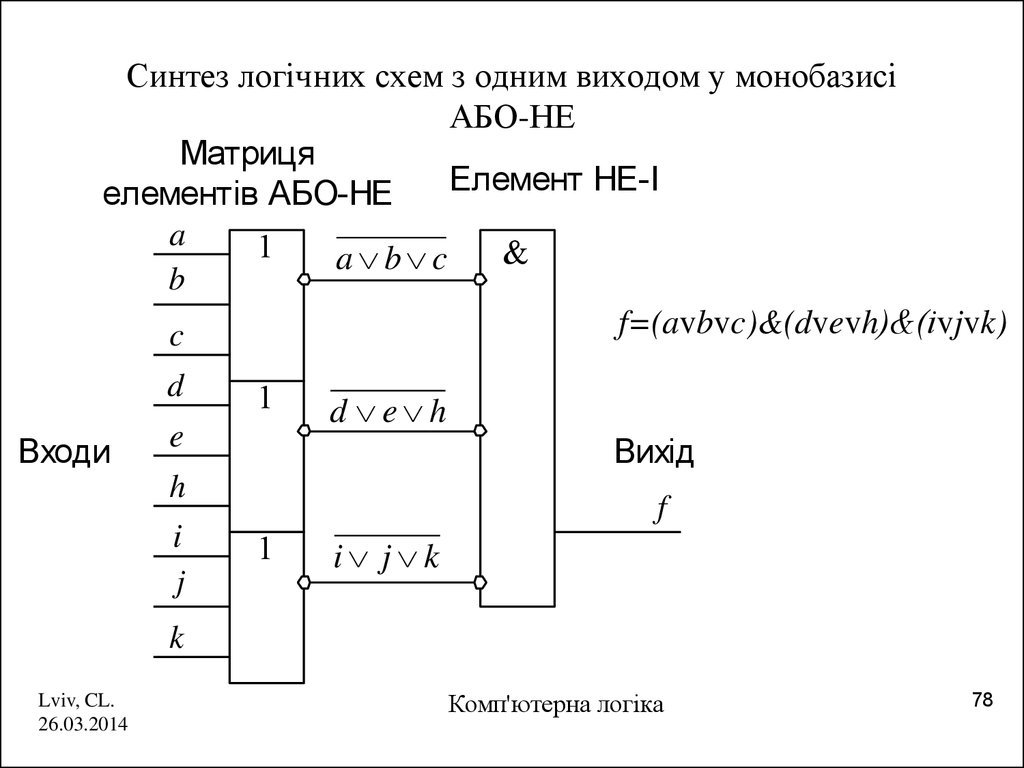
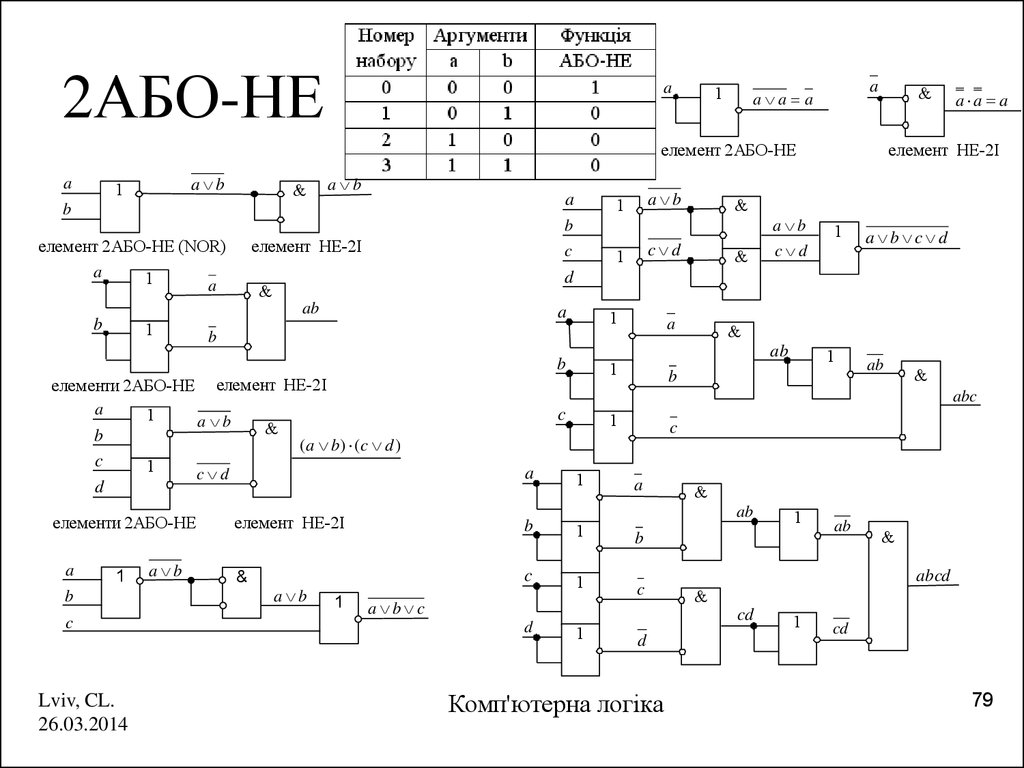
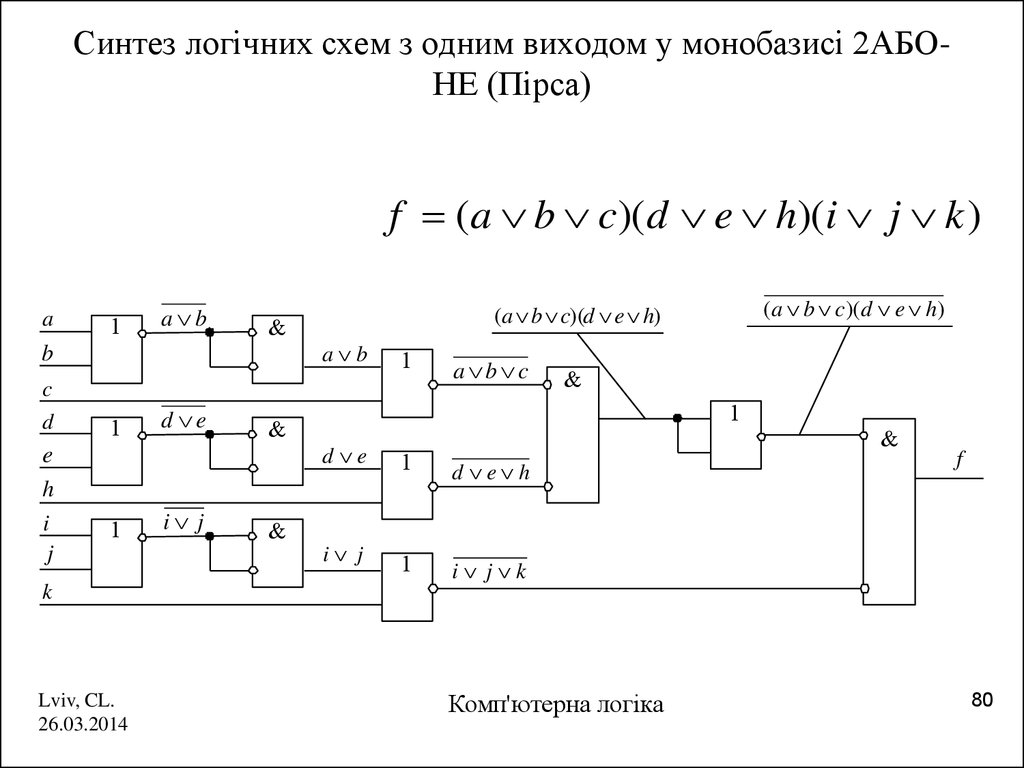


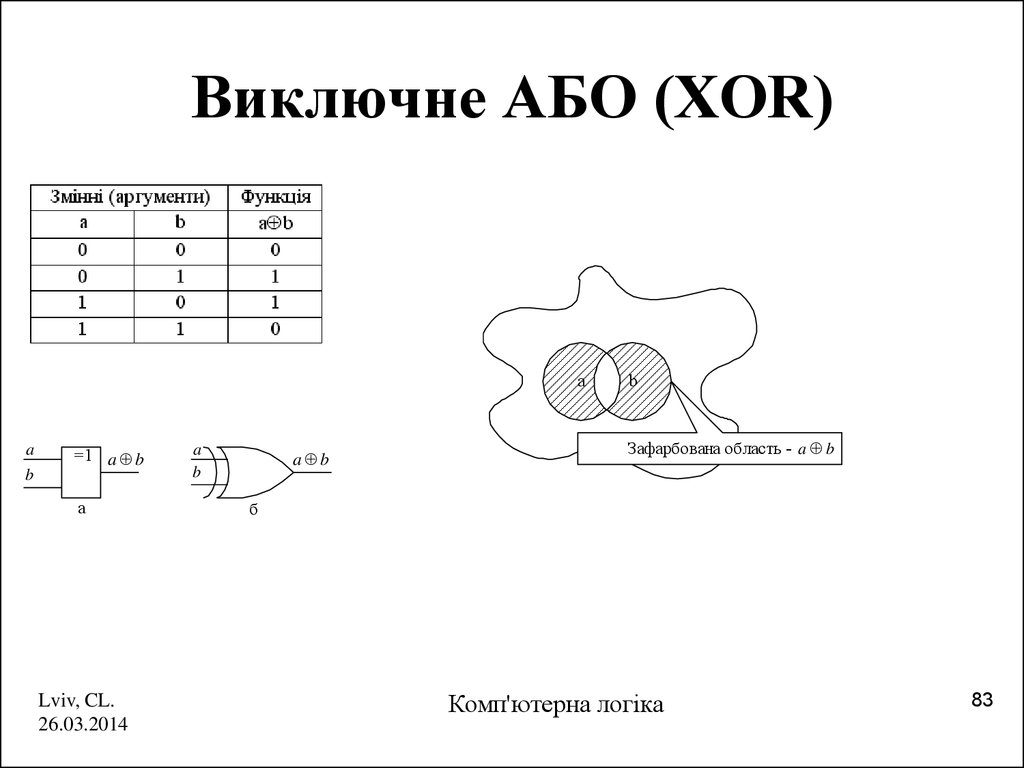
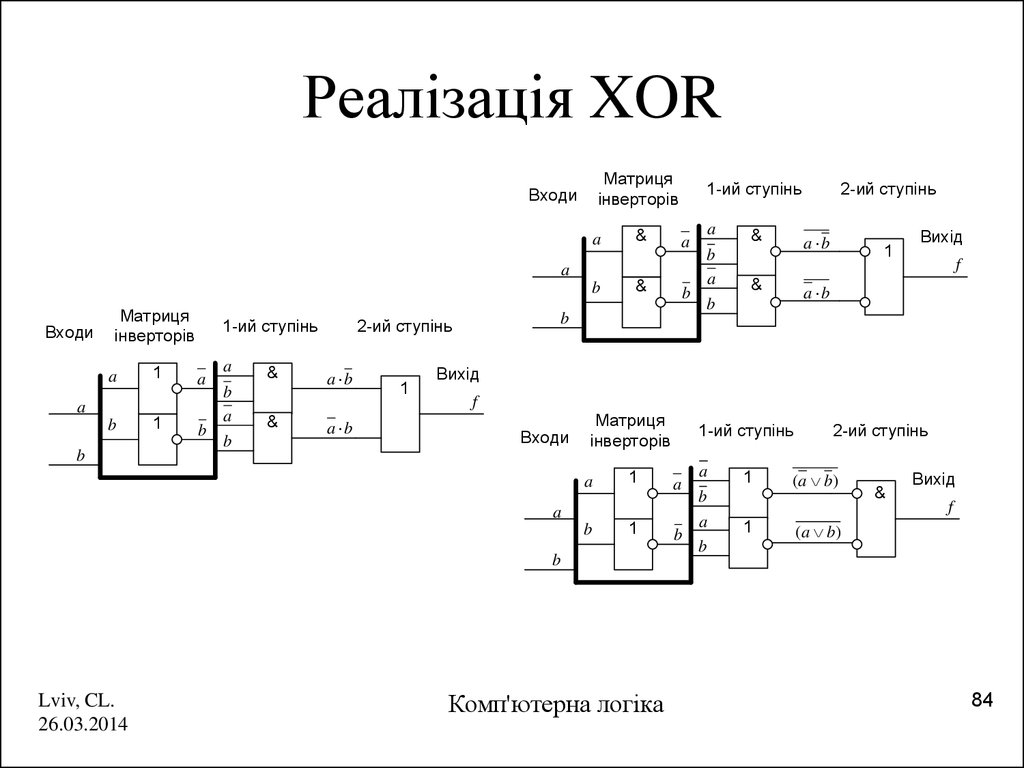
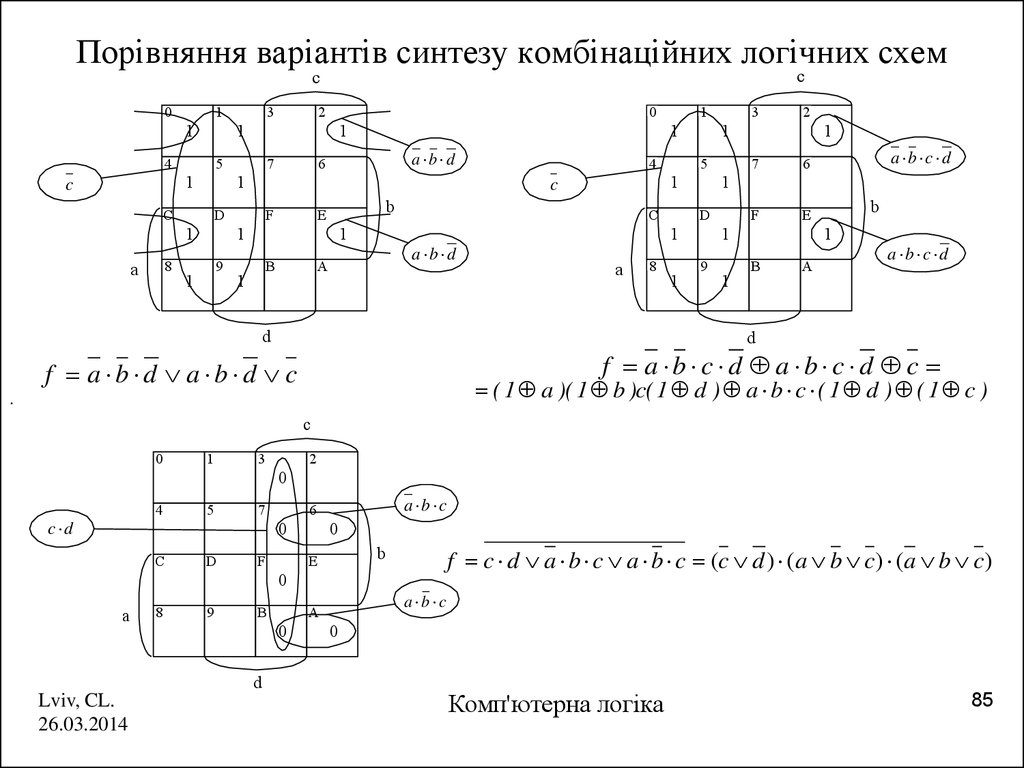
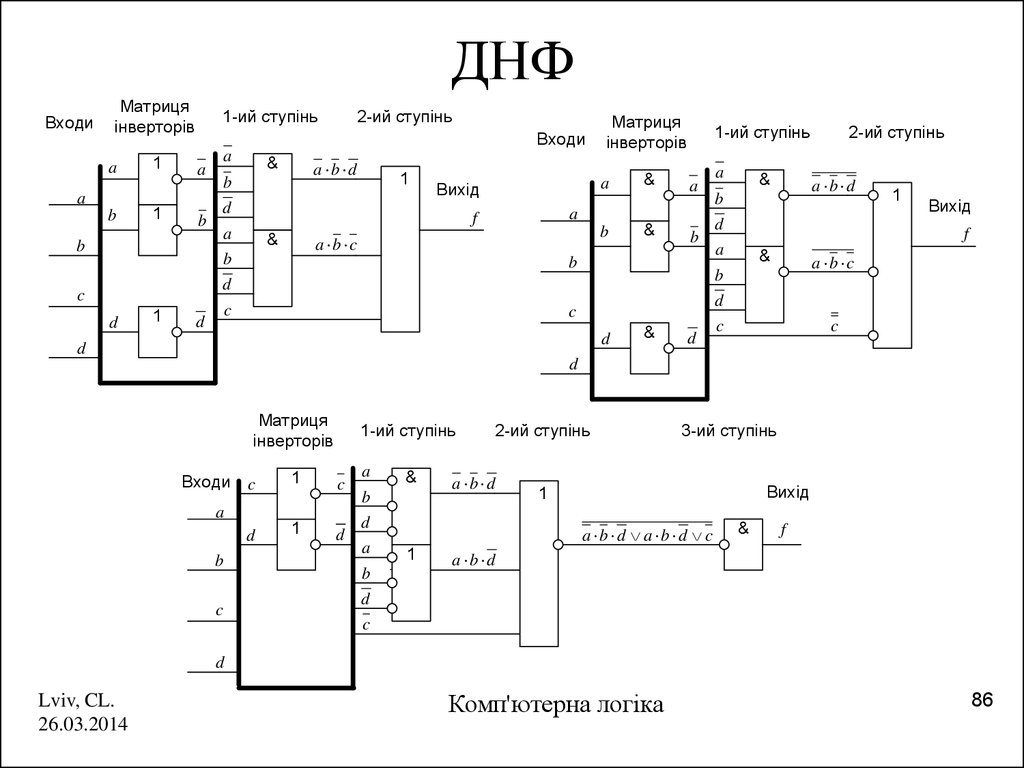
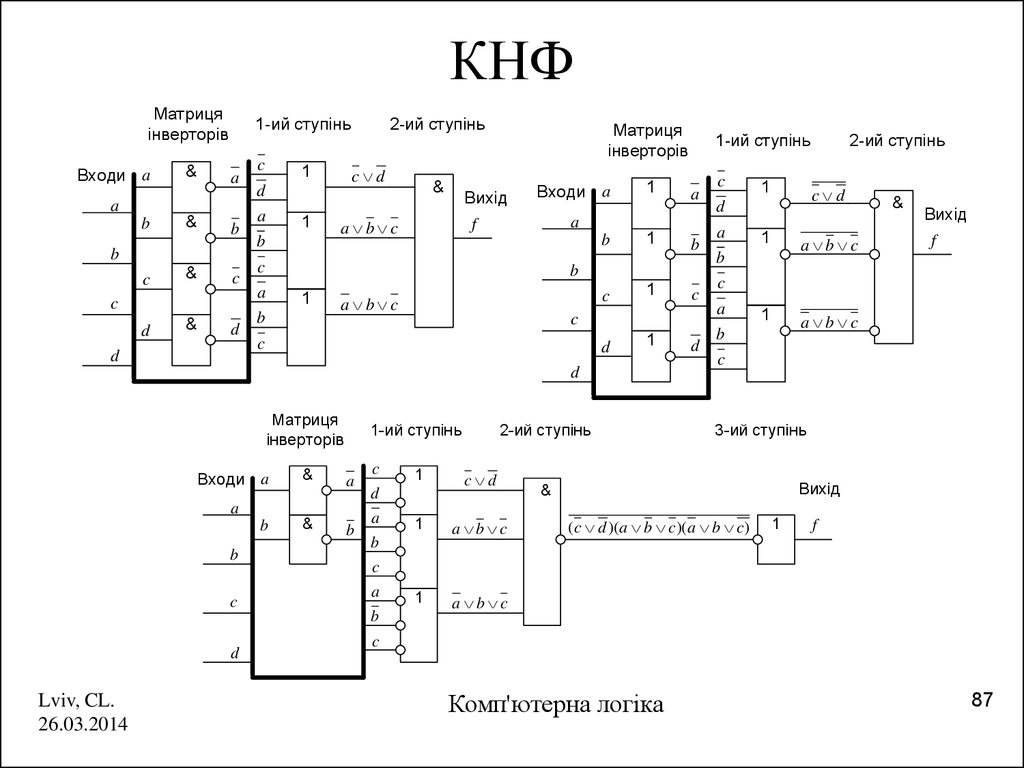
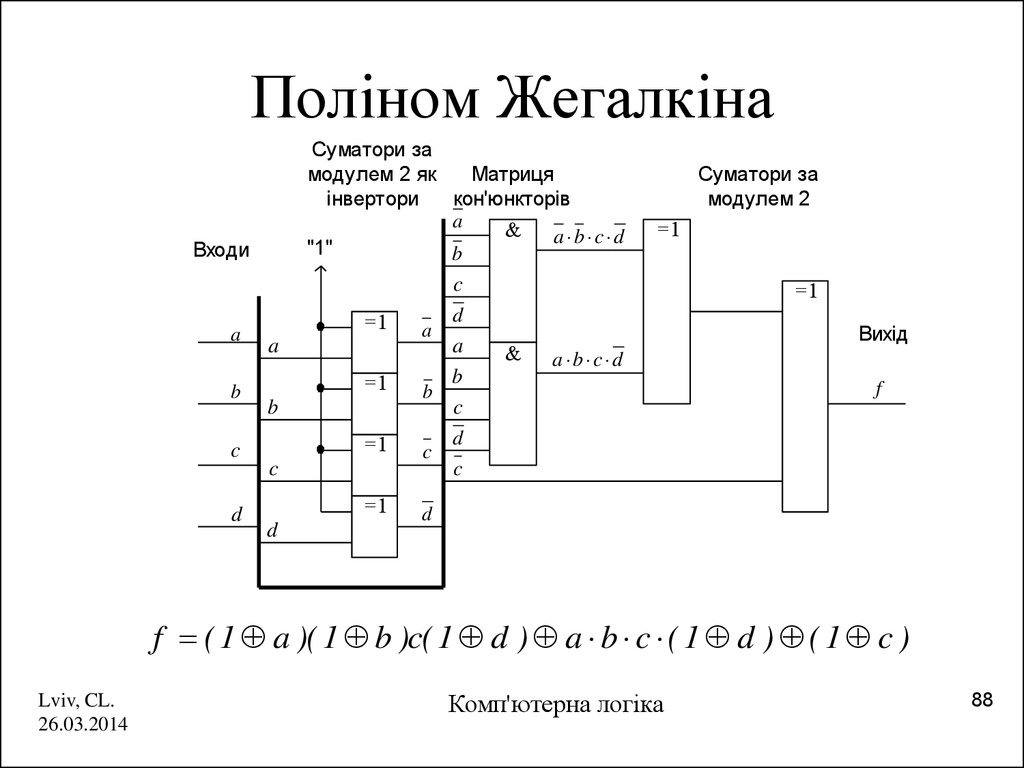














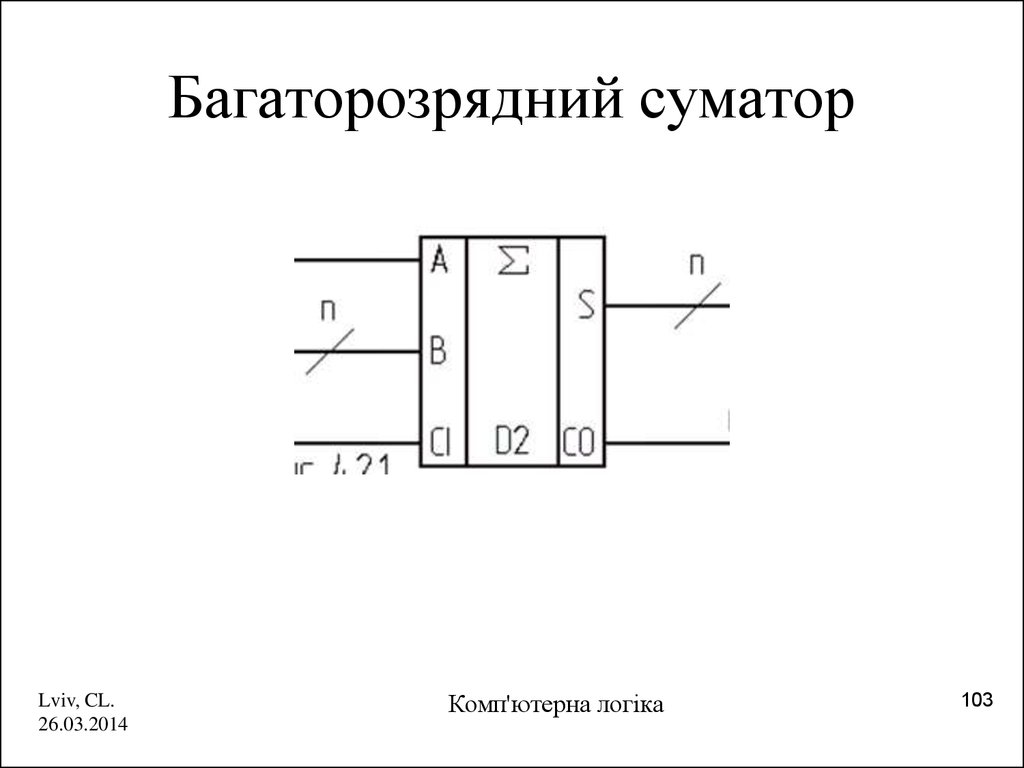


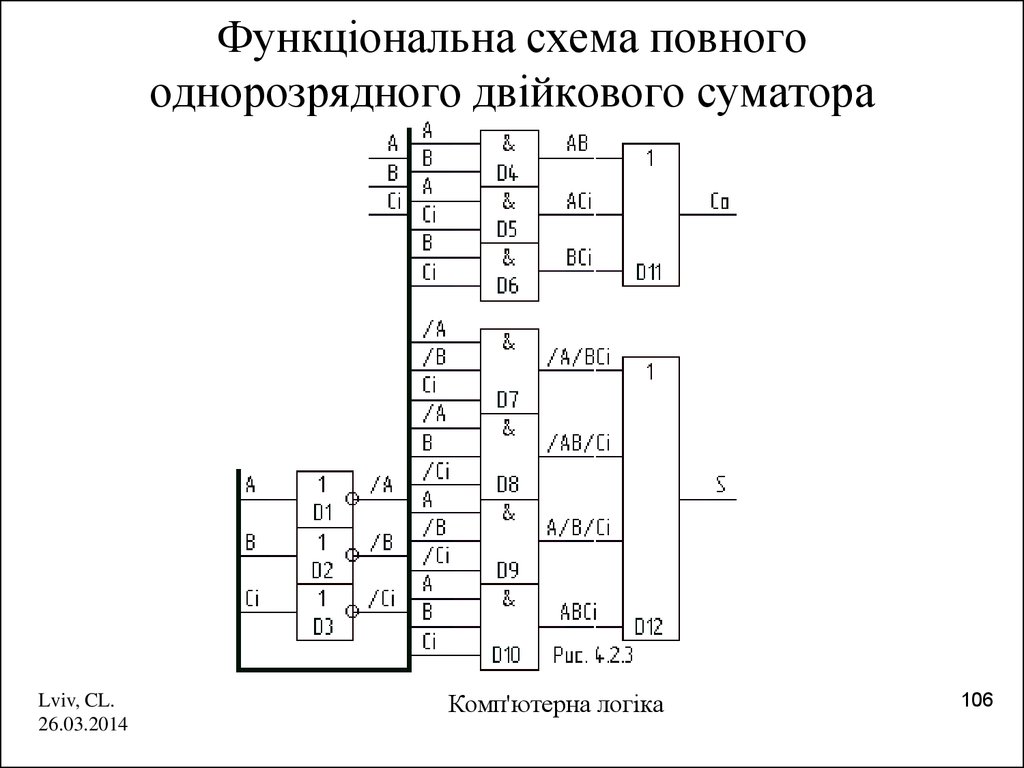




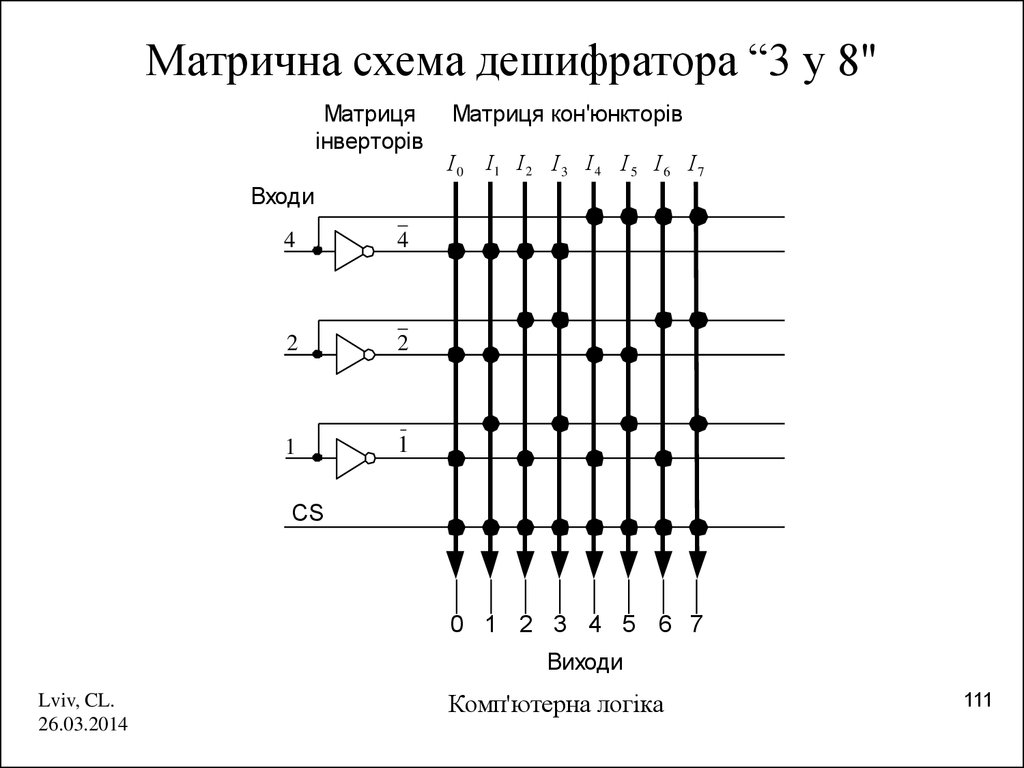



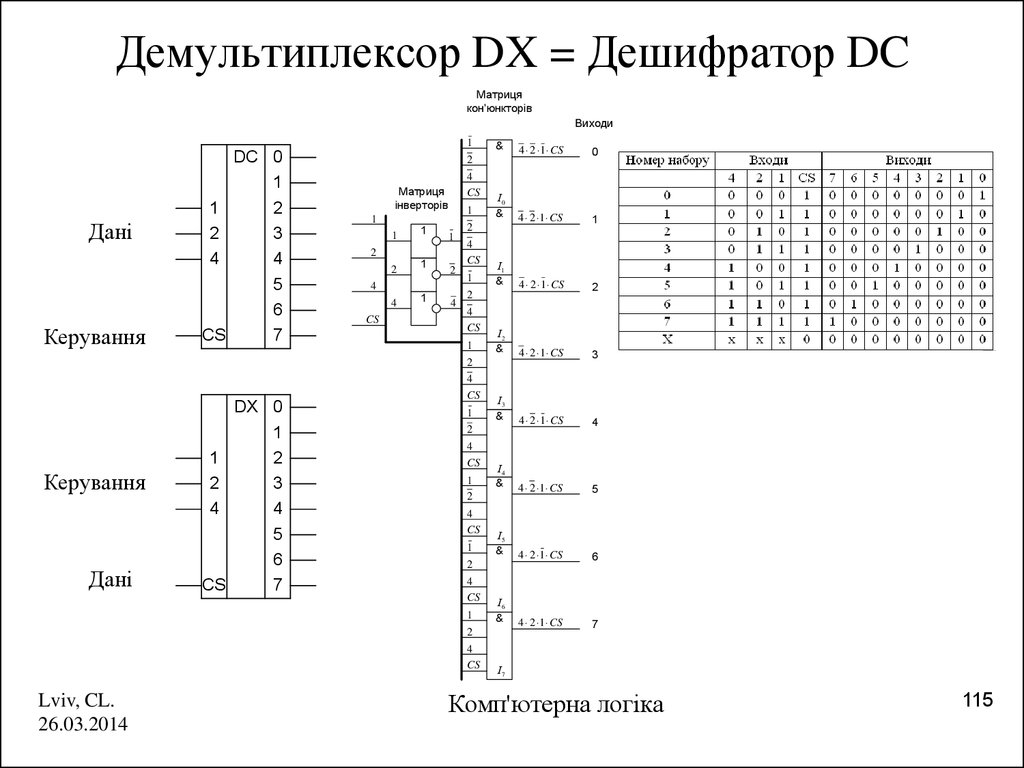
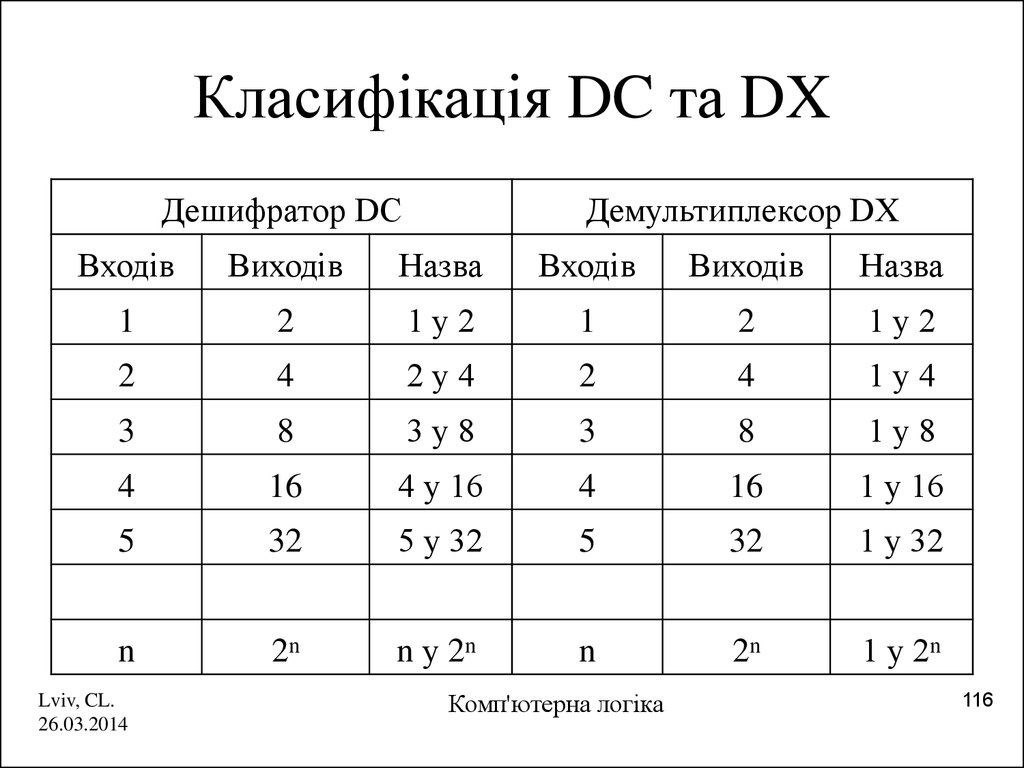


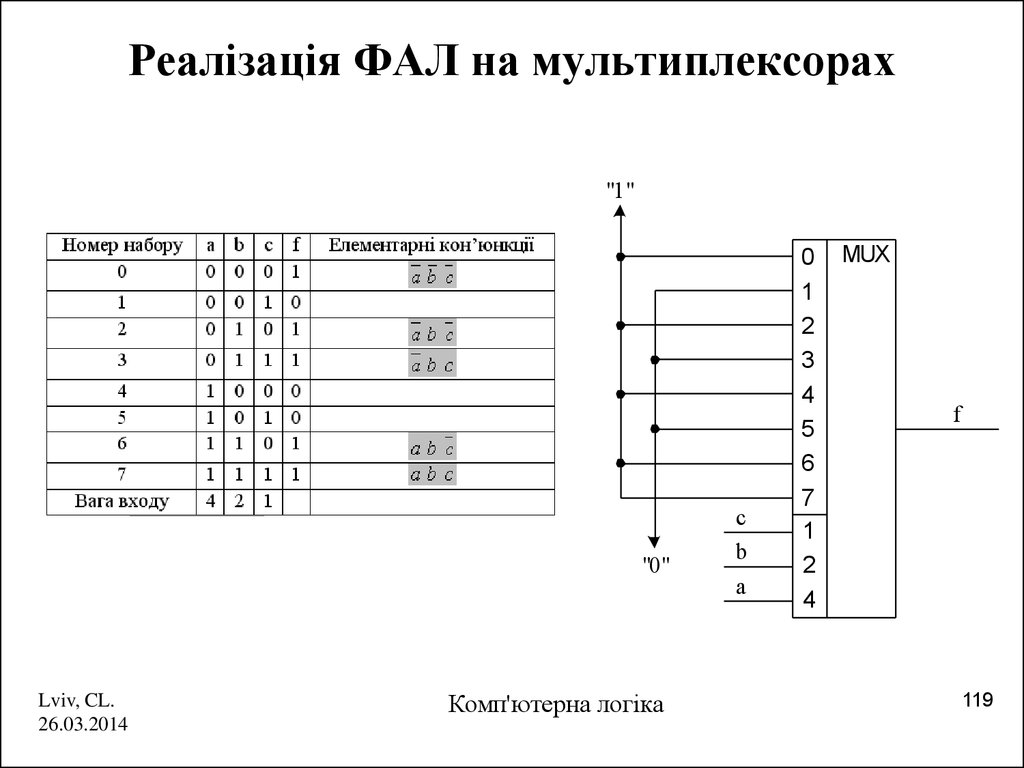
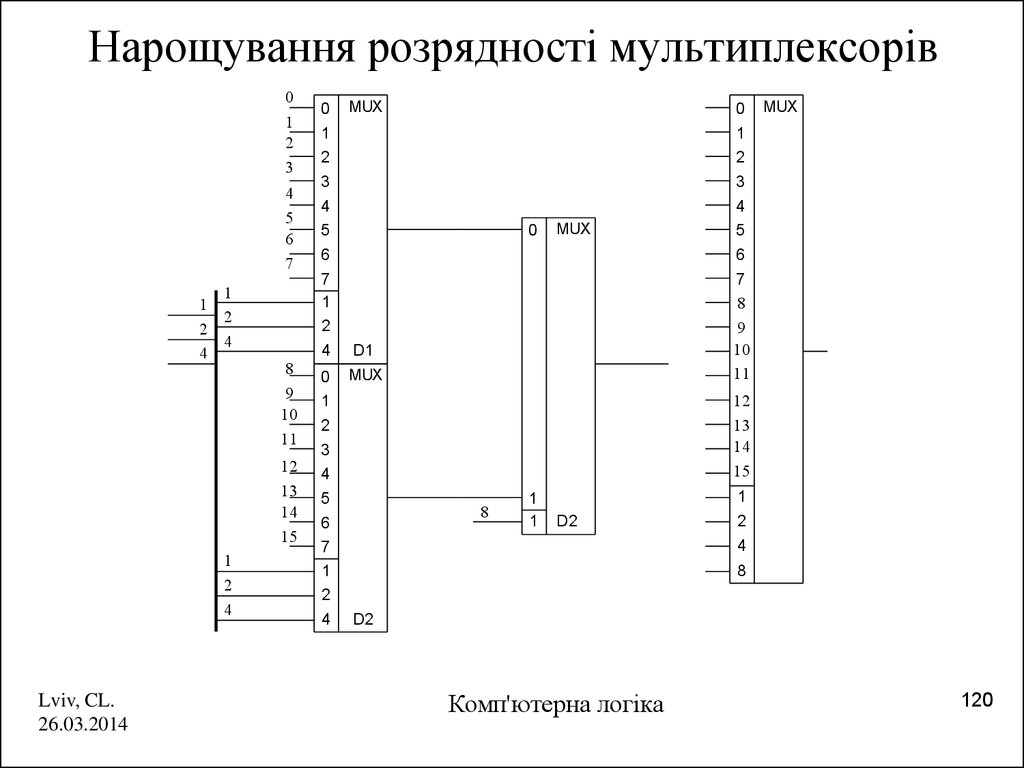
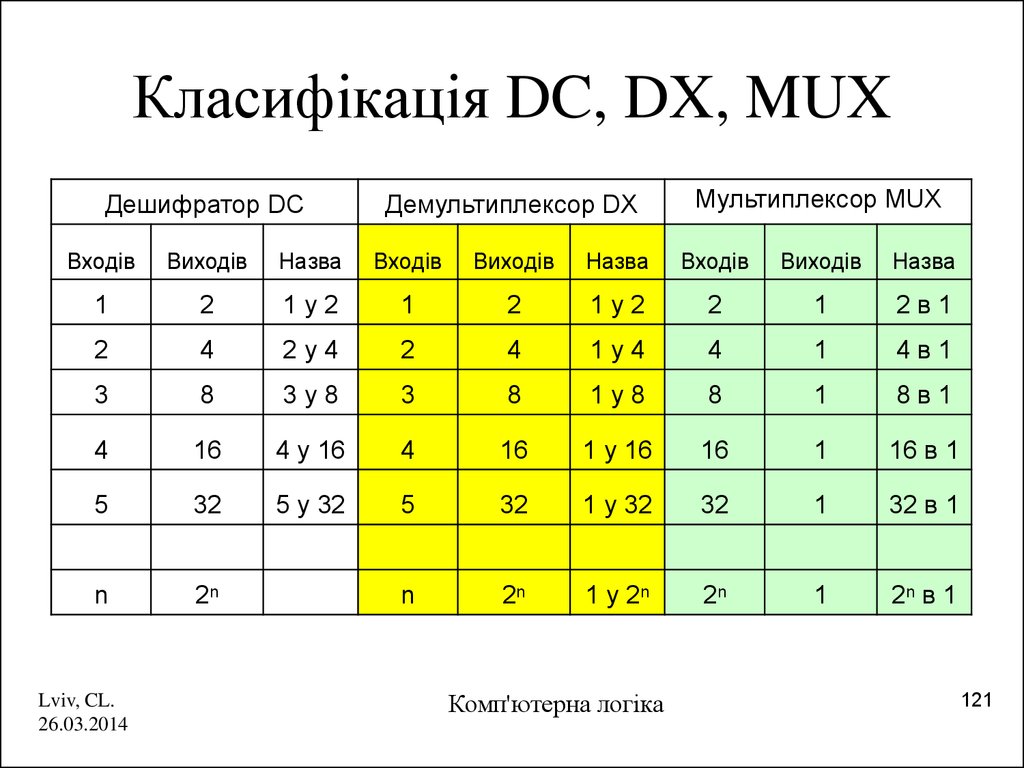
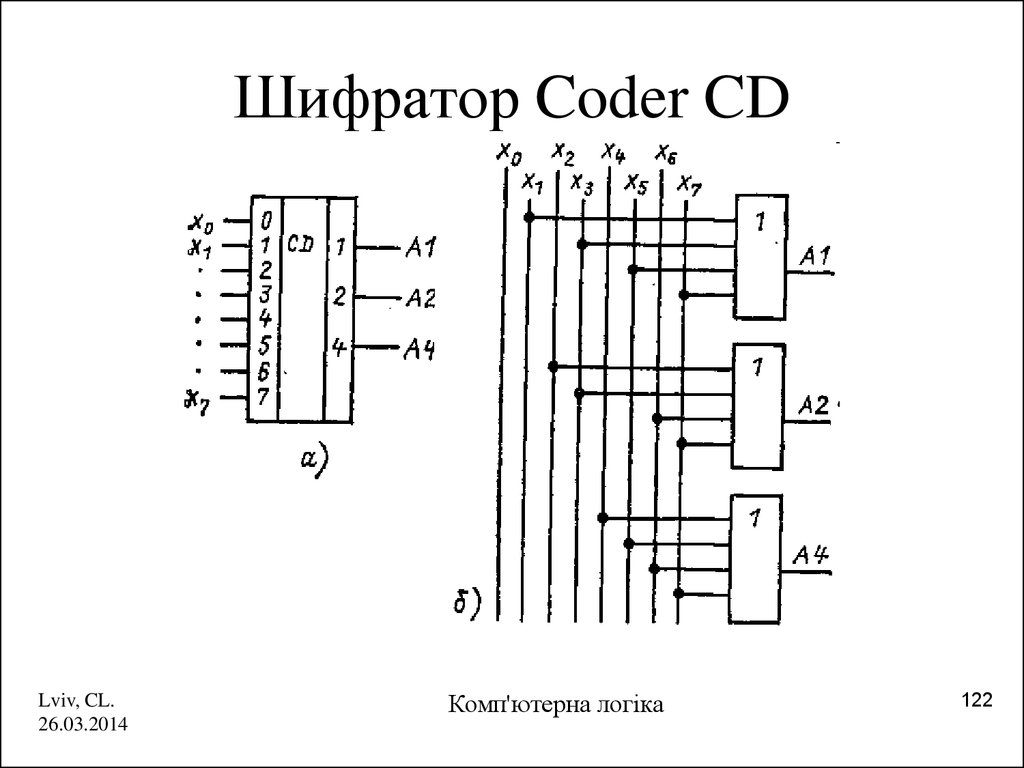
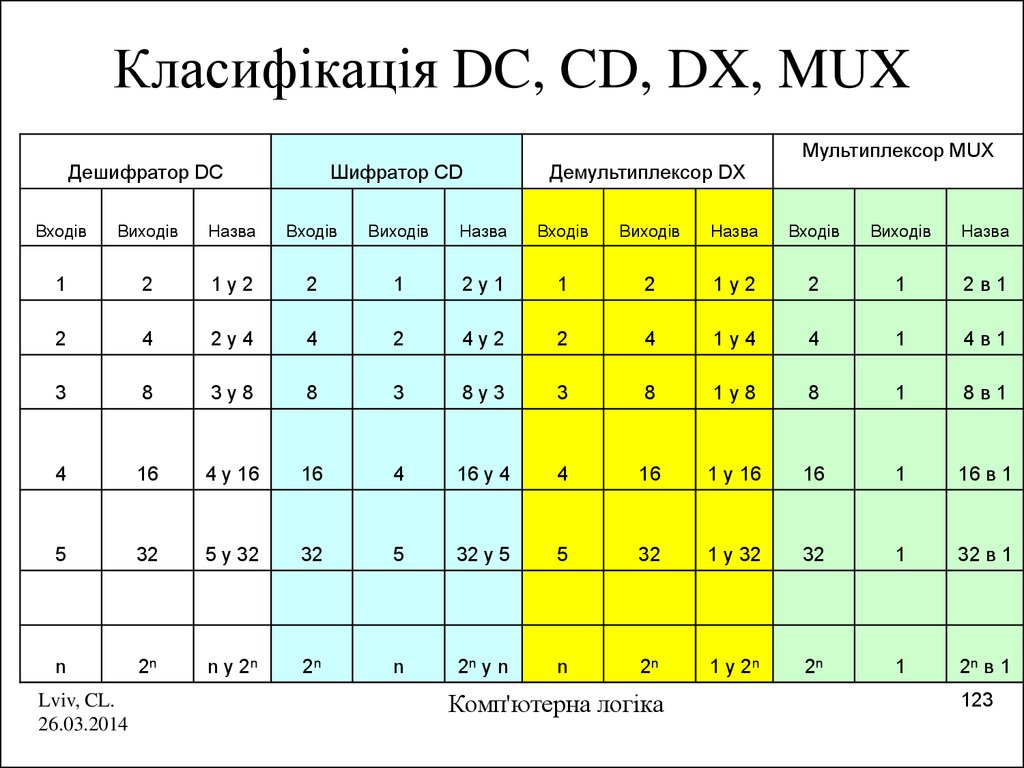
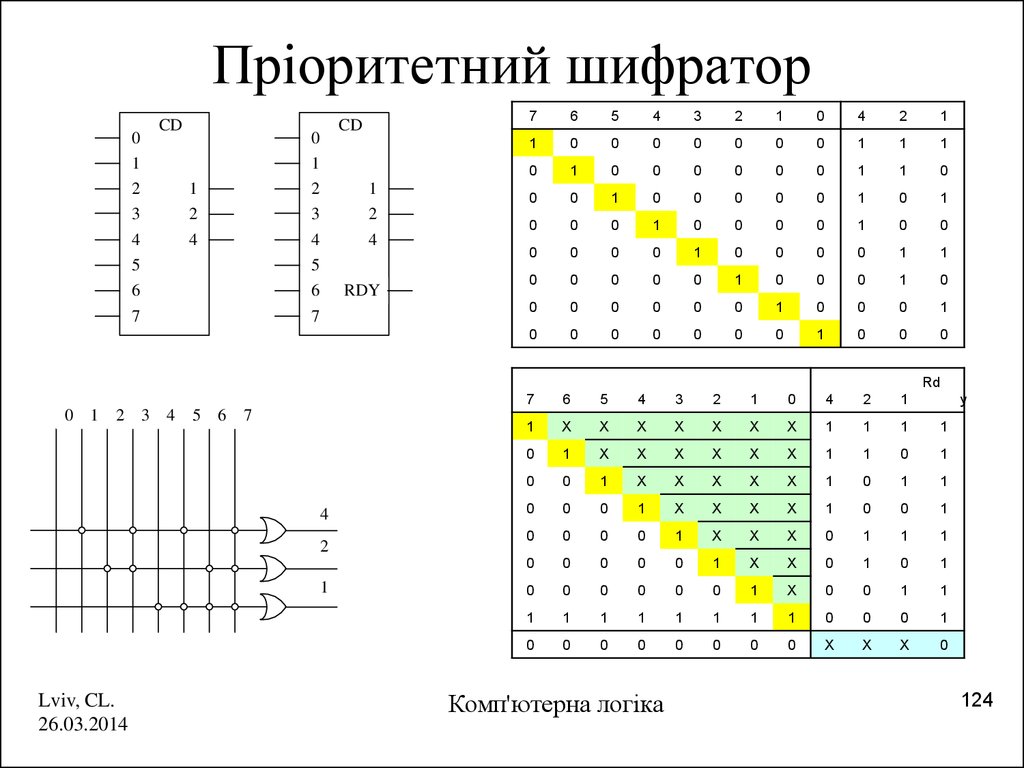

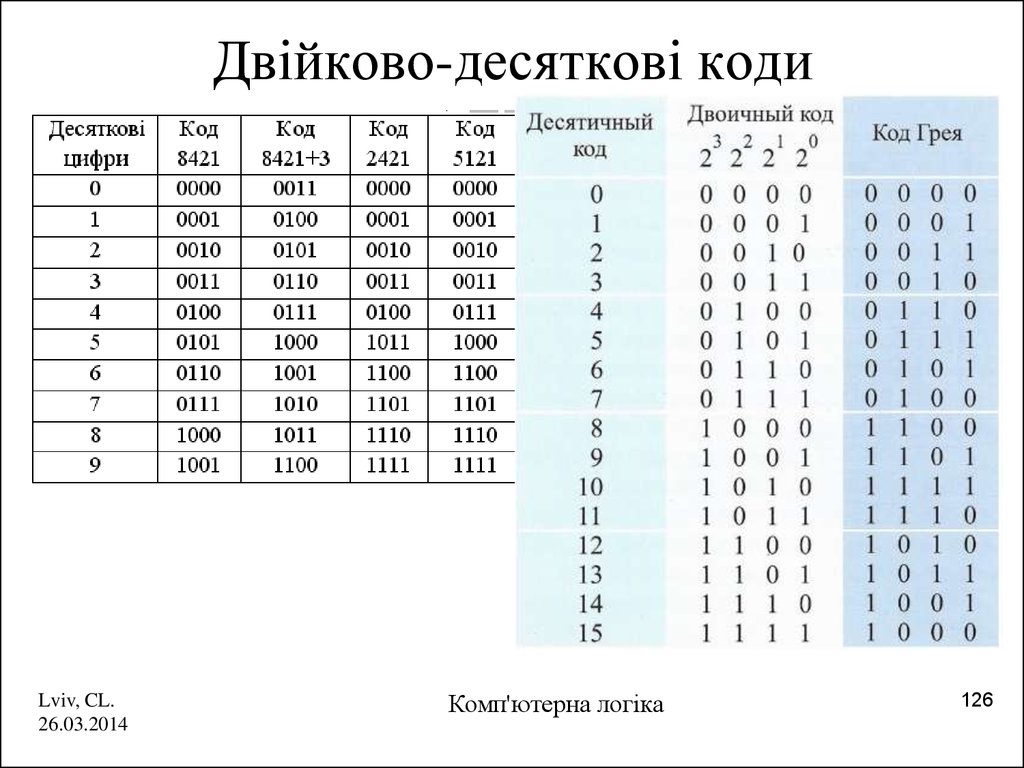

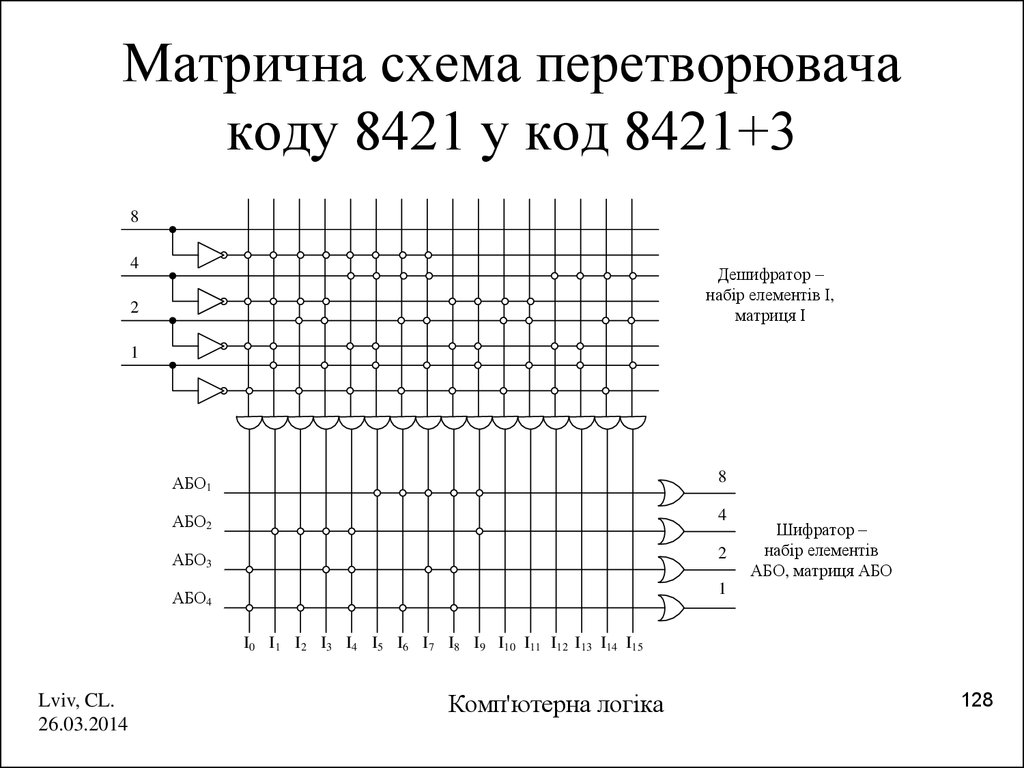
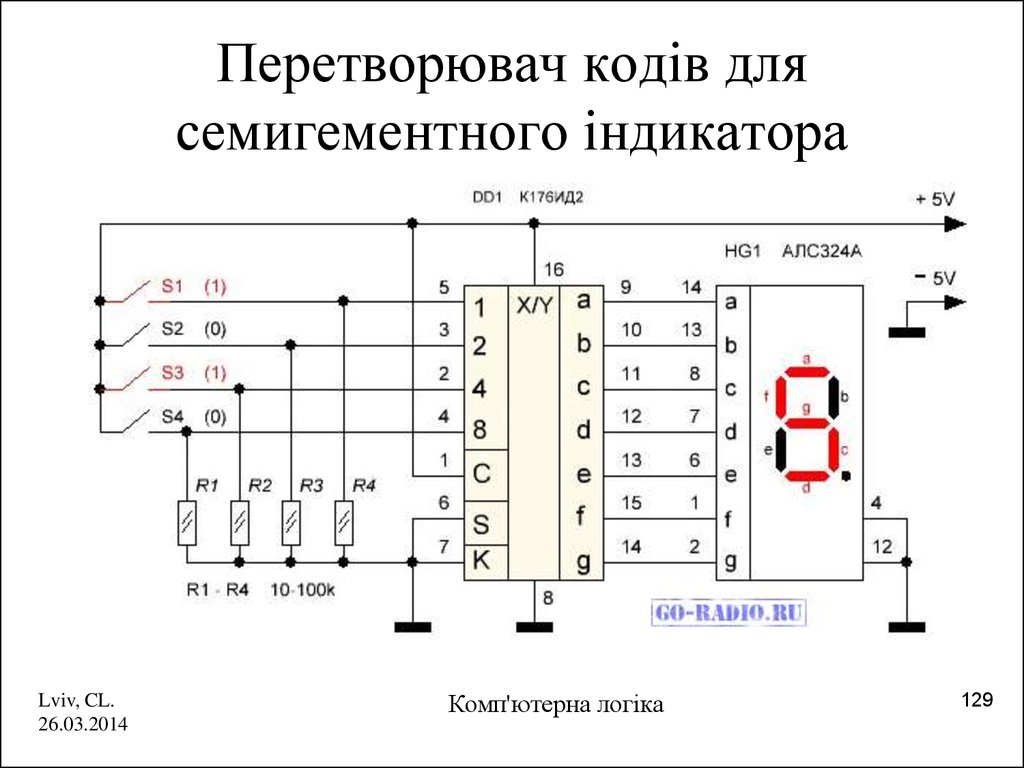
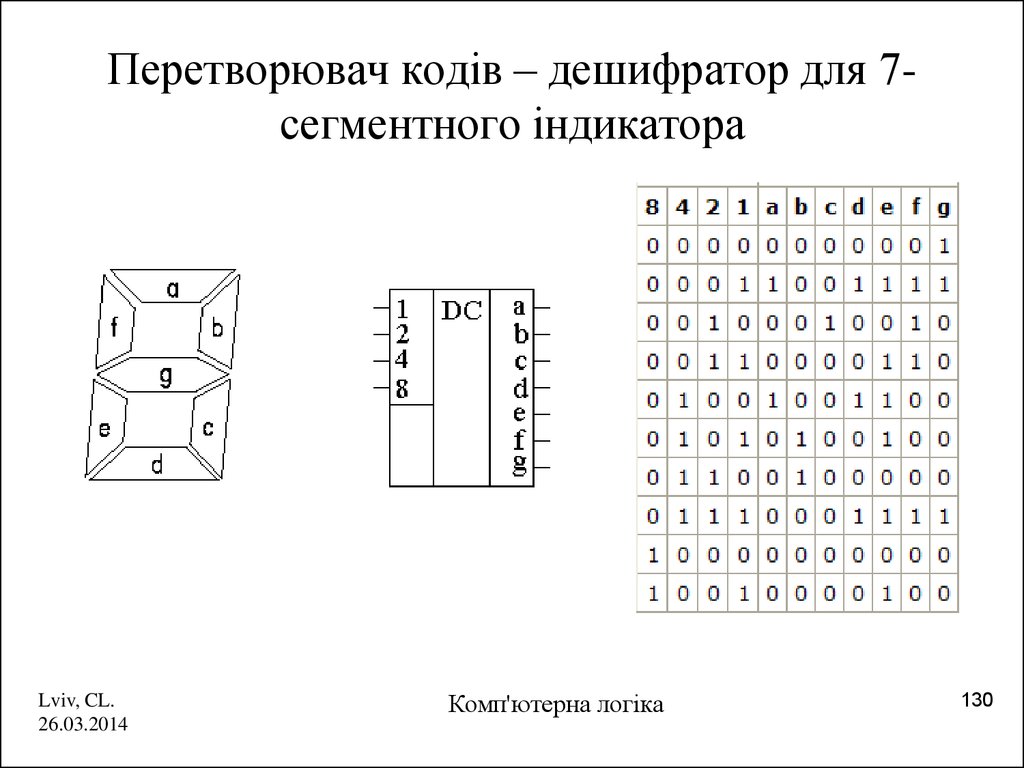
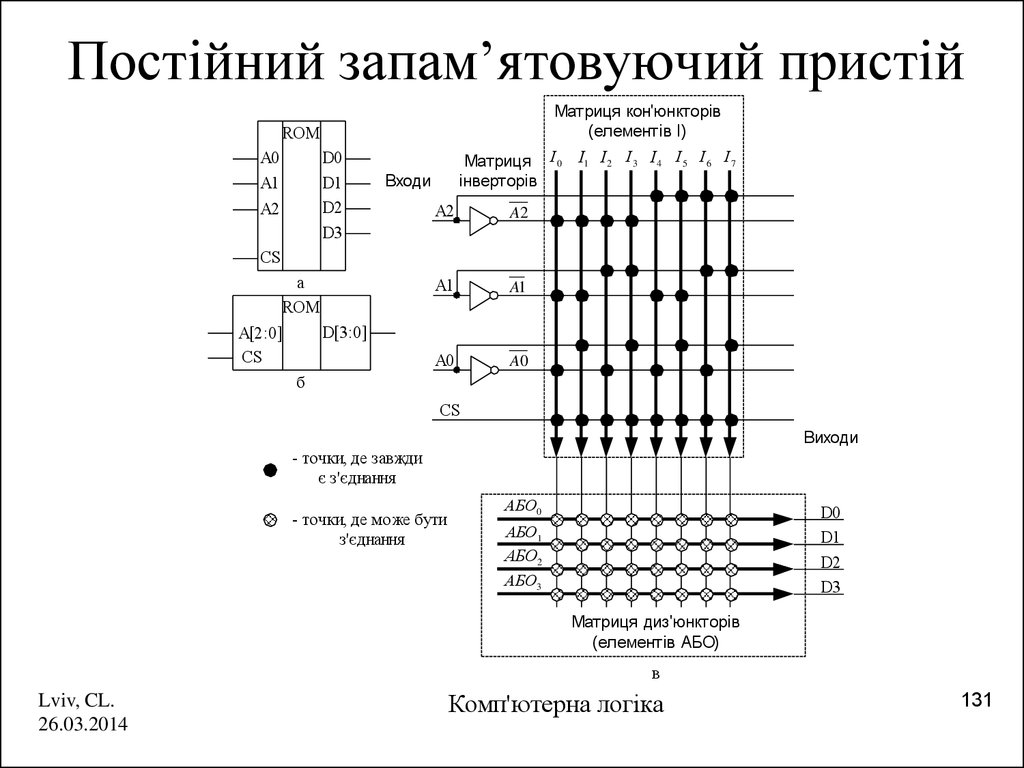
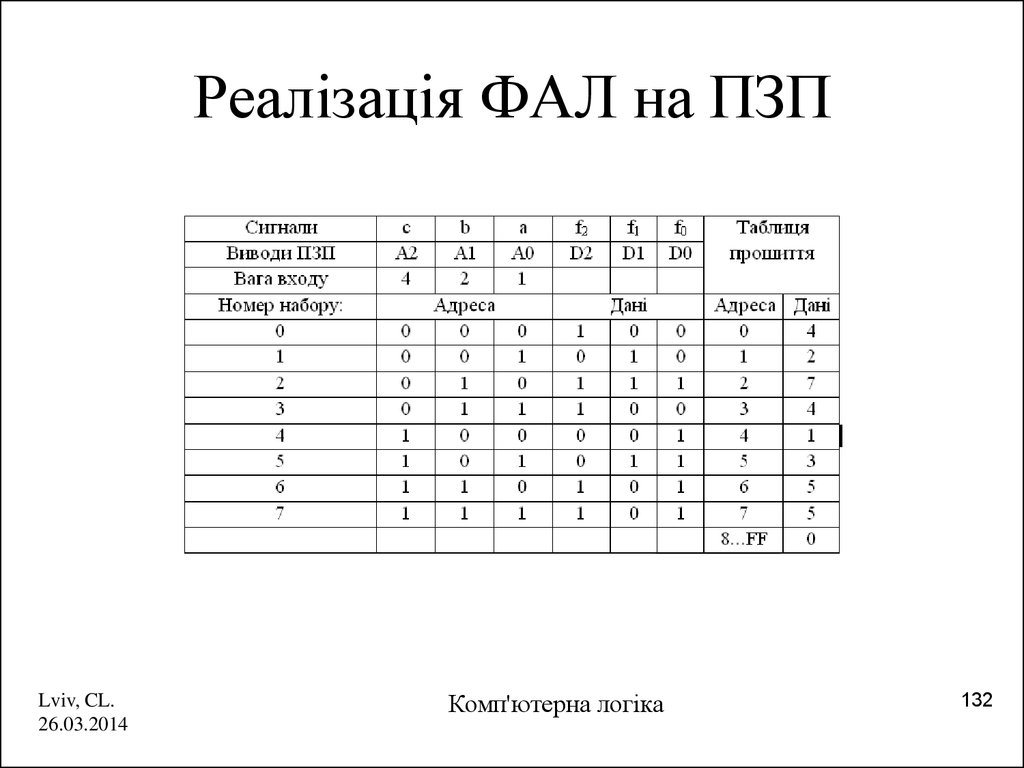


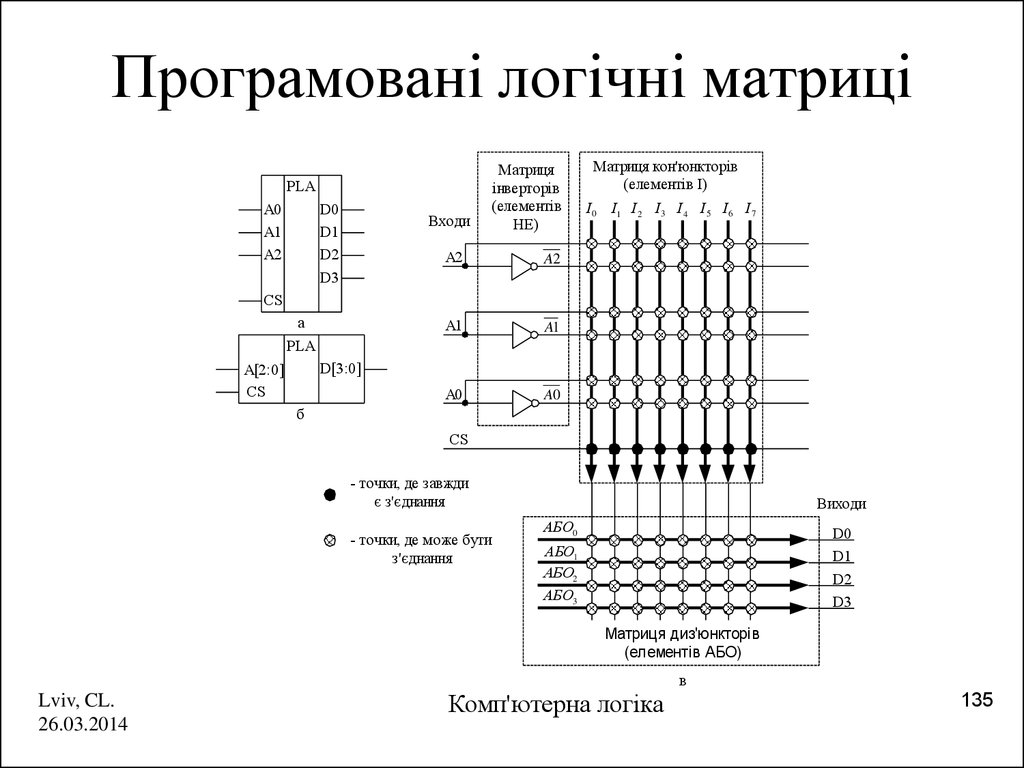
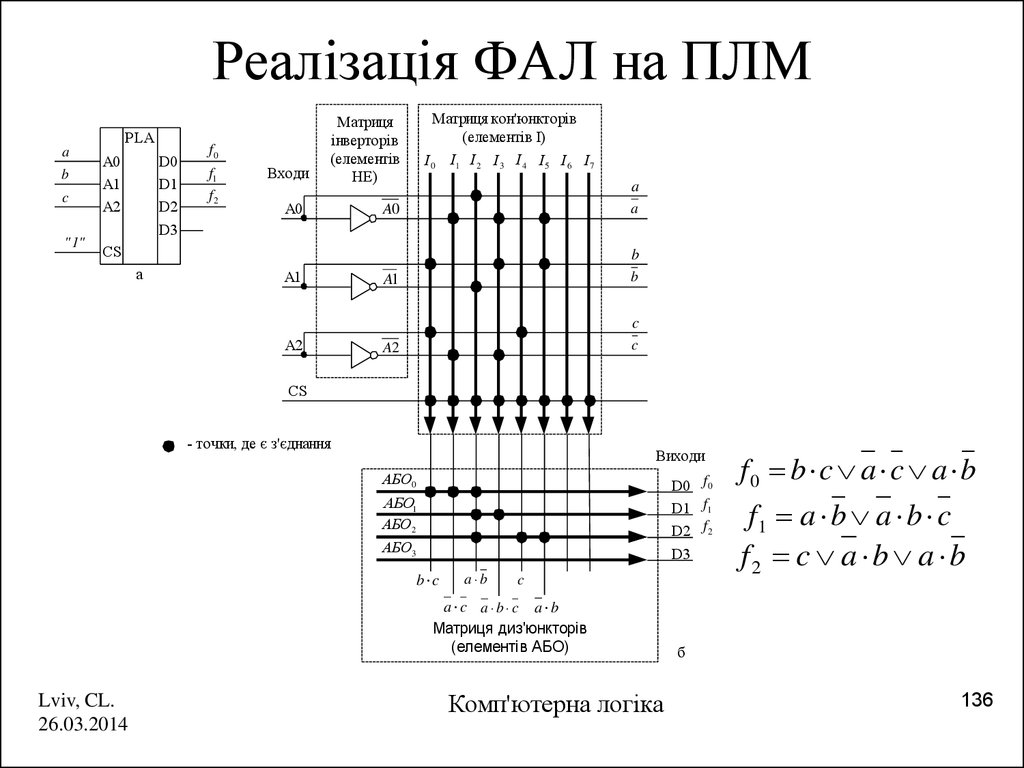


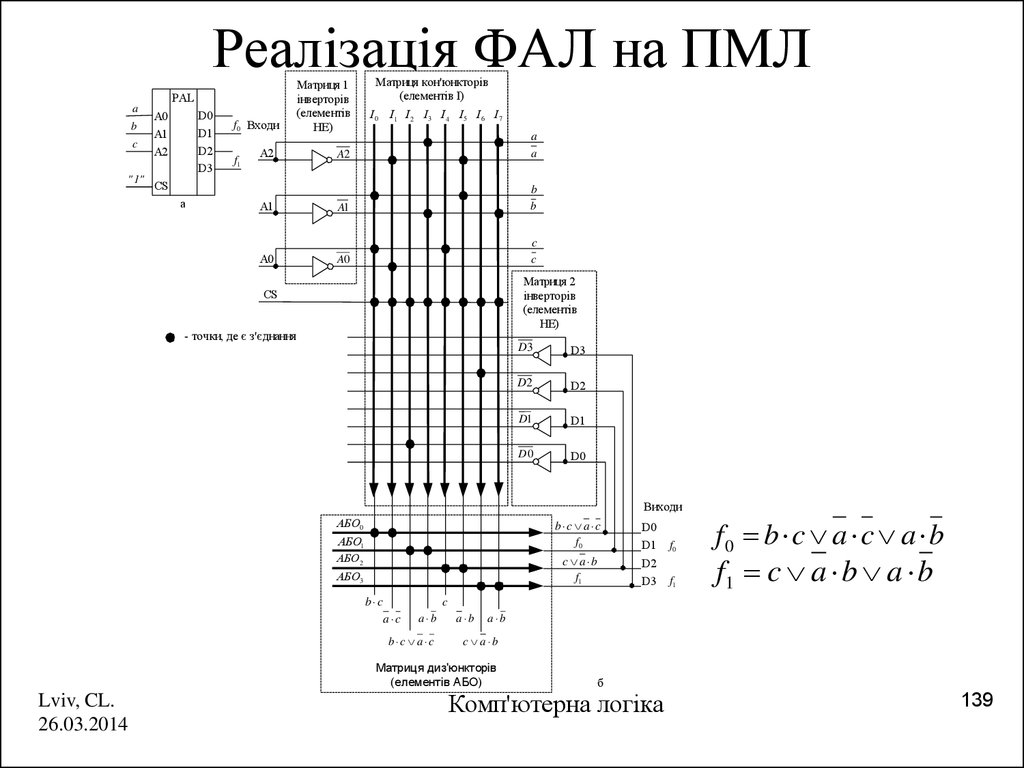
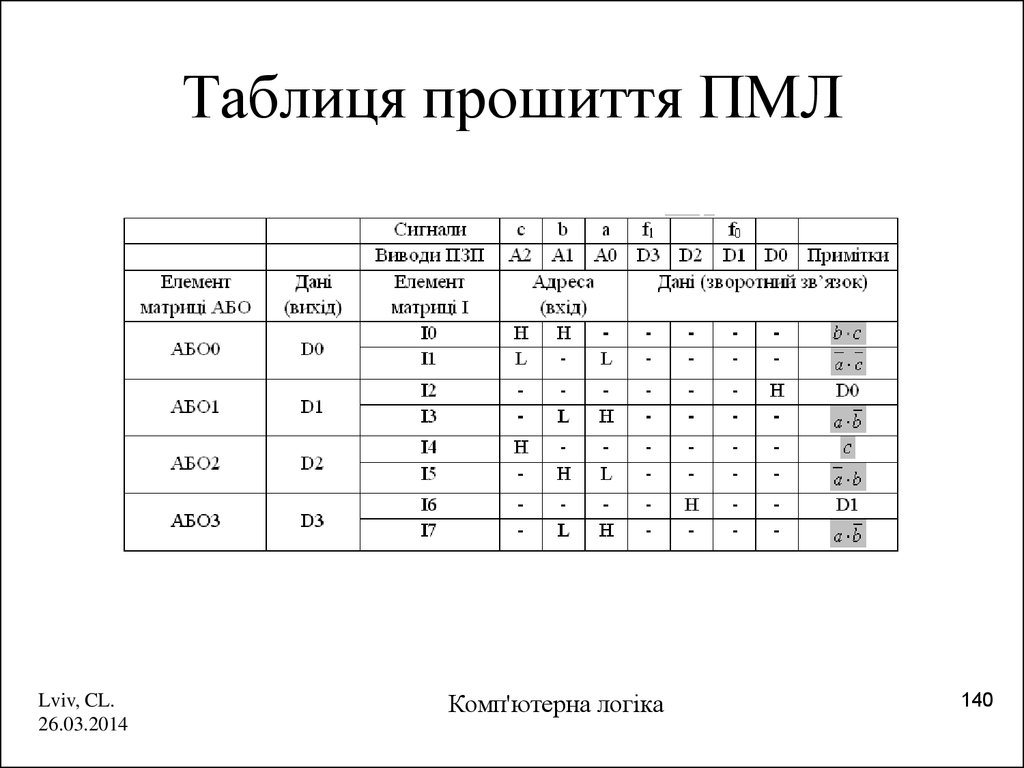
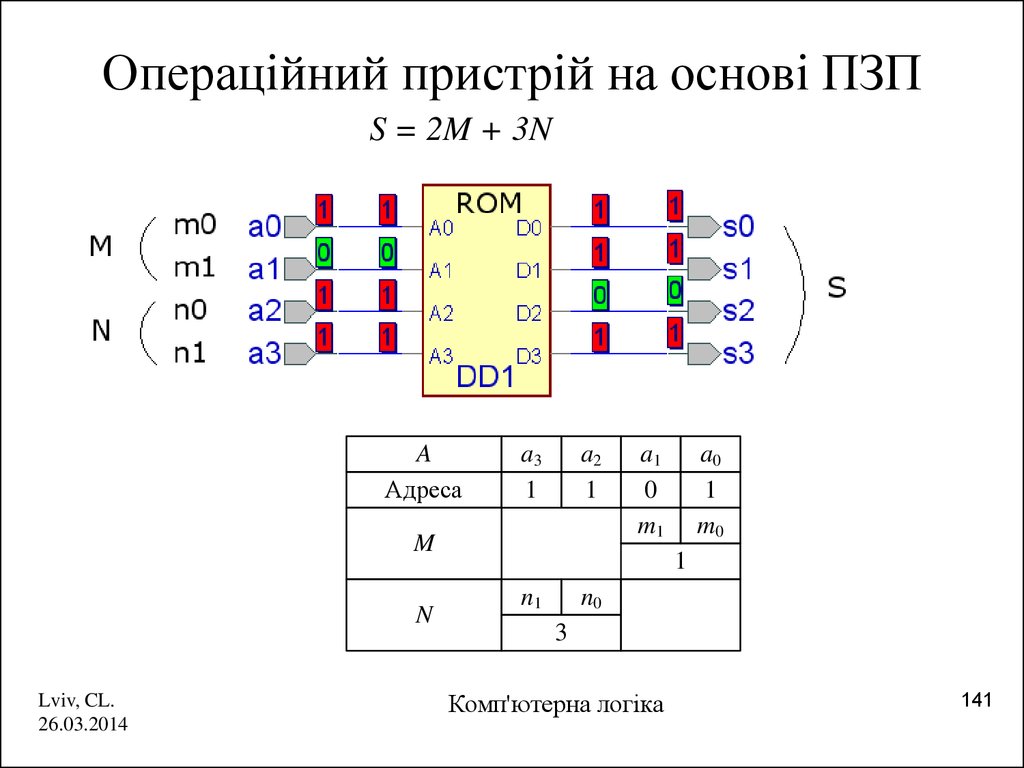
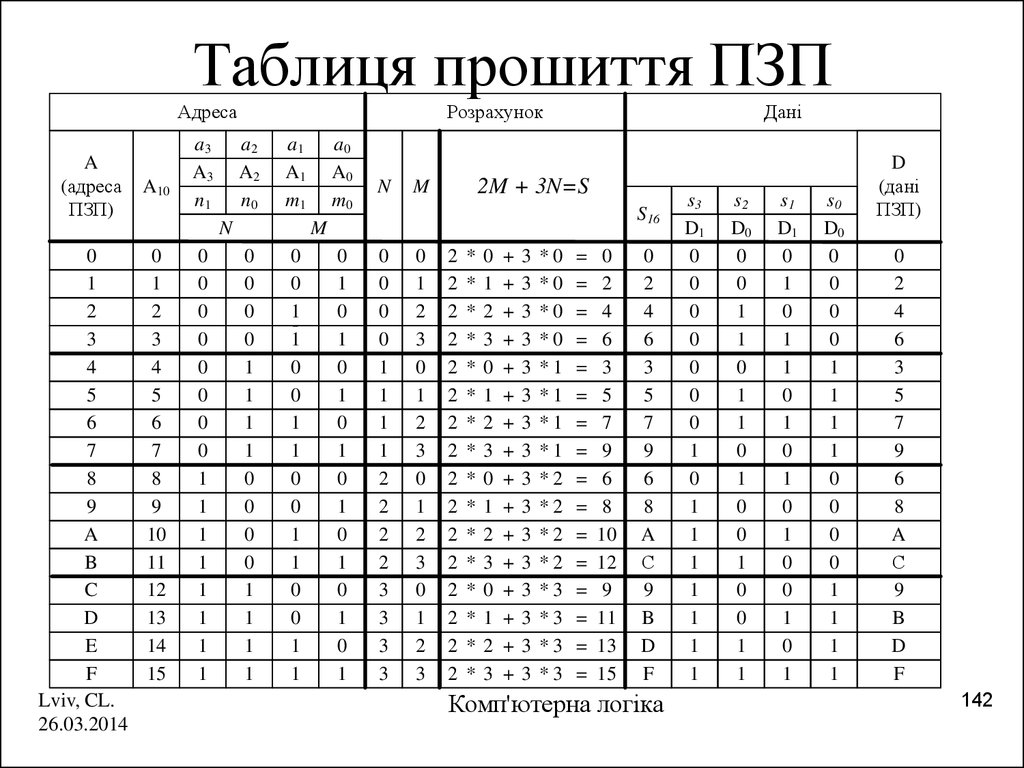


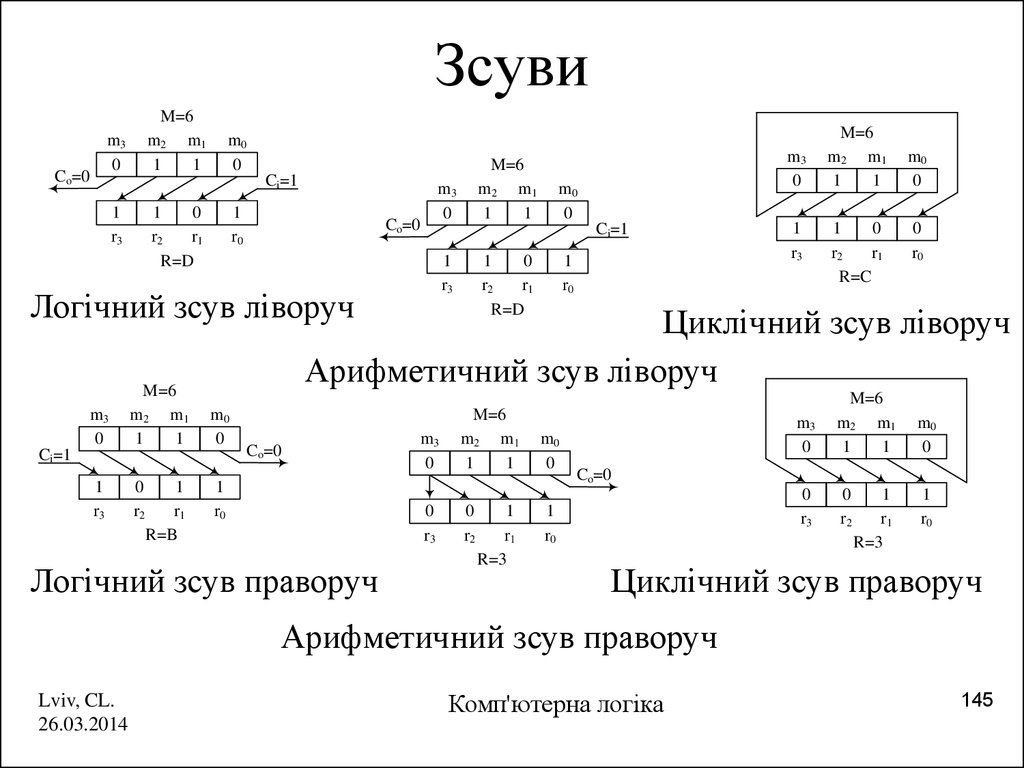
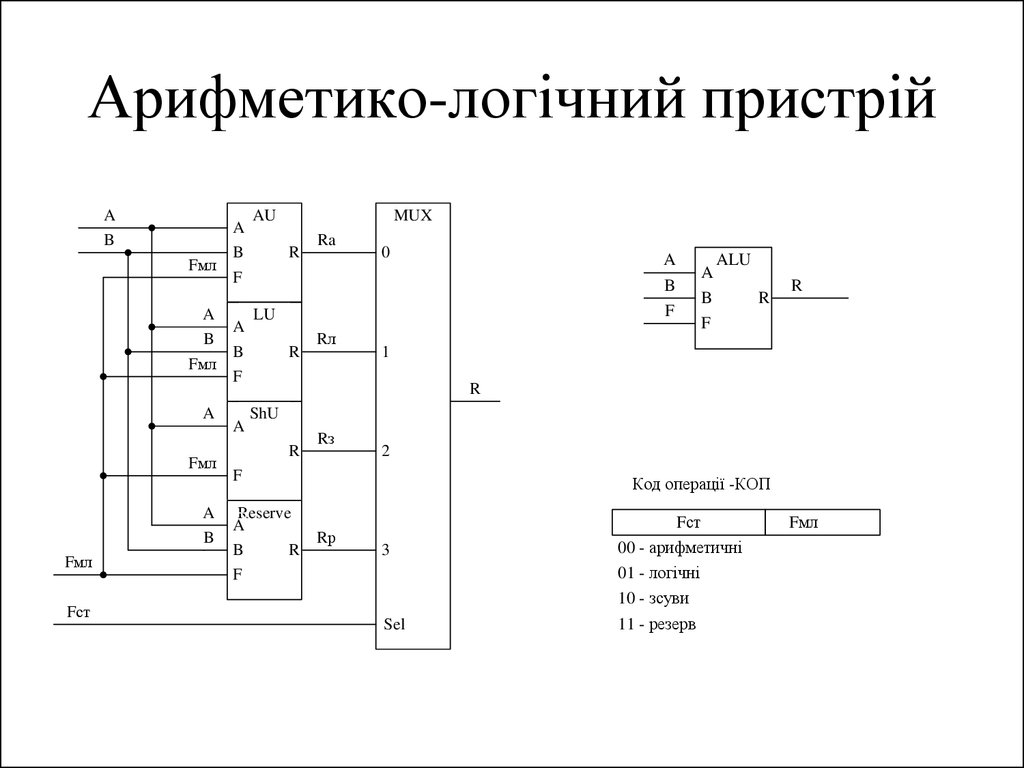
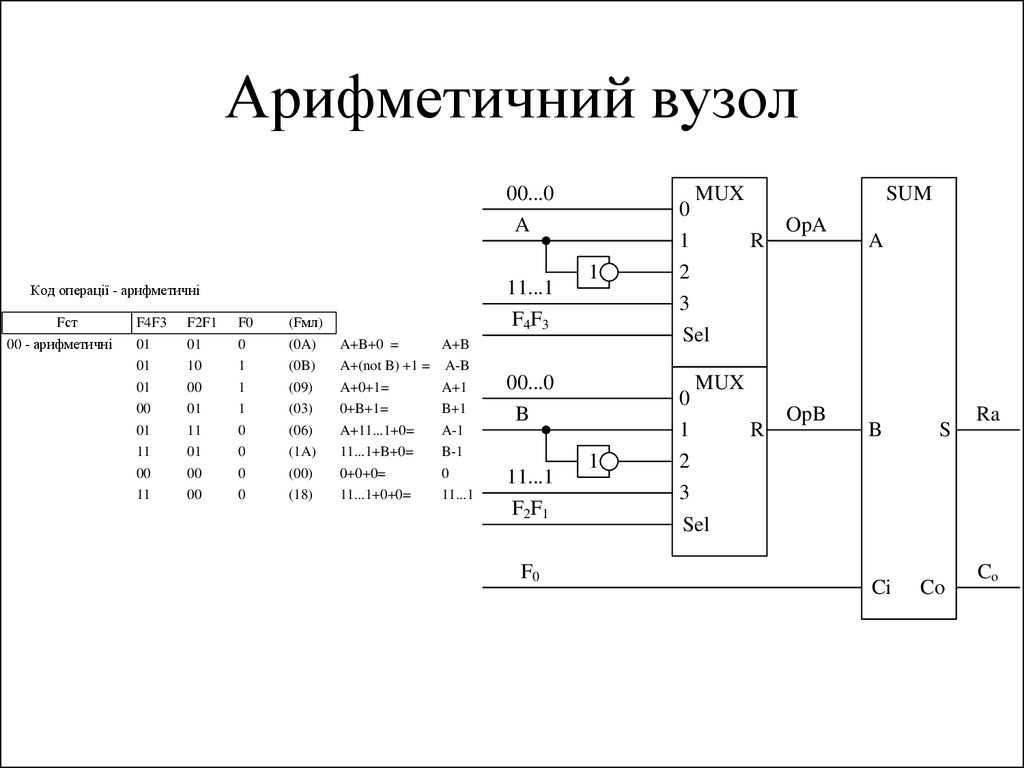
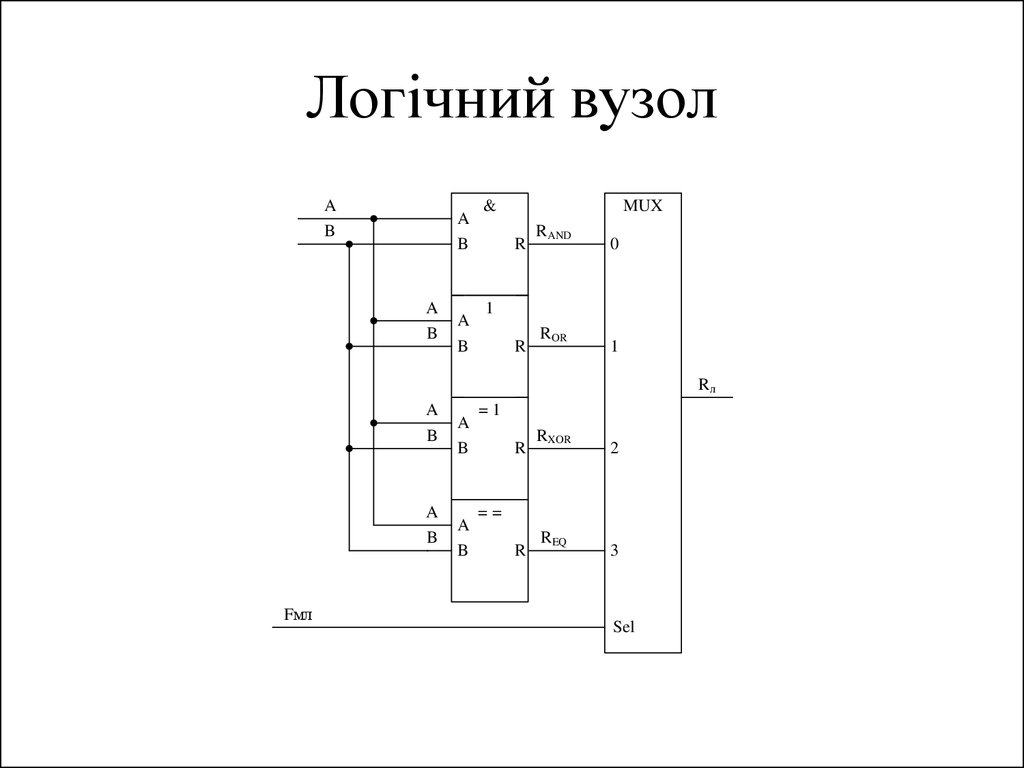
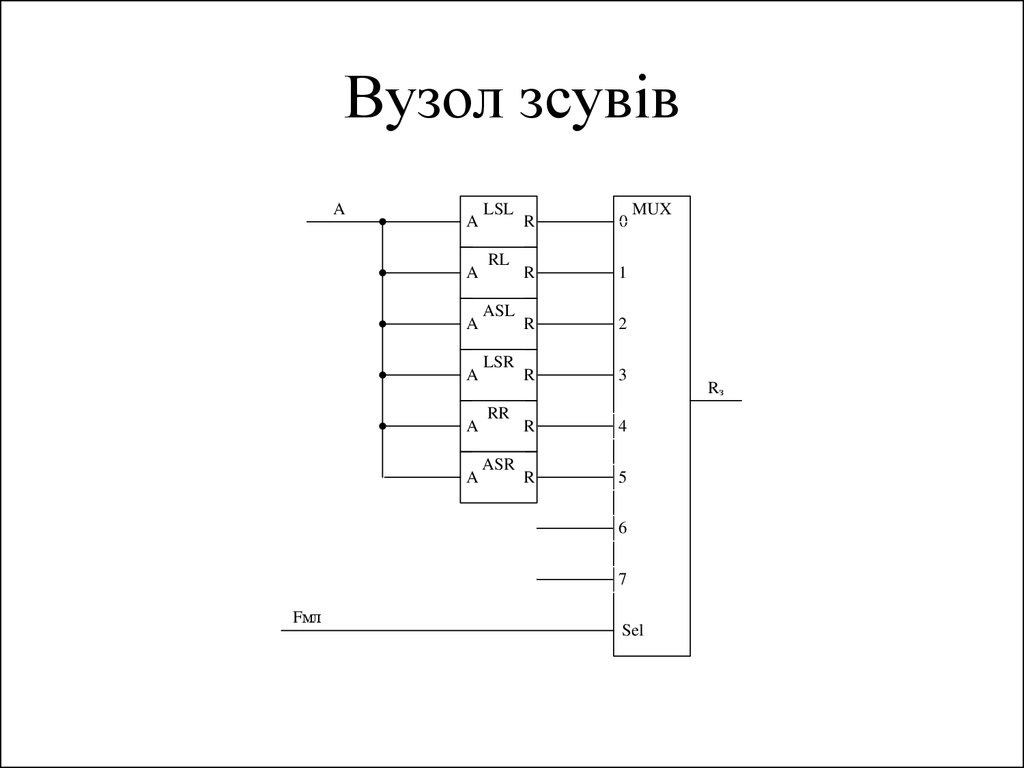
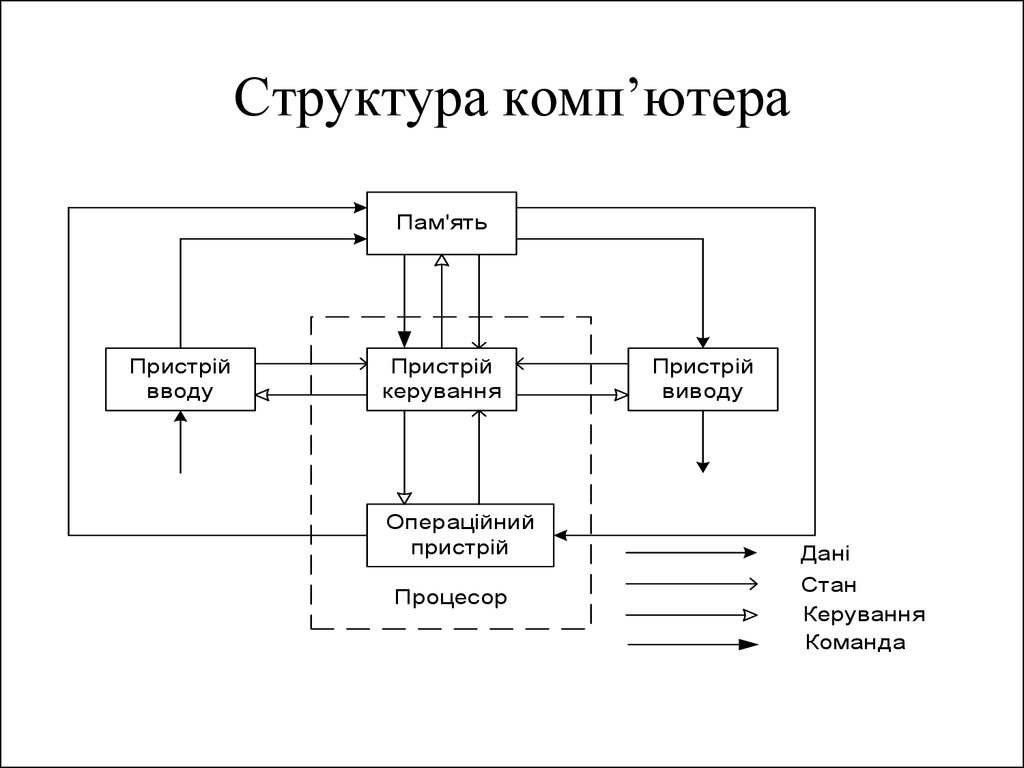
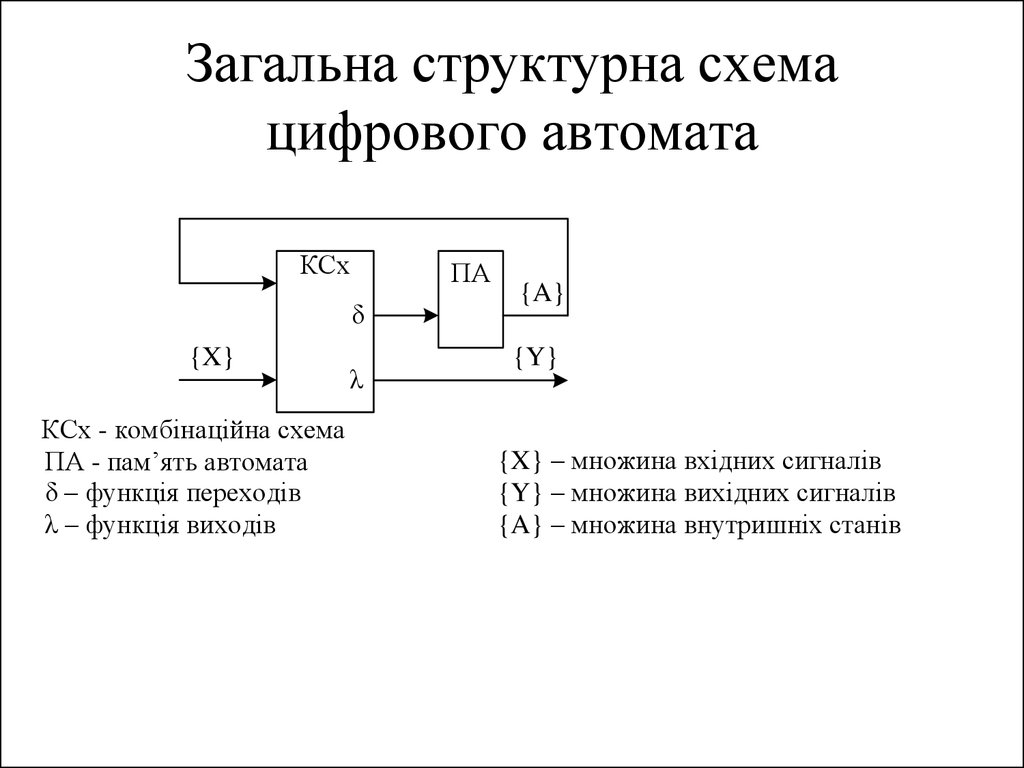
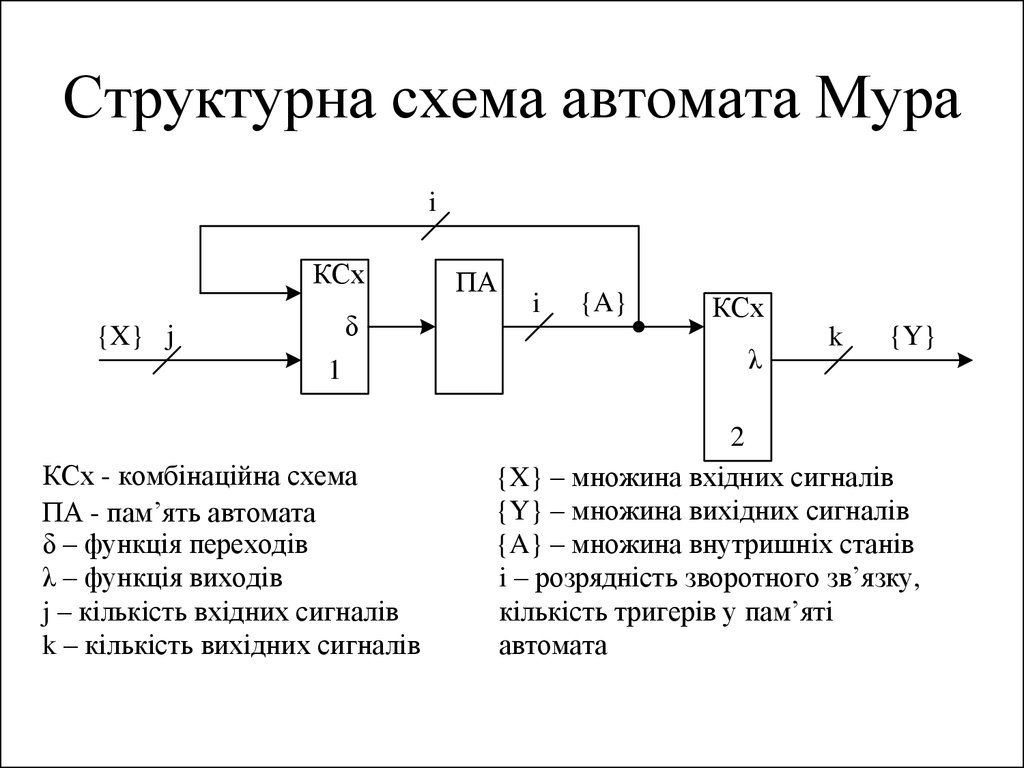
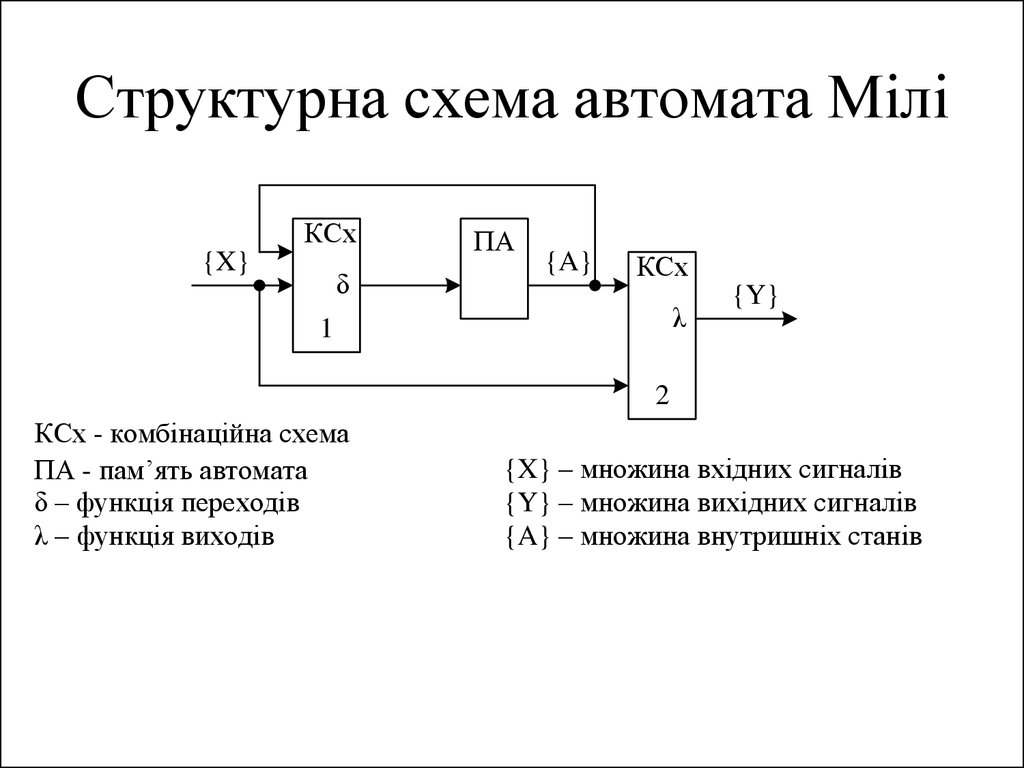

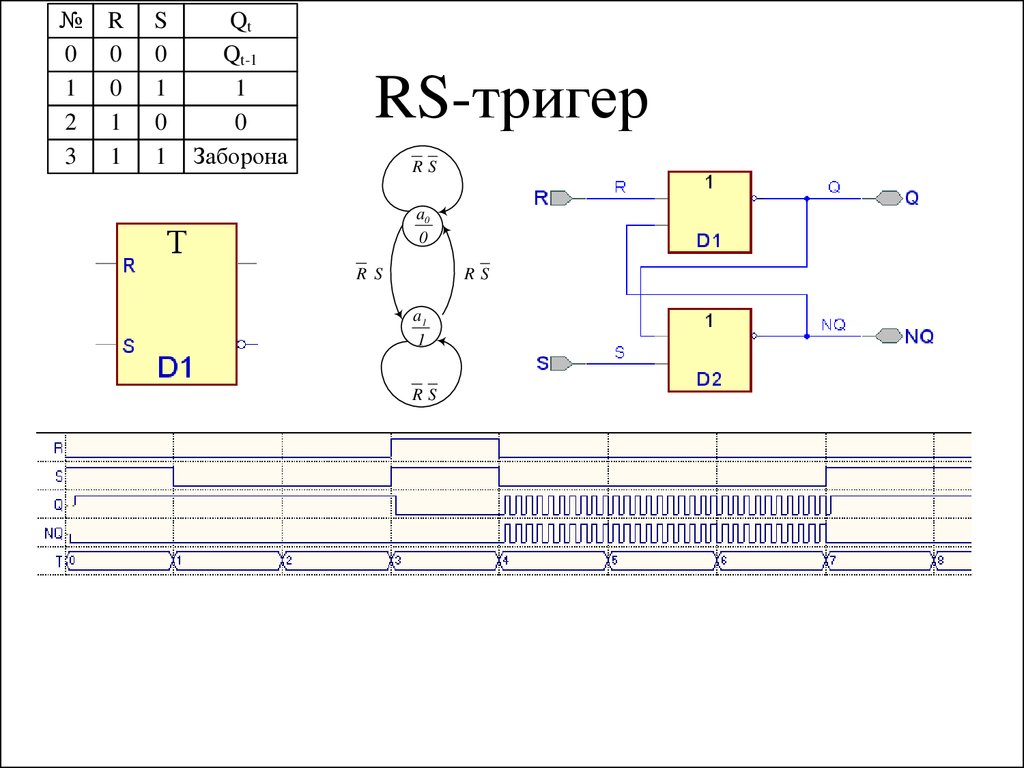

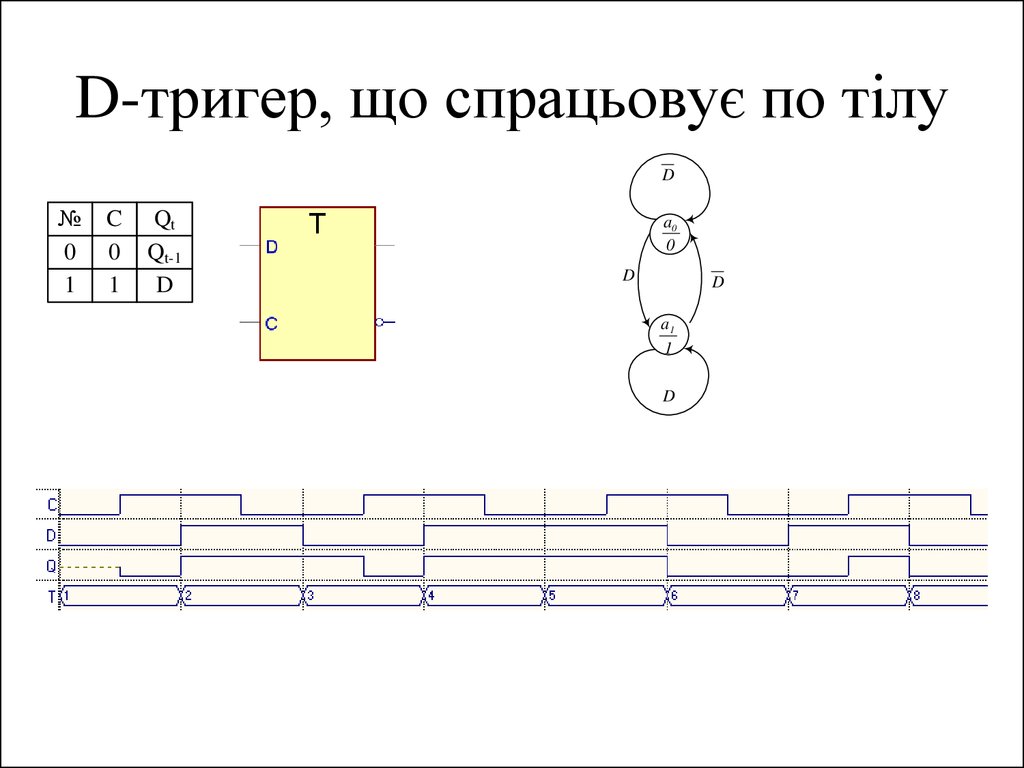



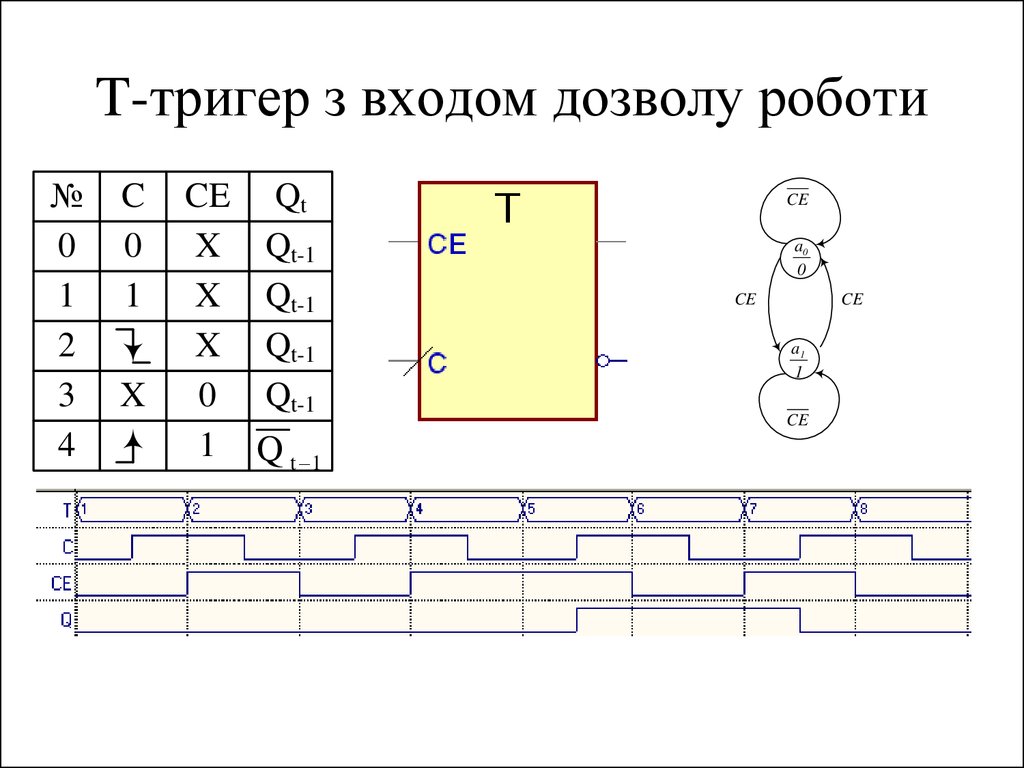
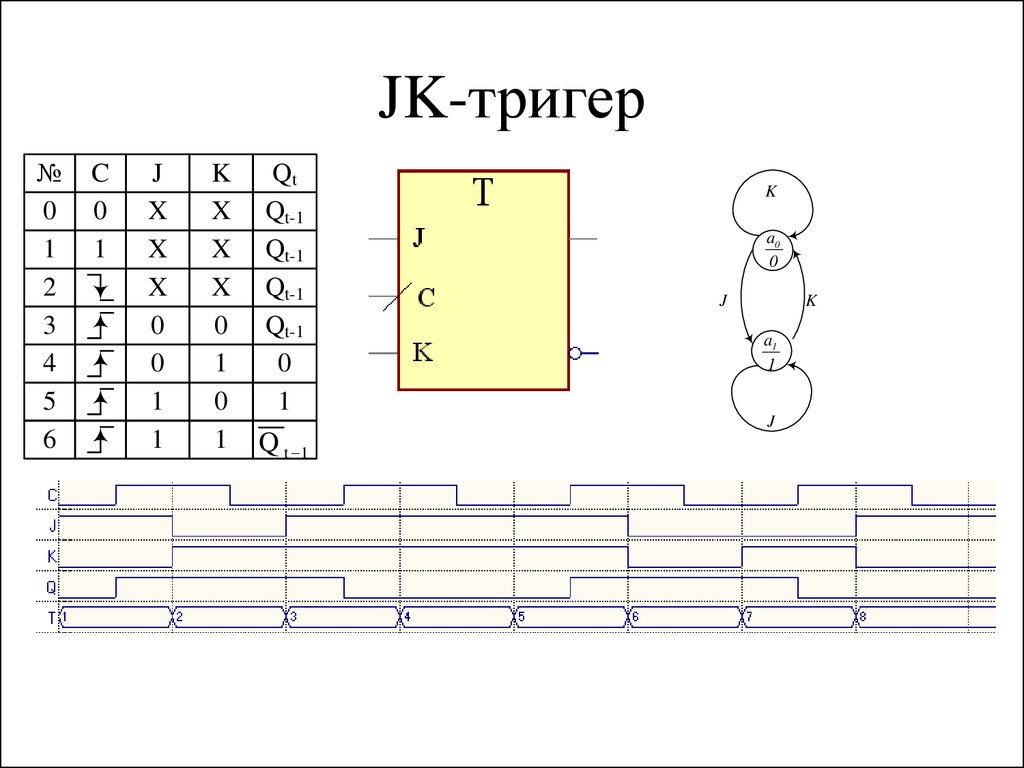

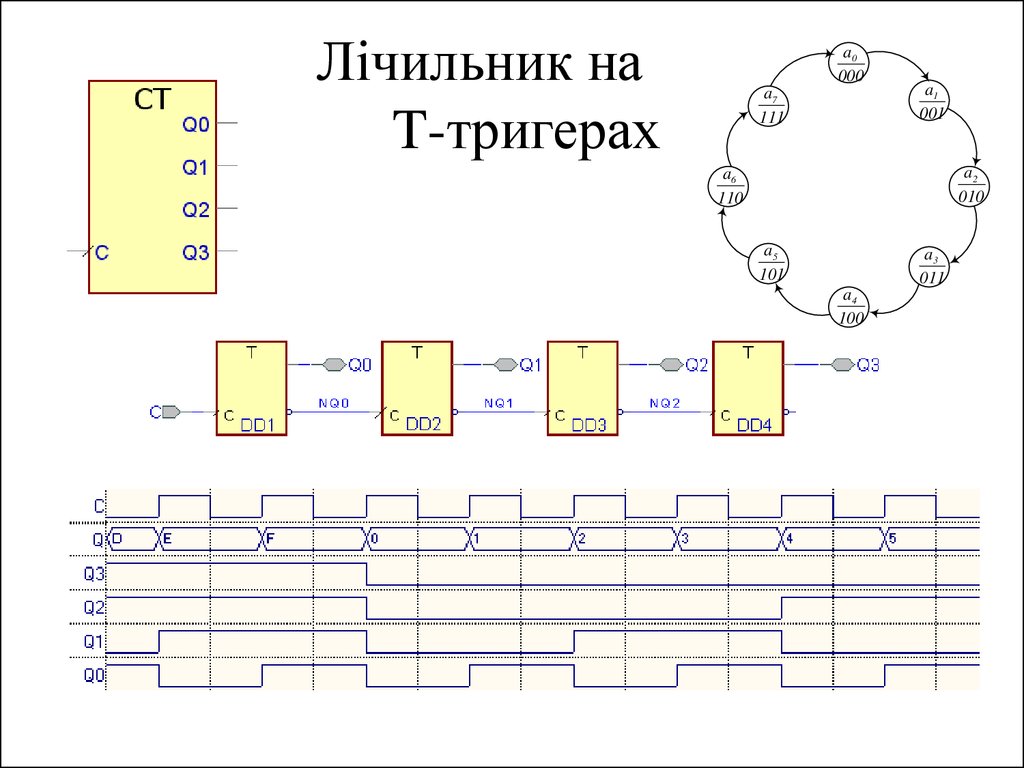
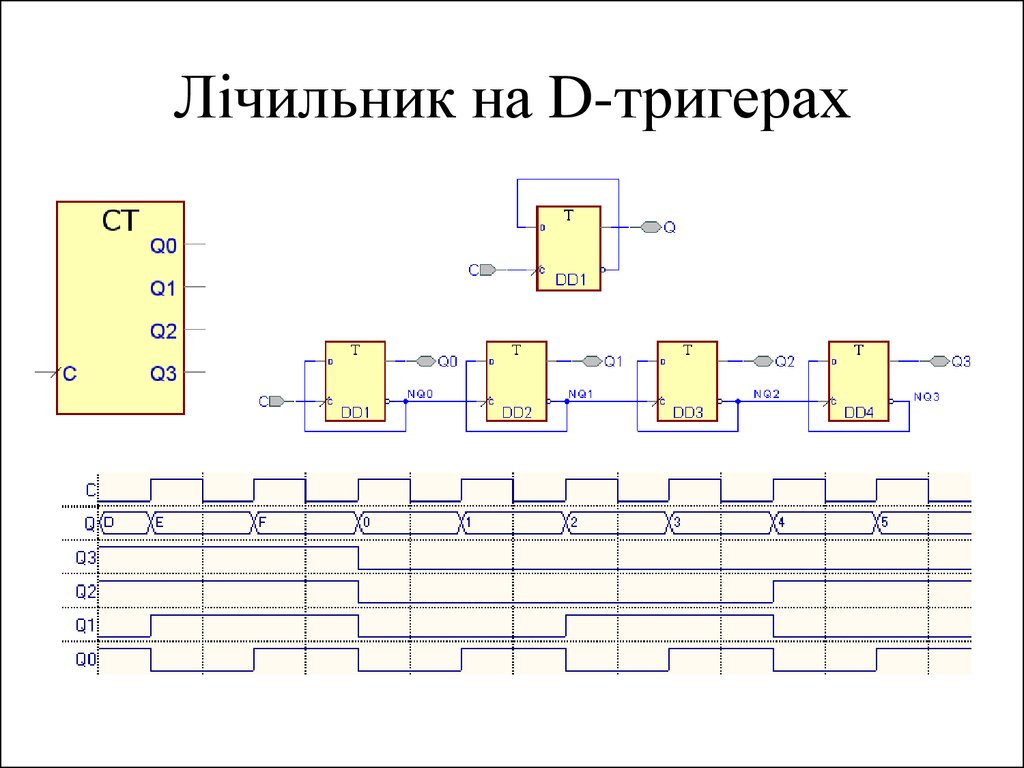
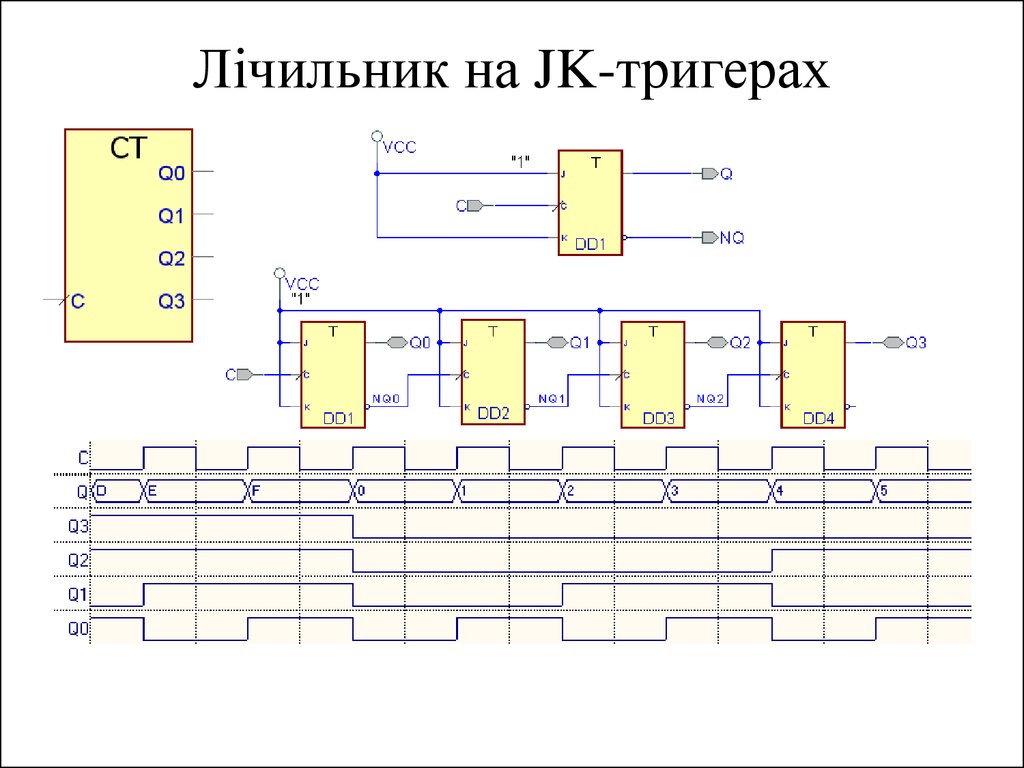

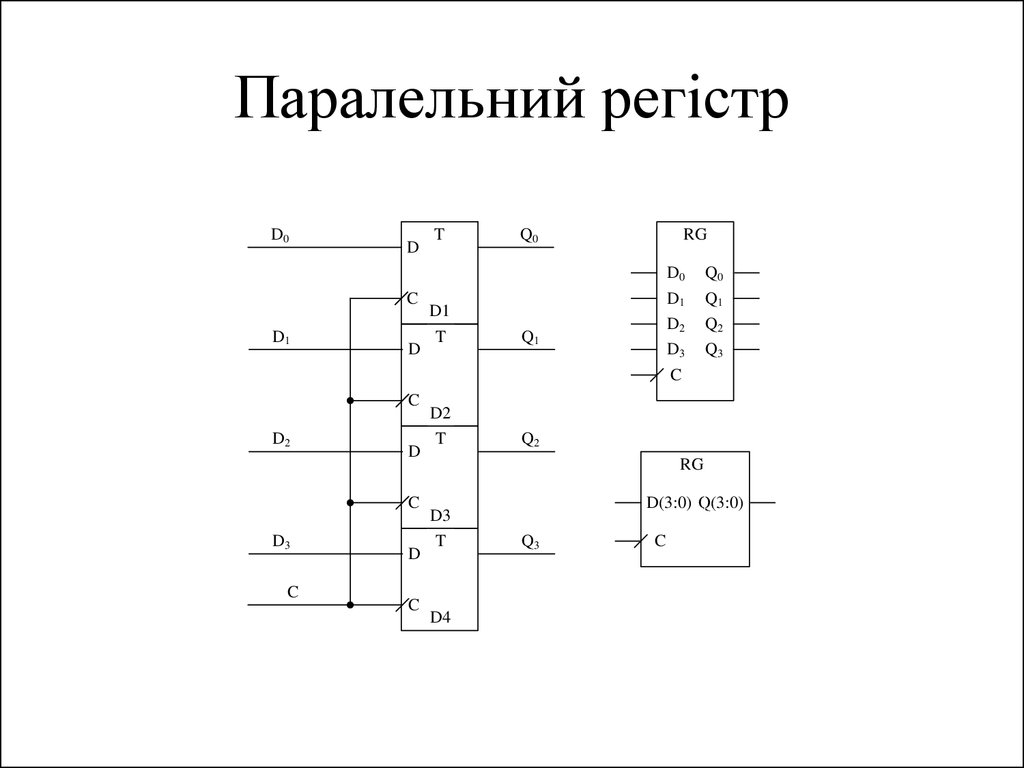
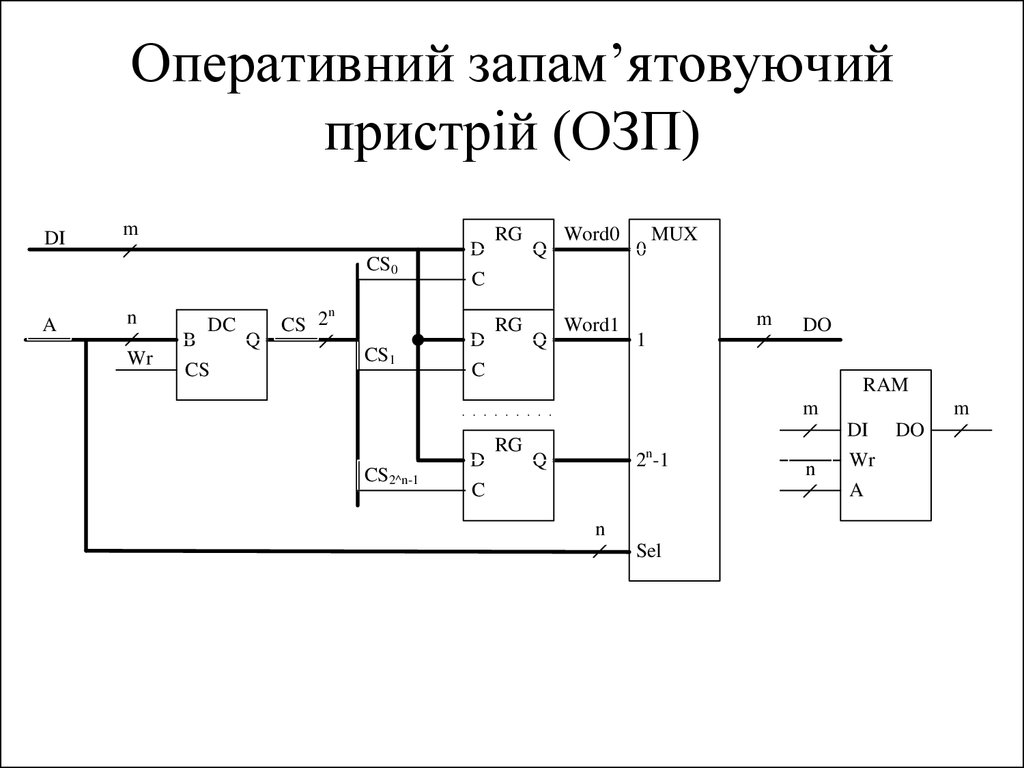

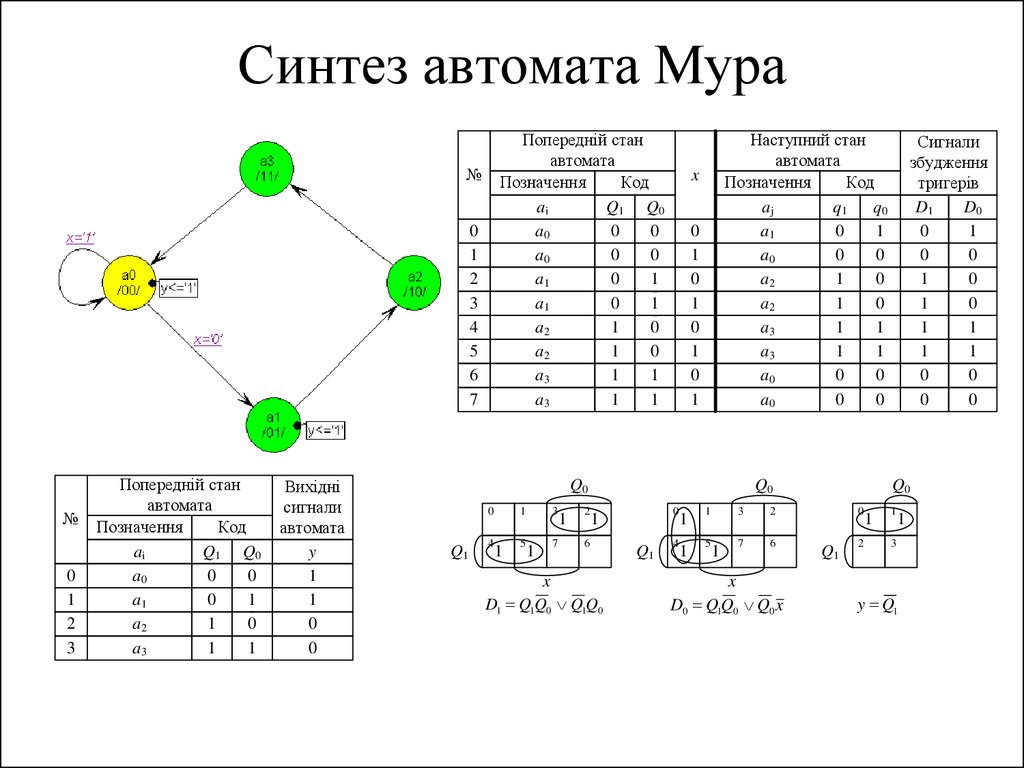
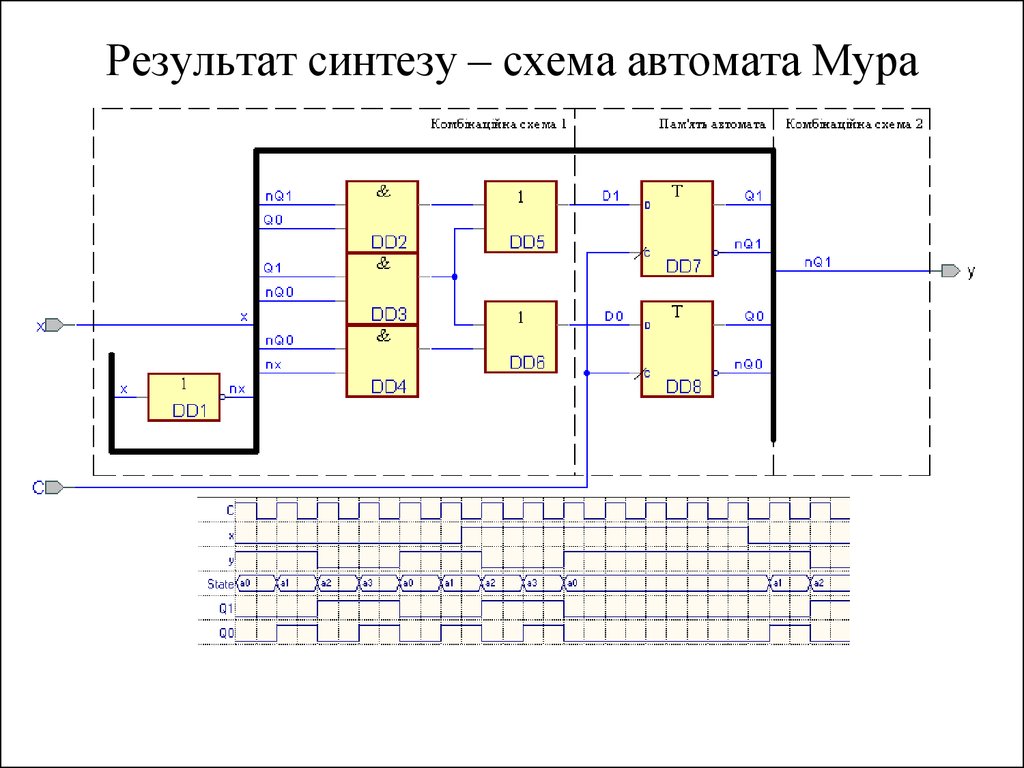
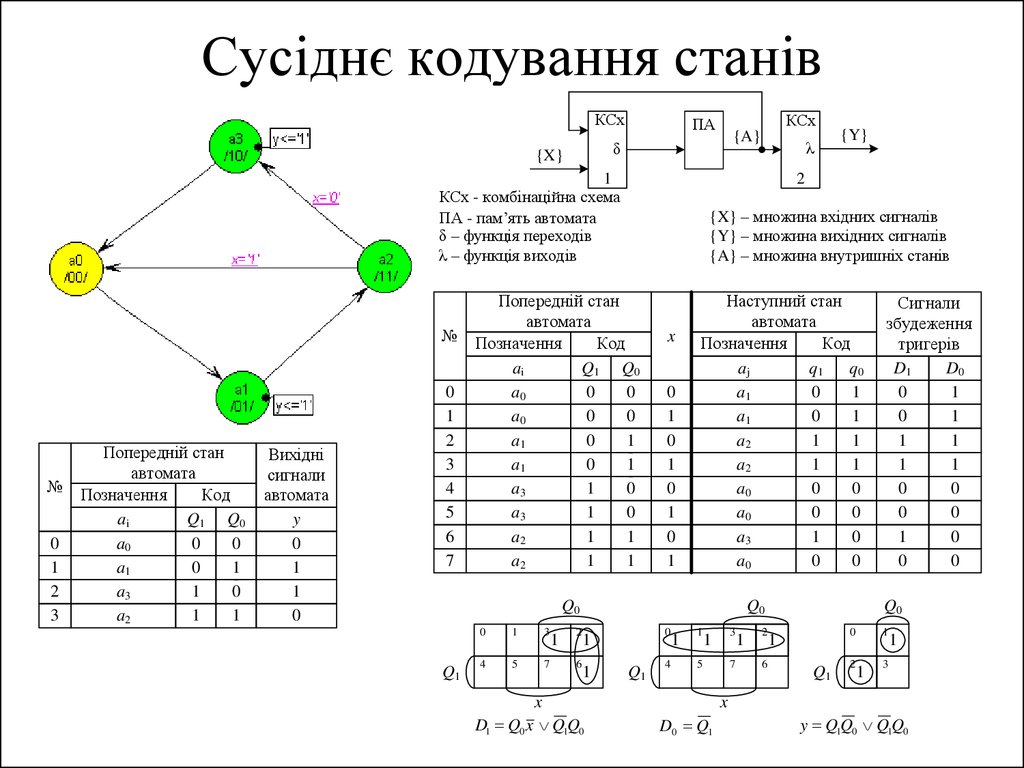
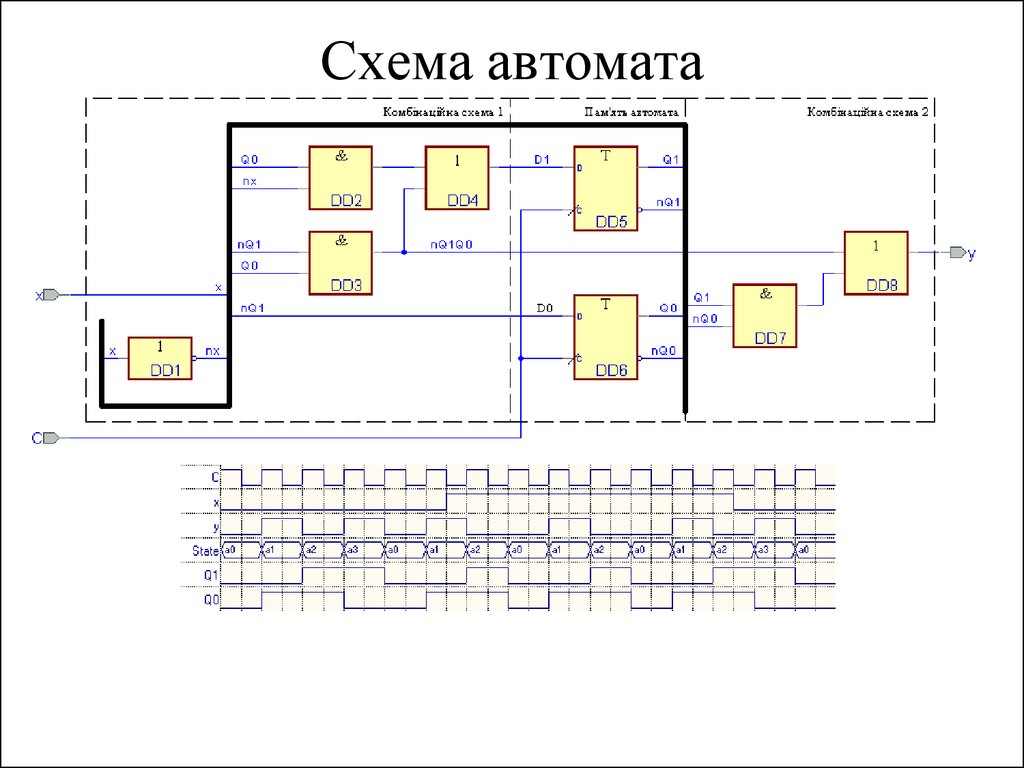

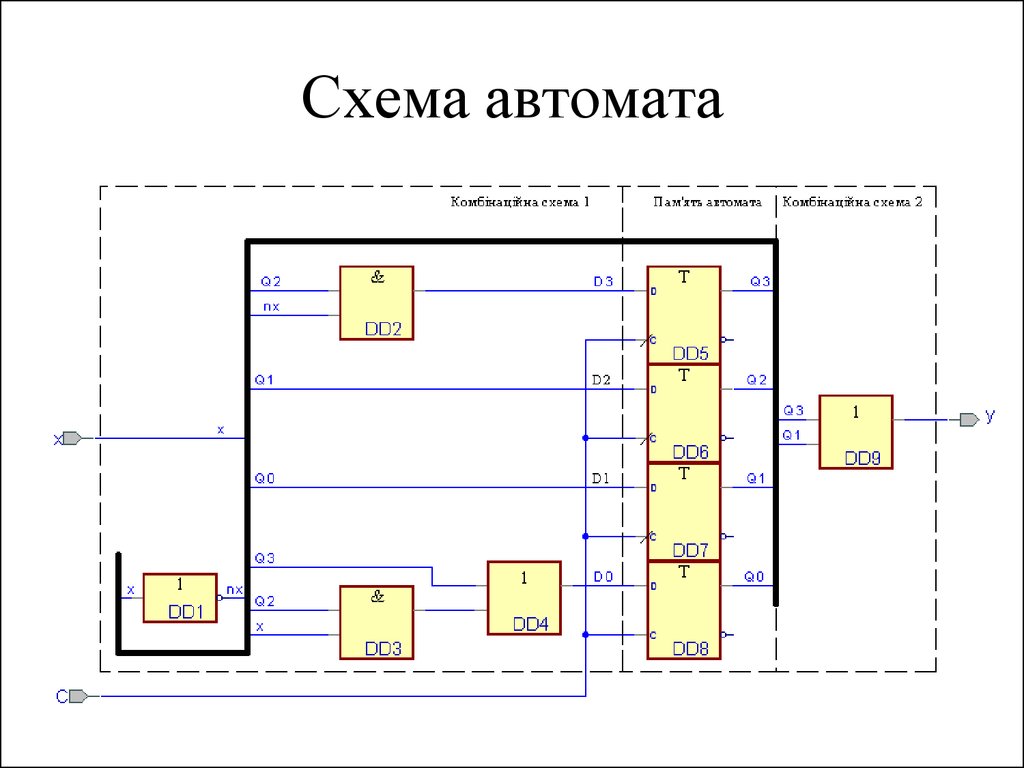

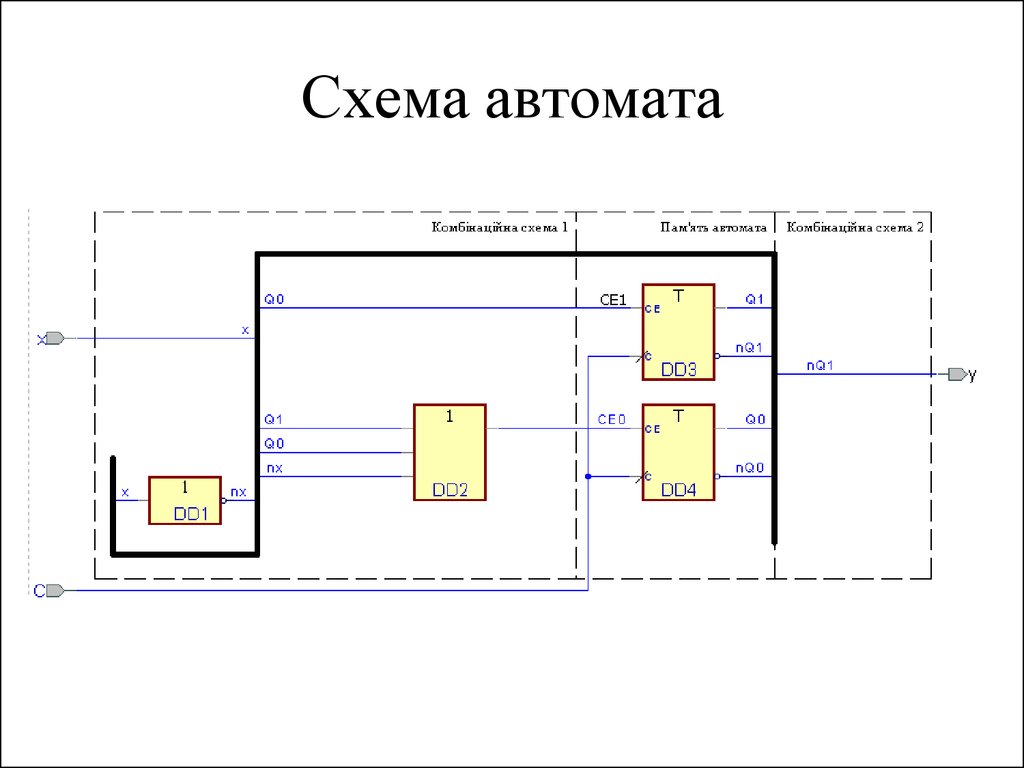
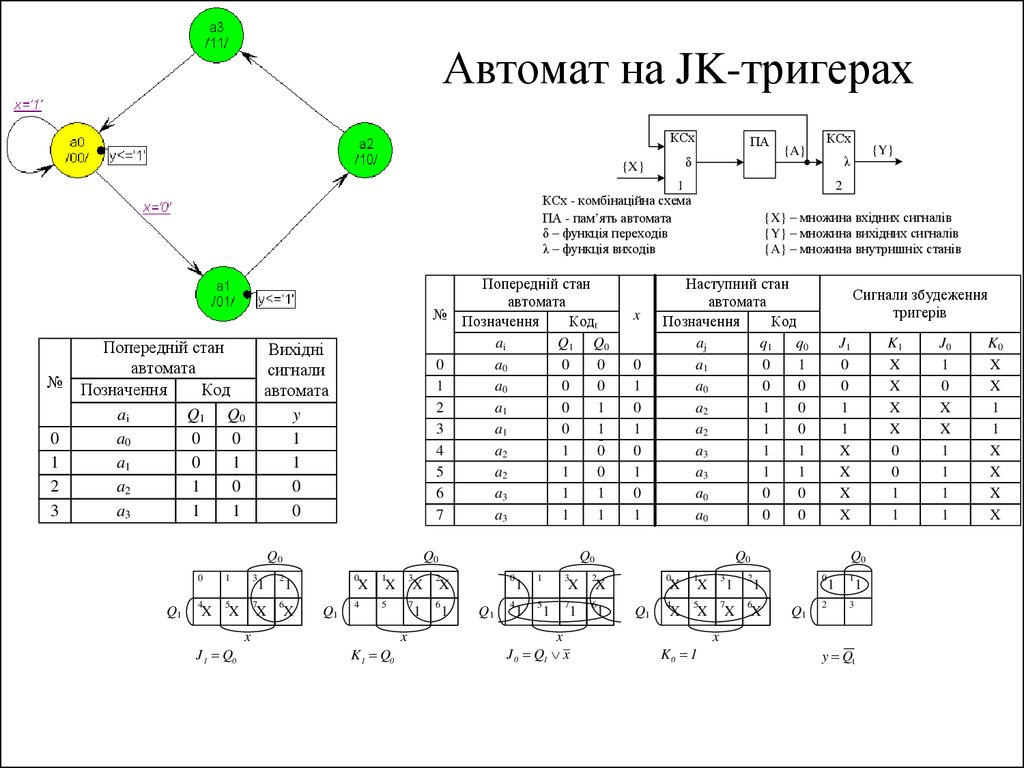
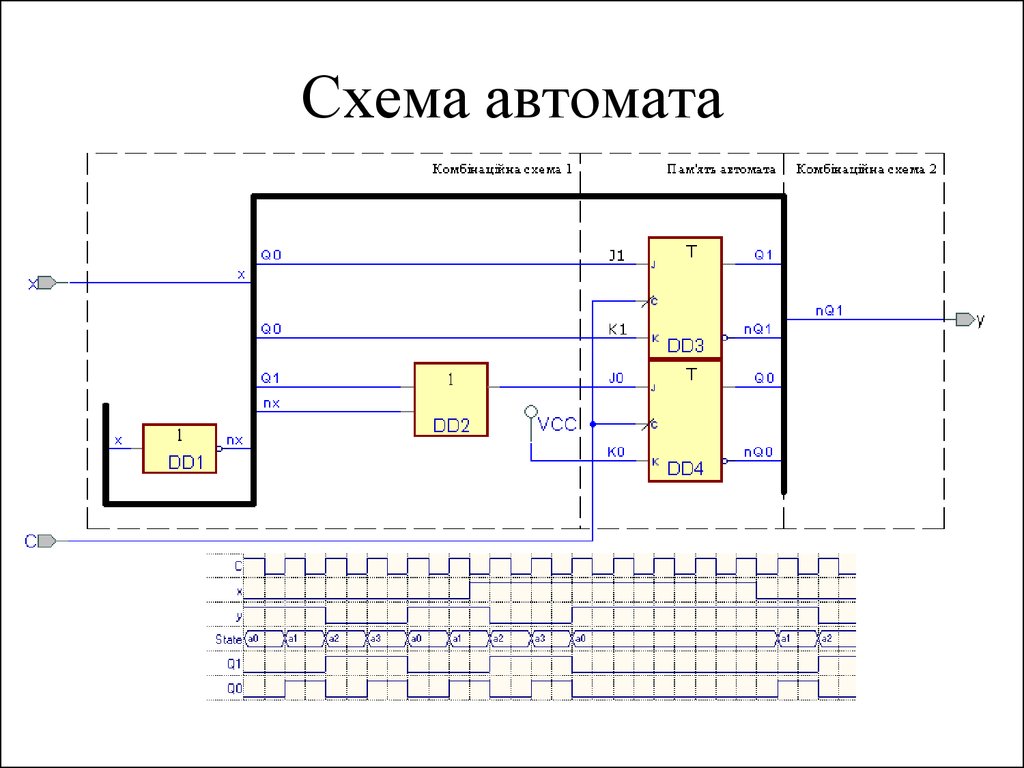
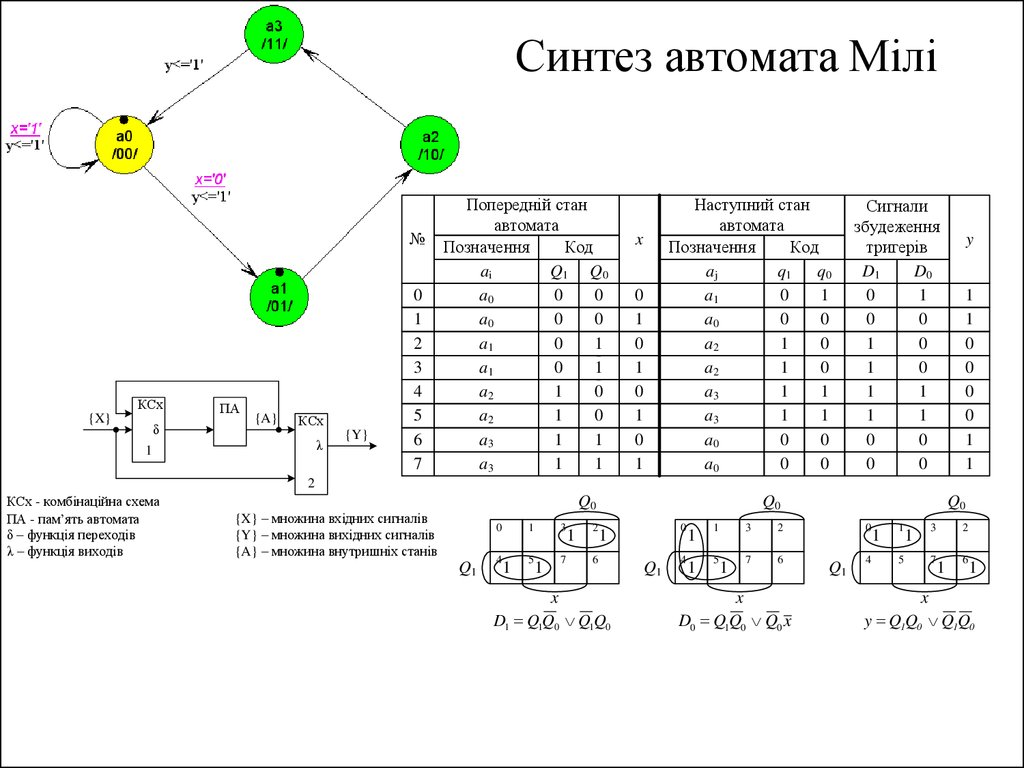

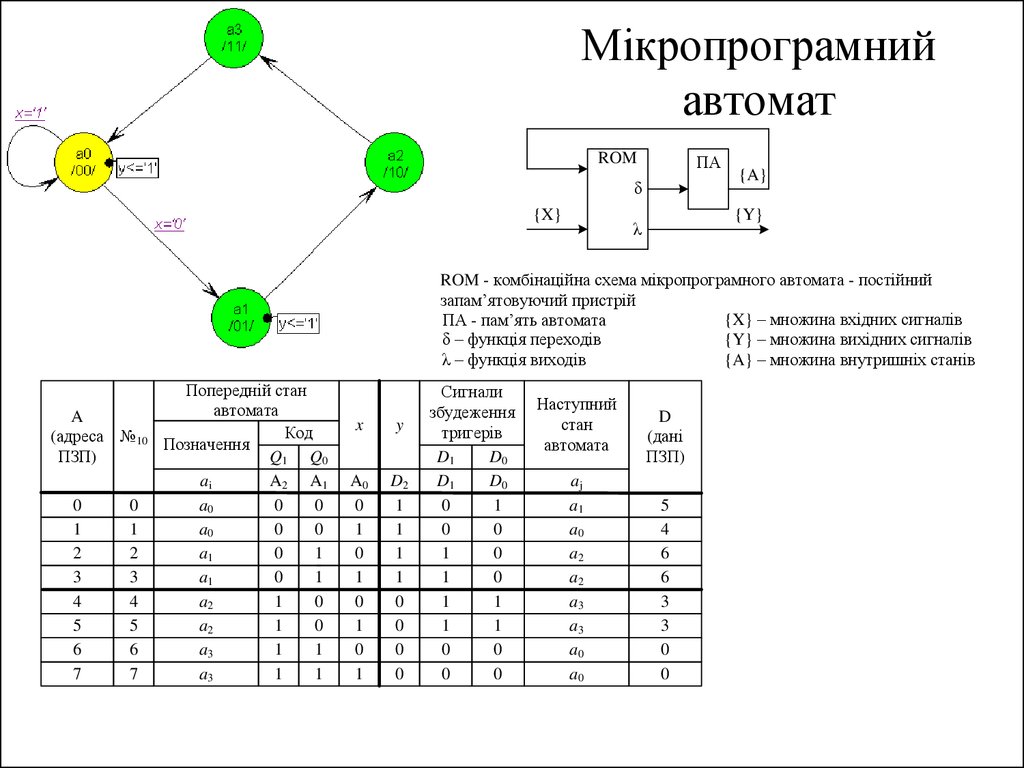
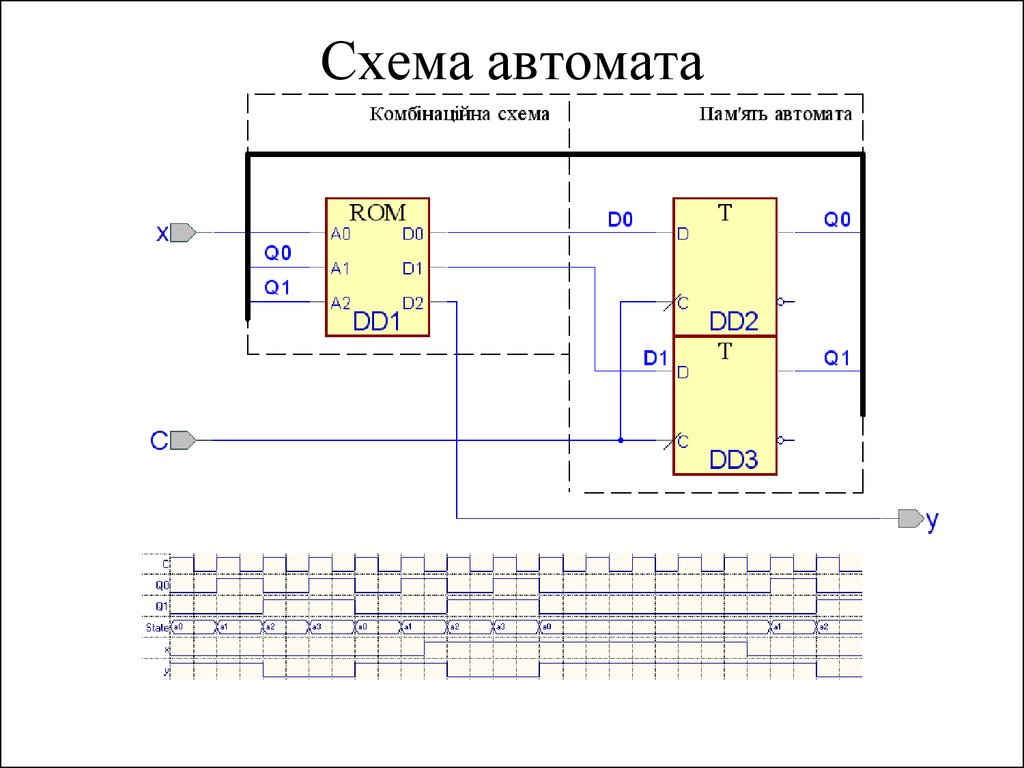

 informatics
informatics electronics
electronics