Розрахунок функції кутового розподілу

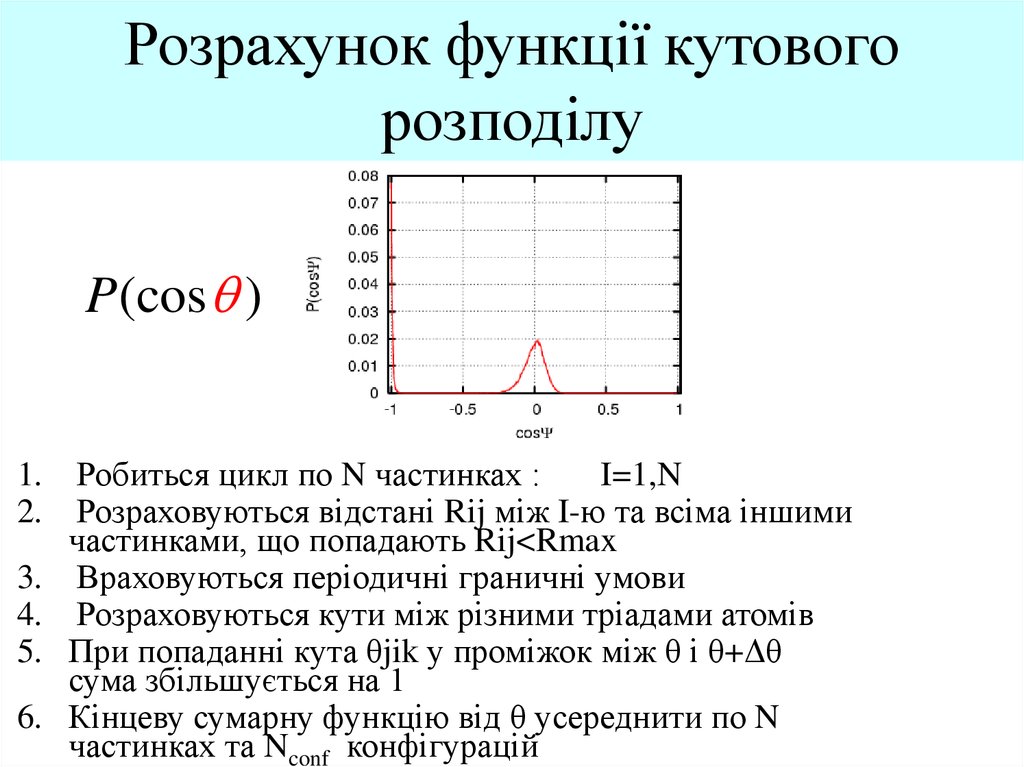
1. Розрахунок функції кутового розподілу

P (cos )
1.
2.
3.
4.
5.
6.
Робиться цикл по N частинках :
I=1,N
Розраховуються відстані Rij між I-ю та всіма іншими
частинками, що попадають Rij<Rmax
Враховуються періодичні граничні умови
Розраховуються кути між різними тріадами атомів
При попаданні кута θjik у проміжок між θ і θ+Δθ
сума збільшується на 1
Кінцеву сумарну функцію від θ усереднити по N
частинках та Nconf конфігурацій

2. Л.15 Метод Монте-Карло

Метрополіс, Розенблат, Теллер, 1953
Метод Метрополіса генерування нерівномірного розподілу
ймовірності являє собою частковий випадок процедури
виборкипо значенню, в якій деякі моливі виборки відкидаються.
Одномірний випадок:
Потрібно згенерувати випадкові змінні (наприклад x) з
довільною густиною ймовірності p(x). В методі Метрополіса
моделюється “випадкове блукання” точок {xi}, розподіл яких
після великої кількості кроків асимптотично прямує до
розподілу ймовірності p(x). Випадкове блукання визначається
заданням ймовірності переходу w(xi->xj) від одного значення
xi до іншого xj для того, щоб розподіл точок x0 ,x1 , x2 ,...
збігався до p(x).

3. Алгоритм одномірних випадкових блукань

Достатньо задовольнити умові “детального балансу”:
p( xi ) w( xi x j ) p( x j ) w( x j xi )
Найпростіший варіант :
w( xi x j ) min[1,
p( x j )
p( xi )
]
Даний перехід можна описати настуними кроками:
1. Вибираємо пробну координату xt xn n , де n є
випадковим числом на відрізку [ : ]
2. Розраховуємо w p ( xt )
p ( xn )
3. Якщо w 1, то перехід приймається і покладаємо xn 1 xt
4.
Якщо
w 1, генеруємо випадкове число r.

4. Алгоритм одномірних випадкових блукань

5. Якщо r w, то перехід приймається і покладаємо xn 1 xt
6.
Якщо пробний перехід не прийнятий, покладаємо xn 1 xn
Асимптотичний розподіл p(x) буде отриманий після достатньо
великої кількості пробних переходів.
Яка роль “розміру кроку” δ ? Якщо δ буде великим, то буде
прийматись лише мала частина пробних кроків і вибірка p(x) буде
неефективною. Якщо δ буде занадто малим, то буде прийматись
більша частина пробних кроків і вибірка p(x) буде знову
неефективною. Критерій вибору величини δ : повинно
прийматись від третини до половини пробних кроків. Бажано
також починати початкове значення x0 так, щоб розподіл xi
якнайшвидше досягав асимптотичного розподілу.

5. Алгоритм Метрополіса

w e
U ( rtN ) U ( rnN )
k BT
1.
Випадково вибирається частинка та розраховується її
N
енергія U (rn )
2.
Дати частинці випадкове зміщення
розрахувати нову енергію U (rt N )
3. Прийняти зміщення
rn
до
rt
rt rn
з ймовірністю
w(rn rt ) min[1, e
U ( rtN ) U ( rnN )
k BT
]
та

6. Найпростіша реалізація методу Монте-Карло

SUBROUTINE MCMOVE
IP=INT(RANF()*NPART)+1
CALL ENERGY(X(IP),U)
XN=X(IP)+(RANF()-0.5)*DELX
CALL ENERGY(XN,UN)
IF(RANF().LT.EXP(-(UN-U)/(BK*T)) X(IP)=XN
RETURN
END

7. Найпростіша реалізація методу Монте-Карло

Для трансляційних рухів
x xi ( Ranf () 0.5)
'
i
y yi ( Ranf () 0.5)
'
i
z zi ( Ranf () 0.5)
'
i
Для орієнтаційних рухів – випадкові ротації кватерніонів
Q (q0 , q1 , q2 , q3 )
q0 cos( ) cos(
)
2
2
q2 sin( ) sin(
)
2
2
q02 q12 q22 q32 1
q1 sin( ) cos(
)
2
2
q3 cos( ) sin(
)
2
2

8. Застосування методу Монте-Карло для обчислень інтегралів

b
f ( x)dx (b a) f
a
b
a
1 n
f ( x)dx (b a ) f ( xi )
n i 1
-визначення інтегралу через
середнє значення
-визначення інтегралу через
генерування випадкових
координат xi

9. Застосування методу Монте-Карло для обчислень багатократних інтегралів

Нехай маса двомірного тіла
визначається розподілом
M ( x, y )dxdy
При обертанні навколо осі z
його момент інерції рівен
I z ( x 2 y 2 ) ( x, y )dxdy
I z ,n
1 n 2
( x2 x1 )( y2 y1 ) ( xi yi2 ) ( xi , yi )
n i 1
- МК вираз для генерування n випадкових
координат (xi yi) в проміжках x1 x x2
y1 y y2