Similar presentations:
Аналіз систем, які працюють за дисципліною обслуговування з очікуванням
1. Лекція 7
Аналіз систем, які працюють задисципліною обслуговування з
очікуванням
Література
1. Омельченко А.В. Основи аналізу систем розподілу інформації.
Навч. посібник. – Харків: ХНУРЕ, 2008. – С 43-55
2. Основні питання
• Визначення ймовірностей станів СРІ• Розподіл часу очікування у випадку
дисципліни черги FIFO
• Формула Літтла
• Формула Полячека-Хінчина
3. Постановка задачі
• Вважається, що повністю доступна СРІ з v приладамиобслуговує найпростіший потік заявок з параметром λ.
При цьому використовується дисципліна обслуговування
з очікуванням. Заявки можуть утворювати чергу
необмеженої довжини. Заявки, що перебувають на
очікуванні, обслуговуються по черзі. Тривалість зайняття
приладу
вважається
випадковою
величиною
з
експоненціальним законом розподілу і параметром
інтенсивності обслуговування μ.
• Необхідно визначити ймовірності різних станів СРІ,
функцію
розподілу
часу
очікування
початку
обслуговування, середній час очікування та середню
довжину черги.
Модель системи
M/M/v/W
4. Визначення ймовірностей станів СРІ
5. Визначення ймовірностей станів СРІ
Отримаємо вирази для станів СРІ типу M/M/v/WEi,v (y)
,0 i v
y
1 Ev (y)
v y
pi
y i v
Ev (y) ( )
v
, i v
1 E (y) y
v
v y
Рекурентні співвідношення для ймовірностей станів для систем
M/M/v/W мають вигляд
y
p
p
(
)
i
i
1
i
y
p
p
(
)
i
i
1
v
i v
i v
6. Друга формула Ерланга
ptE v ( y)
y
1 (1 E v ( y))
v
D v ( y)
Дану формулу часто називають
С-формулою Ерланга.
Agner Krarup Erlang (1878-1929)
7. Вигляд функцій Ерланга
8. Розподіл часу очікування у випадку дисципліни черги FIFO
• У даному випадку імовірність очікування початкуобслуговування понад час t визначається за формулою
(
v
y
)
t
P( t)= P
(
0
)
e
,
P
(
0
)
,
tdF
(
t
)
(
v
y
)
0
.
r
P
(
t
)
(
v
y
)
t
P
(
t
)
e
,
з
P
(
0
)
1
.
з
(v y)
,
9. Формула Літтла
• Формула Літтла встановлює співвідношення між середнімчислом викликів в системі, інтенсивністю вхідного потоку й
середнім часом перебування заявок у системі.
Вона
справедлива для будь-якої системи з очікуванням, що перебуває
у сталому стані.
• Останнє співвідношення означає, що середнє число заявок у
системі дорівнює добутку інтенсивності надходження заявок у
систему на середній час їхнього перебування в системі:
N
T.
При цьому не накладається жодних обмежень на тип потоку
заявок і час обслуговування. Вперше доведення цього факту
дав Дж. Літтл.
10. Доведення формули Літтла
• Рассмотримлюбую
СМО
(одноканальную,
многоканальную, марковскую, немарковскую, с
неограниченной или ограниченной очередью) и
связанные с нею два потока событий:
- поток заявок, прибывающих в СМО;
- поток заявок, покидающих СМО.
• Если
в
системе
установился
предельный,
стационарный режим, то среднее число заявок,
прибывающих в СМО за единицу времени, равно
среднему числу заявок, покидающих её.
• Оба потока имеют одну и ту же интенсивность λ.
11. Доведення формули Літтла
• Обозначим:- α(t) – число заявок, прибывших в СМО до
момента t;
- δ(t) - число заявок, покинувших СМО до
момента t.
• И та и другая функции являются случайными
и меняются скачком (увеличиваются на
единицу) в моменты приходов заявок α(t) и
уходов заявок δ(t).
12. Доведення формули Літтла
• Вид функций α(t) и δ(t) показан на рисунке.• Обе линии – ступенчатые, верхняя - α(t), нижняя - δ(t)
- α(t) – число заявок, прибывших в СМО до момента t;
- δ(t) - число заявок, покинувших СМО до момента t.
13. Доведення формули Літтла
• Очевидно, что для любого момента t ихразность N(t) = α(t) - δ(t) есть не что иное,
как число заявок, находящихся в СМО
• Когда линии α(t) и δ(t) сливаются, в
системе нет заявок
14. Доведення формули Літтла
• Рассмотрим очень большой промежутоквремени T (мысленно продолжив график
далеко за пределы чертежа) и вычислим для
него среднее число заявок, находящихся в
СМО
• Оно будет равно интегралу от функции N(t)
на этом промежутке, деленному на длину
интервала T:
1 T
N N( t )dt.
T 0
15. Доведення формули Літтла
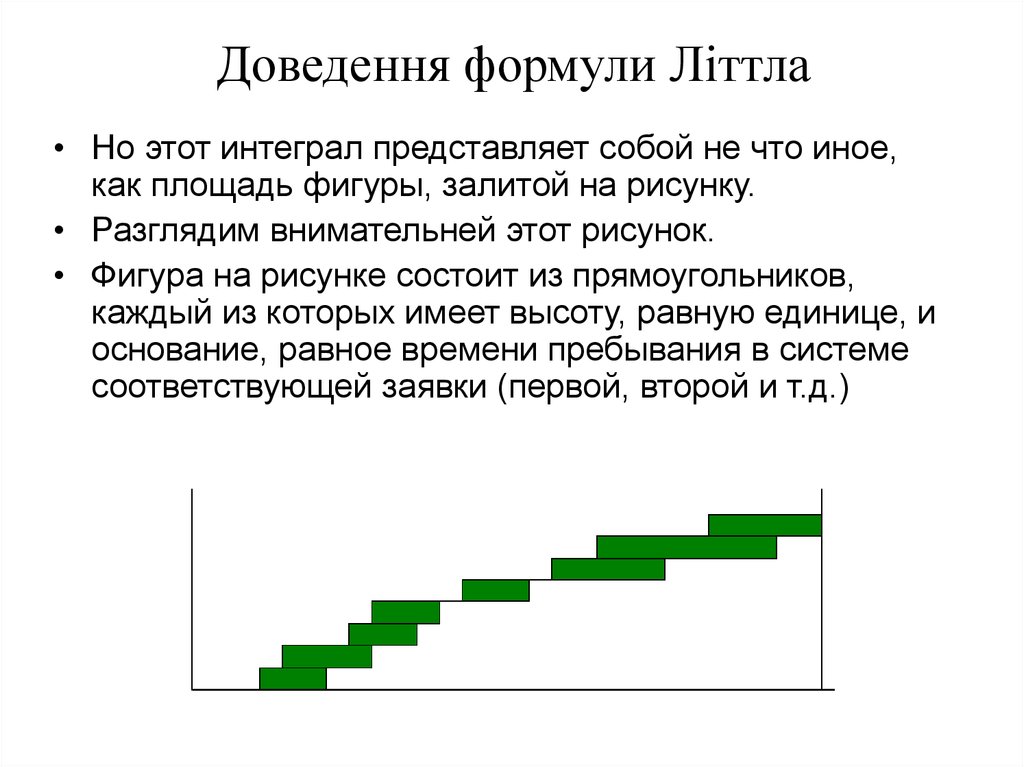
• Но этот интеграл представляет собой не что иное,как площадь фигуры, залитой на рисунку.
• Разглядим внимательней этот рисунок.
• Фигура на рисунке состоит из прямоугольников,
каждый из которых имеет высоту, равную единице, и
основание, равное времени пребывания в системе
соответствующей заявки (первой, второй и т.д.)
16. Доведення формули Літтла
• Обозначим эти времена t1, t2,…• Правда, под конец промежутка T некоторые
прямоугольники войдут в залитую фигуру не
полностью, а частично, но при достаточно большом
T эти детали не будут играть роли
• Таким образом, можно считать, что:
T
N(t)dt t ,
i
0
i
где сумма распространяется на все заявки,
пришедшие за время T
17. Доведення формули Літтла
• Разделим правую и левую часть последнеговыражения на длину интервала T
• Получим
1
N ti.
T i
• Разделим и умножим правую часть на
интенсивность λ:
1
N
ti.
T i
18. Доведення формули Літтла
• Но величина Tλ есть не что иное, каксреднее число заявок, пришедших за время
T
• Если мы разделим сумму всех времен ti на
среднее число заявок, то получим среднее
время пребывания заявки в системе
• Итак:
N T
откуда:
T
1
N.
19. Доведення формули Літтла
• Это и есть формула Литтла:- для любой СМО, при любом характере
потока заявок, при любом
распределении времени обслуживания,
при любой дисциплине обслуживания
среднее время пребывания заявки в
системе равно среднему числу заявок в
системе, деленному на
интенсивность потока заявок
20. Друга формула Літтла
• Точно таким же образом выводится втораяформула Литтла, связывающая среднее
время пребывания заявки в очереди и
среднее число заявок в очереди:
r
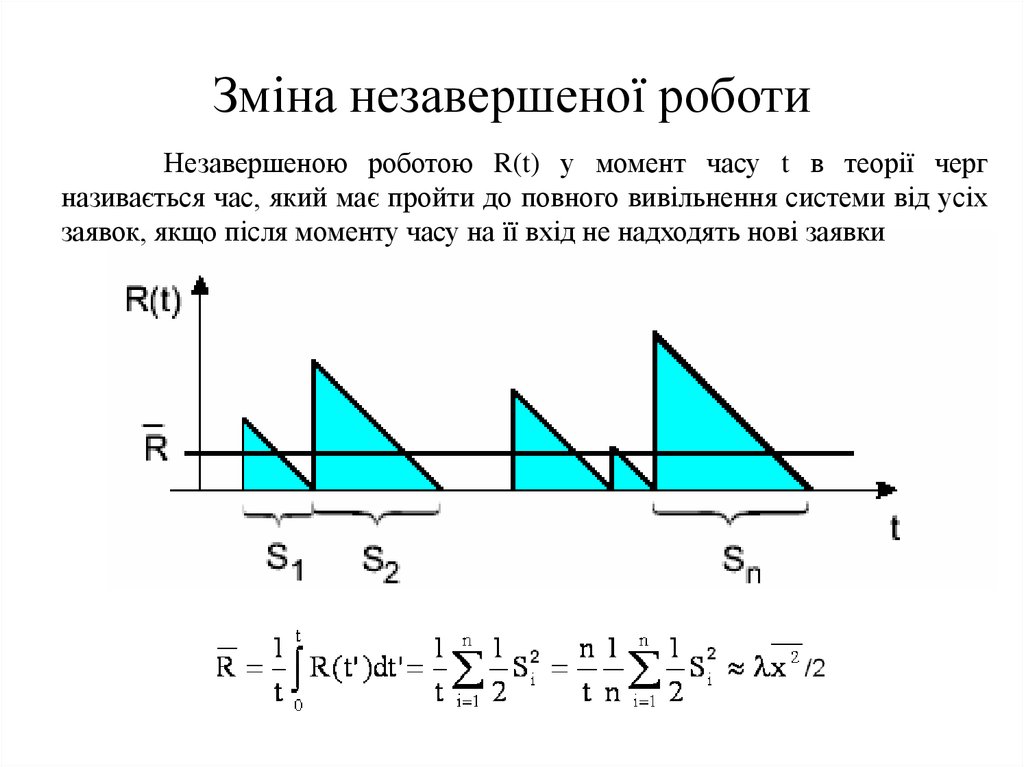
21. Зміна незавершеної роботи
Незавершеною роботою R(t) у момент часу t в теорії чергназивається час, який має пройти до повного вивільнення системи від усіх
заявок, якщо після моменту часу на її вхід не надходять нові заявки
t
1
1 n 1 a n1 n 1 a
R R ( t ' )dt ' Si
Si x 2
t0
t i 1 2
t n i 1 2
22. Аналіз системи M/G/1
Вхідний потік:f ( ) e
Час обслуговування:
p( x )
p(x)dx 1
0
Інтенсивність навантаження:
Середній час очікування:
0
y x
rx R ,
где
Середнє число заявок у черзі:
x x p( x )dx
R
- середня незавершена робота
r
x R
R
1 y
23. Формула Полячека-Хінчина
x 22(1 y)
Середній час очікування початку обслуговування
1 y2
(t ) 2
[1 (
) ]
2(1 y)
t
(Формула ПХ)
Наслідок 1.
2
y
(
t
)
2
r
[
1
(
)
]
2
(
1
y
)t
Наслідок 2.
2
y
(
t
)
2
q
y
[
1
(
)
]
2
(
1
y
)
t
Наслідок 3.
Для моделі M/М/1
Наслідок 4.
Для моделі M/D/1
1 y
(1 y)
1
y
2 (1 y)
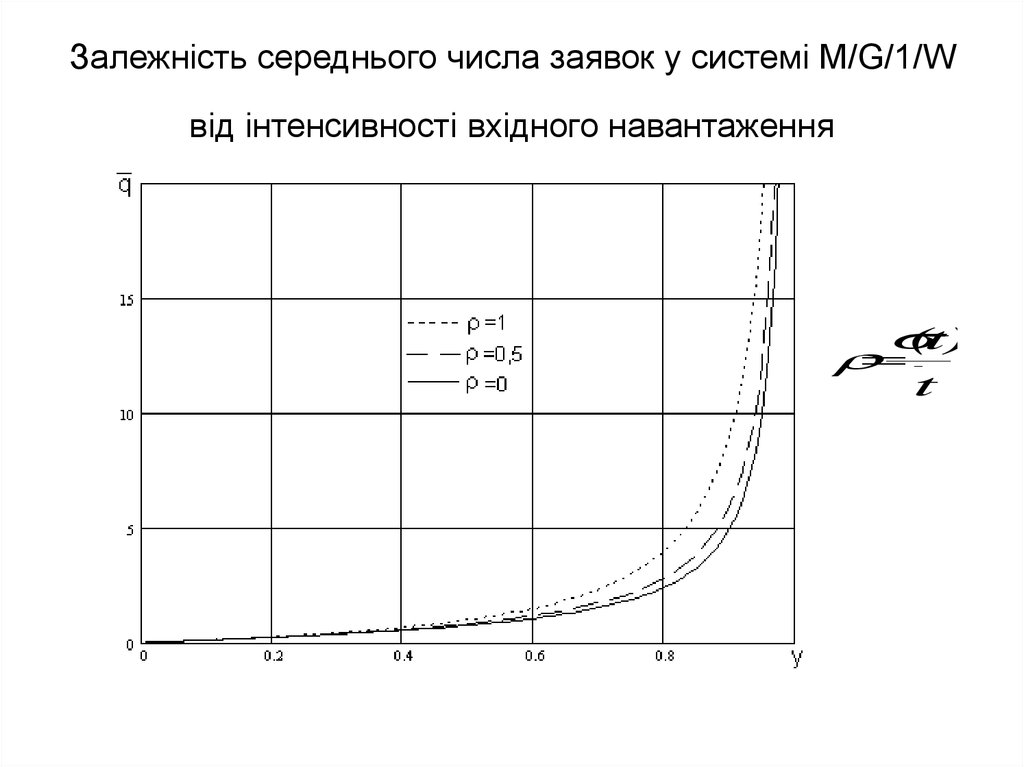
24. Залежність середнього числа заявок у системі M/G/1/W від інтенсивності вхідного навантаження
(t)t
25. Система M/D/v/W
Постановка задачі у даному випадку така сама, як для систем з явними
втратами.
Відмінність полягає лише в законі розподілу тривалості обслуговування:
замість випадкового закону розподілу тривалість обслуговування кожної
заявки вважається постійною величиною, рівною h. Цей випадок вперше у
1932 р. дослідив Кроммелін.
Розглянемо підхід, що використовується у теорії Кроммеліна.
Без обмеження загальності припустимо, що h=1.
26. Система M/D/v/W
27. Система M/D/v/W
28. Система M/D/v/W
29. Криві Кроммеліна для V=1
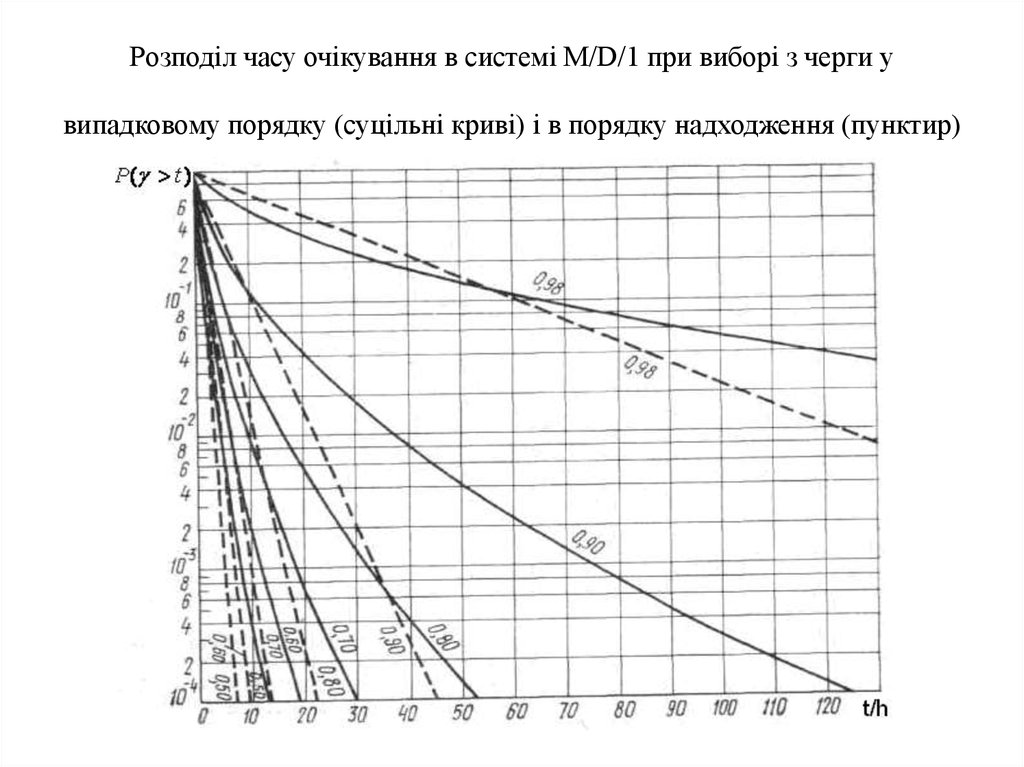
30. Дисципліни вибору з черги
• Практичний інтерес являють дві основні дисциплінивибору заявок з черги: у порядку надходження (FIFO) і у
випадковому порядку (SP). Дисципліна вибору не впливає
на середній час перебування в черзі, а впливає тільки на
момент більш високого порядку: при переході від
упорядкованого вибору в порядку надходження до
випадкового різко зростають імовірності довгого
очікування. На практиці ж часто дисципліна вибору є
чимось середнім між цими двома дисциплінами.




























 informatics
informatics








